CAPITOLO IV ALGORITMO FAST FOURIER TRASFORM

(1)

CAPITOLO IV

ALGORITMO FAST FOURIER TRASFORM

1.1 INTRODUZIONE

1.2 NOTAZIONE E FORMATO DELLA DFT

1.3 ALGORITMO FFT

1.4 UTILIZZO FFT NELLA STIMA SIMULTANEA

1.1 Introduzione

In questo capitolo verrà spiegato in breve il funzionamento dell’algoritmo di Fast Fourier Trasform ( comunemente conosciuto in maniera abbreviata come FFT), le sue caratteristiche per la stima dell’ampiezza e fase di un segnale e verrà inoltre spiegato il modo in cui sarà utilizzato all’interno della procedura per la stima multipla dei parametri di un processo. Saranno inoltre messi in evidenza gli errori della stima di modulo e fase di segnali ai quali verrà sovrapposto rumore bianco con differenti rapporti di potenza segnale rumore.

(2)

1.2 Notazione e formato della DFT

Verrà in questo paragrafo analizzato la notazione ed il formato della trasformata discreta di Fourier ( DFT) [11] in quanto su di essa si basa il principio di funzionamento dell’algoritmo FFT.

La Trasformata discreta di Fourier elabora un segnale di ingresso formato da N punti, in due segnali di output formati da N/2+1 punti. Il segnale di input contiene il segnale che dovrà essere decomposto mentre i due segnali di output contengono le ampiezze delle componenti sinusoidali e cosinusoidali (scalate in ampiezza di un valore che verrà spiegato più avanti). Il segnale di ingresso è detto nel dominio del tempo. Questo perchè la maggior parte dei segnali elaborati dalla DFT è composta da campioni presi in intervalli di tempo regolari. Il temine dominio della frequenza è usato per descrivere le ampiezze delle componenti sinusoidali e cosinusoidali. Il dominio della frequenza contiene esattamente le solite informazioni contenute nel dominio del tempo ma disposte in maniera differente.

Il numero di campioni nel dominio del tempo è di solito rappresentato dalla variabile N; N è un intero positivo e viene solitamente scelto come una potenza di due ( es. 128, 256, 512, ...). Vi sono due principali motivo per la scelta del valore di N come potenza di due:

o È comodo dato che i dati dovranno essere salvati in una digital data storage la quale utilizza indirizzamento binario.

o Il più efficiente algoritmo per calcolare la DFT, la trasformata Veloce di Fourier (FFT), normalmente lavora con N che è una potenza di due.

La notazione standard DSP utilizza le lettere minuscole per rappresentare i segnali nel dominio del tempo (es. x[], y[],...). Le relative lettere maiuscole sono usate per rappresentare il rispettivo valore nel dominio della frequenza (es. X[], Y[],...).

Come si può notare dalla figura IV.2.1 per un segnale di ingresso nel dominio del tempo composto da N punti x [], il suo corrispettivo segnale nel dominio della frequenza è

(3)

campioni. Esse sono chiamate la parte Reale di X[] (scritta anche come Re X[]) e la parte immaginaria di X[] (scritta come Im X[]). I valori in Re X[] sono le ampiezze dei segnali cosinusoidali, mentre i valori contenuti in Im X[] sono le ampiezze dei segnali sinusoidali. Infatti se un segnale nel dominio del tempo ha dei valori che vanno da x[0] a x[N-1], i segnali nel dominio della frequenza vanno da Re X[0] a Re X[N/2] e da Im X[0] a Im X[N/2].

Figura IV.2.1 – Terminologia della DFT. Nel dominio del tempo, x[] consiste in N campioni da 0 a N-1. Nel dominio della frequenza la DFT produce due segnali : la parte reale e la parte immaginaria.

L’asse orizzontale del dominio della frequenza può essere riferito in vari modi. In questo progetto è stato deciso di riferirlo in modo da ottenere sull’asse orizzontale la frequenza in rad/s. Questo significa che i valori lungo l’asse orizzontale variano in modo equispaziato da 0 a freq/2. Freq viene calcolato come 2 /tc, con tc il tempo di

DFT I - DFT N-1 0 N campioni Re X[] 0 N/2 N/2+1 campioni (ampiezza dei coseni)

N/2 0

Im X[]

N/2+1 campioni (ampiezza dei seni) x[]

(4)

Le componenti sinusoindali e cosinusoidali sono anche note come funzioni base della DFT. In altre parole, l’uscita della DFT è un insieme di numeri che rappresentano le ampiezze. Queste funzioni base sono un insieme di onde sinusoidali e cosinusoidali con ampiezza unitaria. La sommatoria delle onde sinusoidali e cosinusoidali del dominio della frequenza, rende il segnale nel dominio del tempo.

Le funzioni di base della DFT sono generate dalle seguenti equazioni:

[ ]

= N ki i ck π 2 cos (IV.2.1)

[ ]

= N ki i sk π 2 sin (IV.2.2)

dove: ck[] è il segnale cosinusoidale per l’ampiezza contenuta in Re X[k] e sk[] è il segnale sinusoidale per l’ampiezza contenuta in Im X[k].

Il fattore di conversione tra le ampiezze delle sinusoidi e i valori nel dominio della frequenza viene calcolato attraverso le formule:

[ ]

2 / Re Re N k X k X = (IV.2.3)

[ ]

Im _/₂

[ ]

Im N k X k X =− (IV.2.4)

e per due casi :

[ ]

N X X 0 Re 0

(5)

[ ]

N

X

X 0 Im 0

Im =− (IV.2.6)

I valori di ReX

[ ]

k e di ImX

[ ]

k sono i valori delle ampiezze convertite per il calcolo del segnale nel dominio del tempo.

1.3 Algoritmo FFT

Utilizzo nell’analisi spettrale

Nell’elaborazione di un segnale, come per l’utilizzo in questa tesi, non si ha a disposizione un’espressione analitica dei valori della sequenza x[n], ma solo i valori medesimi ( ad esempio acquisiti mediante un convertitore A/D) in un intervallo finito, diciamo 0 n N-1. Ciò che si desidererebbe calcolare è la trasformata di Fourier [11] della sequenza aperiodica

[ ]

j fT n e n x f X₍ ₎ +∞ − 2π −∞ = ⋅ = (IV.3.1)

Ovviamente, questa trasformata non potrà essere calcolata per gli infiniti valori della variabile f in un periodo, coiè, ad esempio, nell intervallo [0,1/T]. Ci si accontenterà di ottenere il valore della trasformata per un numero finito di punti normalmente equispaziati nell’intervallo [0,1/T].

Quest’operazione può essere svolta in maniera efficiente tenendo conto della relazione di campionamento in frequenza conseguente di una periodicizzazione:

(6)

1 ,..., 1 , 0 , 1 0 0 − = = k N T N k N Yk (IV.3.2)

e osservando che abbiamo a disposizione un algoritmo veloce per il calcolo delle trasformate discrete. Immaginiamo dunque di perodicizzare la sequenza data con periodo N0=N:

[ ]

+∞

[

]

−∞ = − = m mN n x n y (IV.3.3)

Piochè y[n] è una sequenza periodica, possiamo calcolarne la trasformata discreta di Fourier Y_k,k=0,1,...,N−1 mediante un algoritmo veloce. Sfruttando la (IV.3.2) possiamo poi ricavare i seguenti valori di X( f):

1 . ,... 1 , 0 , = − =NY k N NT k X _k (IV.3.4)

Siamo cioè riusciti a calcolare la funzione X( f) in N punti, e precisamente per le N frequenze equispaziate dell’intervallo [0,1/T]:

1 . ,... 1 , 0 , = − = k N NT k fk (IV.3.5) Complessità di calcolo

Supponiamo di avere disponibile nella memoria di un calcolatore N (potenza di due) valori di una sequenza x[n] e di volerne calcolare la trasformata discreta:

(7)

[ ]

2 /21

[

2 1

]

, 0,... 1 0 2 / 2 2 1 2 / 0 2 / 2 − = + + = − = − − − = − N k e m x e e m x X k k D N m N km j N k j P N m N km j k π π π (IV.3.6)

La prima sommatoria rappresenta la trasformata discreta di una sequenza costituita dagli N/2 campioni di indice pari di x[n], mentre la seconda sommatoria è la trasformata discreta degli N/2 campioni di indice dispari. Possiamo dire che questa scomposizione è “ricorsiva nell’ordine”, nel senso che la trasformata di ordine N è espressa come combinazione lineare di due trasformate di ordine N/2. Il numero di operazioni NFFT(N) necessario a calcolare la trasformata di ordine N secondo questo nuovo criterio può allora essere espresso in maniera ugualmente ricorsiva sulla base di questa scomposizione:

N N N N N N N NFFT FFT FFT 6 2 2 2 ) ( = + + + (IV.3.7)

avendo tenuto conto del fatto che, per ogni valore di k, è necessario moltiplicare Dk per un esponenziale complesso ( 6 operazioni reali) e quindi effettuare la somma con P ( 2 k operazioni reali). Questo procedimento di scomposizione può essere poi ripetuto in modo ricorsivo. Infatti Dk e Pk possono a loro volta essere scomposti suddividendo le sequenze rispettivamente x[2m] e x[2m+1] in due sottosequenze ciascuna di lunghezza N/4. Il calcolo di una trasformata di ordine N/2 comporta allora una complessità:

+ = 2 4 4 2 2 N N N N N_FFT _FFT (IV.3.8)

(8)

N N N N NFFT FFT 2 8 4 4 ) ( = + ⋅ (IV.3.9)

e continuando ad iterare dividendo per 2 progressivamente l’ordine di trasformazione, si ottiene: N N N N N N N NFFT( )= ⋅ FFT +log2 ⋅8 (IV.3.10)

dove NFFT(1) comporta una sola moltiplicazione (

[ ]

0

0 x0ej

X = ) per cui si ricava:

N N N N N N

NFFT( )=6 +8 log2 ≅8 log2 (IV.3.11)

Questa relazione indica che la complessità per l’algoritmo FFT risulta notevolmente inferiore alla complessità (quadratica) dell’algoritmo DFT.

Il tempo di esecuzione reale per l’algoritmo FFT è quello dell’equazione (IV.3.11) dove al posto della costante 8 che corrisponde ad 8 operazioni reali deve essere sostituito con kFFT come in formula: N N k uzione e

Tempo_ sec = FFT log2 (IV.3.11b)

dove kFFT vale circa 10 nanosecondi per un pentium III ad 1 GHz.

Problemi degli analizzatori di spettro numerici

I problemi riscontrati nell’utilizzo di analizzatori di spettro numerici come l’algoritmo FFT sono generalmente di tre tipi:

(9)

o RISOLUZIONE il segnale non può essere campionato da -∞ a +∞ ma per un periodo limitato di tempo (hp. di stazionarietà del segnale numerico.). Si

definisce frame una finestra temporale di 1024, 2048 ... punti.

Risoluzione= ne acquisizio di tempo frame _ _ 1

1 ₌ _{Es: ris=100 Hz tda=3ore.}

o ALIASING Se lo spettro del segnale di ingresso contiene elementi a frequenze più elevate, il campionamento produce sovrapposizioni nella ricostruzione dello spettro. E’ importante anteporre un filtro passa basso anti-aliasing per rispettare le condizioni del Teorema di Shannon

o LEAKAGE Il frame non coincide con il periodo della fondamentale. Si possono utilizzare delle finestre temporali (windows) diverse da quella rettangolare (frame) e tali da pesare i campioni temporali ai margini meno di quelli centrali. Le più note sono quelle di Hamming e la Flattop.

Le soluzioni adottate nello sviluppo di questa tesi per cercare di limitare i tre problemi appena analizzati degli analizzatori di spettro numerici sono esaminate di seguito.

Per quanto riguarda il problema della risoluzione , spesso la scelta di N porta ad una conoscenza insuffuciente della funzione X( f), nel senso che gli N campioni della trasformata discreta sono troppo pochi per ottenere una stima sufficientemente accurata dell’andamento della X( f) stessa. Per evitare questo inconveniente è possibile usare per il parametro N un valore maggiore della durata della sequenza. Il segnale y[n] viene ottenuto cioè dalla ripetizione di una sequenza finita di durata N0 formata dagli N campioni della x[n] a cui vengono postposti N0-N campioni nulli. Si può calcolare adesso la FFT di ordine N0>N della sequenza periodica che nel periodo base vale :

(10)

[ ]

=

[ ]

_≤≤ _≤≤ −₋ 1 0 1 0 0 N n N N n n x n y (IV.3.12)

cioè una sequenza riempita con campioni nulli. Una volta calcolata la trasformata discreta, vengono ricavati N0>N valori della X( f) secondo la relazione del campionamento in frequenza (IV.3.4). Se si fa crescere il valore del parametro N0, si può

aumentare il numero di campioni della funzione X( f), cioè si aumenta la risoluzione dell’analisi spettrale della sequenza x[n] aperiodica e di durata finita.

Per quanto riguarda il problema dell’aliasing, esso può essere eliminato applicando il teorema di Shannon; in altri termini, fissata la banda del segnale B, la frequenza di campionamento deve essere scelta in modo che valga la condizione :

B T

fc = 1 ≥2 (IV.3.13)

Infatti il teorema di Shannon dichiara che: Un segnale il cui spettro è limitato nella banda B può essere ricostruito esattamente a partire dai propri campioni, purchè la frequenza di campionamento non sia inferiore a 2B.

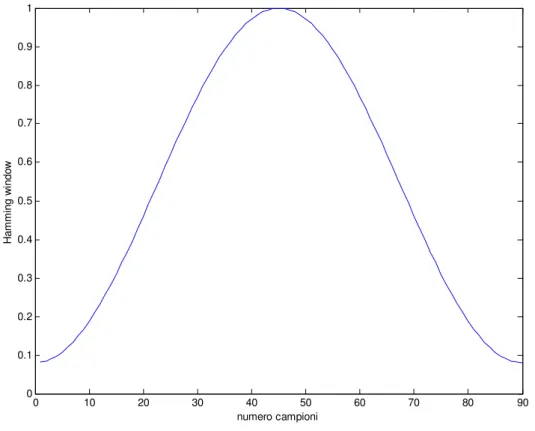
Il problema del Leakage può essere notevolmente attanuato utilizzando le tecniche di Hamming. Questa tecnica consiste nel moltiplicare il segnale da analizzare per un curva detta Hammin window mostrata in figura IV.3.1.

(11)

[ ]

= −

N i i

w 0.54 0.46cos 2π (IV.3.14)

tale finestra infatti viene adattata al numero di punti che verranno passati per il calcolo dell’algoritmo FFT (N=90 nello sviluppo della tesi).

0 10 20 30 40 50 60 70 80 90 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 numero campioni H am m in g w in do w

Figura IV.3.1 – Rappresentazione della Hamming window per limitare il problema di Leakage.

1.4 Utilizzo della FFT nella stima simultamea

Il problema principale nel risolvere il problema della idenfificazione simultanea dei parametri di un sistema con l’utilizzo del criterio del cerchio è quello di poter riuscire a

(12)

stimare tutti i parametri nel minor tempo possibile. Tale tempo deve essere comunque inferiore alla somma dei tempi necessari a stimare tali parametri utilizzando in sequenza uno dei metodi esistenti descritti nel primo capitolo di questa tesi.

Non bisogna però tralasciare troppo l’accuratezza di stima a scapito dei tempi di simulazione. Per questi motivi bisogna cercare un compromesso tra velocità ed accuratezza nelle stime.

Si è deciso quindi di utilizzare l’algoritmo FFT in modo che il tempo di caricamento del buffer non sia eccessivo a basse frequenze ma che allo stesso tempo sia sufficientemente ampio da poter contenere un numero sufficiente di campioni per permetter una stima accurata.

Nella stima simultanea si è deciso di immettere nel sistema una sola frequenza in modo da poter dimensionare ad hoc il buffer e la frequenza di campionamento del segnale che verrà immesso.

In ingresso al sistema si avrà quindi un segnale sinusoidale con frequenza nota. I parametri da dover scegliere affinchè la stima venga effettuata in modo ottimale sono due:

o Numero di campioni all’interno di un periodo o Numero di periodi prima di effettuare una stima

Il numero di campioni all’interno di un periodo non influisce sul tempo di attesa prima che il buffer di calcolo venga riempito ma influisce sulla precisione di stima soprattutto in caso di rumore e sul tempo di calcolo effettivo dell’algoritmo FFT (tempo trascurabile) come da equazione (IV.3.11b). Il numero di periodi prima di effettuare una stima influiscono invece sia sulla precisione della stima dello sfasamento introdotto dal sistema che sul tempo di immissione del segnale nel buffer di calcolo.

(13)

Vediamo adesso attraverso delle simulazioni quali valori per i due parametri appena esposti portano ad un giusto compromesso tra velocità e precisione. Partiremo considerando un tempo di campionamento tale che mi permetta di ottenere 30 campioni del segnale per periodo e vediamo quanti periodi attendere prima di effettuare una stima. E’ stato utilizzato un sistema per effettuare delle prove mettendo in ingresso al sistema una sinusoide di 0.8 rad/s e fase nulla; in uscita al sistema è stata immessa una sinusoide con pulsazione 0.8 rad/s e fase 30 gradi. Sono state effettuate delle prove con diverse modalità di riempimento del buffer di calcolo; è stato calcolato lo sfasamento nel caso in cui è stato immesso nel buffer 1,3,5 periodi del segnale. Nelle figure IV.4.1/2/3/4/5/6 è possibile notare la stima di fase e ampiezza effettuata dal blocco FFT campionando il segnale 30 volte per periodo in assenza di rumore.

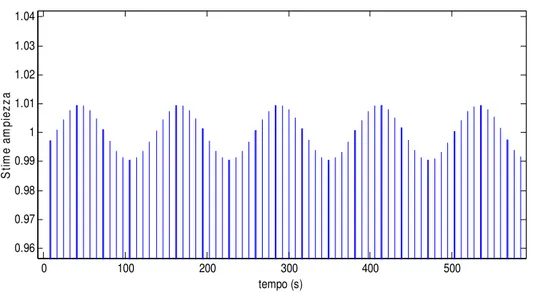
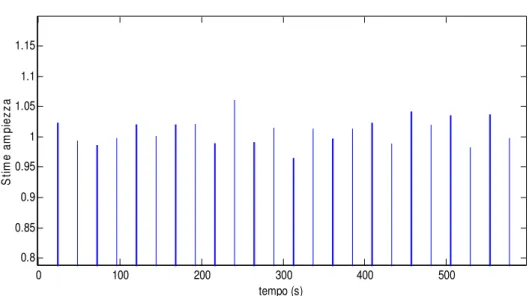
0 100 200 300 400 500 0.96 0.97 0.98 0.99 1 1.01 1.02 1.03 1.04 tempo (s) S tim e am pi ez za

Figura IV.4.1 – Stima di ampiezza in assenza di rumore con buffer di calcolo riempito con 1 periodo del segnale

(14)

0 100 200 300 400 500 -31 -30.8 -30.6 -30.4 -30.2 -30 -29.8 -29.6 -29.4 -29.2 -29 tempo (s) S tim a fa se (g ra di )

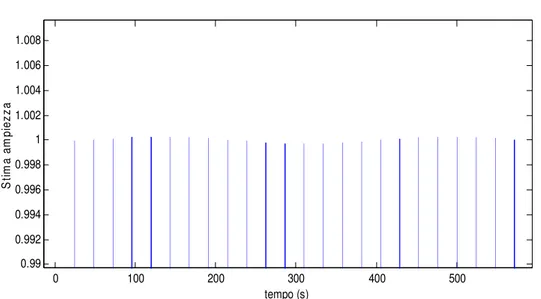
Figura IV.4.2 – Stima di fase in assenza di rumore con buffer di calcolo riempito con 1 periodo del segnale 0 100 200 300 400 500 0.99 0.992 0.994 0.996 0.998 1 1.002 1.004 1.006 1.008 tempo (s) S tim a am pi ez za

Figura IV.4.3 – Stima di ampiezza in assenza di rumore con buffer di calcolo riempito con 3 periodi del segnale

(15)

0 100 200 300 400 500 -30.2 -30.15 -30.1 -30.05 -30 -29.95 -29.9 -29.85 -29.8 tempo (s) st im e fa se (g ra di )

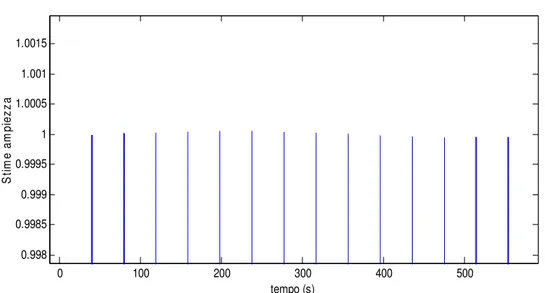
Figura IV.4.4 – Stima di fase in assenza di rumore con buffer di calcolo riempito con 3 periodi del segnale 0 100 200 300 400 500 0.998 0.9985 0.999 0.9995 1 1.0005 1.001 1.0015 tempo (s) S tim e am pi ez za

Figura IV.4.5 – Stima di ampiezza in assenza di rumore con buffer di calcolo riempito con 5 periodi del segnale

(16)

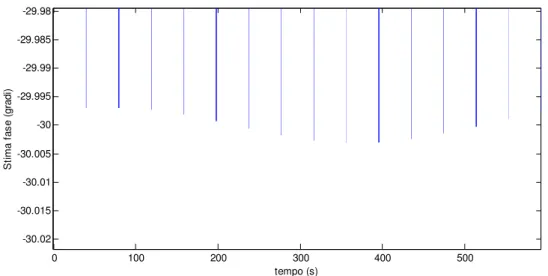
0 100 200 300 400 500 -30.02 -30.015 -30.01 -30.005 -30 -29.995 -29.99 -29.985 -29.98 tempo (s) S tim a fa se (g ra di )

Figura IV.4.6 – Stima di fase in assenza di rumore con buffer di calcolo riempito con 5 periodi del segnale

Dalle figure sopra si può notare che all’aumentare dei periodi contenuti nel buffer di calcolo, la stima effettuata dall’algoritmo FFT aumenta la sua precisione soprattutto nella stima di fase. Si può escludere subito la soluzione che adotta un solo periodo in quanto le stime senza rumore sul segnale sono poco precise. Tra le altre due prove effettuate si nota chiaramente che la stima effettuata con 5 periodi del segnale è precisa con un errore di 5 millesimi di grado mentre quella che utilizza solo 3 periodi del segnale raggiunge una precisione di 1 centesimo di grado. Considerando però i tempi di stima, nel caso a 5 periodi è di 40 secondi circa mentre nel caso di 3 periodi si riesce ad ottenere una stima in circa 23 secondi. Dato che si può ritenere buona un precisione di stima di 1 centesimo di grado, si è deciso di utilizzare nella realizzazione finale un buffer che contenga 3 periodi del segnale. Si può notare inoltre dalle figure IV.4.7/8 che gli errori di stima nel caso in cui venga applicato sul segnale un rumore bianco con un rapporto segnale rumore pari al 40% si ottengono errori simili sia utilizzando 5 periodi che 3 periodi.

(17)

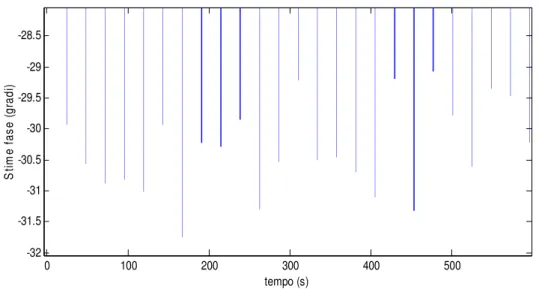
0 100 200 300 400 500 -32 -31.5 -31 -30.5 -30 -29.5 -29 -28.5 tempo (s) S tim e fa se (g ra di )

Figura IV.4.7 – Stima di fase con rumore del 40% con buffer di calcolo riempito con 3 periodi del segnale 0 100 200 300 400 500 -32 -31.5 -31 -30.5 -30 -29.5 -29 -28.5 tempo (s) S tim e fa se (g ra di )

Figura IV.4.8 – Stima di fase con rumore del 40% con buffer di calcolo riempito con 5 periodi del segnale

(18)

Adesso rimane solamente da controllare se l’ipotesi fatta in partenza di campionare il segnale 30 volte per periodo fosse una ipotesi buona o esista un’alternativa frequenza di campionamento che riesca a migliorare ulteriormente le stime di fase. Sono state effettuate anche in questo caso tre prove con 3 periodi del segnale nel buffer di calcolo però a diversa frequenza di campionamento. Nelle figure IV.4.9/10/11/12/13/14 si possono notare gli errori di stima per modulo e fase campionando ripettivamente il segnale 16 – 30 – 60 volte il periodo.

0 100 200 300 400 500 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 tempo (s) S tim e am pi ez za

Figura IV.4.8 – Stima di ampiezza con rumore del 40% con buffer di calcolo riempito con 3 periodi del segnale campionato 16 volte il periodo.

(19)

0 100 200 300 400 500 -34 -33 -32 -31 -30 -29 -28 -27 -26 -25 tempo (s) S tim e fa se (g ra di )

Figura IV.4.9 – Stima di fase con rumore del 40% con buffer di calcolo riempito con 3 periodi del segnale campionato 16 volte il periodo.

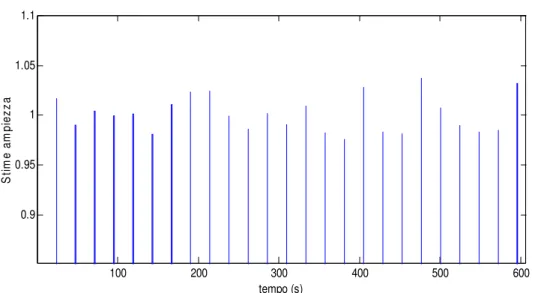
100 200 300 400 500 600 0.9 0.95 1 1.05 1.1 tempo (s) S tim e am pi ez za

(20)

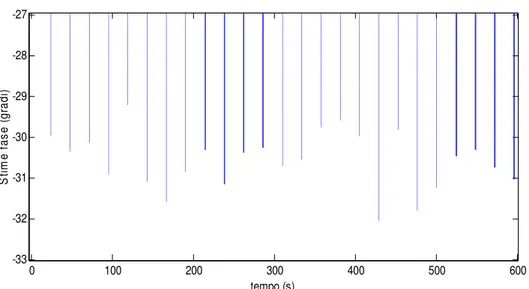
0 100 200 300 400 500 600 -33 -32 -31 -30 -29 -28 -27 tempo (s) S tim e fa se (g ra di )

0 100 200 300 400 500 600 0.7 0.75 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 tempo (s) S tim e am pi ez za

(21)

0 100 200 300 400 500 600 -32.5 -32 -31.5 -31 -30.5 -30 -29.5 -29 -28.5 tempo (s) S tim e fa se (g ra di )

Si nota subito dalle figure IV.4.9/11/13 che gli errori di fase diminuiscono all’aumentare della frequenza di campionamento; questo avviene perchè l’algoritmo FFT diventa più tollerante al rumore più campioni ha a sua disposizione per effettuare il calcolo. Si nota anche che l’errore massimo nel caso di 30 campioni al periodo del segnale e con rumore pari al 40 % del segnale è di 2 gradi. Campionando a frequenza doppia ( 60 campioni al periodo del segnale) l’errore massimo è di 1.5 gradi. Dato il poco vantaggio di precisione si è deciso di mantenere l’ipotesi iniziale di campionare i segnali in ingresso all’algoritmo FFT con una frequenza di campionamento pari a 30 campioni per periodo del segnale. Utilizzando questo campionamento non si incide troppo sui tempi di calcolo effettivo dell’algoritmo FFT come da equazione (IV.3.11b) anche se i tempi sono del tutto trascurabili.