Modelli epidemiologici: proprietà e applicazioni

Capitolo 1

Modelli epidemiologici:

proprietà e applicazioni

Nella prima parte di questo capitolo ci concentreremo sui modelli epidemiologici più semplici elaborati per malattie infettive legate a microparassiti (batteri, virus, protozoi, elminti). In particolare saranno presentati alcuni modelli applicabili a malattie infettive trasmesse solo da persona a persona, e non attraverso vettori (insetti o animali). La loro struttura è basata su equazioni differenziali ordinarie, e la trattazione di riferimento è quella di Herbert W. Hethcote (1989).

Nella seconda parte si approfondiranno i modelli precedenti, proponendo dei modelli di interazione tra gli individui in una popolazione meno semplicistici di quelli precedenti. Si affronterà il problema dell'eterogeneità delle popolazioni introducendo i concetti di mixing proporzionale e ristretto.

Nella terza e quarta parte sarà mostrata l'applicazione dei concetti introdotti rispettivamente ad alcuni modelli sulla gonorrea introdotti da H. W. Hethcote e J. A. York e ad un modello di J. Jacquez sull'HIV.

1.1 Modelli di base

1.1.1 Ipotesi fondamentali e definizioni

Data una popolazione di N individui, si definiscono tre possibili classi di appartenenza per ciascun individuo:

• la classe dei suscettibili S, a cui appartengono gli individui non ancora infetti ma potenzialmente infettabili;

• la classe degli infettivi I, a cui appartengono gli individui infetti e capaci di infettare gli individui della classe precedente;

• la classe dei rimossi R, a cui appartengono gli individui che non possono diventare infettivi, perchè immuni, o isolati, o deceduti.

A ciascuna delle tre classi, si associa una variabile dipendente dal tempo, rispettivamente S(t), I(t), R(t), data dalla frazione di popolazione contenuta in quella classe rispetto alla popolazione totale; la somma delle tre variabili dà 1 per ogni t. La frazione istantanea di infettivi I(t) prende il nome di

prevalenza.

Tutti e tre i modelli utilizzati si fondano sulle seguenti assunzioni semplificative:

nel tempo; anche quando vengono considerati i tassi di natività e mortalità, essi vengono assunti uguali e pari a µ, in modo da mantenere costante N; in genere si ipotizza inoltre che il numero di morti in ogni classe sia proporzionale alla popolazione di ciascun comparto e che tutti i nuovi nati nell'unità di tempo, pari a µ N, entrino nel comparto dei suscettibili.

 Le popolazioni sono mescolate in modo omogeneo; si definisce contatto adeguato ogni contatto di un infetto che è capace di trasmettere l'infezione se avviene con un suscettibile. Sia λ il numero medio di contatti adeguati nell'unità di tempo da parte di un individuo infetto; di questi contatti, una percentuale S avverrà con individui suscettibili, cosicchè λ S rappresenta il numero medio di suscettibili contagiati in un giorno da un infetto. Il numero totale di suscettibili contagiati nell'unità di tempo prende il nome di incidenza (Inc) e sarà dato, per la legge di azione di massa, dal prodotto tra λ S e la popolazione totale contenuta nella classe degli infettivi, data da N I; si avrà dunque:

(1.1) Inc= S N I .

 Il periodo di latenza, definito come la distanza temporale tra l'istante in cui si contrae l'infezione e l'istante in cui si inizia ad essere infettivi, è nullo; se così non fosse, bisognerebbe introdurre un ulteriore classe di appartenenza, quella degli esposti, E, che codifichi lo stato compreso all'interno del periodo di latenza.

 Il numero giornaliero di individui che da infettivi diventano rimossi, in modo definitivo o temporaneo, è proporzionale alla frazione di individui infetti I secondo un coefficiente γ; in altre parole, ogni giorno in media una frazione γ degli infettivi passa nello stato dei rimossi: si definisce di conseguenza il periodo medio di infettività d come:

(1.2) d=1  .

Nel caso in cui si tenga conto anche del tasso di mortalità, il numero giornaliero di rimossi per decesso µ I si aggiunge a quelli rimossi per guarigione, cosicchè l'effetto di µ è quello di sommarsi a γ; in tal caso si ha dunque d=_1 .

Si definisce il numero di contatto σ come il numero medio di contatti adeguati avuti da un individuo durante tutto il tempo in cui è nello stato infettivo, dato da:

(1.3) = 



il numero effettivo di suscettibili infettati da un individuo durante tutto il suo periodo infettivo è dato da σ S e prende il nome di numero di rimpiazzamento: esso determina lo stato di equilibrio di tutti i modelli che vedremo, in quanto rappresenta quanti nuovi suscettibili diventano infettivi al posto di ciascun infetto che diventa rimosso.

1.1.2 Il modello SIS

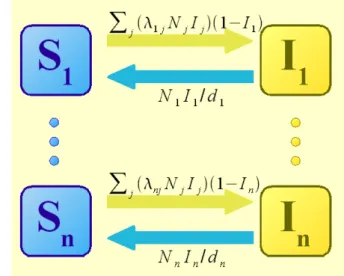
Quando la guarigione dallo stato infettivo non garantisce, neanche temporaneamente, l'immunità, la frazione dei rimossi non gioca alcun ruolo e risulta S(t) + I(t) = 1; si parla allora di modello SIS, in quanto le uniche transizioni possono essere dallo stato S allo stato I e viceversa. Tali transizioni sono regolate dalle relazioni suddette e mostrate nella figura 1.1, che rappresenta un generico modello compartimentale SIS.

Le equazioni differenziali che regolano l'andamento temporale delle popolazioni nei due compartimenti sono:

(1.4) N ˙S=− S N I  N I N − N S N ˙I= S N I− N I − N I

o equivalentemente, dividendo tutto per la popolazione totale N: (1.5) _{˙I = S I− I − I}˙S=−S I  I − S .

Questo modello può essere ricondotto ad una sola equazione differenziale non lineare, sostituendo S = 1– I:

(1.6) ˙I =[−] I − I2 _.

Specificando le condizioni iniziali, e ipotizzando costanti tutti i parametri, per questa forma specifica si può ottenere una soluzione analitica (soluzione di Bernouilli o equazione logistica) che fornisce l'andamento temporale di I(t). L'equazione differenziale può essere risolta con il metodo di separazione delle variabili, elaborandola per portarla nella forma:

(1.7) 1

[−] I − I2 dI=dt

e poi integrando tra l'istante iniziale t = 0 e l'istante generico t; si avrà:

∫

∫

Per comodità, da qui in poi porremo λ – (µ + γ) = α . Il primo integrale si risolve scomponendo la frazione integranda in fratti semplici:

1  I − I2= A − I B I ,

da cui si ricava A= λ/α e B=1/α; a questo punto l'integrale si può scomporre nella somma degli integrali delle due frazioni:

/

∫

∫

∫

− I I =

− I0

I0

e− t _,

essendosi posto I(t) = I ed I(0) = I0 .

Alla stessa soluzione si poteva arrivare, con procedimento diverso, attraverso il metodo di sostituzione delle variabili. Si parte dall'equazione (1.6), e si pone:

I= y−1  dI=−1 y2dy , sostituendo la I con l'equivalente in y, si ottiene:

d y−1_ dt = y −1_{− y}−2 _{ −} 1 y2 ˙y= 1 y− 1 y2   ˙y=− y .

Riapplicando il metodo di separazione delle variabili, si ricava:

∫

∫

da cui infine, risostituendo y = 1 / I: −1 I=− 1 I₀e −t_  I − I =  I0− I0 e−t .

Questa espressione è identica a quella trovata in precedenza.

Rielaborando con semplici ma 'ingombranti' passaggi algebrici l'equazione ottenuta, si ottiene l'equazione logistica che esprime l'andamento della frazione di infetti al variare del tempo ed in funzione dei parametri epidemiologici σ e λ:

(1.8) It= −1 I0e −1  t  1−I01−e −1  t 

L'andamento di questa equazione al variare di σ mostra l'esistenza di un valore critico per tale parametro, pari proprio a σ = 1; al di sotto di esso il sistema converge, per t ∞ , verso lo stato (Seq0, Ieq0) = (1, 0) e pertanto la malattia tende a scomparire; per σ > 1 invece lo stato di equilibrio

risulta essere Seqs, Ieqs=

1  , 1 –

1

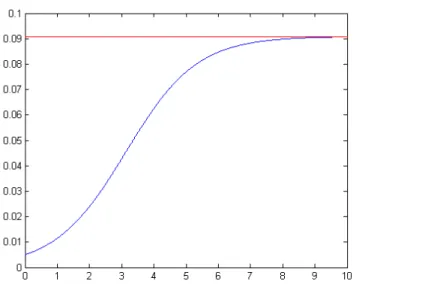
 , detto equilibrio endemico poichè la frazione di infetti rimane identicamente non nulla. In figura 1.2 e 1.3 sono mostrati gli andamenti della (1.8) per due valori di σ al di sotto e al di sopra del valore critico.

Figura 1.2 - Andamento del numero di infetti in un modello SIS per σ < 1 (I0 = 0.5

%, scala dei tempi arbitraria); la linea rossa indica il valore asintotico.

Figura 1.3 - Andamento del numero di infetti in un modello SIS per σ > 1(I0 = 0.5

%, scala dei tempi arbitraria); la linea rossa indica il valore asintotico.

Il diagramma delle fasi di questo sistema riporta in ordinata la derivata di I, e in ascissa la I stessa: dall'equazione del sistema è evidente che esso ha un andamento parabolico; per σ > 1 si ha una intersezione non nulla con l'asse I = 0 e pari proprio al punto di equilibrio previsto, I_eqs=1 – 1

 . Si noti che all'equilibrio il numero di rimpiazzamento σ S vale 1: in effetti, se ciascun infettivo fosse rimpiazzato, nel corso del suo periodo infettivo, da un numero di suscettibili maggiore di uno, la prevalenza I dovrebbe tendere ad aumentare, riducendo S e di conseguenza σ S, fino a tornare al valore di equilibrio; viceversa, se σ S fosse minore di 1, il numero di infettivi scenderebbe aumentando il valore di S con una retroazione negativa.

Allo stato stazionario inoltre tutte le derivate sono nulle per definizione; ponendo a 0 ˙I nella seconda equazione del sistema (1.4), tenendo conto della (1.1) e indicando la prevalenza

all'equilibrio Ieqs con Preveq, risulta la relazione:

(1.9) N Prev_eq=Inceq

=Inceqd .

1.1.3 Il modello SIR senza dinamiche vitali

Nel caso in cui la rimozione dallo stato di infettività conferisca uno stato di immunità permanente, bisognerà aggiungere al modello precedente il comparto dei rimossi R e tenere conto delle relazioni con gli altri comparti. Si ipotizza per il momento che siano trascurabili le dinamiche vitali di natalità e mortalità, e si pone pertanto µ = 0. Questa approssimazione è valida quando il fenomeno che si cerca di modellizzare avviene molto più rapidamente nel tempo rispetto alle dinamiche di natalità, e dunque è adatto per fenomeni epidemici che si esauriscono nell'arco di pochi mesi.

Se tutti i rimossi diventano permanentemente immuni, lo schema del modello è quello di figura 2, che corrisponde al sistema di equazioni:

(1.10) N ˙S_{N ˙I=S N I− N I}=− S N I

N ˙R=N I

;

questo è riconducibile, dividendo tutto per N, a:

Figura 1.5 - Schema compartimentale SIR senza dinamiche vitali

Figura 1.4 - Diagramma delle fasi del modello SIS per σ > 1. I punti evidenziati in rosso rappresentano il punto di equilibrio teorico, che coincidono con l'intersezione del diagramma delle fasi su I=0.

(1.11) _{˙I = S I−I}˙S=−S I ˙R=I

.

Data la relazione S + I + R = 1, che implica anche SI ≤1 , ne deriva che tutte le traiettorie nello spazio delle fasi, determinate dalle coppie di punti (S, I) per ogni t, sono confinate al triangolo delimitato dalla retta S + I = 1 e dagli assi cartesiani. Nel modello SI precedente, invece, tutte le traiettorie si svolgono sulla retta S + I = 1, poichè il modello è monodimensionale (eq. (1.6)).

Se si provano a calcolare i punti di equilibrio del sistema SIR, ponendo le derivate uguali a zero, si ottiene il sistema di equazioni:

(1.12) 0=−SeqIeq

0= SeqIeq− Ieq

,

che ha per soluzione Ieq = 0 ∀ Seq . Il sistema tende dunque ad un equilibrio in cui non vi siano

infetti, ma non è possibile determinare in questo modo il valore di S al termine dell'epidemia.

Ipotizziamo che il numero di infetti iniziale sia trascurabile rispetto alla popolazione totale, I≈0 e che ci possa essere nella popolazione un certo numero di rimossi, ad esempio in seguito a vaccinazione o a una precedente manifestazione della malattia infettiva, tale che la frazione di suscettibili iniziali sia S0. Linearizzando il sistema nell'intorno del punto (S0, 0), si ottiene:

(1.13) J=

[

0 S0−

]

,

che ha autovalori 0 e λ S0 – γ; il secondo autovalore è positivo se 

S0−10  S01 : in

queste condizioni l'infezione tenderà a diffondersi tra la popolazione con andamento esponenziale dando luogo ad una diminuzione monotonica di S(t); a un certo istante t il suo valore raggiungerà St=

= 1

 , che costituisce il valore critico per cui ˙I =0 , come si può vedere sostituendo questo valore nella seconda delle 1.11; per valori ancora più piccoli di S, che sono raggiunti negli istanti immediatamente successivi a t , tale derivata è negativa: allora l'istante t corrisponde al valore massimo di I(t), dopo il quale l'andamento della curva degli infetti inizierà a diminuire fino al valore di equilibrio I = 0.

Riassumendo, si ha che la frazione di infetti decade esponenzialmente al valore nullo se σ S0 < 1;

se invece σ S0 > 1, la prevalenza cresce inizialmente fino ad un valore massimo corrispondente ad

S_picco=1

 , dopodichè diminuisce fino al valore zero, come mostrato in figura 1.6.

L'andamento previsto dal modello in quest'ultimo caso concorda molto bene con l'andamento tipico effettivamente rilevato su casi clinici di molti outbreak epidemici. Il valore di σ può essere stimato a partire da misure sul valore iniziale e finale della frazione di suscettibili.

1.1.4 Il modello SIR con dinamiche vitali

Nel caso in cui la presenza della malattia nella popolazione considerata si protragga per un tempo lungo rispetto ai tassi di natalità e mortalità (cioè la malattia è endemica), questi ultimi non possono essere più trascurati ed il modello va modificato come segue (figura 1.7):

(1.14) ˙S=−S I − S ˙I = S I− I − I ,

dove si è tralasciata l'equazione per R in quanto essa può essere determinata attraverso la relazione R(t) = 1 – I(t) – S(t).

Figura 1.7 - Schema compartimentale SIR con dinamiche vitali

Le derivate di S e di I possono essere viste come le componenti della velocità con cui lo stato del sistema si sposta nello spazio delle fasi, descrivendone la traiettoria; le curve per cui tali componenti si annullano si possono ottenere semplicemente ponendo a 0 la derivata e ricavando S in funzione di I, o viceversa. La curva per cui si annulla ˙S è data da:

(1.15) I= 

1−S S , quelle per cui si annulla ˙I :

(1.16a) S=

 =

1  (1.16b) I=0 .

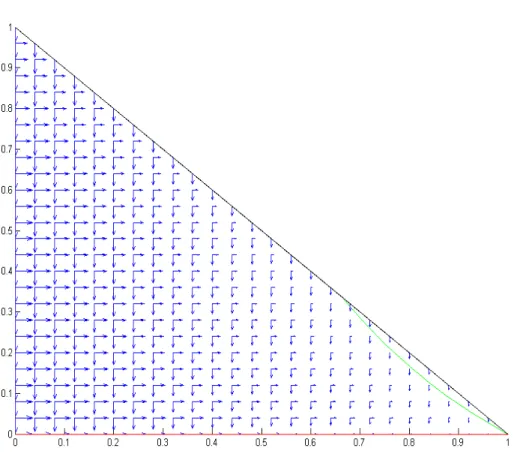
Le intersezioni tra la curva (1.15) e ciascuna delle (1.16) rappresentano i punti in cui entrambe le velocità si annullano, ossia i punti di equilibrio del sistema. Se σ < 1, la curva (1.16a) finisce all'esterno del triangolo dello spazio delle fasi che costituisce il dominio di esistenza del nostro sistema; pertanto, l'unico punto di intersezione è quello dato da B = (1, 0). In figura 1.8 sono mostrate queste curve (eccetto la 1.16a che è fuori dal dominio di esistenza) e le componenti del campo di velocità nei vari punti dello spazio delle fasi per µ = 0,01, γ = 0,01 e λ = 0,015, a cui

corrisponde σ = 0,5. Si vede che il punto B è un punto di equilibrio stabile, poichè il campo di velocità è diretto verso il punto da tutte le direzioni consentite, ossia una perturbazione in una qualsiasi direzione consentita fa sì che il sistema torni nel punto di equilibrio da cui è partito.

In figura 1.9 sono mostrate le curve a velocità nulla e le componenti del campo di velocità nei vari punti dello spazio delle fasi per µ = 0,01, γ = 0,005 e λ = 0,03, a cui corrisponde σ = 2. Stavolta la (1.16a) rientra nel dominio di esistenza del sistema, e il punto A=1

, − 1

  da esso generato è un punto di equilibrio stabile; infatti, il campo di velocità in un intorno del punto è tale da tendere a riportare lo stato del sistema verso l'equilibrio. Il punto B = (1,0) è un equilibrio metastabile: non appena si ha una perturbazione verso le I positive, il campo di velocità tende ad allonanare definitivamente lo stato dal punto di equilibrio in esame; inoltre una perturbazione nella direzione di S, causata ad esempio dall'aumento nel numero dei rimossi in seguito a una campagna di vaccinazione, induce un ritorno verso l'equilibrio, per via della riduzione dei rimossi al passare del tempo causata dal tasso di mortalità e della continua immissione di nuovi suscettibili dovuta alle nascite.

A conferma dei risultati del metodo grafico basato sui campi di velocità, mostriamo ora i risultati di un'analisi quantitativa sulla stabilità locale dei punti di equilibrio, basata sulla linearizzazione del sistema nell'intorno di essi. La matrice jacobiana del sistema è data in generale da:

(1.17) J=

[

∂ S ∂ ˙I∂ I

]

=

[

 Ieq  Seq−

]

.

Figura 1.8 - Andamento del campo di velocità e delle curve a velocità nulla (in verde e in rosso) nel piano delle fasi per σ < 1 (µ = 0,01, γ = 0,01 e λ = 0,015).

Consideriamo il punto di equilibrio A=1 , − 1   : lo jacobiano diventa: (1.18) J=

[

]

il cui polinomio caratteristico p(z) risulta essere: (1.19) p z= z2

 z−1

 .

Poichè siamo sotto l'ipotesi σ > 1 (altrimenti A non sarebbe un punto di equilibrio), sia il coefficiente del termine in z che il termine noto sono positivi: ciò significa che il polinomio caratteristico dello jacobiano nel punto A non ha intersezioni con l'asse z = 0, e dunque non ha radici reali; poichè però i coefficienti del polinomio sono tutti reali, allora le radici dovranno essere complesse e coniugate, ovvero, le traiettorie avranno comportamento oscillatorio intorno al punto di equilibrio.

Sfruttando le relazioni zz=2 ℜ{z} e

∑

da cui si evince la stabilità locale del punto di equilibrio. Le traiettorie nell'intorno del punto A tenderanno a cadere su A con una traiettoria spiraleggiante.

Nella figura 1.10 viene messa in evidenza la traiettoria del sistema a partire dai valori dati per λ, γ

Figura 1.9 - Andamento del campo di velocità e delle curve a velocità nulla (in verde, in rosso e in azzurro) nel piano delle fasi per σ > 1. Il punto evidenziato con il cerchio nero è il punto di equilibrio A (µ = 0,01, γ = 0,005, λ = 0,03).

e µ e da uno stato iniziale in cui I = 0,1, S = 0,9 e pertanto R = 0. Il campo di velocità viene mostrato direttamente con i vettori risultanti, anzichè per componenti. Si vede che l'evoluzione dello stato del sistema segue proprio la direzione indicata punto per punto dal campo vettoriale, e raggiunge il punto di equilibrio A con una traiettoria spiraleggiante (v. dettaglio in fig. 11), come previsto dai risultati analitici dell'articolo di Hethcote.

L'andamento di S(t), I(t) e R(t) è rappresentato in figura 1.12. Il valore costante di regime è in realtà sottoposto a delle oscillazioni sempre più smorzate che la scala dei tempi della figura non riesce a mettere in evidenza, così come è stato necessario guardare un dettaglio della traiettoria per mostrarne l'andamento spiraleggiante.

Per il punto B = (1,0) la matrice jacobiana diventa invece:

(1.21) J=

[

0 −

]

i cui autovalori, essendo una matrice triangolare, sono gli elementi sulla diagonale, uno dei quali (-µ) è sempre negativo;

• per σ < 1, anche − è minore di zero, ed il punto è perciò di equilibrio stabile; • per σ > 1, − è positivo, e dunque il punto è un equilibrio metastabile.

Riassumendo:

• se σ < 1, lo stato di equilibrio stabile è B = (1, 0), qualsiasi sia lo stato iniziale del sistema;

• se σ > 1, tutte le traiettorie, eccetto quelle che iniziano dall'asse I = 0, tendono spiraleggiando allo stato di equilibrio endemico A=1

, − 1

  , mentre le traiettorie che iniziano dall'asse I = 0 tendono all'equilibrio metastabile B = (1, 0).

Figura 1.10 - Traiettoria del sistema SIR con dinamiche vitali (in magenta) nello spazio delle fasi per σ > 1 (µ = 0,01, γ = 0,01 e λ = 0,015).

Figura 1.11 - Dettaglio della traiettoria di figura 10, che ne mette in evidenza l'andamento a spirale. (µ = 0,01, γ = 0,01 e λ = 0,015)

Figura 1.12 - Andamenti nel tempo di S (blu), I (rosso), R (magenta) corrispondenti alla traiettoria di figg. 10 e 11 (µ = 0,01, γ = 0,01 e λ = 0,015); le oscillatozioni delle variabili connessi alla traiettoria a spirale non sono risolvibili con questa scala temporale.

Data una popolazione in cui la malattia sia endemica, è piuttosto semplice determinare σ dai dati epidemiologici: è esattamente l'inverso del valore di equilibrio della popolazione suscettibile Se, che

può essere misurata con metodi serologici: =_S1

1.2 Eterogeneità delle popolazioni

I modelli fin qui introdotti dividono la popolazione in compartimenti solo in funzione della loro condizione rispetto alla possibilità o meno di trasmettere o ricevere la malattia, considerando

omogenea la popolazione all'interno di ciascun comparto: significa che ogni individuo di una classe

si comporta in maniera del tutto identica a tutti gli altri per quanto riguarda i meccanismi di contagio della malattia. Questa ipotesi è estremamente semplificativa e risulta irrealistica; essa trascura infatti le differenze che sussistono tra individuo e individuo a causa delle differenze di genere, di comportamento sociale, di età, di condizioni socio-economiche e demografiche, della sintomaticità o asintomaticità con cui si manifesta la malattia nell’individuo, e così via.

Se da un lato tener conto di tutte queste variabili può complicare la risoluzione del modello e l'identificazione dei parametri, tuttavia è opportuno raffinare i modelli base introducendo una descrizione più approfondita che permetta una maggiore aderenza alla realtà epidemiologica.

Un primo livello di approfondimento si può ottenere suddividendo la popolazione totale in n gruppi, a ciascuno dei quali vengono assegnati parametri diversi dipendenti dalle loro caratteristiche. In figura 1.13 è mostrato il modello compartimentale nel caso di un sistema SIS, ma la rappresentazione può essere banalmente estesa anche al caso SIR. Nel caso SIS, si considerano 2n compartimenti (nel caso SIR saranno 3n), Si ed Ii (nel SIR ci sarà anche Ri), dove l’indice i

rappresenta il gruppo di appartenenza del suscettibile o dell’infetto. Ogni gruppo è costituito da una popolazione totale Ni .

Come nel caso del modello SIS di base, il numero di suscettibili del gruppo i che saranno infettati in un giorno dal gruppo j-esimo sarà dato da λij ( 1 – Ii ) Nj Ij , essendo λij il numero di contatti

adeguati di un individuo del gruppo j-esimo con persone (sia suscettibili che infette) del gruppo i-esimo. La variazione nell'unità di tempo, espressa come derivata, del numero di infetti Ii nel

generico gruppo i sarà allora data dalla somma degli infettati in un giorno da parte di tutti i gruppi (compreso lo stesso gruppo i), a cui va sottratto il numero di individui guariti, dato anche in questo caso da NiIi

d :

(1.22) N_i ˙I_i=

∑

N_iI_i d_i .

Si linearizzi il sistema non lineare e si calcoli l'autovalore a parte reale massima, che indicheremo con s(A), della matrice jacobiana A; si può dimostrare che se s(A) è positivo, si ha un equilibrio non nullo, mentre se è negativo l'equilibrio è lo stato I = 0, cioè la malattia decade.

1.2.1 Il problema delle interazioni

Per poter trovare applicazione pratica, qualsiasi modello deve essere espresso in funzione di un gruppo di parametri di chiaro significato fisico, i cui valori siano determinabili da dati empirici in modo relativamente facile. Il ruolo chiave svolto dai λij in questo tipo di modelli rende necessario

stimare questi parametri in modo piuttosto preciso; tuttavia ciò non è fattibile in modo intuitivo, basandoci semplicemente sulla definizione (numero medio di contatti adeguati nell'unità di tempo da parte di un individuo infetto). Bisogna allora esprimere queste grandezze in funzione di parametri più immediati e dalle stime empiriche accessibili.

Innanzitutto, denominiamo incontro ogni contatto che avvenga con un individuo diverso. Sono gli incontri, e non i contatti ripetuti con uno stesso individuo, a causare la diffusione della malattia da individui infetti a individui suscettibili, sebbene i contatti ripetuti aumentino la probabilità che l'infezione si trasmetta effettivamente. Si definisce poi:

• il livello di attività aj del gruppo j come il numero medio di incontri di una singola persona del

gruppo j nell'unità di tempo; il suo inverso 1/aj rappresenta il tempo medio tra due incontri;

• la probabilità di trasmettere l'infezione qj da parte di un individuo infetto del gruppo j, nel caso

che il contatto avvenga con un suscettibile;

• la frazione di contatti mij che un individuo del gruppo j ha in media con un individuo del gruppo

i rispetto al totale dei contatti. Si avrà

∑

Risulta quindi che λij = aj qj mij.

Mentre aj e qj sono parametri facilmente misurabili, l'incertezza più grande rimane sulla matrice di

interazione, ossia sulle dinamiche sociali dei contatti nella popolazione. Per determinare M si effettuano spesso delle ipotesi, che a seconda dei casi possono risultare arbitrarie o approssimative, ma che comunque permettono di risalire ad una stima sensata dei parametri. La più semplice di queste ipotesi è l'isolamento tra i gruppi, che ipotizza che si abbiano contatti solo all'interno di un gruppo, e cioè mij = 0 per i≠ j : in queste condizioni, il modello a n gruppi può essere

semplificato in n modelli base indipendenti.

Un'ipotesi più complessa ma anche più realistica, introdotta da Nold e ripresa da altri autori è quella di mixing proporzionale. Si definisce attività relativa bj del gruppo j la frazione di attività

totale in quel gruppo rispetto all'attività globale di tutti i gruppi: b_j=ajNj/

∑

avere, come appare immediato,

∑

mij non dipende da i), per le quali la somma degli elementi dà 1.

Anche per un modello a n gruppi si può definire per ciascun gruppo un numero di contatto kj , che

esprime il numero di contatti adeguati di un individuo durante tutto il suo stato infettivo: (1.23) k_j=qjajdj ;

il numero di contatti adeguati con uno specifico gruppo i sarà invece t_ij=kjmij=qjajdjmij=ijdj ,

e la matrice T = { tij } si chiama matrice di trasmissione. Si può calcolare inoltre un numero di

contatto medio

dato dalla somma dei kj, pesata per l'attività relativa di quel gruppo. Si può dimostrare che

l'autovalore a parte reale massima del sistema (1.22) linearizzato ha lo stesso segno di K−1 , e che dunque il valore di K determina l'equilibrio, nullo o endemico della malattia, a seconda che sia rispettivamente minore o maggiore di 1.

Il valore di prevalenza all'equilibrio è dato dal numero di infetti Ei = Ni Ii che si registra quando il

sistema è giunto a regime, e può essere calcolata ponendo a zero la derivata nelle equazioni del modello (1.22).

L'assunzione di mixing proporzionale non è necessariamente valida; ad esempio, alcuni gruppi potrebbero avere dei contatti preferenziali con alcuni gruppi specifici; una tale situazione potrebbe modellizzarsi attraverso un mixing proporzionale ristretto solo all'interno di tali gruppi. Una situazione più plausibile potrebbe essere un certo equilibrio tra le due situazioni: questa ipotesi assume che la matrice di interazione sia data da una combinazione pesata tra la matrice di mixing proporzionale Mp e quella di mixing proporzionale ristretto Mr:

(1.25) M=1 – G M pG Mr ;

la costante G viene detta costante di selettività: per G = 0 torniamo nell'ipotesi di mixing proporzionale puro, per G = 1 siamo nel caso di mixing proporzionale ristretto.

1.3 Alcuni modelli applicati allo studio della gonorrea

La trattazione seguente si rifà ai modelli proposti nel 1984 da H. W. Hethcote e J. A. Yorke, e costituisce un'applicazione ad una malattia infettiva specifica, la gonorrea, di uno dei modelli generali appena proposti.

L'obiettivo dei prossimi paragrafi è mostrare qualche esempio di come si può dedurre nuova conoscenza sui fenomeni epidemiologici a partire da diversi modelli di interazione tra i gruppi e di strutturazione delle popolazioni. Inoltre nella parte finale sarà mostrata l'applicazione di tali modelli al supporto alle decisioni di sanità pubblica, attraverso la determinazione quantitativa delle metodiche di prevenzione e cura più efficaci nella riduzione dei casi clinici.

La gonorrea è una malattia infettiva di origine batterica che si trasmette per via sessuale. Per quanto riguarda gli aspetti di interesse per la modellizzazione, essa è caratterizzata da tempi di latenza estremamente brevi rispetto alla velocità di trasmissione, il che verifica la terza delle ipotesi alla base dei modelli precedenti (par. 1.1.1) e permette di trascurare il compartimento degli esposti E.

In secondo luogo, la guarigione dallo stato infettivo non fornisce immunità temporanea o permanente, e comporta dunque un passaggio dalla condizione di infettivo direttamente a quella di suscettibile: di conseguenza, non esiste il compartimento dei rimossi R.

Infine, l'incidenza rilevata nel corso degli anni mostra che, pur esistendo delle oscillazioni stagionali, queste sono piccole rispetto all'incidenza totale e possono essere trascurate senza perdere troppa informazione sul sistema: ciò significa che i parametri di trasmissione possono essere considerati tempo-costanti.

Le caratteristiche di questa malattia permettono pertanto di utilizzare una modellizzazione di tipo SIS; si può dimostrare comunque che l'introduzione di ritardi nel percorso da un compartimento all'altro, come quelli dovuti al periodo latente o ad un'eventuale immunità temporanea fornita da un vaccino non modificano significativamente l'andamento generale delle variabili di stato ed i valori di equilibrio. Tale dimostrazione, tuttavia, non rientra negli scopi di questa sezione.

1.3.1 Modello base

Il modello più semplice che si può ipotizzare coincide proprio con il modello a due soli compartimenti descritto nel paragrafo 1.1.2: come già visto esso considera una popolazione totalmente omogenea e non tiene conto delle differenze epidemiologiche, ad esempio, tra uomo e donna nella trasmissione della malattia.

Per quanto grossolano possa essere questo modello, esso fornisce un'utile interpretazione della malattia, mettendo in evidenza il fatto che, nell'ipotesi che tutti i parametri del sistema siano stazionari, anche i valori di prevalenza ed incidenza all'equilibrio lo siano. Pertanto, se queste due variabili mostrano un andamento temporale non costante, come di fatto avviene secondo i dati clinici, ciò è dovuto non ad un'evoluzione intrinseca degli stati del sistema, ma semplicemente al fatto che il sistema non si trova all'equilibrio; tale situazione di non equilibrio deve allora essere dovuta a una variazione temporale dei parametri del modello, che sono a loro volta legati a variabili epidemiologiche di diversa natura: sociali, (tassi di contatto tra gli individui, esistenza o meno di programmi di informazione e sensibilizzazione sulla malattia), demografiche (natalità e mortalità), cliniche (durata dell'incubazione del batterio, durata dei periodi infettivi, virulenza degli agenti, resistenza ai farmaci), e così via.

Da una stima approssimata di σ, ottenuta a partire da dati epidemiologici, e dall'equazione analitica della I(t) data dalla soluzione del sistema (1.3), si riesce anche a stimare la velocità con cui

viene raggiunto l'equilibrio. Nel caso della gonorrea, risulta che tali variazioni hanno una costante di tempo piuttosto piccola, attorno ai 40 giorni, che sembra essere confermata dalle misure sperimentali; l'equilibrio segue dunque i cambiamenti delle variabili epidemiologiche in modo molto rapido.

Un secondo modello è quello ad n gruppi descritto nella sezione 1.2. Abbiamo già visto come anche in questo caso l'equilibrio dipenda dal valore del numero di rimpiazzamento rispetto al valore critico 1; anche in questo caso le eventuali variazioni temporali del numero di infetti non vanno attribuite alla dinamica intrinseca del sistema, ma a una variazione continua del valore di equilibrio, causata da variazioni nei parametri epidemiologici che influenzano l'equilibrio stesso.

1.3.2 Modello con core group

In una popolazione si definisce nucleo altamente attivo o core group quella parte di popolazione costituita da persone sessualmente molto attive, che sono dunque efficienti trasmettitori di malattie (cosiddetti superdiffusori); poichè l'obiettivo delle procedure di controllo delle malattie è di ridurre il numero totale dei casi, concentrare tali procedure sul core group anzichè sulla popolazione generica potrebbe rivelarsi più efficace di strategie meno focalizzate.

In tutti i modelli sin qui analizzati esiste un parametro che condiziona il comportamento della malattia in base al valore assunto da esso rispetto ad un valore soglia. Questo parametro può essere individuato nel numero di rimpiazzamento iniziale o numero di riproduzione di base R0, che

intuitivamente si può definire come il numero medio di persone contagiate da un infetto durante il suo periodo infettivo nell'ipotesi di S=1 . Nel modello base, R0 coincide con σ, nel modello a n

gruppi con K .

Quando R0 è maggiore di uno, si ha inizialmente una crescita esponenziale della frazione di

popolazione infetta, che continuerebbe fino al valore di I = 1 se non intervenissero a frenarla dei meccanismi di saturazione. Nelle malattie che conferiscono immunità, il fatto che una certa parte di popolazione diventi immune implica una saturazione della prevalenza, in quanto i contatti adeguati che avvengono con queste persone non si concretizzano in trasmissioni effettive; nel caso della gonorrea e dei modelli SIS in generale, non esistendo immunità, l'effetto di saturazione è dato dalla cosiddetta preemption, cioè dal fatto che, all'aumentare di I, diminuisce la disponibilità di individui suscettibili da contagiare, riducendo il numero di nuovi infetti.

Dai dati utilizzati nel lavoro di Hethcote e Yorke, risulta che negli anni '80 meno dell'1% della popolazione statunitense era affetta da gonorrea, e dunque che l'effetto di preemption era trascurabile. La malattia inoltre non decadeva automaticamente (cioè era a carattere endemico), e pertanto l'R0 complessivo doveva essere maggiore di uno. Ma in assenza di preemption una tale

situazione implicherebbe, secondo il modello base, una crescita esponenziale, e non un valore approssimativamente tempo-costante e non nullo. Questa incoerenza conferma il fatto che l'ipotesi di popolazione uniforme è troppo semplicistica, e lascia intendere che la saturazione del valore di equilibrio sia dovuta ad un effetto di preemption in uno dei sottogruppi che costituiscono la popolazione effettiva.

Ipotizziamo di avere inizialmente suddiviso la popolazione in n gruppi, come nel modello del paragrafo precedente; possiamo accorpare gli n gruppi in due macro-gruppi: il nucleo altamente attivo e la popolazione rimanente, detta gruppo non-core, secondo questo criterio: si considerano facenti parte del core group tutti i sottogruppi della popolazione, la cui prevalenza sia particolarmente alta (ad esempio, >20%); gli altri fanno parte del non-core. Per definizione, il core group presenta un significativo effetto di preemption.

Per renderci conto delle dimensioni dei gruppi, supponiamo di avere una popolazione totale di 1000 persone, di cui 10 siano gli infetti totali (1%), e 20 i componenti del nucleo altamente attivo (2%); per definizione il core group avrà > 4 infetti (prevalenza > 20%), cioè oltre il 40% di tutti gli

infetti della popolazione complessiva. Generalizzando, ciò mostra come il core group possa contenere una grossa percentuale degli infetti totali nonostante la sua dimensione effettiva possa essere anche molto piccola, e ciò a causa della prevalenza molto alta al suo interno.

All'equilibrio, come per il caso monogruppo, varrà sempre la relazione R0S = 1; per il gruppo

non-core la prevalenza è bassa e dunque si può considerare S≈1 ; inoltre, R0non-core deve essere < 1,

altrimenti la frazione infetta crescerebbe, non essendoci effetti di saturazione. Di conseguenza, per mantenersi lo stato endemico a livello di popolazione complessiva, dovrà essere R0core > 1 nel nucleo

altamente attivo, dove infatti rimane valida la relazione R0coreS = 1, ma dove S è invece piccolo. Se

non esistesse il core, la malattia scomparirebbe dal primo gruppo in virtù del suo R0 < 1: il core è

quindi responsabile del permanere della malattia nella popolazione.

Sebbene in questo studio si continuino a trascurare differenze epidemiologiche importanti, ad esempio riguardo il genere e la sintomaticità della malattia, esso dà una valutazione immediata ed efficace degli effetti sulle dinamiche della malattia dovuti a ciascuno dei due gruppi.

1.3.3 Modello uomo-donna

Questo modello si focalizza sulla trasmissione esclusivamente eterosessuale della gonorrea, individuando nella differenza di genere il criterio per la discriminazione dei gruppi. Avremo così un gruppo per gli uomini e uno per le donne, considerati entrambi ad alta attività sessuale; si tratta perciò di una descrizione più dettagliata del nucleo altamente attivo.

Poichè si considerano solo i rapporti eterosessuali, il modello coincide con quello (1.22) per n=2, dove λii = 0 e m12 = m21. La divisione dei gruppi in uomini e donne permette di tenere conto della

differenza epidemiologica nelle probabilità di contagio attraverso due diversi qi; si dice rapporto di

efficacia di contatto il parametro e=q1 q2

.. In questo caso conviene tenere conto, come R0, di un

numero di contatto di seconda generazione k = k1 k2 corrispondente al numero di donne (o uomini)

infettate da uomini (o donne) che in precedenza erano stati infettati da un'unica donna (o uomo).

1.3.4 Modello ad 8 gruppi

Questo modello generalizza ulteriormente l'eterogeneità della popolazione, dividendola in 8 gruppi dati dalle combinazioni possibili di tre caratteristiche:

• genere: uomo o donna;

• livello di attività sessuale: alto o normale (cioè, individuo appartenente al nucleo altamente attivo o no);

• sintomaticità o asintomaticità della malattia.

La suddivisione permette di tenere conto delle notevoli differenze quantitative nei meccanismi di trasmissione in termini di probabilità di contagio, numero giornaliero di incontri sessuali e durata della malattia. La popolazione è supposta anche stavolta eterosessuale in modo da ridurre della metà il numero di λij da stimare; tale ipotesi è comunque giustificata dalla scarsa trasmissione della

malattia tra popolazione omosessuale e eterosessuale, come mostrato da dati sperimentali. I gruppi con indice dispari sono i gruppi femminili, quelli con indice pari i gruppi maschili; la popolazione totale femminile e quella maschile sono assunte essere uguali e normalizzate ad 1.

Si definiscono inizialmente la matrice di interazione e quella di trasmissione secondo l'approccio del mixing proporzionale, tenendo conto che l'attività totale maschile e quella femminile devono essere uguali e riferendo l'attività sessuale relativa bi a quella totale del sesso corrispondente,

anzichè a quella complessiva degli 8 gruppi.

prevalenza conviene tenere presente il valore del numero di contatto di seconda generazione; questo sarà dato dal prodotto dei numeri di contatto medi relativi a ciascun sesso, e calcolati come in (1.24): k= K_uomoK_donna=

∑

∑

1.3.5 Valutazione delle procedure di controllo

Per il controllo delle malattie infettive possono essere applicate diverse misure cliniche, sia di tipo preventivo che curativo; un problema che può essere risolto attraverso l'uso dei modelli matematici è la determinazione dell'efficacia di ciascun tipo di intervento, e conseguentemente della priorità da assegnare a ciascuno, anche sulla base di valutazioni di carattere economico.

Per far ciò occorre modificare le equazioni differenziali sin qui impostate, in modo da tenere conto dei meccanismi causali su cui agisce la specifica metodologia di controllo; calcolando i valori di prevalenza all'equilibrio del nuovo modello si riesce a determinare l'efficacia della metodologia in termini di riduzione dei casi. Nella trattazione seguente continuiamo a focalizzare l'attenzione su un modello con core group, in modo da poter determinare rapidamente dei risultati intuitivi; si osservi però che la modellizzazione delle procedure di controllo rimane del tutto generale.

E' utile tenere presente in questa fase le seguenti definizioni:

• il numero medio di casi per persona in un anno Y, dato dall'incidenza totale in un anno diviso la dimensione della popolazione totale, che è la quantità che una procedura di controllo o una combinazione di procedure dovrebbe minimizzare:

(1.26) Y=365

∑

∑

;

• l'infettività media totale all'equilibrio: (1.27) h=

∑

• l'infettività media frazionaria relativa al gruppo j:

(1.28) Cj=

b_jq_jE_j

h .

Screening e ri-screening diagnostico

Per quanto riguarda la gonorrea, la più semplice metodica di controllo è lo screening diagnostico, che permette di individuare attraverso colture batteriche di campioni biologici gli individui infetti asintomatici, che sono trasmettitori 'nascosti' dell'infezione. Supposto che la frazione giornaliera della popolazione controllata sia g, sarà g Ni il numero di individui appartenenti al gruppo i-esimo

che subirà lo screening; di questi una frazione Ii risulterà essere infetta. Supposto che tutte le

persone trovate infette durante lo screening vengano curate efficacemente, e dunque riportate allo stato di suscettibile, si dovrà considerare, nell'equazione 1.20, un termine sottrattivo pari proprio a – g Ni Ii:

(1.29) N_i ˙I_i=

∑

(1.30) N_i ˙I_i=

∑

Si nota che l'effetto di g è quello di diminuire la durata media dello stato infettivo da di a

D_i= di

1g di

e conseguentemente il ki.

Una procedura più approfondita consiste nel ri-sottoporre a screening diagnostico, dopo un breve periodo di tempo (qualche mese), una certa frazione f delle persone risultate positive al primo screening; questa tecnica è basata sull'intuizione che, con buona probabilità, le persone trovate infette anche allo screening successivo sono dei componenti del core group. Nel caso di ri-screening l'equazione 1.20 viene modificata con un termine – f Ii

2 di : (1.31) N_i ˙I_i=

∑

Una valutazione quantitativa del modello conferma l'intuizione qualitativa, e mostra come questa seconda procedura sia ben più efficace del semplice screening.

Procedure di investigazione dei contatti

Tali metodiche si basano sulla libera segnalazione, da parte di individui a cui è stata fatta una diagnosi di malattia, delle persone da cui pensano di avere ricevuto l'infezione, o a cui pensano di averla trasmessa. Lo studio di questa metodica è incluso nel testo di Hethcote e Yorke, edito nel 1989. Oggi probabilmente questa procedura non è più percorribile per l'aumentata sensibilità verso il rispetto della privacy.

I responsabili della trasmissione all'individuo in esame sono detti infettanti, quelli che hanno subito la trasmissione dall'individuo sono detti infettati. La presa di contatti, la diagnosi e la conseguente eventuale cura di questi individui possono costituire una procedura di controllo efficace.

Il rintracciamento degli infettati permetterà di individuare una proporzione di infetti che è suddivisa in media tra nucleo altamente attivo e gruppo poco attivo in modo analogo all'incidenza dei due gruppi; con il rintracciamento degli infettanti, la proporzione tra le persone individuate nei due gruppi è invece analoga a quella tra le infettività C1 e C2. Ci si aspetta quindi che questo

secondo metodo sia più efficace, in quanto maggiormente orientato ad individuare gli elementi del core.

Rintracciare e trattare gli infettati equivale a ridurre tutti i λij di un fattore percentuale f:

N_i ˙I_i=1− f 

∑

Sostituendo invece il contributo del rintracciamento degli infettatori nelle equazioni differenziali, si ottiene un effetto equivalente duplice: un aumento dei suscettibili, legato all'aumento del numero delle persone curate, e la riduzione della durata media analoga a quella dello screening semplice:

Ni ˙Ii=

∑

Risolvendo analiticamente il modello, risulta, come previsto, che a parità di f il rintracciamento degli infettanti è più efficace del rintracciamento degli infettati.

Procedure di vaccinazione

solo temporanea. La scelta della popolazione da vaccinare può essere fatta in vari modi: qui ci limitiamo a considerare le differenze tra una vaccinazione applicata alla generalità della popolazione esposta alla malattia (vaccinazione generalizzata), e una vaccinazione limitata agli individui che sono stati trovati infetti durante lo screening, subito dopo la cura (vaccinazione

post-trattamento). Sia r la durata media degli effetti di immunizzazione, e u la percentuale di vaccinati in

un giorno.

Nel primo caso il modello si modifica assumendo l'esistenza, per entrambi i gruppi, di un comparto di individui resi immuni dal vaccino, e che gli S di entrambi i gruppi vi entrino con un tasso di u Ni Si e vi escano con un tasso di

N_iV_i

r ; Vi rappresenta la frazione di popolazione immune in ogni istante, pari a (1 – Si – Ii) (figura 1.14). Impostando le equazioni classiche del

modello compartimentale, risulta che il modello è equivalente al modello (1.20), in cui λij è stata

sostituita da ij

1ru .

Nel secondo caso si ipotizza che la vaccinazione faccia passare una frazione u degli individui inizialmente infetti e poi guariti e vaccinati nel comparto degli immuni (la frazione restante 1 – u degli immuni torna invece direttamente tra i suscettibili); dal comparto immune si torna al comparto dei suscettibili con un tasso NiVi

r analogo a quello del caso precedente. Il modello compartimentale risulta essere quello di figura 1.15.

Risolvendo il sistema e calcolando le prevalenze di equilibrio, si dimostra che la vaccinazione post-trattamento è molto più efficace di quella generalizzata, come si spiega intuitivamente dal fatto che in questo modo si riescono a immunizzare temporaneamente una quantità maggiore di individui appartenenti al core group.

1.4 Il modello di Jacquez per l'AIDS

L'AIDS è un'altra malattia infettiva a trasmissione sessuale, causata probabilmente da un unico retrovirus, detto virus dell'immunodeficienza umana e meglio noto con la sigla HIV–1 (Human Immunodeficiency Virus). Subito dopo l’infezione si ha una manifestazione acuta dovuta all’aumento della carica virale nel sangue, simile ad un attacco di mononucleosi infettiva e caratterizzata da febbre, mialgia, diarrea, encefalite, linfoadenopatia. Dopodichè il titolo virale diminuisce in conseguenza della risposta anticorpale e la malattia rimane latente finchè a un certo punto la quantità di cellule T-helper diminuisce, dando luogo alla sindrome da immunodeficienza (AIDS) e lasciando spazio all'aggressione dell'organismo da parte di malattie opportunistiche; alla fine il virus invade anche le aree cerebrali, producendo demenza.

La trasmissione dell’HIV avviene principalmente per trasfusione di sangue infetto, per l’uso condiviso di siringhe da parte di tossicodipendenti, e tramite rapporti sessuali. I tempi di latenza tra l’infezione e la manifestazione dell’AIDS sono dell'ordine della decina di anni. E’ probabile che tutti coloro che contraggono l’HIV sfocino prima o poi in AIDS.

L'evoluzione dell'infezione avviene in una sola direzione, nel senso che non esiste guarigione o regressione della malattia, sebbene alcuni stadi di evoluzione possano essere caratterizzati da una sintomatologia meno spiccata.

Focalizzandoci strettamente sulla trasmissione sessuale, questa malattia può essere descritta in modo convincente prendendo a riferimento il modello SIR con dinamiche vitali; lo stato infetto rappresenta tutti gli stadi della malattia in cui l'individuo può contagiare altri suscettibili, mentre a quello rimosso appartengono quegli individui che avendo manifestato l'AIDS sono ormai impossibilitati ad avere rapporti sessuali e dunque a trasmettere ulteriormente l'infezione. Vanno tenute in conto le dinamiche vitali in quanto la malattia evolve in un arco temporale molto superiore a un anno.

John Jacquez ha proposto nel 1987 un modello SIR ad n gruppi per una popolazione omosessuale con la seguente struttura:

• ogni gruppo, identificato dall'indice i, ha un tasso di reclutamento Ui di nuovi individui

sessualmente attivi, che finiscono nel comparto dei suscettibili Si;

• il comparto degli infetti Ii è diviso in m sottocomparti Ii, r collegati in cascata, ciascuno dei quali

rappresenta uno stadio di avanzamento della malattia ed è caratterizzato da una diversa trasmissibilità della malattia; questi vengono identificati dall'indice r. Da uno stadio di infettività all'altro e dall'ultimo stadio infettivo allo stato rimosso si passa con una probabilità k (ovvero la permanenza in ciascuno stadio infettivo dura 1/k);

• da ciascun comparto, compreso quello dei suscettibili, ma escluso quello dei rimossi, si può uscire anche con una probabilità µ << k, per tutti i motivi che non siano l'evoluzione della malattia, come ad esempio il decesso o la cessazione dell'attività sessuale; µ è detto tasso di

mortalità competitivo.

• dal comparto dei rimossi Ri si esce con probabilità δ, che rappresenta la mortalità causata

dall'AIDS;

• il numero di suscettibili del gruppo i che vengono infettati nell'unità di tempo da un individuo infetto del gruppo j e nello stadio r di evoluzione della malattia è dato, come nei modelli visti sinora, da: (1.32) ij , r X_iY _{j , r} X jYj =aimijqr X_iY_{j ,r} X jY j ;

si è mantenuta la notazione usata più sopra per il modello sulla gonorrea di Hethcote, ad eccezione di due significative variazioni: in primo luogo, il qr è assunto invariante rispetto al gruppo di

appartenenza, ma è supposto variabile a seconda dell'evoluzione della malattia; inoltre, anzichè le frazioni di popolazione suscettibile S ed infetta I, si sono usati i loro valori assoluti X ed Y, pari rispettivamente a:

Xi = Si Ni ,

Yj, r = Ij, r Nj ,

Yj = Ij Nj =

∑

L'uso delle quantità X e Y è consigliato dal fatto che, non esistendo in questo caso vincoli tra il valore del tasso di reclutamento e quello di mortalità competitiva, la popolazione complessiva può non essere costante nel tempo.

Le equazioni finali del modello di Jacquez sono le seguenti:

(1.33)

{

∑

∑

∑

∑

∣

Il modello di Jacquez si differenzia dai modelli SIR introdotti nei paragrafi 1.1.3 e 1.1.4 per due caratteristiche peculiari che lo rendono particolarmente complesso:

• le dinamiche vitali sono contemplate senza porre vincoli di uguaglianza tra Ui e µ, introducendo

inoltre un tasso di mortalità δ legato alla malattia stessa; questo fa sì che la popolazione totale Ni

non sia costante, ma segua la seguente equazione differenziale, data dalla somma delle (1.31): (1.34) ˙N_i=Ui− Ni− Zi ;

nel caso del modello del par. 1.1.4, la (1.32) continua a valere ma i valori dei parametri sono δ = 0 e Ui = µ Ni , cioè ˙Ni=0 e dunque Ni = costante.

La non costanza della popolazione complica notevolmente i termini Yi , r X _jY j

che risultano quindi essere espressioni non lineari delle variabili di stato;

• vengono esplicitamente considerati gli stadi di evoluzione della malattia caratterizzati da valori differenti dei parametri epidemiologici (in particolare, la probabilità di trasmettere l'infezione).

1.4.1 Condizioni per l'invasione nel modello di Jacquez

Ci limitiamo a studiare il comportamento del modello di Jacquez nei primi istanti di diffusione della malattia all'interno di una popolazione, e di individuare le condizioni per cui la malattia sfoci in epidemia, cioè si abbia invasione, o meno.

Studiare le sole condizioni iniziali permette di introdurre delle notevoli semplificazioni sul modello di Jacquez: innanzitutto, nel periodo iniziale dell'evoluzione della malattia, il comparto dei rimossi è vuoto, visto che esiste un periodo di latenza di diversi anni prima della manifestazione

dell'AIDS; in secondo luogo, possiamo ipotizzare che le dinamiche vitali connesse ad Ui e a µ

abbiano raggiunto una popolazione di equilibrio (dunque costante) che, secondo l'equazione (1.32) calcolata con Zi = 0, risulta data da Ni=

U_i

 = XiYi . Infine, negli istanti iniziali praticamente

tutta la popolazione è suscettibile, cioè X_i≈ Ni .

Semplifichiamo ulteriormente il modello tenendo in considerazione l'intero sovracomparto degli infetti, senza la suddivisione in stadi di infettività, la cui popolazione è data, come visto, da

Y_j=

∑

Nel modello così ridotto possiamo considerare la sola equazione relativa al comparto degli infetti, dal momento che quella relativa ai suscettibili è da essa dipendente. Sostituendo tutte le ipotesi introdotte, si ha:

(1.35) ˙Yi=qaiNi

∑

Y_j

N_j−k Yi ;

il modello semplificato è quindi lineare e si può scrivere nella forma matriciale:

(1.36)

[

]

[

]

[

]

{

}

La soluzione del modello linearizzato sarà una combinazione lineare di esponenziali, il cui esponente è dato dagli autovalori della matrice A. Pertanto, se tutti gli autovalori di A risultano essere a parte reale negativa, tutte le Yi decadranno a zero nel volgere di qualche costante di tempo e

la malattia sparirà; se invece almeno un autovalore risulterà a parte reale positiva, tutte le Yi

tenderanno a crescere finchè non insorgano fenomeni di saturazione quali quelli visti nel par. 1.3.2. Inoltre, se esistono autovalori complessi (e necessariamente coniugati dato che gli elementi della matrice sono reali), si evidenzieranno andamenti oscillanti delle prevalenze.

Nel caso n = 2, il polinomio caratteristico di A risulta della forma (1.40) p=2

−tr  Adet  A , essendo trA=

∑

Il discriminante dell'equazione di secondo grado p(λ) = 0 risulta essere: =[tr  A]2 −4 detA= A11 2 2 A11A22 A22 2 −4  A11A22− A12A21=A11 2  A22 2 −2A11A224 A12A21 e dunque:

= A11− A22 2

4 A12A21 .

Essendo A12, A21 ed il termine al quadrato certamente positivi, anche il discriminante lo è, e

dunque gli autovalori del sistema saranno reali e l'andamento della prevalenza nel tempo non sarà di tipo oscillante.

Il discriminante è inoltre nullo solo nel caso in cui A11=A22 e contemporaneamente A12 = 0 oppure

A21 = 0; esplicitando la seconda condizione, risulta che

q a1 N1/ N2 m12=0 oppure q a2N2/N1m21=0 ;

essendo q, N1, N2, a1 e a2 necessariamente non nulli (altrimenti il modello si ricondurrebbe a un

solo gruppo), significherebbe che m12 = 0 oppure m21 = 0, ma ciò significherebbe che uno dei due

gruppi ha rapporti solo al suo interno, e cioè che i gruppi non comunichino tra loro. In conclusione, potrebbero esserci autovalori coincidenti solo nel caso banale in cui il sistema a 2 gruppi possa essere studiato come 2 sistemi monogruppo indipendenti tra loro.

Da queste considerazioni risulta che in tutti i casi di interesse esistono 2 autovalori distinti, che possono essere calcolati come:

=trA±



Il termine sotto radice risulta molto complicato, e diventa impossibile arrivare ad una espressione degli autovalori compatta e facilmente interpretabile da un punto di vista epidemiologico. Introduciamo a questo punto una ulteriore ipotesi, che semplifica notevolmente il calcolo simbolico: supponiamo che il pattern di interazioni corrisponda al mixing proporzionale (par. 1.2.1); si ha allora:

m₂₁=m11 ,

m₁₂=m22 .

Sostituendo questi valori nell'espressione sotto radice, risulta infine (1.41) 1=−k

2=−kq a1m11a2m22=−k 1−R0

;

il primo autovalore è sempre negativo, mentre il segno del secondo risulta dipendere dal termine (1.42) R₀=q

ka1m11a2m22 .

R0 corrisponde alla definizione di numero di rimpiazzamento iniziale, in quanto è il prodotto del

numero di nuovi infetti nell'unità di tempo, qa1m11a2m22 , per la durata media dell'infezione,

1

k . Anche in questo caso, per R0 > 1 si ha invasione, per R0 < 1 la malattia decade.

Per n = 3 la determinazione degli autovalori risulta essere molto faticosa da un punto di vista algebrico, ma si riesce comunque in modo abbastanza intuitivo, seppur rigoroso, a mostrare il ruolo chiave svolto dal parametro R0. Esteso alla terza dimensione R0 si definisce come:

(1.43) R₀=q

k

∑

Il polinomio caratteristico è individuato dall'equazione

(1.44) p=3 p1 2  p2 p3 con

{

∑

∣

Calcolando esplicitamente i valori di p1, p2, p3, sotto l'ipotesi di mixing proporzionale (mij = bj), si

ottiene: p₁=−tr A=q

∑

∑

Gli zeri del polinomio caratteristico possono essere studiati semplicemente sulla base del segno di p1, p2, p3 con metodo grafico: si parte dallo studio degli zeri della parabola 2 p₁ , e si guarda

come questi varino dopo l'aggiunta del termine p2; dopodichè si moltiplica il polinomio di secondo

grado per λ (gli zeri saranno gli stessi, con l'aggiunta di una nuova radice nell'origine) e infine si valuta cosa succede a tutti gli zeri a causa della traslazione dovuta a p3.

Nel nostro caso il segno di tutti i coefficienti dipende unicamente dal valore di R0; si avranno 4

situazioni possibili: [a] R01  p1, p2, p30 [b] 1R0 3 2  p1, p20, p30 [c] 3 2R03  p10, p2, p30 [d ] R03  p1, p2, p30 .

Figura 1.16 - Andamento generale della funzione Q = λ3_+p

1λ2 + p2λ per

Caso [a]: la parabola P = 2

 p1 ha una radice nulla ed una negativa in quanto p1 > 0; poichè

la concavità di P è verso l'alto, una sua traslazione di p2 > 0, porta la radice nulla verso valori

negativi e quella negativa verso lo zero, ma senza cambiarne il segno. La cubica Q = 3

 p1 2

 p2 ha le stesse radici, più una nell'origine. La derivata di Q nell'origine risulta

essere pari a p2 e dunque positiva; l'andamento generale di Q è riportato in figura 1.16: si noti come

la curva passi per l'origine con derivata positiva e si annulli due volte per valori negativi di λ.

La traslazione di questo polinomio verso l'alto dovuta alla somma del termine positivo p3 fa sì che

lo zero nell'origine trasli verso sinistra: tutti gli autovalori del sistema sono dunque in questo caso negativi, e non si ha invasione.

Caso [b]: rimane tutto identico al caso precedente, tranne per il fatto che la traslazione di p3

stavolta avviene verso il basso: la radice nulla di Q diventa in questo caso positiva, e ciò significa nel modello di Jacquez che si avrà invasione.

Caso [c]: qui la parabola P, avente sempre uno zero nullo e uno negativo, viene traslata verso il

basso poichè p2 è negativo: si avrà dunque una radice positiva ed una negativa, a cui si aggiunge nel

polinomio Q la radice nulla. Inoltre, la derivata nell'origine è diventata negativa: il polinomio avrà andamento analogo a quello della figura 1.16, salvo per il fatto che lo zero nell'origine sarà uno dei punti compresi nel tratto discendente tra il massimo e il minimo della curva. La traslazione dovuta a p3, ancora verso il basso, rende negativa quella che era la radice nulla di Q, ma aumenta il modulo di

quella positiva. Anche in questo caso si ha invasione.

Caso [d]: in questo caso la parabola P ha già una radice positiva e l'altra sempre nulla in quanto p1

ha cambiato segno rispetto ai casi precedenti. La traslazione verso il basso di una quantità p2 sposta

sui valori negaivi la radice nulla e su quelli ancora più positivi quella positiva. Q ha andamento analogo al caso [c], e la traslazione ancora verso il basso produce gli stessi risultati.

In conclusione, si ha invasione per tutti i casi tranne il primo, cioè quello con R0 < 1: ciò conferma

ed estende le determinazioni ottenute nel caso di n = 2 e l'interpretazione intuitiva del significato epidemiologico di R0.

Questo risultato può essere generalizzato ad un numero n di gruppi: considerando che che deve essere:

tr A=

∑

det A=

∏

,

e che si ha, per n gruppi:

(1.45) det A=−k

n

1−R0

tr A=−kn−R0=−k [n−11−R0]

, gli autovalori che soddisfano queste condizioni sono:

(1.46) i=−k per i=1, 2,... n−1

n=−k 1−R0

,

in cui il segno dell'autovalore dominante (quello a parte reale massima) che condiziona la situazione di invasione dipende da 1-R0.

1.4.2 Considerazioni su R

e la distribuzione dei contatti

Esplicitando la definizione di R0, si scopre un'altro risultato interessante:

R₀=k q

∑

∑

∑

dividendo numeratore e denominatore per la popolazione totale N, il rapporto Ni / N rappresenta la

probabilità di ciascun gruppo, e le rispettive sommatorie risultano essere i valori attesi di a2 _{ed a}

rispettivamente:

R₀=k_q E{a

2

}

E{a} .

Dalla definizione di varianza, E{a2_{} = Var(a) + E{a}}2_{, da cui, definendo a=E{a} :}

R₀=k q  a2 a  Vara  a = k q a1 Vara a2  ,

da cui risulta che l'invasione dipende non soltanto dal valor medio dell'attività, come ci si poteva aspettare, ma anche per una certa frazione dal modo in cui l'attività è distribuita tra i gruppi: quanto più essa è sparsa tra tutti i gruppi, tanto più facilmente si raggiungerà la condizione di invasione.