1
Ruote
dentate
Capitolo 1
2
1.1
Introduzione
Le ruote dentate sono definite come ruote provviste di denti che permettono di trasmettere il moto di rotazione da un albero ad un altro [1].
Le prime testimonianze di ingranaggi risalgono a tempi molto antichi: circa 2600 anni prima della nascita di Cristo, i Cinesi utilizzarono carri comprendenti serie complesse di ruote, delle quali le più antiche documentate sono presenti nello Zhi Nan Che e consistevano sostanzialmente di dischi di legno, a cui erano attaccati dei perni più piccoli che fungevano da denti:
3
Evidenze dell’impiego di questi componenti meccanici sono state lasciate anche dalle civiltà babilonese (X sec a.C.), egizia (X sec a.C.) e greca (V sec a.C.).
Aristotele, nel quarto secolo avanti Cristo, scrisse di ruote dentate come se fossero di uso comune e, nel quindicesimo secolo dopo Cristo, Leonardo Da Vinci disegnò dispositivi comprendenti molti tipi di ruote dentate:
Figura 1.2 – Schema di una macchina ad ingranaggi (Leonardo Da Vinci, 1500 d.C.
4
Nonostante le antiche origini della trasmissione ad ingranaggi, solo negli ultimi secoli, nel contesto della rivoluzione industriale, si è raggiunto un alto livello tecnologico sulle ruote dentate.
Un anno fondamentale è il 1694 quando Philip De La Hire, basandosi su vecchi studi di Nicholas of Cusa e Albrecht Durer (XV e XVI sec d.C.) propose per primo l’impiego della curva ad evolvente per la realizzazione pratica degli ingranaggi.
In seguito Eulero, nel XVIII secolo, condusse una serie di importantissimi studi sulle proprietà della trasmissione con profili coniugati.
Un anno di grande rilevanza storica per gli ingranaggi è il 1892, quando Wilfred Lewis presentò la prima analisi razionale dello stato di tensione del dente. Ancora oggi le analisi imposte dalle normative si avvalgono della metodologia adottata da Lewis con opportune correzioni.
Le ruote dentate si distinguono per la forma della superficie descritta dai denti, ad esempio le più comuni sono la cilindrica o la conica, e per la conformazione dei denti, ad esempio dritti o elicoidali. Ne conseguono conformazioni diverse ottenute dalle varie combinazioni:
5
Figura 1.4 – Ruota dentata cilindrica con dentatura elicoidale
6
Figura 1.6 – Ruota dentata conica con denti
dritti
7
Per l’elevato rendimento e le grandi potenze trasmissibili sono sempre state il principale mezzo di trasmissione meccanica in campo aeronautico:
Attualmente, la maggior parte degli ingranaggi aeronautici sono utilizzati per i compiti della trasmissione di potenza dall’albero principale del motore ai vari sistemi del velivolo oppure per la riduzione del rapporto di trasmissione per eliche, fan o simili. Per attingere potenza dall’albero motore si usano ruote coniche o, quando lo spazio lo permette, ruote cilindriche; la potenza si distribuisce ai vari utilizzatori per mezzo di ruote cilindriche. Per la riduzione del rapporto di trasmissione, causa i ridotti spazi disponibili, è molto comune l’utilizzo di riduttori epicicloidali.
Gli ingranaggi devono trasmettere elevati valori di potenza tra assi paralleli e sono, in genere, realizzati a denti dritti o bi-elicoidali, in
Figura 1.8 – Motore a pistoni SA8/75 con
trasmissione a ingranaggi per impiego
Figura 1.9 – T700, trasmissione
8
quanto l’impiego di denti elicoidali comporterebbe una complicazione nel disegno dei supporti delle ruote che dovrebbero equilibrare una forte componente assiale.
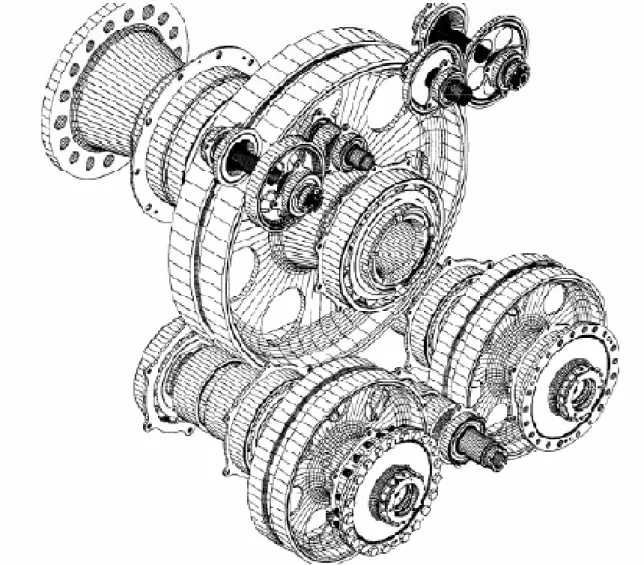
Nella figura seguente è riportato un esempio di trasmissione di impiego aeronautico:
Figura 1.10 – Schematizzazione 3D di una moderna trasmissione di potenza ad
impiego aeronautico
La nostra ricerca si è basata principalmente sullo studio di ruote dentate a denti dritti.
9
1.2
Geometria delle ruote dentate a denti dritti
Le grandezze che caratterizzano ogni coppia ingranante di ruote dentate ad evolvente sono costituite dalla geometria nominale, dalle modifiche di profilo del dente e dalla bombatura del fianco.
La geometria nominale è tale da far rispettare le principali richieste della specifica di progetto, quali ad esempio quella di assicurare determinati rapporti di velocità oppure avere un determinato interasse. Le definizioni e le descrizioni dettagliate sono reperibili su un qualunque testo di costruzione di macchine[1, 2].
Si riporta di seguito l’elenco dei parametri di tale geometria:
10
• rp = raggio primitivo
• rb = raggio di base
• rt = raggio di testa
• rr = raggio di piede
• rrim= raggio della corona dentata, ‘rim radius’ (o raggio interno)
• ha = addendum
• hd = dedendum
• Z = numero dei denti
• p = 2πrp/Z = passo circonferenziale
• m = 2rp/Z = modulo
• b = spessore della fascia dentata o larghezza del dente • I = interasse
• ߶ = angolo di pressione
Per migliorare la cinematica ed il trasferimento dei carichi tra le coppie di denti in presa, nella costruzione di una ruota dentata, le proporzioni standard della geometria nominale (ad es ha=m, hd=1,25m) vengono
modificate [3]. Si apportano anche dei cambiamenti dell’evolvente del profilo del dente, come ad esempio quella dell’arrotondamento per eliminare lo spigolo alla testa del dente che altrimenti asporterebbe del materiale al dente con cui viene in contatto [3].
Nel campo delle alte prestazioni, le coppie trasmesse sono molto elevate e inducono significativi spostamenti elastici dei denti durante l’ingranamento. Queste deformazioni possono causare un certo anticipo
11
nell’ingresso in presa con un conseguente contatto all’estremità:
Figura 1.12 – Contatto di testa del dente della ruota conduttrice che entra in presa
Il contatto di testa è da evitare in quanto provoca dei valori locali di pressioni molto alti, che renderebbero più probabili i fenomeni di pitting ed usura superficiale.
Per rendere più graduale l’ingranamento dei denti ed evitare il contatto di testa, si effettua la modifica di profilo (spoglia [3]) che consiste nell’asportazione di materiale rispetto al profilo definito dalla geometria nominale nella direzione normale all’evolvente.
12
Figura 1.13 – Modifiche di profilo
Come si può notare in figura 1.13 si possono distinguere due tipi di modifiche di profilo:
• Modifiche di testa: quando si asporta il materiale in testa al dente • Modifiche di piede: quando si asporta il materiale a piede dente
La modifica a piede dente può risultare dannosa, perché la diminuzione di materiale causerebbe una concentrazione di tensione dove sono presenti le massime sollecitazioni, quindi sono preferibili le modifiche di testa.
13
Per identificare i punti del profilo del dente si utilizza convenzionalmente l’angolo di rotolamento della retta generatrice dell’evolvente puro, noto come roll-angle [6]:
Figura 1.14 – Roll angle
Dalla figura 1.14 si vede come ad ogni punto P del profilo ad evolvente, che nasce dal punto A appartenente alla circonferenza di base, sia associabile univocamente un valore del roll-angle pari a θ. Quindi la spoglia è definita dalle seguenti caratteristiche [12]:
1. Punto di inizio della modifica Ps definito dal Roll Angle di inizio
14
2. Materiale asportato in testa dente ve
3. Topografia di spoglia v(θ) (relazione tra l’angolo di parametrizzazione del profilo e la profondità della spoglia nel tratto di profilo modificato)
Figura 1.15 – Definizione parametrica della modifica di profilo: Roll Angle (θ),
vettori normale e tangente (n, t), profondità di materiale asportato v(θ), punto d’inizio della modifica lungo il profilo PS, spessore di materiale asportato
all’estremità del dente ve
Le topografie più comuni sono lineari o paraboliche; quest’ultime sono realizzate in modo da avere continuità della curvatura del profilo. Le modifiche di profilo lineari sono più semplici ma possono dare problemi di eccessive forze di contatto dovute alla discontinuità del profilo, che comportano una riduzione della vita a fatica superficiale.
Per avere un contatto più regolare a volte si esegue una bombatura della fascia dentata, che consiste nell’asportazione di materiale in direzione
15
normale alla superficie del dente [3]:
Figura 1.16 – Modifica di bombatura lungo la fascia del dente
Questa modifica è dettata dalla presenza di possibili disallineamenti tra gli assi delle ruote causati dal montaggio o da condizioni di carico del sistema.
A causa del disallineamento, i fianchi dei denti tendono ad entrare in contatto sullo spigolo dell’estremità di fascia, causando locali sovrasollecitazioni che possono portare il fianco ad un rapido deterioramento.
In fase di progettazione si dovrà imporre una bombatura sufficientemente grande da evitare i problemi appena citati, ma allo stesso tempo non eccessiva perché la curvatura provoca un aumento della pressione da contatto (secondo il modello di Hertz [1]).
La bombatura è definita dalle seguenti caratteristiche [14]:
16
2. Forma della bombatura
Figura 1.17 – Definizione parametrica della bombatura
Quando si considerano gli effetti della bombatura su una coppia di ruote ingrananti è stato verificato con studi numerici [14] che, assegnata la topografia della modifica, il parametro che regola gli effetti in termini di pressione di contatto è la “bombatura relativa”, pari alla somma degli ma
delle due ruote ingrananti. Questo aspetto mostra come sia possibile, nella pratica, realizzare la bombatura su una sola delle due ruote, con vantaggi dal punto di vista economico e di produzione.
La ruota reale è soggetta a diversi errori che modificano la geometria rispetto alla condizione nominale. Essi si possono dividere in errori di costruzione o di montaggio [6]. Ci si limita a descrivere quelli relativi allo studio bidimensionale dell’ingranamento; non verranno pertanto trattati fattori quali l’errore d’elica o i disallineamenti. Con queste limitazioni gli errori più comuni risultano:
17
• Eccentricità
• Errori nel profilo (normale o modificato)
Un singolo errore di passo consiste in un’errata spaziatura tra due denti consecutivi con una conseguente differenza tra il passo effettivo e quello teorico pc visto nella figura della geometria. Per ingranaggi ad alte
prestazioni prodotti con tecnologie avanzate, il massimo pitch error è quantificabile nell’ordine di uno scostamento di qualche micron del passo rispetto al valore nominale.
L’eccentricità ec determina un comportamento analogo a quello di una
serie di errori di passo:
Figura 1.18 - Eccentricità
Il centro della circonferenza base della ruota 1 è posizionato in C1’
18
ad alte prestazioni ec non supera i 20 µm. In pratica l’effetto
dell’eccentricità è quello di generare, in assenza di errori di passo ‘reali’, un errore di passo ‘apparente’ variabile ciclicamente ad ogni rotazione:
Figura 1.19 – Errore di passo ‘apparente’ generato dall’eccentricità
L’entità dell’errore di passo ‘apparente’ massimo è facilmente valutabile geometricamente ed è pari a 2ecsin(π/Z).
Per quanto concerne gli errori nella geometria del profilo è sicuramente affermabile che, con le attuali tecnologie per ingranaggi ad alte prestazioni si hanno scostamenti dalla geometria ‘da disegno’ dell’ordine di quantità misurabili con strumenti di verifica; pertanto uno studio che trascuri gli effetti degli errori di profilo può ritenersi esaustivo almeno nell’ambito della progettazione ad alto livello.
19
1.3
Progettazione degli ingranaggi ed analisi necessarie
Le ruote dentate lavorano sempre a fatica, la progettazione si può dividere nelle seguenti fasi [10]:
• Analisi statica: consiste nell’individuare le dimensioni nominali, necessarie per rispettare le richieste di specifica e resistere ai carichi di esercizio, tramite lo studio del comportamento statico dell’ingranamento.
Per la resistenza alla base del dente, secondo gli approcci tradizionali, viene utilizzato il modello di Lewis.
Dimensionata la ruota per la resistenza del dente, si deve anche effettuare un’analisi di resistenza superficiale dei denti tramite la teoria di Buckingham – Hertz.
Queste metodologie possono essere implementate tramite le norme ISO o AGMA, che fanno sempre riferimento al metodo di Lewis, oppure tramite dei software opportuni come quelli per analisi FEM.
• Analisi dinamica: al giorno d’oggi è necessaria anche una analisi della dinamica d’ingranamento più o meno precisa. Per ruote normali può essere sufficiente un approccio normativo, mentre per ruote ad alte prestazioni c’è bisogno di analisi più approfondite tramite software d’analisi FEM o ibridi dedicati. Viene effettuata un’analisi della dinamica dell’ingranamento apportando, se necessario, le modifiche della geometria finché la soluzione non risulta soddisfacente alle richieste della specifica.
20
Nel campo aeronautico, a causa dei piccoli spessori e degli eventuali fori d’alleggerimento presenti, le ruote sono molto deformabili e questo richiede delle analisi sempre più approfondite e precise considerando la geometria variata sotto l’azione del carico. La precisa simulazione degli effetti deformativi sotto carico è di fondamentale importanza per cogliere aspetti della meccanica dell’ingranamento non comprensibili con l’approccio standard normativo e, per ruote fortemente caricate, assume un ruolo di fondamentale importanza la modifica di profilo per migliorare l’ingranamento.
Le moderne specifiche di prestazioni impongono l’impiego di più accurati strumenti di analisi per effettuare una modellazione sempre più fedele.
Le analisi FEM richiedono dei tempi di calcolo molto lunghi, a causa della necessità di dover rigenerare la mesh ad ogni istante d’ingranamento; i software ibridi invece riducono molto i tempi di calcolo.
Quanto accennato sarà trattato più ampliamente nei capitoli successivi.
Questo lavoro di ricerca, iniziato nell’anno 2006-2007 dal Dottor M. A. Moncada, è il tentativo di sviluppare un software che, sfruttando il risultato di una serie di analisi statiche, svolga l’analisi dinamica dell’ingranamento di ruote dentate e che, al tempo stesso, dia risultati accurati in tempi di calcolo relativamente brevi.