Capitolo 2

12

Capitolo 2

La reologia

2.1 Generalità

La reologia è la scienza che studia le relazioni sforzo-deformazione nei corpi, permettendo così di prevedere, ai fini pratici, il comportamento di un materiale sotto determinate condizioni di utilizzo.

Qualsiasi prodotto, compresi quelli dei quali facciamo quotidianamente uso, deve presentare caratteristiche adeguate a tutte le fasi del processo produttivo attraverso il quale giunge al consumatore e deve avere una durata nel tempo accettabile per l’uso al quale è destinato.

Basta pensare ad un lubrificante per motori: deve essere abbastanza fluido da poter essere aspirato dalla pompa, ma non tanto da lasciare scoperta la superficie dei pistoni, mantenendo inoltre inalterate le sue caratteristiche per lungo tempo. Un bitume per pavimentazione stradale deve poter essere facilmente miscelato al materiale litoide per ottenere una mescola adatta alla stesa, ma allo stesso tempo deve poter resistere alle sollecitazioni del traffico stradale senza deteriorarsi. Nell’industria alimentare, cosmetica o farmaceutica, si presentano problemi reologici non trascurabili: per esempio una crema o una pomata deve poter essere spalmata facilmente ma non deve essere tanto liquida da colare.

Come si può capire da questi esempi il campo di applicazione degli studi reologici è vastissimo, poiché ogni materiale, soggetto a sforzi di varia natura, risponde con un comportamento diverso.

Rigorosamente, a livello teorico, tutti i materiali presentano una risposta di tipo viscoelastico alle sollecitazioni imposte. Nei polimeri, sopra la temperatura di transizione vetrosa Tg, tale comportamento è dominante; i bitumi, specialmente quelli modificati sono assimilabili, in termini di proprietà reologiche, a polimeri di basso peso molecolare: sono viscoelastici (con carattere prevalentemente solido) a temperatura ambiente e viscosi (cioè a carattere prevalentemente liquido) ad alta

13 temperatura. In questo capitolo sono illustrate le proprietà viscoelastiche dei materiali ed i metodi sperimentali con i quali tali proprietà possono essere determinate. In particolare si fa riferimento all’analisi dinamica in regime oscillatorio, utilizzata nel corso di questa tesi per studiare le proprietà meccaniche di vari bitumi modificati.

2.2 Comportamento viscoelastico

La teoria della viscoelasticità è di facile comprensione se facciamo riferimento a due modelli ideali: il solido elastico ed il liquido viscoso.

Un solido elastico ha una forma ben definita e l’applicazione di forze esterne lo porta ad una nuova forma di equilibrio. Il solido immagazzina tutta l’energia ottenuta dal lavoro compiuto dalle forze esterne e tale energia, disponibile alla rimozione della forza applicata, permette al solido di ritornare esattamente alla forma originaria. Un solido ideale soggetto ad uno sforzo si deforma elasticamente: l’energia spesa nella deformazione si conserva sotto forma di energia potenziale elastica ed è restituita quando viene rimosso lo sforzo applicato.

Al contrario, fluidi ideali subiscono deformazioni totalmente irreversibili: in altre parole, tutta l’energia spesa per imporre la deformazione è dissipata sottoforma di calore e non può essere restituita annullando la deformazione stessa (comportamento puramente viscoso).

La legge di Hooke e la legge di Newton descrivono rispettivamente il comportamento dei corpi elastici e dei fluidi viscosi, definendo le relazioni sforzo-deformazione per i due casi.

Legge di Hooke:

τ

= G

⋅

γ

     = = = [m/m] [Pa] [Pa] ne deformazio elasticità di modulo G sforzo γ τ _(2.1)

14 Nei corpi elastici lo sforzo è direttamente proporzionale alla deformazione subita dal materiale ed indipendente dalla velocità di deformazione. Il modulo di elasticità definisce la resistenza del solido alla deformazione ed è una proprietà che dipende dal materiale e dalla sua storia termica. La legge di Hooke è valida sia per sforzi normali che per sforzi tangenziali.

Legge di Newton:

τ

=

η

⋅

γ

_&

     = ⋅ = = [m/m] s] [Pa cos [Pa] ne deformazio di velocità ità vis sforzo γ η τ & (2.2)

Nei fluidi puramente viscosi lo sforzo è proporzionale alla velocità di

deformazione ed indipendente dall’entità della deformazione stessa. La viscosità η

definisce la resistenza di un fluido alla variazione irreversibile di posizione dei suoi elementi di volume. Per un liquido Newtoniano ideale la curva di flusso è una retta di pendenza η=τ γ_&=tanα che passa per l’origine degli assi.

La similitudine analitica fra le due leggi è evidente.

Ci sono due tipi importanti di deviazioni dal comportamento puramente Hookeano o Newtoniano [5]:

1. La deformazione in un solido, o la velocità di deformazione in un liquido, possono non essere direttamente proporzionali allo sforzo applicato ma avere una dipendenza più complessa.

2. Lo sforzo può dipendere sia dalla deformazione sia dalla velocità di deformazione, quindi tali anomalie riflettono un comportamento insieme elastico e viscoso, e tale comportamento è chiamato viscoelastico.

Al primo caso appartengono i liquidi non Newtoniani, nei quali la viscosità non è costante, ma dipende dal gradiente della velocità di deformazione con una relazione del tipo τ =η(γ& ⋅) γ&; per questi liquidi la curva di flusso non è una retta ma una curva il cui andamento dipende dalla relazione che lega la viscosità al

15 gradiente della deformazione. Un esempio di questo comportamento sono i fluidi dilatanti, nei quali la viscosità aumenta all’aumentare del gradiente, o i liquidi pseudoplastici, per i quali accade il contrario. Nei solidi tali anomalie si presentano al superamento del limite elastico (fenomeni di snervamento, strizione, ecc.).

Occorre sottolineare che l’entità dello scostamento dal comportamento Newtoniano o puramente elastico non è una proprietà intrinseca di un materiale, ma dipende dallo stato fisico-chimico in cui si trova; in particolare è fortemente

dipendente dalla temperatura.

Nel secondo caso la relazione più semplice che descrive il legame sforzo/deformazione è di tipo lineare:

γ

η

γ

τ

τ

τ

=

_E

+

_V

=

G

⋅

+

⋅

_&

(2.3)

Questa semplice equazione costitutiva rappresenta il comportamento viscoelastico

lineare ed implica che gli sforzi connessi a deformazione e velocità di

deformazione siano additivi.

Nella maggior parte dei materiali il comportamento lineare si ottiene con deformazioni o gradienti di deformazione infinitesimi; nel caso di deformazioni o velocità di deformazione “finite” le relazioni sforzo-deformazione si presentano molto più complesse, in quanto il materiale esce dalla regione di viscoelasticità lineare.

Ovviamente non c’è un valore ben definito che pone il confine fra sollecitazione “infinitesima” e “finita”, ma dipende dal tipo di materiale e dallo stato fisico-chimico in cui si trova. Se sono applicate deformazioni infinitesime la validità della legge di Hooke si estende infatti alla maggior parte dei solidi reali; parimenti i fluidi seguono la legge di Newton per velocità di deformazione infinitesime. Il tipo di materiale oggetto di studio e la strumentazione disponibile suggeriscono se utilizzare tecniche “ad impulso”, cioè con applicazione di stress o strain istantanei (esperimenti di creep o stress relaxation) oppure tecniche dinamiche per analizzare le proprietà meccaniche di un campione da testare.

16

2.3 Creep

Le prove di creep sono condotte applicando uno stress costante al campione e misurando l’andamento temporale della deformazione; tolto il carico si può valutare il creep recovery, cioè il ritorno della deformazione nel tempo.

In figura è riportato il confronto della risposta a creep di un solido elastico e di un generico materiale viscoelastico lineare all’applicazione di due valori di carico σ0 e 2σ0 .

Nel solido elastico la deformazione segue l’andamento del programma di carico, in proporzionalità esatta all’entità del carico applicato. Gli stessi carichi sono applicati ad un materiale viscoelastico lineare; in tal caso lo strain totale è la somma di tre contributi: ε1 ed ε2 sono rispettivamente la deformazione elastica istantanea e ritardata, mentre ε3 è una deformazione residua non recuperabile, dovuta allo scorrimento viscoso.

Figura 2-1: creep e creep recovery

Si definisce in tal modo una grandezza J(t), detta “cedevolezza” o creep

compliance, funzione del tempo e somma di più contributi:

3 2 1 ) ( ) ( J J J t J t _{= = + +} σ ε (2.4)

Nei polimeri reticolati, se il carico è applicato per un tempo sufficientemente lungo, la deformazione raggiunge un valore limite Je (equilibrium compliance), e

17 non si presenta il termine J3, vale a dire che la deformazione è completamente

recuperata; i termini J1 e J2 rappresentano rispettivamente il termine unrelaxed,

cioè la risposta immediata elastica, ed il termine relaxed, il cui valore dipende dal tempo.

Altri materiali, quali i polimeri non reticolati, sotto carico costante raggiungono una condizione di flusso stazionario (steady-state flow) dove la velocità di deformazione è costante e definita da un unico parametro, la viscosità newtoniana h0 (steady-state viscosity).

In questo caso non si presenta il valore limite

J

e, ma si parla di steady-state

compliance

J

e0

,

ottenibile sottraendo il contributo viscoso al tempo t* (Figura

2-2).

Figura 2-2: creep compliance

La presenza di una equilibrium compliance permette di definire un materiale come un solido viscoelastico, mentre nel secondo caso la presenza di scorrimento viscoso indica che abbiamo a che fare con liquidi viscoelastici.

2.4 Stress

relaxation

La controparte delle prove a creep è costituita dagli esperimenti di stress

relaxation. In questo caso è applicata sul materiale una deformazione costante

istantanea e si misura il rilassamento della tensione; questo fenomeno è dovuto alla ridistribuzione delle molecole nel materiale senza che ci siano variazioni macroscopiche di volume. L’assunzione di linearità definisce il linear stress

18 ) ( ) ( 0 t G t = ε σ (2.5)

E’ importante rimarcare che quanto detto è valido esclusivamente nel campo delle piccole deformazioni.

2.5 Principio di sovrapposizione di Boltzmann

Il comportamento lineare ha le sue basi analitiche nel principio di sovrapposizione di Boltzmann [5].

Le ipotesi avanzate dall’autore sono: a) le funzioni J(t) e G(t) dipendono, al tempo t, da tutto quanto è successo al materiale a tempi precedenti; b) il contributo all’istante t a tali funzioni, prodotto ad un tempo qualunque t’ < t da stress o strain imposti, non dipende dai contributi a tempi t’’< t , ovvero i contributi a tempi diversi ti < t vanno semplicemente sommati.

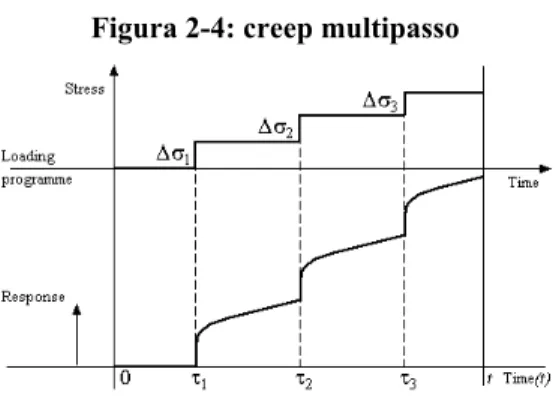
Il principio può essere illustrato mediante un esperimento di “creep multipasso” (Figura 2-4).

Figura 2-4: creep multipasso

Applicando al tempo t = 0 uno stress

σ

0,strain e stress sono legati dall’equazione:

0 ) ( ) ( σ ε t = tJ ⋅ (2.7)

Applicando un carico aggiuntivo al tempo t =τ1la deformazione totale sarà data da:

19 1 1 0 ( ) ) ( ) ( σ τ σ ε t = J t ⋅ +J t− ⋅ (2.8)

Al generico tempo t avremo ( ) ( _i)

i

i J t

t σ τ

ε =

∑

⋅ − . Il passaggio all’integrale, cioè all’applicazione di uno stress continuo, si ottiene per

(

τi+1−τi

)

→0:

ds ds s dJ s t t J t

∫

∞ ⋅ − + = 0 ) ( ) ( ) ( ) 0 ( ) ( σ σ ε (2.9) dove s = t - τi.

La situazione è analoga se si vuole valutare lo stress in funzione di una storia di deformazione continua: ds ds s dG s t t G t

∫

∞ ⋅ − + = 0 ) ( ) ( ) ( ) 0 ( ) ( γ γ σ (2.10)

2.6 Analisi dinamica in regime oscillatorio

Gli esperimenti di creep e stress relaxation sono metodi utili per misurare il comportamento a tempi lunghi di carico. I metodi dinamici in regime sinusoidale, unitamente all’uso del principio di sovrapposizione tempo-temperatura (vedi par. 2.9) permettono di estendere significativamente l’intervallo di caratterizzazione dei materiali. Le prove condotte ad una certa frequenza ω sono infatti qualitativamente equivalenti ai risultati ottenuti ad un tempo di prova t =1/ω [5]. La procedura sperimentale prevede l’applicazione di una deformazione tangenziale (shear strain) oscillatoria con una data pulsazione ω e la misura simultanea dello sforzo di taglio (shear stress), o viceversa. Le prove sono condotte con l’ausilio di un reometro rotazionale(1).

20 Supponiamo che al campione in esame sia applicata una deformazione di ampiezza

γ

₀(2) e andamento sinusoidale:

t) ( sin ) ( =

γ

₀ ⋅

ω

⋅

γ

t (2.11)

La velocità d’applicazione della deformazione (strain rate) è definita come:

t) cos( ) ( =

γ

=

ω

⋅

γ

₀⋅

ω

⋅

γ

dt d t & (2.12)

Se il materiale in studio presenta un comportamento viscoelastico lineare, risponderà alla sollecitazione con uno (shear) stress anch’esso sinusoidale, sfasato di un angolo δ, rispetto alla deformazione applicata, il cui valore dipende dalle caratteristiche del materiale:

t) cos( ' G' t) sin( G' ) ( t) cos( ) sin( t) sin( ) cos( ) ( ) t ( sin ) ( 0 0 0 0 0 ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ = + ⋅ ⋅ =

ω

γ

ω

γ

τ

ω

δ

τ

ω

δ

τ

τ

δ

ω

τ

τ

t t t (2.13) (2.14) (2.15) dove: cos( ) 0 0 _δ γ τ = ′ G sin( ) 0 0 _δ γ τ = ′′ G _(2.16)

Le quantità G’ e G’’ sono definite rispettivamente storage modulus e loss

modulus.

Le equazioni riportate mettono in evidenza che lo sforzo di taglio si può esprimere come la somma di un termine in fase con la deformazione ed un termine in quadratura (in fase quindi con la velocità di deformazione). Un solido elastico presenterà un angolo di fase nullo, mentre δ= π/2 caratterizza il comportamento viscoso; ovviamente se δ è prossimo a π/2 prevarrà il comportamento viscoso, mentre angoli vicini a 0° indicano caratteristiche elastiche prevalenti.

(2)

g e t sono i termini generalmente utilizzati per indicare rispettivamente deformazione e sforzo di taglio, in luogo di e e s che indicano le rispettive quantità elongazionali.

21

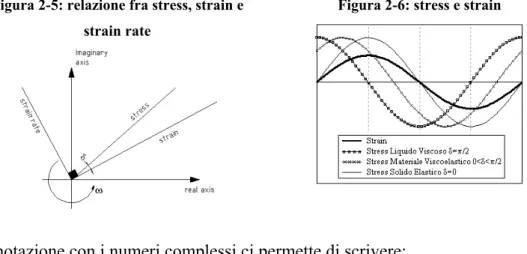
Figura 2-5: relazione fra stress, strain e strain rate

Figura 2-6: stress e strain

La notazione con i numeri complessi ci permette di scrivere:

t i eω

γ

ω

γ

*( )= ₀ ⋅ (2.17) ) t ( 0 ) ( * ω τ ω δ τ _{= ⋅e}i ⋅+ _(2.18) '' ' * * * 0 0 _ei _{=G =G+i⋅G} = δ γ τ γ τ (2.19)

Le misure dinamiche forniscono infatti il valore del modulo complesso G*(

ω

), definito come il rapporto fra lo stress e la deformazione totali subiti dal materiale ad una data frequenza:

) ( '' ) ( ' ) ( * ) ( ) ( _{ω ω ω} ω γ ω τ G i G G = + ⋅ = _(2.20) ) ( ' ω

G descrive la capacità del campione di immagazzinare energia elastica, mentre )G ''(ω è connesso alla capacità di dissiparla; i due termini non rappresentano la componente elastica e la componente viscosa del materiale ad una data frequenza, in quanto la maggior parte dei materiali presenta anche una risposta elastica ritardata, che dipende dal tempo, ma la deformazione conseguente è recuperabile.

In maniera analoga è definita una complex compliance:

) ( '' ) ( ' ) ( * ) ( ) ( _{ω ω ω} ω τ ω γ J i J J = − ⋅ = (2.21)

22 dove J’ e J’’ (storage e loss compliance) hanno lo stesso significato di G’ e G’’. Si fa notare che J* e G* sono uno il reciproco dell’altro, ma non vale la stessa cosa per i termini reali e immaginari delle due funzioni.

Il rapporto fra l’energia persa e quella immagazzinata in ogni oscillazione, definito loss tangent, fattore di perdita o damping, è dato dalla quantità:

) ( ' ) ( ) ( ' ) ( '' ω ω ω ω δ J J G G tg = = ′′ (2.22)

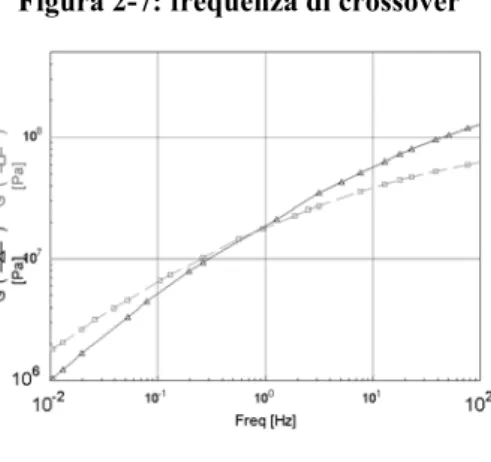
Il valore al quale G’(ω) e G’’(ω) si eguagliano, ossia quando tg è uguale a uno, δ

è definita frequenza di crossover (ωc). Questo valore rappresenta il punto in cui si

passa da un comportamento prevalentemente dissipativo ad un comportamento prevalentemente elastico, o viceversa.

Figura 2-7: frequenza di crossover

Un’ altra quantità indice del comportamento di un materiale è la viscosità

complessa, rapporto fra lo stress applicato e la strain rate; dalle relazioni nel

campo dei numeri complessi si ottiene:

( ) *( ) *( ) '( ) ''( ) ( ) G _i i τ ω ω η ω η ω η ω γ ω ω = = = − ⋅ &       = = ω ω η ω ω η ) ( ' '' ) ( '' ' G G (2.23)

La parte reale η’, definita viscosità dinamica, è un termine atto a descrivere gli

effetti dissipativi; è infatti il rapporto fra lo stress in fase con la strain rate e lo strain applicato.

23 Perω →0, corrispondente a tempi di carico elevati, la viscosità dinamica tende a coincidere con la steady flow viscosity η0, definita nei paragrafi precedenti.

2.7 Modelli meccanici del comportamento viscoelastico

Per schematizzare il comportamento dei materiali dal punto di vista macroscopico si fa riferimento a due ideali modelli meccanici di comportamento: la molla e il pistone idraulico; la prima modella una risposta puramente elastica, il secondo un comportamento puramente viscoso.

L’opportuna combinazione di questi due elementi da vita a modelli utili per la comprensione delle relazioni sforzo-deformazione dei materiali. I più noti sono quelli di Maxwell e di Voigt, ma proprio in virtù della loro semplicità costruttiva non sono adatti a modellizzare le risposte dei materiali reali.

Modello di Maxwell

Il modello di Maxwell è costituito da un elemento elastico ed un elemento viscoso in serie. Applicando una tensione σ0

fra i punti A e B si ottiene una deformazione somma dei contributi dei due elementi. A questo sistema è possibile applicare una deformazione istantaneaε₀, che permette di effettuare prove di stress relaxation; non può invece modellizzare una risposta elastica ritardata.

24

Modello di Voigt

Il modello di Voigt è costituito da un elemento elastico e uno viscoso in parallelo. Applicando una deformazione finita tra i punti A e B, la tensione si ripartisce fra i due elementi; non è adatto a modellizzare una prova di stress relaxation, in quanto non è possibile applicare una deformazione istantanea al sistema per la presenza dell’elemento viscoso. Per lo stesso motivo è adeguato a rappresentare la risposta

elastica ritardata e permette una buona modellizzazione del creep.

Se Gi=1/Ji è la rigidità della molla e ηi la viscosità del pistone, si definisce

i i Gi

λ η= il tempo di rilassamento di un elemento di Maxwell; λι è una misura

del tempo richiesto per il rilassamento della tensione. La stessa quantità, per un elemento di Voigt, è detta tempo di ritardo ed è una misura del tempo che occorre all’elemento elastico per tornare alla configurazione di equilibrio, ritardato dalla presenza dell’elemento viscoso in parallelo. Si ottiene così l’espressione delle funzioni viscoelastiche G(t), J(t), G’(ω), G’’(ω) per i due sistemi:

Maxwell Voigt a) J(t)=J_i +t/η g) J(t)=J_i ⋅

[

1−exp(−t/λ_i)

]

b) G(t)=G_i ⋅exp(−t/λ_i) h) G(t)=G_i c) _{2 2} 2 2 1 ) ( ' i i i G G λ ω λ ω ω + ⋅ = i) G'(

ω

)=G_i d) _{2 2} 1 ) ( '' i i i G G λ ω ωλ ω + ⋅ = _l) G ''(

ω

)=G_i⋅

ωλ

_i =

ωη

_i e) J'(ω)= J_i m) _{2 2} 1 ) ( ' i i J J

λ

ω

ω

+ = f) i i i J J ωη ωλ ω) 1 ( '' = = n) _{2 2} 1 ) ( '' i i i J J λ ω ωλ ω + = (2.24)

25 Come già accennato, queste funzioni sono molto semplici e quasi mai corrispondono all’effettiva risposta di un materiale ad una sollecitazione: infatti la

creep compliance nel modello di Voigt e lo stress relaxation modulus in quello di

Maxwell sono funzioni esponenziali del tempo, ma tale andamento non ha riscontri reali. Di conseguenza nasce la necessità di creare modelli meccanici in grado di simulare l’andamento reale delle relazioni sforzo/deformazione, basandosi sulla combinazione di questi elementi base. Il passo successivo è la definizione di funzioni matematiche in grado di descrivere il comportamento di sistemi eterogenei complessi dove abbiamo distribuzioni praticamente continue dei tempi di ritardo e di rilassamento [5].

2.8 Spettri di ritardo e di rilassamento

Gli elementi di Maxwell e Voigt possono essere combinati per ottenere modelli più complessi di comportamento. Ponendo più elementi di Maxwell in serie i singoli elementi si sommano linearmente:

∑

= Ji

J 1/η=

∑

(1/ηi) (2.25 a,b) vale lo stesso ragionamento per più elementi di Voigt in parallelo:

∑

= G_i

G η=

∑

η_i (2.26 a,b) Entrambi questi modelli comunque non aggiungono niente alle caratteristiche del singolo elemento, modificando solo il valore dei singoli parametri. Se invece si pongono più elementi di Maxwell in parallelo e più elementi di Voigt in serie si ottengono sistemi più complessi.

26

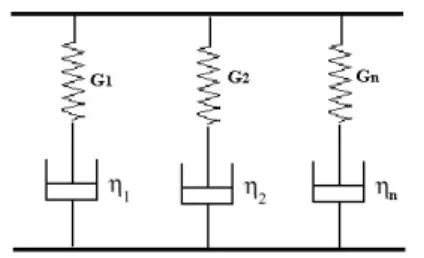
Figura 2-9: elementi di Maxwell in parallelo

Un gruppo di elementi di Maxwell in parallelo rappresenta uno spettro discreto di tempi di rilassamento; in questa disposizione degli elementi le forze applicate sono additive, e l’espressione della funzione G(t) diventa:

1 ( ) _e n _i exp( / )_i i G t G G t λ → = +

∑

⋅ − (2.27)

Analogamente, più elementi di Voigt in serie rappresentano uno spettro discreto di tempi di ritardo; in questo caso sono le deformazioni ad essere additive, e quindi per il modello di Voigt si ottiene:

[

]

0 1 ( ) n _i 1 exp( / )_i / i J t J t λ t η → =

∑

⋅ − − + (2.28)

Se il numero di elementi di Maxwell tende all’infinito si ottiene uno spettro continuo H(λ) definito spettro di rilassamento. In uno spettro continuo il contributo infinitesimo Hdλ al modulo di rilassamento è dato dai λ_i nell’intervallo ( ,λ λ_{i i}+dλ_i). In pratica H(λ) indica la percentuale di elementi che hanno un tempo caratteristico nell’intervallo considerato. Dato l’ampio intervallo di frequenze (di tempi) sul quale sono studiate le proprietà meccaniche, spesso si utilizza una scala logaritmica, considerando quindi gli intervalli ( ln ,lnλ_i λ_i+dlnλ_i), da cui abbiamo le espressioni:

0

( ) _e exp( / ) ln

G t G H t λ d λ

∞

27

( )

( )

2 2 0 ( ) 1 e d G ω G H ωλ λ λ ωλ +∞ ′ = + ⋅ +

∫

(2.30)

( )

2 0 ( ) 1 d G ω H ωλ λ λ ωλ +∞ ′′ = ⋅ +

∫

(2.31)

Con riferimento alle proprietà dinamiche, discretizzando H(λ) con l’ausilio di un numero finito N di elementi di Maxwell, si ottiene:

( )

( )

∑

= + + = N i i i i e g G G 1 2 2 1 ) ( ' ωλ ωλ ω (2.32)

( )

∑

= + = N i _i i i g G 1 1 2 ) ( '' ωλ ωλ ω _(2.33)

Il calcolo dei gi e λi e’ un problema matematico fortemente mal condizionato per

la soluzione dei quali sono disponibili dei software, come per esempio IRIS (Interactive Rheological Software) sviluppato da Baumgärtel e Winter e RSI Orchestrator distribuito dalla Rheometric Scientific.

La procedura per ottenere G’(ω) e G’’(ω) si ripete esattamente per J’(ω) e J’’(ω) considerando un numero infinito di elementi di Voigt in serie dai quali si ottiene lo spettro continuo dei tempi di ritardo L(λ).

2.9 Principio di equivalenza tempo-temperatura

Le proprietà viscoelastiche, specialmente a temperature superiori a quella di transizione vetrosa del materiale, sono fortemente dipendenti dalla temperatura, ed anche in presenza di un comportamento lineare occorre valutare le proprietà meccaniche alle diverse temperature nel range di interesse.

Per alcuni materiali, definiti “termoreologicamente semplici”, è stata provata la validità del principio di sovrapposizione tempo-temperatura o metodo delle

28 meccanica (G’, G’’, tan δ….. ) ottenuta ad una certa frequenza e variando la temperatura, si può ottenere variando la frequenza e tenendo fissa la temperatura.

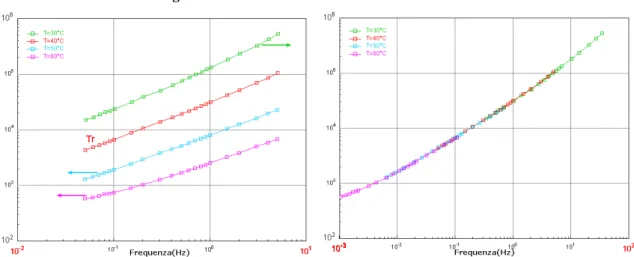
Conseguenza immediata di tale principio è la possibile visualizzazione su una singola curva del comportamento viscoelastico del materiale in un range di frequenze assai più ampio di quello accessibile all’apparecchiatura sperimentale, semplificando notevolmente la visualizzazione degli effetti della temperatura sulle proprietà meccaniche. Il metodo afferma che una qualsiasi funzione viscoelastica, ad esempio G’(ω), nel passare da T a Tr segue l’equazione:

) ( ' ) ( ' T b G T G _r = _T con ρ ρ ⋅ ⋅ = T T b r r T (2.34)

allo stesso modo, prendendo una frequenza di riferimento ω si ottiene:

) ( )

(T_r a_T ω T

ϖ = ⋅ (2.35)

doveϖ è definita frequenza ridotta.

In pratica, se G’(ω,T) è riscalato secondo le equazioni sopra riportate, i dati sperimentali cadono tutti sulla stessa curva (master curve) ottenuta alla temperatura di riferimento Tr. Sperimentalmente la quantità aT (shift factor) è

ottenuta dalla traslazione orizzontale necessaria per sovrapporre i dati ottenuti a qualunque T sulla curva dei dati ottenuti a Tr, mentre bT è legato allo shift

verticale.

La validità del principio implica che gli shift factor siano gli stessi per tutte le proprietà viscoelastiche, quindi è sufficiente costruire la master curve con una delle funzioni per ottenere la curva di tutte le altre. Contemporaneamente alla costruzione della master curve, spesso si riporta in grafico l’andamento degli aT in

29

Figura 2-10: costruzione della master curve

L’andamento con la temperatura dei fattori di shift è generalmente interpolata tramite due equazioni, la Williams-Landel-Ferry (WLF) e l’equazione di Arrhenius. Nel caso di materiali polimerici, la WLF generalmente fornisce un buon “fitting” dei fattori di shift in un intervallo di temperatura compreso fra la temperatura di transizione vetrosa Tg e Tg + 200K:

( )

( )

C T Tr Tr T C T a T a r + − − ⋅ − =       2 ) ( 1 log (2.36)

dove T [°C] è la T selezionata, Tr [°C] la T di riferimento, C1 e C2 sono costanti. La funzione di Arrhenius, generalmente impiegata sotto la temperatura di transizione vetrosa si esprime come:

      − ⋅ = Tr T R E T a_{( )} a 1 1 log (2.37)

Ea è l’energia di attivazione, R la costante reale dei gas.

Il fattore b_T dovrebbe essere correlato alla variazione di densità del materiale con la temperatura; in realtà il termine ha scarsa validità teorica e in letteratura non sono impiegate equazioni che ne interpolano l’andamento, in quanto è influenzato anche dalla storia termica del materiale.

30 Le basi del metodo si fondano sulla teoria molecolare proposta da P.E. Rouse (J.Chem.Phys..1953), illustrata attraverso lo studio del moto di una sistema costituito da masse collegate a catene flessibili polimeriche, nel quale le masse subiscono gli effetti delle forze viscose [6].

2.10 Teoria non lineare dei materiali viscoelastici

E’ importante far notare come finora sia stata utilizzata la teoria della linearità viscoelastica. Questa teoria è però valida solo quando le deformazioni imposte al materiale sono molto piccole o molto lente. Per deformazioni più grandi o più rapide, la teoria lineare non è più valida e la risposta a una deformazione imposta dipende da:

• L’entità della deformazione • La velocità della deformazione • La cinematica della deformazione

Questo significa che non è possibile misurare una risposta ad un tipo di deformazione e usare il risultato per prevedere la risposta a quel tipo di deformazione a meno che sia la velocità che la grandezza della deformazione siano le stesse in entrambi i casi. Per esempio il relaxation modulus misurato per una certa grandezza di shear strain non è lo stesso per una diversa grandezza di shear strain.

Per spiegare i modelli per i comportamenti viscoelastici non lineari bisogna partire dall’analisi delle varie caratteristiche del principio di sovrapposizione di Boltzmann, citato nel paragrafo 2.5, analizzando come queste debbano essere modificate per formulare un modello empirico per la non linearità viscoelastica [6].

Possiamo sviluppare il principio di sovrapposizione di Boltzmann in questa forma:

( )

_∫

(

) ( )

∞ − − = t _ij ij t G t t' γ t' dt τ & (2.38)

31 Ci sono tre caratteristiche principali di questa descrizione del comportamento reologico. La prima è l’uso del tensore di deformazione infinitesimale

γ

ij. La

misura della deformazione non è valida per grandi deformazioni. La seconda, il

relaxation modulus, G(s), è indipendente dalla deformazione: non ci aspettiamo

che ciò sia vero per grandi e rapide deformazioni. Infine l’effetto della storia della deformazione è stato tenuto in conto tramite l’uso di un singolo integrale, e non c’è ragione di credere che una procedura così semplice possa essere adeguata a descrivere la risposta di un materiale a grandi e rapide deformazioni.

Per prima cosa esaminiamo le conseguenze della sostituzione del tensore di deformazione infinitesimale γij nel principio di sovrapposizione di Boltzmann con

un valore finito di deformazione. Il risultato è chiamato modello di viscoelasticità

lineare finita o viscoelasticità quasi lineare: è una procedura empirica, ma porta

ad utili risultati. Due valori di deformazione che sono stati ritenuti utili nella reologia dei polimeri sono il tensore di Cauchy Cij(t1,t2) e il tensore di Finger

Bij(t1,t2) dove t1 è il tempo in cui l’elemento materiale è nella sua configurazione

di riferimento, e t2 è il tempo in cui la deformazione è valutata, relativa alla

configurazione al tempo t1. E’ sufficiente conoscere le componenti di questi 2

tensori per i 2 tipi di deformazione più utilizzati nelle misure reologiche: taglio semplice e allungamento semplice.

Per taglio semplice i tensori sono:

Cij (t1,t2) =           − + − − 1 0 0 0 )] ( ) ( [ 1 ) ( ) ( 0 ) ( ) ( 1 2 1 2 1 2 1 2 t t t t t t γ γ γ γ γ γ (2.39) Bij (t1,t2) =           − − − + 1 0 0 0 1 ) ( ) ( 0 ) ( ) ( )] ( ) ( [ 1 2 1 2 1 2 2 1 t t t t t t γ γ γ γ γ γ (2.40)

32 Per estensione semplice i tensori sono:

A volte è conveniente usare il tensore di Cauchy della deformazione e il tensore

di Finger della deformazione, definiti come:

dove δij è il delta di Kronecker definito cosi:

Noi vogliamo conoscere come lo sforzo al tempo t, τij(t), dipenda dalle

deformazioni avvenute a tempi precedenti, t’, dove t’ ≤ t. Il tensore di Finger, valutato al tempo t’ è allora Bij (t,t’).

Un tensore cartesiano del secondo ordine ha 3 invarianti scalari. Per la nostra trattazione saranno utilizzati gli invarianti scalari del tensore di Finger. Per una data deformazione, possono essere calcolati come segue:

Cij (t1,t2) =

[

]

[ ] [ ]

_



















− − − − − ) ( ) ( ) ( ) ( ) ( ( 2 1 2 1 2 1 ) 2

0

0

0

0

0

0

t t t t t t

e

e

e

ε ε ε ε ε ε (2.41) Bij (t1,t2) =

[

]

[ ] [ ]

_



















− − − − − ) ( ) ( ) ( ) ( ) ( ( 2 2 1 2 1 2 ) 1

0

0

0

0

0

0

t t t t t t

e

e

e

ε ε ε ε ε ε (2.42)

Cauchy strain tensor ≡ Cij - δij (2.43)

Finger strain tensor ≡ Bij - δij (2.44)

δij=1 (i=j) (2.45a)

δij=0 (i≠j) (2.45b)

I1(Bij)=B11+B22+B33 (2.46a)

I2(Bij)=C11+C22+C33 (2.46b)

33 Dal momento che Bij è una funzione dei due tempi t e t’, gli invarianti scalari

dipendono anch’essi da queste due quantità.

Il tensore di Cauchy, quello di Finger o una combinazione dei due possono essere usati per formulare una teoria di viscoelasticità lineare finita.

Osservazioni sperimentali hanno mostrato che se si utilizza un solo tensore, il tensore di Finger dà le migliori indicazioni sul comportamento, quantomeno per deformazioni appena al di sopra della regione di viscoelasticità lineare.

Se si usa il tensore di Finger per generalizzare il principio di sovrapposizione di Boltzmann e quindi formulare una teoria di viscoelasticità non lineare, il risultato è il seguente:

Lodge chiamò questa equazione il modello rubberlike liquid e ha riportato le previsioni del modello per molti tipi di deformazioni.

La relazione tra la memory function e il relaxation modulus del rubberlike liquid può essere trovata usando l’equazione 2.47 per calcolare lo shear stress risultante da uno shear strain step di grandezza γ, imposto su un rubberlike liquid al tempo t=0.

Lo shear stress è dato allora da:

Lo shear strain per t’>0 è zero, poiché non avvengono deformazioni tra i tempi t’ e t. Allora :

oppure, usando la definizione di relaxation modulus:

( )

_∫

( )

∞ − − = t _ij ij t m(t t')B t,t' dt'

τ

(2.47)

( )

_∫

[

( ) ( )

]

∞ − − − = t m t t t t dt t ( ')

γ

γ

' '

σ

(2.48)

( )

=

_∫

∞ − t dt t t m t

γ

( ') '

σ

(2.49)

( )

=

( )

=∞

_∫

− t dt t t m t t G ( ') '

γ

σ

(2.50)

34 oppure, ponendo s = t-t’

Da notare che il relaxation modulus del rubberlike liquid è indipendente dallo strain.

Il rubberlike liquid non è un soddisfacente modello del comportamento viscoelastico non lineare ma è importante perché prevede le principali caratteristiche delle prime deviazioni dal comportamento lineare.

C’è un modello continuo che si è dimostrato molto importante nello sviluppo delle idee più recenti nel campo della viscoelasticità non lineare.

È l’equazione BZK proposta da Bernstein, Kearsley e Zapas. Hanno proposto la seguente forma di equazione costitutiva di un materiale viscoelastico:

dove u è una funzione dipendente dal tempo dell’energia elastica potenziale:

Questa funzione deve essere determinata sperimentalmente, tramite lo studio di grandi e rapide deformazioni.

Un caso speciale della equazione BZK si ottiene introducendo nella BZK una funzione potenziale indipendente dal tempo come :

questo porta al modello BZK fattorizzabile:

( )

=

_∫

∞ t ds s m t G ( ) (2.51)

( )

, ' 2

( )

, ' ' 2 1 1 dt t t B I u t t C I u t ij ij ij

∫

∞ −       ∂ ∂ − ∂ ∂ =

τ

(2.52)

(

I₁,I₂,t t'

)

u u = − (2.53)

(

I1,I2,t t'

)

m

(

t t'

) (

U I1,I2

)

u − = − (2.54)

(

'

)

2

( )

, ' 2

( )

, ' ' 1 1 dt t t B I U t t C I U t t m t ij ij ij

∫

∞ −       ∂ ∂ − ∂ ∂ − =

τ

(2.55)

35 La funzione potenziale deve ancora essere determinata tramite esperimenti.

Da notare come il modello rubberlike liquid di Lodge possa essere visto come un caso speciale di quella sopra.

Molti modelli continui sono stati formulati modificando il rubberlike liquid per migliorare la sua capacità di fitting di dati di risposta non lineari.

L’approccio che si è rivelato più utile prevede di far dipendere la memory function sia dal tempo che dallo strain.

Allora la memory function è assunta come:

e l’equazione costitutiva è:

Paragonandola con la 2.52 si vede che questa è uno speciale caso del modello BZK in cui il termine comprendente il tensore di Cauchy è stato omesso. Ciò semplifica molto l’uso della BZK ma la consistenza termodinamica costruita nella BZK è persa.

E’ stato notato molti anni fa che i dati di stress relaxation possono spesso essere descritti da un relaxation modulus che è il prodotto di un termine dipendente dal tempo e un termine dipendente dalla deformazione. Wagner propose la seguente formula:

dove h

(

I₁, I₂

)

è chiamata damping function [6].

In questo caso la memory function è detta separabile o fattorizzabile, e l’equazione costitutiva diventa:

( )

( )

[

t

t

I

B

ij

I

B

ij

]

M

M

=

−

'

,

₁

(

),

₂ (2.56)

( )

t

M

[

( )

t

t

'

,

I

₁

(

B

_ij

),

I

₂

( )

B

_ij

]

B

_ij

( )

t

,

t

'

dt

'

t ij

=

∫

−

∞ −

τ

(2.57)

( )

[

t t',I1,I2

]

m

( ) (

t t'hI1,I2

)

M − = − (2.58)

( )

t

m

( ) (

t

t

'

h

I

₁

I

₂

) ( )

B

_ij

t

,

t

'

dt

'

t ij

=

∫

−

−

∞ −

τ

(2.59)

36 Paragonandola con la 2.55 si vede che questa è la BZK fattorizzabile con il termine Cij omesso e la chiamiamo equazione di Wagner. Dal momento che la memory function è indipendente dallo strain, è la stessa memory function determinata in esperimenti di piccoli strain.

L’equazione di Wagner non è una equazione costitutiva completa dal momento che contiene la funzione sconosciuta h

(

I₁, I₂

)

che deve essere determinata per ciascun polimero.

Per uno shear strain di grandezza γ, se la memory function è separabile, lo shear stress è dato da:

Dall’equazione 2.60 il non linear relaxation modulus è

dove G(t) è il linear relaxation modulus.

Quindi la separabilità della memory function implica la separabilità del relaxation

modulus. Ogni equazione costitutiva che prevede un relaxation modulus non

lineare separabile fornisce una previsione della funzione h(γ).

Sono stati proposti vari modelli per il fitting della damping function, ne riportiamo alcuni:

( )

t

γ

h

( ) ( )

γ

G

t

σ

=

(2.60)

( ) ( ) ( )

t

h

G

t

G

,

γ

=

γ

(2.61) Wagner h

( )

γ

=e(−nγ) (2.62a) Osaki

h

( )

γ

=

ae

(−n1γ)

+

(

1

−

a

)

e

(−n2γ) _(2.62b) Zapas

( )

₁ 2 1 γ γ a h + = (2.62c)

Soskey and Winter h

( )

γ =_1+aγb

1

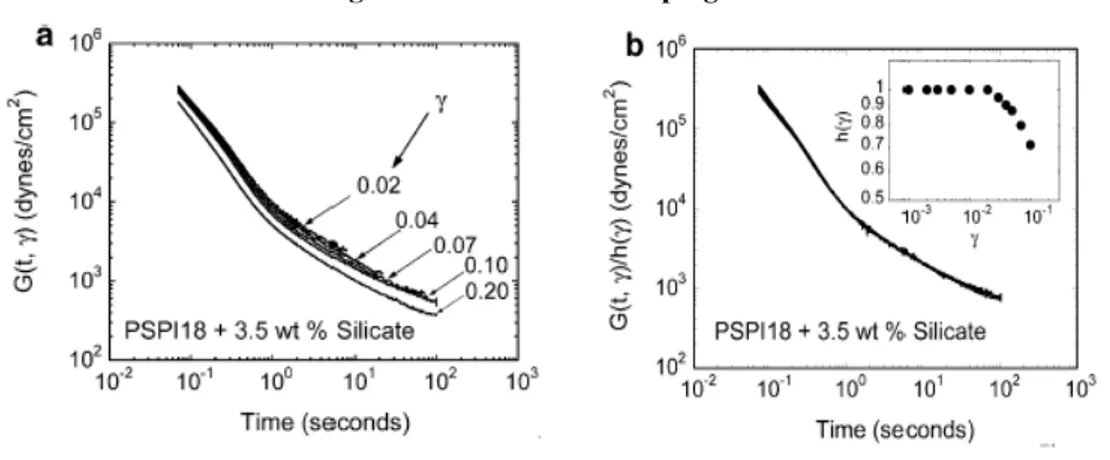
37 Nelle Figure 2-11a e 2-11b è riportato un esempio dell’uso della damping function [7].

Figura 2-11 Uso della damping function

2.11 Viscometria

La valutazione delle proprietà viscoelastiche è uno dei due principali campi di studio della reologia; l’altro argomento di notevole interesse è la determinazione della viscosità del campione in esame, in condizioni di moto di scorrimento. In questa condizione il fluido si può immaginare come un sistema omogeneo costituito da strati di spessore infinitesimo, paralleli e sovrapposti (flusso laminare): la viscosità può essere misurata in funzione della forza necessaria per mantenere una differenza di velocità tra due strati adiacenti. Il fluido è contenuto tra due piani paralleli a distanza h, di cui uno fisso e l'altro che scorre a velocità v. La misura della viscosità deve essere sempre effettuata a flusso laminare, con velocità tanto più limitata, quanto minore è la viscosità da determinare. Nel moto turbolento, oltre una certa velocità critica, si possono generare vortici che provocano uno sbalzo improvviso nella resistenza allo scorrimento.

La viscosità, è una funzione dipendente da cinque parametri: • Struttura chimica

• Temperatura • Pressione • Storia reologica

38 La viscosità ha le dimensioni di una pressione per un tempo e l’unità di misura più usata nel sistema MKS Pascal·secondo [Pa·s], ma è tutt’ora molto impiegata anche il centipoise [cP].

La natura chimica e la temperatura sono parametri che influenzano sempre e in maniera determinante il valore della viscosità.

La pressione è un parametro la cui influenza sui liquidi diventa determinante soltanto quando raggiunge valori molto elevati; per i gas ed i vapori la dipendenza è più marcata, ma le misure di viscometria non riguardano i gas e generalmente sono condotte a pressione atmosferica.

La storia reologica, cioè le condizioni di sollecitazione al quale è stato sottoposto il campione prima della misura, è importante per alcuni fluidi quali le emulsioni o le sospensioni, la cui composizione può cambiare nel tempo.

Infine, prove condotte in condizioni isoterme possono essere influenzate dal

gradiente della velocità di scorrimento γ_{& se il materiale presenta un}

comportamento non-Newtoniano:

Fluido newtoniano: η =costante Fluido non newtoniano: η =η(γ_&)

Per i fluidi non-Newtoniani la possibilità di valutare la viscosità del campione in esame dipende dalla cinematica del sistema di misura.

Secondo la distribuzione della cinematica possiamo avere:

• flusso viscometrico uniforme • flusso viscometrico non uniforme • flusso non viscometrico non uniforme

Se nel reometro si ha una cinematica uniforme, ossia γ& è la stessa dappertutto, le misure forniscono direttamente la viscosità al fissato valore di shear rate.

Se la cinematica non è uniforme si cerca di ottenere un flusso viscometrico, dove cioè la shear rate sia costante lungo la traiettoria della particella di fluido.

39 Nel caso di flusso non viscometrico non uniforme, la γ_{& varia in tutto il campo di} moto. I reometri con un flusso di questo tipo sono utilizzabili solo per fluidi Newtoniani.

Il tipo di cinematica del sistema di misura permette di suddividere i reometri in

non rotazionali e rotazionali.

Nel primo caso si hanno traiettorie aperte e quindi il flusso non è mai a regime; la mancanza degli effetti centrifughi permette di raggiungere elevate shear rate; questi tipi di reometri (a capillare, magnetici, a caduta di sfera…) sono adatti, per esempio, a determinare la viscosità di fluidi che devono essere vaporizzati e quindi sottoposti ad elevatissimi gradienti di velocità.

Nel secondo caso si hanno invece traiettorie chiuse e quindi in teoria si possono sempre raggiungere condizioni stazionarie; per contro occorre fare attenzione agli effetti inerziali della rotazione, cioè le forze centrifughe, e agli effetti di bordo, che limitano necessariamente la valutazione della viscosità a basse shear rate (<100 1/s).

Il reometro può essere equipaggiato con geometrie diverse: per fluidi che presentano una certa consistenza anche a temperature medio alte, quali i bitumi, le più utilizzate sono il piatto-cono ed il piatto-piatto, dei quali è fornita nel seguito una breve descrizione della cinematica di flusso.

Una descrizione dettagliata delle procedure sperimentali per la misura delle proprietà viscose e viscoelastiche, delle geometrie utilizzate e delle problematiche connesse a ciascuna di esse sono riportate nel quarto capitolo.

Geometria piatto-cono

La geometria piatto e cono (Figura 2-12) è una delle più utilizzate per gli studi di viscosità. E’ costituita da un piatto circolare e da un cono con conicità estremamente piccola (1°- 4°max); il campione è posto fra le due superfici, poste in rotazione l’una rispetto all’altra. In genere il piatto superiore è posto in movimento mentre quello inferiore è fermo. Le superfici di scorrimento sono

40 superfici coniche di apertura variabile dalla superficie piana a contatto con il piatto inferiore a quella in contatto con il cono.

Figura 2-12: piatto e cono

Per ogni valore del raggio r la velocità di scorrimento è data dal rapporto fra la velocità del cono in movimento e la distanza fra i due piatti; la conicità estremamente bassa permette l’approssimazione:

θ θ θ ≅ sin ≅

tg (2.63)

Chiamando Ω la velocità angolare, è possibile scrivere:

θ θ θ γ =Ω ⋅ ⋅ Ω ≅ ⋅ ⋅ Ω = = r r tg r r h v & (2.64)

Questa equazione permette di affermare che la shear rate è praticamente costante in tutto il campione. Questa considerazione è particolarmente importante perché implica che con il ricorso alla geometria piatto-cono è possibile valutare la viscosità di fluidi non-Newtoniani, il cui valore dipende cioè dalla shear rate. Anche lo sforzo tangenziale sarà costante in tutto il campo di moto; la coppia M agente sul piatto si può scrivere come:

3 2 (2 ) 3 R M =

_∫

r⋅ ⋅τ πrdr = π ⋅τ (2.65) Sostituendo a τ l’espressione: θ η γ η τ = ⋅_&= ⋅Ω (2.66)

si ottiene l’equazione del reometro piatto-cono:

Ω ⋅ = η θ π 3 2 _R3 M (2.67)

41 Occorre notare che per un dato valore della coppia di torsione lo stress aumenta con 1/r3; questo costituisce un vantaggio nelle prove con materiali di bassa viscosità: per tali materiali occorre applicare stress bassi per mantenere basse shear rate e la sensibilità dello strumento può essere determinante; in tal caso un raddoppio del raggio del cono porta ad aumentare di ben otto volte il valore dello stress misurabile.

All’aumentare della shear rate il flusso di scorrimento diventa irregolare, specialmente per materiali che presentano un’elevata componente elastica. L’uso di questa geometria è limitato quindi sempre a basse velocità di scorrimento, alle quali gli effetti della forza centrifuga sono trascurabili. Di conseguenza nell’equazione del moto il termine inerziale può essere trascurato.

Geometria piatto piatto

Questa geometria non permette la misura diretta della viscosità per materiali non newtoniani poiché la velocità di scorrimento non è la stessa lungo tutte le superfici di flusso; infatti la distanza h fra i due piatti è costante e l’equazione della shear rate diventa:

h r h v Ω⋅ = =

γ& γ& =γ&(r) (2.68)

Di conseguenza per un fluido non-Newtoniano la viscosità varia dal centro alla superficie esterna del campione. E’ comunque possibile stimare con alcune tecniche di calcolo l’andamento della viscosità non lineare; inoltre, per piatti sufficientemente piccoli, l’approssimazione effettuata utilizzando tale geometria può essere considerata accettabile.