Capitolo 2 DUPLICATORE DI TENSIONE

33

Capitolo 2

DUPLICATORE DI TENSIONE

Il ruolo del duplicatore è quello di trasformare una tensione alternata in una tensione continua di ampiezza doppia. Generalmente nei sistemi RFID lo troviamo in cascata alla rete di adattamento e permette al tag di disporre di una tensione continua maggiore rispetto a quella prodotta da un semplice raddrizzatore a doppia semionda.

Per un sistema RFID che utilizza una procedura SEQ è importante che nella fase in cui avviene il trasferimento di energia da reader a tag, il sistema rete di adattamento + duplicatore sia opportunamente dimensionato, in modo da permettere alla capacità C utilizzata come batteria, di caricarsi alla tensione voluta nel tempo a disposizione per questa operazione. Occorre quindi un’analisi temporale per capire quali sono i componenti che maggiormente influenzano la carica della capacità e procedere quindi all’ottimizzazione di tale processo.

In questo capitolo viene fatta una breve introduzione al duplicatore, introdotti alcuni concetti utili (circuito equivalente del diodo, funzione di Bessel modificata), per poi passare a calcolare l’espressione analitica, funzione dei parametri circuitali e del tempo, della tensione ai capi della capacità C posta in uscita. Vengono analizzati tre schemi circuitali di complessità crescente: il primo prevede l’analisi di un duplicatore con generatore di tensione ideale posto ingresso, nel secondo viene studiato l’effetto di una resistenza R posta tra il duplicatore e il generatore di tensione, l’ultimo caso prevede l’inserimento di un’induttanza L in serie ad R, in modo che si venga a creare un circuito risonante serie RLC in ingresso al duplicatore e si possa ottenere una tensione d’uscita superiore rispetto ai casi precedenti.

34

2.1 Introduzione

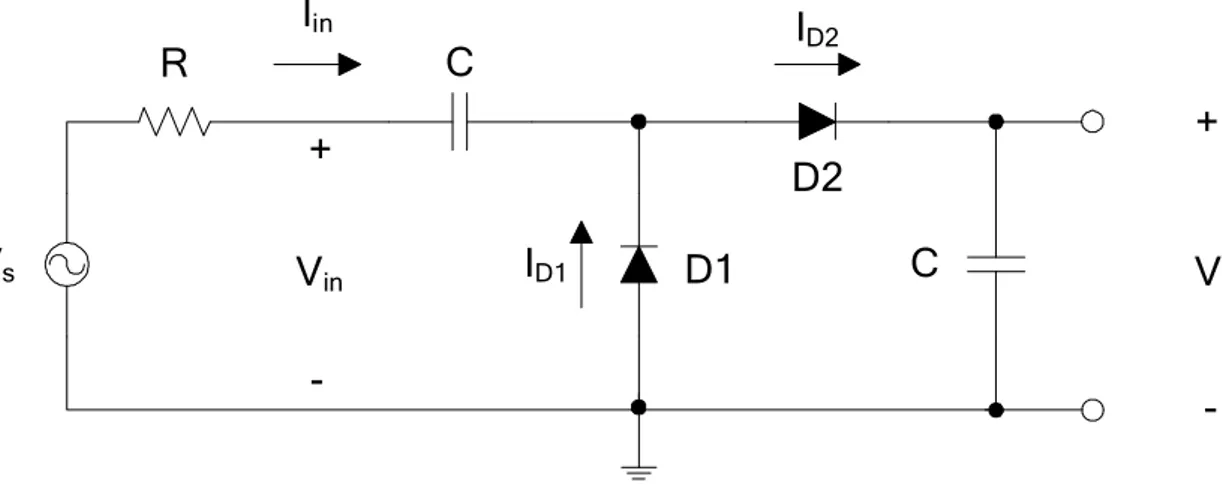
Lo schema di base di un duplicatore di tensione (figura 2.1) è composto da due diodi e due capacita C dello stesso valore. Utilizzando il circuito nella banda UHF, se il valore di C è sufficientemente elevato, è possibile ipotizzare le costanti di tempo del circuito grandi rispetto al periodo del segnale d’alimentazione. Sotto questa ipotesi è possibile considerare le capacità come delle batterie a tensione costante rispetto al segnale in ingresso.

+ -V C C D1 D2 ID2 ID1 + - V/2 + -Vin + -VD1 + VD2

-Figura 2.1 Schema del duplicatore di tensione

Se in ingresso mettiamo un segnale sinusoidale:

0cos( )

in

V =V wt (2.1)

ci possiamo attendere un’uscita a regime:

(

0

)

2

V = V -V_g (2.2)

A regime il circuito può essere visto come un traslatore di livello con in serie un rivelatore di picco: con le ipotesi precedenti le tensioni sulle capacità C sono pressoché costanti rispetto all’ingresso e valgono V e V/2.

35

Mediante simulazione del circuito è possibile vedere che durante tutto il transitorio, le tensioni sui condensatori sono ancora nello stesso rapporto ed è possibile indicarle come V(t) e V(t)/2.

Alle alte frequenze è possibile ipotizzare le due capacità C come dei corto circuiti e quindi i diodi D1 e D2 vengono a trovarsi in parallelo tra loro e con la

sorgente in ingresso; rispetto alla componente continua invece i due diodi vengono a trovarsi in serie e la tensione ai loro capi è uguale e pari a metà della tensione d’uscita [15]. Fatte queste premesse è possibile scrivere le seguenti espressioni:

( )

( )

( )

( )

( )

( )

1 0 2 0 cos 2 cos 2 D D V t V t V t V t V t V t w w = - -= + -(2.3)

In generale V(t) è funzione del tempo, ma essendo lentamente variabile rispetto al segnale d’ingresso, è possibile considerarla costante, quindi d’ora in poi verrà indicata con V.

2.1.1 Circuito equivalente del diodo

Il circuito equivalente di un diodo (figura 2.2) può essere schematizzato come un diodo ideale con in parallelo la capacità della giunzione CD, che risulta essere

funzione del punto di lavoro e la resistenza serie RS, che risulta essere una

resistenza parassita funzione del processo costruttivo.

36

RS gioca un ruolo importante, in quanto avendo a che fare con tensioni di

ampiezza molto piccola occorre minimizzare le cadute di tensione su elementi parassiti che limitano la corrente che attraversa la giunzione. Nel diodo integrato che viene utilizzato nei seguenti circuiti RS = 0 Ω, questo comporta che tutta la

tensione ai capi del diodo reale la rimoviamo ai capi del diodo ideale e della capacità CD.

Più avanti sarà possibile vedere come 2CD risulta essere la capacità

equivalente che si vede dall’ingresso del duplicatore, quindi la scelta del diodo influenza la realizzazione della rete di adattamento e le prestazioni del duplicatore durante il transitorio.

Per valutare CD occorre conoscere il punto di riposo del diodo ed in

particolare la tensione VD ai capi del diodo ideale, oltre ad altri parametri

ricavabili dal modello del dispositivo in uso:

(

)

(

)

0 1 0 1 1 1 1 j D m D D m _D j D C A V FC V V V C V C A FC FC m m V FC V V g g g g -ì < × ï æ ö ï -_{ç ÷} ï = èí ø ï _{é ù} ï _{- ê - + + ú > ×} ï _{êë úû} î (2.4)

Nell’espressione per il calcolo di CD compaiono i seguenti termini:

§ CJ0: capacità della giunzione p-n senza polarizzazione

§ A: area della giunzione

§ m: gradiente della giunzione p-n

§ FC: coefficiente della capacità di svuotamento in polarizzazione diretta § Vγ: potenziale della giunzione p-n

Dall’ espressione (2.3) vediamo che la tensione ai capi del diodo varia nel tempo tra -V0-V/2 e V0-V/2, quindi anche la capacità CD modifica il suo valore

nel transitorio: in realtà vedremo che tale valore non ha forti oscillazioni, ma tali variazioni creano non pochi problemi nel dimensionamento della rete di

37

adattamento. Per semplificare la trattazione è conveniente calcolate una CD

mediata tra tutti i punti di lavoro che il diodo assume nel tempo, in particolare nel nostro caso: 0 0 2 0 2 1 ( ) 2 V V D _V D D D V C C V dV V -=

_ò

(2.5) Sviluppando l’integrale: 0 2 1 _{0 0} 1 (1 ) 1 2 _{0 (1 )} 0 ₂ 1 V V CFV C_J A C_J A _V C_D dV CF m m dV m m V _{V CFV CF} V V V V g g g g é ù ê ú -ê ú é ù ê ú = _{ê ò} + _{ò ê} - + + _{ú ú}= + ë û -æ ö ê_{- - ç} ú ÷ -ê ú ç ÷ ê _{è ø} ú ë û

(

)

1 0 ₁ 0 2 ₀ 1 2 0 2 m m _V C_J A _{V V} V CF V V V V m CFV V _{V V} g _g g g _{g g} g ì é _{æ ö} ùü ï ê _{æ - ö ç - ÷} úï ï _ê æ ö _úï = _í - _{ç ÷} - - - -_{ç ÷ç ÷ ý}+ ê ú - _è - _{ø è øç ÷} ï _{ê ç- - - ÷ ú}ï è ø ï _{êë úû}ï î þ

(

)

(

)

(

)

2 ₂ 1 0 _{1 (1 )} 0 0 1 2 _{0 1} 2 2 2 C_J A _{V m V} CF m V CFV V CFV m V _CF g V_g g ì é æ öùü ï _ê æ ö _çæ ö _÷úï + í _{+ ê} - + _èç - - _ø÷+ _çèç - ÷_ø - _÷úý ï - _{ë è øû}ï î þ (2.6)

Nota la tensione applicata in ingresso al duplicatore e la tensione in uscita è possibile dare una prima stima del valore della capacità CD ai capi del diodo.

Il diodo utilizzato in questo capitolo è di tipo integrato con lunghezza di canale 0.35 μm che presenta una resistenza parassita RS trascurabile e parametri,

quali la corrente di saturazione inversa IS e la capacità CJ0 della giunzione p-n,

proporzionali all’area occupata. Tale diodo presenta una tensione Vγ = 0.69 V, valore che può risultare troppo elevato per applicazioni in cui la tensione in ingresso al duplicatore è dell’ordine di qualche centinaio di mV, ma che risulta accettabile in questa prima fase di analisi delle configurazioni circuitali.

38

Nell’ipotesi che il diodo occupi un’area A = 100 pm2:

S 2 0 I 2 100 _j 93 fA A pm C fF = ìï = _{Þ í} = ïî

Riportiamo per completezza l’intera model del diodo utilizzato nelle simulazioni:

***************** SIMULATION PARAMETERS ***************** * --- * format : PSPICE * model : DIODE * process : CS[ADFI] * revision : 2;

* extracted : CSA C61417; 2000-12; ese(5487) * doc# : 9933016 REV_2

* --- * TYPICAL MEAN CONDITION

* --- * TERMINALS: A=anode=P-region C=cathode=N-region * VARIABLES: M (mulitiplier), AREA [m^2], PERI [m].

* NOTE: The role of a protection DIODE is to conduct ESD current to VDD * (or from VSS). This forward bias is NOT modelled, only leakage current * and capacitance during normal operation. Any inductive load etc that * will give forward bias, must be limited by other components to within * Operating Conditions, otherwise parasitic bipolar action can occur. * D1 A C NDINSUBA {AREA} .ENDS ND * .MODEL NDINSUBA D IS =2.000e-05 N =1.000e+00 CJO =9.300e-04 M =3.100e-01 TT =0.000e+00 FC =0.500e+00 EG =1.110e+00 XTI =3.000e+00 AF =1.000e+00 KF =0.000e+00 VJ =6.900e-01

* --- .MODEL MODNM NMOS LEVEL=7

*

39 2.1.2 Dimensionamento della capacità C

Per dimensionare la capacità C occorre fare delle ipotesi sull’energia che è necessaria per il trasferimento dei dati da tag a reader, ma questo comporta la conoscenza a priori di tutto il circuito che la batteria dovrà alimentare in fase di trasmissione. Vengono quindi fatte delle ipotesi di funzionamento che dovranno essere verificate ed eventualmente adattate al reale funzionamento del circuito.

Il valore minimo di C può essere calcolato conoscendo la tensione necessaria al funzionamento del circuito e dalla potenza dissipata dal tag.

* Q I t C V V D = = D D (2.7)

Se ipotizziamo che nei 20 ms (con riferimento ai transponder TIRIS) utili alla trasmissione dei dati da tag a reader, il circuito assorba una corrente complessiva I = 5 μA e tolleri una variazione della tensione di alimentazione ΔV = 1 V, sfruttando la (2.7), occorre una capacità C = 100 nF.

Nel caso in cui il tag consumi una potenza superiore a quella prevista oppure il circuito alimentato non tolleri un’escursione così ampia della tensione di alimentazione, ovvero le ipotesi iniziali siano state troppo ottimistiche, è necessario aumentare il valore di C e adeguare di conseguenza anche la rete di adattamento.

2.1.3 Funzione di Bessel modificata del primo tipo

Capiterà spesso, nei paragrafi e capitoli successivi, di trovarci di fronte ad espressioni che richiedano l’utilizzo di questa funzione, quindi è utile menzionarne alcune proprietà.

La funzione di Bessel modificata del primo tipo, di ordine n, può essere definita come:

( )

cos

( )

( )

0 cos x t n B x e nt dt p =

_ò

(2.8)

40

Queste funzioni godono delle seguenti proprietà:

( )

( )

( )

( )

( )

n pari n dispari 2 n n n n x n B x B x B x B x e B x x n x p - = = -» _? (2.9)

Nella fig. 2.3 è rappresentato il grafico di Bn(x) al variare dell’ordine e

dell’argomento:

Figura 2.3 Funzione di Bessel modificata del primo tipo

Detta Bn(x) la funzione di Bessel modificata del primo tipo di ordine n,

possiamo scrivere:

( )

( )

cos( ) 0 1 2 cos( ) x t n n e± w B x +¥B x n tw = = ± +

å

± (2.10)

41

2.2 Duplicatore con generatore di tensione

Il primo circuito analizzato (figura 2.4) è composto dal duplicatore con in ingresso un generatore ideale di tensione. E’ un circuito ideale che serve ad introdurre il metodo di analisi che verrà utilizzato nei paragrafi successivi.

+ -V C C Vin _D1 D2 I_D2 I_D1 + - V/2

Figura 2.4 Duplicatore con generatore di tensione ideale

Sfruttando tutte le ipotesi fatte nei precedenti paragrafi, se il generatore Vin è di tipo sinusoidale con ampiezza V0, la tensione ai capi dei diodi risulta:

( )

( )

( )

( )

1 0 0 2 0 cos 2 cos( ) cos 2 D in D V V t V t V V t V V t V t w w w ì _{= -} -ïï = _{Þ í} ï _{= +} -ïî (2.11)

E’ utile ricordare che la tensione in uscita non è costante, ma lentamente variabile rispetto al segnale d’ingresso e quindi per comodità viene indicata con V anziché V(t).

Il diodo utilizzato presenta una RS = 0 Ω, quindi tutta la tensione ai capi del

42

Figura 2.5 Circuito equivalente del diodo con RS = 0 Ω

La corrente ID risulta quindi la somma di due componenti, una dovuta al

diodo intrinseco e una dovuta alla capacità CD:

( )

( )

( )

( )

1 ( ) ( ) D T V t V D S D d D D d D I t I e C t V t V t C t dt dt æ ö ç ÷ = _ç - +_÷ + ç ÷ è ø (2.12)

Trascuriamo per il momento l’ultimo termine, ipotizzando che la capacità CD

sia pressoché costante (vedremo variare di una quantità molto piccola nell’arco di tutto il transitorio):

( )

( )

( )

1 D T V t V D S D d D I t I e C V t dt æ ö ç ÷ = _ç - +_÷ ç ÷ è ø (2.13)

Da momento che a noi interessa capire come varia la tensione in uscita, possiamo concentrare l’attenzione sulla corrente ID2:

( )

( )

( )

cos 2 2 1 0cos 2 o T V V t V D S D d V I t I e C V t dt w w + -æ ö ç ÷ æ ö ç ÷ = _ç - +_{÷ ç} - _÷ è ø ç ÷ ç ÷ è ø (2.14)

43

Considerando V molto più lenta del segnale in ingresso:

( )

( )

( )

cos 2 2 1 0sin o T T V t V V V D S D I t I e e C V t w w w -æ ö ç ÷ = _ç - -_÷ ç ÷ è ø (2.15)

Sostituendo la funzione (2.10) nell’espressione sopra:

( )

0 0 2

( )

2 0 0 1 2 cos( ) T 1 sin V V D S n D T _n T V V I t I B B n t e C V t V V w w w -+¥ = æ_{é ù} ö æ ö æ ö ç ÷ = _{çê ç ÷}+ _{ç ÷ ú} - -_÷ ê è ø è ø ú çë û ÷ è ø

å

(2.16)

La corrente ID2(t) è composta da una componente continua, che corrisponde

alla corrente utile per la carica della capacità in uscita, e da una componente sinusoidale con relative armoniche, introdotte dall’elemento non lineare che è il diodo. La corrente media che attraversa C vale:

2 0 2 T 0 1 V V D S T V I I e B V -æ ö æ ö ç ÷ = _{ç ç ÷}- _÷ è ø ç ÷ è ø (2.17)

Dall’espressione precedente è possibile osservare che la corrente che carica la capacità è massima all’inizio del transitorio quando C è scarica e quindi V = 0 V, mentre tende a diminuire, come era prevedibile, man mano che si carica e tende al valore di regime.

Eguagliando la (2.17) con l’espressione della corrente in una capacità, otteniamo l’interessante relazione:

( )

( )

2 0 0 1 T V t V S T dV t V I e B C V dt -æ ö æ ö ç ÷ - = ç ÷ ç ÷ è ø ç ÷ è ø (2.18)

44

che può anche essere riscritta come:

( )

( )

2 0 0 T V t V S S T C dV t dt V I B e I V -= æ ö -ç ÷ è ø (2.19)

Integrando ambo i membri è possibile ricavare l’espressione di V(t) a meno di una costante d’integrazione k:

( )

(

)

2 0 0 2 ln S T I t k V C S T T S V e I B V V t V I - + æ ö æ ö ç ₊ ÷ ç ÷ ç _{è ø}÷ ç ÷ = ç ÷ ç ÷ ç ÷ è ø (2.20)

Per ricavare K basta imporre la condizione iniziale sul condensatore C, che risulta inizialmente scarico e quindi V(0) = 0 V. Svolgendo i calcoli:

0 0 2 ln T S S S T V V C k I I B I V æ æ öö = - _çç - _{ç ÷÷÷} è ø è ø (2.21) Sostituendo K nell’espressione di V(t):

( )

0 0 2 ln 2 ₀ 0 2 ln S T S S T S T I V C V t I I B V C I V S T T S V e I B V V t V I æ æ æ ööö - ç_ç - ç_ç - ç ÷÷_÷÷_÷ è ø è ø è ø æ ö ç _{æ ö}÷ ç + _{ç ÷}÷ ç è ø÷ = _{ç ÷} ç ÷ ç ÷ ç ÷ è ø (2.22)

45

Con ulteriori passaggi è possibile semplificare la precedente espressione sino ad ottenere:

( )

2 0 0 0 0 2 ln 1 S T I t V C T T T V V V t V e B B V V -æ ö æ æ öö æ ö ç ÷ = _ç ç_ç - ç ÷÷_÷+ ç ÷_÷ è ø è ø è ø ç ÷ è ø (2.23)

E’ possibile osservare che V(t) non dipende dalla frequenza del segnale di alimentazione ma soltanto dalla sua ampiezza, dalla corrente di saturazione inversa IS del diodo e dalla capacità C.

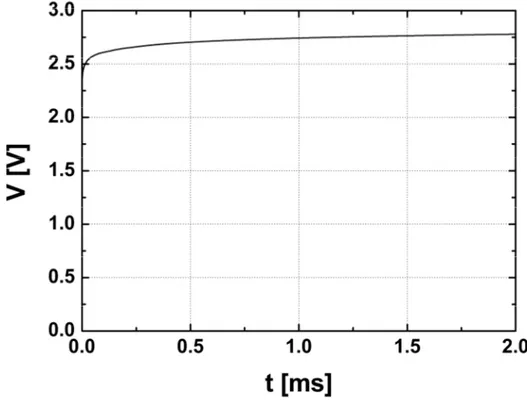
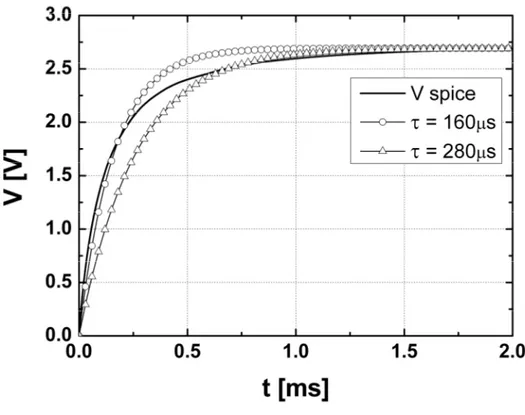
Per verificare l’esattezza dell’espressione trovata è necessario confrontarla con la tensione in uscita al circuito, ottenuta mediante simulazione dello stesso.

Posto in ingresso al duplicatore un segnale sinusoidale di ampiezza V0 = 2 V

e frequenza f = 900 MHz, utilizzando il diodo integrato precedentemente introdotto ed una capacità C = 100 nF, otteniamo la seguente risposta:

46

La tensione di uscita a regime è in accordo a quella che deve essere fornita dal duplicatore:

( )

2

(

0

)

2 2 0.69

(

)

2.62

V ¥ _; V -V_g = - = (2.24)

Tracciando sullo stesso grafico le curve ottenute dall’espressione (2.23) e dalla simulazione del circuito, le due risultano perfettamente sovrapposte.

L’espressione analitica ottenuta risulta quindi un’ottima approssimazione dalla risposta nel tempo del duplicatore, con posto in ingresso un generatore ideale di tensione.

2.3 Duplicatore con generatore di tensione e resistenza R

Rispetto al circuito precedente adesso è presente una resistenza R posta tra il generatore di tensione e il duplicatore.

+ -Vin C C Vs D1 D2 ID2 ID1 R Iin V -+

Figura 2.7 Duplicatore con generatore di tensione e resistenza R

A differenza del circuito precedente, la tensione Vin non è costante ma varia

nel tempo al variare della tensione d’uscita V: nell’ipotesi che V sia costante rispetto alla tensione d’ingresso lo sarà anche l’ampiezza di Vin . Da un’analisi

47

nel dominio della frequenza, fatta mediante simulatore, è possibile ipotizzare la tensione Vin sinusoidale.

( )

0

(

( )

)

cos

( )

in

V t =V V t wt (2.25)

2.3.1 Circuito equivalente del duplicatore

Sfruttando tutte le ipotesi fatte nei precedenti paragrafi sulle capacità C e ipotizzando che la tensione Vin in ingresso al duplicatore sia sinusoidale con

ampiezza V0, la differenza di potenziale ai capi dei diodi risulta:

( )

( )

( )

( )

1 2 2 2 D D V V t Vin t V V t Vin t = - -= + -(2.26)

Se la capacità CD di ogni diodo è pressoché costante e varia lentamente

rispetto alla tensione Vin, è possibile esprimere la corrente che scorre nei due

diodi come:

( )

( )

2 1 2 2 1 2 1 2 T T T T Vin V V V D S D in Vin V V V D S D in d V I t I e e C V dt d V I t I e e C V dt - -+ -æ ö æ ö ç ÷ = _ç - +_{÷ ç}- - _÷ è ø ç ÷ è ø æ ö æ ö ç ÷ = _ç - +_{÷ ç}+ - _÷ è ø ç ÷ è ø (2.27)

Dovendo ricavare il circuito equivalente del duplicatore occorre trovare un’espressione per la corrente Iin, che risulta essere pari alla differenza delle

correnti che scorrono nei due diodi. Sfruttando la funzione di Bessel modificata e le relazioni precedenti:

( )

( )

( )

2 2 1 T T T 2 V Vin Vin V V V in D D S D d in I t I t I t I e e e C V dt - æ - ö ç ÷ = - = _ç - _÷+ = ç ÷ è ø

48 2 0 0 0 1 2 cos( ) T V V n S T _n T V V I e B B n t V V w - é _{æ ö} +¥ _{æ ö} ê ç_ç ÷_÷ ç_ç ÷_÷ ê _{è ø = è ø} ë = +

å

- 0 0 0 1 2 _n cos( ) 2 _{D in} T n T V V d B B n t C V V V w dt +¥ = ù æ ö æ ö - ç ÷- ç- ÷ ú+ = ú è ø

å

è ø _û

(

)

(

)

( )

2 0 2 1 0 1 4 T cos 2 1 2 cos V V S n D T n V d I e B n t C V t V w dt w - +¥ -= æ ö = _{ç ÷} - + è ø

å

(2.28)

Nell’espressione di Iin compaiono soltanto i termini di ordine dispari della

funzione di Bessel modificata in quanto quelli pari, per le proprietà della funzione stessa, si semplificano e danno un contributo nullo.

A questo punto viene fatta un’ipotesi di comodo molto forte sostenuta in parte dal confronto tra funzioni di Bessel aventi stesso argomento ma ordine diverso (fig. 2.3), ovvero si ipotizza di poter trascurare tutti i termini di ordine superiore al primo. In questo caso l’espressione della corrente si semplifica notevolmente:

( )

2 0

( )

( )

1 0

componente in fase componente in quadratura

4 T cos 2 sin V V in S D T V I t I e B t C V t V w w w - _{æ ö} -ç ÷ è ø ; 14444244443 144424443 (2.29)

La corrente Iin ha una componente in fase ed una in quadratura rispetto alla

tensione Vin. E’ possibile quindi calcolare l’ammettenza equivalente vista in

ingresso al duplicatore: 2 0 1 0 4 1 2 T V V S T in eq eq D in eq V I e B V I Y j C j C V R w V w - _{æ ö} ç ÷ è ø = = + = + (2.30)

49 L’espressioni di Req e Ceq risultano: 2 0 0 1 2 4 T V V eq eq D S T V e R C C V I B V = = æ ö ç ÷ è ø (2.31)

Il circuito equivalente del duplicatore di tensione (fig. 2.8) è composto da una resistenza Req in parallelo ad una capacità Ceq.

+

-Vin 2CD

Iin

Req

Figura 2.8 Circuito equivalente del duplicatore di tensione

La resistenza Req è funzione di V e V0, grandezze che modificano il loro

valore durante il transitorio, quindi anche Req assume valori diversi durante la

carica di C.

La capacità equivalente Ceq è multipla di CD, funzione del punto di lavoro dei

diodi, quindi anche in questo caso c’è da aspettarsi una variazione del suo valore nell’arco del transitorio.

Per avere un’idea di come e quanto varia la capacità CD, posto R = 100 Ω

(valore che giustificheremo nel paragrafo successivo) e alimentato il circuito di fig. 2.7 con un generatore VS di ampiezza 2 V, è possibile osservare le tensioni V

50

valore iniziale di 763 mV a 1.98 V, mentre V passa da un valore iniziale di 0 V a 2.69 V.

Figura 2.9 Risposta nel tempo del duplicatore

Sostituendo nell’espressione (2.6) i parametri del diodo integrato ed alcuni punti delle curve sopra, è possibile ottenere una stima di come varia la capacità Ceq nell’arco del transitorio.

t [ms] 0 0.03 0.06 0.1 0.136 0.2 0.3 0.4 0.5 1 1.5 2

V0 [V] 0.763 1.20 1.38 1.53 1.63 1.73 1.84 1.89 1.93 1.96 1.97 1.98

V [V] 0 0.641 1.04 1.40 1.63 1.90 2.16 2.31 2.40 2.60 2.66 2.69

Ceq[fF] 195 189 179 171 167 162 158 155 154 150 149 148

Tabella 2.2 Valori di CD nell’arco del transitorio

Sempre per punti, è possibile tracciare il comportamento della capacità Ceq al

51

Figura 2.10 Comportamento di Ceq al variare di V

Avendo sino ad ora ipotizzato Ceq costante, nei conti successivi verrà

utilizzato il valor medio nell’arco del transitorio. Alla fine vedremo se tale valore è una scelta ottima oppure se conviene utilizzare un altro tipo di approssimazione. + -Vin 2CD Vs R Iin Req

52 2.3.2 Analisi del transitorio

Ricavato il circuito equivalente del duplicatore di tensione, occorre trovare delle relazioni che legano tra loro le varie grandezze in modo da ottenere un’espressione della tensione V(t).

Nell’ipotesi che l’alimentazione sia di tipo sinusoidale con ampiezza VS0, il

modulo della tensione in ingresso al raddrizzatore può essere ottenuto applicando il partitore di tensione. C’è da osservare che questa operazione non è rigorosamente corretta, in quanto applichiamo la teoria per le reti lineari pur avendo dei componenti variabili nel tempo.

0 1 2 1 0 1 2 1 2 eq eq D in S S eq D eq D _eq R j R C V V V V R _R R _{j R C} j R C _R w w w + = = = + _{+ +} + (2.32) Passando al modulo:

(

)

0 ₂ 0 2 1 1 2 S D eq V V R R C R w = æ ö + + ç ÷ ç ÷ è ø (2.33)

Dalla precedente equazione è anche possibile ricavare un’espressione per Req:

(

)

2 2 0 0 2 1 eq S D R R V R C V w = æ ö - -ç ÷ è ø (2.34)

Dalla (2.18) si desume che per ridurre il tempo di carica della capacità in uscita occorre dimensionare il circuito in modo tale che il modulo della tensione V0 in ingresso al duplicatore, sia elevato. Per soddisfare questa condizione,

53

All’aumentare della tensione in uscita V, man mano che le capacità C si caricano, la Req vista ai capi del duplicatore aumenta: questo fatto è in accordo

con l’altra espressione di Req (2.31) ed confermato dal fatto che, una volta

esaurito il transitorio, la corrente in ingresso Iin (2.29) tende a scorrere soltanto

nelle capacità parassite dei diodi CD. C’è quindi da aspettarsi che il primo

termine a denominatore della (2.33), non essendo il valore di R troppo elevato, tenda all’unità molto velocemente.

Per velocizzare il transitorio, mettiamoci nella condizione in cui:

(

₂

)

2 _{1 R} 1 2 D D R C C w w Þ = = (2.35)

Alla frequenza f = 900 MHz, se per CD utilizziamo i valori ottenuti nel

paragrafo precedente, la relazione (2.35) è verificata per una resistenza R di valore inferiore al centinaio di ohm. Sotto questa ipotesi è possibile semplificare l’espressione (2.33): 0 1 0 0 1 eq S S eq eq R V V V R R R R = + æ ö + ç ÷ ç ÷ è ø ; (2.36)

Un’approssimazione di questo tipo porta allo stesso risultato che si avrebbe se la capacità parassita CD dei diodi fosse nulla.

L’approssimazione (2.35) permette inoltre di ottenere un’espressione semplificata della Req: 0 0 1 eq S R R V V = -(2.37)

54

Uguagliando la relazione precedente con la (2.31), ottenuta dal calcolo del circuito equivalente del duplicatore, otteniamo:

2 0 0 ₀ 1 0 1 4 T V V S S T V e R V _V I B V _V = æ ö - _{ç ÷} è ø (2.38)

Questa corrispondenza permette di ottenere due interessanti relazioni, da utilizzare nel calcolo della tensione d’uscita V(t):

0 1 0 0 4 2 ln S T T S V RI B V V V V V æ æ öö ç ç ÷÷ è ø ç ÷ = _{ç ÷} -ç ÷ ç ÷ è ø (2.39)

(

0 0

)

2 0 1 4 T V V S T S V V V B e V RI -æ ö = ç ÷ è ø (2.40)

La prima equazione esprime la relazione tra la tensione V0 in ingresso al

duplicatore e la tensione in uscita V, in funzione dell’ampiezza VS0 e degli altri

parametri circuitali. La seconda equazione permette di sostituire alla funzione di Bessel modificata, un’espressione in cui compaiono i vari parametri del circuito.

Osservando il comportamento del circuito durante il transitorio (fig. 2.9) è possibile fare la seguente ipotesi:

0 ₁

T

V

55

Dalle proprietà della funzione di Bessel (2.9), essendo l’argomento molto maggiore dell’ordine della funzione stessa, l’espressione (2.39) può essere riscritta come: 0 0 0 0 4 2 ln 2 T V V S T S T RI e V V V V V V

p

æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø -; (2.42)

Espandendo l’argomento del logaritmo è possibile cercare di semplificare l’espressione, eliminando eventuali termini che non danno un contributo significativo durante il transitorio.

0 0 0 0 4 1 2 ln ln ln 2 1 1 2 1 1 S S T T T RI V V V V V V V V V V V V

p

é æ ö ù ê ç ÷ ú æ ö æ ö ê ç ÷ ú ç ÷ ç ÷ ê ç ÷ _{è ø è ø}ú ê ç_ç ÷_÷ ú ê _{è ø} ú ë û -= + - - (2.43)

Tracciando singolarmente le varie parti (fig. 2.12) dell’espressione (2.43), possiamo vedere che il terzo termine è sempre trascurabile mentre l’ultimo lo è per gran parte del transitorio, ma tende a divergere a regime, quando Req diventa

molto elevata e V0 tende a VS0. I termini 1V che compaiono nell’equazione

servono a renderla coerente dal punto di vista dimensionale.

Dal momento che V0 non raggiungerà mai il valore VS0, se non per tempi

molto lunghi, semplifichiamo la (2.43) eliminando gli ultimi due contributi.

0 4 2 ln 2 2 1 1 S T T RI V V V V V V p æ ö ç ÷ ç _{÷ +} ç ÷ ç ÷ ç ÷ è ø ; (2.44)

56

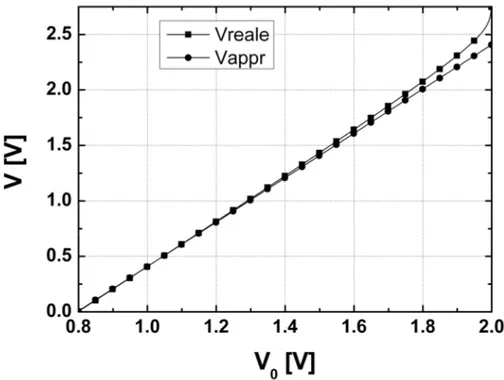
Figura 2.12 Termini dell’espressione (2.43)

Confrontando graficamente l’espressione (2.39) e la sua versione approssimata (2.44), si vede (fig. 2.13) che l’errore commesso tende a divergere a regime, quando V0 tende a VS0.

57

Dal momento che vogliamo ricavare un’espressione analitica di V(t) durante il transitorio, dove l’errore è accettabile, ipotizziamo valida la (2.44). La tensione in ingresso al duplicatore di tensione risulta:

0 ln 4 2 2 1 1 S T T RI V V V V V V p æ ö ç ÷ ç ÷ - _{ç ÷} ç ÷ ç ÷ è ø ; (2.45)

Se l’argomento della funzione di Bessel è sufficientemente grande, sfruttando le proprietà della funzione stessa, dalla (2.40) otteniamo:

(

0 0

)

2 0 0 0 1 ₄ T V V S T T S V V V V B B e V V RI -æ ö æ ö = ç ÷ ç ÷ è ø; è ø (2.46)

Sostituendo la relazione precedente nell’espressione (2.17) della corrente media che attraversa la capacità in uscita:

(

)

2 0 0 0 2 0 1 1 4 T V V S D S S T S V V V I I e B I V RI -æ ö æ - ö æ ö ç ÷ = _{ç ç ÷}- _{÷ ç} - _÷ è ø è ø ç ÷ è ø ; (2.47)

Andandovi a sostituire anche l’espressione (2.45) ottenuta per V0:

0 2 ln 4 4 8 4 2 1 1 S T S D S T V V V RI I I R R R V V V p æ ö ç ÷ ç ÷ = - + _{ç ÷} -ç ÷ ç ÷ è ø (2.48)

A questo punto procediamo come nel paragrafo 2.2, eguagliando la relazione precedente all’espressione della corrente in una capacità.

58 0 _ln 4 4 8 4 2 1 1 S T S S T V V V RI dV I C R R R dt V V V p æ ö ç ÷ ç ÷ - + _{ç ÷}- = ç ÷ ç ÷ è ø (2.49) Raccogliendo i termini in dt e in dV: 0 1 1 8 4 2 2 ln 8 2 1 1 S S T S T dt dV RC RI V V V RI V V V p = æ ö ç ÷ ç ÷ - + + _{ç ÷} -ç ÷ ç ÷ è ø (2.50)

Integrando ambo i membri:

0 4 ln 2 2 ln 8 8 2 1 1 S S T S T RI t K V V V RI RC V V V p æ æ ö ö ç ç ÷ ÷ ç ç ÷ ÷ + = - _ç - - _{ç ÷}+ _÷ ç ç_ç ÷_÷ ÷ ç _{è ø} ÷ è ø (2.51)

Dalla (2.51) è possibile ottenere l’espressione di V(t) a meno di una costante d’integrazione K:

( )

8 0 4 2 2 ln 8 2 1 1 t K RC S S T S T RI V t V V RI e V V V p æ ö -_ç + _÷ è ø æ ö ç ÷ ç ÷ = + _{ç ÷}- + ç ÷ ç ÷ è ø (2.52)

Per ricavare K basta imporre la condizione iniziale sul condensatore C, che risulta inizialmente scarico e quindi V(0) = 0 V.

59 0 4 ln 2 2 ln 8 2 1 1 S S T S T RI K V V RI V V V p æ æ ö ö ç ç ÷ ÷ ç ç ÷ ÷ = - _ç- - _{ç ÷}+ _÷ ç ç_ç ÷_÷ ÷ ç _{è ø} ÷ è ø (2.53)

L’espressione finale della V(t), una volta sostituita la costante K, risulta:

( )

8 0 4 2 2 ln 8 1 2 1 1 t S _RC S T S T RI V t V V RI e V V V p -æ æ ö ö ç ç ÷ ÷æ ö ç ç ÷ ÷ç ÷ =_ç + _{ç ÷}- _÷ -ç ÷ ç ç_ç ÷_÷ ÷è ø ç _{è ø} ÷ è ø (2.54)

Dall’espressione ottenuta si possono facilmente individuare il valore della tensione di uscita a regime VREG e della costante di tempo τ :

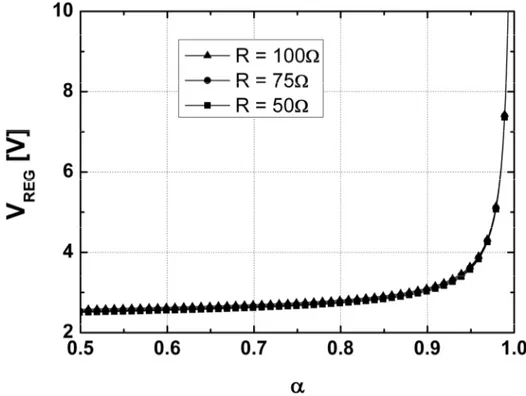
0 4 2 2 ln 8 2 1 1 S REG S T S T RI V V V RI V V V p æ ö ç ÷ ç ÷ = + _{ç ÷} -ç ÷ ç ÷ è ø (2.55) 8RC t = (2.56)

Nella (2.55) il primo termine è positivo mentre gli altri due sono negativi in quanto il logaritmo ha argomento minore di uno. In particolare l’ultimo termine risulta sempre trascurabile rispetto agli altri due, in quanto R è dell’ordine delle decine di ohm mentre IS, per il diodo utilizzato, è dell’ordine del fA.

Il valore di R non influisce significativamente su VREG mentre determina la

60

Figura 2.14 VREG al variare di VS0

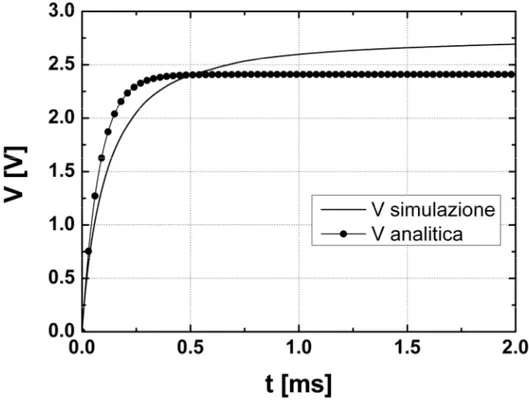
Proviamo a confrontare la risposta nel tempo ottenuta mediante simulatore, con la risposta che si ottiene utilizzando il diodo integrato introdotto nei paragrafi iniziali ed i seguenti valori:

0 2 2.41 100 80 s S REG V V V V R

t

m

ì ì ï ï í í ï ï î î = = Þ = W =

Rappresentando le due curve sullo stesso grafico (fig. 2.15), si osserva chiaramente che le due risposte differiscono nel tempo, sia per quel che riguarda il valore di regime che per l’evoluzione temporale.

Per quel che riguarda la costante di tempo τ si vede che non sono molto diverse tra loro, ma la risposta del circuito raggiunge il valore di regime in un tempo più lungo rispetto al modello trovato.

61

Figura 2.15 Confronto tra risposta reale e espressione ricavata

Occorre verificare se effettivamente la risposta del duplicatore di tensione sia di tipo esponenziale oppure segua un’altra legge. Confrontando la risposta del circuito con un’esponenziale avente lo stesso valore di regime ma costanti di tempo diverse (fig. 2.16), si vede che il sistema non evolve secondo una legge di tipo esponenziale.

Per quel che riguarda la tensione a regime abbiamo visto che l’approssimazione fatta cade in difetto man mano che V0 tende al valore VS0 in

quanto anche l’errore commesso tende a divergere, quindi occorre trovare un’approssimazione migliore che leghi V e V0 rispetto alla (2.44).

62

Figura 2.16 Confronto tra uscita ed esponenziali con costanti di tempo diverse

2.3.3 Sviluppo al primo ordine di V rispetto a V0

Nel paragrafo precedente è stata fatta l’ipotesi che il legame tra V e V0 sia di

tipo lineare (2.44) osservando il contributo dato da ogni termine dell’argomento del logaritmo. Un’approssimazione migliore del transitorio della tensione in uscita al duplicatore, può essere ottenuta dalla facendo lo sviluppo in serie di V rispetto a V0 e scegliendo opportunamente il punto attorno al quale fare lo

sviluppo stesso. Partendo dalla (2.42):

(

)

(

)

0 0 0 0 0 0 0 0 4 4 1 2 ln 2 2 ln 2 2 T V V S S T T S S T T RI e RI V V V V V V V V V V V V p p æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø = + - -; (2.57)

63

Lo sviluppo al primo ordine del secondo termine rispetto a V0, attorno a V0*,

si ottiene come:

(

*

)

0 0 0 0 0 0 0 0 0 * 0 0 4 1 4 1 ln ln 2 2 * 0 0 S S S S T T RI d RI V V V V V dV V V V V _{V V} V V V p p é ù æ ö æ ö ê ú ç ÷ ç ÷ ê ú ç ÷ ₊ ç ÷ -ê ú ç _- ÷ ç _- ÷ ê ú ç ÷ ç ÷ ç ÷ _ê ç ÷_ú è ø ₌ ë è øû = (2.58)

La derivata calcolata in V0* vale:

(

)

0 0 0 0 0 0 0 * 0 0 * 0 0 4 1 1 1 ln 2 2 S S S T V V V V RI d dV V V V V V V V

p

é æ öù ê ç ÷ú _{æ ö} ê ç ÷ú _{ç ÷} ê ç ÷ú _{è ø} ê ç_ç ÷_÷ú = ê _{è ø}ú ë û = = - = -

-(

)

* 0 0 * * 0 0 0 3 2 S S V V V V V -= - (2.59)

Sostituendo l’espressione sopra, nella (2.57):

(

)

(

)(

)

* * 0 0 0 _{* * * *} 0 0 0 0 ₀ 0 0 0 4 1 3 2 2 ln 2 2 S S T S S T RI V V V V V V V V V _V V V V V p é æ ö ù ê ç ÷ ú ê ç ÷ - ú + _{ê ç ÷}+ - _ú - -ê ç ÷ ú ê ç ÷ ú è ø ë û ; (2.60)

64

(

)

(

)

(

)

* * 0 0 0 0 0 _{* * * * *} 0 0 0 0 0 0 0 0 3 4 1 3 2 1 2 ln 2 2 2 S S S T T S S S T V V RI V V V V V V V V V V V V V V V p é æ ö ù ê ç ÷ ú é ù _{ê ú} ç ÷ - -ê ₊ ú_{+ +} ê ç ÷ ú ê _- ú _- -ê ç ÷ ú ê ú ë û _{ê ç ÷ ú} è ø ë û ; (2.61)

Dal momento che la tensione V0, a regime, tende a VS0, il punto V0* attorno

al quale viene fatto lo sviluppo può essere espresso come una frazione di VS0:

*

0 S0

V = ×

a

V (2.62)

In questo modo l’espressione di V dipende, oltre che dai parametri circuitali e da V0, anche dal punto attorno al quale viene fatto lo sviluppo:

(

)

(

)

(

)

0 0 0 0 4 3 1 1 1 3 2 1 2 ln 2 1 1 2 1 2 S T T S S S T RI V V V V V V V V a a a a _p a a a é æ ö ù ê ç ÷ ú é _- ù _{ê ç ÷ - ú} + + + ê _- ú _{ê ç ÷ - ú} -ë û _{ê ç ÷ ú} ç ÷ ê è ø ú ë û ; (2.63)

Per semplificare l’espressione precedente è utile sostituire ai termini che dipendono da α due funzioni:

(

)

0 3 1 ( ) 1 2 1 T S V V a j a a a -= + - (2.64)

(

)

(

)

0 0 4 1 1 3 ( ) ln 2 1 1 2 S S S T RI V V V a g a a a a p æ ö ç ÷ -ç ÷ = _{ç ÷}+ -ç ÷ ç ÷ è ø (2.65)

65

L’espressione semplificata risulta:

0

2 ( ) 2 _T ( )

V = V ×j a + V ×g a (2.66)

Adesso è possibile procedere come nel paragrafo precedente, ricavando l’espressione di V0 in funzione di V (dove per semplicità è stata omesso la

dipendenza da α): 0 ₂V T V g V j j = - (2.67) sostituirla nell’espressione (2.47) di

I

_D2: 0 2 4 8 4 S T D V V V S I I R R R g j j = - + - (2.68)

ed uguagliarla alla corrente che scorre in una capacità C:

0 4 8 4 S T S V V V dV I C R R R dt g j j - + - = (2.69)

Riscrivendo l’espressione precedente in una forma diversa:

(

0

)

1 1

8RCdt V 2V_S 8RI_S 2V_T dV

j = - +j - + g (2.70)

ed integrando ambo i membri:

(

)

(

0

)

ln 2 8 2 8 S S T t K V V RI V RCj + = - -j - - g (2.71)

Dalla (2.71) è possibile ottenere l’espressione di V(t) a meno di una costante d’integrazione K.

66

( )

(

)

8 0 2 8 2 t K RC S S T V t j V RI V g e j æ ö -_ç + _÷ è ø = - + + (2.72)

Per ricavare K basta imporre la condizione iniziale sul condensatore C, che risulta inizialmente scarico e quindi V(0) = 0 V.

(

)

(

0

)

ln 2 _S 8 _S 2 _T

K = - -j V - RI - V g (2.73)

L’espressione finale della V(t), una volta sostituita la costante K, risulta:

( )

(

)

8 0 2 8 2 1 t RC S S T V t j V RI V g e- j æ ö ç ÷ é ù =_ë - + _{û ç}× - _÷ ç ÷ è ø (2.74)

Dall’espressione ottenuta si possono facilmente individuare il valore della tensione di uscita a regime VREG e della costante di tempo τ:

(

0

)

( ) ( ) 2 8 2 ( ) REG S S T V a =j a × V - RI + V ×g a (2.75) ( ) 8RC ( ) t a = ×j a (2.76)

E’ possibile vedere che cambiando il punto attorno a quale viene fatto lo sviluppo al primo ordine, ovvero cambiando il valore di α e quindi di φ e γ, cambiano sia la costante di tempo che il valore della tensione che raggiunge V(t) a regime. In particolare, tracciando le due espressioni sopra, si vede che entrambe sono monotone crescenti nell’intervallo di nostro interesse.

67

Figura 2.17 VREG al variare di α

Mentre per quanto riguarda τ(α):

68

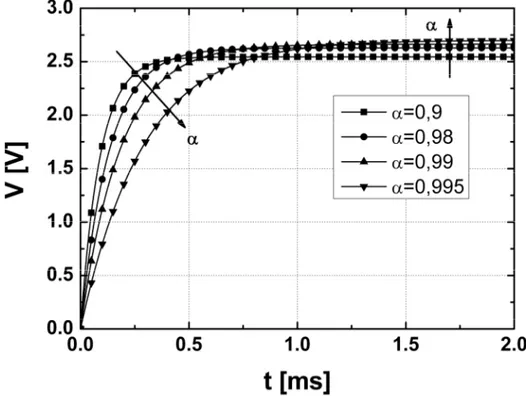
Visto come variano singolarmente i vari termini che compongono l’espressione (2.74), è utile vedere come varia V(t) nel suo complesso al variare del parametro α.

Figura 2.19 V(t) al variare di α

69

Sovrapponendo alle curve tracciate nella fig. 2.19, l’andamento della tensione V(t) in uscita al duplicatore di tensione con R = 100 Ω e VS0 = 2 V, è possibile

scegliere il valore di α che meglio approssima l’uscita (fig. 2.20).

Scegliendo α = 0.99 si ottiene la curva che meglio approssima la risposta del circuito nell’arco di tutto il transitorio. Facendo un confronto con l’espressione (2.54) ottenuta nel paragrafo precedente, senza effettuare lo sviluppo al primo ordine e la risposta del duplicatore di tensione, si può vedere che adesso l’espressione ricavata approssima meglio la tensione in uscita.

Figura 2.21 Confronto tra V(t) in uscita dal duplicatore e modello matematico, con e senza sviluppo

Nello sviluppo è stato utilizzato un valore di α molto prossimo all’unità, il che equivale a considerare V0* molto vicino al valore di regime:

*

0 S0 S0

70

Tracciando l’espressione (2.39) che mette in mostra il legame tra V e V0 e

l’espressione (2.66) ottenuta dallo sviluppo al primo ordine, possiamo vedere che la retta che meglio la approssima il comportamento del circuito è molto diversa da quella che avevamo considerato nel paragrafo precedente, in particolare tende ad approssimare il comportamento nella parte finale del transitorio.

Figura 2.22 Legame tra V e V0 al variare di α

La prima parte del transitorio è molto veloce e quindi per ottenere una tensione d’uscita simile a quella reale, occorre focalizzare l’attenzione sulla parte finale della carica.

71

2.4 Duplicatore con circuito risonante serie RLC

Consideriamo adesso il circuito completo di fig. 2.23: l’idea è quella di dimensionare la rete di adattamento in maniera tale da avere risonanza serie in ingresso al duplicatore, così da poter disporre in ingresso al circuito di una tensione superiore a quella ricevuta all’antenna. Abbiamo visto che il circuito equivalente del duplicatore è rappresentato da una capacità Ceq in parallelo ad

una resistenza Req: per avere risonanza serie occorre dimensionare la rete di

adattamento in modo tale che l’impedenza vista dai terminali di uscita sia di tipo induttivo. In questo paragrafo cercheremo di capire il comportamento del circuito nel transitorio, sostituendo alla rete di adattamento, che verrà trattata nel capitolo successivo, il circuito equivalente visto ai suoi terminali.

+ -Vin C C Vs _D1 D2 I_D2 I_D1 R I_in V -+ L

Figura 2.23 Duplicatore con circuito equivalente della rete di adattamento

2.4.1 Analisi del transitorio

Sfruttando tutte le ipotesi fatte nel paragrafo 2.3.1, che Vin sia di tipo sinusoidale con ampiezza costante rispetto al segnale di ingresso e dipendente dal valore della tensione di uscita V, che la capacità CD dei diodi non vari

significativamente nel transitorio, al duplicatore di tensione può essere sostituito il proprio circuito equivalente. In questo caso, l’ipotesi che la tensione Vin sia di tipo sinusoidale, è rafforzata dal fatto che le armoniche di ordine superiore sono filtrate dal circuito risonante RLC.

72

Per Req e Ceq valgono le espressioni (2.31) calcolate precedentemente:

2 0 0 1 2 4 T V V eq eq D S T V e R C C V I B V = = æ ö ç ÷ è ø (2.31)

Vedremo più avanti che in questo caso entrano in gioco molti fattori durante il transitorio ed il problema maggiore è il dimensionamento della rete di adattamento (L e R), in quanto ci sono alcuni parametri circuitali che variano nel tempo e quindi non è possibile stabilire una condizione di adattamento per tutto il transitorio, ma sarà necessario trovare un compromesso.

+

-Vin

Ceq

Vs

R

I

in

Req

L

Figura 2.24 Circuito equivalente rete di adattamento con circuito equivalente del duplicatore di tensione

Se Req e Ceq possono essere considerate costanti rispetto al segnale di

alimentazione VS, che ipotizziamo sinusoidale con ampiezza VS0 , la tensione

Vin in ingresso al raddrizzatore risulta:

1 1 eq eq eq in S eq eq eq R j R C V V R R j L j R C w w w + = + + + (2.78)

73 Svolgendo i conti:

(

)

2 eq in S eq eq eq eq eq R V V R R jw L RR C w LR C = + + + - (2.79)

e scrivendo Vin in modo da mettere in evidenza i parametri del circuito:

2 1 eq eq in S eq eq eq eq eq eq eq R R R V V RR _L R j C LC R R R R R R w w + = æ ö + ç_ç + ÷_÷ -+ + + è ø (2.80)

è possibile ottenere l’espressione della frequenza di risonanza f0 e del fattore di

risonanza Q: 0 ₂1 1 1 ₂1 1 1 eq eq eq eq eq R f R LC R LC R R p p = = + + (2.81) 0 1 eq eq eq eq Q RR _L C R R R R w = æ ö + ç ÷ ç _{+ +} ÷ è ø (2.82)

Dalle due espressioni ottenute si vede che sia f0 che Q variano durante il

transitorio in quanto Req, funzione della tensione d’uscita V e della tensione in

ingresso al raddrizzatore Vin, tende ad aumentare. Per il momento continuiamo a

supporre Ceq costante, anche se vedremo che questa ipotesi non è completamente

corretta e contribuisce, insieme ad altri fattori, a rendere difficile l’individuazione di un’espressione analitica della tensione V(t) ai capi di C.

74

Vediamo come variano le grandezze f0 e Q al variare di Req e per alcuni valori

di R, ipotizzando che L = 170 nH e che Ceq = 185 fF, valori che verranno

giustificati nel corso del paragrafo.

Figura 2.25 Frequenza di risonanza al variare di R e Req

Per valori di Req di qualche kΩ la frequenza di risonanza f0 dipende dalla

scelta di R ma soprattutto dal valore assunto dalla resistenza equivalente del duplicatore. Questo è sintomo del primo problema che ci troviamo ad affrontare: la f0 del filtro passa banda si sposta durante il transitorio e quindi non sarà

possibile fare in modo che la tensione in ingresso al duplicatore benefici sempre dell’amplificazione massima che abbiamo a centro banda, addirittura se Q è troppo elevato e quindi la banda troppo stretta, c’è il rischio di perdere tutti i benefici per il quale era stata pensata questa configurazione.

Dalla fig. 2.26 si vede che per valori di Req elevati, Q tende a stabilizzarsi e

75

dall’uscita. Per Req dell’ordine delle decine di kΩ, Q dipende ancora da R, ma le

differenze sono meno marcate.

Avremo quindi che nella prima parte del transitorio, qualsiasi sia il valore di R utilizzata, il circuito dovrebbe comportarsi nel medesimo modo, ma all’aumentare della carica immagazzinata dalla capacità in uscita e quindi di Req,

la scelta del valore di R diventa determinante.

Figura 2.26 Q al variare di R e Req

C’è da osservare che se Req non raggiunge valori sufficientemente grandi

durante il transitorio, anche Q non risulta molto elevato: un’idea potrebbe essere quella di abbassare il valore di R ma vedremo nel capitolo successivo che al di sotto di un certo limite non possiamo andare in quanto la diminuzione di R ha come conseguenza un aumento del fattore di risonanza QS, che per limiti

76

Generalmente la frequenza alla quale deve lavorare il dispositivo è una specifica del progetto, quindi fissata f = 900 MHz e gli altri parametri circuitali, è possibile ricavare il valore di L che pone il segnale d’ingresso al centro della banda del filtro RLC, in modo da utilizzare al meglio la risonanza serie.

(

)

2 0 1 1 2 _eq eq R L R f C p æ ö = ç_ç + ÷_÷ è ø (2.83)

Dalla precedente espressione si vede chiaramente che al variare di Req e Ceq,

anche il valore di L necessario a far si che f = f0 cambia, quindi le due frequenze

saranno uguali soltanto ad un certo istante e non sarà possibile sfruttare al meglio gli effetti della risonanza. Occorrerà quindi valutare come conviene dimensionare L, in base al tempo a disposizione per la carica, ai dispositivi utilizzati e all’ampiezza minima del segnale d’ingresso.

77

Per Req sufficientemente grande il valore di L non è problematico in quanto si

attesta, anche al variare di R, intorno ai 169 nH. In realtà vedremo che la scelta di L è molto delicata e necessita di una notevole precisione, dell’ordine di qualche punto percentuale, in quanto scarti maggiori possono compromettere il corretto funzionamento del circuito. Se Req non è sufficientemente grande rispetto a R,

allora anche il valore di L è molto sensibile alla variazione dei parametri circuitali nel transitorio.

Fissati R = 35 Ω, in modo da avere Q il più elevato possibile (Q raggiunge al massimo il valore di 25) compatibilmente alla realizzabilità della rete di adattamento e L = 170 nH, è utile vedere come influisce una variazione di Ceq sul

fattore di risonanza Q e sulla frequenza di risonanza f0 del filtro.

78

Figura 2.29 Influenza di Ceq su Q con R=35 Ω e L = 170nH

Dai precedenti grafici si vede che una variazione di Ceq sposta in maniera

considerevole la frequenza di risonanza f0 mentre ha un effetto trascurabile sul

coefficiente di risonanza Q.

La variazione di f0 implica che la tensione in ingresso al duplicatore sfrutta i

benefici della risonanza serie soltanto in alcuni istanti del transitorio, dunque ci dovremo aspettare, e vedremo che sarà così, risultati ben al disotto di quelli previsti. In particolare, il fatto di considerare la tensione Vin come la tensione

VS0 amplificata del fattore Q, è corretto soltanto quando i parametri circuitali

sono tali da avere f = f0.

Per avere la frequenza di risonanza del circuito sempre uguale a quella del segnale d’ingresso, sarebbe necessaria una induttanza L che muta il suo valore nel tempo in accordo alle variazioni degli altri parametri.

79

Facciamo adesso l’ipotesi, quasi sempre verificata, che la resistenza Req che si

vede in ingresso al duplicatore sia molto maggiore della resistenza R, che si vede in uscita alla rete di adattamento.

eq

R ? R (2.84)

Con questa ipotesi è possibile semplificare l’espressione (2.81) relativa ad f0 e

la (2.82) relativa a Q: 0 ₂1 1 eq f LC p ; (2.85) 0 1 eq eq Q L RC R w æç_ç + ö÷_÷ è ø ; (2.86)

Dalla (2.85) si ricava il valore di L che fissa la frequenza di risonanza, che come abbiamo visto, varia durante il transitorio:

(

)

2

(

)

2 0 0 1 1 2 _eq 2 2 _D L f C f C p = p ; (2.87)

Fissata la frequenza f = 900 MHz e ipotizzando che Ceq = 185 fF, occorre

un’induttanza L = 170 nH.

Per ω = ω0, condizione che si verifica soltanto in alcuni istanti del transitorio,

80 0 eq eq in S eq eq eq eq R R R V V RR _L j C R R R R w + = æ ö + ç ÷ ç _{+ +} ÷ è ø (2.88)

Passando al modulo e ipotizzando valida l’ipotesi (2.84):

0 0 0 0 0 0 1 eq eq in S S S eq eq eq eq eq eq R R R V V V V QV RR _{L L} C RC R R R R R w w + = = = æ ö æ ö + + ç ÷ ç ÷ ç _{+ +} ÷ ç ÷ è ø è ø ; (2.89)

Dall’espressione precedente è possibile ottenere Req:

0 0 0 0 0 0 1 eq S eq eq L L R V C R C R Q V w w w w = = -(2.90)

La (2.90) ha una forma molto simile alla (2.37), ottenuta nel paragrafo 2.3.2 in assenza dell’induttanza L. Uguagliando l’espressione precedente alla (2.31), ottenuta nel calcolo del circuito equivalente del duplicatore di tensione, si ottiene: 2 0 0 0 ₀ 0 ₁ 0 4 T V V S eq _S T L V e V _V C R _{I B} V _V w w = æ ö - _{ç ÷} è ø (2.91)

Questa uguaglianza permette di ottenere due interessanti relazioni, da utilizzare nel calcolo della tensione d’uscita V(t).

81 0 0 1 0 0 0 4 2 ln S T T S eq V LI B V V V V V C R w w æ æ öö ç ç ÷÷ è ø ç ÷ = _{ç ÷} -ç ÷ ç ÷ è ø (2.92)

(

0 0 0

)

₂ 0 1 0 4 T V S eq _V T S V V C R V B e V LI w w -æ ö = ç ÷ è ø (2.93)

L’analisi ricalca quella già vista per il circuito in cui non compariva l’induttanza. La prima equazione esprime la relazione tra la tensione V0 in

ingresso al duplicatore e la tensione in uscita V, in funzione dell’ampiezza VS0 e

degli altri parametri circuitali. La seconda equazione permette di sostituire alla funzione di Bessel modificata, un’espressione in cui compaiono i vari parametri del circuito.

Osservando il comportamento del circuito durante il transitorio, dopo pochi ns, l’ampiezza V0 è dell’ordine di qualche centinaio di mV, quindi è ancora

possibile fare l’ipotesi:

0 ₁

T

V V ?

Dalle proprietà della funzione di Bessel (2.9), essendo l’argomento molto maggiore dell’ordine della funzione stessa, l’espressione (2.92) può essere riscritta come:

(

)

0 0 0 0 0 0 4 2 ln 2 T V V S T S eq T LI e V V V V V C R V w w _p æ ö ç ÷ ç ÷ ç _- ÷ ç ÷ ç ÷ è ø ; (2.94)

82

Portando l’esponenziale fuori dall’argomento del logaritmo, troviamo l’espressione sulla quale andremo a fare lo sviluppo in serie al primo ordine.

(

0

)

0 0 0 0 0 4 1 2 2 ln 2 S T S eq T LI V V V V V V C R V w w _p æ ö ç ÷ ç ÷ + _{ç ÷} -ç ÷ ç ÷ è ø ; (2.95)

Lo sviluppo al primo ordine del secondo termine rispetto a V0, attorno a V0*,

si ottiene come:

(

0 00 0

)

0 * 0 0 4 1 ln 2 S eq S T LI V V V C R V V V w w _p æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø + -=

(

0

)

(

0 0*

)

0 0 0 0 0 * 0 0 4 1 ln 2 S S eq T V V LI d V V dV V V C R V V w w _p = é æ öù ê ç ÷ú ê ç ÷ú + _{ê ç ÷ú} -ê ç_ç ÷_÷ú ê è øú ë û (2.96)

La derivata calcolata in V0* vale:

(

0

)

0 0 0 0 0 0 ₀ 0 0 4 1 1 1 ln 2 2 * * 0 0 0 0 S S S eq eq T LI d V dV V V C R V _V V C R V V V V V w w _p w é æ öù æ ö ê ç ÷ú ç ÷ ê ç ÷ú ₌ç _- ÷ ₌ ê ç _- ÷ú ç _- ÷ ê ç_ç ÷_÷ú ç ÷ è ø ê è øú ë û = =

(

)

* 0 0 0 * * 0 0 0 0 3 2 eq S S eq V C R V V V V C R w w -= - (2.97)

83

Sostituendo il risultato precedente nella (2.96), si ottiene l’espressione di V(t):

(

0

)

0 _* * 0 0 0 ₀ 4 1 2 2 ln 2 S T S eq T LI V V V V V C R _V V w w p é æ ö ê ç ÷ ê ç ÷ + _{ê ç ÷}+ -ê ç ÷ ê ç ÷ è ø ë ;

(

)(

)

* 0 0 0 * 0 0 * * 0 0 0 0 3 2 eq S S eq V C R V V V V V V C R w w ù - _ú + - _ú - _úû (2.98)

Può essere utile mettere in evidenza la parte costante e quella funzione di V0:

(

)

* 0 0 0 0 _{* *} 0 0 0 0 3 2 1 2 eq S T S eq V C R V V V V V V V C R w w é _- ù ê ₊ ú₊ ê _- ú ê ú ë û ;

(

)

(

)

* 0 0 0 0 * _* * 0 0 0 ₀ 0 0 0 3 4 1 2 ln 2 2 S eq S T S eq S eq T V V C R LI V V V C R _V V V C R V w w w w p é æ ö ù ê ç ÷ ú -ê ç ÷ ú + _{ê ç ÷}+ _ú - -ê ç ÷ ú ê ç ÷ ú è ø ë û (2.99)

Se Ceq non cambiasse valore durante il transitorio e quindi la frequenza di

risonanza coincidesse sempre con la frequenza del segnale di alimentazione, la tensione V0, a regime, tenderebbe a QVS0. Supponendo che sia vero, ma

sappiamo che le cose non stanno così, il punto V0* attorno al quale viene fatto lo

sviluppo può essere espresso come una frazione di QVS0:

*

0 S0