Studio del dicroismo locale di nanostrutture metalliche tramite microscopia ottica a campo prossimo

i

Indice

INTRODUZIONE...1

1 INTRODUZIONE ALL’APPARATO ...6

1.1 MICROSCOPIA OTTICA TRADIZIONALE...6

1.2 PROPAGAZIONE E CAMPO PROSSIMO...9

1.3 LO SNOM...10

1.3.1 La sonda...11

1.3.2 La movimentazione ...13

1.3.3 Il controllo della distanza sonda-campione ...14

1.3.4 Lo SNOM utilizzato...17

1.4 LO SNOM A MODULAZIONE DI POLARIZZAZIONE...20

1.4.1 Anisotropia ottica e matrici di Jones ...20

1.4.2 La polarizzazione rotante...23

1.4.3 Misura dell’anisotropia ottica ...25

2 IL TRATTAMENTO DATI...28

2.1 DECONVOLUZIONE DELL’ANISOTROPIA DELLA SONDA...28

2.2 IL PROGRAMMA DI ELABORAZIONE...32

2.2.1 Il linguaggio scelto...33

2.2.2 Introduzione al programma ...35

2.2.3 I filtri ...37

2.2.4 Il programma in azione...45

2.2.5 Le funzionalità del programma...48

3 I CAMPIONI ESAMINATI ...52

3.1 REALIZZAZIONE DEI CAMPIONI...52

ii

4.1 PREPARAZIONE DEL BANCO OTTICO...58

4.2 CALIBRAZIONE DEL TUBO PIEZOELETTRICO...61

4.3 MISURE IN CAMPO PROSSIMO...68

4.3.1 Acquisizione dati ...68

4.3.2 Trattamento dati...73

4.4 MISURE IN CAMPO LONTANO...76

4.5 MODELLO FENOMENOLOGICO...82

CONCLUSIONI...88

APPENDICE ...91

BIBLIOGRAFIA ...95

1

Introduzione

Scopo della tesi è lo studio dell’anisotropia ottica locale di un campione metallico nanostrutturato, tramite la microscopia ottica a campo prossimo con modulazione di polarizzazione. Nanostrutture dotate di forma controllata e dimensionalità ridotta mostrano nuove proprietà in vari campi della fisica della materia, quali nanomeccanica e nanofotonica. Rispetto a quest’ultima, è noto che particelle di metalli nobili ridotte a dimensioni nanometriche mostrano particolari proprietà ottiche nel range spettrale della luce visibile, dovuta all’eccitazione di modi collettivi degli elettroni di conduzione conosciute come risonanze plasmoniche di superficie. Le frequenze di risonanza di tali modi dipendono fortemente dalle dimensioni, dalla forma e dal dielettrico circostante le nanoparticelle, dando quindi un mezzo efficace per variare a piacimento le loro proprietà ottiche. Una possibile applicazione di questi sistemi è la realizzazione delle cosiddette guide ottiche plasmoniche. E’ stato proposto infatti che l’energia elettromagnetica potrebbe essere guidata entro strutture di dimensioni al di sotto del limite di diffrazione, quindi nanometriche, lungo catene di nanoparticelle metalliche ravvicinate, tramite accoppiamento di campo prossimo.

L’adozione di approcci sequenziali come litografia a scansione a sonda o a fascio elettronico ad alta risoluzione per la crescita di nanostrutture metalliche supportate su aree macroscopiche estese è intrinsecamente lenta e quindi non adatta alle applicazioni pratiche. Tramite una tecnica di “scultura ionica,” basata sull’erosione del substrato tramite un fascio di ioni di gas nobili ad incidenza non normale e la successiva deposizione di uno strato metallico, è possibile ottenere un campione nanostrutturato su aree macroscopiche, superando questa limitazione. I campioni studiati in questa tesi sono appunto realizzati, presso l’Università di Genova, producendo uno speciale substrato nanostrutturato sul

Introduzione

2 quale viene depositato un film sottile di metallo nobile. In particolare, il substrato consiste in un vetrino sulla cui superficie vengono create delle ondulazioni monodimensionali (ripples) con una periodicità di circa 150 nm e una profondità di circa 15 nm. Sul substrato così strutturato viene effettuata una deposizione di argento, di spessore nanometrico, che viene ad assumere una morfologia che riproduce quella del substrato. In questo modo il campione può essere rappresentato come costituito da una successione periodica di strutture monodimensionali, cioè di “fili” paralleli. Questo campione realizza in pratica un filtro polarizzatore, ma può avere impieghi potenziali, molti ancora da esplorare, nella cosiddetta “nanoplasmonica”, dove un esempio può essere quello sopra citato delle guide ottiche plasmoniche. In simili sistemi, è basilare l’accoppiamento dei campi prossimi ottici con i modi plasmonici dei metalli nanostrutturati.

Tema centrale di questa tesi e’ la caratterizzazione del dicroismo locale di un tale film metallico nanostrutturato tramite microscopia “SNOM” ad apertura, nella configurazione in modulazione di polarizzazione. Il microscopio ottico a scansione a campo prossimo (SNOM) consente di ottenere una risoluzione laterale dell’immagine ottica di una superficie che non e’ limitata dalla diffrazione come per gli altri strumenti di microscopia ottica tradizionale. Questo è possibile illuminando la superficie da analizzare con un campo elettromagnetico non propagante generato da aperture metalliche del diametro di poche decine di nanometri, dette sonde SNOM, e comunemente realizzate all’apice di fibre ottiche rastremate e metallizzate in cui viene iniettata luce laser. L’elevata risoluzione è data dal fatto che questo campo non propagante, che si estingue su una scala spaziale dello stesso ordine di grandezza dell’apertura, è capace di interagire con le frequenze spaziali (ovvero le periodicità) del campione più elevate di quelle relative alla lunghezza d’onda (k/2π≥1/λ). Gli strati superficiali del campione, per una profondità paragonabile all'estensione spaziale del campo prossimo, interagiscono con il campo elettromagnetico; il risultato dell'interazione, cioè la radiazione diffusa o trasmessa dal campione, viene raccolta in campo lontano, utilizzando configurazioni di riflessione o trasmissione. Eseguendo una scansione

3 della superficie è così possibile costruire una mappa con una risoluzione spaziale confrontabile con il diametro dell’apertura. Commercialmente sono disponibili sonde con aperture tra 50 e 100 nm, che danno la risoluzione necessaria per lo studio locale di strutture con dimensioni nanometriche come quelle dei campioni in esame. L’interesse dell’uso del microscopio a campo prossimo sta inoltre nel modo particolare nel particolare modo di eccitazione ottica, che coinvolge campi evanescenti, e che quindi può fornire indizi utili allo studio del fenomeno dell’accoppiamento ottico di nanoparticelle tra loro.

Questo sistema di indagine può anche essere reso sensibile all’anisotropia ottica locale della superficie, tramite una tecnica detta a “modulazione di polarizzazione”. Questa si basa sull'invio nella fibra che costituisce la sonda SNOM di una radiazione polarizzata linearmente la cui direzione di polarizzazione viene fatta ruotare linearmente nel tempo; accoppiando tale radiazione alla sonda SNOM nella regione di campo prossimo del campione è possibile ottenere un segnale modulato che fornisce una misura delle caratteristiche dicroiche della superficie del campione stesso.

Il lavoro di tesi si inserisce in questo contesto. Lo scopo principale è quello di fornire una valutazione quantitativa del dicroismo del campione in esame, resa più accurata tenendo conto delle proprietà di dicroismo e di birifrangenza proprie della sonda SNOM, che risultano modificare i risultati delle misure. Il dicroismo della sonda dipende principalmente da imperfezioni nella fabbricazione della punta, che ne riducono la simmetria assiale, mentre la birifrangenza è determinata dagli stress meccanici agenti su tutta la fibra al momento della misura, come ad esempio piegature o punti di compressione. Tutti questi effetti vanno a combinarsi nelle misure delle proprietà specifiche del campione. Il problema e' stato affrontato da un punto di vista generale per ottenere le equazioni che descrivono analiticamente il segnale misurato dal rivelatore in funzione del dicroismo del campione e delle proprietà della sonda; ho quindi ricavato l’espressione dei segnali forniti dal demodulatore lock-in del segnale ottico per ricavarne le equazioni che descrivono il dicroismo locale del campione e l’orientazione del suo asse principale a partire da segnale demodulato e dalle caratteristiche della

Introduzione

4 punta. Il passo successivo è stato quello di scrivere un programma con LabView che permettesse di applicare queste equazioni ai dati acquisiti tramite il software di acquisizione dati dello SNOM disponibile in laboratorio. Tramite un’interfaccia grafica, con questo programma si elaborano le immagini acquisite in ogni scansione per migliorarne le qualità in termini di rumore e difetti della scansione e si effettua la deconvoluzione del contributo “residuo” della sonda SNOM alla misura, una volta noto il suo dicroismo. In particolare questo programma e' stato utilizzato per analizzare quantitativamente le scansioni del campione di nanofili di argento, effettuate con due diverse illuminazioni laser per verificarne una possibile dipendenza dalla lunghezza d'onda.

L’analisi in campo prossimo è stata affiancata da una analoga in campo lontano, eseguita convenzionalmente con una misura di estinzione delle luce laser incidente, in modo da verificare la dipendenza dei risultati dalla modalità di eccitazione della nanostruttura.

Il lavoro si è quindi concluso con la presentazione di un modello interpretativo del comportamento ottico del campione, che riproduce i risultati sperimentali e permette quindi di ricavare alcune grandezze incognite quali il rapporto di aspetto delle nanostrutture otticamente attive.

La tesi si svolge in 4 capitoli:

• Nel Capitolo 1 è presentato un quadro generale della microscopia SNOM e in particolare vengono spiegati i principi di funzionamento dello SNOM a modulazione di polarizzazione utilizzato in questo lavoro.

• Nel Capitolo 2 è esposta la teoria che permette di ricavare le equazioni per la deconvoluzione del contributo residuo della sonda alle proprietà del campione, e lo sviluppo del programma che le adopera; sono inoltre presentate le funzionalità che quest’ultimo implementa.

• Nel Capitolo 3 è esposta una panoramica sul metodo di realizzazione del campione di argento nanostrutturato indagato in questo lavoro.

5 • Nel Capitolo 4 sono riportate le misure SNOM effettuate sul

campione e il trattamento dei dati tramite il programma sopra menzionato; sono riportate anche le misure di raffronto effettuate in campo lontano con i risultati ottenuti. Nell’ultima parte è presentato un modello interpretativo dei risultati ottenuti sia in campo lontano che in campo prossimo.

1 - Introduzione all’Apparato

6

1 Introduzione all’Apparato

Da alcuni decenni oramai si assiste ad un crescente sviluppo delle scienze e delle tecnologie su scala nanometrica, sia dal punto di vista della ricerca di base che sul versante applicativo. Il processo di miniaturizzazione delle tecnologie microelettroniche ed optoelettroniche ha portato alla creazione di strutture le cui dimensioni possono essere dell’ordine di un decimo della lunghezza d’onda della luce nel visibile.

Di pari passo anche gli strumenti di indagine si sono evoluti fornendo risoluzioni laterali in grado di evidenziare proprietà ottiche elettriche e meccaniche nella scala nanometrica e quindi in grado di studiare strutture che oramai raggiungo dimensioni traverse dell’ordine dei nanometri. In particolare nel 1984 [1][2] vennero realizzati i primi microscopi di campo prossimo (SNOM – di cui parleremo nei prossimi paragrafi) con una risoluzione laterale di poche decine di nanometri con luce nel visibile; con questo strumento è stato quindi possibile oltrepassare il limite di diffrazione di Abbe [3] cioè ∼λ 2, che è il limite intrinseco di risoluzione della microscopia ottica tradizionale.

1.1 Microscopia ottica tradizionale

Gli strumenti di microscopia ottica tradizionale permettono di ottenere un’immagine di un campione illuminato da una sorgente raccogliendo la luce che esso diffonde. Questi sistemi ottici sono formati in genere da una successione di elementi macroscopici, quali ad esempio le lenti, che hanno lo scopo di

7 condizionare e guidare il fascio di luce diffusa dall’oggetto verso l’osservatore. La finitezza spaziale di questi elementi però determina anche la risoluzione dello strumento. Ogni punto del campione infatti forma una figura di diffrazione sul piano immagine del sistema ottico di raccolta (vedi Figura 1).

Se per oggetti macroscopici questo fenomeno non si manifesta in modo evidente, questo diventa invece cruciale quando vogliamo studiare di un oggetto i suoi dettagli più minuti. Seguendo la teoria di Fraunhofer la diffrazione produce sul piano immagine una distribuzione spaziale di luminosità che può essere interpretata come il modulo quadro della trasformata di Fourier dell’apertura attraverso cui passa la luce nello strumento [4] quindi le informazioni sui dettagli più piccoli sono contenute nelle zone più esterne della figura di diffrazione, la quale contiene le informazioni sulle frequenze spaziali maggiori. Le ottiche di un sistema però possono raccogliere queste informazioni solo entro un certo limite, dato dalla loro geometria, che può essere valutato tramite un fattore detto apertura

numerica e dato da

. . sin

N A =n θ

Figura 1 - Esempio di figura di diffrazione ottenuta da una singola fessura orizzontale (in basso) e profilo della sua intensità luminosa (in alto).

1 - Introduzione all’Apparato

8 dove θ è il semiangolo al vertice del cono di luce che il sistema ottico può accettare quando è posto nel vuoto e n è l’indice di rifrazione del mezzo nel quale si propaga la luce. Proprio seguendo la teoria di Fraunhofer, Abbe [3] ricavò una espressione per la distanza minima necessaria per poter distinguere due oggetti illuminati da luce monocromatica di lunghezza d’onda λ. Secondo il criterio di Rayleigh1 (vedi Figura 2), ad esempio, il limite di diffrazione di Abbe vale:

0,61 sin d n λ θ .

La limitazione della microscopia tradizionale risiede quindi nell’incapacità di raccogliere le informazioni sui dettagli del campione più minuti della lunghezza d’onda.

Tuttavia questa soluzione si basa sull’ipotesi dell’interferenza di onde piane propaganti; il principio di funzionamento della microscopia di campo prossimo è invece basato sull’utilizzo di onde non propaganti le quali, come verrà accennato nel seguito, contengono le informazioni sulle alte frequenze spaziali che sarebbero andate perse con la propagazione.

1 _{Secondo questo criterio due oggetti possono essere considerati distinti nel caso in cui, nel} piano immagine, il massimo principale dell’intensità di uno degli oggetti coincide con i primo minimo dell’altro. Ciò corrisponde all’apparizione di un minimo centrale di intensità ridotta del 19% rispetto ai massimi.

Figura 2 - Sovrapposizione di fronti d'onda da due sorgenti a distanza variabile; la figura centrale rappresenta la condizione di applicazione del criterio di Rayleigh, dove il minimo centrale vale l’81% dei massimi.

9

1.2 Propagazione e campo prossimo

Si può mostrare [5] che la propagazione stessa della luce attraverso una apertura opera come un filtro passa basso. Consideriamo per semplicità solo l’ampiezza scalare del campo elettrico. Se si assume una dipendenza temporale armonica per il campo scalare allora questo verifica l’equazione di Helmholtz

2 2 0 E E c ω Δ + =

e si può ricavare la soluzione generale che descrive il campo scalare E in un punto

(

)

(

)

(

)

(

)

ed α e β indicano le frequenze spaziali.

È quindi chiaro che per frequenze spaziali minori di ω c la componente κ dell’equazione (1) è reale e quindi esprime delle onde che possono propagarsi, mentre per frequenze maggiori κ è immaginario ed esprime il fatto che onde con queste frequenze decadono esponenzialmente. Il valore massimo di k nel piano

( )

MAX

f = λ: i dettagli più piccoli di λ vengono quindi persi con la propagazione, o meglio, le grandi frequenze spaziali decadono esponenzialmente con una lunghezza di scala z=1κ (sono le cosiddette onde evanescenti) mentre le frequenze spaziali più piccole sono libere di propagarsi indefinitamente.

1 - Introduzione all’Apparato

10 La zona z λ dove sopravvivono le alte frequenze spaziali è detta Near

Field (o campo prossimo), mentre la zona z λ è detta Far Field (o campo

lontano).

Gli strumenti ottici che si usano abitualmente, come per esempio i microscopi ottici, illuminano il campione e raccolgono la luce in Far Field e questo limita la loro risoluzione angolare; per superare questo vincolo occorre recuperare le informazioni “nascoste” che si trovano nel Near Field e questo può essere fatto con due metodi complementari:

• illuminare il campione in campo lontano e raccogliere la luce scatterata in campo prossimo (collection mode o modo di raccolta);

• illuminare il campione con una sorgente luminosa di campo prossimo, che contiene le alte frequenze spaziali, e raccogliere quindi la luce in campo lontano (illumination mode o modo di illuminazione).

Il modo che è stato utilizzato in questo lavoro è il modo di illuminazione, il quale può essere configurato in “trasmissione”, per campioni trasparenti, raccogliendo la luce sull’asse della punta oltre il campione, e in “riflessione” per campioni qualsiasi, in cui la luce viene raccolta nel semispazio contenente la punta, in genere tramite un’ottica di raccolta posizionata ad una certa inclinazione rispetto all’asse della punta.

In entrambi i casi, è richiesto che il rivelatore (o l’illuminazione) sia posto in una regione spaziale dove i campi evanescenti non siano ancora estinti, cioè ad una distanza d λ dalla superficie (regione detta “di prossimità”). La misura di

campi evanescenti viene realizzata, tramite un opportuno rivelatore o illuminatore di dimensioni nanometriche e mantenuto nella regione di prossimità del campione, da un particolare tipo di microscopio a scansione a sonda denominato SNOM.

1.3 Lo Snom

I prossimi paragrafi descrivono le parti relizzative fondamentali di un sistema SNOM: la sonda, la movimentazione e il controllo della distanza-punta

11 campione. Le due ultime parti sono di utilizzo generale in microscopia a sonda, mentre la parte che caratterizza lo SNOM è più specificamente la sua sonda. 1.3.1 La sonda

Nonostante l’ipotesi sull’utilizzazione del campo prossimo fosse tutt’altro che recente [6] i mezzi tecnici necessari ad una sua rivelazione sono comparsi solo da pochi decenni; in effetti la prima utilizzazione di un campo prossimo fu fatta per la ricostruzione di proprietà ottiche con risoluzione nell’ambito delle microonde [7], perché essendo queste lunghezza d’onda dell’ordine del centimetro permettevano di ottenere campi prossimi da aperture dell’ordine del millimetro. Il primi profili ottici di un campione con una risoluzione oltre il limite della diffrazione furono ottenuti invece nel 1984 [1] tramite l’utilizzo di un cristallo di quarzo, la cui punta era stata ricoperta da una sottile metallizzazione che lasciava aperta però una apertura di poche decine di nanometri da cui la luce poteva accoppiarsi all’esterno. In un lavoro indipendente [2] veniva dimostrata la possibilità di realizzare praticamente aperture di diametro sub-λ.

Una delle implementazioni più utilizzate per realizzare la microscopia ottica di campo prossimo prevede l’utilizzazione di fibre ottiche appositamente trattate in modo da ottenere una punta dalle dimensioni di decine di nanometri [8]; le due tecniche principali per ottenere queste punte sono l’etching chimico [9] e lo stiramento [10].

La prima consiste nell’utilizzare una soluzione corrosiva in cui immergere un estremo di una fibra ottica; a causa del diverso drogaggio di core e cladding si crea un attacco chimico anisotropo che produce una punta le cui dimensioni possono essere variate regolando i parametri di concentrazione, tempo di posa e tipo di fibra.

La seconda tecnica, quella utilizzata per la fabbricazione delle fibre ottiche commerciali utilizzate in questo lavoro, consiste nello scaldare localmente un punto di una fibra ottica con un laser o con arco elettrico fino al punto di fusione e quindi stirare la fibra per creare un assottigliamento, e quindi con una forte trazione rompere la fibra ormai fredda e creare così una punta con una sezione

1 - Introduzione all’Apparato

12 apicale circolare e piatta; anche in questo caso è possibile regolare i parametri dell’operazione per ottenere il risultato voluto.

In entrambi i casi le fibre vengono ricoperte nella parte rastremata con una metallizzazione di circa 100 nm di spessore (Figura 3 e Figura 4), che nel nostro caso consiste di alluminio. Questo trattamento serve a guidare la radiazione verso l’apertura, in quanto la fibra ottica rastremata non è più in grado di confinare la luce raggiunto un diametro minimo (di cut off). La propagazione nella guida metallica dà comunque luogo ad una attenuazione esponenziale dell’intensità propagata, per cui è conveniente ridurre al minimo la lunghezza del cono dopo il diametro di cut off.

L’apertura stessa è definita a meno dello spessore pelle del metallo, dell’ordine di 10nm per luce visibile, ed ha tipicamente un diametro di 50-100nm.

Figura 4 - Immagini SEM di una fibra stirata senza il rivestimento metallico in vista laterale (a) e con il rivestimento in vista frontale (b) in cui si nota l'apertura apicale che genera il campo prossimo.

Figura 3: Schema di fibra stirata con coating di Al.

13 La potenza che può essere iniettata nella fibra è limitata a circa 1mW in quanto il rivestimento metallico assorbe parte della radiazione aumentando la sua temperatura e generando stress termici che possono creare fratture nella metallizzazione o addirittura fondere il rivestimento.

Tra i parametri più importanti relativi alla fabbricazione delle punte ricordiamo l’angolo di apertura della punta. Un angolo troppo acuto causa uno aumento della distanza tra la regione di cut off e l’apice della fibra, con conseguente aumento dell’attenuazione e drastica riduzione dell’intensità disponibile all’apertura. Attenuazioni (throughput) della luce immessa in fibra di 6-8 ordini di grandezza sono tipiche per queste sonde. Per questo motivo si cercano metodi alternativi per realizzare sonde SNOM con un angolo di apertura più grande possibile (anche oltre 40°) pur mantenendo la dimensione dell'apertura di qualche decina di nanometro.

1.3.2 La movimentazione

In microscopia a scansione di sonda la movimentazione della superficie da analizzare rispetto alla sonda viene effettuata tipicamente tramite trasduttori piezoelettrici – introdotti per questo scopo da Binnig e Smith [11] - in grado di controllare il movimento del campione su scala sub-nanometrica nelle tre direzioni. I più semplici e meno costosi sono realizzati in forma di tubo cilindrico cavo con la superficie interna ed esterna ricoperta da un film conduttore che funge da elettrodo. Di solito la superficie interna è formata da un solo elettrodo mentre quella esterna è divisa in 4 (Figura 5). Applicando una differenza di potenziale (fino al centinaio di Volt) tra l’interno e una sezione esterna si ottiene un allungamento (o accorciamento a seconda della polarità) della sezione stessa lungo l’asse del cilindro. Poiché è possibile controllare selettivamente le sezioni è possibile ottenere un qualsiasi movimento nelle tre direzioni, cioè spostamenti verticali od orizzontali.

1 - Introduzione all’Apparato

14 Osservando la Figura 5 si può notare come un tubo a 4 sezioni (come quello da noi utilizzato) possa eseguire spostamenti laterali solo tramite una sua flessione; questo provoca la comparsa del cosiddetto “artefatto di traslazione” associato al fatto che ad uno spostamento lungo una direzione laterale è associato anche un movimento lungo l’asse verticale. Questi tubi piezoelettrici presentano risoluzioni dell’ordine di grandezza del nanometro, ma il loro comportamento non è lineare con le tensioni applicate e soprattutto presenta fenomeni di isteresi che possono deformare le immagini ottenibili con la microscopia a scansione di sonda [11]. Esistono dei metodi di linearizzazione (sia hardware che software) di questi movimenti, dei quali ometto la descrizione in quanto non utilizzati nell’apparato usato in questo lavoro di tesi.

1.3.3 Il controllo della distanza sonda-campione

Nella microscopia a scansione di sonda esistono due principali modi di operare per quanto riguarda il controllo della distanza punta-campione:

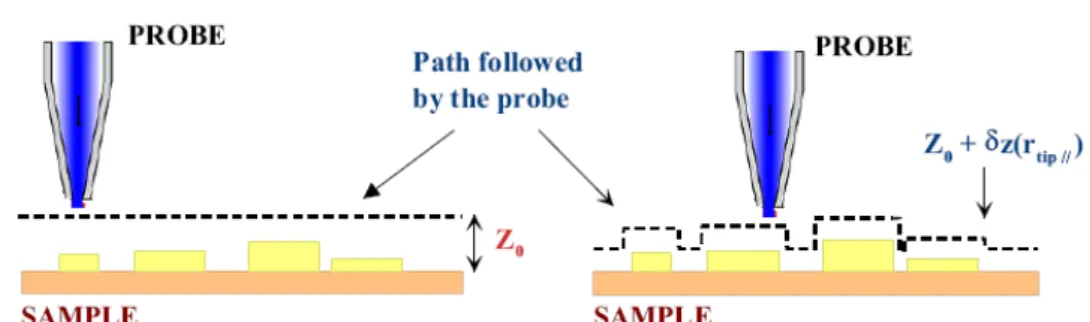
• Altezza costante (CHM): la punta viene mantenuta a distanza fissa dal piano medio del campione (Figura 6 a sinistra);

• Gap costante (CGM): la punta viene mantenuta a distanza fissa dalla superficie localmente affacciata alla sonda (Figura 6 a destra).

Figura 5 - Schema di un tubo piezoelettrico a 4 sezioni.

15 Come accennato in precedenza, per ottenere una risoluzione dell’ordine dell’apertura a della punta è necessario che questa si trovi a distanza di campo prossimo, tipicamente d <a 10 [5]: questo implica che il metodo CHM può essere utilizzato solo in presenza di rugosità sulla superficie inferiori al nanometro, per evitare due inconvenienti: 1) che il movimento della punta durante una scansione provochi un accidentale impatto col campione nel quale la punta potrebbe venire danneggiata irreparabilmente; 2) che avvallamenti di profondità molto maggiori di d non vengano adeguatamente sondati, in quanto la punta sarebbe in quei casi troppo lontana dalla superficie e fuori dalla regione di prossimità.

Il secondo metodo (quello utilizzato nel nostro apparato) risulta quindi più sicuro consentendo di evitare contatti accidentali e dando sempre la garanzia di avere la risoluzione di campo prossimo. Inoltre questo permette l’acquisizione contemporanea del dato ottico assieme a quello topografico, cioè di misurare anche la morfologia della superficie del campione, cosa che non sarebbe possibile nel modo CHM.

La stabilizzazione della punta ad un gap costante dalla superficie necessita di una valutazione continua della distanza punta-campione, che viene effettuata utilizzando una tecnica basata sulla misurazione dell’effetto della cosiddetta shear

force (o forza di taglio) [12][13] tra punta e superficie. Questa forza [14][15] si

manifesta quando, avvicinando una punta in oscillazione parallelamente alla superficie del campione ad una distanza dell’ordine di alcuni nanometri, si ha una

1 - Introduzione all’Apparato

16 diminuzione dell’ampiezza delle oscillazioni dovuta ad una interazione di tipo viscoso, smorzamento che aumenta gradualmente diminuendo la distanza.

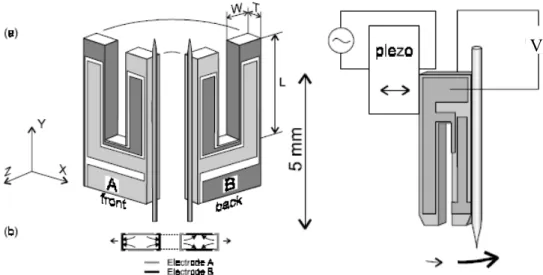
Per mettere in oscillazione la punta e misurarne l’ampiezza delle oscillazioni si utilizza una tuning fork, ovvero un cristallo piezoelettrico a forma di diapason dotato di due elettrodi. Questo elemento viene comunemente utilizzato negli orologi al quarzo ed ha forma e dimensioni tali da oscillare ad una frequenza nominale di 32.768kHz. Una volta incollata con cura l’estremità appuntita di una fibra ottica ad un rebbio della tuning fork (in modo da renderne il moto solidale) e lasciato sporgere solo la punta ad un estremo, come mostrato in Figura 7, è possibile attivare le oscillazioni tramite un segnale AC in tensione applicato ad una lastrina piezoelettrica alla quale la fork è fissata, e monitorare la risposta della stessa quando questa è in risonanza.

La distanza punta-campione viene regolata spostando verticalmente il campione tramite il movimento z del tubo piezoelettrico di scansione descritto nel paragrafo 1.3.2 . Il sistema di controllo del tubo è chiamato feedback loop, un circuito di retroazione che aggiusta in tempo reale la posizione verticale del campione in base ai rilievi incontrati durante la scansione laterale, in modo da mantenere costante l’ampiezza delle oscillazioni della punta ad un valore di set

point impostato dall’utente, di solito pari al 90% dell’ampiezza di oscillazione

libera. La differenza tra l’ampiezza attuale ed il set point viene chiamato segnale

Figura 7 - Schema di montaggio di una tuning fork con la fibra e il sistema di controllo.

17

di errore. La retroazione che pilota il movimento verticale del campione agisce in

modo da cercare di mantenere a zero tale segnale di errore, cioè in modo che la distanza sonda/campione rimanga costante anche durante i movimenti di scansione laterale. Gli allungamenti del tubo in funzione della posizione di scansione vengono registrati durante la scansione simultaneamente al segnale ottico e vengono a formare l’immagine topografica.

1.3.4 Lo SNOM utilizzato

Il microscopio SNOM presente in laboratorio è composto di tre parti fondamentali: la testa, la base e l’elettronica.

La testa (Figura 8 in alto) è la parte che caratterizza maggiormente il microscopio, dal momento che in essa sono contenute: il sostegno della sonda, il sistema di eccitazione e di misura della shear force, e il sistema di raccolta della luce se si lavora nel modo di riflessione. La sorgente luminosa, solitamente un laser, viene posizionata in remoto, in modo tale da permettere una manipolazione più agevole (per esempio quelle che descriveremo più avanti) del fascio accoppiato in fibra.

La base (Figura 8 in basso) ha il compito di sostenere la testa ed il campione, per questo è importante la sua più assoluta stabilità; la sua massa e l’isolamento dal banco ottico tramite isolatori in materiale polimerico ad alto attrito interno (unhappy balls) consentono di limitare le vibrazioni meccaniche derivanti dall’ambiente a frequenze sufficientemente basse da poter essere compensate dal sistema di feedback loop ed evitare impatti della punta con il campione. La base contiene al suo interno, al centro, il sistema di movimentazione del campione costituito dal tubo piezoelettrico sistemato verticalmente in modo tale da non ostacolarne i movimenti; all’interno di questo trova posto l’ottica di raccolta della luce (nel montaggio in trasmissione) mentre il campione viene sistemato sulla parte superiore del tubo piezoelettrico, su un supporto trasparente, in modo da permettere alla luce di raggiungere le ottiche sottostanti.

1 - Introduzione all’Apparato

18 La parte elettronica è composta da tre elementi: una parte si occupa della demodulazione, amplificazione e trattamento del segnale ottico, un’altra gestisce il feedback loop per la stabilizzazione della distanza punta-campione, mentre un’altra ancora gestisce il movimento del campione rispetto alla punta2 e l’acquisizione dei dati. Dal momento che la potenza del segnale ottico SNOM è

2 _{In questa configurazione la punta si può considerare fissa nello spazio, a parte} l’oscillazione dell’ordine del nanometro necessaria per rilevare la shear force.

A OBJECTIV E FIBER HOLDER SHEAR FORCE PIEZO FIBER X-Y TRANSLATOR SAMPLE HOLDER ASPHERIC LENS MICROMETER SCREW LENS INTERFERENCE FILTER SHUTTER PMT FOCUS STAGE PMT SOCKET Z TRANSLATOR TIP PIEZO SCANNER

5 cm

Figura 8 – Schema tecnico della testa e della base del microscopio SNOM rappresentate in sezione verticale [16].

19 dell’ordine dei nW (per potenze in ingresso in fibra dell’ordine di 1 mW) a causa del basso throughput derivante dallo smorzamento esponenziale nella sonda, è necessario raccogliere il segnale tramite un rivelatore abbastanza sensibile; quello impiegato nel nostro apparato è un fototubo miniaturizzato. Tale segnale sarà poi filtrato da un filtro passa-basso, per ottenerne il valor medio (DC), e in simultanea demodulato da un amplificatore lock-in a doppia fase, per ottenere le variazioni indotte dalla modulazione imposta dall’esterno, nel caso specifico dalla variazione della direzione della polarizzazione lineare incidente, come verrà spiegato nel paragrafo seguente. I dati vengono acquisiti in modo sincronizzato al movimento di scansione della punta da un computer dotato di apposite schede di acquisizione e di un software in grado di gestire il processo di scansione del campione. Il software fa muovere il campione relativamente alla punta su una matrice di punti stabiliti dall’operatore, lungo un percorso detto a rastrello (Figura 9) che permette di formare una immagine bidimensionale delle grandezze misurate nella superficie. Eseguire una scansione per ogni riga nelle due direzioni permette di distinguere strutture realmente presenti sul campione da effetti dipendenti dal moto di scansione, come ad esempio l’isteresi del tubo piezoelettrico o un controllo della distanza punta-campione non sufficientemente pronto.

Figura 9 - Schema del percorso a rastrello seguito dalla punta.

1 - Introduzione all’Apparato

20

1.4 Lo SNOM a modulazione di polarizzazione

Lo SNOM descritto nei paragrafi precedenti, operante nel modo di illuminazione in trasmissione, fornisce una caratterizzazione del campione in esame in base al suo assorbimento della radiazione all’apertura; quindi fornisce un meccanismo di contrasto analogo a quello di un microscopio ottico tradizionale nel modo di trasmissione, ma con una risoluzione molto più elevata. In questo lavoro di tesi ho utilizzato una particolare configurazione dello SNOM capace di fornire una caratterizzazione locale delle proprietà di anisotropia ottica dei campioni in esame: lo SNOM a modulazione di polarizzazione (PM-SNOM). Questa configurazione implementata durante precedenti lavori di tesi [17][18][19][20] era stata applicata a campioni dicroici polimerici [21][22], film superconduttori e a polimeri azobenzenici per applicazioni di scrittura ottica [23][24][25]. Nel paragrafo seguente descriverò le basi della tecnica in modulazione di polarizzazione, la sua realizzazione in laboratorio e la sua implementazione al microscopio SNOM.

1.4.1 Anisotropia ottica e matrici di Jones

Si ha anisotropia ottica quando in un cristallo si hanno indici di rifrazione e/o coefficienti di estinzione diversi per direzioni ortogonali. Le onde elettromagnetiche polarizzate linearmente lungo queste due direzioni avranno quindi comportamenti diversi esplicitabili analiticamente utilizzando il formalismo di Jones [26], nel quale si rappresenta la luce polarizzata tramite vettori e gli elementi ottici tramite matrici. In questo formalismo matriciale la luce polarizzata viene rappresentata come

( )

( )

Quindi, definendo un sistema di coordinate destrorso in cui la direzione di propagazione è lungo l’asse z e la direzione verticale è lungo l’asse x, si può scrivere per una polarizzazione lineare verticale:

21

( )

La rappresentazione invece di un campione anisotropo in cui l’asse principale è lungo x avviene tramite una singola matrice:

1 2 0 0 in z in z e C e ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ (3)

Dove n_j =k_j +iα_j è l’indice di rifrazione complesso del materiale di cui è costituito il campione, k è l’indice di rifrazione, che è associato alla _j

birifrangenza (cioè alla variazione di fase rispetto alla radiazione incidente associata al passaggio di luce polarizzata lungo l’asse j del cristallo), α_j è il coefficiente di estinzione per luce polarizzata lungo la direzione j e z è lo spessore

attraversato dalla luce. Moltiplicando le espressioni (2) e (3) si ottiene quindi:

1 1 1 2 2 1 1 2 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 i i in z z ik z z ik z in z ik z z ik z z birifrangenza dicroismo e e P E E e e e e E e e α α α α − + − + − − ⎛ ⎞⎛ ⎞ ⎛ ⎞⎛ ⎞ = _{⎜ ⎟⎜ ⎟}= _{⎜ ⎟⎜ ⎟}= ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞⎛ ⎞⎛ ⎞ = _{⎜ ⎟⎜ ⎟⎜ ⎟} ⎝ ⎠ ⎝ ⎠⎝ ⎠ (4)

Si può quindi osservare che l’anisotropia si manifesta sotto due diversi aspetti: assorbimenti diversi (dicroismo) e sfasamenti diversi (birifrangenza), rappresentati analiticamente nell’ultimo membro dell’espressione (4) e dipendenti dal valore dell’indice di rifrazione.

Normalmente l’indice di rifrazione viene definito caratterizzando proprietà medie di oggetti estesi. In questo lavoro avremo a che fare con strutture nanometriche per le quali è tuttavia possibile definire queste quantità nello stesso modo, considerando che l’interazione che produciamo è di dimensioni estremamente locali ma non a tal punto da trattare le molecole o gli atomi singolarmente. In effetti anche in questo caso si compie un’operazione di media, anche se su una superficie estremamente ridotta; potremo pertanto definire il dicroismo analogamente al caso macroscopico ed utilizzare lo stesso formalismo.

1 - Introduzione all’Apparato

22 Dal momento che il comportamento del campione può dipendere dalla polarizzazione della luce incidente, il metodo di indagine più conveniente consisterà nell’inviare radiazione polarizzata a vari angoli e rilevare così le variazioni presenti nella radiazione trasmessa rispetto a quella incidente. Per realizzare questo tipo di analisi dovremo dotarci quindi di un sistema in grado di produrre in modo controllato luce polarizzata a vari angoli e di una fibra ottica (la stessa che ci farà da sonda) in grado di mantenere il più possibile la polarizzazione in ingresso.

Non è intuitivo che il campo prossimo generato da un’apertura di diametro

a<λ possa presentare una polarizzazione arbitraria, dato che si tratta di un campo che ha una componente non propagante. In particolare applicando la teoria di Bethe-Bouwkamp che descrive i campi elettromagnetici in corrispondenza di un’apertura di diametro a<λ in uno schermo metallico piano infinito [26][28] si trovano le seguenti espressioni di campo:

( )

( )

per luce incidente polarizzata lungo x. Esiste inoltre anche una componente del

campo elettrico lungo z caratteristico di un’onda longitudinale. In conclusione il

problema è molto complesso e nel seguito noi considereremo un effetto medio delle varie polarizzazioni presenti all’apertura che può essere misurato, come media sull’area illuminata, tramite appositi campioni dicroici con spessore minore di λ in modo da agire solo al livello del campo prossimo [21]. Questo tipo di verifica fornisce una misura diretta del grado di polarizzazione lineare, intesa sempre come media sull’area illuminata, e consente di regolare l’ellitticità della polarizzazione in ingresso al sistema in modo da compensarne il contributo residuo. In questa tesi si è usato invece un diverso tipo di approccio, basato sulla misura del dicroismo della punta e sulla sua deconvoluzione software come illustrato nel Capitolo 2.

23 1.4.2 La polarizzazione rotante

Il metodo scelto per ottenere una polarizzazione rotante consiste nell’utilizzo di un modulatore elettro-ottico (EOM), cioè di un dispositivo ottico nel quale un elemento ottico attivo (solitamente un cristallo) mostra un effetto elettro-ottico pilotabile da un segnale elettrico esterno. Il funzionamento di questo dispositivo è paragonabile al principio dell’effetto Pockels (o effetto elettro-ottico lineare), che consiste in una variazione dell’indice di rifrazione di un mezzo ottico proporzionale al campo elettrico applicato, cioè, al primo ordine nel campo elettrico E:

3 0

n n E

Δ ∝

dove Δn è la variazione dell’indice di rifrazione e n l’indice di rifrazione a ₀

campo nullo. Se il campo è applicato lungo un asse di un cristallo di lunghezza l

avremo quindi per i due stati di polarizzazione la seguente differenza di fase:

2 n l π φ λ ⋅ Δ Δ = (6)

Utilizzando il formalismo di Jones si può mostrare come ottenere una rotazione continua dell’asse di polarizzazione lineare tramite un segnale pilota lineare nel tempo.

Supponiamo di applicare un campo elettrico ad un cristallo lungo un suo asse (che definiremo x), a causa dell’effetto Pockels si ottengono quindi due indici

di rifrazione n₀ + Δ e n n associati rispettivamente all’asse lungo cui è applicato ₀

il campo elettrico e quello perpendicolare; se la luce in ingresso è polarizzata lungo uno dei due assi avremo solo una variazione della fase assoluta all’uscita del cristallo, se invece è polarizzata a 45° rispetto all’asse principale, cioè

( )

( )

dove η π è la frequenza della radiazione, all’uscita si manifesta un ritardo di 2

1 - Introduzione all’Apparato 24

(

)

( )

A questo punto è chiaro che applicando un campo elettrico E tale da rendere la differenza di fase (6) uguale a π si ottiene all’uscita dal cristallo una 2

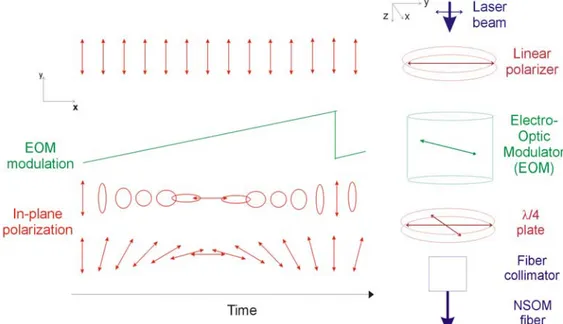
polarizzazione circolare, mentre per Δ uguale a φ π si ottiene in uscita una polarizzazione lineare ortogonale a quella incidente. Se si applica quindi un campo elettrico variabile con una forma d’onda a dente di sega opportunamente calibrato si può passare senza soluzione di continuità da una polarizzazione lineare a quella ortogonale passando attraverso una sequenza di polarizzazioni ellittiche, circolari e di nuovo ellittiche (ma perpendicolari alle precedenti) come mostrato in Figura 10.

L’inserimento successivo di una lamina λ , con il suo asse ruotato a 45° 4

rispetto all’asse x del cristallo, permette di convertire le polarizzazioni circolari ed ellittiche intermedie in polarizzazioni lineari; a questo punto in uscita dalla lamina

4

λ si ha una polarizzazione lineare il cui asse ruota linearmente nel tempo con E come illustrato in Figura 10 e come si ricava nella seguente equazione:

0 0 0 1 0 1 2 1 2 0 1 2 1 2 1 0 _{1 2 1 2} 0 1 _{1 2 1 2} 0 cos 2 sin 2 i t elettro otico e P E i t E t ω ω ω − ⎛ − ⎞⎛ ⎞⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟}⎜_⎜ ⎟_{⎟⎜ ⎟}⎜_⎜ ⎟_{⎟⎜ ⎟}= − ₋ ⎝ ⎠⎝ ⎠⎝ ⎠⎝ ⎠⎝ ⎠ ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ (8)

25 1.4.3 Misura dell’anisotropia ottica

Il microscopio SNOM a modulazione di polarizzazione si realizza accoppiando alla fibra SNOM la radiazione di un laser preparata come sopra esposto, cioè interponendo in sequenza un modulatore elettro-ottico e una lamina

4

λ adatta alla lunghezza d’onda usata.

L’apparato sperimentale va completato con la parte di condizionamento e demodulazione del segnale ottico. Usando le matrici di Jones otteniamo il segnale in intensità misurato dal rivelatore oltre la punta SNOM e il campione che presenti una direzione di anisotropia lungo un asse x che formi un angolo θ rispetto alla direzione di polarizzazione in uscita dalla punta SNOM quando t=0

1 1

2 0

cos sin 0 cos sin

sin cos 0 i sin cos

z ik z z ik z campione e P P e α α θ θ θ θ θ θ θ θ − + − + − ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ =_{⎜ ⎟⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠⎝ ⎠ (9)

( )

( )

(

)

(

)

(

)

1 - Introduzione all’Apparato

26 Nell’equazione (10) I è l’intensità misurata, Δa e a rappresentano rispettivamente l’ampiezza del segnale ottico modulato dalla rotazione della polarizzazione incidente (AC) e il segnale medio (DC). Definiamo il dicroismo come il rapporto tra l’ampiezza di modulazione (AC) e il valore medio del segnale di intensità (DC) che vale quindi:

I I a AC a DC I I γ ⊥ ⊥ − Δ = = = +

Dove I è l’intensità registrata a θ =0 e I_⊥ quella registrata a θ π= 2. Segnali così fatti possono essere misurati direttamente tramite un amplificatore

lock-in a doppia fase, che può fornire il valore di Δa e 2θ una volta riferito alla

frequenza ω che è poi quella di pilotaggio del modulatore elettro-ottico. Il segnale in DC (cioè il segnale medio) potrà essere misurato invece tramite un filtro passa-basso dal segnale prodotto dal rivelatore, una volta impostata una frequenza di taglio molto minore della frequenza di modulazione della polarizzazione.

Nell’equazione (10) i termini di AC e DC sono stati scritti come funzioni solo di α, in quanto nel montaggio non è stato inserito alcun polarizzatore tra campione e il rivelatore. In questo modo infatti i termini di birifrangenza del campione non hanno alcuna influenza sulla misura del dicroismo. Come vedremo, questo è strettamente vero nell’ipotesi che gli assi dicroici e di birifrangenza coincidano [30], che generalmente è una condizione soddisfatta nei comuni materiali.

Come abbiamo accennato nel paragrafo 1.3.2, la scansione del campione avviene su una matrice, che di solito scegliamo di 128 128× punti, stesa su una superficie le cui dimensioni possono essere variate a piacere dall’operatore entro la dimensione massima di _{13 13 μm×} 2 _{stabilita dal software di gestione dello}

27 matrici di dati, rappresentate dal software come pseudoimmagini3, ottenute con i valori acquisiti sui punti della matrice tramite i vari canali di misura: per ogni punto vengono cioè acquisiti i valori di topografia, e le misure di AC in ampiezza e fase e di DC, il tutto reso possibile in tempi non troppo lunghi (30 minuti ad immagine) dalla velocità dell’EOM che in genere viene fatto lavorare a una frequenza di circa 3 kHz, molto superiore quindi a quella dei polarizzatori rotanti impiegati in passato che potevano a stento raggiungere i 100 Hz, provocando per altro vibrazioni deleterie per la misura.

3 _{Per pseudoimmagine si intende un qualsiasi grafico 3D che mostri i valori della variabile} dipendente come colori appartenenti ad una scala cromatica arbitraria. In questo senso le fotografie e le immagini tradizionali possono essere considerate come casi particolari di pseudoimmagini.

2 - Il trattamento dati

28

2 Il trattamento dati

I dati SNOM acquisiti non permettono una valutazione quantitativa immediata delle proprietà di anisotropia del campione in quanto influenzate dalle proprietà ottiche della sonda. Infatti quest’ultima non traduce generalmente la polarizzazione in ingresso alla fibra direttamente nel campo prossimo, ma può introdurre dicroismo e birifrangenza residui. La presenza di imperfezioni microscopiche nella fabbricazione della punta possono portare, ad esempio, alla presenza di un suo dicroismo che andrà quindi a combinarsi con quello proprio del campione. Inoltre il posizionamento stesso della fibra nell’apparato sperimentale può portare un effetto di birifrangenza, dipendente dal modo stesso in cui è stata sistemata ed in particolare dagli stress a cui è sottoposta, anch’esso capace di influenzare il risultato.

È quindi necessario realizzare un programma che permetta di estrarre informazioni quantitative sul dicroismo locale dei campioni analizzati attuando una deconvoluzione dei contributi dovuti alla sonda.

2.1 Deconvoluzione dell’anisotropia della sonda

In questo lavoro si è rappresentato il campo prossimo tramite il formalismo delle matrici di Jones, valido in condizioni di campo propagante, in quanto utilizzando luce polarizzata si è assunto che il campo prossimo presenti caratteristiche di polarizzazione mediate sull’area dell’apertura analoghe a quelle di un campo propagante. Questo approccio, adottato in letteratura [29] ed in

29 precedenti lavori di tesi [3], è in realtà solo un’approssimazione. Abbiamo inoltre assunto che gli assi principali del dicroismo e della birifrangenza dovuti alla sonda siano coincidenti, il che non è vero in generale. Nel seguito esporrò la teoria approssimata alla base dell’algoritmo di deconvoluzione del dicroismo della sonda che verrà poi implementato nel programma descritto più avanti, dimostrando appunto che la sua validità è limitata al caso di birifrangenze lungo un particolare asse. Per ovviare a questa limitazione l’apparato sperimentale è stato dotato di un sistema di controllo della birifrangenza della fibra SNOM, che sarà descritto più avanti, e che potrà essere utilizzato per minimizzare la birifrangenza residua della fibra. Questo sistema, tuttavia, non è stato sfruttato per le misure riportate in questa tesi, dove invece abbiamo verificato che tale birifrangenza residua non fosse troppo alta scegliendo un percorso per la fibra ottica che fosse quanto più possibile privo di piegature e compressioni. È possibile misurare tutte le componenti di dicroismo e birifrangenza, indipendentemente dai loro assi principali, ma questo richiede anche la misura della componente del segnale modulato alla seconda armonica come proposto in [30], comportando però una ulteriore complicazione strumentale.

Riprendendo il risultato dell’equazione (9) possiamo aggiungere il contributo di anisotropia della punta (costituito da termini di birifrangenza e dicroismo nel caso particolare in cui i loro assi principali siano allineati) il cui asse principale verrà considerato d’ora in poi l’asse di riferimento (o asse principale) del sistema. Abbiamo quindi:

1 1 2 1 1 2 0 cos sin 0 sin cos 0 cos sin 0 sin cos 0 i i z ik z z ik z l iw l l iw l e P e e P e α α β β θ θ θ θ θ θ θ θ − + − + − + − + − ⎛ ⎞ ⎛ ⎞ =_{⎜ ⎟⎜ ⎟}⋅ ⎝ ⎠⎝ ⎠ ⎛ ⎞ ⎛ ⎞ ⋅_{⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠ (11)

dove ,α β_{i i} sono i termini di birifrangenza rispettivamente del campione e della fibra relativi all’asse i, ,k w sono i coefficienti di estinzione (dicroismo) del _{i i}

campione e della fibra relativi all’asse i, z è lo spessore del campione, ed l è una lunghezza equivalente a cui sono associati i termini di birifrangenza e dicroismo

2 - Il trattamento dati

30 della fibra. P è invece il vettore definito nell’equazione (8) che rappresenta la ₀

polarizzazione rotante accoppiata in fibra.

Se adesso vogliamo valutare l’intensità raccolta dal rivelatore possiamo calcolare

( )

( )

(

( )

)

(

)

(

)

( ) ( )

cos cos 2 cos

cos 1 2 sin 2 sin

I P P ab a b t a b b t a b b l w w t ω θ ω θ ω = = + ⋅ Δ + Δ Δ + + +Δ − Δ − , (12)

dove per semplificare la notazione si sono operate le sostituzioni seguenti:

(

)

(

)

(

)

(

)

Si può notare anche in questo caso la mancanza dei termini relativi alla birifrangenza del campione, che come avevamo già accennato in 1.4.3, non sono rilevabili in assenza di un polarizzatore posto davanti al rivelatore, più alcuni termini dovuti però alla birifrangenza della sonda SNOM.

La componente DC del segnale può essere facilmente derivata dall’equazione (12) considerando solo la componente continua:

( )

cos 2

DC=ab+ Δ Δa b θ (13)

La componente alternata F_AC = −I DC risulta:

( )

(

)

( )

(

)

(

)

( ) ( )

AC F I DC a b a b t a b b l w w t θ ω θ ω = − = ⋅ Δ + Δ ⋅ + +Δ − Δ − (14)

Se adesso facciamo l’ipotesi che il dicroismo della fibra definito come Δb b sia molto piccolo, cioè

(

)

( )

( )

(

(

)

) ( ) ( )

( )

(

( ) ( )

(

(

)

) ( ) ( )

)

cos 2 cos cos 1 2 sin 2 sin

cos cos 2 cos cos 1 2 sin 2 sin

AC F b a a t l w w t DC b a a b a t t l w w t b a θ ω θ ω ω θ ω θ ω Δ Δ Δ = + + − = Δ Δ = + + − ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ₍₁₅₎

31 Si nota quindi che nel caso in cui l’asse di birifrangenza e quello dicroico della fibra siano allineati ma il contributo di birifrangenza di questa non sia trascurabile si ottiene che la misura di dicroismo viene sottostimata. Questo inconveniente viene eliminato solo tramite l’ipotesi aggiuntiva w₁ ≅w₂ cioè avendo una birifrangenza trascurabile.

In questo caso, dall’equazione (15) possiamo ottenere una espressione molto semplice del segnale al rivelatore:

( )

(

)

In una rappresentazione vettoriale (Figura 11) il segnale alternato è caratterizzato da una ampiezza AC DC e da una fase 2ϕ:

(

)

( )

( )

( )

( )

( )

Nella coppia di equazioni (18) i termini AC e 2φ sono in realtà noti perché sono forniti dal demodulatore lock-in e lo stesso vale per DC che viene fornito dal

Figura 11 – Rappresentazione vettoriale dell’equazione (16) [31]; nella notazione utilizzata in questa tesi φ →ϕ.

2 - Il trattamento dati

32 filtro passa-basso. Se supponiamo noto il dicroismo della punta, la precedente coppia di equazioni forma quindi un sistema di due equazioni in due incognite che può essere risolto per ottenere Δa a, il dicroismo del campione, e 2θ che rappresenta l’angolo tra l’asse principale della fibra e quello del campione. Invertendo queste equazioni si può ottenere:

( )

( )

( )

Quindi le due equazioni (19) ci permettono di ottenere il valore locale del dicroismo e l’angolo relativo del suo asse principale per ogni punto di scansione del campione. Le ipotesi utilizzate sono due: 1) che il dicroismo della punta sia piccolo, ma non è necessario che questo sia minore del dicroismo del campione; 2) la birifrangenza della fibra sia trascurabile. Nel caso ciò non fosse la misura del dicroismo del campione viene sottostimata. Come accennato in precedenza, con l’uso di un sistema di controllo della birifrangenza della fibra, come ad esempio un fiber paddle, o un compensatore Babinet-Soleil posto all’ingresso della fibra, si può soddisfare l’ipotesi 2), mentre la soddisfazione dell’ipotesi 1) dipende dalla qualità della punta SNOM e dalla preparazione del fascio laser accoppiato in fibra.

2.2 Il programma di elaborazione

Lo sviluppo del programma per utilizzare le equazioni ricavate sopra fa parte del lavoro originale che ho svolto per questa tesi. In base alla mia valutazione del problema e alle esigenze di avere un programma semplice e facile da utilizzare, ho scelto il linguaggio che ho ritenuto più adatto.

33 2.2.1 Il linguaggio scelto

La scelta del linguaggio di programmazione è certamente il primo scalino che si incontra quando si deve realizzare un programma che assolva uno scopo ben preciso, come quello di valutare il dicroismo di campioni studiati con lo SNOM, partendo da zero. Nel laboratorio erano presenti vari programmi di trattamento di immagini anche molto sofisticati. I programmi commerciali non davano l’accesso al codice sorgente per una eventuale modifica. Erano tuttavia presenti due programmi, uno in Visual Basic, che sarebbe stato possibile modificare, ed un altro scritto come insieme di macro comandi di Igor [32], un software di analisi per spettroscopia, che già implementava alcune routine di deconvoluzione [19][20]. Ritenendo le piattaforme di sviluppo dei precedenti programmi obsolete o non facilmente esportabili, ho preferito optare per la realizzazione di un nuovo programma in linguaggio LabView4 _{[33] che è molto} diffuso nell’ambiente della ricerca scientifica ed è compatibile con la maggior parte dei sistemi. Questa scelta comporta una serie di vantaggi, tra i quali:

1. Interfaccia grafica

2. Facile accessibilità nel caso fosse necessaria una modifica 3. Semplicità di utilizzo e trasportabilità

LabView era in grado di soddisfare le tre condizioni, e inoltre avendo già dimestichezza con tale linguaggio, avrei potuto essere più autonomo ed efficiente nella realizzazione del progetto. Con questo linguaggio è possibile creare eseguibili con una interfaccia grafica che non necessitano di un compilatore per poter funzionare e l’accessibilità è data dalla particolare natura del linguaggio che risulta in breve tempo intuitivo almeno nella sua interpretazione.

4 _{Acronimo di Laboratory Virtual Instrumentation Engineering Workbench; è l’ambiente} di sviluppo di un linguaggio di programmazione grafica chiamato “G” basato sul concetto di flusso di dati, per cui una istruzione viene eseguita solo quando si hanno a disposizione tutti gli input senza altri vincoli; nei linguaggi tradizionali invece l’ordine delle istruzioni determina l’esecuzione del programma. È sviluppato dalla National Instruments.

2 - Il trattamento dati

34 LabView è un linguaggio di programmazione di alto livello che consente di scrivere programmi tramite una semplice interfaccia grafica. In questo linguaggio le funzioni sono rappresentate da icone con vari connettori per gli input ed output, mentre il flusso dei dati, cioè i collegamenti degli input e degli output tra le varie funzioni, viene gestito tramite fili5 _{che collegano tra loro le vari parti del progetto;} in questo modo la stesura di un programma consiste nella realizzazione dei percorsi che devono seguire i dati attraverso le varie funzioni/icone.

I programmi, che in questo linguaggio sono detti Virtual Instruments (VI), si presentano formati da due parti distinte ma interdipendenti: il pannello di controllo e il diagramma a blocchi. Nel primo sono presenti gli elementi di interfaccia del programma con l’utente, mentre il secondo contiene le routine di funzionamento del programma; quest’ultima parte può essere, se necessario, resa inaccessibile al fine di evitare modifiche del VI.

A fini illustrativi In Figura 12 e in Figura 13 riporto un semplice programma dimostrativo che ho scritto.

5 _{In questo linguaggio i fili rappresentano quello che sono le variabili per i linguaggi} tradizionali.

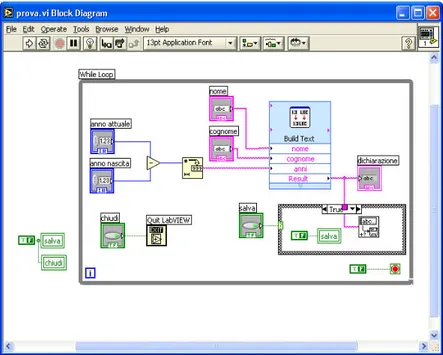
Figura 12 – Screen capture del pannello frontale di una semplice VI.

35 Questo programma legge i campi immessi da tastiera dall’operatore (nome, cognome, anno attuale e anno di nascita) con cui compila una semplice dichiarazione nella quale vengono calcolati gli anni dell’operatore stesso; questa frase, che può essere letta in un riquadro, può essere anche salvata in un file di testo; è anche presente un pulsante per chiudere il piccolo programma. Sono chiaramente visibili i fili che escono dagli input del programma (chiamati

controlli) e, passando per le funzioni interne (le icone con fili in ingresso e in

uscita), raggiungono gli output, chiamati indicatori; il while loop che racchiude il tutto è necessario per mantenere il programma costantemente vigile riguardo le modifiche che l’operatore può introdurre nei controlli e modificare di conseguenza anche i valori mostrati dagli indicatori.

2.2.2 Introduzione al programma

Per prima cosa è stato necessario fornire al programma una procedura per estrarre le informazioni che il software di acquisizione dello SNOM scrive all’interno del file di salvataggio delle immagini; questo file contiene un header

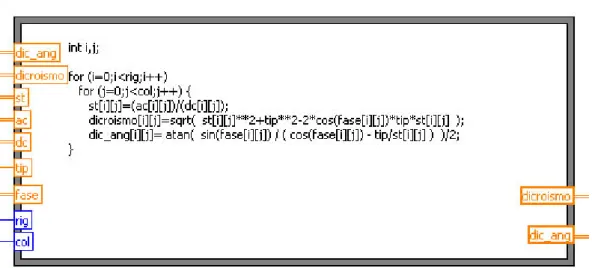
Figura 13 – Screen capture del diagramma a blocchi corispondente al pannello di controllo dell’immagine precedente.

2 - Il trattamento dati

36 dove sono scritti, tra l’altro6, i numeri di righe e colonne delle matrici delle immagini (di solito 128x128) e in coda a questo vengono elencati in ordine tutti gli elementi delle 7 matrici che corrispondono ai seguenti canali dello SNOM:

1. topografia 2. topografia reverse7 3. AC 4. AC reverse 5. errore 6. fase 7. DC

Dopo aver letto nell’header le dimensioni delle matrici (che chiameremo n e

m) è stato quindi possibile estrarre i valori delle entrate delle singole matrici per

costruire una matrice tridimensionale (chiamata nel programma matrice totale) di dimensioni

(

)

colonna. Una volta fatto questo è possibile agire sulle singole matrici o su più

matrici contemporaneamente a partire dallo stesso filo selezionando il giusto indirizzo di pagina. La quantità 7 2+ si riferisce alle 7 matrici presenti nel file alle quali si è scelto di aggiungerne altre due vuote in cui inserire i due dati che vengono forniti dalle equazioni della deconvoluzione (19); è possibile accedere alle varie matrici tramite una selettore con i nomi dei 7 canali più quelli di

6 _{Nell’header sono contenuti tutti i parametri della scansione; ho scelto però di estrarre solo} i parametri indispensabili al funzionamento del programma.

7 _{Nel percorso di scansione a rastrello che esegue lo SNOM (Figura 9), sono i dati che} vengono raccolti percorrendo a ritroso le linee orizzontali, cioè da destra a sinistra.

8 _{Nel programma l’indice di pagina assume in realtà valori da 0 ad 8 percorrendo così i} canali dello SNOM nello stesso ordine in cui sono stati presentati; per evitare la confusione dell’indice zero nel testo sono numerati da 1 a 9.

37

deconvoluzione e deconvoluzione ang relativi alle due matrici prodotte dalla

deconvoluzione.

È stato necessario creare anche un cluster (simile alle strutture del C ) in cui inserire i vari parametri della scansione tra i quali ad esempio il dicroismo della punta, il valore della fase di riferimento impostata sul demodulatore lock-in, e il suo fattore di sua amplificazione. Questi valori vengono utilizzati per tradurre i dati forniti dal lock-in e dal filtro passa-basso nelle giuste unità di misura.

Una volta caricati i dati nella matrice totale, le matrici che la compongono possono essere visualizzate una per volta scegliendole da un selettore multitab in base al nome. Dato il loro numero ho preferito optare per questa soluzione invece di visualizzarle tutte contemporaneamente sullo schermo; questa configurazione permette anche di lasciare molto spazio libero dove distribuire i vari comandi e i settaggi del programma. La visualizzazione delle immagini è indipendente dal flusso dei dati: in base al canale scelto nel selettore (topografia, AC, …) il programma estrae la matrice corrispondente e da questa calcola una nuova matrice, scalando linearmente i dati, in modo da adattarli all’intervallo 0-255 tipico delle immagini in scala di grigio a 8 bit (dove per 0 si intende il tono nero e per 255 il tono bianco). Per migliorare la percezione delle immagini ho anche inserito un semplice grafico 3D che consente di visualizzare meglio alcuni elementi caratteristici delle immagini, come l’intensità del rumore o la dimensione di certe strutture; queste infatti potrebbero essere non facilmente riconoscibili se poste in zone di luminosità troppo elevata: l’occhio umano (la cui curva di sensibilità è circa logaritmica) è infatti più sensibile alle variazioni nei toni scuri che non di toni chiari.

2.2.3 I filtri

Dopo aver scelto il linguaggio è stato necessario stabilire cosa questo programma dovesse essere in grado di fare. Ovviamente la parte relativa alla deconvoluzione era necessaria, ma oltre a questa erano necessarie anche alcune funzioni utili per trattare le immagini grezze fornite dal software dello SNOM.

2 - Il trattamento dati

38 Il set di strumenti utilizzabili per elaborare le immagini acquisite è mostrato in Figura 14 le immagini possono contenere linee difettose9 _{(in genere} orizzontali), piani indesiderati10 o fluttuazioni dovute a oscillazioni della potenza del laser…

È importante notare che questi filtri funzionano operando direttamente sui dati e modificandoli, non sulle immagini visualizzate che sono solo una rappresentazione di quanto contenuto nelle matrici. Nonostante questo, per facilitare la comprensione ho scelto di confondere nel seguito la dicitura dati con quella di luminosità e le matrici con le immagini, data la visualizzazione - appunto per immagini - dei dati stessi.

9 _{Può capitare per esempio che a causa di strutture particolari sulla superficie del campione} la punta perda il contatto per qualche pixel: nelle immagini topografiche queste linee si presentano discontinuità in direzione verticale.

10 _{Sempre nelle immagini topografiche, l’artefatto di traslazione può provocare la} formazione di un gradiente predominate sommato alla vera topografia della superficie analizzata, oppure la superficie del campione può non risultare perfettamente parallela al piano di scansione.

Figura 14 - Screen capture con l'elenco dei filtri disponibili nel programma