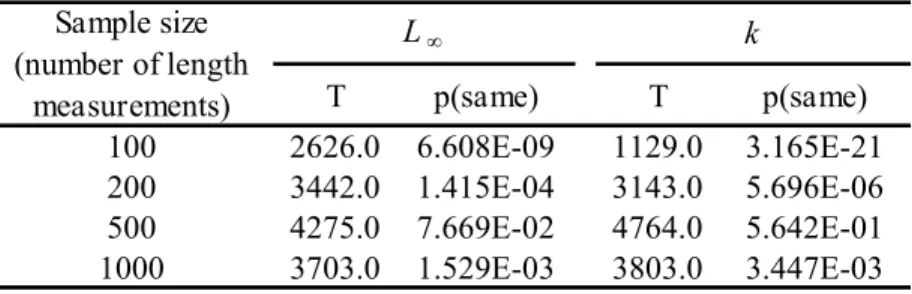
New insights into fish growth parameters estimation by means of length-based methods
Testo completo
Figura


Documenti correlati
Heterocyclic analogs of benzanilide derivatives as potassium channel activators. 1,2,3-Triazol-carboxanilides and 1,2,3-(N-benzyl)-carboxamides as BK- potassium
A tutti quelli che hanno creduto in me senza caricarmi del peso delle loro aspettative e mi hanno sostenuto nei momenti
Al ritorno negli Stati Uniti, nel 1874, fu accolta con grande ammirazione sia a Boston che a Filadelfia, ricevendo applausi da molta parte della critica dell’epoca; Henry
The method presented in this article is based on three core algorithmic ideas: mean shift clustering to detect soma centers (Section 2.2), supervised semantic deconvolution by means
x the constitutive equations of both parent material and FSWed zone were used as input data in the FE simulation of the cold stamping process of the friction stir welded blanks;.
L’uso del paradigma analitico del morfotipo rurale ha consentito di descrivere e, soprattutto, di spazializzare, con una approssimazione riferibile alla scala
Maximum interbuilding approaches corresponding to the un- controlled configuration (black line with squares), the active controller defined by the control gain matrix K (red line
Resta da stabilire, dunque, quali siano gli strumenti più efficaci per assicurare che effettivamente il ruolo dei consumatori all’interno del mercato non sia