Il Calcolo delle Probabilit: varaiabili aleatorie continue e discrete

Calcolo delle probabilità

Progetto lauree scientifiche

Università dell’Insubria

Facoltà di Matematica

Como

Paola Bertoncello Natalina Drappo

Introduzione

alla probabilità

assumibili dai risultati sia finito o numerabile

Analisi degli esiti di esperimenti aleatori

Grandezza i cui valori siano i possibili esiti di un esperimento

Risultato del lancio Mano di poker

Esito di un esperimento aleatorio

Insieme degli eventi elementari Evento

Sottoinsieme dello spazio campionario

testa testa TT

{TT, TC, CT, CC }

{TT, TC, CT} di due monete

Probabilità classica di un evento E

_____________

P(E)= Casi favorevoli Casi possibili

Proprietà

E = esce almeno una testa IEI = 3 Ω = spazio campionario

del lancio di due

I Ω I = 4 P(E) = ¾ monete

0≤P(E) ≤1 P(Ec)=1-P(E)

Ec= non esce alcuna

testa

IEcI = 1 P(Ec) = 1/4

E כֿ F → P(E) > P(F)

F= esce una testa = {TC, CT} IFI=2 _P(F)=1/2 TT CC TC CT Ω E F

Strumenti matematici

per lo studio della probabilità

Disposizione semplice

Selezione ordinata di k elementi di un insieme finito di dimensione n

Elenco degli studenti seduti nella prima fila Primi tre classificati di una gara

Problema: quante disposizioni si

presentano nell’estrazione di due palline da un sacchetto che ne contiene 4 diverse?

Soluzione: 4 possibilità per la prima pallina

per ogni scelta della prima ci sono 3 possibilità per la seconda per ogni scelta delle precedenti ci sono 2 possibilità per la terza

Regola:

Altri esempi e relative soluzioni:

• Il numero di modi in cui disporre 4 alunni in prima fila in una classe di 25 studenti è 25 · 24 · 23 · 22 = 303600

• le possibili disposizioni dei numeri della prima cinquina della tombola sono 90 · 89 · 88 ·87 · 86 > 5 1010

Il numero di k-disposizioni semplici di n elementi è n · (n-1) ·… · (n-k+1)

Usando il fattoriale di n, definito come n! =n · (n-1) · (n-2) · ….. · 1 ottengo:

D _k,n = _____n! (n-k)!

Disposizione con ripetizione

Elenco di k elementi ordinati di un insieme di dimensione n per cui è prevista la ripetizione

Pin del telefono Lancio di tre dadi

Problema: quanti prefissi telefonici si possono

scrivere con tre cifre?

Soluzione:

9 possibilità per la prima cifra

Per ogni scelta della prima cifra ho 9 possibilità per la seconda Per ogni scelta delle prime due cifre ho 9 possibilità per la terza

Altri esempi e relative soluzioni:

Regola:

• Il numero di colonne possibili del totocalcio è 313 = 1594323

• il numero di targhe che si può ottenere con 4 numeri e 2 cifre finali è 104 · 262 = 6760000

Il numero di k-disposizioni con ripetizione di n elementi è D _k,n = nk

… nota

• il numero di password di 8 cifre che si possono scrivere con cifre alfanumeriche maiuscole e minuscole senza

Permutazione (semplice)

Possibile ordinamento di un insieme finito di elementi

È una n-disposizione semplice di n elementi

Ordine di arrivo ad una gara Posizione dei libri in una libreria

Problema: in quanti modi posso distribuire i 25 studenti di una classe?

Soluzione: partendo dal primo banco, per il quale ho 25 possibilità, ad ogni scelta successiva ho uno studente in meno a disposizione, per cui ho

25 · 24 · 23 · …..2 · 1 = 25! Regola

Estrazioni del lotto Combinazioni

Raggruppamenti di k elementi di un insieme di dimensione n

= possibili sottoinsiemi Studenti interrogati

Problema: quante scelte ha un professore se interroga 4 persone in una classe di 25?

Soluzione:

Il numero di 4-disposizioni di 25 elementi è 25!/21! Le disposizioni con gli stessi elementi in cui cambia solo l’ordine corrispondono alla stessa composizione

Il loro numero corrisponde al

numero di permutazioni: sono 4!

Le combinazioni sono 25!____

Altri esempi e relative soluzioni:

Regola:

• Il numero di combinazioni vincenti del SuperEnalotto è

Il numero di sottoinsiemi di k elementi di un insieme di dimensione n è n!

(n-k)!k! C _k,n = ______ ______ 90!

84!6!

Definisco coefficiente binomiale il valore

Probabilità composta

definizioni

X, Y variabili indipendenti A, B eventi indipendenti

I Ωx J Ωy si haA ∩ A ∩ _{P(I J) = P(I) · P(J)∩} P(A B) = P(A) · P(B)∩

Dico due variabili o due eventi indipendenti se il verificarsi del primo non influenza il verificarsi del secondo.



Ossia se tutti i possibili eventi della prima sono indipendenti dai possibili eventi della seconda



A ={TT, TC} B = {TC, CC}

X = esito lancio del primo dado

Y = esito lancio del secondo dado

Regole

con E ∩ F = Φ ho Dati due eventi E e F

P(E F) = P(E) + P(F) - P(E∩F)∩

P(E F) = P(E) + P(F)∩ TTT TTCTCC CCC CTT TCT CTC CCT E F Ω E = esattamente due teste

F = la prima è testa

E = esattamente due teste

F = esattamente una testa

CTC CCT TCC TTT CCC CTT TCT TTC Ω F E

Nota: nel caso di tre eventi

P(E F G) = P(E) + P(F) + P(G) - P(E∩F) - P(E∩G) - P(F∩G) +∩ ∩ + P(E∩F∩G)

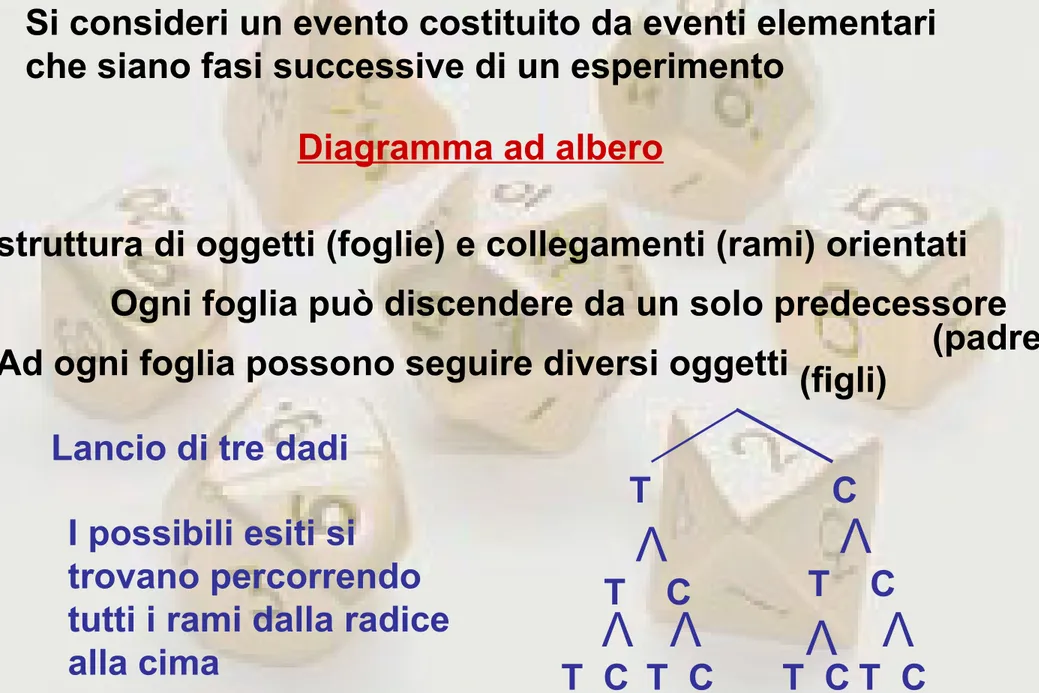
Diagramma ad albero

struttura di oggetti (foglie) e collegamenti (rami) orientati Ogni foglia può discendere da un solo predecessore

(padre) Ad ogni foglia possono seguire diversi oggetti (figli)

Lancio di tre dadi

T C T C T C

V

V

V

V

_V

V

Si consideri un evento costituito da eventi elementari che siano fasi successive di un esperimento

Principio di moltiplicazione

Sia E l’evento che si ottiene percorrendo un ramo dell’albero dalla radice alla cima ed e_i gli eventi

elementari corrispondenti alle foglie del percorso di E P(E) =



Probabilità di un

codice alfanumerico del tipo aabc con a: ±1 b:cifra c:lettera 1 -1

_½

½

_{½ ½}

Probabilità condizionata

e inversa

P(F|E) = Probabilità che l’evento F si realizzi nell’ipotesi che l’evento E si sia già realizzato

F = due esiti su tre sono testa E = il primo esito è testa

P(F)=3/8 _P(F|E)=2/4 TTT TTCTCC CCC CTT TCT CTC CCT E F Ω TTC TCT E F = Ω TCC TTT

Regola

P(F|E)= P(F∩E) P(E) _______

Nota:

F è indipendente da E se (def.) P(F|E) = P(F)

 se sostituisco trovo P(E) · P(F) = P(E∩F)

P(F∩E)=2

Riferendosi all’esercizio precedente

Problema della probabilità inversa Problema:

L’urna I contiene 3 palline rosse e 2 blu, l’urna II contiene 1 pallina rossa e 1 blu. Pesco ad occhi chiusi una pallina rossa: Quale è la probabilità che provenga dall’urna 1?

Soluzione _{Uso il diagramma ad albero:} r b Evento elem. P(e₁)

½

½

½

½

Costruisco il diagramma inverso:

b r I II II I 9/20 11/20 x = 4/9 5/9 6/11 5/11

Come trovare x : la probabilità dei rami equivalenti dei due alberi è uguale, quindi:

9/20 · x = P(E2) = 1/5 3/10 1/5 1/4 1/4 P(b∩I) P(b) P(I|b)

Il problema corrisponde alla ricerca della probabilità dell’urna I condizionata all’aver pescato b

P(II|r) = 5/11 P(I|r) = 6/11 P(II|b) = 5/9 P(I|b) = 4/9

Formula di Bayes Problema:

Si consideri un esperimento in due fasi e si voglia calcolare la probabilità di un evento elementare H_i al

primo stadio nota la probabilità dell’evento E al secondo stadio Regola P(Hi|E) = ________________ P(E|Hi) · P(H_i) Σ P(E|H k) · P(H_k)  m k 1 = __________P(E|Hi) · P(Hi) P(E)

Probabilità discreta

e continua

definizioni Dato uno spazio campionario discreto Ω

def. probabilità su Ω una qualsiasi funzione P : Ω [0,1] che soddisfi P(Ω) = 1 P( Ak) = P(A



U

*

*

Probabilità classica Ω finito o numerabile con Ω = { w_i } IΩI = dimensione (o la cardinalità) di Ω

P(E) = IEI IΩI

___ A _{E Ω}

כּ

definizione equivalente alla probabilità classica: Sia m(x) una funzione m : Ω [0,1]

con P(Ω) = 1



detta funzione di distribuzione di Ω Sia E un sottoinsieme di Ω

definisco P(E) := m(x)



E

x

Le proprietà sono quelle già viste

. le trasmettiamo dagli insiemi agli elementi per il caso numerabile le somme diventano serie

studio della convergenza

X = lunghezza della corda di una circonferenza unitaria Ω = ( 0,2] Si voglia P(E) con E = ( ,2]₃

Scelgo un sistema di coordinate per il punto medio: rettangolari del con origine nel centro della circonferenza

M: (x,y) (x,y) [-1,1]



L’Hp corrisponde a X ≥ lato del triangolo equilatero . M è interno alla circonferenza di raggio ½

Nota:

Se ho uno spazio campionario sottoinsieme di IR2

e ipotizzo che tutti i suoi punti siano equiprobabili

posso associare ad una superficie una probabilità equivalente alla sua area

P(E) = =1/4 ______π(½) 2 π(1)2 Paradosso di Bertrand: P(E) = 1/4 1/2 1/3 M: (ρ;θ) M:(x;y) A:(1;α) B:(1;β)

definizione

F(x) funzione di distribuzione cumulativa di X se

))

,

((

:

)

(

:

)

(

x

P

X

x

P

x

F









F

(

x

)

:

IR

 IR

)

(x

F

0

)

(

lim







F

x

x

(

)

1

lim







F

x

x

)

(x

F

)

(

)

(

lim

t

F

x

F

t

x





definizione

f(x) funzione di densità di X se f: IR IR e vale

P(a ≤ x ≤ b) =



dx

x

f

(

)

_{ b}

_a,

_

Scelta la variabile X non è detto che esista f(x)

+

f(x) non è una probabilità.

P(X E) =





E

dx

x

f

(

)

Sia X una variabile aleatoria con funzione di densità f(x) Teorema Rappresenta la funzione di distribuzione cumulativa di X,





dt

t

f

x

F

(

)

(

)

F

(

x

)

f

(

x

)

dx

d



Da ciò potremmo introdurre un diversa

definizione di funzione densità: f: IR IR+





x

F

dt

t

f

(

)

(

)



(

)



1

dx

x

f

Esempi significativi di distribuzioni e densità Distribuzione uniforme discreta

Sia X una variabile aleatoria con spazio campionario Ω di dimensione n

La distribuzione è rappresentata dalla funzione m(x) = 1/n = costante

continua Distribuzione uniforme

Attenzione!

Sia Ω numerabile e m(x) = costante



dx

x

m )

(

Funzione di densità gaussiana f_x = ______1  2 2 2 2 ) (     x

e

