Elaborazione di modelli statistici della velocita' di propagazione di cricche per effetto di carichi affaticanti

1 Introduzione. 1

2 Generalità 3

3 Geometria dei provini, attrezzature e tipo di carico. 12

3.1 Geometria dei provini. . . 12

3.2 Attrezzature e tipo di carico. . . 14

4 Short Cracks 17 5 Long Cracks 27 5.1 Premesse. . . 27

5.2 Descrizione della curva della velocità tramite un’unica retta. . 32

5.2.1 Elaborazione dei dati. . . 32

5.2.2 Verifica delle 00_capacità00 _{del modello. . . 45}

5.3 Descrizione della curva della velocità tramite due rette. . . 50

5.3.1 Elaborazione dei dati. . . 50

5.3.2 Verifica delle 00_capacità00 _{del modello. . . 71}

6 Sviluppi futuri. 75 7 Conclusioni. 77 Bibliografia 81 A Analisi statistica. 83 A.1 Dati sperimentali . . . 83

A.2 Modello con un’unica retta. . . 86

C Dati sperimentali short crack. 129

D Programmi in Matlab. 143

D.1 Calcolo del valore della velocità di propagazione per le short crack. . . 143 D.2 Approssimazione della curva della velocità di propagazione

delle long cracks tramite un’unica retta. . . 148 D.3 Approssimazione della curva della velocità di propagazione

Introduzione.

La necessità di progettare nuovi aerei e di aumentare la vita operativa dei velivoli già esistenti, cercando di migliorare le caratteristiche di sicurezza e ridurre i costi, ha portato ad un riesame delle attuali metodologie di progetto a fatica di aerei di impiego sia civile che militare.

Gli approcci utilizzati, sia il safe life che il più recente damage tolerance, si basano su valutazioni di tipo deterministico della vita a fatica ed utilizzano dei coefficienti di sicurezza generalmente molto conservativi per evitare rot-ture e malfunzionamenti.

Tali coefficienti non sono ovviamente in grado di cogliere la natura statistica del fenomeno.

Tra gli inconvenienti di questo modo di procedere, i principali sono la man-canza di indicazioni circa il valore del margine di sicurezza e l’impossibilità di risalire, tra i vari parametri che influenzano il fenomeno, a quello che incide maggiormente.

Per superare questi inconvenienti la ricerca si sta concentrando sulla possi-bilità di applicare un approccio di tipo probabilistico più vicino alla realtà fisica del problema.

Tale approccio, in grado di fornire significativi vantaggi, è applicabile sola-mente se sono disponibili le distribuzioni statistiche dei parametri e se si è in grado di simulare numericamente in modo adeguato tutto il fenomeno della fatica.

Ovviamente, prima che questo nuovo approccio possa essere adottato nei regolamenti, è necessario un lungo processo di studio e ricerca per la predisposizione degli strumenti principali per l’applicazione e per le verifiche che gli enti certificanti richiedono prima di accettare una nuova metodologia. Il presente lavoro di tesi ha come obbiettivo lo sviluppo di modelli sta-tistici capaci di caratterizzare la propagazione di cricche per fatica nella lega

Dovendo effettuare un’analisi di natura statistica la campagna di prove è sta-ta effettuasta-ta su trensta-tasei provini appartenenti allo stesso lotto e sottoposti alla stessa condizione di carico.

Nel primo modello sviluppato, il più semplice, le curve sperimentali della velocità, rappresentate in scala doppiamente logaritmica, sono state descritte attraverso delle singole rette di best-fit.

Tale modello però non risulta essere in grado di descrivere efficacemente il fenomeno della propagazione in termini di curva media di propagazione. Dai risultati ottenuti da tale modello si deduce come, descrivendo le curve della velocità attraverso delle singole rette di best-fit, non si ottengano delle curve di propagazione simulate in grado di descrivere accuratamente quelle sperimentali.

Per questo motivo, nel presente lavoro, volendo descrivere accuratamente le curve di propagazione sperimentali, è stato sviluppato un secondo modello capace di descrivere le curve delle velocità attraverso delle coppie di rette di best-fit incidenti.

Quest’ultimo modello risulta fornire una buona descrizione del fenomeno del-la propagazione a fatica sia in termini di curva media di propagazione che di dispersione.

Dai risultati ottenuti dal secondo modello di questo lavoro di tesi risulta chiaro come l’introduzione di un approccio probabilistico possa offrire un valido strumento per il progetto a durability di una struttura aeronautica offrendo un criterio di analisi che permette la valutazione del danneggiamento associato alla fatica in termini probabilistici.

Generalità

Fino alla prima metà degli anni quaranta gli ingegneri progettavano le strut-ture sottoposte a carichi variabili o ripetuti allo stesso modo di quelle sotto-poste a carichi costanti nel tempo, impiegando però maggiori coefficienti di sicurezza.

Infatti, fino ad allora i velivoli erano caratterizzati da una vita operativa estremamente breve ( raramente venivano oltrepassate le migliaia di ore di volo ) ed erano progettati con una certa ridondanza strutturale.

Con l’aumento della vita operativa dei velivoli, soprattutto nel campo dei velivoli civili non imputabili al raggiungimento di un carico eccezionale, si presentarono gravi incidenti; ebbero così inizio studi sistematici finalizzati ad analizzare il fenomeno della fatica.

Da allora la resistenza a fatica ha assunto un ruolo fondamentale nella pro-gettazione, diventando un criterio primario di progetto.

Un ampio lavoro compiuto nell’ultimo secolo ha consentito una crescente comprensione dei meccanismi di base connessi con la rottura per fatica.

Il fenomeno della fatica può essere caratterizzato attraverso quattro stadi:

• formazione di iniziali microfessure;

• crescita fino alla formazione della macrocricca; • propagazione della macrocricca;

• rottura catastrofica finale.

I primi due stadi, nei quali la cricca può essere definita 00_corta00 _{e che} termi-nano indicativamente quando la cricca ha raggiunto la dimensione di circa un millimetro, costituiscono più propriamente la00_nucleazione00_{, gli altri due, nei}

cricca fino alla rottura finale.

Osservando la curva di propagazione per fatica di una cricca , figura 2.1, è possibile definire il valore della lunghezza, cd, corrispondente al minimo valore della lunghezza che può essere osservata in modo affidabile tramite tecniche di ispezione non distruttive ed il valore massimo della lunghezza,

ccr, al di sopra del quale si ha una propagazione instabile.

La propagazione della cricca può avere origine da un difetto iniziale a0 la

cui dimensione, inferiore al millimetro, dipende dalla qualità del processo di fabbricazione del componente strutturale.

Figura 2.1: Tipico andamento della curva della propagazione della cricca.

Su tale curva è possibile definire due regioni: la prima, la regione delle short cracks, relativa a valori della lunghezza della cricca inferiore al mil-limetro, la seconda, la regione delle long cracks, relativa a valori della lun-ghezza maggiori del millimetro.

Per comprendere meglio il comportamento delle cricche quando hanno una lunghezza tale da essere definita 00_corta00_{, sono stati condotti molti studi} circa la loro nucleazione e propagazione.

Da questi studi è emerso che le curve dc/dN - ∆K relative non seguono le leggi classiche e che tali cricche possiedono una velocità di propagazione maggiore, a parità di ∆K, rispetto alle long cracks.

Questo comporta che l’uso delle equazioni valide in LEFM risulta essere inappropriato per il loro studio.

Questo fenomeno è conosciuto come 00_{Short Crack Problem}00_.

La differenza principale tra i modelli validi rispettivamente per le short cracks e le long cracks è mostrato in figura 2.2 nella quale si riportano le curve delle velocità in funzione della variazione del fattore di intensità degli sforzi ∆K.

La curva definita dalla linea continua mostra il tipico andamento della cur-va della velocità delle long cracks sotto l’azione di un carico ad ampiezza costante.

Su tale curva è possibile definire il valore di ∆Kth ottenuto andando ad ef-fettuare delle prove a carico sempre minore fino al raggiungimento del valore di ∆K per il quale non si ha propagazione della cricca.

Secondo il modello delle long cracks, per valori di ∆K inferiori al valore di ∆Kth non si ha la propagazione della cricca.

Figura 2.2: Tipico andamento della curva della velocità di propagazione della cricca.

In figura 2.2 sono riportate anche tre curve tratteggiate relative alla velo-cità di propagazione delle short cracks per tre valori, S1, S2 ed S3 del carico

massimo applicato.

propa-delle long cracks, e crescere più velocemente propa-delle long cracks a parita di ∆K. E’ evidente, quindi, che applicando le equazioni valide in LEFM su tutto l’intervallo dei valori della lunghezza della cricca, si ottiene una pericolosa sovrastima della vita totale a fatica in quanto si associa alle short cracks una velocità di propagazione minore di quella effettiva.

Dagli studi condotti sulle short cracks da Morris e James, [3], è emerso come, per la descrizione della propagazione di queste, giochi un ruolo impor-tante il cosiddetto00_{effetto chiusura}00_{per il quale la cricca propaga solo quando} essa è completamente aperta, cioè si è superato il valore di una tensione di opening, Sop, funzione delle zone plastiche all’apice delle cricche lasciate dal-l’applicazione dei carichi precedenti e maggiore o uguale della Smin del ciclo. In tali zone plastiche infatti sono presenti dei campi di tensione residue di compressione.

La differenza tra il Kmax e il Kop viene chiamata ∆K efficace ( ∆Kef f ), ed è stato ipotizzato che è questo valore che regola il meccanismo di propagazione delle rotture per fatica.

Morris, James & Buck [3] hanno dimostrato con provini in lega di titanio che l’ effetto chiusura aumenta al crescere delle dimensioni della cricca fino a che non raggiunge asintoticamente un certo valore nel campo delle long cracks.

Si capisce quindi come a parità di ∆K, essendo il ∆Kef f maggiore per le short cracks che per le long cracks, la velocità delle short cracks risulti essere maggiore di quella delle long cracks.

Questo spiega perché anche le cricche fisicamente piccole ma grandi rispet-to alle dimensioni medie dei grani e alla larghezza della zona plasticizzata generata dalla cricca stessa crescono con velocità maggiore di quella prevista con le equazioni della meccanica della frattura classica.

Yoder et al. [1], analizzando leghe di alluminio della serie 7000 sotto l’azione di bassi carichi applicati, hanno ricavato delle curve della velocità che, riportate su una scala doppiamente logaritmica, possono essere approssimate molto bene tramite un andamento lineare a tratti come visualizzato in figura 2.3.

Attraverso tale studio sono arrivati alla conclusione che i punti di transi-zione tra i vari tratti si presentano quando il raggio rc _{della zona} plasti-cizzata alla radice della cricca raggiunge le dimensioni caratteristiche della microstruttura.

Questi hanno dimostrato che le transizioni T1, T2 e T3 nella figura 2.3 si

presentano quando rc_{raggiunge rispettivamente la dimensione dei dispersoid}

spacing, subgrain size and grain size.

Figura 2.3: Tipico andamento della curva della velocità di propagazione, [1].

l’azione di bassi carichi ad ampiezza costante utilizzando provini fabbricati in leghe di alluminio 2024-T3 e 2024-T351 per diversi valori dello spessore e diversi valori di Smax/Smin.

Alcuni risultati ottenuti sono riportati nella figura 2.4.

La dipendenza delle curve della velocità dal valore di R è una conferma della dipendenza della crescita della cricca dall’00_{effetto chiusura}00_.

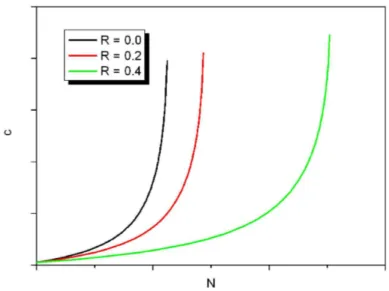
Considerando il modello valido per le long cracks, è stato dimostrato che la propagazione di queste su di un componente risulta essere influenzata da diversi fattori tra cui la lunghezza della cricca stessa, c, l’ampiezza del carico applicato ∆S = Smax - Smin, lo spessore del componente, l’ambiente in cui si trova, la temperatura e il tipo di carico applicato.

A parità di carico massimo, gli effetti dell’ampiezza del carico applicato, in termini di R, definito come Smin/Smax, sono rappresentati in figura 2.5. All’aumentare di R si ha una diminuzione di ∆S e quindi un aumento sia della vita a fatica sia del valore di ccr.

La velocità di avanzamento della cricca è una funzione dell’ampiezza della sollecitazione, della dimensione della cricca, della geometria del componente e dell’ambiente:

dc

dN = f (∆σ, c, β) .

Figura 2.4: Tipico andamento della curva della velocità di propagazione al variare di R, [2].

definito da equazioni del tipo

σ (r, θ) = f (θ) ·√K

2πr, (2.1)

dove con K è stato indicato il fattore di intensità degli sforzi calcolato con la tensione all’infinito σ0.

Poiché il fattore di intensità degli sforzi K risulta essere una misura dello stato di tensione in una regione intorno alla cricca, la velocità di propagazione può essere espressa in funzione dell’ampiezza di ∆K.

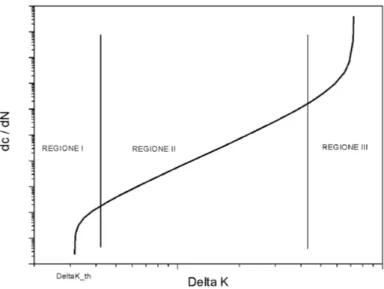
Il tipico andamento ad S della curva di velocità di crescita delle long cracks dc/dN - ∆K è rappresentato, in scala doppiamente logaritmica, in figura 2.6 dove si possono facilmente distinguere tre regioni caratteristiche.

La regione I, dove la cricca risente principalmente della microstruttura del materiale, della tensione media e delle condizioni ambientali, è definita da un valore minimo di ∆K, il valore caratteristico di soglia ∆Kth al di sotto del quale il modello non prevede una propagazione della cricca. Nella regione II, essenzialmente lineare su scala doppiamente logaritmica, si riscontra una piccola influenza da parte della microstruttura del materiale ed una forte dipendenza dall’ambiente e dall’ampiezza media del carico. Nella regione

Figura 2.5: Tipico andamento della curva della propagazione della cricca al variare di R per un valore del carico massimo costante.

III, infine, la curva di velocità di avanzamento della cricca cresce rapidamente mentre il fattore di intensità degli sforzi massimo, Kmax, tende asintotica-mente al valore critico, Kc, in corrispondenza del quale la cricca si sviluppa per propagazione instabile.

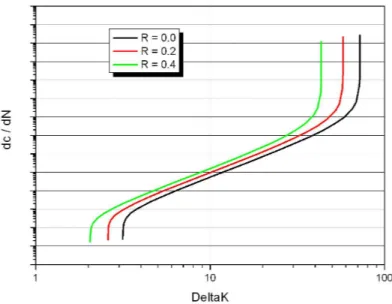
In figura 2.7 si riportano gli effetti dell’ampiezza del carico utilizzato sulla velocità di propagazione della cricca per tre valori diversi di R a parità di carico massimo.

E’ evidente come all’aumentare di R si ha uno spostamento della curva verso sinistra con conseguente aumento della velocità a parità di ∆K.

Molti studi sono stati condotti per cercare di descrivere nel miglior modo possibile la curva in questione attraverso leggi semiempiriche tra le quali quelle maggiormente impiegate sono quella di Paris ( equazione 2.2 ), che descrive solo la regione II del grafico 2.6, e quella di Forman ( equazione 2.3 ), che tiene conto anche della regione III.

dc dN = C∆K m _(2.2) dc dN = C∆Km (1 − R) Kc− ∆K (2.3)

Figura 2.6: Tipico andamento della curva della velocità di propagazione della cricca.

L’attività sperimentale, relativa alle long cracks, svolta nel presente lavoro di tesi,si concentra sulla fase di accrescimento ed è relativa alla sola regione II della curva dc/dN - ∆K.

Per quanto detto sopra, per le analisi e le discussioni dei dati raccolti dalla campagna di prove relativi alle long cracks è stata utilizzata l’equazione di Paris.

Figura 2.7: Tipico andamento della curva della velocità di propagazione della cricca al variare di R.

Geometria dei provini,

attrezzature e tipo di carico.

3.1

Geometria dei provini.

La campagna di prova è stata mirata allo sviluppo di modelli statistici per la descrizione della propagazione di long cracks, sotto l’effetto di carichi af-faticanti ad ampiezza costante, su trentasei provini di tipo Center Crack

Tension, figura 3.1, realizzati in lega alluminio-rame 2024-T3 appartenente

ad un unico lotto.

Dalle figura si può osservare come i provini sono stati protetti con primer, quindi per poter effettuare gli intagli è stato necessario sverniciare e lucidare la zona dei provini intorno al foro centrale.

Figura 3.1: Foto del provino.

Pur mantenendo come obbiettivo principale di questo lavoro lo studio della propagazione di long cracks, durante la campagna di prova sono stati

raccolti anche i dati relativi alla propagazione di short cracks sugli stessi provini utilizzati in seguito, previa modifica degli intagli, per la raccolta dei dati relativi alle long cracks.

In una prima fase, che chiameremo in seguito fase I, sui provini sono stati eseguiti degli intagli adatti allo studio delle short cracks.

Tali intagli, due corner cracks sul boro di un foro centrale, visibili in figura 3.2, sono stati ricavati per elettroerosione.

Figura 3.2: Foto dell’intaglio del provino utilizzato durante la fase I.

La geometria del provino e di tali intagli sono riportati in figura 3.3. Le misurazioni in questa fase sono state interrotte quando il difetto diveniva passante o quando la lunghezza della cricca sulla superficie raggiungeva il valore di 1.2 mm (compreso la dimensione iniziale dell’intaglio).

I provini durante questa fase sono stati identificati con la sigla SC seguita del numero del provino ( SC01, SC02,. . ., SC36 ).

Per lo studio della propagazione fino alla rottura finale, fase II, sono stati utilizzati gli stessi provini della fase I dopo aver modificato la loro geometria. Su ogni provino, infatti, sono stati creati due difetti passanti della lunghezza di 1,5 mm a partire dal bordo del foro. Tale nuovo difetto iniziale è stato creato, tramite una lama seghettata, nella zona precedentemente occupata dalla cricca propagatasi nella fase I. Le dimensioni del provino e del difetto iniziale utilizzato nella fase II sono riportate nella figura 3.4.

Figura 3.3: Geometria del provino relativo alla fase I. [ mm ]

Dopo che la geometria degli intagli è stata modificata i provini sono stati rinominati con la sigla LC seguita dal numero del provino ( LC01, LC02,. . ., LC36 ).

Per poter effettuare le misurazioni della lunghezza della cricca è stato necessario sverniciare e lucidare, prima di andare ad effettuare le prove, tutta la zona dei provini all’interno della quale ha luogo la propagazione della cricca.

Tale zona è stata poi colorata di nero o di rosso per mettere in evidenza il profilo lucido della cricca ed andare ad effettuare una misurazione più precisa.

3.2

Attrezzature e tipo di carico.

Le prove di propagazione, sia per le short cracks che per le long cracks, sono state eseguite, per tutti e trentasei i provini, su una macchina di fatica SERVOTEST avente una capacità di carico massimo di 50 KN. Tramite tale macchina, dotata di un controller analogico, i provini sono stati sottoposti ad un carico di tipo sinusoidale ad ampiezza e frequenza costante. I valori del carico massimo, del carico medio e della frequenza sono stati impostati manualmente tramite potenziometri collocati sul controller. Per tutta la campagna di prova è stato utilizzato un carico di tipo sinusoidale definito

Figura 3.4: Geometria del provino relativo alla fase II. [ mm ].

da un carico massimo di 80 MPa, da un carico minimo di 8 MPa e da una frequenza di 5 MHz.

Per permettere la visualizzazione e la misurazione della lunghezza del-la cricca, sono stati utilizzati due microscopi biocudel-lari, uno 40X ed uno di potenza inferiore, montati su una slitta verticale.

Tali microscopi sono stati montati in modo tale da permettere le misurazioni sui due lati dei provini.

Durante la fase I i provini sono stati montati sulla macchina in modo tale che le misurazioni della lunghezza della cricca sul lato delle corner cracks fosse eseguita tramite il microscopio bioculare 40X, mentre tramite l’altro microscopio, di potenza minore, si controllava se il difetto diveniva passante. Appena il difetto diveniva passante oppure la lunghezza della cricca, dalla parte delle corner cracks raggiungeva il valore di 1.2 mm la prova veniva interrotta.

Durante la fase II, dovendo effettuare solamente misurazioni su uno dei due lati del provino, è stato utilizzato solamente il microscopio bioculare 40X. Le prove nella fase II sono state fatte proseguire fino alla rottura del provino. Per agevolare le misurazioni, la slitta verticale, su cui è stato fissato il mi-croscopio, è stata collegata ad un motore elettrico a passo costante azionabile tramite un telecomando.

In figura 3.5 e 3.6, si riportano le foto della macchina utilizzata e del controller analogico attraverso il quale è stato impostato il suddetto carico.

Figura 3.5: Macchina SERVOTEST.

Short Cracks

I dati raccolti durante la campagna di prove relativa alle short cracks, co-stituiti dal valore della lunghezza della cricca sulla superficie del provino e dal corrispondente numero di cicli di applicazione del carico, sono stati ela-borati per ottenere il valore della velocità di propagazione della cricca ed il corrispondente valore di ∆K.

In letteratura esistono poche soluzioni esatte del fattore di intensità degli sforzi per corpi tridimensionali, e qualche soluzione approssimata attraverso metodi numerici.

Con riferimento alla figura 4.1 e4.2, si è indicato con φ l’angolo lungo il fronte della cricca, con a la lunghezza della cricca nella direzione dello spessore, con c la lunghezza della cricca sulla superficie, con t lo spessore della piastra e con r il raggio del foro.

Seguendo la procedura descritta da Newman e Raju [4], per il calcolo del fattore di intensità degli sforzi è stata utilizzata l’equazione 4.1 ottenuta interpolando i risultati di una analisi agli elementi finiti [5, 6, 7, 8].

In tale equazione St indica la tensione dovuta alla forza di trazione, a indica la lunghezza della cricca lungo la direzione dello spessore, Q indica il fattore di forma ed F indica il fattore di correzione che tiene conto della geometria del provino. K = (St) Ã πa Q !_1/2 · Fch µ_a c, a t, r t, r b, c b, φ ¶ (4.1) Per calcolare il valore del fattore di forma sono state utilizzate le due espressioni empiriche sviluppate da Rawe, vedi riferimento [6], definite dal-l’equazione 4.3 se a/c ≤ 1, oppure daldal-l’equazione 4.14 se a/c > 1.

Figura 4.1: Geometria dell’intaglio iniziale.

Il fattore di correzione F è definito come: Fch= " M1 + M2 µ a t ¶₂ + M3 µ a t ¶₄# g1g2g3g4fφfW (4.2) dove: M1, M2, M3 sono funzioni della configurazione e del tipo di carico;

fφ è una funzione della variabile φ, definita in figura 4.2, che deriva dalla soluzione per una cricca ellittica in un provino di dimensioni infinite; fW è un fattore di correzione che tiene conto della larghezza finita del provino; g è definita da un prodotto di funzioni, g1 g2. . . gn, e risulta essere funzione anche della geometria della cricca.

I valori dei fattori di correzione e delle funzioni sono definiti in modo diverso, a seconda che a/c ≤ 1 oppure a/c > 1.

Per a/c ≤ 1 si ha che:

Q = 1 + 1.464 µ_a c ¶_1.65 ; (4.3) M1 = 1.13 − 0.09a c; (4.4) M2 = −0.54 + 0.89 0.2 + a c ; (4.5) M3 = 0.5 − 1 0.65 + a c + 14 µ 1 − a c ¶₂₄ ; (4.6) g1 = 1 + " 0.1 + 0.35 µ_a t ¶₂# (1 − sin (φ))2; (4.7) g2 = 1 + 0.358λ + 1.425λ2_{− 1.578λ}3_{+ 2.156λ}4 1 + 0.13λ2 ; (4.8) dove λ = 1 1 + c rcos (µφ) ; (4.9) g3 = µ 1 + 0.04a c ¶ h 1 + 0.1 (1 − cos (φ))2i " 0.85 + 0.15 µ_a t ¶_1/4# ; (4.10) g4 = 1 − 0.7 µ 1 −a t ¶ µ_a c − 0.2 ¶ µ 1 −a c ¶ ; (4.11)

fφ = a c ¶₂ cos2_{(φ) + sin}2_{(φ) ; (4.12)} fW = ( sec(πr 2b) sec " π(2r + nc) 4(b − c) + 2nc r a t #)_1/2 . (4.13) Per a/c > 1 Q = 1 + 1.464 µ_c a ¶_1.65 ; (4.14) M1 = µ_c a ¶_1/2µ 1 + 0.04c a ¶ ; (4.15) M2 = 0.2 µ_c a ¶₄ ; (4.16) M3 = −0.11 µ_c a ¶₄ ; (4.17) g1 = 1 + " 0.1 + 0.35 µ_c a ¶ µ_a t ¶₂# (1 − sin (φ))2; (4.18)

g2 e λ sono definite dalle equazioni 4.8 e 4.9;

g3 = µ 1.13 − 0.09c a ¶ h 1 + 0.1 (1 − cos (φ))2i " 0.85 + 0.15 µ_a t ¶_1/4# ; (4.19) g4 = 1; (4.20) fφ = "µ c a ¶₂ sin2(φ) + cos2(φ) #_1/4 . (4.21)

Questo set di equazioni è valido solo se: a/t è compreso tra 0 e 1; a/c è compreso tra 0.2 e 2; r/t è compreso tra 0.5 e 2; (r+c)/b è minore di 0.5; φ è compreso tra 0 e π/2.

La geometria del provino utilizzato, figure 3.3 e 4.1, è tale da consentire l’utilizzo di questo set di equazioni.

Per effettuare il calcolo del valore numerico di K, e quindi di ∆K, è necessario conoscere come la cricca propaga sia nella direzione della spessore, sia sulla superficie.

Poiché i dati raccolti durante la campagna di prova1 _{si riferiscono}

sola-mente al valore della lunghezza della cricca sulla superfice del provino e al corrispondente numero di cicli di applicazione del carico, è stato necessario ricavare una relazione in grado di descrivere la lunghezza della cricca nello spessore in funzione di quella sulla superfice.

Come relazione è stato utilizzato il risultato di una simulazione con il codice di calcolo FASTRAN, [13], eseguita per un provino avente geometria identica a quella dei provini utilizzati nella campagna di prove ed un carico identico a quello impostato sulla macchina SERVOTEST.

Questo codice, particolarmente efficace per il calcolo della propagazione di short cracks è infatti in grado di simulare la crescita di corner cracks lungo lo spessore e la superficie per diverse geometrie e spettri di carico.

Il legame ottenuto è stato rappresentato, in termini di a/c-c, in figura 4.3.

Figura 4.3: Relazione a-c ottenuta tramite simulazione Fastran.

Il calcolo di ∆K e della velocità di propagazione dc/dN è stato effettuato

come dati di ingresso i risultati della campagna di prove e la relazione rica-vata tramite simulazione FASTRAN, attraverso il set di equazioni descritto sopra, si ottengono come uscite i valori della lunghezza della cricca a lungo la direzione dello spessore, i valori di ∆K e quelli di dc/dN.

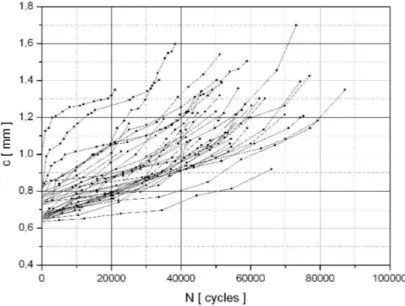
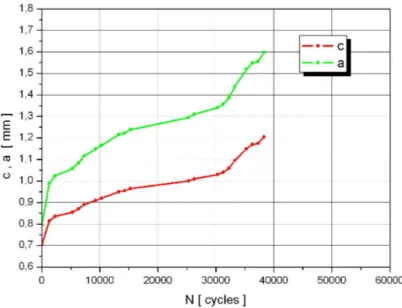
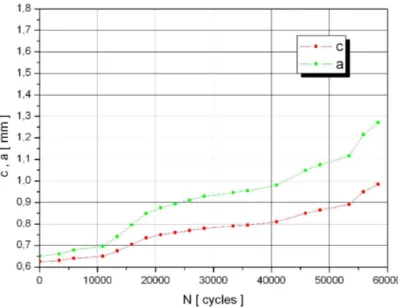
L’elaborazione dei dati relativi alle short cracks quindi si limita solamente al calcolo dei valori della velocità di propagazione della cricca sulla superficie. In figura 4.4 vengono visualizzate le curve di propagazione sperimentali delle short cracks relative a tutti i provini, mentre in figura 4.5 e 4.6 sono riportate le curve di propagazione riferite alla lunghezza della cricca sia nel-la direzione dello spessore che sulnel-la superficie rispettivamente per il provino SC04 e SC07.

Si ricorda che i valori di a, relativi alla lunghezza della cricca lungo lo spessore, sono stati ricavati mediante la simulazione FASTRAN.

Figura 4.4: Curve di propagazione delle short cracks relative a tutti i provini.

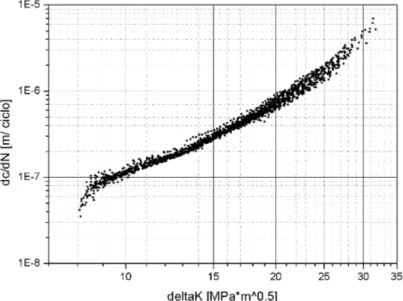
I valori della velocità di propagazione ottenuti sono mostrati in figura 4.7. Come è possibile osservare, confrontandotale figura con quella proposta da Wanhill ( figura2.4 ), i valori del ∆K risultano essere tali che nella curva

Figura 4.5: Curve di propagazione della short crack, sia nella direzione dello spessore che in superficie, relativa al provino SC04.

della velocità di propagazione sia definita solamente l’ultima parte mostrata in figura 2.4 e come quindi non possa essere individuato il valore di ∆Kth.

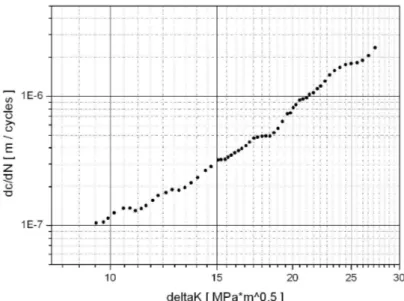
Nelle figure 4.8 e 4.9 si riportano le curve della velocità relative rispetti-vamente ai provini SC09 e SC14.

E’ evidente come valori dei ∆K risultino essere troppo elevati per riuscire ad osservare il tipico andamento delle curve della velocità per le short cracks, e risultano corrispondere a valori della lunghezza della cricca maggiori dei valori per i quali una cricca può essere definita00_corta00_.

Questo risultato potrebbe derivare o da una geometria del provino e dell’in-taglio iniziale non adeguati allo studio in detdell’in-taglio delle short cracks oppure da un carico massimo troppo elevato.

Si ricorda comunque che lo scopo fondamentale di questo lavoro risulta es-sere lo sviluppo di modelli statistici capaci di riprodurre il comportamento a fatica del materiale per quanto riguarda la propagazione delle long cracks. La geometria del provino quindi è stata definita in base allo scopo principale dello studio e considerando che per tale studio era necessario effettuare un intaglio passante è stato fatto uno studio secondario, antecedente a quello principale effettuando degli intagli di tipo corner cracks sul bordo del foro per osservare il comportamento delle short cracks.

Figura 4.6: Curve di propagazione della short crack, sia nella direzione dello spessore che in superficie, relativa al provino SC07.

Figura 4.7: Valori della velocità di propagazione delle cricche in superficie relative a tutti i provini.

Figura 4.8: Valori della velocità di propagazione della cricca in superficie relativa al provino SC09.

Figura 4.9: Valori della velocità di propagazione della cricca in superficie relativa al provino SC14.

lativa alle short cracks ( alle quali corrispondono valori della lunghezza della cricca inferiori approssimativamente al millimetro ) è definita come una fase della nucleazione.

I dati ottenuti dalla campagna di prove relativi alla fase I hanno fornito valori della lunghezza della cricca troppo elevati per poter definire le cricche come short cracks.

Osservando comunque la dispersione delle curve di propagazione mostrate in figura 4.4 è difficile pensare di poter utilizzare un modello, sia esso deter-ministico che statistico, per descrivere il fenomeno.

Per questo motivo non sono stati sviluppati dei modelli in grado di caratte-rizzare la propagazione a fatica delle cricche relative alla fase I.

Long Cracks

5.1

Premesse.

Per quanto riguarda l’analisi dei dati raccolti durante la campagna di prove, relativi alla propagazione delle long cracks, sono necessarie alcune conside-razioni preliminari circa la valutazione del fattore di intensità degli sforzi.

Una forma generale di K risulta essere

K = σ√πc · β (c) (5.1) dove β(c) è una funzione della geometria e c è la lunghezza della cricca, come indicato in figura 5.1

Esistono poche soluzioni in forma chiusa dell’equazione 5.1 mentre molte espressioni sono ottenute tramite approssimazioni numeriche.

Utilizzando l’approccio basato sulla composizione di soluzioni, il fattore di intensità degli sforzi è ottenuto dal prodotto di soluzioni ausiliarie ap-propriate, relative a soluzioni semplici, allo scopo di tener conto degli effetti dovuti alle condizioni al contorno della struttura.

Questo tipo di metodologia è sintetizzata nella seguente relazione:

K = KR_{· β}

1· β2· . . . · βn

KR_{= σ ·}√_{π · ¯c} (5.2)

dove KR _{è la soluzione relativa alla piastra di dimensioni infinite, mentre σ} e ¯c rappresentano rispettivamente la tensione pensata applicata all’infinito. I termini indicati con β1, β2, . . ., βn, sono i fattori di correzione associati alle soluzioni ausiliarie.

Figura 5.1: Disegno del provino.

Per calcolare il valore numerico di K sono stati utilizzati due coefficienti correttivi: il primo, βW, tiene conto dell’ampiezza finita del provino; il secon-do, βh, tiene conto degli effetti che ha la presenza del foro sui valori numerici di K.

Per tener conto della dimensione finita del provino è stata utilizzata una soluzione ausiliaria dovuta a Feddersen che definisce come coefficiente correttivo l’espressione seguente:

βW = 1 r cos³πc W ´. (5.3)

La distinzione tra c e ¯c è ben visibile nelle figure 5.1 e 5.2.

Gli errori commessi nell’utilizzare tale equazione sono inferiori al 0.3% per valori di c/W ≤ 0.35, condizione che in questo caso è sempre verificata. Per tener conto degli effetti della presenza del foro sul valore numerico di K è stata utilizzata, valida per valori di ¯c/R ≤5, la soluzione ausiliaria ricavata da Tweed e Rooke [9], riportata anche in [14]:

βh(c) = exp " 1.21009 − 2.1114 · µ_¯c c ¶ + 0.92466 · µ_¯c c ¶₂# . (5.4) In figura 5.3 si riportano i valori di tale coefficiente in funzione del valore della lunghezza della cricca c.

Figura 5.2: Particolare dell’intaglio iniziale.

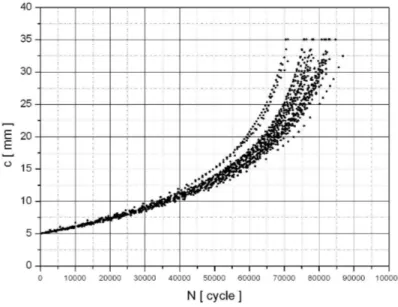
ghezza della cricca al variare del numero di cicli di trentasei provini tutti sottoposti ad un carico massimo di 80 MPa ed R=0.1.

Utilizzando tali dati come ingressi, attraverso un programma implementato in linguaggio FORTRAN sono stati ricavati i valori della velocità di propa-gazione e i corrispondenti valori del ∆K.

Per calcolare il valore di dc/dN il codice effettua un best-fit di un set di punti ricavati dalla curva c-N per mezzo di un polinomio la cui derivata rappresen-ta diretrappresen-tamente la grandezza ricercarappresen-ta.

Il numero dei punti ed il grado del polinomio interpolante vengono inseriti in ingresso.

Il programma richiede inoltre i valori di R, Smax, W necessari per stimare il ∆K.

I valori della velocità di propagazione della cricca in funzione del valore di ∆K di tutti i provini sono riportati in figura 5.4.

Figura 5.4: Valori della velocità relativi a tutti i dati ottenuti dalla campagna di prove.

In tale figura risultano ben visibili le tre regioni definite in figura 2.6: la regione I ( definita da valori di ∆K minori di 9 MPa√m ) dove è visibile

l’andamento della curva per valori di ∆K di poco maggiori del ∆Kth; la regione II ( definita da valori di ∆K indicativamente compresi tra 9 e 28

MPa√m ) avente un andamento rettilineo; la regione III definita da valori

di ∆K maggiori di 28 MPa√m in cui si osserva un aumento della pendenza

della curva in prossimità del ∆K critico.

Nel presente lavoro di tesi sono stati elaborati solamente i valori della lunghezza della cricca compresi tra 5 e 35 mm, corrispondenti ad un intervallo di ∆K compreso tra 9.23 e 27.7 MPa√m. Tale intervallo di ∆K definisce

infatti la regione II.

Osservando la figura 5.5 si nota come la curva delle velocità sia carat-terizzata da un andamento ondulato sovrapposto ad un andamento di tipo lineare.

Tale andamento è dovuto ad errori nelle elaborazioni oppure è dovuto alle caratteristiche proprie del materiale.

L’attività di progettazione a fatica è basata sulla conoscenza della curva della propagazione della cricca e non sono necessarie informazioni circa la velocità di propagazione della stessa.

Per poter sviluppare dei modelli statistici in grado di caratterizzare il com-portamento a fatica del materiale, considerando i valori della velocità interni alla regione II, le curve della velocità di propagazione sono state sostituite, a seconda del modello statistico, con una o due rette definite dall’equazione di Paris (5.5).

Questa sostituzione, non riproducendo gli scalini, comporta degli inevitabi-li errori di approssimazione relativi ai valori della velocità ma non produce degli errori significativi in termini di vita a fatica.

L’operazione di integrazione, necessaria per calcolare la curva della pro-pagazione nota la curva della velocità, infatti, ha l’effetto di ridurre tali errori.

I dati relativi alla propagazione e alla velocità di propagazione della cricca interni agli intervalli sopra definiti sono riportati rispettivamente nelle figure 5.6 e 5.7.

Le coppie di dati, lunghezza della cricca e numero di cicli, e velocità di propagazione e ∆K, sono stati analizzati tramite più modelli attraverso programmi implementati in Matlab 1_.

Figura 5.5: Tipico andamento a scalini della curva della velocità di propagazione.

5.2

Descrizione della curva della velocità tramite

un’unica retta.

5.2.1

Elaborazione dei dati.

Il primo modello utilizzato per analizzare i dati ricavati dalla campagna di prove è stato basato sull’approssimazione dei dati sperimentali della velocità di propagazione della cricca tramite un’unica retta.

Se, come in figura 5.7, si visulizza l’andamento della velocità in scala bi-logaritmica l’equazione 2.2 assume la forma di una retta avente un’equazione del tipo:

log10(

dc

dN) = log10(C) + m · log10(∆K). (5.5)

Considerando i valori dei logaritmi dei dati relativi alla velocità di propaga-zione è stato possibile ricavare i valori dei coefficienti dell’equapropaga-zione di Paris andando a calcolare i coefficienti della retta di best-fit sia per ogni singola prova, sia per tutti i dati della campagna di prova.

Figura 5.6: Curve di propagazione sperimentali per valori della lunghezza della cricca interni all’intervallo analizzato.

tutti i dati come log10(C)tot ed mtot, sono stati ricavati andando a costruire la retta di best-fit con il metodo dei minimi quadrati.

Utilizzare il metodo dei minimi quadrati significa andare a cercare la retta definita come

y = A + Bx

in grado di interpolare i dati sperimentali, Xk e Yk, e tale che, definiti con

yk = A + BXk

i valori numerici, contenuti sulla retta e corrispondenti all’assegnato valore

Xk, renda minima la sommatoria seguente n X k=1 d2 k dove dk = Yk− yk

ed n è il numero dei dati del singolo provino nel caso di retta di best-fit di un singolo provino, oppure il numero dei dati di tutti i provini nel caso di retta di best-fit di tutti i dati raccolti.

Figura 5.7: Curve della velocità di propagazione sperimentale per valori di ∆K interni all’intervallo analizzato.

I coefficienti A e B si ricavano risolvendo il seguente sistema:

( nA + BPn k=1Xk = P_n k=1Yk APn k=1Xk+ B P_n k=1Xk2 = P_n k=1XkYk (5.6) Sono stati così ricavati i valori dei coefficienti log10(C) ed m ed i relativi

valori dell’errore per ciascuna prova e per tutti i dati della campagna di prova. L’errore è stato definito come:

errore = v u u tPnk=1(Yk− yk)2 n − 2 . (5.7)

In figura 5.8 si riportano i valori della velocità di propagazione del provino LC12 e la relativa retta di best-fit calcolata con il metodo dei minimi quadrati. Nella tabella 5.1 sono stati riassunti ciascuno dei trentasei valori dei coefficienti log10(C)i e dei coefficienti mi relativi ai singoli provini.

In figura 5.9 vengono visualizzate tutte le rette di best-fit e i dati speri-mentali della velocità ricavati dall’intera campagna di prove e interni all’in-tervallo considerato.

Figura 5.8: Retta di best-fit per il provino LC12.

la retta di best-fit di tutti i dati della campagna di prova interni all’intervallo considerato.

Si ricorda che, se una distribuzione di n dati xi risulta essere di tipo gaussiana [10], questa risulta essere caratterizzata dal valor medio µ ( il parametro di scala ) definito come:

µ =

P_n

i=1xi

n , (5.8)

e dalla relativa deviazione standard ( parametro di forma ) definita come:

σ = v u u tPni=1(xi− µ)2 n − 1 . (5.9)

Per questo tipo di distribuzione dei dati è possibile definire la funzione densità di probabilità come:

p (x) = 1 σ√2πe

−1₂(x−µ_σ )2_{. (5.10)} Per verificare se una distribuzione di dati xi, possa o meno essere considerata gaussiana nel presente lavoro si utilizza la procedura riportata nelle norme ESDU 68013.

Secondo tale procedura riportando su una carta delle probabilità come ascisse i valori della distribuzione di dati xi e come ordinate i valori di (1 − p(x)) · 100 la distribuzione risulta essere di tipo gaussiana se i punti sulla carta hanno l’andamento di una retta.

Noti i coefficienti mi relativi alle rette di best-fit dei 36 provini è stato calcolato il loro valore medio, definito con ¯m.

Tale valore di ¯m corrisponde alla media delle pendenze di tutte le rette di

best-fit dei singoli provini e risulta essere pari a 2.9436.

La distribuzione dei valori di mi, può essere considerata gaussiana come dimostrato in figura 5.10 ed è definita da un valor medio pari a 2.9436 e da una deviazione standard pari a 0.115616, (tabella 5.3), mentre quella dei

log10(C)i, anch’essa considerabile gaussiana, come visibile in figura 5.11, è definita da un valor medio pari a -9.955128 e da una deviazione standard pari a 0.123473, (tabella 5.4).

Da una osservazione dei dati riportati in tabella 5.1 emerge come l’errore dei dati sperimentali di ogni singola prova risulti essere nella maggior parte dei casi più bassa rispetto all’errore relativo alla retta di best-fit di tutti i dati.

provino log10(C)i mi errore 01 -9.959807 2.9984 0.037597 02 -10.077558 3.0698 0.058854 03 -10.005900 3.0340 0.066994 04 -10.045369 3.0382 0.060426 05 -10.188157 3.1649 0.060996 06 -10.049428 3.0450 0.068123 07 -10.096083 3.0734 0.053449 08 -10.026248 3.0208 0.058416 09 -10.039033 3.0066 0.049650 10 -10.051172 3.0287 0.061458 11 -10.034817 3.0000 0.035098 12 -9.836551 2.8241 0.045164 13 -9.934388 2.9203 0.050189 14 -9.771195 2.7698 0.039423 15 -9.751126 2.7724 0.031331 16 -9.937072 2.9226 0.053508 17 -9.990962 2.9694 0.042701 18 -9.799865 2.7897 0.057547 19 -9.710986 2.7292 0.069796 20 -10.060492 3.0486 0.056806 21 -9.947168 2.9335 0.051531 22 -9.956953 2.9398 0.051716 23 -9.848686 2.8542 0.046721 24 -10.013674 2.9824 0.050620 25 -9.873562 2.8552 0.044544 26 -9.846520 2.8387 0.029279 27 -9.867846 2.8530 0.044687 28 -9.899245 2.8750 0.044205 29 -9.952708 2.9437 0.045909 30 -10.037225 3.0183 0.058797 31 -9.656204 2.6713 0.042990 32 -9.982247 2.9525 0.049425 33 -9.933254 2.9032 0.042536 34 -10.181249 3.1315 0.060355 35 -9.933242 2.9073 0.061067 36 -10.088631 3.0844 0.046047

log10(C)tot mtot errore

tutti dati -9.964251 2.9536 0.059496

Tabella 5.2: Coefficienti log10(C)tot, mtoted errore relativi alla retta di best-fit

di tutti i dati.

Figura 5.10: Distribuzione dei valori di mi.

valor medio standard deviation

mi 2.9436 0.115616

Tabella 5.3: Valor medio e standard deviation dei coefficienti mi. valor medio standard deviation

log10(C)i -9.955128 0.123473

Tabella 5.4: Valor medio e standard deviation della distribuzione dei coefficienti log10(C)i.

Figura 5.11: Distribuzione dei valori di log10(C)i.

Tra i coefficienti che definiscono le equazioni di Paris, o meglio tra i valori del log10(C)i ed mi di tutte le prove risulta esistere una correlazione, sul-la quale si entrerà più in dettaglio successivamente, che è stata messa in evidenza in figura 5.12.

In seguito sono stati ricavati i valori dei coefficienti delle rette di best-fit dei dati relativi alla velocità di propagazione andando a fissare il valore della pendenza pari a ¯m.

Dovendo calcolare solo uno dei due coefficienti, definito come log10(C)mi¯ ,

che definiscono le rette è stata utilizzata solamente la prima equazione del sistema 5.6.

La retta di best-fit con pendenza fissata ( ¯m) relativa a tutti i dati interni

all’intervallo ha un valore del coefficiente log10(C)m¯ pari a -9.95212 e fornisce

un valore dell’errore pari a 0.059508.

L’equazione di tale retta risulta essere quindi:

log10 Ã dc dN ! = −9.95212 + 2.9436 · log10(∆K) . (5.11)

I valori dei coefficienti log10(C)mi¯ e dell’errore per i trentasei provini sono

01 -9.893630 2.9436 0.038169 02 -9.924072 2.9436 0.061083 03 -9.895667 2.9436 0.068052 04 -9.930056 2.9436 0.061774 05 -9.917697 2.9436 0.067269 06 -9.925051 2.9436 0.069395 07 -9.937387 2.9436 0.055986 08 -9.934102 2.9436 0.059213 09 -9.962646 2.9436 0.050272 10 -9.948310 2.9436 0.062429 11 -9.966800 2.9436 0.035820 12 -9.980302 2.9436 0.047792 13 -9.962631 2.9436 0.050271 14 -9.982123 2.9436 0.044782 15 -9.959083 2.9436 0.038320 16 -9.962375 2.9436 0.053570 17 -9.959513 2.9436 0.042825 18 -9.986626 2.9436 0.060610 19 -9.973003 2.9436 0.074489 20 -9.933198 2.9436 0.058355 21 -9.959383 2.9436 0.051545 22 -9.961619 2.9436 0.051718 23 -9.957562 2.9436 0.047928 24 -9.966520 2.9436 0.050846 25 -9.982070 2.9436 0.045935 26 -9.974009 2.9436 0.032021 27 -9.979399 2.9436 0.046164 28 -9.982621 2.9436 0.045111 29 -9.952623 2.9436 0.045909 30 -9.947875 2.9436 0.059604 31 -9.988396 2.9436 0.056318 32 -9.971310 2.9436 0.049436 33 -9.981807 2.9436 0.042838 34 -9.954079 2.9436 0.065043 35 -9.977554 2.9436 0.061234 36 -9.916579 2.9436 0.049472

Figura 5.12: Relazione tra i coefficienti log10(C)i ed mi.

Si fa notare come i valori dell’errore risultino essere ovviamente maggiori di quelli riportati in tabella 5.1.

Anche in questo caso la distribuzione dei valori dei log10(C)mi¯ può essere

considerata gaussiana, come visibile in figura 5.13, e definita dal valor medio e dalla deviazione standard riportati nella tabella 5.6.

valor medio deviazione standard log10(C)mi¯ -9.955213 0.025221

Tabella 5.6: Valor medio e standard deviation per la distribuzione dei valori di log10(C)mi¯ .

Di seguito, in figura 5.14, vengono visualizzate le due rette di best-fit, quella libera e quella con pendenza ¯m per il provino rappresentato in figura

5.8.

Le rette di best-fit con pendenza pari a ¯m di tutti e trentasei i provini

sono riportate in figura 5.15.

A questo punto è stato calcolato anche il valore medio dei coefficienti log10(C)mi¯ , definito come log10(C)m¯. Tale coefficiente risulta essere pari a

Figura 5.13: Distribuzione dei valori di log10(C)mi¯ .

Figura 5.14: Retta di best-fit00_propria00_{e retta di best-fit con pendenza fissata} per il provino LC12.

Figura 5.15: Rette di best-fit con pendenza fissata e dati sperimentali di tutti i provini.

La retta di Paris definita dai coefficienti medi risulta essere:

log10 Ã dc dN ! = −9.955213 + 2.9436 · log10(∆K) (5.12)

Il corrispondente valore dell’errore è pari a 0.05958799.

In tabella 5.7 si riportano i valori dei coefficienti e degli errori per la retta di best-fit, la retta di best-fit con pendenza fissata e la retta definita dai coefficienti medi log10(C)m¯ e ¯m.

log10(C) m errore

best-fit -9.964251 2.9536 0.059496 m fissato -9.95212 2.9436 0.059508 coef. medi -9.955213 2.9436 0.059588

Tabella 5.7: Coefficienti della retta di best-fit, della retta di best-fit con pendenza fissata, della retta definita dai coefficienti medi e relativi valori dell’errore.

definita da log10(C)tot e mtot, si riporta la figura 5.16 dove vengono riportati i dati sperimentali e le due rette.

Figura 5.16: Dati sperimentali di tutti i provini e loro retta di best-fit.

Di seguito, nella figura 5.17, viene riproposta la figura 5.14 in cui sono stati inseriti i valori della velocità relativi alla retta di Paris definita da ¯m e log10(C)m¯.

Per verificare come le rette di best-fit ricavate approssimano i valori sper-imentali della velocità, sono state calcolate le curve di propagazione c-N come integrazione della legge di Paris 2 _{e messe a confronto con le curve di}

propagazione sperimentali.

Nella figura 5.6 sono già state tracciate le curve sperimentali della propa-gazione della cricca per i trentasei provini, nelle figure 5.18 e 5.19 si riportano, per i provini LC11 e LC12, le curve c-N sperimentali, quelle relative all’in-tegrazione della retta di best-fit, quelle relative all’inall’in-tegrazione della retta di best-fit con pendenza fissata e quella relativa all’integrazione della retta definita dai coefficienti medi.

E’ evidente, soprattutto in figura 5.19, come la curva di propagazione derivante dall’integrazione della retta di Paris definita dai valori medi ¯m e

Figura 5.17: Retta di best-fit00_propria00_{, retta di best-fit con pendenza fissata} per un singolo provino, retta media delle velocità relative al provino LC12.

log10(C)m¯ risulti fornire, a parità di numero di cicli, un valore della lunghezza

della cricca inferiore alla lunghezza ottenuta dalle prove.

5.2.2

Verifica delle

_capacità

_{del modello.}

Per effettuare la verifica delle capacità del modello è stata utilizzata la distri-buzione gaussiana dei log10(C)mi¯ definita dal valor medio e dalla deviazione

standard riportati in tabella 5.6

Volendo verificare il modello utilizzato sono state costruite le rette aventi la stessa pendenza di quella definita dai coefficienti medi ma un valore di log10(C) dato dal valore di log10(C)m¯ più l’effetto dovuto alla deviazione

standard della distribuzione dei log10(C)mi¯ .

Dalla figura 5.20 si può osservare come soltanto i dati sperimentali con-tenuti nella parte centrale dell’intervallo di ∆K siano interni alle due rette che intersecano l’asse delle velocità nel valore log10(C)m¯ ± 3σ.

Integrando tali rette è possibile andare a ricostruire le curve di propaga-zione della cricca ed andare a visualizzare la curva relativa alla retta definita dai coefficienti medi e quelle definite da ± σ e da ± 3σ.

Figura 5.18: Curve c-N del provino LC11.

Figura 5.20: Verifica del modello tramite le curve della velocità di propagazione dc/dN.

soddisfacenti: è evidente come la curva di propagazione ottenuta integrando la retta definita dai coefficienti medi presenti un andamento che si discosta molto da quelli dei provini fin da valori della cricca intorno ai 5 mm.

Per rendere più evidente come il modello non risulti approssimare bene i dati sperimentali si riporta in figura 5.22 la prima parte delle curve di propagazione ingrandita.

La curva della propagazione media fornisce valori della lunghezza della cricca più bassi a parità di numero di cicli rispetto ai dati sperimentali.

Un’ulteriore analisi statistica è stata effettuata sul numero di cicli ne-cessario per avere una determinata crescita della cricca. Le curve prese in considerazione sono quelle sperimentali e quelle ottenute dall’integrazione della retta definita dai coefficienti medi e quelle definite da ±3σ.

Considerando sei valori di lunghezza della fessura - 10, 12.5, 15, 17.5, 20, e 28 mm - sono stati calcolati i valori dei logaritmi in base dieci dei numeri di cicli necessari per passare dal valore della lunghezza di fessura di 5 mm fino ad ognuno di questi sei valori3_{. Per ognuna delle sei lunghezze sono stati}

quindi calcolati i valori del logaritmo del numero di cicli di ogni provino, il

Figura 5.21: Verifica del modello tramite le curve di propagazione c-N.

loro valore medio e la deviazione standard. Tali valori sono riportati nella tabella 5.8.

lunghezza di fessura valor medio deviazione standard 10.0 4.55705682919378 0.0205293104 12.5 4.67462420983092 0.0195312831 15.0 4.74318126422596 0.0185054059 17.5 4.78843173516547 0.0191010135 20.0 4.82134804314807 0.0194102045 28.0 4.87985501372526 0.0212071578

Tabella 5.8: Valor medio e deviazione standard del logaritmo del numero di cicli che producono un’assegnata variazione della lunghezza della cricca.

Da tale tabella è possibile osservare come, all’aumentare della lunghezza della cricca, la deviazione standard tenda inizialmente a diminuire, raggiunga un valore minimo per un valore di c prossimo a 15, e poi tenda ad aumentare. Tale andamento di ∆N evidenzia come attraverso delle singole rette non sia possibile descrivere accuratamente le curve della velocità.

Nel paragrafo successivo sarà per questo motivo sviluppato un modello capace di descrivere le curve della velocità attraverso coppie di rette incidenti fissato il punto di intersezione in corrispondenza del valore di ∆K che rende minimo l’errore commesso in tale descrizione.

Tale valore di ∆K corrisponde infatti ad un valore della lunghezza della cricca prossimo a 15.

In figura 5.23 vengono visualizzate le corrispondenti funzioni di

distribu-zione di probabilità di massa.

Tali andamenti ne evidenziano la buona corrispondenza con l’andamento descritto dalla distribuzione sperimentale dei dati raccolti.

La variabilità emersa dalla campagna di prove, evidenziata in figura 5.6, è ora mostrata in termini di probabilità.

In figura 5.23, i valori dei log dei ∆N, riferiti alla curva di propagazione media che producono l’aumento della lunghezza della cricca da 5 mm fino ad uno dei sei valori considerati, sono definiti dalla probabilità del 50 % sulle linee continue.

Come si può osservare il log dei ∆N della curva media risultano essere, quasi in tutti i casi, maggiori di quelli relativi ai valori sperimentali.

E’ evidente che la curva di propagazione media risulta essere troppo 00_lenta00 _{rispetto ai dati sperimentali.}

Figura 5.23: Distribuzione c vs. N relativa al modello utilizzato.

di propagazione dei singoli provini, ottenute integrando le rette della velocità con pendenza fissata.

Per questi motivi l’analisi dei dati raccolti durante la campagna di prova è stata ripetuta sviluppando un secondo modello capace di approssimare le curve della velocità, sullo stesso intervallo, tramite due rette.

Tale modello è esposto nel paragrafo successivo.

5.3

Descrizione della curva della velocità tramite

due rette.

5.3.1

Elaborazione dei dati.

Dopo aver analizzato i dati con il primo modello e avendo osservato che le curve di propagazione, ottenute dall’integrazione delle singole rette di best-fit delle curve della velocità, non risultano essere in grado di descrivere le curve di propagazione sperimentali, è stato costruito un secondo modello.

Quest’ultimo consiste nell’approssimare le curve di velocità, visualizzate in scala bilogaritmica, tramite due rette, come mostrato in figura 5.24.

Figura 5.24: Esempio dell’approssimazione utilizzata.

Lo scopo della ricerca, infatti, è quello di ottenere un’approssimazione migliore delle curve di velocità sperimentali e quindi una migliore approssi-mazione delle curve di propagazione della cricca simulate.

Anche in questo modello sono stati analizzati solamente i dati della velo-cità di propagazione aventi un ∆K compreso tra 9.23 e 27.7 MPa√m e quindi

i dati, relativi alla propagazione della cricca, interni all’intervallo di estremi 5 e 35 mm già riportati rispettivamente in figura 5.6 e 5.7.

A differenza del modello precedentemente illustrato, in questo caso tale intervallo è stato diviso in due intervalli più piccoli: il primo definito da valori di ∆K compresi tra 9.23 MPa√m e il valore di ∆K scelto come valore

di divisione dei due intervalli, ed il secondo definito da valori di ∆K compresi tra tale valore e 27.7 MPa√m.

Indicando con y e x rispettivamente i valori di log10

³

dc dN

´

e di log10(∆K)

le due rette sono definite come:

y = a1+ b1x (5.13)

per valori di x interni al primo intervallo e

y = a2+ b2x (5.14)

due intervalli definito come il valore di ∆K che rende minimo l’errore, definito dall’equazione 5.15, prendendo in considerazione tutti i dati sperimentali relativi alla velocità di propagazione (∆K compreso tra 9.23 e 27.7 MPa√m).

L’errore è stato definito come:

errore = v u u tPni=11 (Yk− a1− b1Xk)2+ P_n2 j=1(Yj − a2− b2Xj)2 n1+ n2− 2 (5.15) dove con Yk e Yj sono stati definiti i valori sperimentali della velocità di pro-pagazione relativi rispettivamente al primo ed al secondo intervallo, con Xk e Xj i valori di ∆K relativi rispettivamente al primo ed al secondo intervallo, e con n1 e n2 il numero dei dati sperimentali rispettivamente nel primo e nel

secondo intervallo.

Per calcolare tale valore di ∆K è stato implementato un programma in linguaggio Matlab4_{, attraverso il quale, al variare di ∆K in un intervallo}

compreso tra 9.5 e 26 MPa√m, sono stati calcolati i valori dei coefficienti

della coppia di rette di best-fit dei dati della velocità che rendono minima l’errore definito dall’equazione 5.15.

Le due rette sono state costruite in modo che si incontrino in corrispondenza del valore di ∆K che divide i due intervalli così da non presentare dei salti nel valore della velocità.

Tra tutti i valori di ∆K è stato poi scelto quello che fornisce il valore minore dell’errore.

Il voler calcolare, per un assegnato valore di ∆K, i quattro coefficienti del-la coppia di rette di best-fit che rendono minimo l’errore equivale a risolvere un problema di minimo relativo vincolato.

Indicando con i pedici k ed 1 i dati ed i parametri relativi al primo in-tervallo e con i pedici j e 2 quelli relativi al secondo inin-tervallo, i punti della retta di best-fit corrispondente ai dati del primo tratto e quelli della retta di best-fit corrispondente al secondo tratto sono definiti dalle equazioni 5.16 e 5.17

yk= a1+ b1Xk (5.16)

yj = a2+ b2Xj (5.17)

nelle quali con Xk e Xj sono indicati i valori sperimentali di ∆K, e con yk e

yj i valori delle velocità appartenenti alle rette di best-fit in corrispondenza di Xk e Xj.

Si osserva come i coefficienti a1 e b1 corrispondono rispettivamente ai

coefficienti log10(C) ed m dell’equazione di Paris (5.5) del primo intervallo e

i coefficienti a2 e b2 ai coefficienti della retta del secondo.

Per come è costruito il modello, minimizzare l’errore equivale a minimiz-zare la sommatoria, su entrambi gli intervalli, della distanza al quadrato tra le ordinate dei dati sperimentali e i valori numerici sulla coppia di rette di best-fit per lo stesso valore delle ascisse, cioè rendere minima la seguente equazione: f (a1, a2, b1, b2) = N1 X k=1 (Yk− a1− b1Xk)2+ N2 X j=1 (Yj− a2− b2Xj)2. (5.18) Le due rette, essendo costruite in modo che si incontrino in corrispondenza del ∆Kf issato che divide gli intervalli, sono legate tra loro e quindi i quattro coefficienti che le definiscono risultano soddisfare la seguente equazione:

g (a1, a2, b1, b2) = a1− a2+ (b1− b2) log10(∆Kf issato) = 0. (5.19) Il metodo utilizzato nel programma implementato in Matlab è quello dei moltiplicatori di Lagrange 5 _[11].

Voler calcolare i coefficienti delle rette che minimizzano l’errore, assegnato il valore di ∆K di divisione, corrisponde quindi a risolvere il seguente sistema:

               fa1+ λga1 = 0 fa2+ λga2 = 0 fb1+ λgb1 = 0 fb2+ λgb2 = 0 g = 0 (5.21) 5

Teorema 5.1 (Metodo dei moltiplicatori di Lagrange)

Sia f : A ⊂ Rn _{→ R una funzione definita nell’insieme aperto A e sia} f ∈ C1_(A).

Supponiamo che il vincolo S sia l’insieme

S = {P = (x1, x2, . . . , xn) ∈ A : g(P ) = 0} , con g : A ⊂ Rn _{→ R, g ∈ C}1 _{(A) e ∇g (P) 6= 0 per ogni P ∈ S.}

Se un punto P0=(x1,x2,. . ., xn) ∈ S è di massimo ( o di minimo ) relativo vincolato, allora esiste λ ∈ R tale che

funzione da minimizzare che dell’equazione che definisce il vincolo, rispetto a quest’ultime.

Dopo aver calcolato i valori dei coefficienti delle rette (log10(C)tot1_i ed

m_{tot1_i} per il primo intervallo e log10(C)tot2_i ed mtot2_i per il secondo) e il

relativo errore per diversi valori del ∆K di divisione è stato poi scelto, come valore di ∆K di divisione quello che fornisce un errore minimo. Tale valore di ∆K è stato definito come ∆Kbest.

Per ottenere l’andamento dell’errore al variare di ∆K è stato eseguito un primo calcolo dei coefficienti delle rette e dell’errore per diversi valori di ∆K utilizzando un passo di quest’ultimo pari a 0.01 MPa√m.

Come si può osservare dalla figura 5.25 si ha un valore di minimo dell’errore per un valore di ∆K compreso tra 16 e 16.5 MPa√m.

Per ottenere un valore di ∆Kbest più preciso, è stato ripetuto il calcolo

Figura 5.25: Valore della deviazione standard al variare di ∆K.

andando ad analizzare un intervallo di ∆K di estremi 15.5 e 16.5 MPa√m

utilizzando un passo di ∆K di 0.001 .

Il valore minimo dell’errore risulta essere pari a 0.04192 in corrispondenza di un valore di ∆Kbest di 16.308 MPa

√

m e quindi in corrispondenza di un

Di seguito, in tabella 5.9, si riportano i valori dell’errore e dei coefficienti delle due rette di Paris al variare del ∆Kf issatocon un passo di 0.001 MPa

√ m

in un piccolo intervallo intorno al valore di ∆Kbest.

m1tot_i log10(C)1tot_i m2tot_i log10(C)2tot_i ∆K_i errore 2.3549 -9.304959 3.6265 -10.846422 16.300 0.0419156949 2.3550 -9.305075 3.6266 -10.846585 16.301 0.0419156794 2.3551 -9.305191 3.6267 -10.846748 16.302 0.0419156658 2.3552 -9.305307 3.6269 -10.846911 16.303 0.0419156543 2.3553 -9.305423 3.6270 -10.847074 16.304 0.0419156447 2.3554 -9.305540 3.6271 -10.847236 16.305 0.0419156370 2.3555 -9.305656 3.6272 -10.847399 16.306 0.0419156314 2.3556 -9.305772 3.6273 -10.847561 16.307 0.0419156277 2.3557 -9.305888 3.6275 -10.847723 16.308 0.0419156260 2.3558 -9.306005 3.6276 -10.847886 16.309 0.0419156262 2.3560 -9.306121 3.6277 -10.848048 16.310 0.0419156284 2.3561 -9.306238 3.6278 -10.848210 16.311 0.0419156326 2.3562 -9.306355 3.6279 -10.848372 16.312 0.0419156387 2.3563 -9.306471 3.6281 -10.848534 16.313 0.0419156468 2.3564 -9.306588 3.6282 -10.848695 16.314 0.0419156569 2.3565 -9.306705 3.6283 -10.848857 16.315 0.0419156689 2.3566 -9.306821 3.6284 -10.849019 16.316 0.0419156829 2.3567 -9.306938 3.6285 -10.849180 16.317 0.0419156989

Tabella 5.9: Coefficienti delle coppie di rette di best-fit ed errore al variare di ∆K in prossimità di ∆Kbest.

In tabella 5.10 si riportano i valori dei quattro coefficienti e dell’errore relativi a ∆Kbest.

m1tot log10(C)1tot m2tot log10(C)2tot ∆Kbest errore 2.3557 -9.305888 3.6275 -10.847723 16.308 0.0419156260

Tabella 5.10: Coefficienti delle rette di best-fit ed errore per tutti i dati sperimentali per ∆K pari a ∆Kbest .

La coppia di rette di best-fit relativa a tutti i dati risulta essere definita quindi dalle seguenti equazioni:

log10 Ã dc dN ! = −9.305888 + 2.3557 · log10(∆K) (5.22)

log10 Ã dc dN ! = −10.847723 + 3.6275 · log10(∆K) (5.23)

per valori di log10(∆K) interni al secondo intervallo.

A questo punto, definito il valore di ∆K che rende minimo l’errore di tutti i dati della velocità interni all’intervallo considerato, è stato possibile dividere, in maniera definitiva, tale intervallo in due.

Il primo intervallo compreso tra il valore di ∆K di 9.23 MPa√m e il valore

di ∆Kbest, il secondo compreso tra il valore di ∆Kbest e 27.7 MPa

√ m.

In figura 5.26 vengono visualizzati tutti i dati sperimentali relativi alla velocità e la coppia di rette di best-fit.

Si osserva, andando a confrontare tale figura con la figura 5.16 relativa ai valori della velocità definita dai coefficienti medi del primo modello, come il secondo modello fornisca una approssimazione migliore dei dati sperimentali.

Figura 5.26: Valori sperimentali della velocità e relative rette di best-fit.

Definiti i due intervalli, e quindi il valore di ∆Kbest, sono stati calcolati per ciascuno dei trentasei provini, utilizzando ancora una volta il metodo dei moltiplicatori di Lagrange, definito dal sistema 5.21, i valori dei quattro coef-ficienti che definiscono le due rette di best-fit, m1i, log10(C)1i, m2i, log10(C)2i

e l’errore.

Così facendo sono stati calcolati i coefficienti delle rette che rendono minimo l’errore di ogni singolo provino.

Ovviamente in questo caso i dati considerati sono quelli della velocità riferiti al singolo provino.

Di seguito, in tabella 5.11, sono stati riportati tali coefficienti con i relativi valori dell’errore.

Le distribuzioni dei valori degli m1i, m2i, log10(C)1i, log10(C)2i possono

essere considerati gaussiane come visibile rispettivamente nelle figure 5.27, 5.28, 5.29, 5.30.

Figura 5.27: Distribuzione dei valori degli m1i.

Nelle tabelle 5.12 e 5.13 sono stati riportati i valori medi e le devia-zioni standard rispettivamente per le distribudevia-zioni dei log10(C)i e per le distribuzioni degli mi sia per il primo che per il secondo intervallo.

Anche per questo modello, come per il precedente, esiste una relazione che lega i valori dei log10(C)1i e m1i e una che lega i valori dei log10(C)2i e

m2i.

Tali relazioni è visibile nelle figure 5.31 e 5.32.

Di seguito, in figura 5.33, vengono visualizzate, come esempio, le due rette di best-fit del provino LC05.

01 -9.554736 2.6309 -10.530572 3.4358 0.0282951184 02 -9.250942 2.3186 -11.155409 3.8894 0.0201054499 03 -9.069488 2.1815 -11.222074 3.9569 0.0216430216 04 -9.206019 2.2657 -11.229492 3.9347 0.0245699142 05 -9.312311 2.3714 -11.270718 3.9867 0.0250752825 06 -9.077073 2.1619 -11.242871 3.9483 0.0307163608 07 -9.391666 2.4344 -10.978836 3.7436 0.0289228376 08 -9.329579 2.3849 -11.147536 3.8844 0.0256368566 09 -9.438884 2.4630 -10.849833 3.6268 0.0286572376 10 -9.181515 2.2369 -11.258611 3.9501 0.0186034434 11 -9.634520 2.6356 -10.603916 3.4352 0.0219734246 12 -9.271504 2.3074 -10.647280 3.4422 0.0242263388 13 -9.580676 2.6006 -10.406419 3.2817 0.0443385168 14 -9.369972 2.4076 -10.320664 3.1917 0.0279258274 15 -9.440111 2.4890 -10.177500 3.0972 0.0238232915 16 -9.289418 2.3296 -11.061782 3.7915 0.0254906992 17 -9.403817 2.4367 -10.775632 3.5682 0.0187859877 18 -9.058068 2.1168 -10.825957 3.5750 0.0316935324 19 -8.825153 1.9273 -10.935379 3.6679 0.0389035679 20 -9.220085 2.2837 -11.218431 3.9320 0.0178470648 21 -9.273144 2.3246 -10.882062 3.6516 0.0283679059 22 -9.122122 2.1936 -10.866519 3.6324 0.0194304229 23 -9.287658 2.3478 -10.615642 3.4431 0.0296020144 24 -9.333440 2.3663 -10.943230 3.6940 0.0237704806 25 -9.159139 2.2087 -10.714397 3.4915 0.0208427870 26 -9.483718 2.5111 -10.313402 3.1954 0.0176647164 27 -9.379543 2.4118 -10.433061 3.2808 0.0339698745 28 -9.309905 2.3368 -10.718695 3.4988 0.0197209432 29 -9.498325 2.5312 -10.633833 3.4678 0.0339943512 30 -9.233388 2.2847 -11.168088 3.8805 0.0224780926 31 -9.218240 2.1576 -10.749784 3.1923 0.0211894352 32 -9.218240 2.2451 -10.749784 3.5084 0.0243845640 33 -9.388432 2.4058 -10.778025 3.5519 0.0203301177 34 -9.450758 2.4678 -11.159943 3.8776 0.0361480250 35 -9.213697 2.2543 -10.901105 3.6461 0.0406760571 36 -9.516795 2.5660 -10.816737 3.6382 0.0274334066

Tabella 5.11: Coefficienti delle coppie di rette di best-fit ed errori per ciascun provino per ∆K pari a ∆Kbest .

Figura 5.28: Distribuzione dei valori degli m2i.