“SISTEMAZIONE IDRAULICA DEL BACINO DEI CORSI D’ACQUA BALBANO E DOGAIA”

(1)

INTRODUZIONE... 5

CAPITOLO 1 - CARATTERISTICHE GENERALI DEL BACINO... 6

1.1 Caratteristiche del bacino... 6

1.2 Caratteristiche geologiche e geomorfologiche... 7

1.3 Corsi d’acqua ... 10

1.3.1 Rio di Dogaia ... 10

1.3.2 Rio di Balbano ... 11

1.3.3 Affluenti del rio di Balbano... 11

1.4 Pericolosità e Rischio idraulico ... 11

CAPITOLO 2 – L’ALLUVIONE DEL 7 NOVEMBRE 2000... 15

2.1 Condizioni del bacino e danni provocati... 17

CAPITOLO 3 – ANALISI IDROLOGICA E IDRAULICA... 22

3.1 Precipitazioni con assegnati periodi di ritorno... 23

3.2 Raccolta dei dati ed elaborazioni statistiche ... 24

Ripafratta [520]... 26

3.3 Elaborazioni statistiche... 27

3.3.1 Metodo di Gumbel... 27

3.3.2 Metodo di Fuller Coutagne ... 28

3.4 Adattamento dei dati dei campioni alle varie distribuzioni... 29

3.4.1 Tabella riassuntiva... 33

3.5 Curve di possibilità pluviometrica ... 34

3.5.1 Tempo di pioggia > 1 ora ... 35

(2)

3.7 Analisi dei bacini... 42 3.7.1 Fosso Dogaia ... 51 3.7.2 Fosso Ciucchi ... 52 3.7.3 Fosso Balbano... 53 3.7.4 Fosso Castiglioncello... 53 3.7.5 Fosso Fontana ... 54 3.8 Analisi Idraulica ... 57

CAPITOLO 4 - INTERVENTI PROPOSTI... 64

4.1.1 Interventi sulla sezione di deflusso e sulla pendenza d’alveo ... 65

4.1.2 Interventi sulla scabrezza d’alveo ... 65

4.1.3 Casse di espansione ... 66

4.2 Cassa in derivazione laterale alimentata da soglia sfiorante a monte di un restringimento di sezione ... 70

4.2.1 Calcolo idraulico dei restringimenti... 70

4.2.2 Verifica dell’energia ... 70

4.2.3 Calcolo dell’altezza in corrispondenza della sezione subito a monte restringimento e tracciamento del profilo di rigurgito ... 71

4.2.4 Calcolo idraulico delle soglie sfioranti... 72

4.2.5 Cassa in derivazione laterale(Balbano) ... 77

4.2.6 Cassa in derivazione laterale(Dogaia)... 81

4.2.7 Cassa in derivazione laterale(Balbano alle cateratte)... 84

4.2.8 Cassa in derivazione laterale(Dogaia alle cateratte) ... 87

4.3 Sistemi di svuotamento delle casse di espansione ... 91

4.4 Profili longitudinali calcolati per lo stato di progetto... 95

(3)

5.2 Terre armate... 100

5.3 Rivestimenti ... 103

5.4 Influenza della vegetazione sulle sponde... 105

APPENDICE ... 107

RINGRAZIAMENTI... 119

(4)

(5)

INTRODUZIONE

L’argomento di questa tesi è stato proposto dal Consorzio di Bonifica del Bientina nell’ambito dei lavori per la sistemazione idraulica del bacino dei corsi d’acqua Balbano e Dogaia e dei loro affluenti. Il lavoro ha evidenziato situazioni di particolare rischio e ha proposto una soluzione per la sistemazione dell’area oggetto di studio. La complessità del bacino è data dalla ramificazione della rete idrografica, nella quale si possono contare almeno cinque corsi d’acqua, e dai vincoli presenti nel territorio. La zona interessata dall’intervento si trova nel comune di Lucca.

Oltre alla sistemazione dei corsi d’acqua suddetti si procede anche alla realizzazione di due casse di espansione(una sul rio di Dogaia e l’altra dopo la confluenza tra il rio di Balbano e il rio di Castiglioncello) con lo scopo di laminare le piene per tempi di ritorno di 200 anni e alla realizzazione di una terza cassa che oltre a laminare le piene ha lo scopo di invasare le acque per il periodo in cui l’altezza liquida del fiume ricettore (Serchio) si trova ad una altezza superiore della quota di scarico delle due aste finali.

Pertanto, allorché il fiume Serchio è in piena, oppure ha una altezza di acqua tale da non consentire lo scarico dei corsi d’acqua, l’unica possibilità che rimane alle acque è quella di permanere all’interno degli alvei fino a che la loro capacità lo permette, dopodichè non vi è altra possibilità se non quella di sormontare le sponde e le arginature ed esondare allagando vaste zone sia agricole che urbanizzate. Quindi la terza cassa ha lo scopo sia di laminare l’onda in arrivo che quello di invasare i volumi che non possono essere scaricati direttamente nel fiume Serchio.

Il lavoro attuale si divide nelle seguenti fasi:

• raccolta dei dati geomorfologici del bacino in esame

• descrizione e analisi dell’evento alluvionale del novembre 2000 • analisi idrologica del sistema

• analisi idraulica allo stato attuale • descrizione degli interventi proposti

(6)

CAPITOLO 1 - CARATTERISTICHE GENERALI DEL

BACINO

1.1 CARATTERISTICHE DEL BACINO

Il sistema idrografico è costituito da 5 sottobacini (fig.1). Partendo da nord-est e ruotando in senso antiorario abbiamo i seguenti corsi d’acqua: rio Dogaia, rio dei Ciucchi, rio di Balbano, rio di Castiglioncello e rio di Fontana. Il bacino in esame si estende per una superficie di circa 12.8 Kmq ed è delimitato a nord dall’autostrada “Bretella”, ad est dal fiume Serchio, a sud ed ad ovest da colline racchiudendo i paesi di Nozzano, Balbano,Castiglioncello e Santa Maria a Colle.

(7)

Il bacino imbrifero complessivo è compreso tra le quote di 300 e 10 m s.l.m.. Le pendenze medie di bacino sono variabili tra 9.40-40.6% per le zone montuose-collinari, in corrispondenza delle quali i corsi d’acqua assumono le caratteristiche torrentizie, mentre in pianura abbiamo valori di pendenza media tra 0.32-2.4%.

(8)

(9)

Fig. 1.3 – Carta geologica

Dal punto di vista geologico si nota che il settore nord-ovest del bacino è caratterizzato da arenarie quarzoso-felspatiche alternate a sottili interstrati di argilliti e siltiti con la presenza di oligocene medio superiori, mentre al sud-ovest si ha prevalenza di argilliti silicee sottilmente stratificate, prevalentemente rosse, e calcari selciferi bianco latte. La zona a nord-est (aree vallive e di foce) è ampiamente occupata da sedimenti, quali “depositi alluvionali recenti e ologene attuali.

Tali formazioni, classificate dal punto di vista idrogeologico sulla base delle caratteristiche litologiche e di fratturazione, presentano una permeabilità secondaria moderatamente bassa (Classe C, relativa al metodo dell’SCS Curve Number).

Dallo stralcio della carta dell’uso del suolo del Piano di Assetto Idrogeologico del Bacino del fiume Serchio si deduce che la parte più elevata del bacino non presenta urbanizzazione; il suolo è essenzialmente forestato con area a vegetazione boschiva ed arbustiva e in piccola parte con “boschi misti”; la porzione centrale del bacino è riservata a ”colture annuali e permanenti, aree prevalentemente occupate da colture agrarie con spazi naturali” e, in minor quantità, a “zone urbanizzate”.

Il bacino prevalentemente ha una permeabilità medio alta con una piccola percentuale di aree a bassa permeabilità come è possibile valutare dalla figura sottostante.

(10)

1.3 CORSI D’ACQUA

All’interno del bacino i 5 corsi d’acqua presenti individuano 2 aste principali: rio di Dogaia (sviluppo 3.92 km)e rio di Balbano (sviluppo 3.35 km). Tutti gli altri fossi possono essere considerati loro affluenti.

Il rio dogaia nasce direttamente nel paese di Santa Maria a Colle, mentre il rio di Balbano nasce dalla confluenza di corsi d’acqua a carattere torrentizio che hanno origine nella parte nord-ovest del bacino. I due corsi convergono a valle del bacino dove si trova un sistema di chiuse (Cateratte),con un impianto di pompe idrovore che con il presente studio verrà sostituito con una cassa di espansione per regolare le portate da addurre al fiume Serchio. Il rio di Balbano prima di convergere con il rio Dogaia riceve le acque dal rio di Castiglioncello e dal rio di Fontana.

Il rio Dogaia si estende essenzialmente in pianura con una pendenza dello 0.32 mentre il rio Balbano è suddiviso praticamente in tre tronchi con pendenze che vanno dal 18% al 5% per poi giungere nel tratto finale ad una pendenza dell’1%, determinando una pendenza media del 2.72%.

Descrizione dei corsi d’acqua: 1.3.1 Rio di Dogaia

• Praticamente il rio di Dogaia non ha veri e propri affluenti ma scoline e canalette che scaricano le proprie acque lungo il percorso del rio stesso, raccogliendo le acque di una superficie di 3.3 Kmq in parte collinare e in parte pianeggiante, interessata sia da urbanizzazione che da insediamenti agricoli. L’asta presenta andamento prevalentemente pianeggiante, con pendenza media pari al 0.32%. La confluenza con il rio di Ciucchi avviene subito a valle del passaggio sotto la ferrovia prima di giungere alle cateratte

• Rio dei Ciucchi: asta principale di lunghezza 1900 m circa, sottobacino di superficie pari a circa 2.23 kmq, presenta carattere montano nel primo tratto con variazione di pendenza abbastanza brusca nel tratto

(11)

importanza. Il rio si immette nella parte finale del rio di Dogaia, quindi non si può considerare come affluente

1.3.2 Rio di Balbano

• Rio di Balbano: raccoglie le acque di un sottobacino di superficie pari a 2.79 Kmq, poco interessato da urbanizzazione. L’asta principale, di lunghezza 1150 m circa, scorre quasi per intero lungo la ferrovia con una pendenza del 1.2% e raccoglie le acque del rio di Castiglioncello nella zona dei Pratacci. A monte dell’asta principale del rio di Balbano confluiscono solco di Nertola, fosso della Sanza e solco del Pera. Nel tratto finale raccoglie le acque del rio di Fontana per poi giungere al sistema di chiuse delle Cateratte

1.3.3 Affluenti del rio di Balbano

• Rio di Castiglioncello: la prima parte dell’asta riguarda una superficie di 3.27 Kmq con tre affluenti: rio di Batano, fosso delle Cavine, solco del Bosco. Zona in prevalenza collinare, poco urbanizzata, che si chiude con la confluenza con il rio di Balbano

• Rio di Fontana: l’asta principale misura 1106 m e raccoglie le acque di un sottobacino di superficie pari a 0.43 Kmq, poco urbanizzato e completamente montano

1.4 PERICOLOSITÀ E RISCHIO IDRAULICO

La morfologia presenta la parte alta dei bacini caratterizzata da elevate pendenze e compluvi molto incisi, dove, soprattutto nel caso di eventi di una certa intensità, si originano fenomeni di erosioni che danno origine a trasporto solido verso valle.

I tratti in erosione diffusa sono situati nella parte superiore dei bacini; le zone in erosione poste a valle sono puntuali e dovuti a fenomeni localizzati di tipo idraulico . Questo vale sia per l’asta principale che per gli affluenti.

(12)

Principali problematiche del sistema

• Presenza di ampi tratti con sezione di deflusso insufficiente: questo problema si presenta in modo particolare in corrispondenza di ponti, tombamenti, sezioni ridotte dalla presenza di materiale detritico e/o vegetale mai rimosso, interventi non appropriati sul corso d’acqua, errati dimensionamenti di opere idrauliche precedentemente realizzate, condizioni morfologiche generali ; riassumendo si ha:

• Tratti a sezione sottodimensionata

• Opere idrauliche (ponti e tombamenti) di sezione insufficiente

• Confluenze non regolate, con apporto di materiale solido all’asta principale di provenienza dai sottobacini; rigurgiti non controllati sugli affluenti

• Problemi di stabilità locale delle opere di sponda e delle strutture arginali

• Elevata disposizione alla erosione delle zone alte di alcuni bacini; assenza di opere idrauliche specifiche (briglie selettive) per il contenimento del materiale soggetto a trasporto

(13)

(14)

Fig.1.4 – Carta rischio idraulico

Per quanto riguarda le zone a rischio, in particolare si fa presente come tutta la zona valliva in prossimità della foce e del sistema di chiuse faccia parte delle zone golenali del fiume Serchio (colore ciano). La zona gialla è soggetta ad elevato rischio di esondazione per il carattere dei corsi d’acqua , impossibilitati a scaricare in modo adeguato. Infine la zona verde è soggetta a un rischio idraulico moderato.

(15)

CAPITOLO 2 – L’ALLUVIONE DEL 7 NOVEMBRE 2000

Il 7 novembre 2000 si è verificato nella zona in esame un eccezionale evento alluvionale caratterizzato da grande afflusso idrologico. Pertanto l’intero bacino è stato sottoposto a sollecitazioni molto vicine a quelle di progetto e di conseguenza è stato possibile valutare l’inadeguatezza di tutto il sistema. Così l’eccezionalità delle piogge, unita alle condizioni del bacino, sicuramente inadeguato per sopportare un fenomeno di tale portata, hanno causato il verificarsi di danni di vario genere e gravità.

Qui di seguito vengono proposti articoli di giornali editi nei giorni successivi l’evento.

(16)

Fig.2.2 –Articolo del Tirreno nei giorni successivi l’evento

(17)

Il sistema dell’intero bacino non era sicuramente nelle condizioni ottimali per poter smaltire un evento di tale portata. Analizziamo, quindi, i motivi che non hanno permesso il regolare deflusso delle acque:

• Degrado del territorio

• Mancanza di risorse per la gestione del territorio

• Mancanza di una programmazione territoriale uniforme

Un fattore importante per analizzare l’evento consiste nel constatare che nei pressi della foce i fossi analizzati hanno sezioni definite e in certi casi anche sufficienti a contenere onde di piena abbondanti. Viceversa, quando si arriva nel tratto vallivo, gli alvei subiscono delle progressive restrizioni.

(18)

Fig 2.5 – Fosso nei pressi della foce: si noti la riduzione di sezione rispetto alla foto precedente

Un altro fattore importante è stato individuato nell’instabilità dei versanti, responsabile dell’elevato trasporto solido nelle aste del reticolo idrografico e delle conseguenti ostruzioni verificatesi in esso.

I danni verificatesi sono la conseguenza della non adeguatezza del bacino idrogeologico stesso, il quale non è stato in grado di sopportare le sollecitazioni cui è stato sottoposto.

La risposta del sistema, evidentemente nelle condizioni in cui si trovava al momento dell’evento, ha evidenziato quanto segue:

• Esondazioni diffuse nella parte valliva del sistema, particolarmente concentrate in corrispondenza delle confluenze e delle strade comunali

(19)

attraversamenti in stretta correlazione con il trasporto solido originato a monte

• Altre zone oggetto di esondazione sono state localizzate in destra del fosso Balbano e in sinistra del fosso Dogaia nella zona della foce. Queste esondazioni sono dovute alle problematiche di rigurgito che hanno determinato il mancato smaltimento delle acque dei fossi. Il difficile smaltimento di queste è dovuto a tre fattori: una scarsa pendenza del fondo dei canali, il rigurgito causato dal livello liquido nei tratti finali a valle della confluenza fra Ciucchi e Dogaia e la presenza di materiale flottante e detritico proveniente da monte

I danni provocati globalmente nell’area in esame sono stati di vario genere. Come è possibile verificare dalla foto di archivio riportate di seguito si possono contare danni alla rete idraulica, alle strutture ed agli impianti (dalle abitazioni private ad edifici pubblici, dalla rete elettrica alla rete fognaria) e disagi di vario genere come avviene in questi casi.

(20)

(21)

Fig.2.8 –Abitazioni sommerse

(22)

L’analisi idrologica ha lo scopo di individuare per ogni sottobacino la portata massima che defluisce alla sezione di chiusura. Non è possibile determinare questa portata massima in senso deterministico, quindi il problema sarà affrontato esclusivamente in termini probabilistici. La portata di piena va considerata come variabile casuale, di conseguenza dovrà essere stimata in relazione ad un livello di probabilità che non può essere superato, vale a dire facendo riferimento ad un periodo di tempo (tempo di ritorno) che intercorre mediamente tra due eventi in cui il valore di tale portata viene superato. Lo studio idrologico, quindi, si rende necessario per le verifiche idrauliche delle aste del reticolo idrografico oggetto di studio, per la conseguente valutazione del rischio idraulico effettivo e per la progettazione di opere atte a diminuire tale rischio.I fenomeni che danno origine ai deflussi attraverso i canali sono le precipitazioni meteoriche; per la modellazione delle piogge è stato effettuato uno studio basato su metodi statistici riguardanti distribuzioni del valore estremo (in particolare sono stati utilizzati il metodo di Gumbel di Fuller-Coutagne ). A seguito degli eventi meteorici le acque pluviali vengono raccolte nei vari bacini e convogliate nei corsi d’acqua; le modalità con cui avviene questo trasferimento, dipendono dalle caratteristiche geografiche, morfologiche e geologiche del bacini stessi, che, nel presente studio, sono stati schematizzati mediante il modello del Soil Conservation Service (SCS), basato sul metodo CN (Curve Number). In base a questa relazione è stata definita una legge di trasformazione “afflussi-deflussi”.

Andando più in dettaglio la procedura di calcolo consiste nelle fasi seguenti: • analisi statistica dei dati di pioggia e verifica dell’adattamento delle

suddette distribuzioni statistiche ai dati a disposizione

• determinazione delle curve di possibilità pluviometrica caratterizzate dal tempo di ritorno deucentennale così come richiesto

• analisi dei bacini afferenti ai principali corsi d’acqua attraverso la parametrizzazione delle caratteristiche morfometriche, litologiche (permeabilità dei terreni) e di uso del suolo

(23)

• costruzione di un modello idrologico su codice di calcolo HEC-HMS 2.2.2 del bacino complessivo per la determinazione delle portate di progetto

• analisi degli effetti di eventi meteorici di durata variabile per i bacini in esame (con tempi di ritorno pari a 200 anni), con ricerca dei fenomeni pluviometrici critici per sezioni significative poste alla chiusura dei bacini parziali e in zone di interesse per l’individuazione degli interventi di messa in sicurezza; in questa fase vengono definiti i valori delle portate di progetto

3.1 PRECIPITAZIONI CON ASSEGNATI PERIODI DI RITORNO

Per lo studio delle precipitazioni è stato ipotizzato uno ietogramma rettangolare con base tp(durata della precipitazione) e altezza un’intensita media che rimane costante durante l’evento. L’entità della precipitazione, cioè l’altezza d’acqua precipitata durante l’intero evento, ragguagliata sulla superficie S del bacino, viene ricavata dalla seguente equazione che determina la curva di possibilità climatica:

n

t a

h=ψ⋅ ⋅ (3.1) dove:

• y è il coefficiente di ragguaglio all’area e alla durata della precipitazione, da valutare per il bacino in base all’estensione della sua superficie

• h è l’altezza totale della precipitazione espressa in mm

• a e n sono coefficienti determinati mediante analisi statistiche • t è la durata del fenomeno meteorico, espressa in ore

Ogni curva di possibilità pluviometrica è relativa ad un determinato periodo di ritorno e mette in correlazione l’altezza di pioggia e la sua durata.

(24)

3.2 RACCOLTA DEI DATI ED ELABORAZIONI STATISTICHE

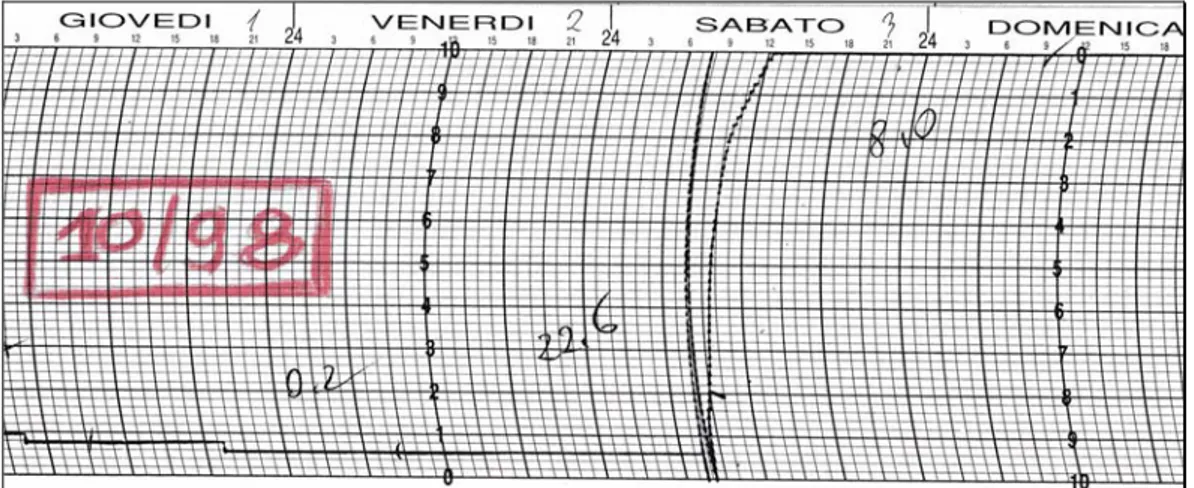
I dati di partenza dell’analisi idrologica sono forniti dal pluviografo registratore della stazione pluviometrica di Ripafratta, la più vicina al bacino in esame. Il periodo di osservazioni dei valori estremi di pioggia pubblicati sugli annali idrologici, disponibili presso l’ufficio idrografico e mareografico di Pisa, parte dal 1971, e termina nel 1998, per un totale di 27 anni. Si è proceduto nel seguente modo: dai tabulati delle piogge giornaliere, per ogni anno è stato definito un numero limitato di eventi meteorici significativi; fatta questa selezione, sono stati esaminati i pluviogrammi relativi a tali fenomeni, suddividendoli in intervalli temporali di 30’. In questo modo si sono potuti stabilire i massimi annuali di pioggia relativi alle durate di 30’, 1 ora, 3 ore, 6 ore, 12 ore e 24 ore.

Di seguito riportiamo due stralci di pluviogramma a titolo di esmpio.

(25)

Nella tabella di seguito sono riportati i campioni analizzati delle massime altezze di precipitazione di durata 5’, 10’, 15’, 20’, 30’, 1, 3, 6, 12 e 24 ore. I campioni delle piogge con durate inferiore ad un’ora non sono molto numerosi, ma nonostante ciò sono stati elaborati, in modo da avere almeno dei riferimenti indicativi; è inoltre da tenere presente che il tempo critico per i corsi d’acqua in esame è molto prossimo all’ora o di poco superiore e per queste durate l’analisi risulta più attendibile essendo i campioni più numerosi.

(26)

Ripafratta [520] Anno 5' 10' 15' 20' 30' 1h ₃h ₆h ₁₂h ₂₄h 1971 32.0 35.8 44.6 59.6 59.6 96.4 1972 24.0 28.0 41.8 42.4 43.0 57.8 1973 17.6 48.2 96.8 104.8 118.0 133.6 1974 24.0 24.8 35.2 37.2 38.0 43.8 1975 16.6 22.6 29.0 38.2 56.8 57.8 1976 25.6 40.8 45.0 45.0 45.0 51.6 1977 10.2 25.0 29.0 34.4 45.4 47.8 1978 14.8 18.4 31.0 39.4 48.6 72.8 1979 9.0 21.4 29.6 49.8 94.8 142.6 1980 13.0 25.2 26.8 32.0 50.2 92.8 1981 13.6 30.4 46.2 52.2 52.4 97.8 1982 12.0 18.6 22.0 27.2 56.0 69.0 1983 12.8 22.0 29.2 43.4 48.0 60.0 1984 13.0 32.2 35.8 40.2 42.6 47.8 1985 15.2 17.6 26.4 30.4 43.0 67.4 1990 16.0 26.2 37.0 65.0 116.6 124.2 124.4 124.4 1991 14.0 25.0 27.4 34.4 66.6 97.0 103.4 103.4 1992 11.2 15.1 20.9 29.3 54.9 59.0 66.0 70.0 1993 10.4 15.4 17.4 18.6 24.2 29.6 48.4 61.4 1994 12.4 18.4 25.0 44.6 84.0 101.0 120.0 135.8 1995 15.0 21.2 34.8 52.4 66.8 78.2 83.6 87.2 1996 11.2 15.4 19.4 37.0 38.4 47.4 49.4 59.4 1997 24.2 30.8 40.8 49.2 53.4 62.4 1998 19 28.4 52.2 67.6 74 78.4

(27)

3.3 ELABORAZIONI STATISTICHE

Per l’individuazione dei punti statistici si è fatto riferimenti ai metodi statistici di Gumbel (o del valore estremo del 1°tipo), di Fuller-Coutagne. Per la stima dei parametri di ogni metodo sono stati utilizzati la media campionaria e lo scarto quadratico medio, le cui espressioni sono

m h M n i n

∑

= = 1 _(3.2) 1 ) ( 1 2 − =

∑

= m n i n ε σ (3.3)

In cui m è il numero dei dati del campione e en è la differenza fra la generica altezza di pioggia e la media campionaria.

3.3.1 Metodo di Gumbel

Per quanto riguarda il metodo di Gumbel il valore h(TR) dell’altezza di pioggia complessiva corrispondente ad un fenomeno di una certa durata, avente tempo di ritorno TR è dato dalla formula seguente:

y N t h r = +_α ⋅ 1 ) ( (3.4) dove:

• h(TR) altezza di pioggia espressa in mm, di una determinata durata, avente periodo di ritorno pari a TR anni

• TR tempo di ritorno espresso in anni

• Y parametro funzione del tempo di ritorno dato da

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − = t y ln ln 1 1 (3.5)

(28)

• N e a parametri della distribuzione statistica di Gumbel rispettivamente pari a : σ ⋅ − =M 0.45 N (3.6) σ α = 77970. ⋅ 1 (3.7) in cui

• M valore medio dell’altezza di precipitazione avente una determinata durata relativo alle osservazione estreme

• s scarto quadratico medio dei dati relativi ad una determinata durata di pioggia

I parametri M e N sono ricavabili direttamente dai dati disponibili; mediante la 3.1, fissando il valore del periodo di ritorno, è possibile calcolare il valore della grandezza idrologica in esame.

3.3.2 Metodo di Fuller Coutagne

Per quanto riguarda il metodo di Fuller-Coutagne il valore h(TR) dell’altezza di pioggia complessiva, corrispondente ad un fenomeno pluviometrico di una certa durata e avente un determinato tempo di ritorno, è ricavabile dalla seguente formula

) log 1 ( ) (t_r N ₁₀T_R h = ⋅ +β⋅ (3.8) dove:

• h(TR) altezza di pioggia espressa in mm, di una determinata durata, avente periodo di ritorno pari a TR anni

• TR tempo di ritorno espresso in anni

• N parametro della distribuzione statistica di Gumbel

• b parametro relativo alla distribuzione di Fuller-Coutagne

dato da N

σ

(29)

Anche in questo caso, dopo aver direttamente determinato dai dati i valori di M e N, fissando un certo tempo di ritorno è possibile stabilire il valore della grandezza idrologica considerata.

3.4 ADATTAMENTO DEI DATI DEI CAMPIONI ALLE VARIE DISTRIBUZIONI

Una volta stimati i parametri delle varie distribuzioni è necessario verificare l’adattamento di queste ultime ai dati del campione a disposizione, per ogni tempo di pioggia. Questo controllo si può fare con test statistici oppure semplicemente con un controllo visivo su carte probabilistiche dette “piani di Gumbel” (uno per ogni tempo di pioggia studiato), nei quali in ascissa compaiono i valori della variabile y (che è funzione del tempo di ritorno) già espressa in precedenza, mentre in ordinata abbiamo i valori delle varie altezze di pioggia. Su tali piani cartesiani i campioni sono rappresentati da una serie di punti (le cui coordinate sono rispettivamente la y corrispondente al tempo di ritorno valutato con la formula di Weibul e le altezze di pioggia misurate), mentre le distribuzioni studiate sono visualizzate con delle curve.

Il procedimento seguito per riportare un campione analizzato sulla carta di Gumbel è così riassumibile: ordinate in ordine crescente le osservazioni disponibili, la durata probabile associata all’osservazione di ordine n risulta data (secondo Weibul) dalla formula:

1 + = Φ m n n (3.10) A tale durata probabile è legato un tempo di ritorno così esprimibile:

n n Tr Φ − = 1 1 (3.11)

In tale modo, ad ogni altezza di pioggia misurata si può associare un tempo di ritorno e , mediante la (3.5) un valore della variabile y; a questo punto il campione è rappresentabile sulla carta di Gumbel.

(30)

La rappresentazione sul piano di Gumbel della curva associata ad una determinata distribuzione, è invece immediata: ad una data altezza di pioggia si associa un determinato valore della probabilità di non superamento e dunque un tempo di ritorno, diverso a seconda del tipo di legge analizzata, come si può desumere dalle (3.4) (3.8) (3.10) (3.16). Trovato il tempo di ritorno, mediante la (3.5) si risale alla variabile y e dunque per punti si può disegnare la funzione relativa alla distribuzione in esame sul piano di Gumbel.

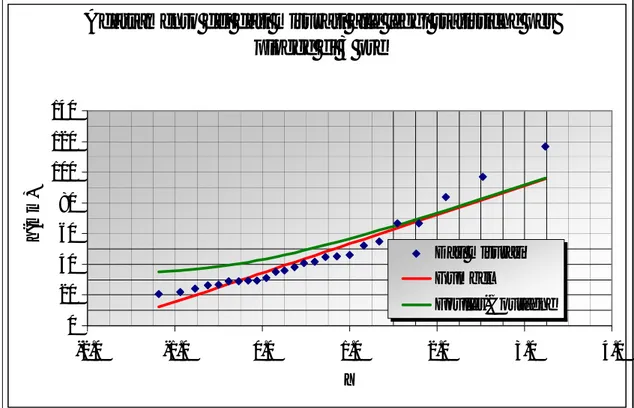
Di seguito si riportano i piani di Gumbel per le piogge di durata pari a 30 minuti, 1 ora, 3 ore, 6 ore, 12 ore e 24 ore.

Adattamento dei dati misurati alle leggi statistiche per

piogge di 1 ore

0 10 20 30 40 50 60 70 -2.0 -1.0 0.0 1.0 2.0 3.0 4.0 Y h( mm ) Dati misurati Gumbel Fouller-Coutagne

(31)

Adattamento dei dati misurati alle leggi statistiche per

piogge di 3 ore

0 20 40 60 80 100 120 140 -2.0 -1.0 0.0 1.0 2.0 3.0 4.0 Y h( m m ) Dati misurati Gumbel Fouller-Coutagne

Fig 3.4 – Adattamento dei dati misurati alle leggi statistiche per piogge di 3 ore

Adattamento dei dati misurati alle leggi statistiche per

piogge di 6 ore

0 20 40 60 80 100 120 140 -2.0 -1.0 0.0 1.0 2.0 3.0 4.0 Y h (mm) Dati misurati Gumbel Fouller-Coutagne

(32)

Adattamento dei dati misurati alle leggi statistiche per

piogge di 12 ore

0 20 40 60 80 100 120 140 -2.0 -1.0 0.0 1.0 2.0 3.0 4.0 Y h( m m ) Dati misurati Gumbel Fouller-Coutagne

Fig 3.6 – Adattamento dei dati misurati alle leggi statistiche per piogge di 12 ore

Adattamento dei dati misurati alle leggi statistiche per

piogge di 24 ore

0 20 40 60 80 100 120 140 160 -2.0 -1.0 0.0 1.0 2.0 3.0 4.0 Y h( m m ) Dati misurati Gumbel Fouller-Coutagne

(33)

Dall’analisi dei piani di Gumbel si può giungere alle seguenti conclusioni:

• I punti rappresentativi del campione si concentrano nella zona con bassi valori di y (inferiori a 2) e cioè danno buone informazioni per quanto riguarda tempi di ritorno piccoli ; viceversa abbiamo pochi punti con ascissa superiore a 2 (corrispondente a un TR pari a 13 anni) e il valore più alto della y dei campioni analizzati corrisponde a un tempo di ritorno pari a 26 anni: per questo motivo, per quanto riguarda eventi con tempi di ritorno elevati (in particolare la pioggia duecentennale, alla quale si farà riferimento per i dimensionamenti idraulici), si utilizzano metodi di stima diversi. Tuttavia per il presente studio si è deciso di utilizzare i dati ottenuti con i metodi di Gumbel e Fuller-Coutagne anche se non disponiamo di un alto numero di dati • La distribuzione di Fuller-Coutagne fornisce valori dell’altezza di

pioggia maggiori rispetto alla distribuzione di Gumbel per y basse, cioè per tempi di ritorno non elevati, che hanno scarsa rilevanza dal punto di vista progettuale. Viceversa, per tempi di ritorno elevati, la distribuzione di Fuller-Coutagne coincide con la distribuzione di Gumbel; entrambe sottostimano i punti rappresentativi degli “eventi eccezionali” del campione

Da un’analisi accurata dei dati è possibile verificare che queste due distribuzioni approssimano in modo soddisfacente il campione solo per piogge di durata un’ora e sono meno precise per la stima di piogge con elevati tempi di ritorno per le altre durate di pioggia. Comunque per il presente studio si è deciso di utilizzare i dati ottenuti da questi due metodi.

3.4.1 Tabella riassuntiva

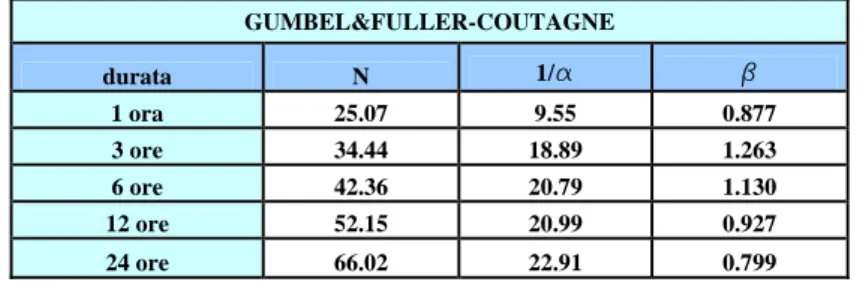
Di seguito si riportano i valori dei parametri delle diverse distribuzioni ottenute con i metodi sopra descritti e le altezze di pioggia, per i tempi di pioggia di 1 ora, 3 ore, 6 ore, 12 ore e 24 ore, in funzione del tempo di ritorno.

(34)

GUMBEL&FULLER-COUTAGNE durata N 1/a b 1 ora 25.07 9.55 0.877 3 ore 34.44 18.89 1.263 6 ore 42.36 20.79 1.130 12 ore 52.15 20.99 0.927 24 ore 66.02 22.91 0.799

Tab. 3.2 – Valori dei parametri delle distribuzioni di Gumbel e Fuller-Coutagne

GUMBEL Tr 1h 3h 6h 12h 24h 20 anni 53.43 90.56 104.13 114.49 134.06 50 anni 62.33 108.17 123.50 134.05 155.41 100anni 68.99 121.36 138.02 148.70 171.40 200 anni 75.63 134.50 152.49 163.30 187.34 FOULLER-COUTAGNE Tr 1h 3h 6h 12h 24h 20 anni 53.67 91.04 104.66 115.03 134.65 50 anni 62.42 108.35 123.71 134.26 155.64 100anni 69.04 121.45 138.12 148.80 171.51 200 anni 75.66 134.55 152.54 163.35 187.39

Tab 3.3 – Valori delle altezze di pioggia per vari tempi di pioggia e diversi tempi di ritorno secondo le distribuzioni analizzate

Come già sostenuto si può notare come i valori ottenuti dalle due stime siano simili e che le altezze di pioggia crescono molto limitatamente per durate superiori alle 3 ore. Quindi entrambi i metodi utilizzati sono in accordo sul fatto che le curve di possibilità pluviometrica presentano un pronunciato smorzamento nella loro parte terminale.

3.5 CURVE DI POSSIBILITÀ PLUVIOMETRICA

Lo scopo ultimo dell’analisi delle piogge è quello di fornire delle curve di possibilità pluviometriche che permettano di stabilire, fissato il tempo di ritorno dell’evento, il valore dell’altezza di pioggia per una determinata durata dell’evento

(35)

state determinate varie curve di possibilità pluviometrica, tutte per un tempo di ritorno pari a 200 anni, per il quale dovranno poi essere stimate le portate e dimensionati i canali della rete in esame. Le curve di possibilità pluviometrica sono state determinate in due modi diversi: per tempi di pioggia inferiori ad un’ora si è usata l’elaborazione dei vari casi critici;,per tempi superiore all’ora si è usato il metodo statistico di Gumbel.

3.5.1 Tempo di pioggia > 1 ora

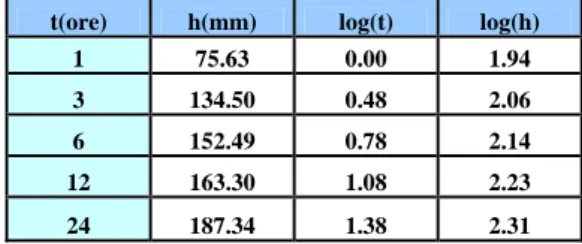
• Si calcola il logaritmo dei valori delle altezze di pioggia di durata da 1 a 24 ore (con tempo di ritorno di 200 anni), e il logaritmo delle durate

t(ore) h(mm) log(t) log(h) 1 75.63 0.00 1.94 3 134.50 0.48 2.06 6 152.49 0.78 2.14 12 163.30 1.08 2.23 24 187.34 1.38 2.31

Tab. 3.4 – Valori delle altezze di pioggia misurate e dei tempi in scala logaritmica

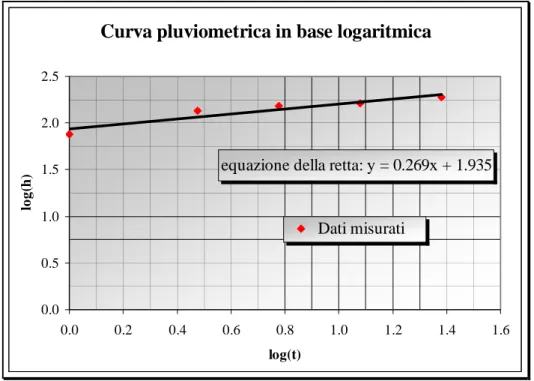
• Si riportano i suddetti punti nel piano logaritmico [ log(t), log(h) ] e si traccia la retta interpolante

(36)

Curva pluviometrica in base logaritmica

equazione della retta: y = 0.269x + 1.935

0.0 0.5 1.0 1.5 2.0 2.5 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 log(t) lo g (h ) Dati misurati

Fig. 3.8 – Rappresentazione in scala logaritmica della curva di possibilità pluviometrica

• I parametri a e n della curva di possibilità pluviometrica si ricavano dall’equazione della retta interpolante (che non è altro che la curva di possibilità pluviometrica nel piano logaritmico) essendo:

a=101.935 =86.15(mm) n=0.269

• Si ricava l’equazione della curva di possibilità pluviometrica: 0.269

15 .

86 t

h= ⋅ per tr = 200 anni

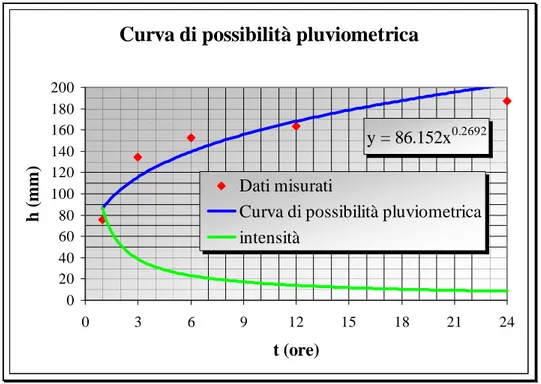
• Di seguito si riporta la rappresentazione grafica delle curva di possibilità pluviometrica duecentennale. Nel grafico viene tracciato anche l’andamento qualitativo dell’intensità di pioggia l che risulta decrescente con la durata secondo la legge:

₌ _⋅ n−1 t a

(37)

Curva di possibilità pluviometrica

y = 86.152x0.2692 0 20 40 60 80 100 120 140 160 180 200 0 3 6 9 12 15 18 21 24 t (ore) h ( mm) Dati misurati

Curva di possibilità pluviometrica intensità

Fig. 3.9 –Curva di possibilità pluviometrica per piogge di durate superiori all’ora e per tempi di ritorno di 200 anni

3.5.2 Tempo di pioggia < 1 ora

Questa elaborazione è la più semplice: scelto il campo delle durate di pioggia nel quale la curva deve avere validità, si raccolgono, per ciascuno degli anni di osservazioni disponibili per la stazione pluviometrica, i valori massimi delle altezze di pioggia di ciascuna durata compresa nel campo di interesse, nel caso in esame 10’- 15’- 20’- 30’- 60’, pubblicati nell’annale idrologico.

• Ordinati quindi, per ciascuna durata, in ordine decrescente i valori delle altezze di pioggia h verificatisi nel periodo di osservazione, i massimi valori relativi alle varie durate costituiscono il I° caso critico, i valori immediatamente successivi il II° caso critico e così via

• Per determinare le costanti a e n delle curve è opportuno linearizzare l’equazione, passando alla rappresentazione logaritmica:

) log( ) log( ) log(h = a +n⋅ t (3.13)

(38)

Tale equazione nel piano logaritmico ( log (h) ; log (t) ) è l’equazione di una retta. Casi critici 10' 15' 20' 30' 60' 1° 16 24 32 37 65 2° 15.2 17.6 26.2 34.8 52.4 3° 15 13.6 25 27.4 48.2

Tab. 3.5 – Altezze di pioggia dei primi tre casi critici

• Le costanti a e n relative a un dato caso critico possono essere determinate mediante un inviluppo o per interpolazione. Il metodo di regolarizzazione per interpolazione dei dati relativi a un certo caso critico consiste nel ricavare i parametri delle costanti log a e n della retta ( 3.13 ) col metodo dei minimi quadrati, che rende minima la somma dei quadrati degli scarti tra i valori osservati e quelli corrispondenti che si ricavano dalla ( 3.13 ). Questo metodo è preferibile rispetto al metodo mediante inviluppo, purché non lasci troppo al di sotto i punti rappresentativi delle altezze di pioggia di durata prossima a quella critica per il problema di interesse

= ∑ ⋅ ⋅∑log( ) ) log( 10 i i t m n m h a (3.14)

∑

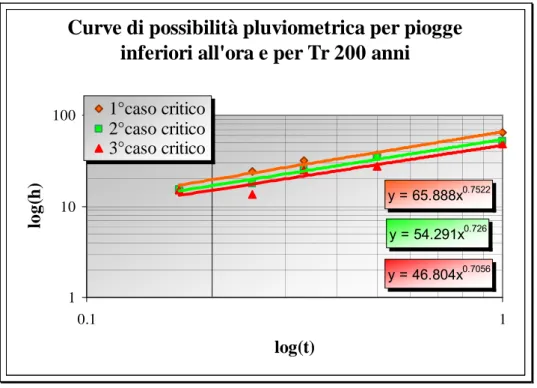
⋅ − ⋅ ⋅ − ⋅ = 2 2 ) log ( 1 ) (log ) log ( ) log ( 1 ) (log ) (log i i i i i i t m t h t m h t n (3.15)

(39)

Curve di possibilità pluviometrica per piogge

inferiori all'ora e per Tr 200 anni

y = 46.804x0.7056 y = 54.291x0.726 y = 65.888x0.7522 1 10 100 0.1 1 log(t) log( h ) 1°caso critico 2°caso critico 3°caso critico

Fig. 3.10 –Curva di possibilità pluviometrica per piogge di durate inferiori all’ora e per tempi di ritorno di 30 anni

• Le curve ottenute non sono del tutto soddisfacenti a causa del non perfetto parallelismo, per cui si verifica che in un certo campo di durate le altezze di pioggia del caso critico inferiore sono maggiori di quelle relative al caso critico d’ordine superiore. Le intersezioni tra le curve tuttavia risultano all’esterno del campo di durate di pioggia oggetto di studio. Queste imprecisioni sono causate dai pochi dati disponibili che non hanno permesso una corretta regolarizzazione dei dati pluviometrici

• Al fine di individuare una curva rappresentativa dei valori di altezza di pioggia per le durate inferiori all’ora, visto i difetti dei risultati trovati è sembrato opportuno adottare l’equazione con il coefficiente angolare più basso, vale a dire quella del I° caso critico in quanto rende la stima più cautelativa inducendo altezze di pioggia più elevate a parità di ordinata iniziale:

0.7522 88 .

65 t

(40)

Le piogge di durata inferiore all’ora hanno ordinata iniziale minore di quelle superiori all’ora. Data però la minore disponibilità di dati si è ritenuto adottare per entrambi la ordinata iniziale di quelle superiori all’ora, ottenendo l’equazione:

0.7522 15 .

86 t

h= ⋅ per tr = 200 anni

Curva di possibilità pluviometrica per Tr 200 anni y = 86.152x0.2692 y = 86.152x0.7522 0 20 40 60 80 100 120 140 160 180 200 220 0 3 6 9 12 15 18 21 24 t (ore) h (mm)

dati misurati t > 1ora

dati misurati t < 1ora

Fig. 3.11 –Curva di possibilità pluviometrica per tempi di ritorno di 200 anni

Curva di Possibilità climatica per Tr=200 anni

• 0.7522

15 .

86 t

h= ⋅ per t minore di 1 ore

• 0.269

15 .

86 t

h= ⋅ per t maggiore di 1 ore

La curva duecentennale sarà adoperata per il dimensionamento dei canali, per le verifiche nei riguardi delle portate massime e per il progetto delle casse di espansione; le altre curve, con tempi di ritorno inferiori, saranno utilizzate per stabilire che tempo di ritorno ha la pioggia che causa la crisi dell’attuale reticolo idrografico e per quantificare l’intervallo temporale con cui vengono allagate le aree di espansione dei corsi d’acqua previsti per la sistemazione del bacino.

(41)

3.6 COEFFICIENTE DI RAGGUAGLIO

Le elaborazione dei dati pluviometrici cui finora si è fatto riferimento permettono di determinare le equazioni della curva di possibilità climatica , aventi prefissate probabilità di verificarsi, relative alle località di osservazione.

Per i problemi relativi alle costruzioni idrauliche occorre invece spesso riferirsi a curve di possibilità climatica valide per superfici di una certa estensione (nel nostro caso, per il calcolo della portata di progetto, occorre riferirsi alla superficie del bacino sotteso da una data sezione). Se la superficie non è molto piccola, non risulta lecito supporre che l’altezza di pioggia a essa relativa sia uguale a quella verificatasi nel centro di scroscio, in quanto l’altezza e l’intensità media di pioggia di una certa durata diminuiscono man mano che ci si allontana da tale punto.

D’altra parte le curve di possibilità pluviometrica vengono determinate prendendo in esame le massime altezze di altezze di precipitazione di varie durate registrate nella stazione di misura in un certo periodo di osservazione e quindi, proprio perché si tratta di altezze massime, è da presumere che esse si siano verificate durante eventi con centro di scroscio nelle vicinanze della stazione stessa.

Occorre perciò ragguagliare le altezze di pioggia all’area dei bacini di interesse. Bisogna al riguardo avere presente che, a parità di area, il coefficiente di ragguaglio varia con la durata della pioggia e più precisamente diviene sempre più piccolo al diminuire di tale durata.

In conclusione, il valore del coefficiente di ragguaglio è stato determinato facendo riferimento alla tabella fornita da Columbo (1960) pubblicata sul Manuale di ingegneria civile. Per il bacino in esame, facendo riferimento ad un’area pari all’incirca a 1000 ha, il coefficiente di ragguaglio non varia molto al variare della durata dell’evento perciò è stato assunto il suo valore medio pari a 0.85.

(42)

Durata [ore] 1000 ha 1500 ha 2000 ha 3000 ha 4000 ha 5000 ha 0.25 0.835 0.804 0.782 0.750 0.722 0.685 0.5 0.840 0.813 0.791 0.759 0.733 0.704 0.75 0.844 0.818 0.798 0.767 0.740 0.714 1 0.846 0.821 0.803 0.772 0.746 0.721 2 0.850 0.827 0.811 0.783 0.757 0.732 3 0.853 0.831 0.815 0.789 0.765 0.741 4 0.857 0.835 0.821 0.796 0.733 0.750 6 0.863 0.843 0.831 0.808 0.788 0.757 12 0.884 0.868 0.858 0.844 0.830 0.816 24 0.923 0.916 0.906 0.900 0.894 0.886

Tab. 3.6 - Coefficienti di ragguaglio alle precipitazioni per aree inferiori a 50 km2

3.7 ANALISI DEI BACINI

Per poter utilizzare il programma di calcolo HEC-HMS 2.2.2 sono state individuate le principali caratteristiche dei vari sottobacini.

L’analisi dei bacini ha lo scopo di giungere alla definizione dei tempi di concentrazione che saranno utilizzati per la determinazione della durata dell’evento pluviometrico critico e per la determinazione dell’idrogramma unitario per la ricostruzione dell’onda di piena.

Oltre ai tempi di concentrazione per ciascun bacino si è determinato il coefficiente CN in funzione delle caratteristiche litologiche, di permeabilità e di uso del suolo, avendo analizzato i bacini elementari sia dal punto di vista geo-morfologico che da quello di permeabilità e attitudine al deflusso delle acque meteoriche.

L’utilizzo di dati di permeabilità ed uso del suolo ha consentito di impiegare un modello di trasformazione da afflussi a deflussi che tiene effettivamente conto delle caratteristiche del territorio oggetto di studio comunemente noto come «Metodo CN» del Soil Conservation Service; in questo modo è possibile determinare lo ietogramma delle piogge nette o efficaci che formano il deflusso attraverso i corsi d’acqua.

(43)

Le caratteristiche geometriche e morfologiche dei bacini oggetto di studio sono espresse attraverso i seguenti parametri:

• Superficie del bacino imbrifero

• Lunghezza asta principale del corso d’acqua in esame

• Quota massima del bacino rilevata direttamente sulla cartografia disponibile

• Quota sezione di chiusura • Pendenza media del bacino

Per quanto riguarda la permeabilità, considerata a livello macroscopico, il territorio afferente a ciascun bacino viene suddiviso in quattro categorie (A, B, C e D) a permeabilità decrescente .

Le caratteristiche di uso del suolo sono state rilevate dalla cartografia allegata al P. A. I. dell’Autorità di Bacino; i coefficienti relativi ai diversi usi del terreno sono stati assegnati per similitudine con quanto previsto in tabelle sperimentali riferite a bacini degli Stati Uniti. Nella tabella 3.21 sono riportate le caratteristiche di permeabilità facenti capo alle classi descritte; nella tabella 3.22 sono invece riportati i coefficienti CN parziali che vengono assegnati alle varie porzioni di territorio in funzione della permeabilità e dell’uso del suolo; nella colonna “Classi” si leggono i numeri assegnati alle porzioni di bacino in questo studio.

Il calcolo del coefficiente CN medio caratteristico di ciascun bacino è stato condotto effettuando una media pesata dei coefficienti parziali sulle rispettive superfici. In particolare, operando per superfici finite, si è calcolato il coefficiente CN parziale di ciascun elemento a partire dalla permeabilità ed uso del suolo locali, procedendo poi al calcolo della media pesata sul complesso del sottobacino considerato.

Il CN così calcolato è quello identificato con l’indice II ed è relativo alla classe AMC media (umidità media prima dell’inizio dell’evento meteorico critico); l’altezza media di pioggia che determina il parametro AMC è stata valutata in 15.13 mm ed è

(44)

la quantità di acqua che statisticamente cade nei cinque giorni precedenti l’evento; ciò si deduce facendo riferimento alla pioggia media annua, che è pari a 1104.8 mm.

Le caratteristiche geometriche, di permeabilità e di uso del suolo individuate permettono di calcolare, per ogni bacino, il tempo di concentrazione.

La formula cui si è fatto riferimento è stata la seguente: Formula del SCS

per il calcolo del tempo di concentrazione di bacini collinari;

(

)

[

]

5 . 0 7 . 0 0.8 1900 9 / 1000 L) (3281 1.67 S CN tc ⋅ − ⋅ ⋅ ⋅ = (3.16) dove: • tc è il tempo di concentrazione

• L la lunghezza dell’asta massima espressa in Km • CN è il valore del coefficiente CN per quel bacino • S è la pendenza media del bacino espressa in %

Le portate di progetto relative alle sezioni di chiusura di ciascun sottobacino, vengono calcolate a partire dagli ietogrammi e dagli idrogrammi unitari ottenuti combinando i dati relativi agli eventi pluviometrici con le caratteristiche dei sottobacini. Per ciascun sottobacino si è fatto riferimento al fenomeno pluviometrico critico che, secondo le elaborazioni effettuate, non coincide con i tempi di concentrazione calcolati ma assume un valore maggiore. L’evento critico è stato individuato, per ciascun bacino, per successive iterazioni di calcolo assumendo come variabile, ovviamente, la durata dell’evento piovoso.

Per la costruzione degli ietogrammi relativi alle piogge nette si è fatto riferimento alla formula seguente, dovuta al Soil Conservation Service:

(

)

S I P P a e + − = 2 a I -P (3.17) dove:

(45)

• Pe è la pioggia efficiente (o netta) misurata in mm • P è la pioggia totale misurata in mm

• S = 25.4·(1000/CN -10) è l’assorbimento potenziale massimo, misurato in mm

• Ia è l’assorbimento iniziale, misurato anch’esso in mm e posto uguale a 0.1•S

L’idrogramma unitario assunto è quello sviluppato dal Soil Conservation Service, basato su una serie di dati raccolti da numerosi bacini agricoli posti sul territorio degli USA. Le equazioni parametriche così ottenute vengono utilizzate per calcolare la portata di picco e la durata dell’idrogramma a partire dalla definizione del tempo di ritardo (lag time) del bacino idrografico considerato, pari al 60% del tempo di concentrazione del bacino.

Il bacino complessivo è stato suddiviso nei seguenti sottobacini: • Bacino Dogaia

• Bacino Ciucchi • Bacino Balbano

• Bacino Castiglioncello • Bacino Fontana

• Le confluenze dei vari fossi sono state indicate con lettere maiuscole: • A – Rappresenta il punto del Dogaia nel quale si ha l’immissione del

Ciucchi

• B – Rappresenta la confluenza tra il Balbano e il Castiglioncello

• C – Rappresenta il punto del Balbano nel quale si ha l’immissione del Fontana

Inoltre i tratti a valle della confluenza B sono stati schematizzati con il metodo cinematico; in effetti questa modellazione dà luogo a laminazioni praticamente trascurabili, dell’ordine di grandezza pari a 0.1 m3_{/s. Di seguito riportiamo una}

(46)

tabella in cui compaiono i valori dei parametri relativi ad ogni sottobacino del modello.

Bacino Area [km2_{] CN I}_a_[mm] _{SCS Lag [m]}

Dogaia 3.30 77.53\81.79 7.36\5.66 27.13\33.84

Ciucchi 2.23 74.14 8.86 31.56

Balbano 2.79 72.99 9.39 48.97

Castiglioncello 3.27 71.03 10.37 57.81

Fontana 0.43 70.92 10.40 33.66

Tabella 3.7 – Caratteristiche dei bacini

Il parametro SCS Lag vale il 60% del tempo di concentrazione.

L’assorbimento iniziale Ia è stato 0.10•S per tutti i bacini stanti le caratteristiche geologiche e a cautela dei calcoli idrologici.

Per quanto riguarda il bacino Dogaia i valori per ogni parametro sono due perché, a differenza degli altri bacini, quello in questione è stato schematizzato con due piani confluenti nello stesso corso d’acqua (vedere 3.7.1 Fosso Dogaia).

Lo ietogramma totale è stato assunto di forma costante. Dal punto di vista matematico l’intensità di pioggia i dell’evento considerato rimane invariata per tutta la durata della pioggia e pari ad h(tp)/tp, con riferimento alla curva di possibilità pluviometrica adottata.

Di seguito si espongono i passaggi per la realizzazione del modello idrologico con HEC-HMS 2.2.2:

• Determinazione dello ietogramma delle piogge totali per diverse durate con tempo di ritorno pari a 200 anni a partire dalle curve di possibilità pluviometrica. Immissione in HEC-HMS 2.2.2 dei valori ottenuti per le precipitazioni (precipitation gage)

(47)

• Schematizzazione del bacino mediante sottobacini elementari (basin Model)

• Determinazione dell’idrogramma unitario (modello del SCS), calcolo del CN e del Ia per ogni sottobacino

• Assegnazione dei parametri precedentemente calcolati per ciascun bacino

• Immissione dei dati relativi al componente Metereologic Model (interazione fra modello di bacino e modello meteoreologico definito in funzione delle diverse durate degli eventi)

• Immissione dei dati relativi al componente Control Specifications (inizio e fine simulazione idrologica fissato lo step temporale di calcolo, che nello studio compiuto è stato posto pari ad 1 minuto per le piogge con durata minori e uguali all’ora e 5 minuti per pigge di durata superiore)

• Determinazione degli idrogrammi di piena a 200 anni nelle sezioni in esame in funzione della durata dell’evento meteorologico

Sono stati simulati gli eventi di pioggia ad intensità costante di durata variabile da 0.5 a 5 ore, con variazioni temporali di 15 minuti; per ogni simulazione sono stati calcolati gli idrogrammi nelle varie aste del reticolo idrografico e in particolare i valori di picco delle portate; confrontando tra loro questi valori si sono potuti stabilire i massimi di portata allo stato attuale, in pratica raggiungendo l’obiettivo dell’analisi idrologica.

Nel seguito riportiamo le carte utilizzate per la valutazione delle caratteristiche morfometriche dei bacini suddetti ed i risultati ottenuti al termine dell’analisi idrologica.

(48)

Fig 3.12 – Carta litologica e relativa legenda per la valutazione delle caratteristiche di permeabilità del terreno

(49)

Fig. 3.13 – Carta di uso del suolo

Caratteristiche geomorfologiche e di permeabilità

Gruppo Caratteristiche

A Scarsa potenzialità di deflusso. Comprende sabbie profonde con scarsissimo limo e argilla; anche ghiaie profonde, molto permeabili.

B Potenzialità di deflusso moderatamente bassa. Comprende la maggior parte dei suoli sabbiosi meno profondi che nel gruppo A, ma il gruppo nel suo insieme mantiene alte capacità di infiltrazione anche a saturazione.

C Potenzialità di deflusso moderatamente alta. Comprende suoli sottili e suoli contenenti considerevoli quantità di argilla e colloidi, anche se meno che nel gruppo D. Il gruppo ha scarsa capacità di infiltrazione a saturazione. D Potenzialità di deflusso molto alta. Comprende la maggior parte delle argille con alta capacità di rigonfiamento,

ma anche suoli sottili con orizzonti pressoché impermeabili in vicinanza della superficie.

(50)

Coefficienti CN

USO DEL SUOLO A B C D

Terreno coltivato

Senza trattamenti di conservazione 72 81 88 91 Con interventi di conservazione 62 71 78 81

Terreno da pascolo

Senza trattamenti di conservazione 68 79 86 89 Con interventi di conservazione 39 61 74 80

Praterie

Buone condizioni 30 58 71 78

Terreni boscosi o forestati

Terreno sottile, sottobosco povero, senza foglie

45 66 77 83 Sottobosco e copertura buoni 25 55 70 77

Spazi aperti, prati rasati, parchi

Buone condizioni con almeno il 75% dell'area

con copertura arborea 39 61 74 80 Condizioni normali con copertura erbosa

intorno al 50%

49 69 79 84

Aree commerciali (impermeabilità 85%) 89 92 94 95

Distretti industriali (impermeabilità 72%) 81 88 91 93

Aree residenziali (impermeabilità 72%) Estensione lotti Impermeabilità

media %: 1/8 Acre 65 % 77 85 90 92 1/4 Acre 38 % 61 75 83 87 1/3 Acre 30 % 57 72 81 86 1/2 Acre 25 % 54 70 80 85 1 Acre 20 % 51 68 79 84

Parcheggi impermeabilizzati, tetti, piazzali ecc.

98 98 98 98

Strade

Pavimentate, con cordoli e fognature 98 98 98 98 Inghiaiate o selciate con buche 76 85 89 91 In terra battuta (non asfaltate) 72 82 87 89

Tab. 3.9 . Parametri CN relativi alla classe II di umidità (AMC II) per le quattro classi litologiche e per i vari tipi di uso del suolo

DETERMINAZIONE DEL PARAMETRO AMC (ANTECEDENT MOISTURE CONDITION)

CLASSE AMC STAGIONE DI RIPOSO STAGIONE DI CRESCITA

I <12.7 <35.5

II 12.7 – 28.0 35.5 – 53.3

III > 28.0 > 53.3

Tabella 3.10 – Condizioni di umidità iniziali individuate in base all’altezza totale di pioggia (in mm) caduta nei 5 giorni precedenti

(51)

3.7.1 Fosso Dogaia

Il Fosso Dogaia nasce direttamente dal paese di S.Maria a Colle nella parte nord-est del bacino in esame, sviluppandosi prettamente in zona pianeggiante fino a raggiungere il sistema di chiuse alle cateratte. Per tutta la suo lunghezza raccoglie le acque delle numerose scoline che servono per lo scolo dei campi circostanti. Le prime arginature si trovano a circa 800 metri dal paese di Nozzano. Prima di giungere alle cateratte riceve le acque dal fosso Ciucchi. Nel programma di calcolo HEC-HMS 2.2.2, il bacino è stato diviso a sua volta in due bacini (uno collinare e l’altro pianeggiante) simulando due piani con pendenze diverse con in mezzo il corso d’acqua.

I dati morfometrici principali relativi al bacino sono i seguenti: • Estensione: 3.30 Kmq

• Bacino 1a

• Larghezza : 0.765 Km • Pendenza: 0.02 % • Rugosità: 0.06 • Percentuale del bacino: 47 % • Bacino 1b

• Larghezza : 0.570 Km • Pendenza: 0.0062 % • Rugosità: 0.06 • Percentuale del bacino: 53 %

Con riferimento alle tabelle 3.8 e 3.9 sono state analizzate le caratteristiche litologiche e dell’uso del suolo del bacino.

I terreni facenti parte del bacino imbrifero hanno una potenzialità di deflusso moderatamente alta (classeC) con scarsa capacità di infiltrazione a saturazione.

(52)

Per il bacino si è ottenuto un coefficiente CNII medio (relativo cioè alla classe di umidità AMC II) pari a:

CNII = 77.53 bacino 1a CNII = 81.79 bacino 1b

con un tempo di concentrazione, calcolato con la formula del SCS, pari a: tc = 0.75 ore bacino 1a

tc = 0.94 ore bacino 1b

3.7.2 Fosso Ciucchi

Il Fosso Ciucchi nasce nella parte alta del bacino nella zona denominata ‘Al Seminario’. Nel tragitto da monte a valle il fosso attraversa il centro abitato prima di confluire con il Dogaia.

I dati morfometrici principali relativi alla sezione di chiusura del bacino sono i seguenti:

• Estensione: 2.23 kmq • Lunghezza asta principale: 2.35 km • Quota massima del bacino: 267.2 m s.l.m. • Quota sezione di chiusura: 11.09 m s.l.m. • Pendenza media del bacino: 13.62 %

CNII = 74.14

con un tempo di concentrazione, calcolato con la formula del SCS, pari a: tc = 0.88 ore.

(53)

3.7.3 Fosso Balbano

Il Fosso Balbano nasce dall’unione di tre fossi a carattere torrentizio sviluppati nella parte nord-ovest . Anche se il bacino imbrifero è più piccolo del bacino del Castiglioncello, il ramo a valle della confluenza prende il nome di Balbano.

Dalla tavola allegata si nota che il bacino è costituito per la maggior parte da terreni con permeabilità medio alta. Il bacino nella zona collinare è prevalentemente di tipo boschivo, a mano a mano che la zona collinare degrada nella pianura i boschi lasciano il posto ad aree poco urbanizzate e concentrate soprattutto nelle vicinanze della sezione di chiusura del bacino.

CNII = 72.99

3.7.4 Fosso Castiglioncello

Il fosso Castiglioncello nasce a sud – ovest dalla Foce di Casalina e prosegue il suo cammino per la parte montano- collinare per pochi centinaia di metri. Prima di

(54)

confluire con il Balbano raccoglie le acque del rio di Batano, del fosso delle Cavine, e del solco del Bosco.

Con riferimento alle tabelle 3.8 e3.9 sono state analizzate le caratteristiche litologiche e dell’uso del suolo del bacino.

Il bacino nella zona collinare è prevalentemente di tipo boschivo.

Nella parte pianeggiante i boschi lasciano il posto ad aree di tipo seminativo. L’urbanizzazione è poco rilevante, e concentrata soprattutto nelle vicinanze della sezione di chiusura del bacino.

CNII = 71.03

3.7.5 Fosso Fontana

Il fosso Fontana sottintende il bacino più piccolo. Nasce dalle Muracce. Il suo corso lambisce il centro abitato e si immette nel Balbano prima che questo corra parallelamente alla ferrovia.

(55)

Dalla tavola allegata si nota che il bacino è costituito maggiormente da terreno collinare.

Per quanto riguarda l’uso del suolo, il bacino è costituito principalmente da terreni boscosi nella parte collinare, mentre nella zona valliva, di dimensioni meno estese, si ritrovano l’area urbanizzata.

CNII = 70.92

Per calcolare le portate nelle varie aste nel sistema considerato, il bacino è stato modellato con codice di calcolo HEC-HMS 2.2.2, schematizzandolo come appare dalla figura di seguito. Ogni sottobacino del sistema è stato definito mediante i parametri sopra scritti; la portata massima di ciascun corso d’acqua è stata definita simulando eventi di pioggia con diverse durate (più precisamente da 0.5 ore fino a 4 ore con variazioni temporali di 15 minuti) e ad intensità costante, ovviamente con tempo di ritorno pari a duecento anni; confrontando le portate al colmo fornite nell’output del programma si sono potuti stabilire i massimi ricercati.

(56)

Fig 3.14 – Schematizzazione del bacino con modulo di calcolo HEC-HMS 2.2.2

PORTATE MASSIME ALLO STATO ATTUALE

PER PIOGGE DI INTENSITA COSTANTE

(Tr=200ANNI)

Sottobacini 0.5 ore 1 ora 1.5 ore 2 ore 2.5 ore 3 ore

Dogaia 24.25 29.77 28.22 27.32 25.9 25.08

Ciucchi 22.41 27.36 26.76 25.84 24.5 23.21

Balbano 23.53 27.53 29.98 28.73 27.37 26.65

Castiglioncello 22.36 26.59 30.8 29.99 28.88 27.64

Fontana 3.81 4.75 4.54 4.13 3.67 3.09

Tab 3.11 – Tabella riassuntiva delle portate nelle varie aste del sistema per varie durate di pioggia e tempo di ritorno pari a 200 anni; le celle evidenziate rappresentano i massimi di

(57)

3.8 ANALISI IDRAULICA

I dati ottenuti dal programma di calcolo HEC-HMS 2.2.2 sono stati utilizzati in un altro programma, HEC-RAS 3.1.3, che consente il calcolo del pelo libero una volta stabiliti i valori massimi di portata nei vari corsi d’acqua. E’ stato costruito, quindi, un modello idraulico del reticolo idrografico tenendo conto delle sezioni dei corsi d’acqua, delle pendenze, della scabrezza dei vari tratti e si è proceduto alla simulazione dell’andamento delle acque all’interno della rete idrografica. A causa della presenza di numerose singolarità idrauliche, della irregolarità delle sezioni allo stato attuale e della bassa pendenza nel tratto terminale dei fossi non è possibile effettuare le verifiche delle varie aste a moto uniforme, ma si è ritenuta necessaria la costruzione di un modello di deflusso a moto permanente.

Il modello geomorfologico dei corsi d’acqua è stato costruito a partire dalle sezioni rilevate per essere implementato su codice di calcolo HEC-RAS 3.1.3. Per la schematizzazione del sistema in esame sono stati adoperati i seguenti dati:

• Geometria della sezioni rilevate (mediante la definizione delle coordinate dei punti del contorno dell’alveo rispetto a un sistema di riferimento ben definito)

• Distanza fra le sezioni adiacenti

• Coefficienti di scabrezza (con la possibilità di fornire valori differenti di tali coefficienti per quanto riguarda le sponde e il fondo)

• Condizioni al contorno (quali l’altezza liquida nella sezione di sbocco in mare e le equazioni mediante le quali si definiscono i livelli idraulici in corrispondenza delle confluenze fra i vari corsi d’acqua; in particolare nel modello utilizzato si sono utilizzate le equazioni dell’energia)

Il codice di calcolo HEC-RAS 3.1.3 impone di individuare per ogni sezione l’ascissa limite sulla sponda destra e sulla sponda sinistra, cioè l’ascissa dei punti che hanno ordinata di valore maggiore per la sponda destra e sinistra rispettivamente; se in un certo tratto la sezione del corso d’acqua non è sufficiente al deflusso della

(58)

portata di progetto il livello del pelo libero viene calcolato dal programma come se ci fossero due paramenti verticali liquidi (cioè senza superfici solide) nei punti di ascissa limite. Il profilo liquido risulta in questo modo di livello superiore a quello reale, perché in tale condizione non appena si supera la quota del rilevato arginale si ha l’esondazione del corso d’acqua e gli argini funzionano come sfioratori laterali con un battente molto inferiore a quello rilevato dai risultati del modello. Se questi punti non vengono definiti il programma può condurre a risultati ingannevoli. Concludendo, le sezioni per le quali i livelli liquidi sono tali da non permettere il deflusso all’interno degli alvei con il rispetto dei franchi prestabiliti, o sono addirittura superiori all’altezza dei rilevati arginali presenti, si ritengono insufficienti e necessitano di interventi: questi potranno essere di varia natura (innalzamento degli argini, diminuzione della scabrezza, riduzione a monte della portata e così via).

Modellando in tal modo lo “stato attuale” si trovano i profili nei vari canali del reticolo idrografico (relativi alle portate massime generate da eventi duecentennali) e si evidenziano le zone di crisi che dovranno essere oggetto di sistemazione. Per una lettura dei profili longitudinali si tenga presente che:

• Con la linea di colore blu (a tratto continuo e di spessore maggiore) è indicato il pelo libero

• Con la linea viola e con la linea celeste (tratteggiate) sono indicati le sommità dei rilevati arginali posti in destra e sinistra idrografica

(59)

reach1 32 28 26 25 22 2119 ₁₈ _{17 16 15} 11 10 9 bal_b ano

(60)

reach1 12 11 10 8 7 6 5 3 2 1 0.8 do ga ia

(61)

(62)

(63)

Con i risultati di HEC-RAS 3.1.3 si può verificare che le situazioni più critiche si hanno in corrispondenza dei forti cambiamenti di pendenza, dove si riscontrano livelli idraulici notevoli che provocano profili di rigonfiamento in tutti i corsi d’acqua, rendendoli inadeguati al contenimento delle piene. Oltre al problema del rigurgito, nei tratti terminali dei corsi d’acqua, come già esposto precedentemente, i corsi d’acqua hanno sezioni ridotte e in certi casi neanche arginate, dunque inadeguate al contenimento della piena duecentennale. Per risolvere il problema, oltre alla sistemazione delle sezioni, si interverrà anche su quelle zone in cui il letto del fosso è in contropendenza in modo da rendere più regolare il deflusso senza creare innalzamenti del pelo libero.