Capitolo 2
Tempo di percorrenza di una
traiettoria
In questo capitolo è descritto l’algoritmo sviluppato per il calcolo del tempo di percorrenza di una traiettoria, assegnate le caratteristiche di aderenza di una vettura. Seguirà uno studio di convergenza per la scelta dell’opportuno passo d’integrazione necessario al calcolo del tempo con una precisione del centesimo di secondo.
2.1
Caratteristiche di aderenza
La risultante sul piano stradale delle forze tangenziali esercitate dai pneu-matici deve restare approssimativamente all’interno di un ellisse, se il carico verticale, agente sul pneumatico stesso, rimane costante. Uscire dall’ellisse significa avere perdita di aderenza.
Le due componenti della risultante sono la forza laterale (che è presente quan-do la vettura è in curva) e la forza longitudinale (che è presente durante le fasi di accelerazione e frenata).
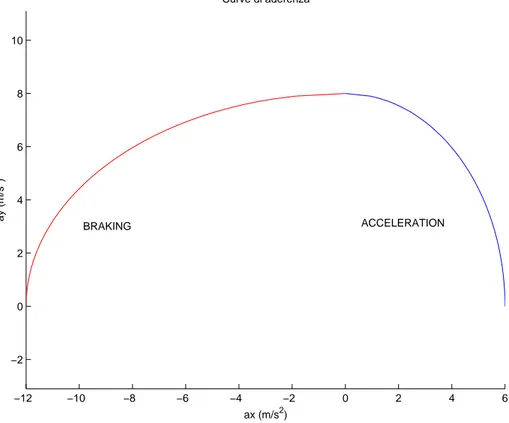
Come si può notare in figura 2.1, al crescere di una componente diminuisce l’altra per cui si ha una massima forza laterale se non c’è componente lon-gitudinale e viceversa. Quest’ultimo punto spiega perché non è proprio
con-2.1 Caratteristiche di aderenza
veniente frenare o accelerare in curva quando la risultante è già prossima al limite. Si avrebbe un’improvvisa riduzione di forza laterale (aumenta la forza blu, diminuisce quella viola) con conseguente perdita di aderenza.
Tale ellisse viene comunemente indicato come diagramma g − g. Il nome,
Figura 2.1: Componenti della forza risultante nel piano stradale nel contatto tra pneumatici e strada
diagramma g − g, deriva dal fatto che il valore delle forze longitudinali e laterali viene prima diviso per la massa del veicolo, ottenendo le seguenti accelerazioni ax = Flong m ay = Flat m
Tali accelerazioni vengono poi riportate sul diagramma normalizzate rispetto all’accelerazione di gravità g. Il diagramma utilizzato in seguito per l’ottimiz-zazione della traiettoria è del tipo mostrato in figura 2.2.
Considereremo tale ellisse simmetrico rispetto all’asse delle ascisse. Ovvero si ipotizza che il veicolo abbia comportamento analogo nelle curve a destra ed a sinistra (curvatura k(s) negativa e positiva rispettivamente).
2.2 Algoritmo di calcolo del tempo −12 −10 −8 −6 −4 −2 0 2 4 6 −2 0 2 4 6 8 10 ax (m/s2) ay (m/s 2) Curve di aderenza BRAKING ACCELERATION
Figura 2.2: Ellisse d’aderenza
2.2
Algoritmo di calcolo del tempo
2.2.1
Velocità massima
Sia assegnata una curva sul piano {x y} p(s) con s ascissa curvilinea. Dalle equazioni che descrivono la curva assegnata è possibile ricavare l’espressione della curvatura k(s), come mostrato nel paragrafo 1.1. Tale caratteristi-ca geometricaratteristi-ca è legata all’accelerazione laterale sviluppata da un veicolo che percorre tale traiettoria. In condizioni stazionarie, infatti è possibile scrivere:
ay(s) =| k(s) | v(s)2 (2.1)
sis-2.2 Algoritmo di calcolo del tempo
tema di assi corpo definiti nel capitolo precedente.
Dalle curve di aderenza di un veicolo è possibile ricavare l’accelerazione latera-le massima sviluppabilatera-le dal veicolo in condizioni di puro impegno d’aderenza laterale da parte dei pneumatici. Sostituendo il valore ricavato da tali dia-grammi nell’equazione (2.1), è possibile ricavare la velocità massima, punto per punto, con cui il veicolo può percorrere tale traiettoria.
vmax(s) =
r ay max
k(s) (2.2)
Nei tratti di rettilineo in cui il valore della curvatura k è nullo, la velocità mas-sima consentita dall’aderenza laterale del veicolo è infinita. Tale condizione non è fisicamente realizzabile, in quanto la velocità massima in rettilineo è limitata dalla potenza del motore e dalle forze che si oppongono al moto; in particolare le forze aerodinamiche aumentano molto velocemente con il crescere della velocità. Pertanto la velocità massima ammissibile ha come vincolo superiore la velocità massima del veicolo in rettilineo. Nel nostro studio tale limite superiore è posto pari a 60 m/s, circa 210 km/h.
Ovviamente la velocità definita dalla 2.2 rappresenta un limite superiore e la velocità effettivamente posseduta dal veicolo risulta inferiore. Infatti se il veicolo possedesse in un istante la velocità massima, non sarebbe possibile per esso variarla. Infatti per poter modificare la velocità longitudinale è
in-dispensabile generare delle accelerazioni ax, ma tali accelerazioni richiedono
un impegno di aderenza longitudinale, impegno che non è possibile richiedere ai pneumatici, essendo già impiegati al limite di aderenza dall’accelerazione laterale sviluppata. La richiesta di tali accelerazioni comporta quindi la perdita d’aderenza da parte del veicolo. Il tracciamento delle curve della velocità massima in laterale puro sono comunque importanti per la verifica del corretto funzionamento dell’algoritmo di calcolo del tempo.
2.2 Algoritmo di calcolo del tempo
2.2.2
Tempo di percorrenza
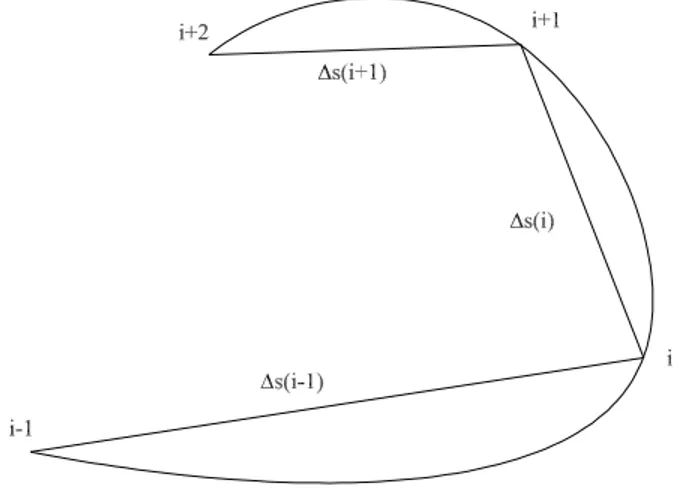
Nota una traiettoria p(s) e la sua curvatura k(s), prendiamo n punti ap-partenenti alla curva e tracciamo la poligonale congiungente tali punti (vedi figura 2.3).
In ogni punto i è noto il valore della curvatura k(i) ed il valore della velocità
Figura 2.3: Poligonale inscritta nella curva
massima ammissibile tramite la relazione (2.2) vmax(i). Supponiamo che sia
nota nel punto i la velocità v(i) effettiva del veicolo e tale che v(i) sia minore
di vmax(i). É allora possibile ricavare l’accelerazione laterale ay(i) sviluppata
dal veicolo in tale punto tramite la relazione (2.1)
ay(i) = k(i)v(i)2
Poichè la velocità posseduta dal veicolo è inferiore alla velocità massima, per come l’abbiamo definita, risulta
2.2 Algoritmo di calcolo del tempo
Risulta quindi disponibile una parte dell’aderenza massima, sfruttabile per accelerare il veicolo. Noto il valore dell’accelerazione laterale è possibile ri-cavare dalle curve d’aderenza il valore massimo dell’accelerazione
longitudi-nale sviluppabile nel punto i, ax(i) > 0.
Definendo
∆s(i) =k p(i + 1) − p(i) k (2.3)
è possibile ricavare il tempo necessario a percorrere il tratto di poligonale in-tercorrente tra il punto i ed il punto i + 1, supponendo che il moto in questo tratto avvenga ad accelerazione costante. Tale tempo risulta infatti
t(i) = −v(i) +pv(i)2+ 2ax(i)∆s(i)
ax(i)
(2.4)
Noto tale valore è possibile calcolare la velocità posseduta dal veicolo nel punto i + 1
v(i + 1) = v(i) + ax(i)t(i) =
p
v(i)2 + 2ax(i)∆s(i) (2.5)
Se la velocità risultante è inferiore alla velocità massima calcolata secondo la relazione (2.2) nel punto i + 1 si effettuano le stesse operazioni appena descritte e si procede verso punto il successivo della curva, in tal caso infatti l’accelerazione laterale sviluppata dal veicolo è inferiore a quella massima sviluppabile in condizioni di totale impegno laterale. Nel caso in cui la ve-locità nel punto i sia pari alla massima possibile su strada diritta, condizione possibile solo nel caso in cui effettivamente il veicolo si trovi a percorrere un tratto rettilineo, la velocità nel punto i + 1 è posta uguale alla velocità nel
punto i e l’accelerazione longitudinale ax(i) è considerata nulla. In tal caso il
2.2 Algoritmo di calcolo del tempo uniforme)
t(i) = ∆s(i)
vmax(i)
(2.6)
Nel caso in cui la velocità nel punto i + 1 sia superiore alla velocità mas-sima ammissibile in tale punto bisogna operare in modo differente. Infatti tale condizione rileva il superamento del limite d’aderenza, ciò comporta che la velocità appena calcolata non è fisicamente realizzabile da tale veicolo in questo determinato punto.
Nota l’accelerazione laterale nel punto i è possibile ricavare il nuovo valore dell’accelerazione longitudinale che questa volta risulterà essere minore di zero (frenatura). Dalle curve di aderenza del veicolo è possibile ricavare il massimo valore dell’accelerazione longitudinale in frenatura nel punto i. Uti-lizzando questo nuovo valore dell’accelerazione longitudinale si puo procedere al calcolo del nuovo tempo di percorrenza e della nuova velocità v(i + 1) at-traverso le relazioni (2.4) e (2.5). Nel caso in cui tale nuovo valore sia inferiore al massimo realizzabile nel punto i + 1 si può procedere al calcolo del tempo nel tratto successivo; nel caso in cui tale valore risulti ancora superiore a quello massimo è necessario compiere un ulteriore passo indietro. Infatti un singolo tratto in frenatura precedente al punto in cui si verifica la perdita dell’aderenza può non essere sufficiente.
Ci si riporta quindi al punto i − 1. Poichè è nota in questo punto la velocità, è possibile ricavare l’accelerazione laterale sviluppata dal veicolo e da questa ricavare la massima decelerazione sviluppabile in tale punto. In questo modo è possibile ricalcolare il tempo di percorrenza del tratto ∆s(i − 1) e la nuova velocità v(i), che sarà chiaramente inferiore alla precedente. Nota la nuova velocità nel punto i è possibile inserire un successivo tratto in frenatura come fatto in precedenza e calcolare la nuova velocità nel punto i + 1. Se tale velo-cità risulta ancora troppo elevata si inserisce un ulteriore tratto in frenatura precedente agli ultimi due. La procedura si ripete finchè v(i + 1) non risulta essere inferiore alla massima realizzabile nel medesimo punto. Ottenuto un
2.3 Scelta del passo d’integrazione
valore ammissibile è possibile procedere al calcolo del tempo del tratto suc-cessivo.
Noti i tempi impiegati a percorrere i singoli tratti di poligonale, per conoscere il tempo di percorrenza complessivo della traiettoria è sufficiente sommare i singoli tempi intermedi.
2.3
Scelta del passo d’integrazione
La precisione, nel calcolo del tempo di percorrenza, dell’algoritmo esposto nel paragrafo precedente è funzione della dimensione del passo d’integrazione ∆s scelto. La scelta della dimensione di tale variabile è un compromesso tra la corretta rappresentazione della curva ed un tempo di calcolo ragionevole per poter effettuare successivamente un processo di ottimizzazione, in cui molte traiettorie saranno confrontate per poter determinare quella ottima. Due fattori portano a dover ridurre il ∆s necessario ad una adeguata soluzione
• Individuando sulla curva n punti, in cui valutare la velocità e le accele-razioni, la poligonale risultante è composta di n − 1 tratti di lunghezza ∆s(i). La lunghezza di tale poligonale, come mostrato nel paragrafo 2.1 risulta l(P) = n−1 X i=1 ∆s(i) (2.7)
Tale lunghezza è una approssimazione per difetto della lunghezza effet-tiva della curva, il cui valore reale è dato dall’espressione (1.9), che qui si riporta
L(ϕ) =
Z b
a
k ˙ϕ(t) k dt
Come mostrato in precedenza il valore della sommatoria (2.7) tende al valore reale della lunghezza della curva se i tratti ∆s(i) sono
sufficien-2.3 Scelta del passo d’integrazione temente piccoli.
• All’ingresso di una curva, preceduta da un tratto più o meno lungo di rettilineo, è necessario individuare un punto in cui iniziare la frenata. Inoltre superato il punto in cui la curvatura è massima, è necessario, per sfruttare al meglio l’aderenza disponibile, iniziare ad accelerare. Nell’algoritmo esposto nel paragrafo precedente è evidente come all’in-terno di un singolo tratto ∆s(i) l’accelerazione sia considerata costante. Per tale motivo l’individuazione precisa del punto di frenata all’ingresso della curva e del punto in cui si inizia ad accelerare sono strettamente legati alla dimensione dei tratti in esame. Quindi per poter identifi-care con precisione i punti suddetti è necessario che tali tratti siano sufficientemente piccoli.
2.3.1
Valutazione della lunghezza della curva
Per poter rappresentare correttamente la lunghezza della curva è necessario, come detto in precedenza, imporre un passo d’integrazione sufficientemente piccolo. Per identificare tale dimensione si è proceduto al calcolo della lunghezza di un arco di cerchio (90 gradi), con raggio variabile tra venti e duecento metri, confrontandola con la lunghezza delle poligonali inscritte al variare della dimensione dei segmenti. In figura 2.4 è mostrato il risultato ottenuto per una curva con raggio di cento metri. Come è possibile osservare, quando la dimensione dei tratti ∆s(i) è di circa due metri, la differenza tra la lunghezza effettiva e quella approssimata dal poligono è nell’ordine di pochi millimetri. Come sarà mostrato successivamente i limiti che sono imposti dalla seconda condizione prima enunciata, ovvero la corretta identificazione del punto di frenata e del punto di inizio accelerazione, risultano molto più stringenti.
2.3 Scelta del passo d’integrazione 5 10 15 20 25 30 35 40 156 156.2 156.4 156.6 156.8 157 157.2 delta s (m) lunghezza (m) poligonale curva
Figura 2.4: Confronto tra la lunghezza della curva e la lunghezza del poligono inscritto al variare della dimensione dei segmenti approssimanti
2.3.2
Valutazione del punto di frenata e del punto di
inizio accelerazione
Anche in questo caso sono stati confrontati i risultati ottenuti al variare del-la dimensione dei segmenti ∆s(i), per una serie di curve a raggio costante e variabile tra venti e duecento metri. Sono riportati nelle figure 2.5 e 2.6 i risultati ottenuti per le due curve agli estremi dell’intervallo considerato. Per consentire l’identificazione del punto di frenata è stato inserito antecedente-mente alla curva un tratto di rettilineo lungo 150 metri, in modo da poter consentire al veicolo un sufficiente spazio di frenata per affrontare la curva. Infatti con i valori di decelerazione massima realizzabili in rettilineo sfrut-tando la curva di aderenza mostrata in figura 2.2, è possibile fermare, in tale
2.3 Scelta del passo d’integrazione
spazio, un auto che parte con la velocità massima consentita. Come è
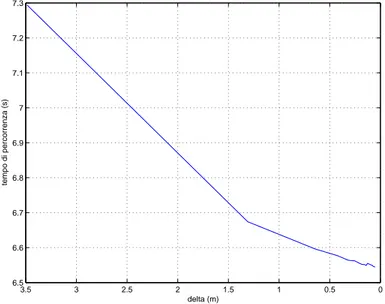
evi-0 0.5 1 1.5 2 2.5 3 3.5 6.5 6.6 6.7 6.8 6.9 7 7.1 7.2 7.3 delta (m) tempo di percorrenza (s)
Figura 2.5: Tempo di percorrenza al variare del passo di integrazione per una traiettoria a raggio costante pari a 20 metri
dente dalle figure 2.5 e 2.6, la convergenza del valore del tempo di percorrenza non avviene in modo monotono. Questo andamento si realizza in quanto al diminuire delle dimensioni del passo d’integrazione, da un lato si identifica con crescente precisione il punto ideale di inizio frenata, ma d’altra parte au-menta la lunghezza totale della poligonale che approssima la curva. Per passi di integrazione ampi la crescente precisione nell’identificazione del punto di frenata ha un influenza molto maggiore rispetto al secondo fenomeno. L’im-portanza di questo si fa al contrario sentire quando la dimensione dei tratti ∆s(i) considerati diminuisce drasticamente. E’ possibile notare comunque che l’ampiezza di tali oscillazioni diminuisce decisamente con l’infittimento dei punti di integrazione. Noi considereremo raggiunto un sufficiente grado di precisione quando l’ampiezza di tali oscillazioni sarà inferiore al centesimo di secondo.
Come è possibile notare nelle figure precedenti il raggiungimento di tale con-dizione dipende dal raggio della traiettoria effettuata. I risultati di tale
stu-2.3 Scelta del passo d’integrazione 0 0.5 1 1.5 2 2.5 3 3.5 10.63 10.64 10.65 10.66 10.67 10.68 10.69 10.7 10.71 10.72 delta (m) tempo di percorrenza (s)
Figura 2.6: Tempo di percorrenza al variare del passo di integrazione per una traiettoria a raggio costante pari a 200 metri
dio sono mostrati in figura 2.7. Per confermare l’ipotesi che il passo d’inte-grazione sia funzione della curvatura, si è proceduto ad un analogo studio su curve con raggio di curvatura variabile. Si riportano i risultati ottenuti per due traiettorie realizzate su una ampia curva di 90 gradi con raggio di cur-vatura, calcolato al centro strada, pari a 180 metri (curvatura pari a 0.556
m−1) ed un tornate con raggio 40 metri (curvatura pari a 0.025 m−1). In
entrambi i casi la larghezza della carreggiata è pari a 3 metri. Le traiettorie realizzate sono riportate nelle figure 2.8 e 2.10.
Nelle figure 2.9 e 2.11 è evidenziato con un tratto in rosso il valore, ricava-to dalla figura 2.7, per cui si dovrebbe realizzare la convergenza del tempo di percorrenza, considerando i valori di curvatura massima raggiunti da tali traiettorie. E’ possibile notare come l’ipotesi che il passo di integrazione sia funzione della curvatura massima della traiettoria effettuata trovi riscontro in queste prove.
Si può quindi concludere che il passo d’integrazione da impiegare nel calcolo del tempo di percorrenza di una traiettoria risulta funzione della curvatura
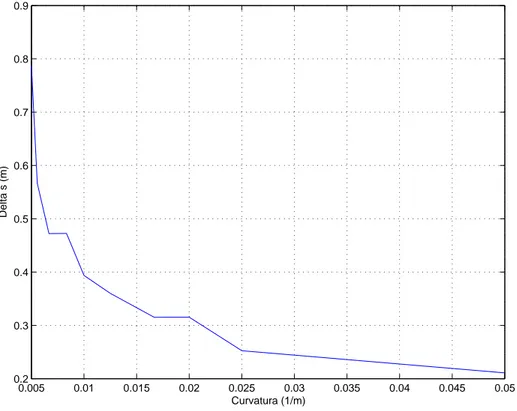
2.3 Scelta del passo d’integrazione 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Curvatura (1/m) Delta s (m)
Figura 2.7: Passo d’integrazione che garantisce la convergenza del tempo di percorrenza al variare della curvatura
massima della traiettoria stessa, ed i valori necessari affinchè il calcolo abbia una precisione del centesimo di secondo sono quelli mostrati in figura 2.7.
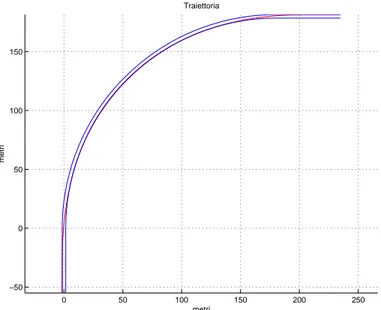
2.3 Scelta del passo d’integrazione 0 50 100 150 200 250 −50 0 50 100 150 Traiettoria metri metri
Figura 2.8: Traiettoria utilizzata per lo studio di convergenza del passo d’integrazione 0 0.5 1 1.5 2 2.5 3 3.5 4 11.46 11.48 11.5 11.52 11.54 11.56 11.58 11.6 delta s (m) tempo (s)
2.3 Scelta del passo d’integrazione −10 0 10 20 30 40 50 60 70 80 90 −50 −40 −30 −20 −10 0 10 20 30 40 Traiettoria metri metri
Figura 2.10: Traiettoria utilizzata per lo studio di convergenza del passo d’integrazione 0 0.5 1 1.5 2 2.5 12.5 12.55 12.6 12.65 12.7 12.75 delta s (m) tempo (s)
2.3 Scelta del passo d’integrazione
2.3.3
Tempo di calcolo
E’ evidente che il tempo di calcolo aumenta al diminuire del passo d’inte-grazione. Infatti al crescere del numero dei tratti in cui è suddivisa una singola traiettoria aumentano il numero delle operazioni necessarie al calcolo del tempo di percorrenza. Inoltre nella ricerca del punto ottimale di frenata l’algoritmo è costretto a compiere un numero sempre crescente di passi in-dietro al diminuire della dimensione dei passi stessi.
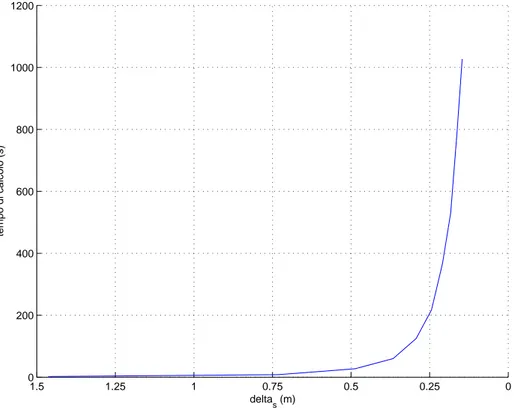
E’ lecito aspettarsi quindi che il tempo di calcolo aumenti molto velocemente con il decrescere del ∆s(i). Tale andamento è infatti mostrato in figura 2.12. E’ evidente come il tempo cresca in maniera repentina, infatti si passa da
0 0.25 0.5 0.75 1 1.25 1.5 0 200 400 600 800 1000 1200 delta s (m) tempo di calcolo (s)
Figura 2.12: Tempo di calcolo al variare del passo d’integrazione
un secondo circa per ∆s pari a 2 metri, ad oltre cinque minuti per ∆s di 25 centimetri, fino ad oltre quindici minuti per il calcolo di una traiettoria con passo d’integrazione di 15 centimetri.
2.3 Scelta del passo d’integrazione
Confrontando i dati ricavabili dalla figura 2.7, con i tempi di calcolo mostrati, ci si rende conto che per il calcolo di una traiettoria come quella mostrata in figura 2.10, ovvero con raggio di curvatura pari a 40 metri, con il passo d’integrazione necessario ad ottenere una precisione del centesimo di secon-do, sono necessari oltre 5 minuti.
Per questa ragione è impensabile utilizzare tali passi d’integrazione per svilup-pare una ottimizzazione su migliaia di traiettorie possibili. Sarà quindi ne-cessario svolgere la nostra ricerca della traiettoria ottima con poche centinaia di curve. Anticipando ciò che verrà più dettagliatamente spiegato in seguito, si opererà una prima ottimizzazione con un passo di integrazione più ampio rispetto a quello necessario per la convergenza, che ci consentirà, con tempi di calcolo ragionevoli, di limitare la nostra successiva ricerca in zone ristrette del tracciato. A tale operazione preliminare seguirà una successiva ottimiz-zazione, questa volta realizzata con il passo d’integrazione ottimale, che andrà ad identificare la traiettoria ottima. In tale modo possiamo confrontare un numero di curve sensibilmente inferiore all’operazione precedente, in quanto risultano escluse quelle curve che sicuramente non sono performanti ai fini del tempo di percorrenza.