ANALISI DI SUPERFICI SELETTIVE IN FREQUENZA CAPITOLO 2

CAPITOLO

2

ANALISI DI SUPERFICI SELETTIVE

IN FREQUENZA

2.1 FSS: superfici selettive in frequenza.

Le Superfici Selettive in Frequenza (FSS) sono strutture bidimensionali, periodiche e nella maggior parte delle applicazioni anche planari. Esse sono formate da elementi disposti periodicamente in due direzioni. Si definiscono superfici selettive in frequenza perché si comportano in maniera selettiva con le onde elettromagnetiche, facendo passare inalterate le onde in un determinato intervallo di frequenze e riflettendo quasi completamente tutte le altre.

I fattori che influenzano maggiormente il comportamento e la struttura della FSS sono: - la conducibilità del materiale che forma la FSS;

- la permittività del substrato della FSS;

- la geometria del singolo elemento della FSS (forma e spessore del conduttore); - la periodicità degli elementi della FSS;

Si possono distinguere due classi di schermi FSS:

- FSS di tipo capacitivo quando un elemento (patch) di materiale conduttore di forma opportuna, viene ripetuto periodicamente. Le celle conduttrici sono separate da aria o da dielettrico.

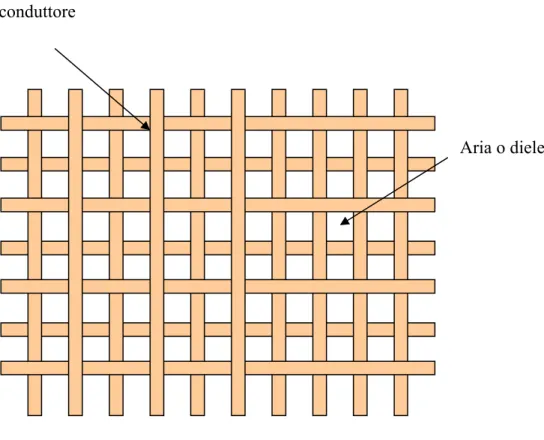
- FSS di tipo induttivo (Fig.2.1), realizzate forando in modo periodico una superficie conduttore oppure nel caso dei tessuti conduttori intrecciando nell’ordito una trama metallica. In questo caso l’elemento base della struttura periodica è l’aperura.

Figura 2.1 FSS ad apertura

Per spiegare teoricamente il funzionamento delle FSS ci si basa sulla considerazione che esistono delle direzioni dello spazio dove si ha la massima irradiazione, mentre in altre direzioni l’irradiazione è nulla. Se consideriamo un’onda elettromagnetica piana che incide su una superficie FSS, l’onda induce delle correnti sulle parti metalliche dello schermo che di conseguenza irradiano un campo elettromagnetico nello spazio circostante. Questo campo si definisce scatterato.

Quando l’onda non incide normalmente sullo schermo, le correnti indotte risulteranno sfasate a causa della differenza di cammino con cui l’onda incide sui vari elementi metallici della FSS. Lo sfasamento delle correnti dipende dalla frequenza della radiazione elettromagnetica e dal tipo di periodicità della struttura dello schermo. Se consideriamo i campi scatterati dalle varie correnti, essi risulteranno anch’essi sfasati delle medesime quantità e quindi il campo totale reirradiato avrà modulo massimo in alcune direzioni mentre sarà nullo in altre. Quando la schermatura è totale, cioè il campo reirradiato ha le stesse caratteristiche dell’onda incidente allora si parla di risonanza dello schermo. Allontanandoci dalla condizione di risonanza lo schermo trasmetterà una parte dell’onda incidente, fino a diventare totalmente trasparente alle radiazioni elettromagnetiche.

Si possono individuare tre categorie nella classificazione delle FSS:

- FSS costituite da uno schermo metallico spesso

Aria o dielettrico conduttore

- FSS costituite da uno schermo metallico spesso con un substrato di dielettrico - FSS costituite da uno schermo metallico sottile con substrato di dielettrico.

Nella trattazione dei tessuti metallici schermanti presi in esame in questa si sede si farà riferimento esclusivamente al caso di schermo metallico sottile con substrato di dielettrico.

Nell’analisi si sfrutta l’approssimazione di schermo infinitamente sottile (lo spessore fisico dello schermo è più piccolo della minima lunghezza d’onda presa in esame). Un'altro parametro molto importante per la caratterizzazione di una FSS è la conducibilità elettrica del materiale utilizzato per la costruzione dello schermo. Una soluzione realizzativa per le FSS può essere quella di fissare uno strato estremamente sottile di metallo (oppure una maschera di fili metallici) su un substrato di dielettrico. In questo modo si conferisce robustezza ed elasticità alla struttura, necessaria nelle applicazioni pratiche. Utilizzando un substrato dielettrico, si cambia però la risposta in frequenza dello schermo. La frequenza di risonanza passa da f0 se consideriamo solo la FSS, a

(

1

)

2 0 + ε = r f

f se sovrapponiamo lo schermo metallico ad un substrato dielettrico (εr).

Negli schermi ad apertura quando lo spessore non è più tale da essere considerato sottile, la frequenza di risonanza dipende dallo spessore del dielettrico.

2.2 Analisi del campo reirradiato da un singolo elemento della FSS.

Facciamo l’analisi nel caso di schermo capacitivo: la cella elementare è costituita da un patch

(Fig. 2.2). Si deve risolvere l’equazione integrale denominata EFIE (Electric Field Integral Equation). Le ipotesi iniziali sono:

- schermo infinito, così da poter trascurare gli effetti di bordo - onda incidente monocromatica o somma di onde monocromatiche - spessore infinitesimo.

Dopo aver definito l’equazione integrale applicheremo il teorema di Floquet per adattare l’equazione al caso periodico che stiamo trattando; poi applicando il MoM (Method of Moments) la trasformeremo in un sistema di equazioni lineari, risolvibile più facilmente.

Il teorema di Floquet afferma che tutte le grandezze relative al campo reirradiato presentano la stessa periodicità delle celle. In particolare se la struttura è periodica nella direzione individuata dall’asse x e _F

(

_{x ,u,v}

)

_ejωt

0 rappresenta la distribuzione di una componente del campo in corrispondenza della sezione x , allora la distribuzione in x + L è pari a _F

(

_x +_L,_u,_v

)

_ejωt_ejβ0L,

dove con β0 si è indicata una costante dipendente dalla frequenza e dalle dimensioni della struttura

(L è il periodo della struttura). Siccome la relazione che lega le distribuzioni delle componenti dei campi in due sezioni che distano tra loro di un periodo deve essere indipendente dall’ascissa x0,

allora si può scrivere che:

(

_{x u v}

)

_f

(

_{x u v}

)

_ej x

F , , = , , β0 (2.1)

dove f

(

x,u,v

)

essendo periodica di periodo L lungo l’asse x si può scrivere nel seguente modo:

(

)

( )

x L i j i ie a v u g v u x f π ∞ −∞ =

∑

= 2 , , , (2.2)

Figura 2.2 Singolo patch conduttore

Sfruttando il teorema di Floquet, possiamo scrivere le componenti del campo come segue:

(

)

( )

j( t x) i i t j g u v ae i e v u x F ∞ ω+β −∞ = ω _{= ,}

∑

, , 0 (2.3) dove x z y Onda incidente θinc

L i i π + β = β ₀ 2

Se consideriamo un singolo elemento della FSS la relazione che esprime il campo scatterato in funzione delle correnti superficiali indotte è la seguente:

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛_∇ ∇ ωε + ωµ − = A A Es r r 0 1 0 _j j (2.4)

dove A è il potenziale vettore, dipendente dalla distribuzione di corrente superficiale J indotta sulla superficie del conduttore in relazione alla seguente legge:

( )

r

( ) ( )

r r'J r' r' J A =

∫

G , d =G⊗ (2.5) con

( )

' 4 ' , ' 0 r r r r r r − π = ejk − G (2.6)

che rappresenta la funzione di Green nello spazio libero, mentre k0 è il numero d’onda.

La funzione di Green può essere interpretata come la risposta del potenziale vettore prodotta da una corrente di tipo impulsivo. Nei casi in cui la distribuzione di corrente assume espressioni più complicate, possiamo sempre rappresentarla come combinazione lineare di correnti di tipo impulsivo e quindi anche il potenziale vettore sarà combinazione lineare di G.

Imponiamo adesso la condizione al contorno: sulla superficie del conduttore la somma delle componenti tangenziali del campo incidente e del campo scatteratto deve essere nulla, quindi:

0 = + = inc t s t E E E La (2.4) diventa quindi:

( )

r A

( )

r

[

(

A

( )

r

)

]

Einc_t ∇∇ ωε − ωµ = r r 0 0 1 j j (2.7)

L’espressione appena trovata rappresenta l’equazione del campo elettrico (EFIE) per un patch perfettamente conduttore. Nel caso di una superficie planare sottile esisteranno solo le componenti Jx e Jy della corrente superficiale e di conseguenza solo Ax e Ay risulteranno non nulli.

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ + ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ + ωµ − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − y x i y i x A A y k y x y x x k k j E E 2 2 2 0 2 2 2 2 2 0 2 0 0 _(2.8) dove A_x =G⊗J_x e A_y =G⊗J_y.

Applichiamo la trasformata e la antitrasformata di Fourier alla (2.8); operando le seguenti trasformazioni si ha: J J G~~ G⊗ ↔ A A α ↔ ∂ ∂ j x A A β ↔ ∂ ∂ j y A A _{↔ αβ} ∂ ∂ ∂2 _j2 y x

Esprimendo il secondo membro nel dominio delle frequenze spaziali e antitrasformando, la (2.8) diventa:

( )

( )

( ) ( )

( )

⎥⎥_⎦ α β ⎤ ⎢ ⎢ ⎣ ⎡ β α β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ β − αβ − αβ − α − ε ω π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ∞ α β ∞ − ∞ ∞ −

∫ ∫

e e d d J J G k k j y x E y x E _{j x j y} y x i y i x , ~ , ~ , ~ 1 2 1 , , 2 2 0 2 2 0 0 0 (2.9) dove I I 2 0 2 2 2 2 2 0 2 1 2 ~ k k j G − β + α = β − α − − =

con I matrice identica.

2.3 Campo scatterato di un array di patch monodimensionale.

Utilizzando il teorema di Floquet possiamo generalizzare l’EFIE ottenuta per un singolo elemento (2.8) al caso periodico monodimensionale. Poniamo che dx sia il periodo di ripetizione della cella

elementare e J(x) sia la corrente indotta sul singolo patch, quindi applicando il teorema di Floquet la corrente sull’elemento distante dx è:

(

) ( )

jkincx dx x J x e d x J + = (2.10) dove inc x

Definiamo la funzione:

( )

( )

jkincx x e x J x J' = − (2.11)

dalle (2.10) e (2.11) segue che:

(

_{x d}

)

_J

(

_{x d}

)

_e ( ) _J

_{( )}

_{x e J}

_{( )}

_x J jk x d jk x x x inc x x inc x ' ' + = + − + = − = _(2.12)

Analizzando la (2.12) si evince che J '

( )

x è periodica di periodo dx ed è per questo motivo

esprimibile attraverso la sua trasformata serie di Fourier:

( )

dx nx j n n e J x J π ∞ −∞ =

∑

= 2 ~ ' (2.13) Dalle (2.11) e (2.13) si ottiene:

( )

j x n n x k d n j n n n inc x x J e e J x J ∞ α −∞ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + π ∞ −∞ =

∑

∑

= = ~ ~ 2 (2.14) Nell’equazione (2.14) è stata effettuata una discretizzazione della frequenza spaziale α ottenendo

inc x n n k d + π =

α 2 che sostituita nella (2.9) consente di ottenere l’equazione integrale nel caso trattato in questo paragrafo. Si ottiene:

( )

( )

∑ ∫

(

) (

(

)

)

∞ −∞ = β α ∞ ∞ − β ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ β − β α − β α − α − ε ω = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n y j x j n y n x n n n n x i y i x d e e J J G k k j d y x E y x E n , ~ , ~ , ~ 1 1 , , 2 2 0 2 2 0 0 0 (2.15)

2.4 Campo scatterato di un array di patch bidimensionale.

Possiamo adesso periodicizzare l’espressione del campo scatterato anche lungo l’asse y applicando nuovamente il teorema di Floquet. Discretizzando anche β come fatto per α si ottiene:

inc y y m m k d + π = β 2

L’equazione integrale diventa quindi:

( )

( )

∑ ∑

(

) (

(

)

)

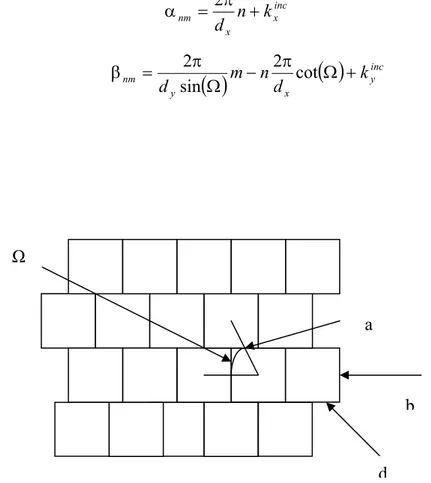
∞ −∞ = ∞ −∞ = β α ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ β − β α − β α − α − ωε π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n m y j x j m n y m n x m n m m n m n n y x i y i x e n e m J J G k k j d d y x E y x E , ~ , ~ , ~ 1 2 , , 2 2 0 2 2 0 0 (2.16)

Nel caso in cui le celle risultino traslate di una certa quantità lungo l’asse x (Fig. 2.3), le variabili discrete αn e βm cambiano come segue:

inc x x nm n k d + π = α 2

( )

( )

incy x y nm k d n m d Ω + π − Ω π = β 2 cot sin 2

Figura 2.3 Celle traslate

Tutte le relazioni ottenute fino ad adesso sono valide nel caso di schermi di tipo capacitivo dove i singoli elementi conduttori sono dei patch. Se invece consideriamo gli schermi induttivi (ad apertura) per ottenere le giuste relazioni dobbiamo applicare il concetto di dualità all’equazione all’operatore, mettendo così in relazione il campo magnetico diffratto con le correnti magnetiche superficiali. Imponendo la continuità del campo magnetico totale su entrambi i lati dell’apertura, si ottiene l’equazione integrale per il campo magnetico (MFIE – Magnetic Field Integral Equation) che è:

( )

( )

∑ ∑

(

)

(

(

)

)

∞ −∞ = ∞ −∞ = β α ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ β − β α − β α − α − ωµ π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n m y j x j m n y m n x m n m m n m n n y x i y i x e n e m M M G k k j d d y x H y x H , ~ , ~ , ~ 1 2 , , 2 2 0 2 2 0 0 (2.17)

dove M rappresenta la corrente magnetica superficiale.

d b a Ω

Per facilitare l’implementazione su un calcolatore e per una maggiore compattezza delle espressioni, queste (valide nello spazio libero) possono essere riscritte come segue:

(

)

(

)

0 2 2 0 , ~ ωε β α ⋅ α − = j G k G n n m XX

(

)

(

)

0 2 2 0 , ~ ωε β α ⋅ β − = j G k G m n m YY

(

)

0 , ~ ωε β α ⋅ β α − = = j G G G n m n m YX XY

dove le funzioni che compaiono al primo membro prendono il nome di Funzioni diadiche spettrali

di Green. Quindi l’equazione all’operatore per il campo elettrico diventa:

( )

( )

∑ ∑

(

(

)

)

∞ −∞ = ∞ −∞ = β α ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ωε π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n m y j x j m n y m n x YY YX XY XX y x i y i x e n e m J J G G G G j d d y x E y x E , ~ , ~ 1 2 , , 0 (2.18)

Analogamente l’equazione all’operatore per il campo magnetico diventa:

( )

( )

∑ ∑

(

(

)

)

∞ −∞ = ∞ −∞ = β α ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ωε π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n m y j x j m n y m n x YY YX XY XX y x i y i x e n e m M M G G G G j d d y x H y x H , ~ , ~ 1 2 , , 0 (2.19)

Le equazioni (2.18) e (2.19) sono valide anche se la superficie selettiva in frequenza risulta immersa in strati di materiale dielettrico. In questi casi si tiene conto della presenza di materiali con costante dielettrica εr diversa da 1 nelle funzioni di Green e le equazioni (2.18) e (2.19) diventano:

( )

( )

∑ ∑

(

(

)

)

∞ −∞ = ∞ −∞ = β α ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ωε π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n m y j x j m n y m n x eYY eYX eXY eXX y x i y i x e n e m J J G G G G j d d y x E y x E , ~ , ~ 1 2 , , 0 (2.20)

( )

( )

∑ ∑

(

(

)

)

∞ −∞ = ∞ −∞ = β α ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ωε π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n m y j x j m n y m n x eYY eYX eXY eXX y x i y i x e n e m M M G G G G j d d y x H y x H , ~ , ~ 1 2 , , 0 (2.21)

Se il conduttore è caratterizzato da una conducibilità finita si deve applicare una modifica alle condizioni al contorno. L’equazione = s + inc =0 _diventa:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ y x S s y s x i y i x J J Z E E E E (2.22) dove

(

)

σδ + = j

Z_S 1 rappresenta l’impedenza superficiale della FSS.

Nell’equazione all’operatore (2.18) andrà aggiunto il prodotto presente nell’equazione (2.22).

2.5 Soluzione dell’equazione all’operatore.

Le equazioni all’operatore scritte in precedenza possono essere riscritte in maniera simbolica come segue:

g u

L∗ = (2.23)

dove g è un vettore rappresentante il campo elettrico (o magnetico) incidente; u è un vettore incognito riferito alla corrente superficiale elettrica (J) o magnetica (M); L è un operatore che mette in relazione il vettore u con quello g. Nel caso del campo elettrico quindi la (2.23) diventa:

E J

L∗ = (2.24)

Un’equazione come la (2.24) si può risolvere utilizzando il Metodo dei Momenti (MoM). Consideriamo la seguente equazione integrale:

( )

x

( ) ( )

x f x g

( ) ( )

x,x' f x'dx'

s =α +

∫

(2.25)

dove f(x) rappresenta la funzione incognita e le funzioni s(x), α(x) e g(x,x’) sono note. La funzione

g(x,x’) spesso dipende solo dalla differenza (x-x’), cioè g(x,x’) = g(x-x’) e rappresenta il kernel

dell’integrale. In base ai limiti di integrazione, l’equazione (2.25) prende il nome di equazione di Fredholm se i limiti sono costanti, o equazione di Volterra se i limiti dipendono da x. Inoltre se α = 0 l’equazione si dice di prima specie, se α = cost di seconda specie e di terza specie se α = α(x). Analizziamo le equazioni di Fredholm supponendo che le variabili x e x’ siano limitate all’intervallo (a,b). Dal punto di vista analitico la soluzione è difficile da ottenere nella generalità dei casi. Per semplicità si utilizza un approccio numerico e quindi si espande la funzione incognita in termini di opportune funzioni note:

( )

( )

( )

( )

_∑

( )

= = + + + ≅ N n n n N N f x a f x a x f a x f a x f 1 2 2 1 1 ... (2.26)

Le funzioni f_n

( )

x sono chiamate funzioni di base o funzioni di espansione. Si può adesso ricondurre il problema alla ricerca dei pesi a1……aN che permettono di esprimere la soluzione

cercata come una combinazione lineare di funzioni base note. Sostituendo la (2.26) nella (2.25) si ottiene:

( )

x a

( ) ( )

x f x a g

( )

x s N _n n n n N n n

∑

∑

= = + α = 1 1 (2.27) con

( )

x g

( ) ( )

x,x' f x'dx' g _n b a n =

∫

(2.28)

Una scelta opportuna delle funzioni base può semplificare notevolmente la ricerca della soluzione. La scelta delle funzioni base f_n

( )

x deve essere tale da permettere di ricostruire l’andamento della

f(x) che come è noto può avere un qualsiasi andamento lungo x.

Per ricavare la forma numerica della (2.27) si impone la stessa equazione su N punti in modo da ottenere un sistema di N equazioni in N incognite per poi effettuare la risoluzione in forma matriciale. I risultati ottenuti con questo metodo sono poco accurati nella maggior parte delle applicazioni.

In alternativa si può utilizzare l’operazione di weighting o testing che consiste nell’introduzione di un ulteriore insieme di funzioni w_n

( )

x , definite nello stesso dominio della funzione f(x), e fissare il prodotto interno w, f , un’operazione scalare che soddisfi le seguenti condizioni:

-simmetria: w, f = f,w

-linearità: αf +βg,w =α f,w +β f,w (2.29) - _f,_f∗ >0 _{per f ≠0, f, f}∗ _{=0 per f =0}

Una possibile scelta è la seguente:

( ) ( )

x f x dx w f w b a

∫

= , (2.30)

Si verifica facilmente che tutte le condizioni (2.29) sono soddisfatte dalla (2.30). Se eseguiamo l’operazione di testing sulla (2.27) otteniamo la seguente espressione:

( )

x a g

( )

x r a s N _mn n n mn N n n m

∑

∑

= = + = 1 1 (2.31) dove

( ) ( )

xs x dx w s b a m m =

∫

(2.32)

( ) ( ) ( )

x w x f x dx r _n b a m mn =

∫

α (2.33)

( ) ( ) ( )

x g x x f x dx dx w g _n b a b a m mn =

∫

∫

, ' ' ' (2.34)

Il problema di partenza definito nella (2.25) può essere rappresentato nel seguente modo:

s

Lf = (2.35)

dove L rappresenta un operatore lineare integro differenziale. La (2.25) è stata discretizzata nella forma della (2.30), diventando così un’equazione di tipo matriciale:

s

Ma= (2.36)

dove a è il vettore delle incognite contenente i pesi delle funzioni di base, M è la matrice i cui elementi sono calcolati secondo la (2.33) e (2.34), mentre s rappresenta il vettore del termine noto i cui elementi sono dati dalla (2.32). La soluzione si ottiene invertendo la matrice risolvente, ovvero:

s M

a= −1 (2.37)

Le funzioni wm sono delle funzioni di base ortonormali e la loro scelta condiziona fortemente il

risultato finale. La scelta wm=fn viene denominata procedura di Galerkin, dal nome del matematico

russo che le ha utilizzate. Scegliendo invece wm=δ(x-xn) si ottiene il metodo di Point Matching o

metodo della collocazione. In questo caso l’equazione (2.37) corrisponde a forzare l’equazione (2.25) ad essere soddisfatta nei punti discreti xn.

Per risolvere l’equazione all’operatore dobbiamo esprimere il vettore incognito J in funzione di un set di funzioni di base note f:

n n n

C f

J =

∑

(2.38)

dove Cn sono i coefficienti incogniti e fn è la generica funzione appartenente alla base scelta. In

questo modo l’equazione all’operatore può essere riscritta come segue: n

n n

C L f

E=

∑

∗ (2.39)

Definiamo il seguente prodotto scalare:

ds erficie b a b a =

∫

∗• sup , (2.40)

ds apertura z b a b a, =

∫

∗× • (2.41)

Se poi si pesano i campi con le funzioni di prova wi si ottiene:

∑

∗ = j j j i i E W C L f W, , (2.42)

che in termini matriciali diventa:

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ... , ... , , ... ... ... ... ... ... ... ... , ... , , ... ... ... ... ... ... , ... , , ... , ... , , 2 1 2 1 2 1 2 2 2 1 2 1 2 1 1 1 E w E w E w C C C f L w f L w f L w f L w f L w f L w f L w f L w f L w n n n n n n n n (2.43)

Limitando la sommatoria e invertendo la matrice, è possibile ricavare il vettore dei coefficienti incogniti: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ... , ... , , ... ... ... ... ... ... , ... , , ... ... ... ... ... ... , ... , , ... , ... , , ... ... 2 1 1 2 1 2 2 2 1 2 1 2 1 1 1 2 1 E w E w E w f L w f L w f L w f L w f L w f L w f L w f L w f L w C C C n n n n n n n n (2.44)

Una volta calcolati i coefficienti Cj che rappresentano quindi le ampiezze incognite delle immagini

delle funzioni f, alle quali viene applicato l’operatore L nello spazio vettoriale definito da W, si risale al vettore J. I prodotti scalari all’interno della matrice possono essere calcolati utilizzando un’integrazione numerica di tipo gaussiano, mentre quelli presenti nel vettore a secondo membro sono, per la forma di Ei, le trasformate di Fourier delle funzioni W di prova, calcolate in inc

x k = α e in inc y k = β .

2.6 Le funzioni di base ROOF-TOP.

Sono enunciate di seguito le caratteristiche che devono avere le funzioni di base per avere una buona velocità e convergenza dell’algoritmo:

- la matrice risultante sia di ordine minimo - siano soddisfatte le condizioni al contorno

- siano trasformabili secondo Fourier per non perdere il vantaggio di lavorare nel dominio della frequenza

- le loro trasformate decadano rapidamente affinché i prodotti scalari nei quali compaiono abbiano un numero di termini ridotto.

Le funzioni che soddisfano a queste caratteristiche possono essere divise in due categorie:

- funzioni definite sull’intero dominio: si prestano ad essere utilizzate efficacemente solo per geometrie caratteristiche

- funzioni definite solo sui sottodomini: consentono di sfruttare una matrice risultante di ordine ridotto ovvero invertibile secondo il metodo dell’eliminazione gaussiana.

Le funzioni di base comunemente utilizzate sono le funzioni roof-top (Fig. 2.4). Sono funzioni di tipo vettoriale che assumono valore unitario allo spigolo congiungente una coppia di rettangoli e valore nullo agli spigoli opposti.

Utilizzando delle funzioni base definite su dei sottodomini rettangolari allora le funzioni roof-top sono definite su ogni coppia di elementi rettangolari attigui.

ε_r y x 1 0 0 a) b)

Figura 2.4 Funzioni di base roof-top su sottodomini rettangolari

Facendo riferimento al particolare problema in esame e alla figura 2.5 scriviamo l’espressione analitica delle funzioni roof-top come prodotto delle seguenti funzioni:

( )

⎪⎩ ⎪ ⎨ ⎧ ∆ ≤ ∆ − = altrove y y m y m H_y , 0 2 , 1 (2.45)

( )

⎪⎩ ⎪ ⎨ ⎧ ∆ ≤ ∆ − ∆ ∆ − − = Λ altrove x x n x x x n x n x , 0 , 1

Figura 2.5 Funzioni di base roof-top per FSS

Per poter rappresentare una corrente su di una superficie per mezzo delle funzioni di base appena scelte è necessario discretizzare la cella elementare, di dimensioni

(

a×b

)

in

(

N×N

)

sottocelle elementari di dimensioni ∆x=a N e ∆y=b N. In questo modo si definisce per ogni subcella un vettore superficiale di corrente; in questo modo nell’equazione all’operatore è possibile utilizzare la FFT (Fast Fourier Trasform) al posto della trasformata continua di Fourier (TCF).

Le espressioni delle componenti della densità di corrente lungo le due direzioni spaziali sono le seguenti:

( ) ( )

m nB m n I J _x N N n N N m x x , , 1 2 2 1 2 2

∑ ∑

− − = − − = = (2.46)

( ) ( )

m nB m n I J N _y N n N N m y y , , 1 2 2 1 2 2

∑ ∑

− − = − − = =

dove Ix e Iy sono le ampiezze delle correnti elementari, mentre Bx e By sono le funzioni di base la cui

espressione è la seguente: x y ∆x ∆y

(

)

[

m x n y

]

B +12∆ , ∆

(

)

[

m x n y

]

B ∆ , +12 ∆

( )

n m n H

( )

m B_{x x} ⎟ _x ⎠ ⎞ ⎜ ⎝ ⎛ + Λ = 2 1 , (2.47)

( )

( )

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Λ = 2 1 ,m H n m n B_{y y y}

Imponiamo adesso le seguenti condizioni e notazioni semplificative:

( )

⎜⎜_⎝⎛ ⎜_⎝⎛ + ⎟_⎠⎞∆ + ∆ ⎟⎟_⎠⎞ ⋅ = ⋅ ⋅

∫

x i j k n x k m y inc y inc x i d e B 2 1 0 , 0 ~ W S E (2.48)

( ) ( )

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₌ =

∑ ∑

∞ −∞ = ∞ −∞ = n m B n m I J TCF J _x n m x x x , , ~ (2.49)

( ) ( )

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = =

∑ ∑

∞ −∞ = ∞ −∞ = n m B n m I J TCF J _y n m y y y , , ~

(

) ( )

[

∑∑

B m,n,x,y ⋅I n,m

]

=

∑∑

I

( ) (

m,n ⋅B~ m,n,α,β

)

TCF _{x x x x} (2.50)

(

) ( )

[

∑∑

B m,n,x,y ⋅I n,m

]

=

∑∑

I

( ) (

m,n ⋅B~ m,n,α,β

)

TCF _{y y y y}

Le equazioni 2.46 possono essere riscritte in forma più compatta: n

n n

C f

I=

∑

(2.51)

Adesso si applicano i seguenti prodotti scalari

∑

∗ = j j j i i E W C L f W, , (2.52)

all’equazione all’operatore per il campo elettrico

( )

( )

∑ ∑

(

(

)

)

∞ −∞ = ∞ −∞ = β α ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β α β α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − n m y j x j m n y m n x YY YX XY XX y x i y i x e n e m J J G G G G d d y x E y x E , ~ , ~ ~ ~ ~ ~ 2 , , (2.53) Imponiamo la condizione di Galerkin, assumendo le funzioni di base uguali a quelle di prova:

W = f = B (2.54)

Si indica poi con P(n,m) la fase _e−j(kxincn∆x+kincy m∆y) _{avendo sostituito x con p∆x e y con p∆y, a causa}

( )

( )

(

)

(

)

(

)

(

)

(

)

(

)

⎥_⎦⎤⋅⎢_⎣⎡

(

(

)

)

⎥_⎦⎤ ⎢ ⎣ ⎡ ⋅ ⋅ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ∗ ∗ ⋅ π π − = =− ∗ ∗ ∗ ∗

∑∑ ∑ ∑

' ,' ' ,' , 0 0 , , ' ~ , ' ~ ' , ~ , ' ~ 2 1 , 0 , 0 ~ , 2 1 0 , 0 ~ 2 2 ' ' 2 2 2 2 0 0 q p q p q p q p e e m n G m n G m n G m n G q p B q p B y x q m N j p n N j p q N N n N N m YX YY XY XX y y x x I I P P P E P E (2.55)

Le variabili discrete p e q sono i punti di applicazione delle funzioni di prova: in corrispondenza dei due indici vengono calcolati i coefficienti incogniti. Le variabili n e m appartengono al dominio trasformato e consentono di individuare i punti dello spazio immagine dell’operatore FFT. Le variabili discrete p’ e q’ identificano i punti in cui vengono applicate le funzioni di base: le sommatorie in cui figurano come indici esprimono la somma dei singoli campi reirradiati relativi ai punti di applicazione delle funzioni di prova. Infine le variabili p= p− p' e q =q−q' tengono conto della traslazione tra le funzioni di prova e quelle di base.

Gli elementi della matrice G di Green sono stati modificati come segue:

(

)

_{∑ ∑}

∞

(

) (

) (

)

−∞ = ∞ −∞ = ∗ = r s x x XX XX G n m B n m B n m N m n G~' , 1₂ ~ ,' ' ~ ,' ' ~ ,' '

(

)

_{∑ ∑}

∞

(

) (

) (

)

−∞ = ∞ −∞ = ∗ = r s y y YY YY G n m B n m B n m N m n G~' , 1₂ ~ ,' ' ~ ,' ' ~ ,' '

( )

(

) (

) (

)

⎟⎠ ⎞ ⎜ ⎝ ⎛ ∆ β + ∆ α ∞ −∞ = ∞ −∞ = ∗

∑∑

= 2 2 2 ' ' ' ,' ~ ' ,' ~ ' ,' ~ 1 , ' ~ j x y r s y x XY XY m n e m n B m n B m n G N m n G

(

)

(

) (

) (

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛_α ∆ _+β ∆ − ∞ −∞ = ∞ −∞ = ∗

∑ ∑

= 2 2 2 ' ' ' ,' ~ ' ,' ~ ' ,' ~ 1 , ' ~ j x y r s YX y x YX m n e m n B m n B m n G N m n G

in cui n'=n+rN, m'=m+sN e le sommatorie in r e s, che derivano dai prodotti scalari che compaiono al secondo membro della (2.52), sono limitabili a pochi termini poiché come visto in precedenza le trasformate di Fourier decadono rapidamente.

Gli elementi che compaiono nella diagonale principale della penultima matrice al secondo membro della (2.55), possono essere scritti come:

(

)

(

)

( ) ( ) _' ' ' 2 ' 2 2 2 2 2

,

'

q y jk p x jk y m j x n j q q y b m k j p p x a n k j q m b b N j p n a a N j y q k x p k j q m N j p n N j inc y inc x n n inc y inc x inc y inc x

e

e

e

e

e

e

e

e

e

e

e

q

p

⋅ ∆ ⋅ ∆ ∆ β ∆ α − ∆ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ π − ∆ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ π π π ∆ + ∆ π π

⋅

⋅

⋅

=

=

=

=

P

(2.56)

L’equazione (2.55), tenendo conto della (2.56) può essere scomposta nel prodotto mostrato di seguito:

( )

( )

(

)

(

)

(

)

(

)

(

)

(

)

j n x m y j( p x q y) y m x n j N N p N N q y x N N n N N m YX YY XY XX y y x x m n q p q p e e e q p q p m n G m n G m n G m n G q p B q p B ∆ β + ∆ α ∆ β + ∆ α − ∆ β + ∆ α − − − = − − = − − = − − = ∗ ∗ ∗ ∗ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⋅ ⋅ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ −

∑ ∑

∑ ∑

' ' ' ' 0 0 0 0 ' , ' ' , ' , ' ~ , ' ~ ' , ~ , ' ~ 2 1 , 0 , 0 ~ , 2 1 0 , 0 ~ 1 2 2 ' 1 2 2 ' 1 2 2 1 2 2 I I P E P E (2.57)

Le fasi presenti a secondo membro si possono riscrivere per mettere in evidenza le funzioni nella base di Fourier:

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _{∆ + ∆} − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _{∆ + ∆} − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{α ∆ +β ∆} −

=

=

=

y m q N j x n p N j y q k y m q N j x n k x n p N j y m x n j

e

e

q

p

e

e

e

inc x inc x q p ' 2 ' 2 ' 2 ' 2

'

,

'

' '

P

(2.58)

Analogamente si può scrivere:

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _∆ − ∗ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _{∆ + ∆} − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π _{∆ + ∆} − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{α ∆ +β ∆} −

=

=

=

y qm N j x pn N j y q k y qm N j x p k x pn N j y m x n j

e

e

m

n

e

e

e

inc x inc x q p 2 2 2 2

'

,

'

' '

P

(2.59)

Invertendo l’ordine dei prodotti e delle sommatorie è possibile ora mettere in evidenza le trasformate di Fourier ed ottenere, in forma simbolica, la seguente espressione:

( )

( )

(

)

(

)

(

)

(

)

(

)

(

)

⎧⎨_⎩

(

)

(

)

⎥_⎣⎢⎡

(

(

)

)

⎥_⎦⎤_⎪⎭⎬⎫⎪ ⎦ ⎤ ⎢ ⎣ ⎡ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − ∗ ∗ ∗ ∗ ∗ ∗ ' , ' ' , ' ' , ' 0 0 ' , ' , ' ~ , ' ~ ' , ~ , ' ~ , 0 0 , 2 1 , 0 , 0 ~ , 2 1 0 , 0 ~ 1 0 0 q p q p q p P q p P FFT m n G m n G m n G m n G FFT q p P q p P q p B q p B y x YY YX XY XX y y x x I I P E P E (2.60)

L’espressione scritta sopra può essere risolta mediante un metodo diretto oppure con l’impiego di metodi iterativi, come ad esempio quello del gradiente coniugato.

Una volta noti i coefficienti delle funzioni base e quindi le correnti superficiali, è possibile ricostruire la componente tangenziale del campo elettrico reirradiato, la cui espressione in termini di armoniche di Floquet vale:

z j y j x j p q pq z j y j x j _{e e e} p _e q _e pq e ∞ α β − γ −∞ = ∞ −∞ = γ − β α ₊

∑ ∑

= s s E E E 0 0 0 00 (2.61) dove 2 0 2 2 _k p p pq = α +β − γ

Volendo esprimere il campo scatterato in termini di potenziale elettrico e magnetico l’espressione precedente diventa:

(

s

)

s s s A A F E ∇∇⋅ ωε + ωµ − × ∇ − = r r r 0 0 1 j j (2.62)

dove As e Fs rappresentano i potenziali vettore elettrico e magnetico, che valutati per z = 0 possono essere scritti come segue:

∑ ∑

∞ −∞ = ∞ −∞ = γ β α = p q z j y j x j TM pq pq q p _{e e} e R zˆ s A (2.63)

∑ ∑

∞ −∞ = ∞ −∞ = γ β α = p q z j y j x j TE pq pq q p _{e e} e R zˆ s F

Esaminando le (2.63) si nota come i potenziali sono funzione dei coefficienti di riflessione.

Sostituendo le (2.63) nella (2.62) e sfruttando l’ortogonalità delle armoniche di Floquet, è possibile risalire ai coefficienti di riflessione (analogamente anche a quelli di trasmissione), per una superficie selettiva in frequenza.

Si riportano di seguito le espressioni dei coefficienti di riflessione e di trasmissione per la polarizzazione TE e per quella TM, ricavati dopo alcuni passaggi dalle equazioni (2.63):

(

)

[

]

[

(

)

]

}

{

(

2 2

)

~ , ~ ~ , ~ n m mn n m m mn n m n TE mn j R β + α δ + β α α − δ + β α β = r y s y r x s x E E E E (2.64)

(

)

[

]

[

(

)

]

}

{

(

)

0 2 2 ~ , ~ ~ , ~ ωε γ β + α δ + β α β − δ + β α α − = mn n m mn n m n mn n m m TM mn R r y s y r x s x E E E E

(

)

[

]

[

(

)

]

}

{

(

2 2

)

~ , ~ ~ , ~ n m mn n m m mn n m n TE mn j T β + α δ + β α α − δ + β α β = t y s y t x s x E E E E (2.65)

(

)

[

]

[

(

)

]

}

{

(

)

0 2 2 ~ , ~ ~ , ~ ωε γ β + α δ + β α β + δ + β α α − = mn n m mn n m n mn n m m TM mn T t y s y t x s x E E E E

In queste espressioni la trasformata di Fourier è stata indicata per mezzo dell’operatore E~.

2.7 Il solver elettromagnetico FSS.

Il programma di simulazione consente di analizzare lo scattering da superfici selettive in frequenza risolvendo l’equazione all’operatore EFIE attraverso l’applicazione del Metodo dei Momenti (MoM). Utilizzando questa procedura si approssimano le correnti indotte con le funzioni roof-top definite sui sottodomini. Le funzioni di prova sono prese uguali alle funzioni di base (metodo di Galerkin) e si risolve l’equazione matriciale mediante il metodo di eliminazione gaussiano. Si suppone implicitamente che la FSS sia di estensione infinita e che essa sia composta da:

- uno o più strati di dielettrico

- uno schermo FSS formato da materiale perfettamente conduttore (PEC) o da materiale con perdite (in questo ultimo caso sarà necessario fornire al simulatore il valore dell’impedenza superficiale complessa Rs)

- un piano di massa perfettamente conduttore (opzionale) come ultimo strato.

Il programma necessita dell’immissione della cella elementare della FSS che è una versione discretizzata attraverso una matrice di dimensione 16×16, composta di 1 o 0 a seconda che la sottocella sia di materiale conduttore o di dielettrico. Le dimensioni della cella possono essere portate a 32×32 o 64×64 cambiando opportunamente il programma.

Nel caso 16×16 il programma controlla ognuna delle 256 locazioni della griglia: se una qualsiasi sottocella e quella immediatamente alla sua sinistra o alla sua destra sono ambedue fatte di materiale conduttore (nella matrice corrisponde 1 in entrambe le locazioni), viene assegnata alle due locazioni una funzione roof-top, centrata tra le due e rappresentante la corrente diretta lungo x; la stessa operazione viene ripetuta lungo le colonne della matrice (in questo caso la funzione roof-top rappresenta la corrente lungo y).

Il programma consente di determinare, per entrambe le polarizzazioni (TE e TM) e per qualsiasi forma della cella elementare (nei limiti della discretizzazione) le seguenti quantità:

- modulo e fase dei coefficienti di riflessione e trasmissione quando è fissata la direzione di incidenza (θinc, φinc)

- i coefficienti delle correnti indotte

- un grado di attendibilità dei risultati ottenuti grazie al calcolo della potenza di ogni singola armonica di Floquet.

Si può calcolare l’efficacia di schermatura di una FSS dopo aver ricavato i coefficienti di trasmissione del campo elettrico, calcolati in un determinato intervallo di frequenza, utilizzando la relazione seguente: ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ τ = e dB SE 20log₁₀ 1 (2.66)

dove τe rappresenta il coefficiente di trasmissione del campo elettrico (in campo vicino si può

utilizzare il coefficiente di trasmissione del campo magnetico τh per determinare la schermatura del

campo magnetico).

Qualora non si riuscisse a soddisfare le condizioni di progetto si possono utilizzare le FSS multischermo che si ottengono alternando strutture a singolo schermo, le cui geometrie possono anche differire tra loro.