CAPITOLO V METODO HYBRID TRAIT

87

CAPITOLO V

METODO HYBRID TRAIT

5.1 Introduzione al metodo “H-TRAIT”

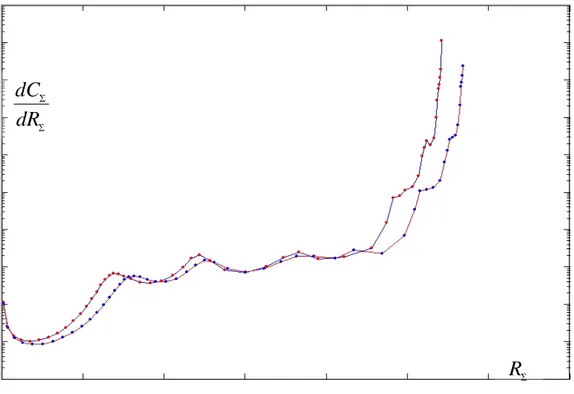
Nel precedente capitolo si è proceduto ad una descrizione del metodo NID, il quale sebbene è in grado di fornire un’elevata risoluzione nell’analisi termica di una struttura di assemblaggio e permetta una rappresentazione a Structure Function , si basa su ipotesi matematicamente non corrette, ovvero l’assunzione di uno spettro di costanti di tempo continuo. Al contrario il metodo TRAIT si fonda sull’ipotesi corretta di spettro discreto, ma non è in grado di fornire un elevato numero di parametri termici caratteristici nell’analisi termica di una struttura di assemblaggio. Sarebbe per noi di grande utilità poter ricorrere ugualmente alla rappresentazione di tipo “structure function”, da un lato perché è assai diffusa e accettata in ambito di ricerca, dall’altro perché condensa in un solo grafico una notevole quantità di informazioni sulle strutture sotto esame. Il punto di forza di tale rappresentazione risiede nella correlazione che opera fra resistenze e capacità termiche di ogni nodo, grazie alla quale divengono evidenti dei dettagli che non sarebbe possibile dedurre dal valore di ciascuna delle due prese singolarmente. Come esempio consideriamo i grafici di figura 1 e figura 2, relativi a misure effettuate su due substrati la cui struttura fisica inizialmente coincide, e comincia a differire soltanto da un certo punto in poi. Nella prima, ottenuta con l’analisi di tipo TRAIT classico, questo non risulta evidente, mentre emerge significativamente nella seconda, ricavata con un nuovo metodo, di cui si discuterà in questo capitolo, che abbiamo denominato TRAIT ibrido (o HTRAIT). L’HTRAIT si è rivelato un sistema di caratterizzazione molto potente, poiché unisce una correttezza teorica di base, dal momento che si basa sull’assunzione dello spettro come infinito e discreto, a una modalità di rappresentazione intuitiva ed efficace.

88

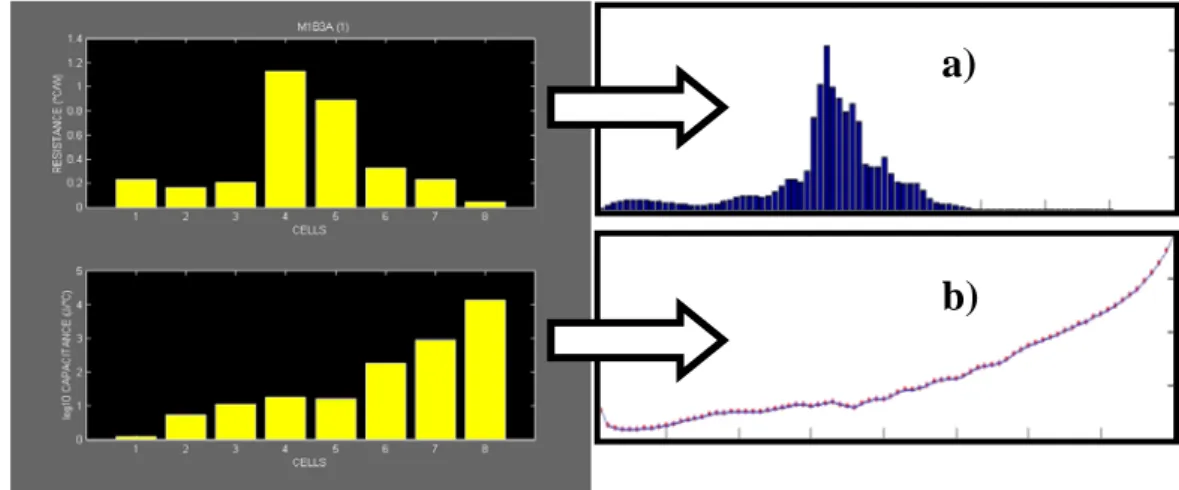
La possibilità di ottenere dei grafici analoghi alla structure function cumulativa e alla structure function differenziale, in verità, è già presente nel pacchetto software TRAIT tradizionale anche se il risultato non è ben interpretabile a causa del basso numero di costanti di tempo (che coincide col numero di nodi) che possiamo ottenere (nel caso particolare 8, ma comunque mai superiore ai 12-13).

Se però riuscissimo ad aumentare il numero di nodi, e conseguentemente il numero di righe dello spettro e delle celle RC, con qualche artifizio matematico, ci avvicineremmo

89

alla condizione di spettro continuo necessaria per poter ottenere una rappresentazione a structure function rilevante, col vantaggio però di essere partiti da un insieme di dati ottenuto in un modo teoricamente corretto. Di seguito descriveremo i passi della procedura che abbiamo adottato.

R

dC

dR

Σ Σ

FIG 2 Structure function ricavata colla procedura HTRAIT a partire dai sistema le cui resistenze e capacità sono mostrate in figura 1

90

5.2 Procedura di allargamento dello spettro

La procedura di distribuzione continua dello spettro discreto operata dal metodo HTRAIT si basa sulla conoscenza dell’impedenza termica Z(s) vista dalla sorgente di calore della struttura sotto esame, ricavata col software TRAIT. I passi necessarii sono i seguenti:

1) Si acquisisce il transitorio di temperatura;

2) Da tale transitorio si estraggono con il metodo TRAIT le costanti di tempo del sistema (discrete) e quindi si calcola la Z(s);

3) Si ottiene una distribuzione continua delle costanti di tempo, grazie a questa relazione:

( )

1

{

( )

}

Im

exp

A z

Z s

z

π

=

⎡

_⎣

= −

−

⎤

_⎦

4) Questa distribuzione continua viene “affettata” con un passo ∆ (abbiamo z

operato il cambiamento di variabile z=ln

( )

( )

5) A partire dai valori A e _i τ_i viene ricavata la rete equivalente di Cauer e da questa si procede al calcolo delle structure function cumulativa e differenziale.

In relazione alla figura 3, definiamo le seguenti espressioni:

b a

z

z

z

N

−

∆ =

( )

A

A z dz

=

_∫

91

1

2

z

= + −

z

⎛

_⎜

i

⎞

_⎟

⋅ ∆

x

⎝

⎠

Dove le A sono le nuove costanti di tempo, ricavate per distribuzione e successiva i

suddivisione di quelle discrete; esse sono tanto più numerose quanto più piccolo si sceglie l’intervallo z∆ . Si è verificato in pratica che il campionamento dello spettro continuo, ottenuto dalla distribuzione di un numero di costanti oscillante fra 8 e 12 ottenute dal metodo TRAIT, con un numero di 200 costanti di tempo, e quindi con 200 valori di resistenze e capacità, è più che sufficiente ad ottenere structure function leggibili.

A(z)

A

A

A

92

Adesso è però necessario fare qualche precisazione in merito all’applicazione della formula (1). Se la applicassimo così come sta scritta otterremmo una fedele trasposizione continua dello spettro discreto, dove al posto delle barre con costante di tempo τ_i e ampiezza A avremmo delle _i δ di Dirac di area pari proprio ad A . Ci _i ritroveremmo esattamente al punto di partenza, a prescindere dal fatto nella pratica che non riusciremmo in alcun modo ad ottenere delle δ di Dirac a causa della limitata potenza di calcolo disponibile, ritrovandoci con un errore di overflow.

Per ovviare a questo inconveniente e ottenere una vera e propria distribuzione dello spettro dobbiamo introdurre un parametro chiamato “angolo di errore δ ” e adottare una formula leggermente differente dalla (1), ovvero dobbiamo calcolarla non sull’asse reale negativo:

( )

(

( )

)

exp

exp

ln

s

= −

−

ζ

= −

−

τ

= −

τ

ma su una retta del piano complesso , come mostrato in figura 5, di equazione

( )

( )

(

cos

)

exp

( )

s

= −

δ

+

jsen

δ

⋅

−

ζ

a)

b)

93

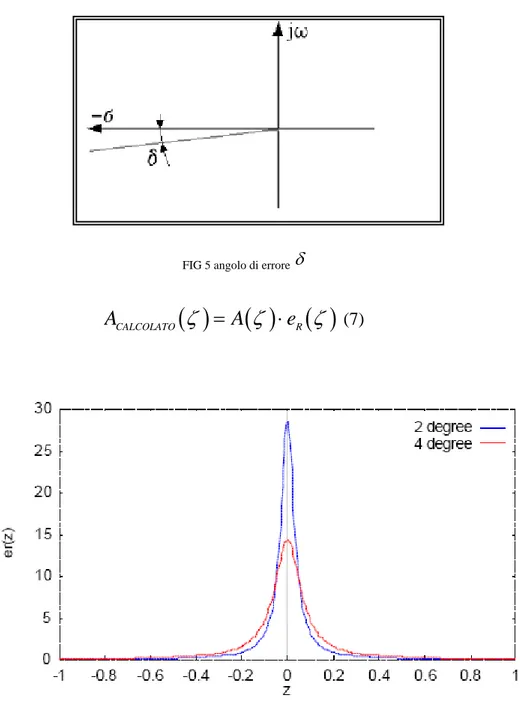
L’angolo di errore δ deve essere abbastanza piccolo (0.01-0.1°) al fine di ridurre le artefazioni che questa tecnica comporta. Si dimostra che lo spettro A z

( )

( )

(rappresentata in figura 6), ovvero:

( )

( ) ( )

CALCOLATO R

A

ζ

=

A

ζ

⋅

e

ζ

FIG 5 angolo di errore δ

94

( )

_{( )}

( )

_{( )}

exp

( )

₍

₎

1 2cos

exp

exp

2

R

sen

z

e

z

z

δ

ζ

δ

⋅

−

=

−

⋅

− +

−

Riducendo δ tale funzione diventa più stretta per cui l’errore diminuisce. L’accuratezza richiesta da un determinato problema può essere ottenuta attraverso la scelta di un certo angolo δ .

Vediamo ora di dedurre matematicamente l’espressione (1).

Per il modello a costanti di tempo discrete, l’impedenza termica vista dalla sorgente si esprime come:

( )

₍

₎

1

1 exp

R

R

Z s

s

τ

S

ζ

=

=

+

+

+

∑

∑

( )

Analogamente per uno spettro di costanti di tempo continuo si ha:

( )

( )

₍

₎

( )

₍

₎

1 exp

1 exp

R

R

z

Z S

d

dz

S

S

z

ζ

ζ

ζ

−

=

=

+

+

+

−

∫

∫

Prendiamo ora tale funzione sull’asse reale negativo del piano complesso:

( )

( )

₍

( )

₎

₍

₎

ln

1

1

exp

R

z

Z

dz

j

z

σ

δ

Σ =

−

−

Σ =

− +

Σ −

∫

95 Che scriviamo come

( )

( )

( )

Z z

=

R

− ⊗

z

W z

( )

₍

₎

_{( )}

( )

( )

( )

( )

(

)

( )

( )

( )

(

)

( )

1

1

1

exp

1 exp

exp

1 exp

exp

1 exp

exp

a ar ai

W z

W

z

jW

z

j

z

z

z

j

z

z

z

z

δ

δ

δ

δ

=

=

+

=

− +

−

=

+

−

+

−

+

La 12 può quindi essere separata in parte reale ed immaginaria:

( )

{

}

( )

( )

( )

{

}

( )

( )

Re

Im

Z z

R

z

W

z

Z z

R

z

W

z

=

− ⊗

=

− ⊗

Si dimostra che se δ →0 W approssima una delta di Dirac moltiplicata per ai π .

Otteniamo quindi:

(

)

1

{

(

( )

)

}

Im

exp

R

ζ

z

Z s

z

π

= − =

= −