CAPITOLO 2

CAPITOLO 2

 

MODELLI MATEMATICI PER LE 

SOSPENSIONI  

2.1 Introduzione 

Nel capitolo precedente sono stati illustrati la struttura e il funzionamento  di  una  sospensione;  il  passo  successivo  è  quello  di  costruire  un  modello  matematico  che  possa  descriverne  il  comportamento.  In  questo  capitolo  verranno  presentati  i  modelli  matematici  per  le  sospensioni  con  cui  verranno sviluppati gli algoritmi di controllo. 

2.2 Modello half car DOF2 

Il  modello  che  sembra  più  completo  per  descrivere  il  comportamento  di  uno  scooter  è  l’  half  car  con  due  gradi  di  libertà  (DOF2)  presentato  di  seguito: 

  Figura 2.1 Modello half car DOF2.[6]

 

Il telaio e il motore sono modellati come corpi rigidi mentre le sospensioni  e  le  ruote  sono  invece  rappresentate  da  un  elemento  elestatico  e  da  uno  smorzante  con  caratteristiche  non  lineari.  I  parametri  che  descrivono  questo sistema sono:  ‐ Mc: massa del telaio (sprung mass).  ‐ Jc: momento di inerzia del telaio  ‐ mwf e mwr: masse della ruota posteriore e anteriore (unsprung masses).  ‐ kwf e kwr: coefficienti di rigidezza del pneumatico anteriore e posteriore.  ‐ kf e kr: coefficienti elastici dell’ammortizzatore anteriore e posteriore  ‐ βwf e βwr: coefficienti di smorzamento delle ruote anteriore e posteriore  ‐ lf e lr: distanza del baricentro del telaio dalle sospensioni.    Le variabili che descrivono il modello sono:  ‐ zrf e zrr: profilo della strada anteriore e posteriore. 

‐ zwf e zwr: posizione verticale della ruota anteriore e posteriore.  ‐ zcf e zcf : posizione anteriore e posteriore del telaio. 

‐ Zc: posizione verticale del baricentro del telaio. 

‐ βf and βr: coefficienti di smorzamento variabili della sospensione anteriore e posteriore. 

 

Questo  modello  fornisce  una  descrizione  accurata  del  comportamento  delle  sospensioni,  permettendo  di  tenere  conto  dell’accoppiamento  tra  forze anteriori e quelle posteriori. Tale modello è però molto complesso e,  in  particolar  modo,  risulta  difficile  l’estrazione  di  tutti  i  parametri  necessari dal veicolo di interesse. Per queste ragioni si è scelto di utilizzare  un  modello  semplificato  detto  “quarter  of  car”.  La  limitazione  di  questo  modello,  come  suggerito  dal  nome,  è  proprio  il  non  poter  tenere  conto  dell’accoppiamento  tra  ruota  anteriore  e  posteriore.  Tale  scelta  è  però  giustificata dal fatto che dati sperimentali mostrano che l’influenza di tali  accoppiamenti sulle dinamiche della sospensione è contenuta, tipicamente  inferiore al 10%. L’utilizzo di tale modello permette, quindi, di  mettere a  punto strategie di controllo in maniera più semplice ottenendo, allo stesso  tempo, risultati molto simili al modello completo “half of car”.    

2.3 Modello a un grado di libertà 

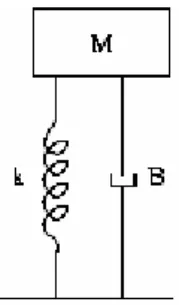
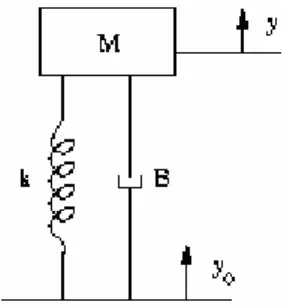
2.3.1 Introduzione al modello 

Si  presenterà  in  seguito  il  modello  a  un  grado  di  libertà  (che  non  tiene  conto  dello  schiacciamento  della  ruota),  andando  a  derivare  le  equazioni  che  tengono  insieme  il  sistema.  Tale  modello  schematizza  la  sospensione  come segue (Figura 2.2): 

 

Figura 2.2 Modello quarter caar DOF1 per sospensione.  

in  cui  k  rappresenta  il  coefficiente  elastico  della  molla  e  B  rappresenta  il  coefficiente  di  smorzamento  dell’ammortizzatore.  Andremo  adesso  ad  analizzare le possibili regolazioni effettuabili su una sospensione e la loro  modellizzazione matematica. 

 

2.3.2 I Coefficienti di frenatura 

Regolando  i  coefficienti  di  frenatura  in  compressione  e  in  estensione  si  varia la velocità con cui la sospensione ritorna alla posizione di equilibrio.   In particolare  si ha la seguente relazione: 

v B F_d =− ⋅  

In  cui  Fd  è  la  forza  di  smorzamento  esercitata  dalla  sospensione  che  è  proporzionale, tramite un coefficiente (B), alla velocità di compressione o  estensione della sospensione stessa.    2.3.3 Il precarico  Come già detto nel capitolo 1 ricordiamo che una sospensione non viene  mai sollecitata in trazione, ma presenta sempre una leggera compressione  iniziale, chiamata precarico. La regolazione del precarico non fa variare la  costante di rigidità della molla ma aumenta o diminuisce la forza minima  necessaria  per  far  reagire  la  molla  o,  più  semplicemente,  varia  la  soglia 

superata  la  quale  la  sospensione  comincia  a  comprimersi.  La  molla  reagisce quindi con una forza pari a:  ) ( _p m k y y F =− ⋅ Δ −  

in  cui  yΔ   rappresenta  la  variazione  della  distanza  tra  gli  estremi  della  sospensione (ossia la variazione  della compressione della molla cambiata  di  segno)  rispetto  alla  condizione  a  vuoto,  y   rappresenta  il  modulo _p

dell’accorciamento iniziale dovuto al precarico ed infine k è il coefficiente  elastico  della  molla  .  Tale  regolazione  serve  a  centrare  la  dinamica  dell’ammortizzatore  in  modo  da  evitare  il  più  possibile  il  fondocorsa  e  il  distaccamento della ruota dal suolo. 

Considerando  che  la  forza  esercitata  dalla  sospensione,  staticamente,  eguaglia la forza peso del sistema moto+pilota si ottiene:  ) ( y y_p k g M⋅ =− ⋅ Δ −  e quindi  y_p k g M y=− ⋅ + Δ  

Come  si  vede  la  compressione  statica  yΔ   dipende  da  y :  in  particolar _p modo  all’aumentare  del  precarico  la  compressione  statica  diminuisce  e  quindi  aumenta  l’altezza  da  terra.  L’aumento  della  compressione  statica  implica  un  allontanamento  della  dinamica  dal  suo  estremo  superiore  ma  un  avvicinamento  al  fondo  corsa  inferiore.  Con  un  precarico  maggiore  sarà  quindi  più  facile  avere  un  distaccamento  della  ruota  dal  suolo.  E’  importante  notare  che  il  precarico  non  deve  essere  mai  superiore al  peso  statico  delle  masse  sospese  perché  se  così  fosse  le  sospensioni  funzionerebbero  solo  per  sollecitazioni  verticali  superiori  al  valore  del  precarico  meno  la  forza  peso  delle  masse  sospese,  comportandosi  invece  come corpi rigidi per sollecitazioni inferiori. In queste condizioni l’energia  trasmessa  dal  fondo  stradale  verrebbe  assorbita  quasi  interamente  dal  pneumatico  che  così  rischierebbe  di  andare  in  crisi  e  non  funzionare  nel  modo  corretto  perché  si  troverebbe  a  fare  un  lavoro  aggiuntivo  (quello  delle sospensioni) per il quale non è stato espressamente progettato [10]. 

 

2.3.4 Equazioni per la descrizione del sistema complessivo passivo  In relazione alle considerazioni appena esposte è possibile, adesso, andare  a ricavare le equazioni complessive che reggono il sistema in Figura 2.3. 

 

Figura 2.3 Modello quarter car DOF1.   L’equazione che descrive questo sistema è la seguente:  d m F F g y M ⋅(&&+ )= +  

in cui  y&&  rappresenta l’accelerazione della massa sospesa, mentre Fm e F  d rappresentano  rispettivamente  la  forza  esercitata  dalla  molla  e  la  forza  esercitata dallo smorzatore. 

Definiamo, a questo punto, un sistema di riferimento in cui  y  rappresenta  la  variazione  di  altezza  della  massa  sospesa  rispetto  alla  condizione  a  vuoto mentre y  rappresenta la variazione del profilo stradale rispetto alla 0 condizione statica di moto ferma (e quindi strada piatta). In questo modo  ricaviamo che le espressioni per le forze diventano:          Fm =−k⋅(y−y0 − yp) e Fd =−B⋅(y−y0).  E quindi l’equazione complessiva diventa:  ) ( ) (y y0 B y y0 k g M y

M ⋅ _&&+ ⋅ =− ⋅ − − ⋅ _&− _&  

Tale  relazione  va  modificata  come  segue  per  tenere  conto  del  raggiungimento delle condizioni limite del fondocorsa e del distacco della  ruota  da  terra.  Definendo  y   come  il  modulo  dell’accorciamento f dell’ammortizzatore corrispondente al fondocorsa, possiamo scrivere: 

        M ⋅(y&&+g)=Fm+Fd  ⎩ ⎨ ⎧ − ⋅ − = ∞ = ⎩ ⎨ ⎧ − ⋅ − = − ⋅ − = ⎩ ⎨ ⎧ = = ) ( ) ( ) ( 0 0 0 0 0 y y B F F y y B F y y k F F F d m d m d m & & & & se se se f f y y y y y y y y − ≤ − < − < − ≥ − ) ( 0 ) ( 0 ) ( 0 0 0  

Spesso  si  trova  un’altra  rappresentazione  del  medesimo  sistema  in  cui  la  grandezza  y  rappresenta, questa volta, la variazione della massa sospesa  rispetto  alla  condizione  di  equilibrio.  Con  questo  nuovo  sistema  di  riferimento l’equazione descrittiva del sistema diventa:   d m F F y M⋅ &&= +   ⎩ ⎨ ⎧ − ⋅ − = ∞ = ⎩ ⎨ ⎧ − ⋅ − = − ⋅ − = ⎩ ⎨ ⎧ = ⋅ − = ) ( ) ( ) ( 0 0 0 0 y y B F F y y B F y y k F F g M F d m d m d m & & & &   se se se p f p p f p y k g M y y y y k g M y y y k g M y y k g M y y − ⋅ + − ≤ − − ⋅ < − < − ⋅ + − − ⋅ ≥ − ) ( ) ( ) ( 0 0 0   Per quanto riguarda la fase di test del controllo si è utilizzato un modello  semplificato  dall’eliminazione  del  precarico.  Tale  condizione  non  è  particolarmente limitativa se si considera che la grandezza   yp

k g M⋅ ₋

 sarà  mantenuta  costante  per  centrare  la  dinamica  dell’ammortizzatore.  Considerazione  analoga  può  essere  fatta  per  quanto  riguarda  il  fondocorsa, la grandezza  k g M y_f + ⋅ −  sarà mantenuta costante (centratura  della dinamica dovuta al precarico) e quindi può essere sostituita con y  f1 costante. In seguito a tali considerazioni si ottengono le seguenti relazioni:   M⋅ &&y =Fm +Fd 

⎩ ⎨ ⎧ − ⋅ − = >> − ⋅ = ⎩ ⎨ ⎧ − ⋅ − = − ⋅ − = ⎩ ⎨ ⎧ = ⋅ − = ) ( ), ( ) ( ) ( 0 0 0 0 0 y y B F k R y y R F y y B F y y k F F g M F d m d m d m & & & &   se se se 1 0 0 1 0 ) ( ) ( ) ( f f y y y k g M y y y k g M y y − ≤ − ⋅ < − < − ⋅ ≥ −   2.3.5 Modello per le sospensioni semi‐attive DOF1  Il modello a un grado di libertà per le sospensioni semi‐attive è identico a  quello  passivo  se  non  per  il  fatto  che  il  coefficiente  B  è  variabile  dal  sistema di controllo, le equazioni rimangono quindi le medesime. 

 

 

2.4  Modello DOF2 

Un modello più completo di quello appena presentato è quello a due gradi  di  libertà,  che  tiene  conto    del  comporatamento  elastico  della  ruota;  esso  consiste nello schematizzare la sospensione come segue: 

  Figura 2.5 Modello half car DOF2 per sospensione semi-attiva.   Con un procedimento analogo a quello presentato per il modello DOF1 si  ottengono le relazioni seguenti:  0 ) ( _{2 1} 2 1 1⋅y −k ⋅ y − y +F +Fd = m &&

 

0 ) ( 2 1 2 2 2⋅y +k ⋅ y −y −Fd = m _&&

 

in cui:  ⎩ ⎨ ⎧ ⋅ + − ⋅ = g m m y y k F ) ( ) ( 1 2 1 0 1

    

( ) / ( ) ) ( / ) ( 0 1 1 2 1 0 1 1 2 1 y y k g m m y y k g m m − < ⋅ + − ≥ ⋅ +

 

) (y2 y1 Cv F_d =− ⋅ _{& − &}

 

F  rappresenta  la  variazione  della  forza  tra  ruota  e  terreno  rispetto  alla 

condizione  di  equilibrio;  Fd  è  la  forza  esercitata  dallo  smorzatore  a  coefficiente  variabile(MRF  damper);  m2  è  la  massa  sospesa,  m1  la  massa  non sospesa, k1 il coefficiente di rigidezza della ruota, k2 il coefficiente di 

rigidezza della sospensione. Come già detto, tale modello è valido sia per  la  sospensione  passiva  con  Cv=costante,  e  per  la  sospensione  semi‐attiva  con Cv=variabile. 

Nelle  figure  seguenti  si  riporta  lo  schema  completo  della  sospensione  sviluppato in ambiente matlab: 

  Figura 2.6 Schema Matlab della sospensione.

  Figura 2.7 Blocco F.

 

In  Figura  2.7  è  mostrato  il  blocco  F  che  rappresenta  la  variazione  della  forza tra ruota e terreno, lo switch finale permette di tener conto delle due  condizioni: ruota in aderenza e distacco dal suolo.    Figura 2.8 Blocco Fd.

 

 

  Figura 2.9 Blocco per la modifica di K2.

 

In Figura 2.9 è mostrato il blocco che tiene conto del fondocorsa, quando 

(

y2 −y1

)

> yf il coefficiente k2 deve essere molto più grosso di quando la 

molla è in condizione normale per tener conto della tamponata, per questa  ragione  viene  moltiplicato  per  1000,  tenendo  conto  delle  caratteristiche  delle  molle  fornite  dal  costruttore.  La  caratteristica  dell’elemento  smorzante nelle sospensioni passive e semi‐attive è riportata nella Figura  2.10. 

  Figura 2.10 Caratteristica dell’elemento smorzante per una sospensione passiva e una

semi-attiva.  

Per i nostri scopi tale caratteristica è stata linearizzata con saturazione. La  Figura  2.11  e  la  Figura  2.12  mostrano  la  caratteristica  linearizzata 

dell’ammortizzatore  nei  casi  di  sospensione  passiva  e  semi‐attiva  rispettivamente.  

  Figura 2.11 Caratteristica lineare della sospensione passiva.  

  Figura 2.12 Caratteristica linearizzata della sospensione semi-attiva.  

In base ai dati disponibili in letteratura si è scelto di avere una sospensione  con le seguenti caratteristiche: 

coefficiente  di  smorzamento  variabile  tra  200  e  3000  [Ns/m]  e  forza  esercitabile dall’ammortizzatore tra ‐6000 e 6000 [N]. 

2.5  Modello lineare 

2.5.1 Modello lineare della sospensione passiva 

Per studiare la problematica del controllo servirà avere un modello lineare  su  cui  studiare  il  problema.  Al  fine  di  ottenere  un  modello  lineare  della  sospensione,  per  prima  cosa,  è  necessario  ricondursi  nella  zona  di  funzionamento  in  cui  le  ruote  sono  attaccate  al  suolo  e  non  si  ha  tamponata.  Questo  significa  che  per  il  modello  ad  un  grado  di  libertà  si  ottiene la seguente equazione del moto: 

 

Figura 2.13 Modello quarter car DOF1 per sospensione passiva.   d m F F y M_{⋅ &&}= +   con ⎩ ⎨ ⎧ − ⋅ − = − ⋅ − = ) ( ) ( 0 0 y y B F y y k F d m & &  

Figura 2.14 Modello quarter car DOF2 per sospensione passiva.  

Per  il  modello  a  due  gradi  di  libertà  si  ottengono  invece  le  seguenti  equazioni del moto:

  

 

0 ) ( 2 1 2 1 1⋅y −k ⋅ y − y +F +Fd = m _&&

 

0 ) ( _{2 1} 2 2 2⋅y +k ⋅ y −y −Fd = m &&

 

in cui:  ) ( 1 y₁ y₀ k F = ⋅ −

 

   

) (y2 y1 Cv F_d =− ⋅ _{& − &}

 

  Per la sospensione passiva è quindi possibile ricavare un modello linerare  a due gradi di libertà.    2.5.2 Modello lineare della sospensione attiva  Consideriamo nuovamente le condizioni di assenza di distacco della ruota  da  terra  e  di  non  raggiungimento  della  tamponata,  questa  volta  per  una  sospensione attiva. La sospensione attiva ad un grado di libertà può essere  schematizzata come segue: 

 

Figura 2.15 Modello quarter car DOF1 per sospensione attiva.  

In cui U è la forza esercitata dall’attuatore attivo. L’equazione del sistema c risulta quindi la seguente: 

) ( ) (y y₀ u t k y m_{⋅ &&}+ ⋅ − = _c

 

Analogamente per il modello a due gradi di libertà si ottiene:   

Figura 2.16 Modello quarter car DOF2 per sospensione attiva.   Quindi anche in questo caso F  è la forza esercitata dall’attuatore attivo e d le equazioni del moto diventano:  0 ) ( 2 1 2 1 1⋅y −k ⋅ y − y +F −Fd = m _&&

 

0 ) ( _{2 1} 2 2 2⋅y +k ⋅ y −y +Fd = m &&

 

) ( 1 y1 y0 k F = ⋅ −

 

 

F_d =u_c(t)

 

d F  questa volta rappresenta la forza esercitata dall’attuatore attivo.  Le grandezze di interesse per ogni sistema risultano le seguenti:    1o _{ord.    2}o _ord. 

Accelerazione Massa Sospesa:  y&&       y&&2 

Tenuta di strada:  k₂⋅(y−y₀)    k₁⋅(y₁ −y₀)  Velocità massa sospesa:  y&       y&2 

Velocità relativa sospensione:  y& −y&0      y& −2 y&1   

Posizione relativa sospensione:  (y−y0)    y2 −y1 

 

2.5.3 Linearità della sospensione semi‐attiva 

La  sospensione  semi‐attiva  è  intrinsecamente  non  lineare,  non  è  infatti  possibile scrivere il sistema nella forma:  u B x A x_&= ⋅ + ⋅  

in  cui  x  è  il  vettore  delle  variabili  di  stato,  mentre  u  è  il  vettore  degli  ingressi.  Nel  caso  di  sospensione  semi  attiva,  infatti,  gli  ingressi  sono  la  strada e il coefficiente di smorzamento, quest’ultimo però compare anche  nella matrice A, il sistema risulta non lineare. E’ importante notare che la  sospensione  semi‐attiva  e  attiva  sono  uguali  almeno  quando  la  sospensione attiva si limita a dissipare energia: 

c

u y y

Cv⋅(&₂ − &₁)=  e k⋅

(

y&−y&0

)

=u_c    se uc⋅

(

y&2 −y&1

)

≤0

 

0 =

Cv

  

e k =0

      

      

se

  

u_c⋅

(

y&₂ −y&₁

)

>0

 

La  sospensione  semi‐attiva  si  comporta  come  una  sospensione  attiva  e  quindi  lineare,  almeno  per  un  certo  periodo  di  funzionamento:  come  si  vedrà  nel  capitolo  successivo  questo  sarà  molto  importante  per  lo  sviluppo di alcuni tipi di controllori.         

2.6 Confronto tra modello lineare DOF1 e DOF2 

Per i fini di questo lavoro si è scelto di utilizzare il modello a due gradi di  libertà  rispetto  a  quello  a  un  solo  grado  di  libertà  poiché  più  completo.  Nonostante questo modello sia utilizzato massicciamente in letteratura, si  trovano anche diversi riferimenti a quello a un grado di libertà: per questa  ragione si è scelto di confrontarli per capire quali siano le differenze tra i 

due.  Poiché  i  controllori  verranno  studiati  sui  sistemi  lineari  (attivi)  per  poi portarli sui non lineari si è deciso di confrontare i due sistemi lineari  DOF1  e  DOF2  per  vedere  come  si  comportano.  I  due  sistemi  possono  essere scritti come segue:  u B x A x_& = ⋅ + ⋅

  (1) 

u D x C y= ⋅ + ⋅

   (2) 

in cui si scelgono come uscite tutte le variabili che vogliamo confrontare e  quindi calcolarne la funzione di trasferimento; per il sistema ad un grado  di libertà si ha:  0 0 0 1 0 0 1 0 1 0 _{U y} m y y y m k y y y & & & & && _⋅ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + ⋅ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⋅ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ₋ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −

       (1) 

0 0 0 0 0 1 0 0 0 0 0 0 0 1 ) ( 0 1 1 0 0 1 0 0 ) ( ) ( ) ( y U m y y y km k y y y y y y y k y & & & & & && ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ₋ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − ⋅

  

(2) 

Mentre per quello DOF2  si ha:  o y U m m y y y y y y m k m k m k y y y y y y & & & && & & && & & ⋅ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − 0 1 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 1 0 1 0 1 2 1 0 1 2 1 2 1 1 1 2 2 2 1 0 1 2 1 2

 (1) 

0 2 1 0 1 2 1 2 1 2 2 1 2 1 2 2 0 1 2 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 y U m y y y y y y k m k y y y y y y y y & & & & & & && ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⋅ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − −

       (2) 

Le  figure  successive  rappresentano  le  funzioni  di  trasferimento  dei  due  sistemi per le diverse grandezze di interesse in funzione dei due ingressi  possibili: la strada e la forza dell’attuatore.  

  Figura 2.17 Funzione trasferimento:accelerazione massa sospesa-forza attuatore.  

  Figura 2.18 Funzione di trasferimento: tenuta di strada-forza attuatore.

  Figura 2.19 Funzione di trasfrimento: velocità massa sospesa-forza attuatore.  

  Figura 2.20 Funzione di trasferimento: compressione sospensione-forza attuatore.

  Figura 2.21 Funzione di trasferimento: velocità sospensione-forza attuatore.  

  Figura 2.22 Funzione di trasferimento: accelerazione massa sospesa-strada.

  Figura 2.23: funzione di trasferimento: Tenuta di strada-strada.

 

  Figura 2.24 Funzione di trasferimento: velocità massa sospesa-strada.

  Figura 2.25 Funzione di trasferimento: compressione sospensione-strada.  

  Figura 2.26 Funzione di trasferimento: velocità relativa sospensione-strada.  

Come si vede dalle figure, il sistema DOF1 è una buona approssimazione  di  quello  DOF2,  per  la  maggior  parte  delle  grandezze,  fino  a  una  frequenza  non  troppo  elevata.  Considerando  che,  in  base  a  dati  sperimentali, generalmente il contenuto spettrale della strada non supera i  100 Hz,  si  capisce  come  utilizzare  il  sistema  a  un  grado  di  libertà  per  progettare  un  controllore  possa  condurre  ugualmente  a  un  risultato  accettabile. Tuttavia, per quanto riguarda gli obbiettivi di questo lavoro, si  è preferito utilizzare il sistema a due gradi di libertà in quanto più preciso  e  allo  stesso  tempo  non  troppo  complesso  dal  punto  di  vista  computazionale.