APPENDICE A La frattalità

APPENDICE A

La frattalità

Introduzione

L'osservazione di molti oggetti naturali, siano essi alberi, foglie, coralli o montagne, ci mostra che questi difficilmente possono essere descritti con gli strumenti della geometria tradizionale.

In altre parole, mentre le ben note figure geometriche quali i triangoli, i rettangoli, i poligoni in genere ed i cerchi, oppure i solidi classici quali piramidi, parallelepipedi, coni, sfere, ecc. sono adatte a descrivere le opere dell’uomo, siano essi palazzi o ponti od oggetti di diverso tipo come imbuti ed altro, male si prestano a rappresentare le forme della natura: una piramide non riproduce fedelmente un monte, al più ne é una sua rappresentazione stilizzata.

Per contro gli oggetti naturali sembrano essere molto irregolari e complessi, e proprio per questo di difficile studio, se non con strumenti molto complicati. Un più attento esame però rivela che questi oggetti sono spesso caratterizzati da evidenti proprietà di auto-similarità su differenti scale. Ad esempio se prendiamo un ramo di un albero, questo è una copia rimpicciolita dell’albero stesso, ed allo stesso tempo è una copia ingrandita di alcune sue parti; così pure se noi guardiamo il profilo di una montagna da lontano esso presenta molte irregolarità che si manifestano simili quando la guardiamo più da vicino: i grossi massi diventano sassolini, ma la struttura è simile [89].

Questi oggetti sono detti frattali.

Nel nostro organismo si trovano diversi esempi di strutture frattali come ad esempio il DNA, i bronchi, i vasi sanguigni ed i neuroni.

In questo lavoro di tesi è stata applicata l’analisi frattale sia alle cellule di Purkinje sia alle reti di neuroni mesencefalici al fine di “misurare” il livello di organizzazione e regolarità.

I frattali

Il termine frattale viene dal latino frangere (rompere) e dall’aggettivo derivato fractus (rotto, ridotto in frammenti). I frattali sono figure geometriche complesse caratterizzate dal ripetersi sino all’infinito di uno stesso motivo su scala sempre più ridotta [90]. Questa è la definizione più intuitiva che si possa dare di figure che in natura si presentano con una frequenza impressionante ma che non hanno ancora una definizione matematica precisa: l’atteggiamento corrente è quello di considerare frattale un insieme F che abbia proprietà simili alle quattro elencate qui di seguito:

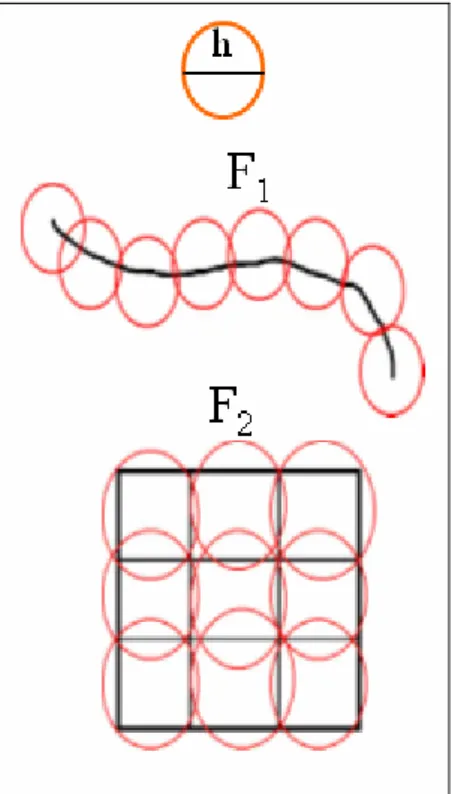
• Autosimilarità: F è unione di un numero di parti che, ingrandite di un certo fattore, riproducono tutto F; in altri termini F è unione di copie di se stesso a scale differenti (Fig. 1)

• Struttura fine: F rivela dettagli ad ogni ingrandimento (Fig. 2)

Figura 2 Successivi ingrandimenti di un oggetto frattale

• Irregolarità: F non si può descrivere come luogo di punti che soddisfano semplici condizioni geometriche o analitiche; la funzione è ricorsiva: F = {Z | Z = f(f(f(...)))}

• Dimensioni di autosimilarità maggiore della dimensione topologica: La caratteristica di queste figure, dalla quale deriva il loro nome, è che, sebbene esse possano essere rappresentate (se non si pretende di rappresentare infinite iterazioni, cioè trasformazioni per le quali si conserva il particolare motivo geometrico) in uno spazio convenzionale a due o tre dimensioni, la loro dimensione non è intera. In effetti la lunghezza di un frattale “piano” non può essere misurata definitamene, ma dipende strettamente dal numero di iterazioni al quale si sottopone la figura iniziale.

È importante tenere presente che, i sistemi naturali, in contrasto con i frattali matematici, sono inevitabilmente finiti e limitati nella scala dalla loro stessa natura. Tali sistemi esprimono le proprietà frattali soltanto in un certo intervallo di scala.

Dimensione frattale

Un parametro importante nell’analisi frattale di strutture biologiche è la dimensione frattale (D), che aumenta di valore all’aumentare della complessità strutturale. D è chiamata frattale perché generalmente non è un intero ed è chiamata dimensione perché fornisce una misura di quanto l’oggetto occupa lo spazio.

In generale un oggetto si dice di dimensione D_t = D_t’; quando ogni punto dell’insieme ha un intorno in F con frontiera di dimensione D_t = (D_t’-1). La dimensione topologica è un numero intero.

Fino agli inizi di questo secolo la geometria ha considerato oggetti per la cui trattazione è sufficiente la definizione classica e intuitiva di dimensione (Dt =

dimensione topologica), già presente almeno implicitamente in Euclide. In questa definizione, data compiutamente da Poincaré, si assegna ad un punto o ad un insieme totalmente sconnesso di punti Dt= 0; per le rette,

induttivamente, la Dt = 1 in quanto possono essere divise da elementi di

Dt = 0 (o meglio, un insieme F ha dimensione 1 se ogni punto ha un intorno in

F arbitrariamente piccolo con frontiera di dimensione zero); e in generale un oggetto si dice di dimensione Dt = Dt’; quando ogni punto dell'insieme ha un

intorno in F con frontiera di dimensione Dt = (Dt’-1). La dimensione

Il concetto di dimensione ha però diverse connotazioni matematiche, in accordo con le seguenti proprietà:

Siano A e B insiemi di punti: 1. A = ℜk ⇒ dim(A) = k

2. A ⊆ B ⇒ dim(A) ≤ dim(B) 3. A ⊆ ℜk (A è aperto) ⇒ dim(A)=k 4. A numerabile ⇒ dim(A) = 0

5. dim(A) non varia se A è sottoposto a rotazioni, traslazioni, cambiamenti di scala (autosimilarità)

6. dim(A∪B) = max{ dim(A), dim(B) }

7. A può essere diviso da una sottoclasse di punti D_t = (D_t’-1). A può essere diviso da una sottoclasse di punti Dt = (Dt’-1).

Considerando l’insieme di Cantor, riportato in Fig. 3, si ha Dt(C) = 0.

Figura 3 L’insieme di Cantor

L’insieme di Cantor è costituito dai punti che “rimangono” sul segmento [0,1] dopo che da questo è stato asportato (prima iterazione, p = 1) il terzo centrale (1/3, 2/3), e da ognuno dei due segmenti risultanti [0, 1/3] e [2/3, 1] è stato asportato il terzo centrale, esclusi gli estremi, e così via per infinite iterazioni. Evidentemente per p→∞ l’insieme C è costituito dagli estremi dei segmenti che si formano ad ogni iterazione ed è quindi costituito da infiniti punti.

La lunghezza dei segmenti asportati, dopo la p-esima iterazione, è data dall’espressione:

( )

( )

( )

∑

che è ovviamente uguale ad 1 per p→ ∞.

Si dimostra così che la lunghezza complessiva dell’insieme di Cantor è zero, e altresì che è costituito da infiniti punti. Quindi la definizione classica di dimensione è assolutamente inefficace. Tale definizione infatti non distingue tra C e l'insieme dei razionali nell'intervallo [0,1]. Per questo B.B.

Mandelbrot, autorevole matematico che ha dato l'impulso allo studio dei

frattali, evidenziò come la dimensione topologica non sia opportuna per le figure frattali.

Interviene quindi la dimensione frattale [90].

Esistono in letteratura diverse definizioni di dimensione frattale, le più comuni sono quella di Kolmogorov-Hausdorff-Besikovicth e quella di

Minkowski-Bouligand.

L’intenzione originaria di Hausdorff era quella di definire un parametro che fosse indipendente dalla risoluzione della misura e che fosse applicabile a tutte le forme. Tale parametro è calcolato coprendo un oggetto con sfere che hanno un raggio decrescente dalla dimensione dell’immagine a zero. Il volume della sfera è pari a eD _{dove e è la risoluzione della misure e D è la}

dimensione frattale. Questa definizione è stata estesa e formalizzata da

Besikovicth.

La dimensione di Hausdorff a volte è molto difficile da calcolare per cui è stata introdotto successivamente da Kolmogorov un parametro D più pratico che è detto dimensione di capacità. La differenza rispetto alla dimensione di Hausdorff-Besikovicth è che in questo caso l’oggetto viene coperto con sfere di raggio identico. La dimensione di Kolmogorov-Hausdorff-Besikovicth può

essere espressa matematicamente nel seguente modo: si misuri un insieme di punti A con un’unità di misura h ogni volta più piccola e si chiami N(h) il minimo numero di figure necessari per coprire per intero la figura (Fig. 4), la capacità di A è data da

( )

(

) ( )

Df =limh→oln /ln 1/

dove Df>DT (DT: dimensione topologica).

Figura 4 Metodo utilizzato per calcolare la dimensione di Kolmogorov-Hausdorff-Besikovicth

La dimensione di Minkowski-Bouligand viene calcolata in modo diverso dalla dimensione di Hausdorff: un cerchio viene fatto scorrere continuamente lungo la linea di contorno dell’oggetto e viene determinata l’area coperta (Fig. 5). Il logaritmo di questo valore poi è graficato in funzione del logaritmo del diametro del cerchio e viene calcolata la pendenza della retta che si ottiene che corrisponde alla dimensione frattale [84].

Figura 5 Metodo utilizzato per calcolare la dimensione di Minkowski-Bouligand

Ritornando all’insieme di Cantor e facendo riferimento alla definizione di dimensione data da Kolmogorov-Hausdorff, si può calcolare D_f(C) prendendo inizialmente un segmento unitario, che, essendo della stessa lunghezza del segmento di partenza, lo copre al meglio; dopo la p = 1, i due segmenti rimanenti sono “misurati” da N(h) = 2 segmenti di h = 1/3; in generale, dopo p iterazioni, N(h) = 2p e h = 3-p. Da questo si ricava che:

D_f(C) = ln 2p / ln 1/3 -p = ln 2 / ln 3 = 0,6309...

Il fatto che la dimensione di C sia 0 < D_f(C) < 1 fa immediatamente capire come l’insieme C non contenga segmenti continui, ma sia costituito da infiniti punti che sono tutti di accumulazione per C stesso [89].

Metodi per determinare la dimensione frattale [89]

La misura della dimensione frattale (D) di un oggetto reale consiste essenzialmente nella ricerca di una relazione tra una certa proprietà (P) dell’oggetto e la risoluzione spaziale con cui l’oggetto è analizzato (r), del tipo P = krf(D), dove k è un fattore costante e f è una funzione lineare in D. Questa relazione può essere riscritta come ln(P) = k’+f(D)ln(r) e quindi il calcolo della dimensione frattale si riduce all’interpolazione lineare dei valori ln(P)−ln(r) in un “intervallo di linearità” delimitato da due valori di “cut-off” della risoluzione (rmin e rmax).

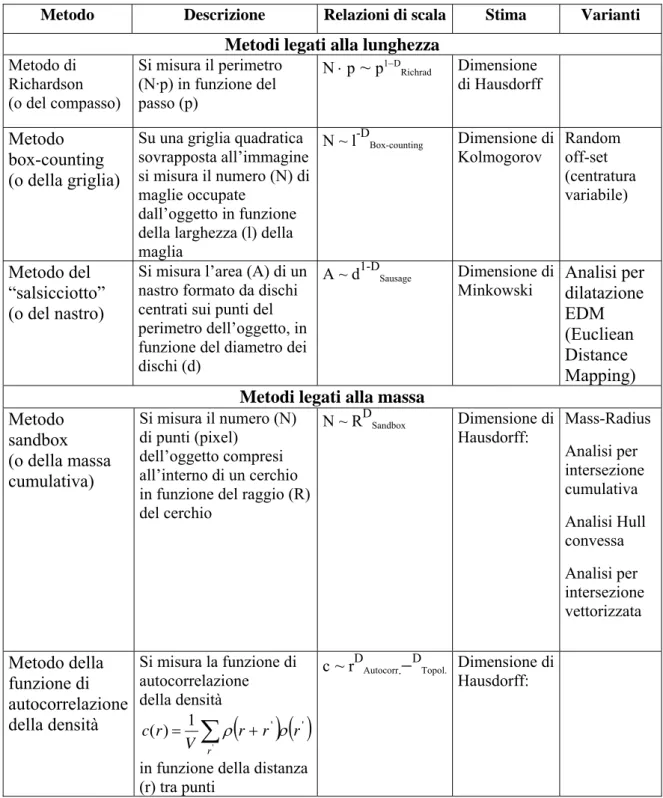
I vari metodi di calcolo della dimensione frattale sono classificabili in due categorie:

1. Con i metodi legati alla lunghezza si analizza il comportamento di scala di proprietà legate all’estensione spaziale (lineare, superficiale o volumetrica), con il singolo pixel dell’immagine digitalizzata dell’oggetto come unità di misura.

2. Nei metodi legati alla massa invece il singolo pixel viene considerato come l’unità di misura della “massa” dell’oggetto e viene analizzato il comportamento di scala di proprietà legate al numero di pixel, ovvero alla ”massa”.

Metodo Descrizione Relazioni di scala Stima Varianti Metodi legati alla lunghezza

Metodo di Richardson (o del compasso) Si misura il perimetro (N·p) in funzione del passo (p) N ⋅ p ~ p1−D Richrad Dimensione di Hausdorff Metodo box-counting (o della griglia)

Su una griglia quadratica sovrapposta all’immagine si misura il numero (N) di maglie occupate

dall’oggetto in funzione della larghezza (l) della maglia N ~ l-DBox-counting Dimensione di Kolmogorov Random off-set (centratura variabile) Metodo del “salsicciotto” (o del nastro)

Si misura l’area (A) di un nastro formato da dischi centrati sui punti del perimetro dell’oggetto, in funzione del diametro dei dischi (d)

A ~ d1-DSausage Dimensione di

Minkowski Analisi per _dilatazione

EDM (Eucliean Distance Mapping)

Metodi legati alla massa

Metodo sandbox (o della massa cumulativa) Si misura il numero (N) di punti (pixel) dell’oggetto compresi all’interno di un cerchio in funzione del raggio (R) del cerchio N ~ RDSandbox Dimensione di Hausdorff: Mass-Radius Analisi per intersezione cumulativa Analisi Hull convessa Analisi per intersezione vettorizzata Metodo della funzione di autocorrelazione della densità Si misura la funzione di autocorrelazione della densità

(

) ( )

∑

in funzione della distanza (r) tra punti

c~ rDAutocorr.−DTopol. Dimensione di

Hausdorff:

I frattali in fisiologia

La geometria frattale si può applicare nel campo biologico-scientifico, un frattale infatti consiste di frammenti geometrici di grandezza ed orientamento variabile, ma con forma simile. Nel corpo umano strutture riconducibili a frattali sono osservabili nei neuroni e nelle fibre nervose, nel muscolo

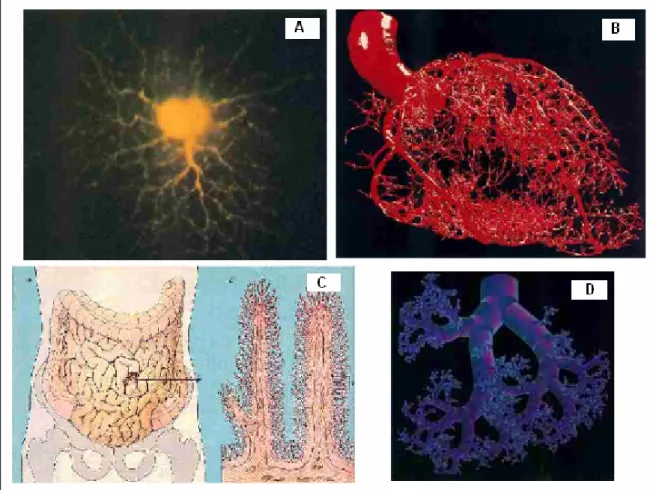
cardiaco, nei vasi sanguigni, nell’intestino e nell’albero bronchiale (Fig. 6).

Figura 6 Strutture biologiche frattali: A. Neurone, B. Vasi sanguigni, C. Intestino, D. Bronchi

Nonostante queste strutture anatomiche di tipo frattale facciano da supporto a funzioni evidentemente diverse in organi differenti, esse hanno in comune tratti strutturali e fisiologici. Ramificazioni o ripiegature frattali amplificano enormemente la superficie disponibile per l’assorbimento (come per

l’intestino), per la distribuzione e la raccolta dei soluti (vasi sanguigni, dotti biliari e albero bronchiale) e per l’elaborazione delle informazioni (reti di neuroni).

La fisiologia sembra uno dei settori più promettenti per lo studio dei frattali e del caos e di altri tipi di dinamiche non lineari. I fisiologi hanno bisogno di sviluppare una migliore comprensione di come i processi di sviluppo possano portare alla formazione di architetture frattali e di come i processi dinamici che si svolgono all’interno del corpo umano generino caos apparente.

Nel prossimo futuro gli studi sui frattali e sul caos applicati alla fisiologia, potranno fornire metodi più sensibili per caratterizzare le disfunzioni dovute a vecchiaia, malattie o sostanze tossiche [91].

L’analisi frattale dei neuroni

L’applicazione dei metodi dell’analisi frattale allo studio della morfologia del neurone risale agli inizi degli anni ’90. Questo studio può essere molto utile per discriminare tra tipi diversi di neuroni.

Caserta ha misurato la dimensione frattale di neuroni della retina in vivo e in

vitro, ottenendo valori che possono “discriminare” tra le due origini (circa

1,67 per i neuroni in vivo e 1,39-1,43 per quelli in vitro) [92]. In un articolo successivo [93] ha poi mostrato che la dimensione frattale può essere utilizzata per classificare tra diverse tipologie fisiologiche di neuroni gangliari della retina. I neuroni analizzati sono stati classificati (in base alla loro risposta a stimolo elettrici) come cellule X, cellule W toniche, cellule W fasiche. Ai neuroni sono state poi applicate svariate tecniche di misura della dimensione frattale, ottenendo vari risultati. Ma in generale le dimensioni frattali medie dei neuroni nelle tre rispettive classi differiscono in maniera

consistente: gli intervalli formati dalle deviazioni standard intorno a queste medie non si sovrappongono quindi la dimensione frattale può essere utilizzata come misura discriminante tra le tre classi.

Una ricerca abbastanza simile a quella di Caserta è stata pubblicata da Jelinek [94]. E’ stata misurata la dimensione frattale di 192 cellule, appartenenti a cinque classi fisiologiche di neuroni gangliari di retina di gatto, mediante tecniche, implementazioni e addirittura operatori differenti. I molteplici risultati mostrano chiaramente l’attitudine alla classificazione dei neuroni (più o meno marcata) dei vari metodi di analisi frattale.

Alves ha invece analizzato 111 cellule di Purkinje, mostrando come la dimensione frattale dendritica (1,68) sia nettamente differente da quella del segmento terminale dell’assone (1,28) [95].

Ancora in riferimento alle cellule di Purkinje, Takeda ha mostrato che la dimensione frattale cresce con la filogenesi: da 1,13 (lampreda) a 1,86 (uomo) [96].

Studi più recenti realizzati da Milošević e Ristanović su neuroni del cordone spinale, hanno dimostrato che l’analisi frattale è in grado di discriminare tra neuroni appartenenti a lamine diverse. Tra i vari metodi applicati quello del

box-counting è risultato il migliore nell’effettuare la classificazione dei

neuroni [97, 98].

Infine Fernandez ha analizzato la possibilità che i neuroni (gangliari di retina) abbiano una struttura multifrattale, siano cioè oggetti con una dimensione frattale che varia da punto a punto [99].