Capitolo 2
Uno degli effetti che si viene a determinare quando una cellula è esposta ad un campo elettrico, è la differenza di potenziale indotta attraverso la membrana cellulare, che prende il nome di TMP (Transmembrane Potential).
La stima del TMP e delle variazioni indotte dai campi elettrici è stata affrontata in tre maniere differenti a seconda della forma della cellula. Il potenziale, infatti, dipende non solo dalla forma, ma anche dalle dimensioni dell’unità biologica e in particolare dalle varie configurazioni che può assumere. In genere gli autori hanno fatto riferimento a poche e semplici forme geometriche.
Per cellule sferoidali la distribuzione del potenziale è stata ottenuta con un approccio di tipo analitico risolvendo semplicemente l’equazione di Laplace [17]. Il modello di cellula usato è quello classico a strati, in cui la membrana non è conduttiva e il suo spessore non è costante. Per questa ragione, il metodo non è accurato per analizzare cellule molto lunghe nelle quali lo spessore della membrana è molto più largo e le correnti conduttrici su questa diventano rilevanti.
Un secondo approccio si serve del modello del cavo con perdite (Leaky cable model) adottato per geometrie cilindriche.
Figura 2.1 Leaky cable model. L’interno (ri) e l’esterno (re)
della cellula sono connessi in parallelo dalla membrana (rm).
Cooper [18] è stato il primo a proporre questo modello (figura 2.1) per descrivere il potenziale indotto in una cellula biologica di lunghezza finita; in seguito quest’idea è stata rivista da altri autori, che hanno introdotto anche l’impedenza della membrana. Questo tipo di approccio ha delle limitazioni; infatti, è usato solo per cellule cilindriche parallele al campo applicato, che risulta essere inoltre imperturbato dalla presenza delle stesse.
Capitolo 2 Infine, per geometrie più complesse sono usate delle tecniche numeriche [19] che tengono conto delle più grandi variazioni della forma della cellula, che in ogni caso ha la stessa composizione generale (membrana, citoplasma e mezzo) utilizzata per i precedenti metodi.
Nelle sezioni successive si presenterà una soluzione analitica per il potenziale di transmembrana.
2.1. Determinazione della tensione di transmembrana
Per determinare la tensione indotta si esprime il campo E in funzione del potenziale elettrico Φ :
Φ −∇ =
E
dove Φ deve soddisfare l’equazione di Laplace ∇2Φ=0, con le seguenti condizioni:
1. Il campo lontano dalla cellula è omogeneo:
(
)
0r
lim −∇Φ =E
∞
→ .
2. Nella cellula il potenziale è limitato: Φ<∞
→0 r
lim
.
3. La continuità del potenziale e la densità di corrente sulla superficie tra il citoplasma e la membrana e tra la membrana e l’esterno vale:
(
Φ −Φ)
=0 i S m i ⇒ nˆ⋅(
σi∇Φi −σmΦm)
Si =0(
Φ −Φ)
=0 e S e m ⇒ nˆ⋅(
σm∇Φm −σeΦe)
Se =0 iS e S sono l’interno e l’esterno della superficie della membrana; e Φ , i Φ , m
e
Φ sono i potenziali rispettivamente nell’interno della cellula, sulla membrana ed infine all’esterno della cellula stessa; σi, σm, σe sono le conducibilità delle tre regioni; nˆ è il vettore normale alla superficie in esame. La tensione di transmembrana ∇Φ indotta dal campo elettrico sulla membrana della cellula è la differenza tra i valori del potenziale elettrico sulle due superfici:
e i S S −Φ Φ = Φ ∇
Nel caso in cui la membrana è non conduttiva esistono delle semplificazioni: nel citoplasma non c’è campo e la variazione di potenziale elettrico si ha solo nella membrana cellulare.
A questo punto si può introdurre il principio d’invarianza che è importante per successive derivazioni.
Per un oggetto con una membrana non conduttiva posto in un campo elettrico omogeneo:
(i) il potenziale elettrico fuori dell’oggetto è determinato solo dalla sua forma; (ii) se tale oggetto presenta una simmetria rispetto al piano nel quale il campo
esterno è perpendicolare, allora anche la tensione transmembranale indotta è determinata dalla sola forma dell’oggetto.
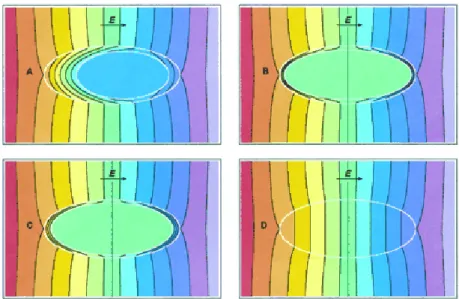
La dimostrazione di tale principio è illustrata in figura 2.2 con un esempio.
Figura 2.2 Principio di invarianza
Si deduce, dalla figura, che in presenza di un campo esterno assegnato, il potenziale fuori della cellula è lo stesso. Per gli oggetti B, C, D, simmetrici rispetto al piano a cui il campo è perpendicolare, il potenziale elettrico all’interno, e quindi la tensione transmembranale, è la stessa. Per l’oggetto D, che è interamente di materiale non conduttivo (la membrana riempie interamente l’oggetto), si definisce la tensione di transmembrana come la differenza tra i valori del potenziale elettrico nel suo centro e quello sulla sua superficie.
Per cellule con simmetria planare e con una membrana non conduttiva, lo spessore della membrana è quindi irrilevante per la tensione transmembranale indotta, che può essere determinata risolvendo l’equazione di Laplace.
Capitolo 2 In figura 2.2, tutti gli oggetti hanno la stessa forma esterna sferoidale (prolate). Con uno spessore di membrana uniforme, l’oggetto B è un modello realistico di cellula, ma la superficie interna della membrana non è uno sferoide prolate e di conseguenza l’equazione di Laplace non può essere risolta analiticamente. Diversamente per C e D, le due superfici sono tutte sferoidi prolate, e quindi per questi due oggetti l’equazione di Laplace si può risolvere in coordinate sferoidali separando le variabili. Ricapitolando, per calcolare la tensione indotta in cellule con simmetria planare e con membrana non conduttiva, sono necessari e sufficienti due requisiti. Il primo implica che la forma della cellula sia modellata tramite coordinate superficiali in un certo sistema di riferimento, tra cui quello sferico e quelli sferoidali prolate ed oblate, mentre il secondo implica che l’equazione di Laplace sia a variabili separate nel sistema di riferimento considerato.
Scrivendo in coordinate sferiche la tensione di transmembrana, si ha:
( )
+ × > − + − − − = = + × < − − − − = ∆Φ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ 2 2 2 2 2 1 2 2 1 2 2 2 2 1 1 2 2 2 1 2 2 1 2 2 2 1 2 1 2 1 2 2 2 2 2 1 2 2 1 1 2 1 2 2 1 2 1 2 2 2 2 2 1 2 2 cos cos log cos 2 3 cos 2 3 cos cos cot R sen R R R R R R R R R R R R R R E R R ER ER R sen R R R R R R R R arc R R R R R E (2.1.1)dove E è il campo elettrico esterno, R1 è il raggio lungo l’asse di simmetria rotazionale (raggio polare), R2 è il raggio equatoriale (perpendicolare a quello polare) ed infine ϕ è l’angolo polare misurato dal centro della cellula rispetto alla direzione del campo elettrico.
Tale equazione è stata implementata con il software Matlab e il grafico risultante è riportato in figura 2.3.
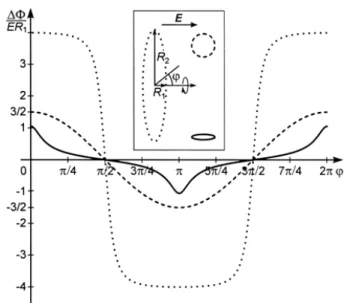
Figura 2.3 Tensione di Transmembrana normalizzata a ER1 in funzione dell’angolo polare
Il grafico mostra la tensione di transmembrana ∆Φ
( )
ϕ , normalizzata rispetto a ER1, in funzione dell’angolo polare ϕ per le tre cellule sferoidali con stesso raggio polareR1 ma differente raggio equatoriale: infatti, per la linea continua si è scelto1 2 1 R5
R = , per quella tratteggiata R2 = R1 ed infine per quella punteggiata
1
2 5 R
R = .
La forma dello sferoide determina non solo il valore massimo di ∇Φ, ma anche la frazione di membrana esposta a più alti valori di potenziale.
Una generalizzazione dell’equazione (2.1.1) è riportata in figura 2.4, che grafica il massimo valore del potenziale, normalizzato a ER1, in funzione del rapporto
1 2 R
R (linea continua); la linea tratteggiata, invece, mostra il grafico di un’ipotetica funzione max
( )
∆Φ = ER2.Per una cellula perfettamente sferica R2 R1=1, il massimo valore di tensione è uguale a 3 2. Tale grafico è stato verificato con il software Matlab.
Capitolo 2
Figura 2.4 Generalizzazione dell’equazione (1)
2.2. Calcolo del potenziale in cellule sferoidali
2.2.1 Cellula Sferica
Consideriamo una cellula di forma sferica posta in un campo elettrico omogeneo. In questa sezione ricaveremo la distribuzione spaziale del potenziale elettrico in un sistema di riferimento sferico
{
(
r,ϕ,ϑ)
∈R3 :r ≥0 ,0≤ϕ ≤π ,0≤ϑ ≤2π}
, le cui coordinate sono così definite:ϕ
cos r
x= , y=r senϕcosϑ, z =r senϕsenϑ. (2.2.1) Per geometrie simmetriche rispetto a x, il potenziale elettricoΦ
(
r,ϕ,ϑ)
è indipendente da ϑ e quindi il potenziale è funzione solo di r e ϕ; è possibile scrivere l’equazione di Laplace nella forma:0 cot 1 2 2 2 2 2 2 2 = ∂ Φ ∂ + ∂ Φ ∂ + ∂ Φ ∂ + ∂ Φ ∂ ϕ ϕ ϕ r g r r r r . (2.2.2)
Il caso più semplice che si può presentare è quello di campo elettrico in uno spazio uniforme.
In questo caso la distribuzione Φ risulta essere lineare e, per un campo elettrico 0 parallelo all’asse x, si può scrivere:
Φ0
( )
r,ϕ =−Ercosϕ. (2.2.3) La situazione è diversa se nel campo s’introduce una sfera, il cui centro è posto nell’origine del sistema di riferimento.Considerando ancora la simmetria rispetto a x e risolvendo rispetto a Φ , separando le variabili si ha:
( )
r ϕ =G( ) ( )
r H ϕ Φ , , (2.2.4) l’equazione (2.2.2) diventa:( )
( )
( )
( )
( )
ϕ( )
ϕ ϕ ϕ H H H r G r G r r G r ′′ + ′ − = ′ + ′′ 2 cot 2 . (2.2.5) Tale uguaglianza si ha solo nel caso in cui le costanti siano uguali.In questo modo si ottengono due equazioni differenziali:
( )
( )
( )
( )
( )
( )
= + ′ + ′′ = − ′ + ′′ 0 cot 0 2 2 ϕ ϕ ϕ ϕ H KH H r KG r G r r G r (2.2.6)Per r >0 la soluzione generale della prima equazione del sistema (2.2.6) è data da:
( )
> + = + − < − − + − − = + + − + − − − − − 4 1 -K 4 1 -K 4 1 K log 2 4 1 cos log 2 4 1 ) 4 1 1 ( 2 1 2 ) 4 1 1 ( 2 1 1 2 1 1 2 1 2 2 1 1 K K C r r C C r C r K r C r K sen r C r G (2.2.7) con C1 e C2 costanti.Lontano dalla sfera il campo è omogeneo e dall’equazione (2.2.3) si deduce che la funzione G
( )
r è proporzionale a r ed è ottenuta da (2.2.7) solo se K =2, e in tal caso:( )
22 1 r C r C r G = + (2.2.8)Capitolo 2 Per K=2, da (2.2.6) H
( )
ϕ assume la seguente forma:( )
( )
− + − + = ϕ ϕ ϕ ϕ ϕ cos 1 cos 1 log cos 1 cos 4 3 C C H , (2.2.9)con C e 3 C4 costanti. La costante C4 si assume nulla, H
( )
ϕ è sempre continua quindi il suo valore in[ ]
0,π diventa:( )
ϕ C3cos( )
ϕH = . (2.2.10)
Unendo le due soluzioni (2.2.8) e (2.2.9), in accordo con (2.2.4) si ottiene:
( )
,ϕ cosϕ 2 cosϕ r B Ar r = + Φ , (2.2.11) con A e B costanti.La distribuzione dentro e fuori una sfera omogenea, non conduttiva ha una forma simile a quella dell’equazione (2.2.11), ma con valori differenti delle costanti A e B:
( )
( )
( )
≤ + = Φ ≤ ≤ + = Φ = Φ r R cos cos , R r 0 cos cos , , 2 2 ϕ ϕ ϕ ϕ ϕ ϕ ϕ r B r A r r B r A r r e e e i i i (2.2.12)Applicando le condizioni di continuità e assumendo che σm =0 si ottengono le varie costanti: E Ai 2 3 − = , Bi =0, E Ae =− , 2 3 ER Be =− . (2.2.13)
Allora la tensione di trasmembrana indotta è l’opposto del potenziale elettrico della superficie esterna:
( )
(
ϕ)
cosϕ 2 3 , ER R r =−Φ = ∆Φ . (2.2.14)Con valori fisiologici di conducibilità, ∆Φ differisce al massimo per diverse parti per
mille dal risultato esatto dato da Kotnik e altri [20]:
(
)
(
)
[
]
(
)(
) (
) (
)(
)
[
]
ϕ σ σ σ σ σ σ σ σ σ σ σ σ cos 2 1 2 3 3 2 3 3 3 3 2 2 ER d R R d R d dR m i m e i m e m i m i e − − − − + + − − + = ∆Φ , (2.2.15)dove σi, σm e σe sono le conducibilità, rispettivamente, del citoplasma, della membrana cellulare e del mezzo esterno e d è lo spessore della membrana.
È da notare che tale equazione si applica solo nel caso in cui lo spessore e la conducibilità della membrana sono costanti; inoltre è facile dimostrare che ponendo
0 =
m
σ l’equazione (2.2.15) si semplifica nella (2.2.14).
2.2.2. Cellula Sferoide “Prolate”
Consideriamo in un campo elettrico omogeneo una cellula “prolate” con il raggio polare parallelo al vettore del campo. In questo caso, la distribuzione di potenziale elettrico è calcolata in un sistema di riferimento
(
)
{
u,v,ϑ ∈R3:u≥0 ,0≤v≤π ,0≤ϑ ≤2π}
, in cui le coordinate sono così definite:v u a
x= cosh cos , y=a senhusenvcosϑ, z=asenhusenv senϑ, (2.2.16) dove a è la distanza tra i fuochi.
Per geometrie simmetriche rispetto a x, come prima, il potenziale è indipendente da ϑ e l’equazione di Laplace è: 0 coth coth 2 2 2 2 = ∂ Φ ∂ + ∂ Φ ∂ + ∂ Φ ∂ + ∂ Φ ∂ v v v u u u . (2.2.17)
La distribuzione del potenziale elettrico in un mezzo uniforme è lineare e per un campo parallelo all’asse x si può esprimere in questo modo:
Capitolo 2
( )
u,v Eacoshucosv0 =−
Φ . (2.2.18) La sfera è descritta dal raggio, mentre esistono due modi equivalenti per caratterizzare lo sferoide prolate. Il primo considera la distanza a tra i fuochi e il valore U che descrive la superficie dello sferoide scegliendo a come u=U . Il secondo, più intuitivo rispetto al primo, considera il raggio polare R1 e il raggio equatoriale R2. Le relazioni che uniscono questi parametri sono:
U a R1 = cosh , R2 =asenhU, (2.2.19) 2 2 2 1 R R a= − , 2 1 2 1 1 2 log arctan R R R R R R h U − + = = . (2.2.20)
Se lo sferoide è immerso nel campo in modo che il suo raggio polare (quello più lungo) sia sull’asse x e il centro sia coincidente con l’origine del sistema di riferimento, con lo stesso procedimento adottato per la cellula sferica, si ottiene un sistema d’equazioni differenziali simile a (2.2.6):
( )
( )
( )
( )
( )
( )
= + ′ + ′′ = − ′ + ′′ 0 cot 0 coth v KH v H v v H u KG u G u u G (2.2.21)Trovando le soluzioni per K = 2 e raggruppando le equazioni trovate, si ottiene:
( )
− + − + = Φ 1 cosh 1 cosh log cosh 1 cos cosh , u u u B v u A r ϕ ; (2.2.22)tale espressione varia a seconda che ci si trovi dentro o fuori la cellula, infatti:
( )
( )
≤ − + − + = Φ ≤ ≤ − + − + = Φ = Φ u U cosv 1 cosh 1 cosh log cosh 1 cos cosh , U u 0 cosv 1 cosh 1 cosh log cosh 1 cos cosh , u u u B v u A v u u u u B v u A v u e e e i i i (2.2.23)(
)
(
U)
senh U U hU E a Ai 2 2 coth log cosh sec − − = , Bi =0, Ea Ae =− ,(
(
)
)
hU U U E a Be csc coth 2 coth log − − = . (2.2.24)Anche in questo caso la tensione di trasmembrana indotta è l’opposto del potenziale elettrico:
( )
( )
(
(
)
)
v U senh U U E a v U v cos 2 coth log cosh , 2 − = Φ − = ∆Φ , (2.2.25)Per poter scrivere l’equazione (2.2.25) come la (2.2.14) trovata per la sfera, è sufficiente esprimere la variabile v in funzione di ϕ, trovando così una relazione biunivoca tra le coordinate utilizzate in questa sezione e quelle sferiche
(
r,ϕ,ϑ)
usate nella precedente:
( )
= a re h r u jϕ ϕ Re arccos , ,( )
= a re h r v jϕ ϕ Im arccos , . (2.2.26) Viceversa, si ha:( )
2 2 cos 2 cosh ,v a u v ur = + , ϕ
( )
u,v =arctan(
coshucosv,senhusenv)
. (2.2.27) Dato cheU
indica la superficie dello sferoide prolate, r si può scrivere così:( )
ϕ ϕ ϕ 2 2 2 2 2 1 2 1 cos R sen R R R r U + = . (2.2.28)Inserendo questa relazione in (2.2.26) e applicando la (2.2.20), dopo qualche calcolo si arriva ad esprimere v in funzione della superficie
U
:( )
ϕ ϕ ϕ ϕ 2 2 2 2 2 1 2 cos cos arccos R sen R R v U + = : (2.2.29)Capitolo 2 la tensione di trasmembrana indotta in uno sferoide prolate formulata in coordinate sferiche ha la seguente espressione:
( )
ϕ ϕ ϕ ϕ 2 2 2 2 2 1 2 2 2 2 2 1 1 2 2 2 1 2 2 1 2 2 2 1 cos cos log R sen R R R R R R R R R R R R E + − + − − − = ∆Φ (2.2.30)2.2.3. Cellula Sferoide “Oblate”
In questo caso per analizzare la distribuzione spaziale del potenziale elettrico in uno sferoide “oblate”, prendiamo in considerazione il seguente sistema di riferimento
(
)
{
w,η,ϑ ∈R3:w≥0 ,0≤η ≤π ,0≤ϑ ≤2π}
, in cui le coordinate sono così definite: ηcos senhw a
x= , y=acoshwsenηcosϑ, z=acoshwsenη senϑ, (2.2.31) dove a è la distanza tra i fuochi.
Il potenziale è indipendente da ϑ se si hanno geometrie simmetriche rispetto all’asse x, e analogamente ai precedenti casi l’equazione di Laplace diventa:
0 cot tanh 2 2 2 2 = ∂ Φ ∂ + ∂ Φ ∂ + ∂ Φ ∂ + ∂ Φ ∂ η η η w w w . (2.2.32) Nel caso più semplice, la distribuzione nello spazio uniforme è lineare e per un campo parallelo all’asse x si ha:
( )
,η cosη0 w =−Easenhw
Φ . (2.2.33)
Lo sferoide oblate, come quello prolate, può essere rappresentato in due modi; il primo considera la distanza a tra i fuochi e la superficie dello sferoide come w = W, l’altro, invece, considera i due raggi R1 e R2, che sono rispettivamente quello polare e quello equatoriale.
Le relazioni sono: asenhW R1 = , R2 =acoshW , (2.2.34) 2 2 2 1 R R a= − , 2 1 2 1 1 2 log arctan R R R R R R h W − + = = . (2.2.35)
Poniamo lo sferoide nel campo in modo che il suo centro coincida con l’origine del sistema di riferimento e che il raggio più piccolo (R1) sia lungo l’asse x. Seguendo un procedimento uguale a quello usato per lo sferoide prolate, si arriva a scrivere
( )
,η = cosη+(
cot(
)
−1)
cosηΦ w Asenhw B senhwarc senhw (2.2.36)
con A e B costanti.
In particolare dentro e fuori lo sferoide si ha:
( )
( )
(
)
(
)
( )
(
)
(
)
≤ − + = Φ ≤ ≤ − + = Φ = Φ w W cos 1 senh cot arc senh cos senh , W w 0 cos 1 senh cot arc senh cos senh , , η η η η η η η w w B w A w w w B w A w w e e e i i i (2.2.37)in cui le costanti sono:
(
senhW)
W senhW arc hW E a Ai − − = 2 cosh cot csc , Bi =0, Ea Ae =− ,(
)
senhW arc hW W E a Be cot sec tanh − − = . (2.2.38)La tensione indotta è pari all’opposto del potenziale elettrico:
( )
η(
η)
(
)
cosη cosh cot , 2 senhW W senhW arc E a W − = Φ − = ∆Φ . (2.2.39)Tenendo conto delle seguenti relazioni:
( )
= a jre h r w ,ϕ Re arccos jϕ ,( )
− = a jre h r ϕ π jϕ η Im arccos 2 , , (2.2.40)Capitolo 2
( )
2 2 cos 2 cosh ,η =a w+ η wr , ϕ
( )
w,η =arctan(
sinhwcosη−coshwsenη)
, (2.2.41) è possibile esprimere la distribuzione del potenziale elettrico in funzione del sistema di riferimento sferico:( )
ϕ ϕ ϕ ϕ 2 2 2 2 2 1 2 1 2 1 2 2 1 2 1 2 2 2 2 2 1 2 2 cos cos cot R sen R R R R R R arc R R R R R E + − − − − = ∆Φ (2.2.42)2.3. Variazione della tensione di transmembrana con
deformazioni elettromeccaniche
La polarizzazione della membrana cellulare produce una forza elettrica che agisce sulla membrana stessa e porta ad una deformazione della cellula nella direzione del campo. Le cellule sferiche sono deformate in sferoidi prolate e quindi potremo analizzare le variazioni della tensione di transmembrana all'allungarsi della cellula. Si può generalizzare lo studio includendo gli sferoidi oblate, ma i risultati non devono modificare quelli ottenuti per le cellule prolate. Le due restrizioni che si possono imporre durante la deformazione sono:
1. Area superficiale della membrana costante, S; tale superficie è pari a:
arcsin 2 4 arcsin 2 2 1 2 1 2 2 2 1 2 1 2 2 2 1 2 2 2 1 2 1 2 1 2 1 2 1 2 2 2 1 2 2 2 1 2 2 > − − + = < − − + = R R R R R R R R R R R R R R R R R R R h R R R R R S π π π
2. Volume cellulare costante, V:
2 2 1 3 4 R R V = π .
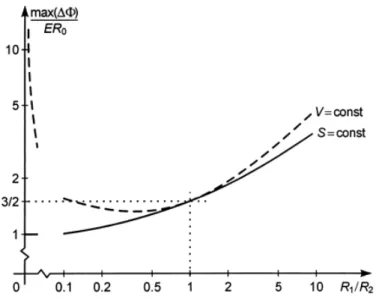
La prima condizione è valida per una membrana non comprimibile e non espandibile, mentre la seconda per membrane non permeabili (per esempio il citoplasma). Non possono coesistere entrambe le condizioni poiché la cellula risulterebbe indeformabile. Ognuna di queste condizioni è una possibile approssimazione della situazione realistica. Per entrambe, il grafico, in figura 2.5, mostra la tensione di transmembrana in funzione del rapporto R1 R2.
Figura 2.5 Funzione di transmembrana in funzione di R1 R2
La figura mostra che i risultati sotto le due condizioni divergono all'aumentare dell'eccentricità della cellula. Ciò nonostante, la deformazione nelle forme molto eccentriche non è stata mai osservata sulle cellule biologiche poiché questo è preceduto dalla rottura della membrana. Ad eccezione di cellule molto eccentriche naturalmente, ovvero i bacilli, le reali deformazioni si hanno nella regione dove i due raggi hanno lo stesso ordine di grandezza. Bisogna tenere a mente, in ogni modo, che la forza elettrica tende ad allungare la cellula nella direzione del campo, e così per le cellule che sono inizialmente sferiche, solo la parte in cui il rapporto tra i raggi è maggiore di uno è d’interesse pratico [21].