CAPITOLO III METODO BEM-RM APPLICATO ALLA TEORIA DELLA DIFFUSIONE DEI NEUTRONI

(1)

CAPITOLO III

METODO BEM-RM APPLICATO ALLA TEORIA DELLA

DIFFUSIONE DEI NEUTRONI

Introduzione al capitolo: l’ applicazione del metodo agli elementi di frontiera (o BEM: Boundary

Element Method) alla teoria della diffusione dei neutroni è stata proposta da Koskinen nel 1965 e poi, nel 1985, da Itagaki.

Si può osservare che il metodo BEM può essere applicato solo a sistemi fisici costituiti da regioni omogenee. Nella diffusione dei neutroni significa che il metodo BEM può essere applicato nel caso di regioni caratterizzate da un insieme di sezioni d’urto costanti spazialmente. Questa non è una condizione di per sé restrittiva per un reattore in quanto è considerato costituito da assembly omogeneizzate, anche se bisogna comunque esaminare un numero elevato di regioni per ottenere una rappresentazione soddisfacente della potenza del core del reattore. A causa di questa difficoltà il metodo BEM è stato dapprima applicato alla teoria della diffusione solo in casi particolari, come per esempio in problemi del riflettore (nel 1976 è stata elaborata la teoria del riflettore di Kalambokas-Henry e poi, più tardi, i problemi del riflettore sono stati trattati in un contesto più generale da Itagaki e Trebbia nel 1991 e poi da Temesvary e Makai nel 1992).

La situazione per il metodo BEM inizia a cambiare con la pubblicazione di due lavori (Dhandhang e altri), nei quali viene presentato un metodo generale per problemi di criticità multigruppo ed in numerose regioni. Ma la tecnica risolutiva adottata (basata sul metodo di Newton direttamente applicato alla matrice globale rappresentante il reattore, allo scopo di determinarne la criticità) risulta eccessivamente onerosa.

Il metodo BEM-RM (RM = Response Matrix o matrice di risposta), che qui viene presentato, prende spunto da un metodo BEM-RM per problemi bidimensionali elaborato presso il Dipartimento di Ingegneria Meccanica, Nucleare e della Produzione della Facoltà di Ingegneria di Pisa (in particolare durante il dottorato di Maurizio Maiani), nel quale il metodo BEM viene combinato con la tecnica della matrice di risposta. Ciò permette di superare o almeno di alleviare le difficoltà sopra esposte.

Nel presente capitolo viene applicato il metodo agli elementi di frontiera al problema stazionario della diffusione dei neutroni. Nel seguito verranno trattati soltanto problemi ad un solo gruppo energetico. Partendo dall’equazione stazionaria della diffusione dei neutroni in una regione omogenea tridimensionale, si ricava la corrispondente equazione integrale di frontiera che caratterizza il metodo. Questa viene poi espressa essa stessa nel formalismo della matrice di risposta, impiegando come dati e come incognite le semi-correnti entranti ed uscenti. Successivamente viene adottato uno sviluppo in polinomi di Legendre definiti sulla frontiera e l’equazione integrale di frontiera viene in tal modo discretizzata. Si ottiene quindi un sistema di equazioni algebriche che, risolto, fornisce, per una data distribuzione delle semi-correnti entranti, le semi-correnti uscenti di neutroni e, se occorre, il flusso neutronico all’interno del dominio.

(2)

1) EQUAZIONE INTEGRALE DI FRONTIERA

Si considera l’equazione stazionaria della diffusione dei neutroni ad un gruppo energetico in una regione tridimensionale omogenea V , delimitata dalla superficie A :

( )

( ) ( )

2 0 . . r a D q V c c

φ

 _∇ _{− Σ} ₊ ₌ _{∀ ∈}   +  r r r r

( )

1 dove: D : coefficiente di diffusione; a

Σ = sezione d’urto di assorbimento macroscopica;

( )

φ

r = flusso neutronico in r ;

( )

q r = sorgente di neutroni in r ;

r: punto appartenente alla regione V .

Si intende riformulare in forma integrale (o in forma debole) il problema individuato dalla

( )

1 e dalle condizioni al contorno e si vuole introdurre una soluzione fondamentale il cui laplaciano è noto. Inoltre ci si propone di trasformare gli integrali volumetrici in integrali superficiali. Nel seguito viene illustrata la procedura che permette di raggiungere questi obiettivi.

Sia

φ

ɶ

( )

r r, ' la soluzione fondamentale dell’equazione

( )

1 . Ossia

φ

ɶ

( )

r r, ' si annulla all’ infinito e soddisfa l’equazione:

D∇2_r

φ

ɶ

( )

r r, ' − Σ_a

φ

ɶ

( ) ( )

r r, ' +

δ

r r, ' =0 ∀r

( )

2

dove:

( )

, '

δ

r r è la delta di Dirac, che rappresenta una sorgente puntiforme ed unitaria posta in 'r (emette un neutrone nell’unità di tempo e di volume).

Quindi

φ

ɶ

( )

r r, ' indica il flusso di neutroni generato in r da una sorgente puntiforme ed unitaria posta in 'r in un mezzo omogeneo infinito. Dunque, come è noto,

φ

ɶ

( )

r r, ' risulta essere espresso dalla relazione:

( )

, ' 1 4 R L e DR

φ

π

− = r r ɶ

( )

3 essendo 2 a D L =

Σ dove L : lunghezza di diffusione ed R= −r r'.

Il problema differenziale individuato dall’equazione

( )

1 e dalle condizioni al contorno viene riformulato con una relazione integrale attraverso le seguenti operazioni:

1) Si sostituisce r ad r nell’equazione '

( )

1 , che viene poi moltiplicata per

φ

ɶ

( )

r r, ' ed integrata rispetto ad r nell’intero volume V : '

(3)

( )

2

( )

( ) ( )

( )

( ) ( )

( )

' , ' ' ' ' _a , ' ' ' ' , ' ' ' ' 0 V V V D dV dV q dV

φ

∇

φ

− Σ

φ

+

φ

=

∫

ɶ r r r r r

∫

ɶ r r r r

∫

ɶ r r r r

( )

4

2) Si prende in considerazione la seconda identità di Green:

2 2 S V g f f g dS f g g f dV n n ∂ ∂  ₋  ₌ _ _{∇ − ∇} _    _∂ _∂   

∫

( )

5.1

dove: f e g sono funzioni di r definite nel dominio V ;

n è la normale esterna ad S ;

S = ∂V è la frontiera di V .

Questa identità viene applicata al primo termine della

( )

4 , assumendo f corrispondente a

φ

ɶ

( )

r r, ' e g corrispondente a

φ

( )

r . Perciò:

( )

_{( ) ( ) ( )}

( ) ( )

_{( ) ( )}

' 2 2 ' ' ' ' ' ' ' ' ' , , ' ' ' ' ' , ' ' ' ' , ' A A A V V A A A A A A A D dV D dV D dA n D dA n

φ

∂ ∇ = ∇ − ∂ ∂ + ∂

∫

r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

5.2 dove: n r

( )

A' è la normale esterna ad A in ' A r , pertanto

( )

' A n ∂

∂ r è la derivata direzionale lungo la

normale esterna ad A in r_A' .

Si considera il primo termine del secondo membro della

( )

5.2 e si sostituisce il termine

( )

2

' , '

D∇_r

φ

ɶ r r con la corrispondente espressione che si ottiene dalla

( )

2 :

( )

( ) (

)

( )

( ) ( )

( )

( ) (

)

( )

( ) ( )

( ) ( ) ( )

2 ' , ' ' ' ' ' , ' ' ' ' ' , ' ' ' ' ' ' ' ' , ' ' ' a V V a A A a A D dV dV dV dV dV c

φ

δ

φ

δ

φ

  ∇ = _Σ − − _ = Σ − − = Σ −

∫

r r r r r r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

5.3

dove, per una nota proprietà della funzione di Dirac,

( ) ( )

(

) ( )

( )

0 se esterno a 1 ' , ' ' ' se * 2 se interno a V V c dV A V V

φ

δ

φ

   = − = ∈ = ∂  

∫

r r r r r r r r r r r r

(4)

in cui per la relazione

( )

* si è assunto che la frontiera sia regolare, priva di punti angolosi. Se

A V

∈ = ∂

r è un punto angoloso, allora risulta

( ) ( )

( )

2

c φ ϑ φ

π

=

r r r dove in problemi

bidimensionali ϑ è l’angolo compreso tra le tangenti destra e sinistra ad A in r . In tre dimensioni

ϑ è l’angolo solido (visto dall’interno) compreso tra le facce che concorrono nel punto (o nel segmento di contorno singolare).

Pertanto l’equazione

( )

5.2 diventa:

( )

( ) ( )

( ) ( ) ( )

( )

( ) ( ) ( )

( ) ( )

2 ' ' ' ' ' ' ' ' ' , ' ' ' ' ' , ' ' ' , ' , ' a V A A A A A A A A A A A D dV dV c D dA D dA n n

φ

∇ = Σ −  _∂ _∂    − − ∂ ∂    

∫

r r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

5.4

Sostituendo la

( )

5.4 nell’equazione

( )

4 si ottiene:

( ) ( )

( )

_{( ) ( ) ( )}

' ' '

( ) ( )

'

_{( ) ( )}

' '

( ) ( )

( )

' ' , ' , ' , ' ' ' ' 0 A A A A A A A A A A V c D dA D dA q dV n n

φ

 ∂

φ

∂ 

φ

− − − + = ∂ ∂   

∫



∫

r r r r r r r r r r r r r r r r ɶ ɶ ɶ

( )

6

Si definisce poi la funzione:

J_n

( )

_A D

( )

_A n

φ

∂ = − ∂ r r

( )

7.1

si tratta della componente normale del vettore corrente nel punto r_A∈A e, corrispondentemente, si definisce la funzione di trasferimento:

(

)

(

)

( )

, , A n A A J D n

φ

∂ = ∂ r r r r r ɶ ɶ

( )

7.2

Pertanto l’equazione

( )

6 diventa:

( ) ( )

( ) ( ) ( )

' ' '

( ) ( ) ( )

' ' '

( ) ( )

( )

, ' , ' , ' ' ' '

n A A A n A A A

A A V

c r φ r +

∫

Jɶ r r φ r dA r +

∫

J r φɶ r r dA r =

∫

φɶ r r q r dV r

( )

8

Nota: esiste un’analogia formale tra la

( )

8 e l’equazione ottenuta nel metodo diretto (equazione

(

28.2

)

del capitolo II). Infatti:

metodo diretto: c

( ) ( )

u q*

( ) ( ) ( )

, u d q

( ) ( ) ( )

u* , d

Γ Γ

= −

_∫

Γ +

_∫

Γ

(5)

eq.

( )

8 :

( ) ( )

( ) ( ) ( )

' ' '

( ) ( ) ( )

' ' '

( ) ( )

( )

, ' , ' , ' ' ' '

n A A A n A A A

A A V

c r φ r +

∫

φɶ r r q r dV r

In conclusione, in corrispondenza di un qualsiasi punto r∈V è soddisfatta la seguente equazione:

( )

( ) ( ) ( )

' ' '

( ) ( ) ( )

' ' '

( ) ( )

( )

, ' , ' , ' ' ' ' n A A A n A A A A A V J dA J dA q dV V φ r +

_∫

ɶ r r φ r r +

_∫

r φɶ r r r =

_∫

φɶ r r r r ∀ ∈r

( )

8.1

la quale lega il flusso in ogni punto interno ai valori del flusso stesso e della corrente netta sulla frontiera.

Ponendo nella

( )

8 r= ∈rA A, si ottiene:

( ) ( )

(

'

) ( ) ( )

' '

( ) (

' '

) ( )

'

(

) ( )

( )

, ' , ' , ' ' ' ' A n A A A A n A A A A A A A A V c r φ r +

∫

φɶ r r q r dV r ∀ ∈r A

( )

8.2

la quale è un’equazione integrale di frontiera.

Fissate le condizioni al contorno, che possono coinvolgere i valori alla frontiera del flusso o della corrente o di entrambe le grandezze, le equazioni sopra riportate permettono di ricavare tutte le incognite. Si supponga, per esempio, che siano noti i valori della corrente normale in tutti i punti della frontiera (J_n

( )

r_A ∀ ∈r_A A), allora tramite la

( )

8.2 si ricava il flusso nei punti di frontiera,

( )

A

φ

r , ed in seguito attraverso la

( )

8.1 si ottiene il flusso nei punti interni del dominio. Occorre osservare che se l’equazione integrale di frontiera venisse risolta senza approssimazioni, allora si otterrebbe la soluzione esatta, ossia il valore esatto del flusso in tutti i punti della regione V .

Se sono presenti regioni omogenee con caratteristiche differenti, allora le

( )

8.1 e

( )

8.2 sono valide in ogni regione omogenea e bisogna imporre la continuità del flusso e della corrente normale nei punti di interfaccia tra due regioni omogenee confinanti.

La tecnica appena presentata è quella utilizzata nei vecchi metodi BEM: essa conduce ad una matrice di grandi dimensioni, la cui inversione può dare origine a problemi o risultare comunque un’operazione complessa. Una possibile alternativa è l’impiego di metodi iterativi, che però possono essere piuttosto pesanti dal punto di vista computazionale, soprattutto in problemi coinvolgenti numerose regioni omogenee. Esiste infine un altro metodo, semplice, che permette di ovviare a queste difficoltà: tale soluzione viene presentata nel paragrafo che segue.

2) EQUAZIONE INTEGRALE DI FRONTIERA IN TERMINI DI SEMI–CORRENTI ENTRANTI ED USCENTI

Si considera l’equazione integrale di frontiera

( )

8.2 ottenuta nel paragrafo precedente:

( ) ( )

(

'

) ( ) ( )

' '

( ) (

' '

) ( )

'

(

) ( )

( )

, ' , ' , ' ' ' ' A n A A A A n A A A A A A A A V c r φ r +

∫

φɶ r r q r dV r ∀ ∈r A

( )

9 Si definiscono le semi-correnti:

( )

1

( )

1

( )

4 2 n A A n A J± r =

φ

r + J r

( )

10

(6)

( )

n A

J+ r è la semi-corrente uscente dalla regione considerata;

( )

n A

J− r è la semi-corrente entrante nella regione considerata.

La convenzione adottata per il segno + o – come apice di J_n± è legata ad n , normale esterna alla frontiera del dominio: se la semi-corrente è nel verso di n (quindi è uscente), ad essa è associato il segno +; viceversa, se la semi-corrente è nel verso opposto di n (perciò è entrante), allora ad essa è associato il segno –. Quindi risulta: φ

( )

A 2 Jn

( )

A Jn

( )

A + −   = _ + _ r r r

( )

10.1 J_n

( )

r_A =_J_n+

( )

r_A −J_n−

( )

r_A _

(

10.2

)

Allo stesso modo si definiscono le funzioni di trasferimento:

(

, '

)

1

(

, '

)

1

(

, '

)

4 2 n A A A A n A A Jɶ± r r = φɶ r r ± Jɶ r r

( )

11 Si introducono le espressioni di

φ

( )

rA , Jn

( )

rA ,

(

)

' , A A

φɶ r r e Jɶ

(

r rA, A'

)

in termini delle semi-correnti

nell’equazione integrale di frontiera

( )

9 e pertanto si ottiene:

( )

(

)

(

)

( )

( ) ( )

( )

(

)

(

) ( )

(

) ( )

( )

' ' ' ' ' ' ' ' ' ' 2 , , 2 ' 2 , , ' , ' ' ' ' A n A n A n A A n A A n A n A A A n A n A n A A n A A A A A V c J J J J J J dA J J J J dA

φ

q dV + − + − + − + − + −      ₊ ₊ ₋ ₊           + _ − _{ } + _ =

∫

r r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ ɶ

_{( )}

12.1

Si esplicitano i vari addendi della

( )

12.1 :

( )

( ) (

) ( )

( ) (

) ( )

( ) (

) ( )

( ) (

) ( )

( ) (

) ( )

( ) (

) ( )

( ) (

) ( )

' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' 2 2 , ' 2 , ' 2 , ' 2 , ' 2 , ' 2 , ' 2 , ' A n A n A n A n A A A n A n A A A A A n A n A A A n A n A A A n A n A A A A A A n A n A A A n A n A A A A A c J J J J dA J J dA J J dA J J dA J J dA J J dA J J dA + − + + + − − + − − + + + − − +  ₊ ₊ ₋   + − + + +

∫

r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ ɶ ɶ ɶ

( ) (

' '

) ( )

'

(

) ( )

( )

2 n A n A, A ' A A, ' ' ' ' A V J− J− dA

φ

q dV − =

∫

r ɶ r r r

∫

ɶ r r r r

(

_12.2

)

Eliminando gli elementi uguali ma di segno opposto e dividendo l’intera equazione per quattro, si ricava:

( ) ( )

_{( ) (}

_{) ( )}

( ) ( )

_{( ) (}

_{) ( )}

(

) ( )

( )

' ' ' ' ' ' , ' 2 1 , ' , ' ' ' ' 2 4 A n A n A n A A A A A n A n A n A A A A A A V c J J J dA c J J J dA

φ

q dV A + + + − − − + = − + + ∀ ∈

∫

r r r r r r r r r r r r r r r r r ɶ ɶ ɶ

( )

13

(7)

Nota la sorgente q r

( )

in tutti i punti della regione V , se si conoscono in tutti i punti della frontiera i valori della semi-corrente entrante nel dominio V attraverso la frontiera A , Jn

( )

A

+

r , allora la

( )

13 fornisce la semi-corrente uscente J_n−

( )

r_A in tutti i punti della frontiera A .

La

( )

13 è equivalente alla

( )

8.2 , ma ha un legame naturale con la tecnica della matrice di risposta. Il fulcro di questa tecnica è la matrice di risposta o Response-Matrix (R-M), che individua la risposta del sistema (o di un suo elemento) in termini di semi-corrente uscente dal sistema (o dall’elemento) ad una sollecitazione che è rappresentata dalla semi-corrente entrante nel sistema (o nell’elemento) stesso. Quindi l’equazione

( )

13 , essendo espressa in termini di semi-correnti entranti ed uscenti, risulta ideale per la determinazione della matrice di risposta del sistema (o di un suo elemento).

3) TRASFORMAZIONE DEGLI INTEGRALI VOLUMETRICI RELATIVI ALLE SORGENTI ESTERNE IN INTEGRALI DI FRONTIERA

La

( )

13 è un’equazione integrale di frontiera espressa in termini di semi-correnti. Spesso il termine di sorgente q r

( )

risulta uguale a zero, quindi nella

( )

13 sono presenti solo integrali superficiali. Tuttavia, soprattutto alle alte energie, q r

( )

è diverso da zero e pertanto nella

( )

13 compare il termine di sorgente, che, essendo espresso attraverso un integrale di dominio, priva il metodo agli elementi di frontiera della sua eleganza e della sua efficacia. Questo inconveniente può essere superato: se infatti la sorgente è individuata da una funzione regolare (o più precisamente poli-armonica), allora il relativo integrale volumetrico può essere trasformato in un integrale di frontiera. Nel presente paragrafo viene mostrato come sia possibile trasformare l’integrale volumetrico di sorgente in un integrale di frontiera.

Si considera il termine di sorgente:

1

( ) ( )

, ' ' '

( )

' oppure

4_V

∫

φ

r r q r dV r ∀ ∈r V ∀ ∈ = ∂r A V

ɶ

( )

₁₄

e si suppone che q r

( )

sia una funzione armonica.

( )

'

,

φ

ɶ r r è la soluzione fondamentale dell’equazione stazionaria della diffusione e quindi soddisfa l’equazione: D∇2r

φ

ɶ

( )

r r, ' − Σa

φ

ɶ

( ) ( )

r r, ' +

δ

r r, ' =0 ∀r

( )

15 Si riscrive la

( )

15 invertendo r ed 'r : D∇2r'

φ

ɶ

( )

r r', − Σa

φ

ɶ

( ) ( )

r r', +

δ

r r', =0 ∀r'

( )

15.1 Poiché

( )

, ' 1 4 R L e DR

φ

π

− = r r ɶ dove 2 a D L =

Σ essendo L lunghezza di diffusione ed

(8)

allora risulta

φ

ɶ

( ) ( )

r r, ' =

φ

ɶ r r', . Inoltre:

δ

( ) ( )

r r', =

δ

r r, ' .

Perciò la

( )

15.1 può essere riscritta nella seguente forma:

D∇2r'

φ

ɶ

( )

r r, ' − Σa

φ

ɶ

( ) ( )

r r, ' +

δ

r r, ' =0 ∀r'

(

15.2

)

quindi, ricavando l’espressione di

φ

ɶ

( )

r r, ' in funzione degli altri termini che compaiono nella

(

15.2

)

, risulta:

( )

, ' 1 2_r_'

( ) ( )

, ' , ' a D φ ₌ _ _∇ φ ₊δ _ Σ r r r r r r ɶ ɶ

(

15.3

)

dove si è supposto Σ ≠_a 0.

Perciò, sostituendo nella

( )

14 l’espressione di φɶ

( )

r r, ' ottenuta, si ricava:

( ) ( )

( )

2

( ) ( )

( )

( ) ( )

( )

' 1 1 , ' ' ' ' , ' ' ' ' , ' ' ' ' 4_Vφ q dV 4 _a _V D rφ q dV _Vδ q dV   =  ∇ +  Σ _ _

∫

ɶ r r r r

∫

ɶ r r r r

∫

r r r r

( )

16

Per la nota proprietà della funzione di Dirac la

( )

16 diventa:

( ) ( )

( )

2

( ) ( )

( ) ( ) ( )

' 1 1 , ' ' ' ' , ' ' ' ' 4V 4 a V r q dV D q dV c q φ =  ∇ φ +  Σ _ _

∫

ɶ r r r r

∫

ɶ r r r r r r

( )

17 dove

( )

0 se 1 se 2 1 se V c A V V ∉    = ∈ = ∂   _∈  r r r r

Si considera la seconda identità di Green:

2 2 S V g f f g dS f g g f dV n n ∂ ∂   _ _ − = _ ∇ − ∇ _  _∂ _∂   

∫

( )

18

dove f e g sono funzioni di r definite nel dominio V , delimitato dalla superficie S ed n è la normale esterna ad S

e si applica tale identità al secondo membro della

( )

17 (si assume φɶ

( )

r r, ' corrispondente a g ,

( )

(9)

( ) ( )

( )

( ) ( )

_{( )}

( )

( ) ( )

_{( ) ( )}

( )

' ' 2 ' ' ' ' ' _' _' 2 ' , , ' ' ' ' ' , ' , ' ' ' ' A A r A A A A V A A A A r V q q dV q dA dA n n q dV

φ

∂ ∂ ∇ = − ∂ ∂ + ∇

∫

r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

19 ossia

( ) ( )

( )

( ) ( ) ( )

( ) ( )

_{( ) ( )}

( )

' 2 ' ' ' ' ' ' _' 2 ' , ' ' ' ' , ' , ' , ' ' ' ' A r A n A A A A V A A A r V q D q dV q J dA D dA n D q dV

φ

∂ ∇ = − ∂ + ∇

∫

r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

20 dove

( )

' ' ' , , A n A A J D n

φ

∂ = ∂ r r r r r ɶ ɶ _.

Pertanto il termine di sorgente

( )

14 assume la seguente forma:

( ) ( )

( ) ( ) ( )

' ' '

( ) ( )

'

_{( ) ( )}

' '

( )

2

( )

' ' 1 , ' , ' , ' ' ' ' 4 A A n A A A A r a A A A V q c q q J dA D dA D q dV n φ φ  _∂   ₊ ₋ ₊ _∇  Σ _

∫

∂

∫

_ r r r r r r r r r r r r r r r ɶ ɶ ɶ

( )

21

La

( )

21 è un’espressione generale valida sempre.

Per ipotesi si è supposto che q r

( )

sia una funzione armonica, quindi ∇2r'q

( )

r' =0, pertanto la

( )

21

diventa:

( ) ( )

( ) ( ) ( )

' ' '

( ) ( )

'

_{( ) ( )}

' ' ' 1 , ' , ' 4 A A n A A A A a A A A q c q q J dA D dA n φ  _∂   ₊ ₋  Σ _

∫

∂ _ r r r r r r r r r r r ɶ ɶ

( )

22

Perciò, nell’ipotesi che q r

( )

sia una funzione armonica e che il mezzo sia assorbitivo (Σ ≠_a 0), ponendo r=r , si può sostituire con l’espressione _A

( )

22 il termine di sorgente presente nell’equazione integrale di frontiera

( )

13 , che quindi risulta costituita solo da integrali di frontiera. E’ possibile estendere il risultato appena ottenuto al caso di una sorgente q r

( )

descritta da una funzione non armonica, ma caratterizzata da una certa regolarità. Si suppone per esempio che sia:

( )

2 ' ' 0 rq ∇ r ≠

( )

4 ' ' 0 rq

∇ r = (per esempio q r

( )

è un polinomio di terzo grado), allora si definisce la funzione q rɶ

( )

tale che:

qɶ

( )

r = ∇2_rq

( )

r

(10)

Inoltre si estende q rɶ

( )

per continuità su tutti i punti del bordo. Allora si considera l’integrale volumetrico presente nella

( )

21 :

( )

, ' 2_r_'

( )

' '

( )

' V q dV φ ∇

∫

ɶ r r r r

( )

23 in cui si introduce q rɶ

( )

:

( ) ( )

, ' ' '

( )

' V q dV φ

∫

ɶ r r ɶ r r

( )

24

La

( )

24 è formalmente uguale alla

( )

14 e quindi è possibile ripetere tutte le operazioni che hanno condotto dalla

( )

14 alla

( )

21 , al termine delle quali la

( )

24 si trasforma nella seguente espressione:

( ) ( )

( ) ( ) ( )

' ' '

( ) ( )

'

_{( ) ( )}

' '

( )

2

( )

' ' 1 , ' , A ' , ' ' ' ' A n A A A A a A A A V q c q q J dA D dA D q dV n φ φ  _∂   ₊ ₋ ₊ _∇  Σ _

∫

∂

∫

r _ r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ ɶ ɶ ɶ

( )

25

che, essendo per ipotesi ∇2rqɶ

( )

r =0, diventa:

( ) ( )

( ) ( ) ( )

' ' '

( ) ( )

'

_{( ) ( )}

' ' ' 1 , ' , A ' A n A A A A a A A A q c q q J dA D dA n φ  _∂   ₊ ₋  Σ _

∫

∂ _ r r r r r r r r r r r ɶ ɶ ɶ ɶ ɶ

( )

26

Perciò, sostituendo l’integrale volumetrico, che compare nella

( )

21 , con l’espressione

( )

26 e ponendo r=r , è possibile rimpiazzare l’integrale volumetrico della _A

( )

13 con questa somma di integrali di frontiera e di termini costanti.

Poiché una qualsiasi funzione regolare q r

( )

può essere approssimata mediante uno sviluppo polinomiale di grado sufficientemente elevato e dal momento che la procedura sopra illustrata può essere ripetuta innumerevoli volte, allora in generale l’integrale volumetrico della sorgente esterna può essere trasformato in una somma di integrali superficiali.

Deve ancora essere esaminato il caso di un mezzo non assorbitivo, per il quale quindi risulta Σ =a 0 Il termine di sorgente è espresso dalla solita formula:

1

( ) ( )

, ' ' '

( )

' oppure

4_V

∫

φ

ɶ r r q r dV r ∀ ∈r V ∀ ∈ = ∂r A V

( )

27

Se Σ =_a 0, allora la soluzione fondamentale dell’equazione stazionaria della diffusione, φɶ

( )

r r, ' , è espressa dalla formula:

(11)

( )

, ' 1 4 DR φ π = r r ɶ dove R= −r r'

( )

28 Si definisce la funzione:

( )

, ' 8 R D ψ π = r r ɶ essendo R= −r r'

( )

29

Il laplaciano di

ψ

ɶ

( )

r r, ' , in coordinate sferiche, è espresso dalla formula:

( )

(

( )

)

2 2 2 1 , ' d R , ' R dR ψ ψ ∇ ɶ r r = ɶ r r Poiché

( )

2 , ' 8 R R D ψ π = r r ɶ , allora

(

( )

, '

)

4 d R R dR ψɶ r r = πD

(

( )

)

2 2 1 , ' 4 d R dR ψɶ r r = πD quindi 2

( )

, ' 1

( )

, ' 4 DR ψ φ π ∇ ɶ r r = = ɶ r r

( )

30

Pertanto il termine di sorgente espresso dalla

( )

27 diventa:

( ) ( )

( )

2

( ) ( )

( )

' 1 1 , ' ' ' ' , ' ' ' ' oppure 4_V

∫

φ

ɶ r r q r dV r =4

∫

_V∇r

ψ

ɶ r r q r dV r ∀ ∈r V ∀ ∈ = ∂r A V

( )

31 (Nota:

ψ

ɶ

( )

r r, ' =

ψ

ɶ

( )

r r', ; ∇2_r

ψ

ɶ

( )

r r, ' = ∇_r2

ψ

_' ɶ

( )

r r, ' ).

La

( )

31 viene riformulata facendo ricorso alla seconda identità di Green (formula

( )

18 ), ottenendo così:

( ) ( )

( )

( ) ( )

_{( )}

( )

( ) ( )

_{( ) ( )}

( )

2 ' ' ' ' ' ' ' 2 ' ' ' 1 , ' ' ' ' 4 , 1 ' , ' , ' ' ' ' 4 V A A A A A A A A A A V q dV q q dA dA D q dV n n

ψ

∇ =  _∂ _∂   ₋ ₊ _∇  ∂ ∂    

∫

r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

32

(12)

Se q r

( )

è una funzione armonica, allora l’integrale volumetrico presente nella

( )

32 è nullo e perciò la procedura termina, poiché il termine di sorgente che compare nella

( )

27 è stato convertito in una somma di integrali di frontiera.

Se q r

( )

non è armonica, ma è una funzione regolare, allora, come già osservato, essa può essere approssimata da uno sviluppo polinomiale di grado sufficientemente elevato. Si supponga, per esempio, che q r

( )

sia espressa da un polinomio di terzo grado, allora ∇4q

( )

r =0. Dunque si definiscono una funzione qɶ

( )

r = ∇2q

( )

r (quindi ∇2qɶ

( )

r =0) ed una funzione

ψ

ɶ( )1

( )

r r, ' , il cui laplaciano coincide con la funzione

ψ

ɶ

( )

r r, ' (quindi ∇2

ψ

ɶ( )1

( )

r r, ' =

ψ

ɶ

( )

r r, ' ). Pertanto, l’integrale volumetrico che compare nella

( )

32 può essere così riscritto:

( )

, ' 2_'

( )

' '

( )

' 2_' ( )1

( ) ( )

, ' ' '

( )

'

V V

q dV q dV

ψ

∇ = ∇

ψ

∫

ɶ r r r r r

∫

r ɶ r r ɶ r r

( )

33

che, attraverso la seconda identità di Green (formula

( )

18 ), viene trasformato in una somma di integrali superficiali e di un integrale volumetrico. Se, come supposto, ∇2qɶ

( )

r =0, allora tale integrale volumetrico è nullo e quindi il procedimento termina, perché l’integrale volumetrico iniziale (formula

( )

27 ) è stato trasformato in una somma di soli integrali di frontiera. Se

( )

2

0

q

∇ ɶ r ≠ (ossia lo sviluppo polinomiale che approssima q r

( )

coinvolge polinomi di grado maggiore di tre), allora si ripete il procedimento appena illustrato fino alla definizione di una funzione qɶ( )p

( )

r il cui laplaciano è nullo.

4) DISCRETIZZAZIONE DELL’EQUAZIONE INTEGRALE DI FRONTIERA ESPRESSA IN TERMINI DI SEMI–CORRENTI MEDIANTE UNO SVILUPPO IN POLINOMI DI LEGENDRE

4.1) Introduzione

Nel presente paragrafo l’equazione integrale di frontiera espressa in termini di semi-correnti entranti ed uscenti viene discretizzata tramite il metodo dei momenti.

Dunque si considera l’equazione integrale di frontiera:

( ) ( )

₍

_{) ( ) ( )}

( ) ( )

₍

_{) ( ) ( )}

' ' ' ' ' ' , ' 2 , ' 2 A n A n A A n A A A A n A n A A n A A q A A c J J J dA c J J J dA V A + + + − − − + = − + + ∀ ∈

∫

r r r r r r r r r r r r r ɶ ɶ

( )

34

dove V è il termine di sorgente ed è individuato da una delle formule ricavate nel paragrafo q 3

)

.

Si introduce una base ortonormale completa di funzioni reali,

{ }

0

l _l

w ∞₌ , definite sulla frontiera A del dominio V . Le semi-correnti entranti ed uscenti vengono espresse in termini di tali funzioni, quindi risulta:

(13)

( )

_,

( )

0 n A n l l A A l J J w A ∞ ± ± = =

∑

∀ ∈ r r r

( )

35 dove n l, n , l n

( ) ( ) ( )

A' l A' ' A' A J± = <J± w > =

∫

J± r w r dA r

(

35.1

)

, n l

J± sono i coefficienti con cui è necessario “pesare” le funzioni w r_l

( )

_A per ottenere le semi-correnti J_n±

( )

r_A . Tali coefficienti vengono determinati attraverso il prodotto scalare delle semi-correnti con le funzioni peso w r_l

( )

_A (equazione

(

35.1

)

).

Allo stesso modo il termine di sorgente q r

( )

A , che compare in V , ed il kernel q

(

)

'

,

n A A

Jɶ± r r vengono proiettati sulle funzioni peso w r_l

( )

_A . Tali sviluppi sono introdotti nell’equazione integrale di frontiera

( )

34 e, attraverso il prodotto scalare dell’equazione ottenuta con un’arbitraria funzione peso della base ortonormale, per esempio w_m

( )

r_A , si ottiene un sistema lineare di infinite equazioni algebriche. Risolvendo tali equazioni, si ricavano le incognite J_n+

( )

r_A in termini di J_n−

( )

r_A e di

( )

A

q r che sono assegnate.

E’ opportuno adottare come funzioni peso w r_l

( )

_A funzioni semplici, come per esempio dei polinomi. Tuttavia bisogna osservare che nei problemi tipici di analisi dei reattori la frontiera del dominio è dotata di spigoli, i quali rappresentano una sorgente di difficoltà nell’applicazione della tecnica BEM. In particolare, in corrispondenza dei punti spigolosi della frontiera, dove la normale esterna alla frontiera non è definita univocamente, la semi-corrente può presentare una discontinuità, che non viene riprodotta in modo adeguato da un’espansione polinomiale in termini di funzioni continue in tutto il dominio di definizione. Un rimedio a tale problema consiste nella suddivisione della frontiera A in elementi As

(

s=1, 2,...,N

)

, tali per cui i punti spigolosi sono

posti alle estremità degli elementi. In questo modo tutti i punti interni di un qualsiasi elemento A _s

sono punti non singolari. In accordo con questo approccio, si definisce per ognuno degli elementi

s

A una base ortonormale completa locale costituita dalle funzioni peso e r_l

( )

_A :

( )

se 1, 2, 3,..., ; 0,1, 2,..., 0 altrimenti l A A s l A w A s N l e = ∈ = = ∞  r r r

quindi s individua l’elemento di frontiera A ; l individua la funzione peso l_s –esima.

Si può osservare che le funzioni e rl

( )

A , sebbene siano state definite come una base ortonormale

locale distinta in ogni elemento A , rappresentano anche un sistema ortonormale nell’intero _s

dominio costituito dalla frontiera A . Infatti le funzioni e rl

( )

A che hanno lo stesso indice s, sono

uguali a zero nei punti esterni ad A e soddisfano la condizione locale di ortonormalità: _s

( ) ( ) ( )

' _' ' ' '

( ) ( ) ( )

' _' ' ' ' _' s sl A sl A A sl A sl A A ll A A e e dA = e e dA =

δ

∫

r r r

∫

r r r

Inoltre il prodotto scalare di due funzioni peso, aventi indici s ed 's diversi tra loro, è uguale a

(14)

_sl

( ) ( ) ( )

_A' _{s l}_{' '} _A' ' _A' 0

A

e e dA =

∫

r r r

Perciò il prodotto scalare definito sull’intera frontiera A tra due funzioni peso e ed _sl e_{s l}_{' '} è uguale ad uno solo se s=s' e l=l', mentre è uguale a zero in tutti gli altri casi, ossia:

' '

( ) ( ) ( )

' ' ' ' ' 1 se ' e ' , ' 0 altrimenti sl s l sl A s l A A A s s l l e e e e dA  = = < > = = 

∫

r r r

Le corrispondenti espansioni per le semi-correnti e per il termine di sorgente sono:

( )

_,

( )

0 1, 2, 3,.., 6 n A n sl sl A A s l J J e A s ∞ ± ± = =

_∑

∀ ∈ = r r r

( )

0 1, 2, 3,.., 6 A sl sl A A s l q q e A s ∞ = =

∑

∀ ∈ = r r r

Nel seguito il metodo appena descritto viene applicato al caso in cui il dominio in esame sia un cubo. Come funzioni peso vengono adottati i polinomi di Legendre normalizzati 1.

4.2) Regione omogenea: cubo. Discretizzazione dell’equazione integrale di frontiera espressa in termini di semi-correnti entranti ed uscenti mediante un’espansione in polinomi di Legendre.

Si considera una regione omogenea la cui frontiera delinea un cubo:

l = lato del cubo

Sono note tutte le caratteristiche fisiche e geometriche della regione omogenea che si intende analizzare.

L’equazione integrale di frontiera che viene discretizzata è la seguente:

( ) ( )

₍

_{) ( ) ( )}

( ) ( )

₍

_{) ( ) ( )}

' ' ' ' ' ' , ' 2 , ' 2 A n A n A A n A A A A n A n A A n A A q A A c J J J dA c J J J dA V A + + + − − − + = − + + ∀ ∈

∫

r r r r r r r r r r r r r ɶ ɶ

( )

36 l

(15)

Nel seguito viene esaminata la

( )

36 , assumendo che il termine q r

( )

A sia costante, ossia

( )

A costante

q r = =q . Perciò, considerando la formula

( )

22 del paragrafo 3

)

, V rq

( )

A risulta essere

dato dalla seguente espressione:

( )

( ) ( )

( ) (

) ( )

(

) ( )

_{( ) ( )}

( )

(

) ( )

(

) ( )

' ' ' ' ' ' ' ' ' ' ' 1 , ' , ' 4 1 , ' , ' 4 A q A A A A n A A A A A A a A A A A n A A A n A A A a A A q V c q q J dA D dA n c q q J dA q J dA

φ

+ −  _∂    = + − Σ _ ∂ _   = _Σ  + −   

∫

r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

37

avendo assunto Σ ≠_a 0 ed avendo sostituito Jɶ_n

(

r r_A, _A'

)

con la corrispondente espressione in termini di Jɶ_n±

(

r r_A, _A'

)

in base alla formula

( )

11 .

Quindi l’equazione integrale di frontiera in esame ha la seguente espressione:

( ) ( )

₍

_{) ( ) ( )}

( ) ( )

₍

_{) ( ) ( )}

( )

(

) ( )

(

) ( )

' ' ' ' ' ' ' ' ' ' , ' 2 , ' 2 1 , ' , ' 4 A n A n A A n A A A A n A n A A n A A A A n A A A n A A A A a A A c J J J dA c J J J dA c q q J dA q J dA A + + + − − − + − + = − +   +  + −  ∀ ∈ Σ _ _

∫

r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ

( )

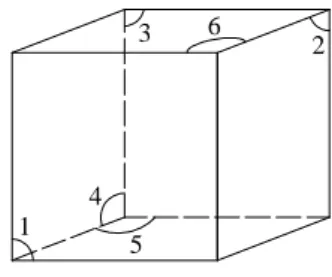
38

La superficie A , frontiera del cubo V , è costituita da sei facce. Si individua ognuna di tali facce con l’indice s=1, 2, 3,.., 6. Quindi nella notazione delle semi-correnti viene introdotto il pedice s, che individua la faccia a cui appartiene il punto r in cui sono valutate le correnti. _A

(Gli archi nella figura 2 servono per individuare in modo univoco le facce.)

Si scompongono gli integrali superficiali su A nella somma degli integrali sulle varie facce e

pertanto la

( )

38 è ricondotta alla seguente equazione:

3 6 ₂

4 5 1

(16)

( )

_{( )}

₍

_{) ( ) ( )}

( )

_{( )}

₍

_{) ( ) ( )}

( )

(

) ( )

(

) ( )

' ' ' ' 6 ' ' ' , , ' , ' ' 1 6 ' ' ' , , ' , ' ' 1 6 6 ' ' ' ' , ' , ' ' 1 ' 1 , ' 2 , ' 2 1 , ' , ' ; 1, 2,... 4 s s s s A n s A n ss A A n s A A s A A n s A n ss A A n s A A s A A n ss A A A n ss A A A A s s a A A c J J J dA c J J J dA c q q J dA q J dA A s + + + = − − − = + − = = + = − +   +  + −  ∀ ∈ = Σ _ _

∑ ∫

∑

∫

∑

∫

r r r r r r r r r r r r r r r r r r r r ɶ ɶ ɶ ɶ , 6

( )

39

Su ogni faccia A della frontiera del cubo si fissa un sistema di riferimento cartesiano locale, con s

l’origine posta al centro della faccia stessa.

Vista dall’alto:

Gli assi delle basi 5 e 6 sono:

3 6 ₂ 4 5 1 3 2 4 1 y 2 x 2 y 3 y 1 3 x 4 x 1 y 4

Gli assi z dei sistemi di riferimento relativi alle facce 1,2,3,4 escono dal piano della pagina

6 5 z₆ 4 2 y₆ x₆ y₅ z₅ x₅

Figura 3: facce del cubo

(17)

(Si noti che, fissato il sistema di riferimento della faccia 1, i sistemi di riferimento delle facce 2,3,4 sono stati definiti attraverso una rotazione del sistema di riferimento della faccia 1. Ciò, come sarà chiaro in seguito, permette di ridurre il numero dei calcoli).

Dunque un generico punto r appartenente ad una qualsiasi delle sei facce del cubo è individuato _A

dalle coordinate

(

x ys, s

)

che possono assumere valori compresi nell’intervallo ,

2 2 l l   −    .

Su ognuna delle sei facce del cubo si definiscono i polinomi di Legendre normalizzati e applicati a variabili che appartengono all’intervallo ,

2 2

l l

 

−

 

 , essendo l la lunghezza del lato del cubo. Tali

polinomi costituiscono una base ortonormale completa locale e quindi è lecito esprimere le semi-correnti entranti ed uscenti definite sulle singole facce attraverso un’espansione in polinomi di Legendre, pertanto:

( )

(

)

1 2 1

( ) ( )

2 1 2 , , , , 0 0 , 1, 2, 3,.., 6 n s A n s s s n s l l l s l s l l J J x y J P x P y s ∞ ∞ ± ± ± = = = =

_∑∑

= r 1 dove:

(

) ( ) ( ) (

)

1 2 1 2 , , , , , 1, 2, 3,.., 6; 1, 2 0,1, 2, 3,..., s n s l l n s s s l s l s s s A J± =

∫

J± x y P x P y dA x y s= l l = ∞ 1 2 , , n s l l

J± : momenti di Legendre delle semi-correnti entranti ed uscenti J_{n s}±_,

( )

r_A =J_{n s}±_,

(

x y_s, _s

)

;

( )

1 , 2

l s l s

P x P y : polinomi di Legendre normalizzati definiti in ; , , 2 2

s s s

l l

A x y ∈ −_ _

 .

Allo stesso modo si espande in polinomi di Legendre normalizzati il Kernel

(

'

)

(

)

, ' , , , , ', ' n ss A A n s s s s s Jɶ± r r =Jɶ± x y x y , perciò:

(

)

(

)

1 2 1 2 1

( ) ( ) ( ) ( )

2 1 2 1 2 1 2 ' , ' , ' ' ' , ', , ' ' ' ' ' ' 0 0 ' 0 ' 0 , , , , n ss A A n ss s s s s n ss l l l l l s l s l s l s l l l l J J x y x y J P x P y P x P y ∞ ∞ ∞ ∞ ± ± ± = = = = = =

_{∑∑ ∑ ∑}

r r ɶ ɶ ɶ , ' 1, 2, 3,.., 6s s = dove:

1_{I polinomi, che vengono qui impiegati, sono polinomi normalizzati e definiti su variabili che appartengono}

all’intervallo , 2 2 l l   −  

 . Quindi sarebbe opportuno individuare ognuno di tali polinomi con la dicitura NPˆl, come

correttamente viene fatto nell’appendice A al presente capitolo. Tuttavia si è preferito utilizzare solo la lettera P

accompagnata dall’indice dell’ordine del polinomio, P , per non rendere eccessivamente pesante la forma delle _l

(18)

(

) ( ) ( ) ( ) ( ) (

) (

)

1 2 1 2 1 2 1 2 ' , ', , ' ' , ' ' ' ' ' ' ' ' ' 1 2 1 2 , , , , ' , 1, 2, 3,.., 6; , , ' , ' 0,1, 2, 3,..., s s n ss l l l l n ss s s s s l s l s l s l s s s s s A A J J x y x y P x P y P x P y dA x y dA x y s l l l l ± ₌ ± = = ∞

∫ ∫

ɶ ɶ

(Si noti che 's individua la faccia di partenza, s la faccia di arrivo.)

Si introducono tali sviluppi nella

( )

39 , che quindi diventa:

(

)

_{( ) ( )}

( ) ( ) ( ) ( )

( ) ( )

(

)

(

)

1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 1 , , 0 0 6 , ', , ' ' ' ' ' ' ' 1 0 0 ' 0 ' 0 , ', ' ' ' ' ' ' ' ' ' 0 ' 0 , , , 2 ' , , 2 s s s n s l l l s l s l l n ss l l l l l s l s l s l s s A l l l l n s m m m s m s s s m m s s n s l c x y J P x P y J P x P y P x P y J P x P y dA x y c x y J ∞ ∞ + = = ∞ ∞ ∞ ∞ + = = = = = ∞ ∞ + = =   +       ×  =   −

∑∑

∑ ∑∑ ∑ ∑

∫

∑ ∑

ɶ

( ) ( )

( ) ( ) ( ) ( )

( ) ( )

(

)

(

)

2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 1 2 0 0 6 , ', , ' ' ' ' ' ' ' 1 0 0 ' 0 ' 0 , ', ' ' ' ' ' ' ' ' ' 0 ' 0 , ', , ' , , 4 4 s l l s l s l l n ss l l l l l s l s l s l s s A l l l l n s m m m s m s s s m m s s n ss l l l a a P x P y J P x P y P x P y J P x P y dA x y c x y q q J ∞ ∞ − = = ∞ ∞ ∞ ∞ − = = = = = ∞ ∞ − = =   +       ×    + + Σ Σ

∑∑

∑ ∑∑ ∑ ∑

_∫

∑ ∑

ɶ ɶ

( ) ( ) ( ) ( )

(

)

( ) ( ) ( ) ( )

(

)

1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 1 2 1 2 1 2 ' 6 ' ' ' ' ' ' ' ' ' 1 0 0 ' 0 ' 0 6 , ', , ' ' ' ' ' ' ' ' ' 1 0 0 ' 0 ' 0 ' , ' , 4 s s l l s l s l s l s s s s _A l l l l n ss l l l l l s l s l s l s s s s l l l l a A P x P y P x P y dA x y q J P x P y P x P y dA x y ∞ ∞ ∞ ∞ + = = = = = ∞ ∞ ∞ ∞ − = = = = =         −   Σ _ _

∑ ∑∑ ∑ ∑

∫

∑ ∑∑ ∑ ∑

∫

ɶ

( )

40

Si considerano separatamente i vari addendi dell’equazione

( )

40 . I simboli di sommatoria ed i polinomi di Legendre in x ed in _s y vengono posti fuori dagli integrali ed è possibile sfruttare _s

l’ortonormalità dei polinomi di Legendre. Pertanto sono valide le seguenti relazioni:

▪ Dal secondo addendo del primo membro della

( )

40 :

( ) ( ) ( ) ( )

( ) ( )

(

)

( ) ( )

1 2 1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 1 , ', , ' ' ' ' ' ' 0 0 ' 0 ' 0 , ', ' ' ' ' ' ' ' ' ' 0 ' 0 , ', , ' ' , ', ' ' ' ' ' ' 2 ' , s n ss l l l l l s l s l s l s l l l l A n s m m m s m s s s m m l l s l s n ss l l l l n s m m l s m s l J P x P y P x P y J P x P y dA x y P x P y J J P x P x ∞ ∞ ∞ ∞ + = = = = ∞ ∞ + = = + + −         ×  =  

∑∑ ∑ ∑

∫

∑ ∑

ɶ ɶ

( ) ( )

2 2 1 2 1 2 1 2 2 2 ' ' ' ' ' ' 0 0 ' 0 ' 0 ' 0 ' 0 2 l s l s m s s l l l l m m l dx P y P y dy ∞ ∞ ∞ ∞ ∞ ∞ = = = = = = −

∑∑

∑ ∑ ∑ ∑

∫

(19)

(

40.1.1

)

In virtù della ortonormalità dei polinomi di Legendre normalizzati:

( ) ( )

1 1 2 1 1 ' ' ' ' ' 1 1 2 1 se ' ' 0 se ' ' l l s m s s l l m P x P x dx l m − =  = ≠ 

∫

( ) ( )

2 2 2 2 2 ' ' ' ' ' 2 2 2 1 se ' ' 0 se ' ' l l s m s s l l m P y P y dy l m − =  = ≠ 

∫

Pertanto la

(

40.1.1

)

diventa:

( ) ( ) ( ) ( )

( ) ( )

(

)

( ) ( )

1 2 1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 1 2 , ', , ' ' ' ' ' ' 0 0 ' 0 ' 0 , ', ' ' ' ' ' ' ' ' , ', , ' ' , ', ' ' ' 0 ' 0 0 ' 0 ' 0 ' , s n ss l l l l l s l s l s l s l l l l A n s m m m s m s s s l s l s n ss l l l l n s l l m m l l l J P x P y P x P y J P x P y dA x y P x P y J J ∞ ∞ ∞ ∞ + = = = = ∞ ∞ ∞ ∞ + + + = = = = =         ×  =  

∑∑ ∑ ∑

∫

∑ ∑

ɶ ɶ 1 0 l ∞ ∞ =

∑∑

(

40.1.2

)

▪ Dal secondo addendo del secondo membro della

( )

40 :

( ) ( ) ( ) ( )

( ) ( )

(

)

1 2 1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 , ', , ' ' ' ' ' ' 0 0 ' 0 ' 0 , ', ' ' ' ' ' ' ' ' ' 0 ' 0 ' , s n ss l l l l l s l s l s l s l l l l A n s m m m s m s s s m m J P x P y P x P y J P x P y dA x y ∞ ∞ ∞ ∞ − = = = = ∞ ∞ − = =         ×   

∑∑ ∑ ∑

∫

∑ ∑

ɶ

(

40.2.1

)

Per la

(

40.2.1

)

sussistono le stesse operazioni valide per la

(

40.1.1

)

, perciò la

(

40.2.1

)

viene ricondotta alla seguente formula:

( ) ( ) ( ) ( )

( ) ( )

(

)

( ) ( )

1 2 1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 1 2 , ', , ' ' ' ' ' ' 0 0 ' 0 ' 0 , ', ' ' ' ' ' ' ' ' , ', , ' ' , ', ' ' ' 0 ' 0 0 ' 0 ' 0 ' , s n ss l l l l l s l s l s l s l l l l A n s m m m s m s s s l s l s n ss l l l l n s l l m m l l l J P x P y P x P y J P x P y dA x y P x P y J J ∞ ∞ ∞ ∞ − = = = = ∞ ∞ ∞ ∞ − − − = = = = =         ×  =  

∑∑ ∑ ∑

∫

∑ ∑

ɶ ɶ 1 0 l ∞ ∞ =

∑∑

(

40.2.2

)

(20)

( ) ( ) ( ) ( )

(

)

( ) ( )

( ) ( ) (

)

1 2 1 2 1 2 1 2 1 2 1 2 ' 1 2 1 2 1 2 1 2 1 2 1 2 _' , ', , ' ' ' ' ' ' ' ' 0 0 ' 0 ' 0 , ', , ' ' ' ' ' ' ' ' 0 0 ' 0 ' 0 ' , ' , s s n ss l l l l l s l s l s l s s s l l l l A n ss l l l l l s l s l s l s s s l l l l A J P x P y P x P y dA x y J P x P y P x P y dA x y ∞ ∞ ∞ ∞ + = = = = ∞ ∞ ∞ ∞ + = = = =   =   

∑∑ ∑ ∑



∫

∑∑ ∑ ∑

∫

ɶ ɶ

(

40.3.1

)

Poiché P x₀

( )

_s P y₀

( )

_s 1 l

= = allora 1=l P x P y₀

( ) ( )

_s ₀ _s , dove l è il lato del cubo. Quindi:

( ) ( ) (

)

( ) ( ) ( ) ( ) (

)

( ) ( )

1 2 1 2 ' ' 1 2 ' ' ' ' ' ' 0 ' 0 ' ' ' ' ' ' ' 2 2 0 ' ' ' ' 0 ' ' ' ' 2 2 ' , ' , s s l s l s s s s s l s l s s s A A l l s l s s s l s s l l P x P y dA x y l P x P y P x P y dA x y l P x P x dx P y P y dy − − = =

∫

In virtù della ortonormalità dei polinomi di Legendre normalizzati:

( ) ( )

1 2 1 0 ' ' ' ' 1 2 1 se ' 0 0 se ' 0 l s l s s l l P x P x dx l − =  = ≠ 

∫

( ) ( )

2 2 2 0 ' ' ' ' 2 2 1 se ' 0 0 se ' 0 l s l s s l l P y P y dy l − =  = ≠ 

∫

Perciò la

(

40.3.1

)

diventa :

( ) ( ) ( ) ( )

(

)

( ) ( )

1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ' , ', , ' ' ' ' ' ' ' ' , ', ,00 0 0 ' 0 ' 0 0 0 ' , s n ss l l l l l s l s l s l s s s n ss l l l s l s l l l l l l A J P x P y P x P y dA x y l J P x P y ∞ ∞ ∞ ∞ ∞ ∞ + + = = = = = =   =   

∑∑ ∑ ∑



∑∑

∫

ɶ ɶ

(

40.3.2

)

▪ Dal quinto addendo del secondo membro della

( )

40 :

( ) ( ) ( ) ( )

(

)

1 2 1 2 1 2 1 2 1 2 1 2 ' , ', , ' ' ' ' ' ' ' ' 0 0 ' 0 ' 0 ' , s n ss l l l l l s l s l s l s s s l l l l A J P x P y P x P y dA x y ∞ ∞ ∞ ∞ − = = = =     

∑∑ ∑ ∑



∫

ɶ

(

40.4.1

)

Per la

(

40.4.1

)

sussistono le stesse operazioni valide per la

(

40.3.1

)

, perciò la

(

40.4.1

)

viene ricondotta alla seguente formula: