4.4.4 Sistema non coibentato

Capitolo 4 – Sistema di accumulo termico

4.4.4 Sistema non coibentato

Al fine di mettere in evidenza l’efficacia del sistema di coibentazione è stata effettuata una simulazione transitoria, relativa ad un raffreddamento notturno della durata di dieci ore, in cui le pareti del sistema di accumulo termico si sono mantenute dimensionalmente le medesime ma strutturalmente costituite da acciaio e quindi con resistenza al trasferimento di calore decisamente minore. L’intervallo temporale coincide con il primo sottointervallo relativo alla simulazione del paragrafo 4.4.2.1 in modo da poter confrontare le due situazioni.

Dall’analisi dei gradienti termici di parete ( figura 4.37 e 4.38 ) risulta evidente il considerevole aumento della temperatura di parete esterna dovuto al prevedibile incremento delle dispersioni termiche.

Figura 4.37 : sistema coibentato – gradiente termico di parete [ T ] = K

Figura 4.38 : sistema non coibentato – gradiente termico di parete [ T ] = K 148

-Capitolo 4 – Sistema di accumulo termico

Considerando le dispersioni termiche attraverso la parete laterale, relative alle due situazioni si ottengono i seguenti risultati :

Qcon_coibente = 0,11 MWt

Qsenza_coibente = 0,31 MWt

Si ha pertanto un aumento del 200% delle dispersioni attraverso la parete laterale.

La mancanza di coibentazione non penalizza il sistema di accumulo soltanto da un punto di vista energetico, ma si ripercuote negativamente anche sulla temperatura di lavoro del guscio metallico. Indicando con TL tale temperatura , che nel caso del sistema non coibentato è

quella relativa ad un punto posto alla stessa distanza dai Sali fusi, rispetto al punto in cui è posto effettivamente il guscio metallico del sistema ciobentato, si ottiene :

TL_con_coibente = 327 °C

TL_senza_coibente = 423 °C

Si nota come il sistema di coibentazione garantisce all’acciaio di trovarsi in un range di temperatura al di sotto del valore critico di 400 °C oltre il quale la resistenza meccanica non è più garantita:

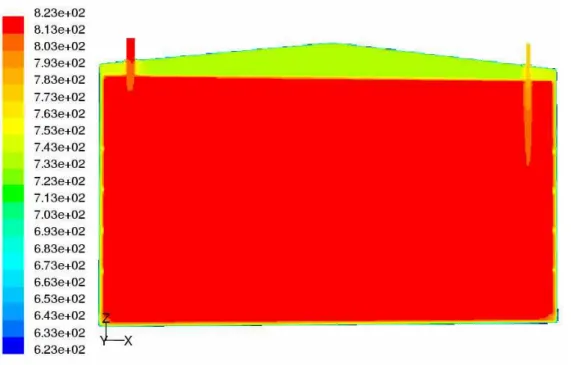
L’analisi del campo di temperatura sul piano di simmetria del sistema ( figure 4.39 e 4.40 ), consente di esporre alcune considerazioni di natura fluidodinamica.

Figura 4.39 : sistema coibentato 149

-Capitolo 4 – Sistema di accumulo termico

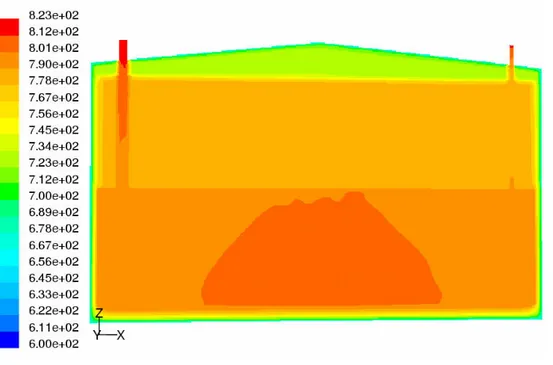
Figura 4.40 : sistema non coibentato

Il bulk dei Sali fusi contenuto dal sistema coibentato presenta un campo di temperatura omogeneo, quello contenuto dal sistema non coibentato presenta una stratificazione termica dovuta al valore più elevato delle dispersioni. In tali condizioni si ha un raffreddamento più pronunciato verso le pareti e conseguentemente la comparsa di un nucleo interno più caldo. La particolare forma della massa calda è dovuta ad una maggiore resistenza termica della fondazione che consente il mantenimento di una maggiore temperatura sul fondo, nasce pertanto una componente di spinta di Archimede che tende a portare il fluido caldo più leggero verso l’alto il quale però tende a raffreddarsi esternamente.

Il fenomeno appena descritto non si verifica per il serbatoio coibentato perché, essendovi minori dispersioni, l’elevata conducibilità termica dei Sali fusi consente al sistema di distribuire omogeneamente la temperatura.