Sistema di interpolazione digitale di fase 2

2

Sistema di interpolazione digitale di fase

Gli anelli ad aggancio di ritardo detti DLL (Delay Locked Loop), costituiscono il blocco fondamentale per la realizzazione di un sintetizzatore digitale di frequenza. In questo capitolo si introducono i concetti generali per la comprensione del funzionamento delle DLL, quindi si procede ad una analisi dettagliata dell’architettura utilizzata in ambito di questo lavoro di tesi.

2.1 Anelli ad aggancio di ritardo (DLL)

Un anello ad aggancio del ritardo è un circuito digitale che riceve in ingresso un segnale periodico ad onda quadra, e produce in uscita un certo numero di repliche di questo segnale sfasate l’una rispetto all’altra di una quantità che è frazione intera del periodo del segnale in ingresso.

Una DLL è composta da un certo numero di celle di ritardo, variabile a seconda dell’architettura utilizzata, e da un circuito di controllo, che consente di compensare le variazioni dei parametri di processo e di mantenere costante lo sfasamento fra le varie repliche prodotte a fronte di variazioni delle condizioni operative. Le celle di ritardo sono solitamente realizzate mediante due inverter posti in cascata, in modo da mantenere inalterata la polarità del segnale. Per rendere possibile il controllo in retroazione, il ritardo introdotto da ciascuno dei due inverter è controllabile tramite un opportuno segnale che può essere una tensione analogica o una parola digitale. In tutte le architetture il circuito di controllo riceve in ingresso due segnali provenienti da due differenti celle di

ritardo, e fa in modo, agendo sui ritardi di tutte le celle, di mantenere costante e pari al valore desiderato, la relazione temporale tra i segnali d’ingresso. In particolare tale circuito è costituito da un rivelatore di fase e dal circuito che effettivamente produce il segnale (digitale o analogico) per il controllo dei ritardi. L’uscita del rivelatore di fase è proporzionale allo sfasamento fra i due segnali d’ingresso, tale informazione è utilizzata dalla logica di controllo per modificare i ritardi delle celle. Normalmente il sistema si trova a regime quando lo sfasamento fra i due segnali d’ingresso al rivelatore di fase è nullo. In tale condizione si dice che la linea di ritardo è agganciata. Ad aggancio effettuato esiste una precisa relazione temporale tra le uscite della linea la quale viene mantenuta nonostante eventuali variazioni di temperatura e tensione di alimentazione che altererebbero pesantemente tale relazione in mancanza del circuito di controllo..

In letteratura si trovano le seguenti architetture di DLL:

• DLL seriali: le celle di ritardo sono connesse serialmente.

• DLL parallele: le celle di ritardo sono connesse parallelamente.

Una DLL seriale è mostrata in Figura 2.1, come si può osservare essa è costituita da N celle di ritardo, tutte identiche tra loro, poste in cascata. Il circuito di controllo riceve in ingresso i segnali IN e OUT ed agisce in modo identico su tutte le celle, dunque quando il sistema è a regime avremo che il ritardo complessivo introdotto dalla linea è pari a T , ossia al periodo del segnale d’ingresso. Per cui _CK

l’uscita i-esima della DLL è una replica del segnale IN sfasata rispetto a tale segnale della quantità:

N T i T CK i = ⋅ ∆ ( 2-1 )

In funzione del valore di N si può ottenere la risoluzione temporale desiderata. La massima risoluzione ottenibile con questa architettura è il minimo ritardo introdotto da una delle celle, il quale dipende dalla tecnologia utilizzata.

Nella Figura 2.2 è visibile la struttura di una DLL di tipo parallelo. Il segnale d’ingresso IN è inviato parallelamente a tutte le N celle di ritardo. In questo caso i ritardi delle varie celle non sono uguali tra loro. In particolare le celle sono dimensionate in modo tale che la i-esima introduca un ritardo pari a:

( )

i T

t_R + −1 ⋅∆ ( 2-2 )

Con i appartenente all’intervallo [1, N]. Avremo quindi che il ritardo passa da t_R, per la cella numero 1 a t_R +

(

N −1

)

⋅∆T, per la cella N.

Figura 2.2 Struttura di una DLL di tipo parallelo.

Le uscite di queste due celle vengono confrontate dal circuito di controllo, pertanto a regime avremo che la differenza fra i ritardi di queste sarà pari a T . _CK

Dunque possiamo concludere che l’uscita i-esima della DLL sarà una replica del segnale IN sfasata della quantità:

( ) ( )

−1 ⋅ −1 + = ∆ N T i t T CK R i ( 2-3 )

Quindi anche in questo caso in funzione del numero di celle N si possono ottenere risoluzioni sufficientemente elevate.

Le prestazioni di un anello ad aggancio del ritardo possono essere valutate in termini di differenze fra la risposta di ritardo ideale e quella reale. Infatti, in generale una DLL consente di creare dei riferimenti temporali e può quindi essere

utilizzata per convertire una parola digitale d’ingresso in un valore temporale (DTC: Digital to Time Converters) o viceversa per convertire un intervallo temporale in una parola digitale (TDC: Time to Digital Converters). Il comportamento di una DLL può essere rappresentato mediante la sua risposta di ritardo (vedi Figura 2.3). In particolare le prestazioni della DLL sono valutate in termini di non linearità differenziale (DNL) e integrale (INL), dove la prima è definita come lo scostamento dell’ampiezza degli intervalli di quantizzazione reali da quelli nominali (LSB), mentre la seconda è definita come la differenza tra i livelli di transizione reali e quelli nominali.

Figura 2.3 Caratteristica di conversione di una DLL.

La Figura 2.3 riporta in termini grafici le definizioni di DNL e INL. Le cause di non linearità sono da attribuire alla mancanza di uniformità dei ritardi generati dalle celle, i quali portano a caratteristiche di conversione differenti da quella ideale. E’ importante a questo punto distinguere fra errori di non linearità sistematici e casuali; definiremo con DNL e INL l’errore di non linearità dovuto a fattori casuali, mentre con SDNL (Systematic Differential No linearity) e SINL (Systematic Integral No linearity) l’errore di non linearità dovuto a cause sistematiche. Bisogna osservare che mentre la SDNL e la SINL sono dipendenti dal tipo di architettura utilizzata, e quindi possono essere ridotte utilizzando strutture maggiormente ottimizzate, la DNL e la INL derivano da fattori casuali e

impredicibili, come il mismatch dei dispositivi, per cui non possono essere eliminate.

Alla luce di quanto detto, cerchiamo di effettuare un confronto fra le due architetture di DLL. Lo svantaggio principale di una architettura di tipo seriale risiede nel fatto che il valore N è limitato dal ritardo minimo t_min ottenibile in una data tecnologia. Infatti tenendo conto che t_min e T sono fissati avremo che il _CK

valore massimo di N risulta essere:

min

t T

N CK

MAX = ( 2-4 )

Una linea di ritardo parallela non presenta questo inconveniente in quanto in esse il quanto temporale che definisce la risoluzione coincide con la differenza tra i ritardi introdotti da due celle successive. Questo comporta che il ritardo di propagazione della singola cella non risulti essere importante. Cerchiamo di capire meglio questo concetto. Nella linea seriale si ha che il ritardo delle singole celle viene a sommarsi, passando dalla cella 1 alla cella N, in modo che a regime il ritardo introdotto fra la prima e l’ultima cella sia uguale a T . Nell’architettura _CK

di tipo parallelo invece si sfrutta il fatto che il ritardo fra una cella e la successiva differisce della quantità

( ) ( )

1 1 − ⋅ − N T

i CK _{, la quale non dipende dal ritardo di} propagazione della singola cella. Abbiamo quindi un sistema completamente indipendente dal ritardo minimo consentito dalla tecnologia, dunque il numero N potrà essere grande quanto si vuole. Per contro una architettura parallela risulta essere difficilmente controllabile in quanto le varie celle sono diverse ed è difficile mantenere la linearità della risposta di ritardo. Questo problema limita l’uso delle DLL parallele come secondo livello d’interpolazione necessario per incrementare la risoluzione rispetto alla linea seriale.

2.2 Celle di ritardo

Abbiamo visto nel paragrafo precedente come una DLL sia sostanzialmente composta da celle con ritardo variabile. Si tratta adesso di andare ad analizzare le possibili implementazioni circuitali di tali elementi.

Figura 2.4 Inverter CMOS con carico capacitivo.

L’elemento utilizzato in ambito digitale per realizzare un ritardo è l’inverter. Risolvendo le equazioni integrodifferenziali di un inverter con un carico capacitivo in uscita (vedi Figura 2.4), si può ricavare l’espressione del ritardo di propagazione sul fronte in salita.

P P ox p P P L R L W C con C K t β µ β = ⋅ = ( 2-5 )

In modo analogo è possibile determinare l’espressione per il ritardo di propagazione del fronte in discesa, la quale risulta essere:

N N ox n N N L F L W C con C K t β µ β = ⋅ = ( 2-6 )

In queste espressioni K è in prima approssimazione un valore costante e identico in entrambe6. Osserviamo nelle due relazioni sopra come i tempi di ritardo dipendano dal valore del carico capacitivo e dal β dei due transitori. Dunque si capisce che per ottenere una variazione del ritardo è possibile agire sui valori di tali parametri. Avremo quindi una distinzione in due architetture:

• Current-starved: La variazione del ritardo è ottenuta agendo sul β dei

transistori.

• Shunt-capacitor: Si agisce sul carico capacitivo visto dall’inverter.

6 _{Il valore di K delle due espressioni è dato da due relazioni identiche a differenza del fatto che nel}

caso del ritardo sul fronte in salita vi compare il valore in modulo della tensione di soglia del transistore PMOS, mentre nel caso di ritardo del fronte in discesa vi compare il modulo della tensione di soglia del NMOS, da cui effettivamente i due K sono identici solo se i moduli delle due tensioni lo sono.

Nei seguenti paragrafi saranno presentati i due tipi di architetture [5]. Ci riferiremo in particolare alle realizzazioni in cui il controllo del ritardo viene effettuato attraverso una parola digitale.

2.2.1 Current-Starved

Lo schema elettrico di una cella di ritardo di tipo current-starved a controllo digitale è mostrato in Figura 2.5.

Figura 2.5 Cella di ritardo di tipo current-starved a controllo digitale.

Si osservi in questo esempio la presenza di 2 transistori centrali, i quali sono nella classica connessione ad inverter, e 10 transistori esterni, di cui due sempre attivi e 8 attivabili mediante un opportuno bit di controllo7_{. Le dimensioni dei transistori}

esterni variano con la potenza del 2 passando dal primo all’ultimo transistore. Nel seguito useremo β e _P β_N per i transistori centrali, e β_PC e β_NC per i transistori posti in parallelo che risultano essere sempre attivi. In particolare in prima approssimazione M transistori in parallelo possono essere ricondotti ad un unico transistore con: M β β β β = ₁ + ₂ +...+ ( 2-7 )

Per quanto riguarda il β di M transistori in serie, questo risulta essere equivalente a: M β β β β 1 ... 1 1 1 2 1 + + + = ( 2-8 )

Applicando queste due relazioni al circuito otteniamo una struttura inverter equivalente con valori di β per il transistore PMOS e per quello NMOS, che valgono rispettivamente:

(

)

[

]

(

)

(

P P

)

P P P P P P P P P P P C C C C TOT N N b b b b b b b b β β β β β β β β β β β β β + + ⋅ + = + + + + + + + + + ⋅ = 0 0 0 0 3 2 1 0 3 2 1 0 8 4 2 8 4 2 ( 2-9 )

(

)

[

]

(

)

(

N N

)

N N N N N N N N N N N C C C C TOT N N b b b b b b b b β β β β β β β β β β β β β + + ⋅ + = + + + + + + + + + ⋅ = 0 0 0 0 3 2 1 0 3 2 1 0 8 4 2 8 4 2 ( 2-10 ) Dove N risulta essere la parola digitale di comando; se chiamiamo n il numero di transistori controllabili in parallelo otteniamo che N è espressa su un numero di bit pari a:

W

n=log₂ ( 2-11 )

Dove con W indichiamo il massimo valore che può assumere N. Se adesso applichiamo alla struttura inverter equivalente le relazioni del ritardo (2-5) e (2-6), otteniamo:

(

)

P P P P P P L P L R C C TOT N N C K C K t β β β β β β β + + ⋅ + ⋅ = ⋅ = 0 0 ( 2-12 )

(

)

N N N N N N L N L F C C TOT N N C K C K t β β β β β β β + + ⋅ + ⋅ = ⋅ = 0 0 ( 2-13 )

Svolgendo ulteriormente i calcoli si ottengono le relazioni seguenti:

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ + ⋅ ⋅ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ + ⋅ + ⋅ ⋅ = N N C K t C C C C P P P P P P P P L R β β β β β β β β 0 0 1 1 ( 2-14 )

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ + ⋅ ⋅ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ + ⋅ + ⋅ ⋅ = N N C K t C C C C N N N N N N N N L F β β β β β β β β 0 0 1 1 ( 2-15 )

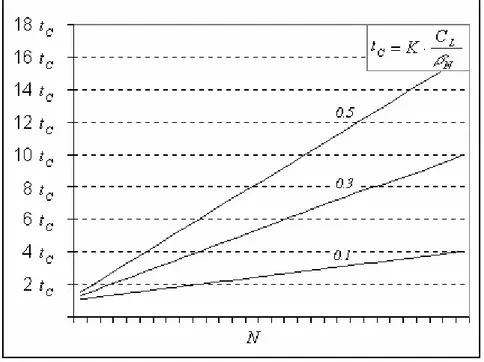
Il valore di N può assumere i valori compresi nell’intervallo [0, W-1]. In particolare l’andamento dei due ritardi sarà funzione del rapporto fra i β dei transistori esterni. Al variare di tale rapporto si ottiene una famiglia di curve, il cui andamento è mostrato in Figura 2.6.

Figura 2.6 Andamento del ritardo sul fronte in discesa in funzione di N e del rapporto fra i β. In figura è visibile l’andamento del ritardo sul fronte in discesa; quello in salita avrà andamento identico ma con valore di t differente. Inoltre in figura abbiamo _C

assunto di variare il rapporto tra i β, mantenendo costante il valore di

C

N

β , altrimenti si avrebbero avute variazioni sul valore di t . _C

E’ importante osservare come il valore massimo del ritardo sul fronte in salita e di quello sul fronte in discesa risultino essere:

P P P P L R C C MAX C K t β β β β + ⋅ ⋅ = ( 2-16 )

N N N N L F C C MAX C K t β β β β + ⋅ ⋅ = ( 2-17 )

I valori minimi, ottenibili per N = W-1, invece risultano essere:

P L R C K t MAX = ⋅β ( 2-18 ) N L F C K t MAX = ⋅β ( 2-19 )

Ovviamente tali valori dipendono dalle dimensioni scelte per i transistori interni ed esterni. Scegliendo opportunamente tali dimensioni, possiamo ottenere intervalli di variazione utili all’applicazione per la quale la cella di ritardo è stata progettata.

Si noti come per valori di N elevati il circuito sia equivalente ad un inverter composto dai due soli transitori centrali.

Figura 2.7 Andamento della differenza di ritardo fra due valori di N consecutivi.

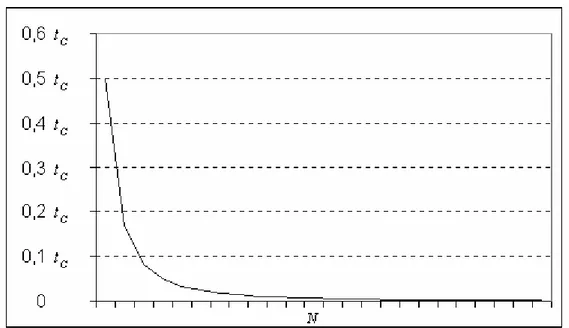
Una delle caratteristiche di questo circuito risiede nel fatto che la risoluzione temporale ottenibile non è costante al variare di N ma risulta avere l’andamento

riportato in Figura 2.7. In altre parole la risposta di ritardo non è lineare e questo può rappresentare un problema in alcune applicazioni. Dal punto di vista della risoluzione temporale il caso peggiore si ha quando N passa da 0 a 1. Otteniamo

Mediante simulazioni è possibile constatare che il comportamento reale della cella rispecchia in modo approssimativo, quello deducibile dal modello analitico. La principale limitazione del modello risiede nella stima del massimo ritardo il quale si discosta notevolmente da quello realmente ottenibile. Il valore del minimo ritardo invece, coincide sia nel caso del sistema teorico che nel caso del sistema reale. Inoltre l’andamento del ritardo in funzione di N è con buona

approssimazione iperbolico, in completo accordo con quanto previsto in modo analitico.

L’uso di un modello teorico permette di tracciare le linee guida per la progettazione di una cella di questo tipo, consentendoci di comprendere su quali parametri agire al fine di ottenere un determinato intervallo di variazione del ritardo. Dal modello si evince che la dimensione dei transistori centrali incide sul minimo ritardo ottenibile, mentre quella dei transistori esterni deve essere scelta in modo da ottenere il valore massimo desiderato.

La risoluzione temporale ottenibile con la cella risulta essere superiore a quella stimata in modo teorico, e il valore esatto può essere determinato solo mediante simulazioni.

2.2.2 Shunt-capacitor

In una architettura di tipo shunt-capacitor si ottiene la variazione del ritardo della cella andando ad agire sul carico capacitivo. Nel particolare caso delle celle di ritardo a controllo digitale dobbiamo utilizzare una struttura capace di far variare il valore della capacità in funzione di una parola di controllo ad n bit. L’elemento

base di tale struttura costituito da un transistore NMOS con drain e source cortocircuitati8, prende il nome di shunt-capacitor.

8 _{L’unico motivo per cui non si utilizzano transistori PMOS, è dovuto al fatto che questi devono}

stare nella n-well, da cui a causa delle regole di layout avremo occupazioni di area superiori rispetto all’uso di transistori NMOS.

Figura 2.8 Struttura di una cella di ritardo a shunt-capacitor.

Un dispositivo di questo tipo si comporta da carico variabile in quanto il valore della capacità presente fra i due terminali, risulta essere funzione della tensione applicata ai due terminali stessi. Quindi variando tali tensioni possiamo ottenere valori di capacità e dunque di ritardo differenti. In Figura 2.8 è mostrato lo schema di una cella di ritardo basta su questa configurazione. Si osservi la connessione di più shunt-capacitor in parallelo, in modo tale da poter ottenere variazioni del ritardo differenti in funzione del numero di elementi attivati. In funzione del terminale che viene utilizzato per effettuare il controllo possiamo ottenere due configurazioni:

• Configurazione a controllo di gate: i terminali di drain e source sono

connessi sull’uscita dell’inverter, mentre il controllo è applicato sul gate.

• Configurazione a controllo drain/source: il terminale di gate è

applicato sull’uscita dell’inverter, mentre il controllo è applicato al terminale drain/source.

Le due configurazioni consentono di ottenere intervalli di variazione della capacità differenti, in quanto a seconda di come viene connesso il dispositivo, il carico visto in uscita risulterà essere diverso.

Prima di addentrarci nell’analisi delle due configurazioni, vediamo qual è l’andamento del ritardo ottenibile in funzione del numero di celle shunt-capacitor attivate. Poiché ciascuna cella introduce una capacità ∆C, avremo che i ritardi sul fronte in salita e su quello in discesa risultano essere:

(

)

[

L n

]

N F C C b b b K t = ⋅ +∆ ⋅ ₀ + ₁+...+ β ( 2-20 )

(

)

[

L n

]

P R C C b b b K t = ⋅ +∆ ⋅ ₀ + ₁+...+ β ( 2-21 )

Elaborando le due espressioni si ottiene:

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ ∆ + ⋅ ⋅ = ∆ ⋅ + ⋅ = N C C C K C N C K t L N L L N F _{β β} 1 ( 2-22 )

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ ∆ + ⋅ ⋅ = ∆ ⋅ + ⋅ = N C C C K C N C K t L P L L P R _{β β} 1 ( 2-23 )

Dove N rappresenta la parola digitale di controllo, espressa in codifica termometrica. Per una maggior chiarezza in Tabella 2 si è riportata la codifica termometrica nel caso di N espressa su 3 bit.

Tabella 2 Codifica termometrica espressa su 3 bit.

N Codifica termometrica

0 000 1 001 2 011 3 111

Dalle relazioni (2-22) e (2-23) si osserva che una volta fissate le dimensioni dei transistor dell’inverter, il ritardo del sistema risulta essere dipendente dal rapporto fra le capacità, in particolare al variare di questo si ottiene una famiglia di curve il cui andamento è mostrato in Figura 2.9. Si noti come il valore minimo del ritardo sia fissato dal valore della capacità C_L, la quale tiene di conto di tutti i contributi capacitivi che non variano in funzione del segnale di comando, da cui sarà comprensiva della capacità dello stadio a valle, e delle capacità parassite degli shunt-capacitor. Per quanto riguarda la minima variazione temporale ottenibile, questa è fissata dal valore ∆C, da cui per i due fronti del segnale avremo:

N F C K T β ∆ ⋅ = ∆ ( 2-24 )

P R C K T β ∆ ⋅ = ∆ ( 2-25 )

Dall’analisi effettuata si evince che i parametri fondamentali di uno shunt-capacitor saranno relativi al valore ∆C che introduce, in quanto da esso dipende la risoluzione del sistema, e al valore delle capacità parassite che aumentando il valore di C_L limitano il minimo ritardo ottenibile. Si tratta adesso di analizzare le due configurazioni ed effettuare un confronto fra queste.

Figura 2.9 Andamento del ritardo sul fronte in discesa al variare del rapporto ∆C/C_L.

Nel seguito daremo per nota la conoscenza del circuito equivalente di ampio segnale di un dispositivo NMOS, rimandando il lettore all’appendice A per maggiori approfondimenti.

2.2.2.1 Configurazione a controllo di gate

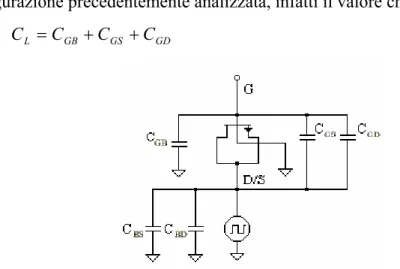
In Figura 2.10 è riportato il circuito elettrico equivalente dello shunt-capacitor, dove sono state messe in evidenza le capacità del dispositivo. Osservando la figura si ricava facilmente il valore della capacità di carico vista dall’uscita dell’inverter: GD GS BD BS L C C C C C = + + + ( 2-26 )

Figura 2.10 Circuito elettrico equivalente dello shunt-capacitor a controllo di gate.

Tale capacità varia in modo non lineare in funzione delle tensioni applicate ai terminali G e D/S, e in funzione della zona di funzionamento del transistore. Innanzitutto osserviamo che il dispositivo non può trovarsi mai in saturazione in quanto la tensione V è sempre nulla, quindi il suo funzionamento è ristretto alla _DS

zona di interdizione e alla zona triodo.

Figura 2.11 Zone di funzionamento del transistore per la configurazione a controllo di gate. In Figura 2.11 è riportata la zona di funzionamento al variare delle tensioni presenti sui due terminali. L’andamento della curva che separa le due zone di funzionamento è in prima approssimazione lineare, in quanto un aumento del potenziale di source e drain tende ad allontanare il dispositivo dalla condizione di inversione, da cui il valore della tensione di gate necessaria alla formazione del canale risulterà aumentato. Se si tiene conto anche dell’effetto body l’andamento della curva è espresso dalla relazione:

S D B S D B t V V V =γ ⋅ 2φ − _/ +2φ + _/ ( 2-27 )

Dove φ rappresenta il potenziale di superficie e γ è il coefficiente di effetto _B body. A seconda del valore della tensione di controllo il punto di lavoro del

dispositivo si sposterà sulla retta A o sulla retta B, alle quali competono valori di capacità differenti, infatti in zona triodo e in zona di interdizione avremo un valore di capacità che vale rispettivamente:

) ( ) ( 2 3 s GD s GS OX BD BS L C C C W L C C C TRIODO = + + ⋅ ⋅ + + ( 2-28 ) ) ( ) ( s GD s GS BD BS L C C C C C _INTERDETTO = + + + ( 2-29 )

In Figura 2.12 è riportato l’andamento della capacità nelle due zone di funzionamento A e B del dispositivo.

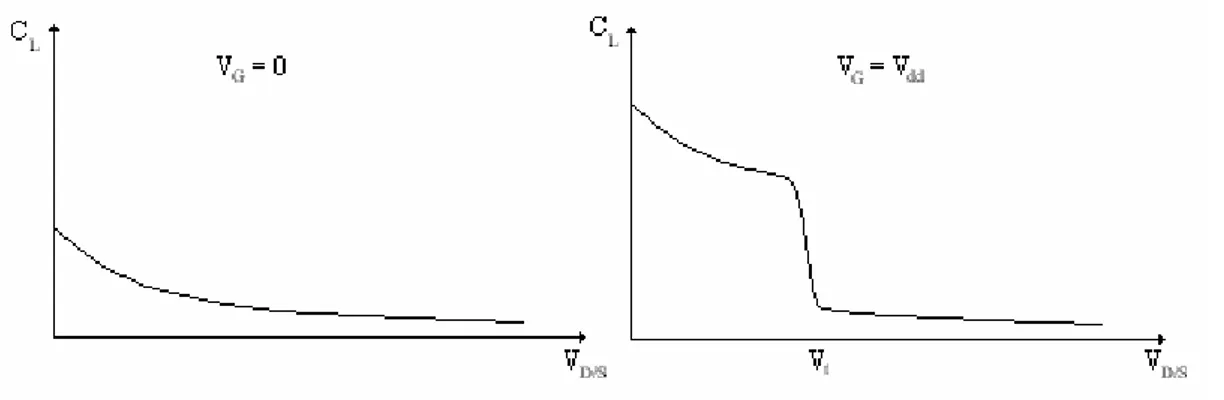
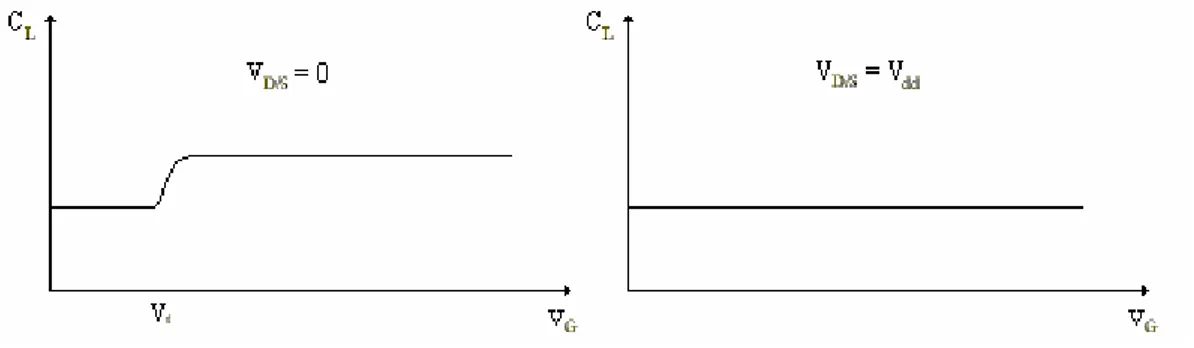
Figura 2.12 Variazione della capacità in funzione della tensione V_D/S.

Si noti come nel caso V_G =0 l’andamento della capacità sia quello classico di una giunzione pn polarizzata in inversa, questo accade in quanto il dispositivo funziona sempre in zona di interdizione, e quindi la capacità di carico che presenta è quella data dall’espressione (2-30). Nel caso V_G =V_dd, abbiamo invece che all’andamento esponenziale si viene a sommare il comportamento dovuto all’attraversamento delle due zone di funzionamento, quindi per valori di

t dd S

D V V

V _/ < − avremo che la capacità è data dalla relazione (2-29), mentre per i valori di V_D/S >V_dd −V_t, la capacità sarà data dalla relazione (2-30). Abbiamo quindi ottenuto un sistema capace di variare il valore della sua capacità in funzione della tensione di gate, ossia siamo riusciti ad ottenere una capacità variabile in modo digitale. Quindi, utilizzando questa configurazione come carico di un inverter, si riesce a variare il ritardo di questo in modo digitale.

2.2.2.2 Configurazione a controllo drain/source

La configurazione a controllo drain/source può essere analizzata in modo analogo a quella a controllo di gate. Come si può osservare in Figura 2.13, il valore della capacità di carico vista dall’inverter risulta essere differente da quello della configurazione precedentemente analizzata, infatti il valore che assume è:

GD GS GB

L C C C

C = + + ( 2-30 )

Figura 2.13 Circuito elettrico equivalente dello shunt-capacitor a controllo drain/source.

Tale capacità varia in funzione delle tensioni applicate ai terminali e della zona di funzionamento del dispositivo, da cui avremo che quando il transistore è in interdizione e quando è in zona triodo assumerà rispettivamente i seguenti valori:

) ( ) ( ) ( 2 3 s GB s GD s GS OX L C W L C C C C _TRIODO = ⋅ ⋅ + + + ( 2-31 ) ) ( ) ( ) ( s GB s GD s GS OX L C W L C C C C _INTERDIZIONE = ⋅ ⋅ + + + ( 2-32 )

In modo analogo a quanto visto nel paragrafo precedente, possiamo andare a valutare le zone di funzionamento del dispositivo in funzione delle tensioni applicate, in modo da poter trarre conclusioni sull’andamento della capacità al variare del segnale di comando (vedi Figura 2.14).

Anche in questo caso la crescita lineare della tensione di soglia è solo una approssimazione del primo ordine, in quanto si è trascurato l’effetto body, dovuto alla differenza di potenziale fra i terminali di source e bulk. Il punto di lavoro del dispositivo si sposterà a seconda del valore della tensione di controllo V_D/S, dalla retta A alla retta B, pertanto avremo un comportamento capacitivo, variabile in funzione di un segnale di controllo digitale, che è quello mostrato in Figura 2.15

Figura 2.15 Variazione della capacità in funzione della tensione V_G.

Quindi anche questa configurazione se utilizzata come carico di un inverter consente di variarne il ritardo in funzione del segnale di comando applicato sul terminale di controllo drain/source.

Pertanto entrambe le configurazioni analizzate possono essere utilizzate per realizzare un carico capacitivo variabile, in modo tale da consentire la variazione del tempo di propagazione dell’inverter che compone la cella di ritardo. Le due configurazioni si distinguono però per il valore del ritardo minimo

min

T introdotto e per il valore ∆T, da cui la scelta fra una delle due ricade sul particolare tipo di applicazione per la quale devono essere utilizzate. Vediamo di mettere in luce tali differenze. La configurazione a controllo di gate presenta un

min

T superiore rispetto a quella con controllo drain/source, in quanto le capacità parassite dovute ai pozzetti di drain e source presentano un valore comparabile con quello della capacità di gate da cui la capacità minima introdotta dal sistema è nettamente superiore a quella dell’altra configurazione. Questo comporta un limite inferiore sul ritardo minimo ottenibile con questa configurazione, ed inoltre tale limite cresce all’aumentare del numero di celle shunt-capacitor connesse in

parallelo9. Per quanto riguarda il valore del ∆T, avremo che risulta essere proporzionale alla variazione di capacità ottenibile passando dalla condizione di carico disattivo a quella di carico attivo. Dunque poiché tale variazione è superiore per la configurazione a controllo di gate otteniamo per questa un ∆T maggiore rispetto a quello ottenibile per la configurazione a controllo drain/source.

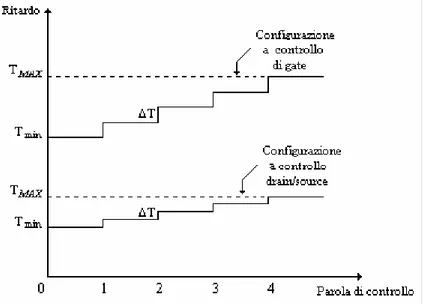
Figura 2.16 Andamento del ritardo della cella in funzione degli shunt-capacitor attivati.

In Figura 2.16 abbiamo effettuato un confronto fra le due configurazioni per un ugual numero di shunt-capacitor nel caso in cui i condensatori controllabili sono delle dimensioni minime consentite dalla tecnologia (massima risoluzione sul controllo). Si noti come la configurazione a controllo drain/source consenta di ottenere valori di T_min più piccoli e risoluzioni temporali maggiori, questo lo si paga con un minore intervallo di variazione del ritardo per questo tipo di cella. Concludendo, se si necessita di un controllo molto fine della variazione del ritardo e tempi di propagazione piccoli, dobbiamo preferire una configurazione a controllo drain/source, se invece si necessita di un ampio intervallo di variazione del ritardo la configurazione da utilizzare è quella a controllo di gate. Si deve osservare comunque che il comportamento del ritardo nei due tipi di approccio

9 _{Il confronto fra le due architetture è basato sulla tecnologia CMOS 0.35 um della AMS, dunque}

dipende fortemente dai valori dei parametri dello specifico processo tecnologico utilizzato.

Mediante simulazioni si può constatare che il comportamento della cella di ritardo rispecchia fedelmente il modello teorico, infatti l’andamento del ritardo risulta essere lineare al variare del carico capacitivo. Inoltre il confronto fra le due configurazioni, stimato a livello teorico e mostrato in Figura 2.16, trova completa conferma nei risultati delle simulazioni.

Infine bisogna osservare che a causa della variazione della capacità al variare della tensione di uscita dell’inverter avremo un comportamento sui fronti in salita diverso rispetto a quello sui fronti in discesa. Tuttavia grazie al fatto che una cella di ritardo è composta da due inverter regolabili in cascata questo effetto è eliminato e quindi entrambi i fronti del segnale risultano essere ritardati della medesima quantità.

2.3 Sistema a due livelli di interpolazione

L’architettura utilizzata in ambito di questa tesi per la realizzazione dell’interpolazione digitale di fase prevede l’uso di un sistema a due livelli di interpolazione.

Figura 2.17 Schema a blocchi dl sistema a due livelli d’interpolazione.

Il primo livello di interpolazione è costituito da una DLL di tipo seriale mentre il secondo da una DLL innovativa la cui struttura può essere ricondotta a quella di tipo parallelo. La Figura 2.17 mostra lo schema a blocchi semplificato del sistema.

La DLL di tipo seriale consente di ottenere _{2 repliche del segnale di clock CK,} n sfasate fra loro della quantità:

n CK S T T 2 = ∆ ( 2-33 )

Tali repliche possono essere selezionate mediante un multiplexer, il quale in funzione della parola di controllo al suo ingresso selezionerà una sola di queste. Due uscite consecutive della DLL seriale sono inviate in ingresso al secondo livello d’interpolazione, il quale suddivide l’intervallo temporale del quale sono sfasate in ulteriori _{2 intervalli. In funzione della parola digitale di controllo al} m suo ingresso questo introduce un ritardo pari a:

m n CK m S P T j t T j t T = + ⋅∆ = + ⋅ ₊ ∆ 2 2 0 0 ( 2-34 )

con j appartenente all’intervallo [0, 2m −1_{]. La Figura 2.18 mostra la suddivisone} del periodo di clock ottenibile con questo sistema (per semplicità di rappresentazione si è considerato il caso di n = 2 e m = 5).

Figura 2.18 Frazionamento del clock in sottointervalli mediante due livelli di interpolazione. Per analizzare il funzionamento del sistema supponiamo che il fronte del segnale MSB (che vogliamo ritardare in modo controllato) si presenti in ingresso al DTC senza alcuno sfasamento temporale rispetto al segnale CK. In funzione dei segnali di comando avremo selezionato la i-esima uscita della DLL seriale, per cui il segnale MSB verrà campionato con un clock che presenta uno sfasamento rispetto al segnale CK pari a: n CK S T i T_i 2 ⋅ = ∆ ( 2-35 )

Pertanto il segnale in uscita dal primo flip-flop sarà ritardato della medesima quantità. Si è quindi realizzato il primo livello di interpolazione, il quale consente un riposizionamento del fronte di MSB con una risoluzione data dalla relazione (2-34). Il segnale in uscita dal multiplexer è allo stesso tempo inviato in ingresso al secondo livello di interpolazione, il quale in funzione dei segnali di controllo introduce su questo un ritardo espresso dalla relazione (2-35). Tale segnale va a campionare l’uscita del primo flop da cui il segnale in uscita dal secondo flip-flop è ritardato della quantità:

m n CK n CK TOT T j t T i T = ⋅ + + ⋅ ₊ ∆ 2 2 0 ( 2-36 )

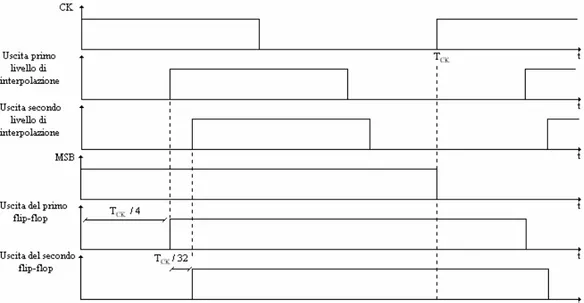
Concludendo abbiamo che il numero di livelli di interpolazione complessivi del sistema è pari a ₂n+m_{. In questa semplice analisi abbiamo anche considerato nulli i} tempi di propagazione dei flip-flop campionatori i quali comunque introducono lo stesso ritardo su tutti i fronti non influenzando le relazioni temporali relative tra di essi. La Figura 2.19 riassume le operazioni di interpolazione sul segnale MSB, in modo tale da fare comprendere in modo migliore il funzionamento del sistema. Nell’esempio in figura viene scelta la prima replica di CK sia per il primo che per il secondo livello di interpolazione.

Figura 2.19 Forme d’onda del circuito d’interpolazione.

La scelta dei valori di n ed m deve essere effettuato in modo opportuno, infatti un valore di n piccolo porta la DLL seriale ad operare con tempi di propagazione

della singola cella di ritardo abbastanza grandi, da cui se scegliessimo un m elevato in modo da ottenere alte risoluzioni temporali, avremmo il problema che l’errore di matching presente sulle celle della DLL seriale potrebbe essere troppo elevato.

Adesso che è stato descritto il funzionamento generale analizzeremo in modo dettagliato la struttura reale del sistema realizzato. Vedremo le architetture scelte per implementare le celle di ritardo e il loro dimensionamento; inoltre descriveremo il circuito di controllo utilizzato, soffermandoci sulla scelta del rivelatore di fase e sulla tecnica di controllo utilizzata. Il multiplexer verrà descritto nel capitolo 3, in quanto prima di parlare di questo devono essere introdotti concetti non ancora noti al lettore.

2.3.1 Primo livello di interpolazione

Il primo livello di interpolazione è costituito da una DLL di tipo seriale, composta da 34 elementi di ritardo e progettata per funzionare ad una frequenza di clock di 120 MHz. Dei 34 elementi di ritardo solamente 32 sono inseriti nell’anello di controllo mentre i restanti due costituiscono delle celle di tipo dummy, necessarie per uguagliare i carichi capacitivi di tutte le celle della DLL. Poiché i segnali della prima e della trentaduesima cella devono essere prelevati per effettuare il controllo, si ha che queste due celle a differenza delle altre vedono un carico capacitivo maggiore da cui avremo una disuguaglianza sui ritardi. Per ovviare a questo abbiamo inserito un buffer in corrispondenza a ciascuna uscita della DLL, e prelevato i segnali dopo tali buffer.

In base a quanto detto avremo che la risoluzione temporale di tale livello di interpolazione è: ps T T CK S 260.41 32 = = ∆ ( 2-37 )

Da cui il numero di bit della parola di controllo necessari a selezionare una unica uscita della DLL seriale risulteranno essere n = 5.

La struttura seriale si presta bene all’applicazione anche perché il tempo di propagazione minimo realizzabile nella tecnologia utilizzata è notevolmente inferiore ai 260.41 ps. Un ulteriore blocco fondamentale del primo livello

d’interpolazione è costituito dal multiplexer, il quale deve presentare un tempo di propagazione costante rispetto a qualunque ingresso. Tale proprietà risulta essere fondamentale in quanto una diversità sui tempi di propagazione altererebbe le relazioni temporali fra i segnali in uscita della DLL seriale.

2.3.1.1 Celle di ritardo

Poiché il ritardo di propagazione di una cella varia notevolmente a seconda del processo di fabbricazione, dovremo fare in modo che la DLL seriale riesca in tutte le condizioni operative ad agganciarsi sulla frequenza del clock. Per fare questo abbiamo utilizzato delle celle di ritardo controllabili digitalmente. La struttura utilizzata è quella del tipo a shunt-capacitor con controllo di gate. Si è preferito il controllo a shunt-capacitor rispetto a quello a current-starved in quanto come visto consente un legame lineare fra ritardo introdotto e carico capacitivo inserito, nonché una risoluzione costante su tutto l’intervallo di variazione. Inoltre dal punto di vista del layout una cella di questo tipo è più compatta consentendo una minimizzazione dell’area occupata dalla DLL. La scelta del sistema a controllo di gate deriva dalla possibilità di ottenere intervalli di variazione del ritardo maggiormente estesi. L’uso della struttura a controllo drain/source ci avrebbe costretto ad utilizzare un numero di condensatori inseribili nettamente superiore, per ottenere un intervallo di variazione del ritardo della stessa ampiezza. Il dimensionamento del sistema è stato possibile effettuando simulazioni sulle celle di ritardo. Come prima cosa abbiamo effettuato simulazioni parametriche sulla cella in modo tale da determinare le dimensioni dei transistori dell’inverter. Quello che dobbiamo fare è porci nel caso peggiore per la velocità (WS = Worst Speed) e determinare i valori delle larghezze dei transistori tali da consentire un ritardo di propagazione di 260.41 ps. In questo modo siamo sicuri che nelle condizioni peggiori la linea riesce ad agganciare il clock senza nessun condensatore inserito (funzionamento a vuoto)10. In Figura 2.20 è riportato

10 _{In realtà conviene fare in modo che il ritardo in queste condizioni sia sufficientemente più}

piccolo di 260.41 ps, in modo da avere un buon margine di aggancio, ed evitare quindi possibili malfunzionamenti.

l’andamento del tempo di propagazione al variare del parametro W dei transistori NMOS, con lunghezza di canale fissata al valore minimo consentito dalla tecnologia. Si osservi che abbiamo scelto una W doppia per il transistore PMOS rispetto a quella del NMOS. Si noti come al crescere della larghezza di canale dei transistori, il tempo di propagazione ha andamento iperbolico, questo accade in quanto la riduzione del tempo di propagazione in seguito all’aumento del β è limitata dalla crescita delle capacità parassite dei transistori.

Figura 2.20 Andamento del tempo di propagazione della cella al variare della larghezza di canale. Le dimensioni ottenute per i transistori sono riportate in Tabella 3.

Tabella 3 Dimensioni dei transistori della cella di ritardo della DLL seriale.

NMOS PMOS

Wn = 20 um Wp = 40 um

Ln = 0.3 um Lp = 0.3 um

Una volta determinate tali dimensioni è necessario fare in modo che la linea agganci il clock anche nelle condizioni di massima velocità (WP = Worst Power), da cui è necessario determinare il carico capacitivo mediante il quale il ritardo della singola cella diviene 260.41 ps in tali condizioni operative. Infatti le dimensioni dei transistori sono tali da darci un ritardo di 260.41 ps nel caso WS, da cui la stessa cella nel caso WP presenterà un tempo di propagazione nettamente inferiore ai 260.41 ps, dunque per poter aumentare tale ritardo è necessario

aggiungere dei carichi capacitivi. Notiamo che nella scelta delle dimensioni dei carichi shunt-capacitor e del loro numero, si deve raggiungere un compromesso tra ottenere una regolazione fine, raggiungere il range di variazione desiderato, limitare le capacità parassite e l’occupazione di area della cella. Per ottenere una risoluzione elevata si sono ricercate le dimensioni minime delle capacità, tuttavia una tale scelta porta ad avere un intervallo di variazione del ritardo limitato che per essere esteso necessità di un numero molto elevato di carichi shunt-capacitor; aumentare il numero degli shunt-capacitor ha per contro un aumento delle capacità parassite notevole, che tenderebbe ad aumentare il minimo ritardo ottenibile per la cella di ritardo e quindi potrebbe portarci a non riuscire a ottenere un ritardo di 260.41 ps nel caso WS a vuoto. Quello che si è deciso di fare è stato allora utilizzare anziché un maggior numero di condensatori in parallelo, dei condensatori più grandi il cui ritardo introdotto fosse circa 8 volte il ritardo introdotto da uno piccolo. Per tali condensatori si è fatto in modo di mantenere le dimensioni dei pozzetti di drain e source le più contenute possibile in modo appunto da non aumentare notevolmente la capacità parassita. In questo modo abbiamo che il ritardo introdotto da un condensatore grande è circa otto volte il ritardo di uno piccolo, mentre la capacità parassita che introduce è nettamente inferiore a quella che avremmo avuto utilizzando otto condensatori piccoli in parallelo. La struttura complessiva prevede 12 condensatori piccoli e 15 condensatori grandi. I condensatori piccoli sono 12 anziché 8 a causa del fatto che il ritardo del condensatore grande non è perfettamente pari ad 8 volte il ritardo di quello piccolo, da cui per evitare di avere intervalli di ritardo non coperti con la risoluzione desiderata si sono inseriti un maggior numero di condensatori piccoli. Il metodo di inserimento dei condensatori, verrà dettagliatamente analizzato nel paragrafo successivo dove sarà descritto il circuito di controllo, quello che importa comprendere adesso è solamente che l’inserimento di tutti i condensatori consente di ottenere un ritardo di 260.41 ps nel caso WP. Le dimensioni utilizzate per i condensatori piccoli e grandi sono riportate in Tabella 4.

Si noti che affinché un condensatore grande introduca un ritardo 8 volte maggiore di uno piccolo, non basta realizzare un condensatore con area otto volte maggiore, come ci si potrebbe aspettare. Questo accade in quanto il ritardo dello

shunt-capacitor non dipende solo dall’area di gate, ma anche dalla forma e dalla distanza delle varie parti del canale dai contatti di drain e source, questo effetto è dovuto alla presenza delle resistenze parassite di canale e di gate.

Tabella 4 Dimensioni degli shunt-capacitor delle celle di ritardo della DLL seriale.

Shunt-capacitor smaller Shunt-capacitor bigger

Area 1.2 um² 7.56 um²

Bisogna osservare che le zone più lontane dei contatti di drain e source a causa della resistenza parassita subiscono un ritardo nella distribuzione di carica che di fatto diminuisce la superficie efficace del condensatore portando quindi ad una riduzione del ritardo. Il layout dei condensatori piccoli e grandi è riportato in appendice C, si osservi la differenza rispetto al classico layout di un NMOS, dovuta al fatto che drain e source sono cortocircuitati e quindi si possono realizzare layout maggiormente compatti. In particolare poi nei condensatori piccoli il terminale drain/source è condiviso a coppie in modo da ridurre l’effetto delle capacità parassite di questi pozzetti. Il layout dei condensatori grandi è invece realizzato con una struttura a bottone dove la formazione del canale avviene in modo periferico al contatto drain/source il quale viene a trovarsi in posizione centrale.

E’ importante osservare che per effettuare il dimensionamento dei condensatori e quindi le relative simulazioni elettriche è stato necessario prevedere un opportuno circuito elettrico equivalente [6]. Infatti a causa della notevole influenza delle resistenze parassite di canale e di gate, per poter simulare correttamente i condensatori, non possiamo lasciare che il simulatore veda lo shunt-capacitor come un semplice transistore con il drain e il source cortocircuitati. Durante le simulazioni transitorie, infatti, un qualsiasi MOSFET viene trattato attraverso un modello equivalente i cui parametri dipendono dalla geometria. Nel caso di funzionamento in zona triodo si tiene conto della resistenza globale di canale in quanto la corrente che scorre tra drain e source è determinata in base alla differenza di potenziale presente tra essi. Se però questi due terminali sono cortocircuitati, la resistenza di canale scompare e la corrente risulta sempre uguale a zero. Il transistore diventa in pratica una pura capacità, con resistenza

delle armature nulla; quindi questo modello è sicuramente inesatto in quanto nella realtà la corrente scorre nelle armature e incontra sia la resistenza del gate che quella del canale. In particolare quest’ultima è tutt’altro che trascurabile ed il suo valore dipende dalla differenza tra la tensione fra gate e source rispetto a quella di soglia del transistore ad effetto di campo. D'altronde non possiamo rinunciare del tutto al modello classico del transistore in quanto solamente tramite questo possiamo tenere conto della formazione o della scomparsa del canale al variare della V_D/S. Per simulare la distribuzione delle cariche sulle armature possiamo allora utilizzare un modello costituito da una catena di transistori ciascuno dei quali rappresenta una porzione di condensatore. Per ottenere una simulazione che sia il più vicino possibile alla realtà, ognuno dei transistori che costituiscono la catena deve essere di lunghezza minima e deve avere una larghezza pari a quella della striscia concentrica di armatura che rappresenta. La catena si sviluppa a partire dal contatto drain/source verso l’esterno del condensatore con l’ultimo terminale che deve essere flottante in quanto non vi può fuoriuscire corrente. In realtà per consentire la simulazione non possiamo lasciare un terminale flottante per cui è necessario connetterlo a massa mediante una resistenza di valore molto alto. In Figura 2.21 è mostrato lo schema elettrico del circuito descritto nel caso la catena sia composta di soli due transistori.

Figura 2.21 Circuito elettrico equivalente di uno shunt-capacitor.

Il modello finora descritto deve essere ulteriormente perfezionato per quanto riguarda i transistori intermedi. Per essi infatti la capacità introdotta deve essere solamente quella di canale e quindi è necessario annullare l’area e il perimetro di drain e source. Bisogna notare inoltre che l’area e il perimetro di uno dei terminali di source o drain devono essere annullati anche per il primo transistore della catena. Infine poiché per i condensatori piccoli abbiamo che il terminale

drain/source è condiviso a coppie, i parametri di area e perimetro di tale pozzetto devono essere divisi di un fattore due.

Tabella 5 Parametri dei transistori utilizzati per fare le simulazioni. N° transistor Parametri capacità grandi Parametri capacita piccole 1 W = 6 um L = 0.3 um AD = 0 um² AS = 1.44 um² PD = 0 um PS = 0 um W = 1 um L = 0.3 um AD = 0 um² AS = 0.6 um² PD = 0 um PS = 1.2 um 2 W = 8.4 um L = 0.3 um AD = 0 um² AS = 0 um² PD = 0 um PS = 0 um W = 1 um L = 0.3 um AD = 0 um² AS = 0 um² PD = 0 um PS = 0 um 3 W = 10.8 um L = 0.3 um AD = 0 um² AS = 0 um² PD = 0 um PS = 0 um W = 1 um L = 0.3 um AD = 0 um² AS = 0 um² PD = 0 um PS = 0 um 4 W = 1 um L = 0.3 um AD = 0 um² AS = 0 um² PD = 0 um PS = 0 um

In Tabella 5 sono riportate, per ogni condensatore, le dimensioni dei transistori nei quali l’abbiamo scomposto per effettuare la simulazione e i relativi parametri di area di source e drain, si osservi come il modello del condensatore piccolo utilizzi 4 NMOS, mentre quello del condensatore grande ne utilizzi 3.

Le simulazioni effettuate sulle celle di ritardo, riportate in Figura 2.22, dimostrano il comportamento perfettamente lineare della DLL realizzata. E’

importante osservare inoltre come in tutte le condizioni possibili di funzionamento il sistema riesca ad agganciarsi sulla frequenza di clock d’ingresso, con la risoluzione desiderata. Infine la stima della variazione del ritardo relativa all’inserimento di un condensatore piccolo è risultata essere di 2 ps, mentre quella relativa all’inserimento di uno grande è risultata essere di 15.96 ps, con un rapporto uno ad otto fra le due, come appunto si desiderava ottenere.

Figura 2.22 Variazione del ritardo di una cella della DLL seriale.

Come già detto nel paragrafo precedente le uscite delle celle di ritardo prevedono dei buffer necessari per equalizzare i carichi e quindi evitare differenze sui valori dei ritardi introdotti. Il metodo utilizzato è mostrato in Figura 2.23, si noti come ciascuna cella di ritardo veda lo stesso carico capacitivo indipendentemente dal fatto che la sua uscita debba essere inviata o meno al rivelatore di fase.

Le dimensioni dei due buffer utilizzati riportate in Tabella 6 sono state determinate mediante simulazioni. In particolare la dimensione del buffer che pilota l’ingresso del multiplexer è stata realizzata facendo si che il ritardo introdotto sia il più piccolo possibile in modo da non introdurre inutili ritardi sulle uscite della DLL.

Tabella 6 Dimensioni dei transistori dei buffer di uscita della DLL seriale.

NMOS PMOS

Primo inverter W = 5 um L = 0.3 um W = 10 um L=0.3 um Secondo inverter W = 7.5 um L = 0.3 um W = 15 um L = 0.3 um

Mediante simulazioni Montecarlo abbiamo valutato infine l’entità del mismatch della linea seriale, compatibilmente alle dimensioni scelte dei vari transistori. Tale simulazione è stata effettuata andando a valutare la differenza fra i ritardi introdotti tra due celle della DLL seriale; i risultato ottenuto è stato uno scostamento massimo fra i ritardi della linea inferiore ad 1 ps.

2.3.1.2 Circuito di controllo

Il circuito di controllo è composto da un rivelatore di fase e una logica di controllo necessaria a comandare le celle di ritardo. Il compito svolto da questo circuito è quello di annullare la differenza di fase presente tra i due segnali al suo ingresso.

Figura 2.24 Schema a blocchi del rivelatore di fase.

Innanzitutto è necessario osservare che mentre la parte di controllo vera e propria può essere realizzata a livello semicustom, in quanto non presenta specifiche stringenti, il rivelatore di fase deve essere inevitabilmente realizzato a livello

fullcustom, in modo da ottenere le prestazioni necessarie. Nel seguito analizzeremo dapprima il circuito del rivelatore di fase, quindi andremo ad analizzare la struttura del sistema di controllo realizzato a standard cells.

Il rivelatore di fase in funzione dello sfasamento presente fra i segnali al suo ingresso genera un segnale up/down che vale 1, se il ritardo della linea è superiore al periodo del segnale di riferimento e 0 in caso contrario. In Figura 2.24 è riportato lo schema a blocchi del rivelatore di fase; si osservi la presenza di due Half-Transparent-Register (HT-R) e di un latch-SR.

Figura 2.25 Circuito elettrico di un Half-transparent-register.

Per comprendere il funzionamento del sistema è necessario analizzare il comportamento degli R. La Figura 2.25 mostra lo schema elettrico di un HT-R. La struttura è formata da un p-latch seguito da un n-latch in tecnica True Single Phase Clock. Un sistema di questo tipo è sensibile ai fronti dei segnali d’ingresso, in particolare abbiamo che l’uscita assume sempre valore logico alto a parte il caso in cui il fronte in salita del segnale X anticipa il fronte in salita di Y; in questo caso l’uscita va a livello logico basso per un tempo pari alla distanza temporale presente tra i due fronti.

Abbiamo quindi un sistema capace di generare un impulso a livello basso la cui durata è pari al tempo con il quale X anticipa Y. In Figura 2.26 è riportato un esempio di andamento dei segnali in un HT-R. Si riesce quindi a capire molto semplicemente il funzionamento del rivelatore di fase. Infatti se il segnale PD 0 è in anticipo rispetto al segnale PD 31 avremo che il segnale UP presenterà un impulso sul livello logico basso, mentre il segnale DOWN sarà sempre a livello alto, da cui il latch viene settato e quindi l’uscita Up/down assume valore logico basso11. Nell’altro caso se PD 31 è in anticipo con PD 0 avremo che il latch viene resettato da cui l’uscita Up/down assume valore logico alto. La Figura 2.27 riassume il comportamento del rivelatore di fase in entrambe le condizioni descritte.

Figura 2.27 Andamento del segnale Up/down nelle due possibili condizioni operative.

A causa della struttura degli HT-R il sistema funziona in modo non ambiguo per ritardi tra DP 31 e DP 0 compresi nell’intervallo:

CK CK T T T 2 1 2 1 _{<∆ <} − ( 2-38 )

Poiché inizialmente le celle di ritardo funzionano con carico capacitivo nullo può accadere che la condizione inferiore venga violata, in questo caso accadrebbe che il segnale Up/down assumerebbe valore logico 1 indicando erroneamente la condizione di anticipo del segnale DP 31 rispetto al segnale DP 0. Per ovviare a tale problema abbiamo previsto un’opportuna modifica circuitale (vedi Figura 2.28) al rivelatore di fase mostrato in Figura 2.24. La soluzione trovata è basata sul fatto che il segnale Up/down non è significativo fintanto che il ritardo tra i

11 _{Il fatto che l’uscita del latch assuma valore logico basso quando esso viene settato è evidente se}

segnale DP 0 e DP 31 non rientra nell’intervallo di non ambiguità dato dalla relazione (2-40), quindi si deve fare in modo di forzare il sistema affinché entri nell’intervallo utile; per fare ciò si campiona tramite un flip-flop sensibile al fronte in discesa il segnale DP 0 mediante il segnale DP 24 (corrispondente all’uscita della ventiquattresima cella di ritardo). Il segnale d’uscita di tale flip-flop, detto Upforcing, viene inviato assieme al segnale Up/down ad una porta NOR, in modo da costituire il nuovo segnale U/D il quale assume valore logico alto se DP 31 è in ritardo rispetto a DP 0 e basso nel caso opposto. La Figura 2.28 mostra lo schema a blocchi del sistema proposto e le relative temporizzazioni necessarie per comprenderne in modo migliore il funzionamento. Osservando le temporizzazioni notiamo che se il segnale DP 31 anticipa DP 0 di un tempo superiore a T_CK /2, il segnale DP 24 campiona DP 0 quando esso è a valore logico basso, da cui il segnale Upforcing assume il valore logico alto forzando l’uscita U/D a zero, per indicare che il ritardo della DLL deve essere aumentato. Al crescere del ritardo introdotto dalle celle della DLL arriveremo alla condizione in cui DP 24 campiona DP 0 quando esso assume valore logico alto.

Figura 2.28 Schema a blocchi completo del rivelatore di fase.

In tale condizione accade che il segnale Upforcing torna al valore logico basso da cui l’uscita U/D viene a coincidere con il segnale Up/down negato. Si comprende quindi che quando il segnale di Upforcing torna a valore logico basso il ritardo fra DP 31 e DP 0 risulta essere pari a:

6 2 2 24 32 T_CK T_CK T_CK T = ⋅ = + ∆ ( 2-39 )

Si a quindi che il sistema viene forzato ad entrare nell’intervallo di non ambiguità con un margine di sicurezza di 1/6 del periodo di clock.

Si potrebbe obbiettare che all’aumentare del ritardo tra i due segnali il segnale DP 24 potrebbe nuovamente tornare a campionare DP 0 sul valore basso portando l’uscita Upforcing a livello alto e quindi andando a forzare il segnale U/D sul valore logico basso, condizione che comporterebbe un malfunzionamento del sistema di controllo. Tuttavia è necessario osservare che questo accade quando il valore del ritardo è:

3 24 32 CK CK CK T T T T = ⋅ = + ∆ ( 2-40 )

Tale condizione potrebbe essere verificata solamente quando la frequenza del clock d’ingresso risultasse essere oltre il limite massimo agganciabile dalla linea.

Le simulazioni effettuate sul dispositivo rispecchiano il comportamento teorico descritto. In particolare sono state eseguite simulazioni mirate, atte a determinare la sensibilità del rivelatore. Bisogna infatti osservare che i rivelatori di fase presentano una dead zone intorno al punto di sfasamento nullo che porta ad errori di rivelazione. Nel caso del nostro rivelatore di fase idealmente si dovrebbe avere che il segnale U/D sia a valore logico alto per sfasamenti positivi e a valore logico basso per sfasamenti negativi, da cui l’andamento del segnale U/D in funzione dello sfasamento sarebbe un gradino con fronte in salita centrato sullo sfasamento nullo.

Nella situazione reale mostrata in Figura 2.29, si osservi come il comportamento sia con buona approssimazione coincidente con quello ideale, a parte la presenza di una dead zone di estensione stimata attorno ai 13 ps, nel caso tipico. Un tale errore di rivelazione è non significativo per il nostro sistema in quanto il ritardo fra DP 0 e DP 31 è fissato dal minimo ritardo introducibile dalla DLL seriale, che risulta essere pari al ritardo minimo introducibile dalla singola cella di ritardo moltiplicato per il numero di celle della DLL, che nel nostro caso è 32. Da cui avremo una precisione di aggancio della linea ben maggiore alla dead zone e di valore di circa 64 ps nel caso tipico.

Adesso che abbiamo discusso la generazione del segnale U/D da parte del rivelatore di fase, non resta che vedere come sia possibile sfruttare la conoscenza di tale segnale per effettuare la funzione di controllo sulle celle di ritardo della DLL seriale. Nel paragrafo 2.3.1.1 è stata descritta la struttura delle celle di ritardo. Ricordiamo che il sistema di shunt-capacitor è organizzato su 12 condensatori piccoli e 15 condensatori grandi raggruppati in quattro gruppi con peso crescente secondo la potenza del due. In particolare sappiamo che il ritardo introdotto da ciascun condensatore grande è circa otto volte quello introdotto da uno piccolo, per cui i condensatori piccoli sono pilotati mediante una codifica termometrica, mentre il pilotaggio di quelli grandi è stato realizzato mediante una codifica binaria. I condensatori piccoli sono pilotati mediante uno shift-register a 12 bit il quale consente di realizzare la codifica termometrica, mentre i condensatori grandi sono pilotati mediante un contatore up-down a 4 bit, il quale verrà incrementato o decrementato in funzione del numero di condensatori da inserire. In Tabella 7 sono indicati alcuni casi particolari delle due codifiche necessarie al pilotaggio dei condensatori e il relativo numero di condensatori attivati, in modo che sia possibile comprendere meglio quanto detto.

Descriviamo ora la strategia di aggancio del sistema. Inizialmente tutte le celle di ritardo presentano tutti i condensatori controllabili spenti, in modo tale che il ritardo complessivo della linea sia quello minimo. In queste condizioni l’uscita U/D del rivelatore di fase si trova a livello logico basso indicando al circuito di controllo che il ritardo delle celle deve essere aumentato. Il controllore

campiona ad ogni ciclo di clock il segnale U/D e, finché questo è basso, aumenta di uno il numero di condensatori piccoli inseriti.

Tabella 7 Esempio di codifiche di pilotaggio in funzione del numero di condensatori attivati. Codifica condensatori grandi Codifica condensatori piccoli N° condensatori grandi attivati N° condensatori piccoli attivati 0000 000000000000 0 0 0000 000000000001 0 1 0000 111111111111 0 12 0001 000011111111 1 8 0010 000011111111 2 8 1111 111111111111 15 12

Qualora tutti i dodici condensatori piccoli fossero attivati e il segnale U/D si trovasse ancora a livello logico basso, il controllore procederebbe aumentando di 1 la parola di controllo che pilota i condensatori grandi e disattivando 8 dei 12 condensatori piccoli12. Il sistema di controllo continua ad operare in questo modo fintanto che non si arriva nella condizione di aggancio identificata dalla transizione a livello logico alto del segnale U/D. Il valore dell’uscita U/D alto indica al circuito di controllo di ridurre il ritardo delle celle, da cui il sistema provvederà a disattivare uno dei condensatori piccoli, riportando il valore del ritardo totale della DLL ad essere inferiore al periodo di clock. Si osservi che in questa condizione abbiamo che l’uscita U/D è nuovamente a livello logico basso dunque il controllore provvede ad attivare un ulteriore condensatore piccolo, da cui si capisce che in un sistema di questo, nella condizione di aggancio, avremo una continua commutazione di uno dei condensatori piccoli. Tali commutazioni sono indesiderate in quanto comportano un assorbimento di potenza non trascurabile, pertanto sono state eliminate mediante un circuito, detto Stand-by-controller che si accorge del raggiungimento della condizione di aggancio. Per

12 _{Si ricordi che il ritardo introdotto da un condensatore grande è in prima approssimazione}

quanto detto precedentemente la condizione di aggancio è caratterizzata da un segnale U/D che commuta continuamente fra il livello logico alto e quello basso, pertanto il circuito di stand-by può sfruttare questa proprietà per rilevare tale condizione. Quello che si è deciso di fare è campionare l’uscita U/D del rivelatore di fase ad ogni ciclo di clock mediante uno shift-register ad 8 bit. Il contenuto di tale registro consente di valutare o meno il raggiungimento dell’aggancio in base al numero di 1 che contiene, infatti in caso di aggancio conterrà un ugual numero di 1 e 0. Se si verifica tale condizione, il circuito del controllore viene disabilitato per un tempo pari a 256 cicli di clock sfruttando un contatore ad 8 bit. Al termine dei 256 cicli il controllore viene riattivato, in modo tale che questo possa riprendere a monitorare il ritardo della linea. Si ha quindi che il controllore di fase risulta attivo per un tempo inferiore al 2% del tempo complessivo, cosa che comporta un notevole risparmio di potenza. Si osservi che la disabilitazione del circuito di controllo non costituisce un grave problema in quanto le variazioni dei ritardi delle celle sono dovute ad effetti termici i quali hanno costanti di tempo notevolmente maggiori rispetto al tempo in cui il circuito è disattivo. La Figura 2.30 riporta lo schema a blocchi del sistema di controllo utilizzato. La frequenza di clock di tale sistema è stata scelta pari a 30 MHz, ossia ¼ della frequenza di clock della DLL seriale, per motivi di risparmio di potenza. In base a tale scelta avremo che il circuito di controllo risulta essere disabilitato per un tempo pari a 8.533 us, nettamente inferiore ai tempi caratteristici dei fenomeni termici.

Le uscite del circuito di controllo non possono essere connesse direttamente agli shunt-capacitor, a causa della loro scarsa capacità di pilotaggio dei carichi, che in questo caso sono considerevoli13. Cerchiamo di comprendere quanto detto considerando il circuito di Figura 2.31.

Figura 2.31 Circuito elettrico di pilotaggio dello shunt-capacitor a controllo di gate.

In tale circuito abbiamo supposto di pilotare lo shunt-capacitor mediante un inverter, componente che potrebbe rappresentare l’uscita del circuito di controllo (anche se l’uscita del circuito di controllo non fosse un inverter, le cose cambierebbero poco in quanto si potrebbe ricondurre l’analisi ad un inverter equivalente). Andiamo a studiare il comportamento dinamico del sistema supponendo che la tensione V_A imposta dall’inverter sia a livello logico alto, in modo da avere attivato lo shunt-capacitor.

Figura 2.32 Circuito equivalente di pilotaggio dello shunt-capacitor.

In queste condizioni il circuito può essere schematizzato mediante il circuito equivalente mostrato in Figura 2.32, dove lo shunt-capacitor è stato sostituito con una capacità e sono stati messi in evidenza i diodi dei pozzetti di drain dell’inverter. Si noti come il transistore PMOS in queste condizioni funzioni in zona triodo in quanto la sua tensione tra drain e source è nulla, e quindi possa essere sostituito con la sua resistenza differenziale R . Allora trascurando la _dP

presenza dei diodi il circuito da risolvere si riduce ad una semplice squadra RC, per cui l’andamento della tensione V_A(t) quando il segnale IN commuta da livello logico alto a livello logico basso risulta essere stimato dalla seguente relazione:

dd C R t dd A t V e V V = ⋅ dP + − ) ( ( 2-41 )

Quando invece il segnale IN effettua la commutazione opposta l’andamento di ) (t V_A risulterà essere: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⋅ = −R C t dd A P d e V t V ( ) 1 ( 2-42 )

La Figura 2.33 riporta l’andamento delle forme d’onda nel caso ideale (fronti istantanei)una completa commutazione del segnale IN.

In particolare si osservi come la tensione V_A(t) non possa superare il valore

γ

V

V_dd + grazie al presenza del diodo superiore. Si noti inoltre come per tutto l’intervallo di tempo _{t , la tensione} * _{V (t)}

A risulti essere inferiore alla tensione di soglia del transistore NMOS, pertanto in questo intervallo di tempo lo shunt-capacitor risulta essere disattivo. Si osservi che _{t dipende dalla costante di tempo} * del circuito ossia dal valore della capacità da pilotare e dal valore della resistenza dinamica del transistore PMOS. Dunque per ridurre tale tempo possiamo aumentare la larghezza di canale dl transistore PMOS in modo da ridurre la sua resistenza differenziale.

Nel circuito preso in considerazione non si è tenuto conto che il buffer pilota contemporaneamente i carichi capacitivi di entrambi gli inverter che costituiscono la cella di ritardo. Per questi l’andamento della tensione IN è opposto, da cui gli effetti complessivi sulla V_A(t) tendono a compensarsi. Quindi avremo che le dimensioni del transistore PMOS del buffer non devono essere così elevate come era stato dedotto dall’analisi precedentemente fatta. Inoltre i fronti reali dei segnali in uscita agli inverter della linea di ritardo non sono istantanei (tempi di commutazione dell’ordine dei 100 ps) da cui l’effetto capacitivo è più limitato di quello descritto. Mediante simulazioni effettuate facendo funzionare effettivamente la linea di ritardo è possibile dimensionare i buffer di pilotaggio in modo che la tensione VA sia sufficientemente stabile nel tempo.

Tabella 8 Dimensione dei transistori dei buffer di pilotaggio degli shunt-capacitor.

PMOS NMOS

CP0-CP11 W = 14 um L = 0.3 um W = 6 um L = 0.3 um CG0-CG1 W = 28 um L = 0.3 um W = 12 um L = 0.3 um CG2-CG3 W = 42 um L = 0.3 um W = 24 um L = 0.3 um

In modo complementare si potrebbe effettuare una analisi quando il valore di V_A imposta dall’inverter sia a livello logico basso in modo da avere disattivato lo shunt-capacitor. In questo caso si ricaverebbe una condizione sul dimensionamento del transistore NMOS. Tuttavia si deve osservare che in questo caso la capacità dello shunt-capacitor è nettamente inferiore al caso precedente da