2 Fluidodinamica Computazionale

2 Fluidodinamica Computazionale

2.1 Introduzione

Per fluidodinamica computazionale (CFD) si intende l’analisi numerica di sistemi che coinvolgono moto di fluidi, scambio termico e fenomeni connessi come le reazioni chimiche. La CFD permette di risolvere, con l’ausilio di codici di calcolo, le equazioni di Navier-Stokes in un dominio di interesse, per il quale siano state definite le condizioni al contorno ed iniziali.

I primi passi nel campo della simulazione numerica di problemi fluidodinamici risalgono alla prima metà del 19008. I primi codici numerici furono sviluppati per lo studio di specifiche classi di problemi e solo a partire dagli anni 80 ebbe inizio, in Europa, la diffusione di codici CFD per applicazioni generali9. Tuttavia, l’impiego della CFD in applicazioni ingegneristiche è stato reso possibile solo di recente, grazie allo straordinario sviluppo dei calcolatori, che ha permesso di ridurre i tempi di calcolo, e all’introduzione delle griglie non strutturate e ibride, che permettono una riproduzione accurata dei dettagli anche nel caso di geometrie molto complesse. Infine, l’introduzione del calcolo parallelo ha ridotto ulteriormente il problema del tempo di calcolo che, pertanto, cessa di essere, a parità di disponibilità economiche, il fattore limitante nella diffusione della CFD.

Come Scienza emergente la Fluidodinamica Computazionale ha destato molto interesse nella comunità scientifica internazionale. Essa costituisce, infatti, uno strumento predittivo molto attraente, potenzialmente capace di affrontare qualsiasi tipologia di problema, senza le limitazioni caratteristiche della sperimentazione. In particolare, la Fluidodinamica Computazionale può essere impiegata per lo studio di condizioni di flusso difficilmente riproducibili in laboratorio oppure di sistemi operanti in condizioni pericolose (analisi di rischio e scenari incidentali). Inoltre, il ricorso alle simulazioni numeriche consente di ottenere risultati ad alta risoluzione, in tempi molto minori e con costi ridotti rispetto alla tradizionale pratica sperimentale. Tuttavia, non è ancora possibile impiegare la CFD in sostituzione della sperimentazione. I codici di calcolo, infatti, sono basati su modellazioni e

8 _{Nel 1933 fu affrontato, per la prima volta, uno dei problemi classici in campo fluidodinamico: il cilindro}

investito da un flusso. La prima soluzione numerica per tale problema fu ottenuta nel 1953 da Kawaguti, a mezzo di un calcolatore funzionante 20 ore al giorno per 18 mesi.

9 _{Lo sviluppo della CFD in Europa ebbe luogo grazie all’intensa attività di ricerca condotta dal gruppo di Brian}

Spalding presso l’Imperial College di Londra. L’equipe londinese sviluppò numerosi codici di calcolo, implementando gli algoritmi della famiglia SIMPLE, il modello di turbolenza k-ε nella sua versione attuale, gli schemi di risoluzione UPWIND e i modelli di combustione Eddy Break Up e Presumed Pdf.

rappresentazioni semplificate delle realtà fisiche che, come tali, non garantiscono la validità assoluta del risultato. È, quindi, necessario affiancare alla fluidodinamica computazionale una procedura di validazione, che accerti la correttezza della modellazione utilizzata e l’attendibilità dei risultati ottenuti.

I campi di applicazione dei codici CFD sono molteplici ed includono: ƒ l’industria aerospaziale, per la progettazione dei velivoli;

ƒ l’industria automobilistica, per la progettazione dei motori a combustione interna; ƒ l’industria energetica, per la progettazione di sistemi di combustione ad elevata

efficienza e basso impatto ambientale;

ƒ l’industria elettronica, per lo studio dei sistemi di raffreddamento dei circuiti elettrici; ƒ l’industria di processo, per lo studio dei processi di miscelamento e dei reattori agitati; ƒ l’industria civile, per la progettazione dei sistemi di aerazione degli edifici;

ƒ il settore medico, per lo studio del flusso d’aria nei polmoni, di sangue nelle arterie e nelle vene;

ƒ il settore ambientale, per lo studio della dispersione degli inquinanti in mezzi gassosi e liquidi (scarico di sostanze inquinanti in atmosfera, fiumi, laghi e mare);

ƒ il settore meteorologico, per la comprensione di fenomeni naturali come gli uragani.

2.2 Equazioni di conservazione per flussi reagenti

I modelli matematici per lo studio del moto dei fluidi si fondano sulla cosiddetta ipotesi del continuo. Sulla base di tale ipotesi, un fluido viene considerato come un corpo continuo e non costituito da molecole in grado di collidere tra di loro o con corpi solidi. Ciò implica che il valore puntuale di una qualsiasi proprietà intensiva (densità, pressione, temperatura, velocità) è uguale al suo valore medio misurato in di un volume elementare, δ , V

di fluido. Per la validità dell’ipotesi è necessario, tuttavia, che il volume di riferimento sia sufficientemente piccolo da poter essere considerato infinitesimo rispetto alle variazioni spaziali delle grandezze macroscopiche, ma grande abbastanza per contenere un numero di molecole sufficiente a rendere il valore di ciascuna grandezza statisticamente stazionario. Volendo definire, ad esempio, il valore della densità, ρ, in un punto P dello spazio, detto δ V

un volume di fluido di cui P è il baricentro e δ la massa di fluido in esso contenuto, si ha: M

V M V δ δ ρ δlim→0 = . 2.1

I problemi fisici che coinvolgono flusso di fluidi, scambio termico e reazioni chimiche sono governati dai principi di conservazione della massa, della quantità di moto e dell’energia. Questi principi sono espressi, da un punto di vista matematico, da un insieme di equazioni differenziali alle derivate parziali che, sulla base dell’ipotesi del continuo, descrivono il comportamento di un volume infinitesimo di fluido (particella di fluido).

Con riferimento ad un sistema di coordinate cartesiane e utilizzando, secondo la consuetudine tensoriale, la notazione di sommatoria10_{, le equazioni di conservazione per}

flussi reagenti possono essere espresse come segue: ƒ Equazione di conservazione della massa totale:

0 = ∂ ∂ + ∂ ∂ i i x u t ρ ρ 2.2 ƒ Equazione di conservazione della massa delle singole specie chimiche:

k i k i i i k k _w x J x u Y t Y & + ∂ ∂ − = ∂ ∂ + ∂ ∂ρ ρ k =1,2,...,NC 2.3

ƒ Equazione di conservazione della quantità di moto: j i ij j i i j j g x x p x u u t u ρ τ ρ ρ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ j=1,2,3 2.4

ƒ Equazione di conservazione dell’entalpia specifica11: rad i j ij i i i i Q x u Dt Dp x q x hu t h _{+ &} ∂ ∂ + + ∂ ∂ − = ∂ ∂ + ∂ ∂ρ ρ _τ . 2.5

Nelle equazioni 2.2-2.5 l’indice i indica una componente di un vettore tridimensionale (i=1, 2, 3), mentre k denota una specie chimica (k =1, 2,…, NC). Quanto al significato dei

termini:

ƒ ρ è la densità del fluido;

ƒ u è la velocità del fluido, i.e. u=u₁+u₂+u₃;

ƒ Y è il vettore delle frazioni massiche delle specie chimiche; ƒ h è l’entalpia specifica del fluido;

ƒ N è il numero di specie chimiche; C

ƒ p è la pressione statica del fluido;

ƒ g rappresenta una forza di volume per unità di massa;

10 _{La notazione di sommatoria sottintende una sommatoria su tutti gli indici ripetuti.} 11 _{Ritenendo trascurabili gli effetti delle forze di volume.}

ƒ τ è il tensore degli sforzi viscosi;

ƒ k

J è il flusso diffusivo della specie chimica k;

ƒ q è il flusso diffusivo di calore;

ƒ w& è la velocità di reazione massica del componente k; _k

ƒ Q&_rad rappresenta il flusso di calore radiante.

2.3 Equazioni costitutive

Le equazioni 2.2-2.5 non costituiscono un sistema determinato. Il numero di incognite risulta, infatti, superore alle equazioni disponibili. È necessario, pertanto, formulare delle relazioni costitutive che permettano di esprimere la pressione, p , il tensore degli sforzi viscosi, τ , il flusso diffusivo della specie k, k

J e il flusso termico diffusivo, q .

Nella maggior parte dei processi di combustione è possibile ritenere valida l’equazione di stato dei gas perfetti. Applicando la legge di Dalton, la pressione statica del fluido, p , può essere ottenuta dalla somma delle pressioni parziali, p , dei singoli componenti: k

cRT RT c p p C C N k k N k k

∑

∑

dove R è la costante universale dei gas, T è la temperatura mentre c ed k c rappresentano, rispettivamente, la concentrazione della specie k e della miscela gassosa.

Nell’ipotesi di poter ritenere il fluido newtoniano, il tensore degli sforzi viscosi è espresso dall’equazione di Newton:

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = i i ij i j j i ij x u x u x u _µδ µ τ 3 2 2.7

dove µ è la viscosità del fluido e δij è il simbolo di Kronecker. Il flusso di materia delle specie chimiche, k

J , viene generalmente espresso

utilizzando la legge di Fick:

i k k k i x Y Sc J ∂ ∂ − = µ . 2.8

Nella 2.8 Sc è il numero di Schmidt della specie chimica k, definito come: k

dove D rappresenta la diffusività del componente k nella miscela. L’impiego della legge di _k

Fick è molto frequente poiché permette di semplificare fortemente la risoluzione delle equazioni di bilancio. Tuttavia, ricorrendo a tale approssimazione, la somma delle frazioni massiche, Y , risulta diversa da 1. Questo problema viene aggirato sostituendo l’equazione di k bilancio di un componete, generalmente N2, con l’equazione:

∑

Il flusso termico, q , può essere espresso come: ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ∂ ∂ − =

∑

Nella 2.11 Pr rappresenta il numero di Prandtl, definito come:

λ µ p c = Pr 2.12

dove c è il calore specifico a pressione costante e _p λ è la conducibilità termica della miscela.

L’equazione 2.11 contiene un termine diffusivo espresso dalla legge di Fourier e un termine caratteristico dei sistemi multicomponente, associato alla diffusione di specie chimiche con differenti entalpie specifiche.

A questo punto è possibile introdurre il numero di Lewis, Le , della specie k, definito come _k

rapporto tra il trasporto diffusivo di calore e di materia:

k p k k D c Sc Le ρ λ = = Pr . 2.13

Nell’ipotesi in cui il numero di Lewis possa essere considerato unitario, l’equazione 2.11 si semplifica per dare:

i i x h q ∂ ∂ − = Pr µ . 2.14

Nella maggior parte dei problemi di combustione, inoltre, è possibile trascurare le variazioni di pressione e l’effetto delle forze di volume e di quelle viscose. Sulla base di tali ipotesi, e nel caso in cui sia Q&_rad =0, le equazioni di conservazione 2.3 e 2.5 diventano formalmente identiche:

2.4 Risoluzione delle equazioni di conservazione

La risoluzione diretta (DNS12) delle equazioni 2.2-2.5, generalmente indicate come equazioni di Navier-Stokes, è possibile sono nel caso di flussi con bassi numeri di Reynolds. La DNS richiede, infatti, una discretizzazione spaziale e temporale molto fine, tale da risolvere completamente anche le più piccole scale dei fenomeni in gioco. Il livello di dettaglio ottenuto è massimo e non vi sono perdite sostanziali di informazioni. Tuttavia, all’aumentare del numero di Reynolds si riducono le dimensioni delle strutture vorticose più piccole ed il costo computazionale delle simulazioni risulta, pertanto, proibitivo. È necessario sottolineare, inoltre, che l’applicazione della DNS ai flussi reagenti è particolarmente complessa a causa della forte non-linearità dei termini di generazione delle specie chimiche, e all’esistenza di scale spaziali e temporali molto più piccole rispetto a quelle tipiche del campo di moto.

Nell’ambito delle applicazioni ingegneristiche si fa riferimento, quindi, a metodi di risoluzione semplificati che si basano su operazioni di filtraggio delle equazioni di Navier-Stokes con medie spaziali e temporali. Prima di passare alla descrizione di tali metodi è opportuno fornire, comunque, alcuni cenni sulle caratteristiche dei flussi turbolenti.

2.4.1 Caratteristiche fondamentali della turbolenza

La turbolenza è un fenomeno irregolare, transitorio e tridimensionale, caratterizzato da fluttuazioni di tutte le proprietà locali. Gli studi sulla turbolenza hanno evidenziato che il passaggio da flusso laminare a flusso turbolento rappresenta un fenomeno critico (Mauri, A.A. 2003-2004). All’aumentare del numero di Reynolds, infatti, il flusso si ritrova con un eccesso di energia che non riesce a dissipare in regime laminare e comincia a destabilizzarsi a livello macroscopico, con la formazione di vortici. Inizialmente la dimensione dei vortici è paragonabile alla dimensione caratteristica del sistema e il numero di Reynolds ad essi associato è molto alto. In tali condizioni l’effetto delle forze viscose risulta trascurabile e l’energia viene semplicemente trasferita da vortici più grandi a vortici più piccoli, come in una cascata, fino a quando non si generano vortici sufficientemente piccoli che il numero di Reynolds loro associato è dell’ordine dell’unità. In corrispondenza di questa scala di lunghezze, l'energia meccanica viene finalmente dissipata.

Il flusso d’energia da una scala di dimensioni all’altra è fornito da una grandezza nota come dissipazione, ε , dell’energia cinetica turbolenta, k. Indicate con L e '

u la scala di

lunghezza macroscopica e la fluttuazione di velocità turbolenta ad essa associata, la dissipazione ε si valuta dal rapporto tra l’energia cinetica turbolenta, '2

u , e il tempo

caratteristico di trasferimento d’energia nei vortici più grandi, _{/ u}'

L L = τ : L u u L u '3 ' 2 ' = = ε . 2.15

Il numero di Reynolds riferito alla scala macroscopica del sistema è dato da: ν L u L ' Re = 2.16

dove ν è la viscosità cinematica del fluido.

Nella cascata di trasformazione dell’energia il numero di Reynolds decresce passando da Re_L

a valori prossimi all’unità, quando le forze di inerzia e quelle viscose diventano tra loro paragonabili. Questo limite identifica la scala di dimensioni più piccola di un flusso turbolento, chiamata scala di Kolmogorov, η_k, e controllata esclusivamente dalle proprietà locali del fluido, la viscosità cinematica ν e la dissipazione ε . Si ha:

4 1 3 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ε ν ηk 2.17

cui corrisponde un numero di Reynolds unitario

1 Re 3 4 3 1 ' = = = ν η ε ν η η k k k u k . 2.18

Le espressioni della velocità e del tempo caratteristico della scala di Kolmogorov sono:

( )

I rapporti tra scale macroscopiche e microscopiche sono espressi dalle relazioni:

2 1 4 1 4 3 L k L L k L k Re Re u u Re L _{= = =} τ τ η . 2.20

L’equazione 2.20 evidenzia che, all’aumentare di ReL, le micro e macroscale divergono sempre di più e la turbolenza sviluppa una microstruttura progressivamente più fine (e dunque difficile sia da determinare sperimentalmente che da simulare numericamente).

La caratteristica principale di un flusso turbolento è la forte intensità dei processi di miscelamento. La diffusività del fluido in regime turbolento può essere, infatti, anche due o tre ordini di grandezza maggiore rispetto alla diffusione molecolare, tipica dei flussi laminari.

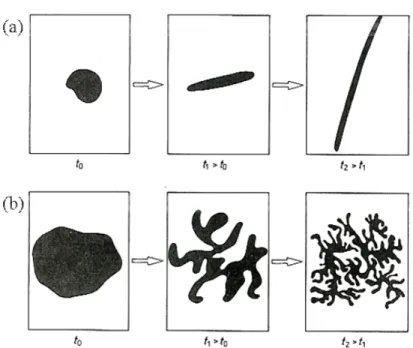
Il processo di trasferimento dell’energia dalle grandi strutture vorticose verso scale sempre più piccole determina la riduzione delle disomogeneità delle grandezze scalari (temperatura e concentrazione dei componenti) da una dimensione macroscopica ad una microscopica. A questo fenomeno, noto come diffusione turbolenta o di Taylor, è associata anche una significativa accelerazione dei processi di trasporto molecolare. La deformazione degli elementi di fluido ad opera dei vortici turbolenti determina, infatti, una significativa estensione delle superfici di contatto tra zone con differenti proprietà e facilita, pertanto, il miscelamento del sistema. L’intensificazione dei fenomeni di miscelamento molecolare rappresenta l’aspetto determinante in processi puramente molecolari come la combustione. La deformazione di un elemento di fluido soggetto a diverse scale di turbolenza è illustrata in Figura 2.1.

Figura 2.1 - Deformazione di un elemento di fluido soggetto a scale di turbolenza (a) maggiori e (b) minori rispetto alla dimensione caratteristica dell’elemento considerato.

2.4.2 Equazioni di Navier-Stokes mediate secondo Reynolds

Anche se la risoluzione numerica delle equazioni di Navier-Stokes fosse praticabile, l’elevato grado di dettaglio spaziale e temporale ottenibile avrebbe scarso interesse pratico. Nelle applicazioni ingegneristiche, infatti, l’attenzione è posta sui valori medi delle grandezze in gioco, come la velocità media di consumo del combustibile o il tasso medio di formazione delle sostanze inquinanti. Le equazioni di conservazione che descrivono il sistema vengono, pertanto, mediate sulla base di una descrizione statistica del flusso turbolento.

Nel precedente Paragrafo è stato sottolineato che la turbolenza costituisce un fenomeno irregolare, transitorio e tridimensionale, caratterizzato da fluttuazioni di tutte le proprietà locali. Per questa ragione, è possibile suddividere qualsiasi quantità, f , in una componente media, f , ed una fluttuante, '

f :

' f f

f = + con f'=0. 2.21

Nel caso della componente i della velocità del fluido si ottiene, ad esempio:

( )

( ) ( )

( )

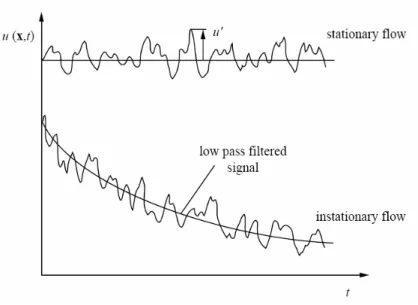
Il valore medio della velocità (o della temperatura, concentrazione) è definito diversamente per flussi globalmente stazionari o non-stazionari (Figura 2.2). Se il flusso è stazionario rispetto alla media, è possibile definire una media temporale come:

( )

( )

_∫

Per flussi transitori, u_i

( )

( )

( )

∑

dove u_i,k

( )

l’esperimento n volte e nelle stesse condizioni iniziali.

La definizione 2.21 è nota come decomposizione di Reynolds ed è diffusamente impiegata nell’analisi fluidodinamica di sistemi non reagenti per la derivazione di equazioni di trasporto delle quantità medie, note come equazioni di Navier-Stokes mediate secondo Reynolds (RANS13).

Figura 2.2 – Flussi turbolenti stazionari e non stazionari.

I processi di combustione sono caratterizzati da forti variazioni di densità. L’approccio classico utilizzato per descrivere il flusso turbolento con medie temporali deve essere, quindi, modificato al fine di considerare gli effetti di una densità non costante. Ciò si realizza introducendo la cosiddetta media di Favre, definita come:

.

ρ ρf

f = . 2.25

La proprietà f può essere, ancora una volta, decomposta in una media e una fluttuazione:

'' f f

f = + . 2.26

Moltiplicando l’equazione 2.26 per la densità e mediando si ottiene:

(

)

Applicando la definizione 2.25 si ricava, infine:

0 ''₌ f

ρ . 2.28

Sostituendo la relazione 2.25 nelle equazioni 2.2-2.5 e mediando, si ottiene: ƒ Equazione di conservazione della massa totale:

0 = ∂ ∂ + ∂ ∂ i i x u t ρ ρ 2.29 ƒ Equazione di conservazione della massa delle singole specie chimiche:

k i k i i i k i i k k w x J x u Y x u Y t Y & + ∂ ∂ − ∂ ∂ − = ∂ ∂ + ∂ ∂_{ρ ρ ρ} '' '' C N k =1,2,..., 2.30

ƒ Equazione di conservazione della quantità di moto: j i ij j i i j i i j j g x x p x u u x u u t u ρ τ ρ ρ ρ + ∂ ∂ + ∂ ∂ − ∂ ∂ − = ∂ ∂ + ∂ ∂ '' '' 3 , 2 , 1 = j 2.31

ƒ Equazione di conservazione dell’entalpia specifica: rad i j ij i k i i i i i Q x u Dt p D x J x u h x u h t h & + ∂ ∂ + + ∂ ∂ − ∂ ∂ − = ∂ ∂ + ∂ ∂ τ ρ ρ ρ '' '' 2.32 Le equazioni 2.29-2.32 sono formalmente identiche alle equazioni di Navier-Stokes mediate secondo Reynolds, valide per flussi incomprimibili. La relazione che intercorre tra le media di Reynolds e quella di Favre è esprimibile come:

(

)(

)

L’equazione 2.33 evidenzia che il passaggio dalla media di Reynolds a quella di Favre richiede la conoscenza, o la modellazione, delle fluttuazioni di densità.

Le equazioni di conservazione mediate 2.29-2.32 contengono, rispetto alle equazioni di Navier-Stokes, alcuni termini aggiuntivi che è necessario modellare per rendere determinato il problema. Tali termini sono:

ƒ Il tensore degli sforzi (stress) di Reynolds, '' ''

i ju

u , espresso utilizzando i modelli di

turbolenza (Paragrafo 2.4.3).

ƒ I flussi turbolenti di materia, '' ''

i ku

Y , e di calore, h''u_i'' . Questi termini sono

generalmente modellati ricorrendo all’ipotesi del trasporto del gradiente:

i k t k t i k x Y Sc u Y ∂ ∂ − = µ ρ '' '' _2.34 i t t i x h u h ∂ ∂ − = Pr '' '' µ ρ 2.35

dove µ_t è la viscosità turbolenta, valutata a mezzo del modello di turbolenza, mentre t

k

Sc e Pr rappresentano, rispettivamente, il numero di Schmidt turbolento della specie _t

k e il numero di Prandtl turbolento.

Numerosi lavori sperimentali hanno dimostrato, tuttavia, che l’ipotesi del trasporto del gradiente risulta non verificata per alcune fiamme turbolente premiscelate, nelle quali i flussi turbolenti di materia e di calore sono diretti in direzione opposto rispetto a quanto predetto dalle equazioni 2.34 e 2.35 (counter-gradient turbulent transport).

ƒ I flussi molecolari di materia, k

J , e di calore, q . Nel caso di elevati numeri di

Reynolds, questi termini sono generalmente trascurabili rispetto a quelli di trasporto turbolento.

ƒ La velocità di reazione delle specie chimiche, w&k , valutate con opportuni modelli di combustione.

ƒ Il flusso di calore radiante, Q&_rad , valutato con i modelli di radiazione.

2.4.3 Modelli di turbolenza

I modelli di turbolenza permettono di esprimere il tensore degli sforzi di Reynolds in funzione delle variabili mediate nel tempo. Esistono due classi principali di modelli di turbolenza:

ƒ I modelli di diffusione per gradiente (Eddy viscosity models); ƒ I modelli diretti.

2.4.3.1 Modelli di diffusione per gradiente

I modelli di diffusione per gradiente sono basati sull’ipotesi di Boussinesq, secondo la quale gli stress di Reynolds possono essere espressi in funzione del gradiente di velocità media del fluido, attraverso una relazione analoga all’equazione di Newton per gli sforzi viscosi: ij i i t i j j i t i j x u k x u x u u u µ ρ µ δ ρ _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = − 3 2 '' '' _2.36

dove µ_t è la viscosità turbolenta (eddy viscosity) e k è l’energia cinetica turbolenta, definita

come:

∑

nell’’equazione 2.36 è stato introdotto per recuperare il valore esatto della traccia del tensore degli sforzi di Reynolds.

Sostituendo le equazioni 2.34-2.37 nelle equazioni RANS si ottiene: ƒ Equazione di conservazione della massa totale:

0 = ∂ ∂ + ∂ ∂ i i x u t ρ ρ 2.38 ƒ Equazione di conservazione della massa delle singole specie chimiche:

k i k t k t k i i i k k w x Y Sc Sc x x u Y t Y & + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ = ∂ ∂ + ∂ ∂ρ ρ µ µ C N k =1,2,..., 2.39

ƒ Equazione di conservazione della quantità di moto:

(

)

(

)

ƒ Equazione di conservazione dell’entalpia specifica: rad i t t i i i Q Dt p D x h x x u h t h & + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ = ∂ ∂ + ∂ ∂ Pr Pr µ µ ρ ρ 2.42

dove il termine di dissipazione degli sforzi viscosi i j ij x u ∂ ∂

τ è stato ritenuto trascurabile.

Dall’analisi delle equazioni 2.38-2.42 si deduce che le ipotesi del trasporto del gradiente (equazioni 2.34 e 2.35) e di Boussinesq (2.36) spostano il problema di chiusura delle equazioni di conservazione alla determinazione della viscosità turbolenta, µt.

Modello della lunghezza di miscelamento di Prandtl

Prandtl (1925) ha proposto di legare la viscosità turbolenta al gradiente di velocità del fluido tramite la relazione algebrica:

S l_m t 2 ρ µ = 2.43

Nella 2.43 S rappresenta il tensore degli sforzi medio, definito come:

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = i j j i x u x u S 2 1 2.44

Il modello di Prandtl è molto semplice e non richiede la risoluzione di nessuna equazione di trasporto aggiuntiva (zero equation model). Tuttavia, la sua applicazione nei codici di calcolo CFD è limitata a causa della insufficiente accuratezza.

Modello di Prandtl-Kolmogorov

Il modello di Prandtl-Kolmogorov si basa, invece, sulla risoluzione di un’equazione di trasporto per l’energia cinetica turbolenta, k (one equation model). La viscosità turbolenta

viene, quindi, espressa come:

k l

C _{PK pk}

t ρ µ,

µ = 2.45

dove C_µ,PK è una costante del modello, generalmente porta pari a 0.09, mentre l è una _pk

lunghezza caratteristica valutata, ancora una volta, con correlazioni empiriche.

Anche il modello di Prandtl-Kolmogorov trova scarsa applicazione nei codici CFD commerciali, a causa del modesto miglioramento di accuratezza conseguibile rispetto al zero

equation model.

Il modello k-ε e le sue varianti

Una formulazione più generale del problema di chiusura viene realizzata con il modello k-ε, sviluppato da Launder (1972). In tal caso la viscosità turbolenta è valutata come:

ε ρ

µt = C_µ k2 2.46

L’energia cinetica turbolenta, k, e la sua dissipazione, ε , sono ottenute dalla risoluzione

delle seguenti equazioni di trasporto:

ε ρ σ µ µ ρ ρ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ = ∂ ∂ + ∂ ∂ k i k t i i i P x k x x k u t k 2.47 k C P k C x x x u t i k t i i i 2 2 1 ε ρ ε ε σ µ µ ε ρ ε ρ ε ε ε − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ = ∂ ∂ + ∂ ∂ 2.48 Il termine di sorgente, P , è dato da: k

j i i j k x u u u P ∂ ∂ − = _ρ '' '' _2.49

I valori delle costanti relative al modello k- ε standard sono: 92 . 1 44 . 1 3 . 1 0 . 1 09 . 0 = = ₁ = ₂ = = _{ε ε ε} µ σ σ C C C _k 2.50

Il modello k-ε è molto popolare per la sua semplicità e robustezza numerica, ed è diffusamente impiegato nell’analisi numerica dei processi di combustione. Tuttavia, esso presenta numerose limitazioni:

ƒ Le equazioni sono ricavate nell’ipotesi di alti numeri di Reynolds e non possono essere impiegati per flussi con forte vorticità o anisotropia della turbolenza;

ƒ Il trattamento del flusso alla parete è realizzato a mezzo di espressioni algebriche (Paragrafo 2.4.4);

ƒ Il modello k-ε deve essere modificato nel caso di fluidi comprimibili. Ciò si realizza esprimendo la costante C in funzione del numero di Mach_µ 14 e dividendo il termine di

dissipazione ε in una componente solenoidale ed una di dilatazione (Sarkar et al., 1991).

ƒ Il modello k-ε tende a sovrastimare la dispersione di getti circolari (Morse, 1977; Launder et al., 1972; Pope, 1978). In letteratura sono state proposte numerose correzioni al modello base, che spesso si riducono a modificare la costante C o ad _ε1

esprimerla con una funzione delle coordinate locali.

Tra le diverse varianti del modello k-ε classico si distingue, per la sua robusta base teorica, il cosiddetto modello RNG15 _{k-ε. Il modello affonda le sue radici nella complessa}

teoria dei gruppi di normalizzazione (Yakhot e Orszag, 1986) ma si riduce, in pratica, a esprimere la costante C come: _ε1

3 0 0 , 1 , 1 1 1 βη η η η ε ε ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = _RNG RNG C C con µ ε η=k Pk _2.51 dove 0 , 1 RNG

C_ε è assunto pari al valore della costante C del modello standard. I valori delle _ε1

altre costanti relative al modello RNG k-ε sono:

68 . 1 72 . 0 72 . 0 0845 . 0 4 . 4 015 . 0 0 ≈ , = , = , = 2, = − = η CµRNG σkRNG σε RNG Cε RNG β 2.52

14 _{Il numero di Mach è definito come il rapporto fra il valore locale della velocità del flusso e il valore locale}

della velocità del suono. Al fine di definire il campo di validità dell'ipotesi di incomprimibilità, viene analizzato il valore il numero di Mach. Generalmente, gli effetti della comprimibilità di un fluido possono essere trascurati per numeri di Mach inferiori a 0.3.

2.4.3.2 Modelli diretti

I modelli diretti (Reynolds Stress Model) rinunciano all’ipotesi di isotropia della turbolenza, implicita nell’ipotesi di Boussinesq, e realizzano la chiusura delle equazioni di Navier-Stokes mediate la risoluzione di equazioni di trasporto per i componenti del tensore degli stress di Reynolds. Ciò implica che, nel caso di problemi tridimensionali, è necessario risolvere sei equazioni di trasporto addizionali16. I modelli RSM sono indicati nel caso di flussi complessi, caratterizzati da forti componenti tangenziali (swirl) e rapidi cambiamenti nella velocità di deformazione. Il loro impiego risulta, tuttavia, limitato dall’elevato costo computazionale richiesto e dalla minore robustezza numerica rispetto ai modelli di diffusione per gradiente.

2.4.4 Trattamento del flusso alla parete

La trattazione numerica del flusso in prossimità di pareti solide è molto complessa a causa delle rapide variazioni del profilo di velocità del fluido e per la necessità di rappresentare, in maniera opportuna, gli effetti delle forze viscose.

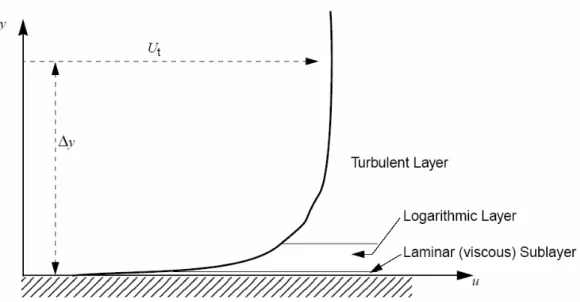
Da un punto di vista fenomenologico, è possibile suddividere uno strato limite turbolento in tre zone (Figura 2.3). Nello strato più interno, generalmente indicato come

sublayer viscoso, il flusso è laminare e la viscosità molecolare esercita un ruolo dominante sui

fenomeni di scambio termico e di quantità di moto. Più lontano dalla parete, invece, nello strato logaritmico, i processi di miscelamento risultano controllati dalla turbolenza. Esiste, infine, una regione intermedia, nota come buffer layer, in cui gli effetti della viscosità molecolare e della turbolenza si bilanciano.

Supponendo che la distribuzione di velocità in prossimità della parete possa essere approssimata con il profilo logaritmico, le caratteristiche del flusso nello strato limite turbolento possono essere valutate dalla cosiddetta legge di parete:

( )

Nell’equazione 2.53 U è la velocità del flusso turbolento completamente sviluppato ad una _t

distanza y∆ dalla parete, u è la velocità di taglio, _τ τ_w è lo sforzo di taglio, y è la distanza +

adimensionale dalla parete, κ è la costante di Von Karman e CR è una costante dipendente

dalla rugosità della parete.

Figura 2.3 – Rappresentazione dello strato limite turbolento.

Il ricorso alla legge di parete permette di valutare il profilo di velocità del fluido nello strato limite sulla base di relazioni empiriche. Non è necessario considerare l’effetto delle forze viscose nel modello di turbolenza e ciò permette di ridurre, in modo significativo, il costo computazionale richiesto.

I modelli di turbolenza per bassi numeri di Reynolds (Low-Reynolds-number models) consentono, invece, di risolvere completamente il sublayer viscoso, utilizzando una griglia molto fine in direzione normale alla parete. Il numero di nodi nello strato limite turbolento deve essere, infatti, sufficiente per riprodurre le rapide variazioni del profilo di velocità del fluido. Ciò determina un forte incremento dei tempi di elaborazione richiesti rispetto all’approccio basato sulla funzione di parete.

2.4.5 Modelli di combustione

La definizione della velocità di reazione, w&k , che appare come termine sorgente nell’equazione di conservazione delle specie chimiche mediata secondo Favre, rappresenta un problema chiave nella modellazione dei flussi reagenti.

In generale, una reazione di combustione può essere descritta in termini di M reazioni elementari che coinvolgono NC componenti:

k N k j k k N k j k R R C C ⋅ ⇔ ⋅

∑

∑

dove νkj è il coefficiente stechiometrico del componente R nella reazione elementare j, k definito come: ' '' j k j k j k ν ν ν = − . 2.55

La velocità di reazione netta per il componente k è data dalla relazione:

∑

dove W è il peso molecolare della specie k. Il termine k Q rapprese4nta il grado di j avanzamento della reazione j, esprimibile come:

∏

∏

reazione j, mentre _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ k k W Y ρ

è la concentrazione molare della specie k.

Le costanti cinetiche sono generalmente espresse utilizzando la relazione di Arrhenius e la costante di equilibrio, K : eq ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = T exp RT exp j aj j f j a j j f j f T T A E T A k β β 2.58 eq j f j r K k k = 2.59

dove Af j è il fattore pre-esponenziale, β j è l’esponente della temperatura mentre Eaj e Taj rappresentano, rispettivamente, l’energia e la temperatura di attivazione.

Dalle espressioni riportate per il calcolo della velocità di reazione (equazioni 2.56-2.59) si evince che il termine w&_k è fortemente non lineare e non può essere espresso

semplicemente in funzione delle frazioni massiche medie, Y_k , della densità media, ρ e

della temperatura media, T . Un approccio diretto consiste nell’espansione della velocità di

reazione media in serie di Taylor. Consideriamo, per semplicità, una reazione irreversibile tra un combustibile, F, ed un ossidante, O:

P s sO

F+ →(1+ ) . 2.60

La velocità di consumo del combustibile può essere espressa come: ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − = T T Y Y T A w a O F F 1 1 2 1 exp β ρ & . 2.61

Espandendo in serie di Taylor i termini _Tβ1 _{e ⎟}

⎠ ⎞ ⎜ ⎝ ⎛− T T_{a 1}

exp , espressi in funzione delle variabili medie, si ottiene (Borghi, 1978):

(

)

(

)

( )

₍

(

_{) (}

_[

)

₎

_]

∑

(

) (

)

L’equazione 2.63 comporta numerose difficoltà. In primo luogo, essa introduce nuove quantità ( '' ''

O FY

Y e Yk''T'' ) che è necessario modellare con relazioni algebriche o equazioni di

trasporto. Inoltre, l’errore di troncamento risulta inaccettabile quando solo pochi termini dell’espansione in serie sono presi in considerazione. Infine, l’equazione 2.63, è valida solo per reazioni irreversibili e non è estendibile a schemi di combustione realistici. Per le ragioni illustrate, la chiusura del termine w&_k non viene realizzata con la 2.63 ma ricorrendo a modelli

derivanti da analisi fisiche. Tali modelli sono stati sviluppati per lo studio delle fiamme premiscelate e diffusive e sono brevemente illustrati di seguito.

2.4.5.1 Modello Eddy Break-up

Il modello Eddy Break-up, sviluppato da Spalding (1971) per lo studio delle fiamme premiscelate, si basa sull’analisi fenomenologia della combustione turbolenta nell’ipotesi di elevati numeri di Reynolds (Re>>1) e di Damköhler (Da>>1). L’ipotesi alla base del

modello è che la velocità globale del processo di combustione sia controllata dal miscelamento turbolento e non dalla chimica delle reazioni di ossidazione. La velocità di reazione media, w&k , risulta, quindi, proporzionale al tempo caratteristico del miscelamento turbolento (k/ε). Nel caso di sistemi caratterizzati da un eccesso di ossidante si ottiene

(reazione 2.60):

( )

dove C_EBU è una costante del modello, dell’ordine dell’unità, e Y indica la varianza della _F''

frazione massica del combustibile.

2.4.5.2 Modello Eddy Dissipation e le sue varianti

Il modello Eddy Dissipation, sviluppato da Magnussen e Hjertanger (1976) costituisce l’estensione del modello Eddy Break-up alle fiamme non premiscelate. Il grado di avanzamento medio della reazione j è valutato dalla conoscenza della frazione molare media di reagenti,

[ ]

[ ]

[ ]

[ ]

∑

∑

dove CED e BED sono due costanti del modello. Il grado di avanzamento Q è limitato, j pertanto, dalla specie chimica presente in difetto all’interno sistema.

Esistono alcune varianti del modello Eddy Dissipation che permettono di considerazione gli effetti di una cinetica non infinitamente veloce. Questi modelli, noti come modelli combinati Eddy Dissipation/Finite Rate Chemistry, valutano il grado di avanzamento della reazione j come:

(

)

dove Qj mix e

Arr j

Q rappresentano i gradi di avanzamento ottenuti, rispettivamente,

nell’ipotesi di miscelamento e cinetica controllante. Il termine Qj Arr è valutato in base alla relazione 2.57, sostituendo ai valori istantanei della densità, delle frazioni massiche e della temperatura i corrispondenti valori medi:

∏

∏

Questo approccio è valido solo nel caso di bassi numeri di Damköhler (Da≈1) e numeri di

Reynolds molto elevati (Re>>1). In tali condizioni, infatti, la turbolenza all’interno del sistema è così intensa che il sistema evolve verso condizioni tipiche di un reattore perfettamente miscelato (well stirred reator limit).

2.4.6 Modello di radiazione

La valutazione del flusso di calore radiante, Q&rad , assorbito ed emesso da una fiamma risulta particolarmente importante nella simulazione numerica della combustione turbolenta. È noto, infatti, che la radiazione costituisce il meccanismo di scambio termico dominante nelle applicazioni di combustione, a causa delle elevate temperature in gioco17.

Il linea di principio, Q&rad potrebbe essere calcolato dalla conoscenza della distribuzione di temperatura nel sistema in esame. Tuttavia la temperatura costituisce un’incognita del problema e viene fornita come risultato delle simulazioni numeriche. Di conseguenza, il calcolo dello scambio termico radiativo risulta accoppiato alla risoluzione dell’equazione di bilancio energetico.

L’equazione di trasporto dell’energia termica radiante (Radiative Transfer Equation o RTE) può essere espressa come:

( ) (

) ( )

( )

( ) ( )

∫

17 _{L’equazione di Stephan-Boltzmann evidenzia che lo scambio di energia radiante emessa da un corpo è}

dove:

ƒ ν è la frequenza;

ƒ r e s rappresentano, rispettivamente, il vettore posizione e direzione;

ƒ s è la distanza percorsa dalla radiazione dal punto di emissione a quello di

assorbimento (path lenght),

ƒ K e a K indicano, rispettivamente, i coefficienti di assorbimento e riflessione ν

(scattering);

ƒ I è l’intensità della radiazione emessa da un corpo nero; b

ƒ I è l’intensità della radiazione emessa in corrispondenza della frequenza _ν ν , funzione

della posizione, r, e della direzione, s;

ƒ Ω è l’angolo solido18 _{(Figura 2.4);}

ƒ Φ indica la probabilità che la radiazione sia riflessa dalla direzione s a s (scattering ' phase function);

ƒ SR indica una sorgente di radiazione.

Figura 2.4 – Definizione dell’angolo solido.

L’equazione 2.69 è un’equazione integro-differenziale del primo ordine, funzione delle coordinate spaziali, della direzione e della frequenza. La sua risoluzione analitica è, pertanto, molto complessa e possibile solo in casi estremamente semplici. In generale si

18 _{L'angolo solido con cui una superficie dA}

j è vista da certo punto P è definita come la proiezione della

ricorre, quindi, ad alcune semplificazioni che permettono di approssimare la dipendenza direzionale e spettrale della RTE.

2.4.6.1 Metodo delle armoniche sferiche

Il metodo delle armoniche sferiche, anche noto come metodo PN, è basato sull'idea che

la soluzione della RTE possa essere semplificata esprimendo l’intensità della radiazione emessa, I , come una serie di prodotti di funzioni angolari e spaziali. Il numero di termini _ν

utilizzati nell’espansione in serie fornisce l’ordine ed il relativo nome al metodo. Si hanno, ad esempio, approssimazioni P1 o P3. Le approssimazioni di ordine pari non sono mai impiegate

poiché è noto che i metodi di ordine dispari sono più accurati di quelli successivi di ordine pari. Il modello PN è particolarmente adatto per la modellazione di sistemi in cui la radiazione

è emessa isotropicamente, come accade nei processi di combustione. Lo svantaggio del metodo è che, all’aumentare dell’ordine N, l’accuratezza dell’approsimazione aumenta in modo trascurabile mentre la complessità matematica cresce fortemente.

2.4.6.2 Metodo delle ordinate discrete

Il metodo delle ordinate discrete, conosciuto come metodo SN, si basa anch’esso sulla

dipendenza angolare dell’intensità della radiazione emessa. A differenza del modello PN,

tuttavia, il metodo SN discretizza l’intero angolo solido Ω , utilizzando un numero finito di

direzioni, a ciascuna delle quali è associato un fattore peso. L'intensità della radiazione in ciascuna direzione è ritenuta uniforme e risulta funzione della sola coordinata spaziale. Gli integrali sull’angolo solido, per il calcolo del flusso di calore radiante e delle sorgenti di radiazione, sono valutati utilizzando opportune formule di quadratura. Il numero di direzioni utilizzate fornisce l’ordine ed il relativo nome al metodo. Si hanno, ad esempio, approssimazioni S2 o S4. Le approssimazioni di ordine pari sono generalmente usate per

disporre di direzioni e pesi simmetrici, invarianti rispetto a rotazioni di 90°. Il metodo delle ordinate discrete è in grado di fornire un’approssimazione sufficientemente accurata della RTE nel caso di ordini N elevati (N>8). In presenza di sorgenti radianti localizzate, il metodo può risentire, tuttavia, di errori significativi, dovuti alla discretizzazione angolare e spaziale.

2.4.6.3 Metodo a zone

Il metodo a zone si basa sulla suddivisione del sistema in esame in un numero finito di volumi e superfici all’interno dei quali la temperatura e le proprietà radiative possono considerarsi costanti. Un’equazione di bilancio energetico viene, quindi, introdotta per ciascuna coppia di volumi e superfici a contatto. Si ottiene un sistema di equazioni algebriche per la valutazione delle temperatura e dei flussi di calore.

Il metodo a zone è attraente per molte applicazioni ingegneristiche, poiché l’approccio impiegato è pratico e potente. Tuttavia, esso è difficilmente implementabile in un codice CFD che utilizza, per la risoluzione delle equazioni di conservazione, la tecnica ai volumi finiti. Infatti, il costo computazionale richiesto dal metodo a zone risulterebbe proibitivo se per la sua risoluzione fosse adottata la stessa griglia di calcolo utilizzata per le equazioni di Navier-Stokes.

2.4.6.4 Metodo Monte Carlo

Il metodo Monte Carlo è un metodo puramente statistico, particolarmente adatto per la risoluzione dell’equazione di trasporto dell’energia radiante, che simula le interazioni tra i fotoni, responsabili del trasporto dell’energia radiante, e l’ambiente che li circonda. La storia di un numero rappresentativo di fotoni viene ricostruita e tracciata dal punto di emissione fino a quello di assorbimento. In presenza di fenomeni di scattering, la direzione dei fotoni viene

aggiornata attraverso un campionamento della distribuzione degli angoli di riflessione. Il

metodo Monte Carlo è in grado di fornire risultati che oscillano intorno alla soluzione esatta della RTE. Tuttavia, esso è soggetto ad errori statistici ed è caratterizzato da tempi un costo computazionale molto elevato..

2.4.6.5 Valutazione delle proprietà radiative

L’equazione di trasporto dell’energia radiante evidenzia che l’intensità della radiazione, I , varia nello spettro delle frequenze. La valutazione della dipendenza spettrale _ν

di I costituisce uno dei problemi più complessi nella risoluzione della RTE e richiede, _ν

Il modello spettrale Gray assume che le proprietà radiative del mezzo siano uniformi in tutto lo spettro. Ciò elimina la dipendenza di I da _ν ν e l’intensità della radiazione risulta

costante per tutte le lunghezze d’onda.

Il modello Weighted Sum of Gray Gases (WSGG) assume che l’assorbimento e l’emissione di energia radiante da parte di un mezzo gassoso sia rappresentabile come somma pesata del contributo di N gas grigi, caratterizzati da proprietà radiative costanti.

Il modello Multiband suddivide lo spettro in N bande di ampiezza finita all’interno delle quali le proprietà radiative possono essere considerate quasi uniformi e mediate senza perdita di accuratezza.

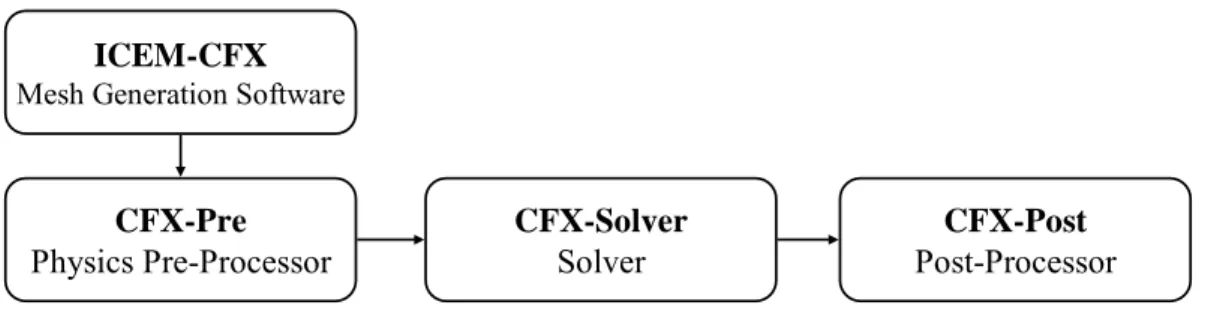
2.5 Struttura di un codice di calcolo CFD

I principali elementi che compongono un codice di calcolo CFD sono: ƒ Il modello matematico;

ƒ Il modello numerico; ƒ L’algorittmo di risoluzione; ƒ I criteri di convergenza.

2.5.1 Modello matematico

Il modello matematico è l’insieme delle equazioni differenziali, delle relazioni costitutive e dei modelli di turbolenza, di combustione e di radiazione impiegati per la rappresentazione del sistema fisico considerato. La scelta del modello matematico dipende strettamente dal problema in esame. Non esiste, infatti, un modello universale, ma è necessario stabilire, caso per caso, quello più appropriato e capace di fornire il miglior grado di approssimazione.

Al fine di ottenere un modello matematico ben posto è necessario stabilire, inoltre, le condizioni al contorno per le equazioni di Navier-Stokes. I contorni di un dominio di calcolo sono, generalmente, di tre tipi: contorni senza passaggio di fluido (Wall), contorni con flusso entrante (Inlet) e contorni con flusso uscente (Outlet). In corrispondenza delle sezioni di ingresso devono essere assegnate le caratteristiche del flusso convettivo (portata, velocità, temperatura, composizione), mentre i flussi diffusivi sono posti pari a zero o opportunamente approssimati. Alle sezioni di uscita non sono note, normalmente, le caratteristiche del flusso e deve essere, pertanto, specificato il valore della pressione sul confine. Per i contorni

impermeabili del dominio, infine, devono essere indicate le condizioni di parete (no slip, free

slip) e i flussi di calore (conduzione, convezione, irraggiamento).

Infine, è necessario fornire la dipendenza delle proprietà termodinamiche che compaiono nelle equazioni di conservazione (viscosità, conducibilità termica, diffusività, calore specifico) dalle variabili dipendenti.

2.5.2 Modello numerico

La risoluzione delle equazioni differenziali viene realizzata per via numerica, ricorrendo al concetto di discretizzazione. Esso è alla base di qualsiasi metodo numerico e consiste nel definire, all’interno del dominio di calcolo, dei punti, detti nodi, in corrispondenza dei quali sono valutate le grandezze incognite. Nel caso del Metodo ai Volumi Finiti (FVM) i nodi individuano il centro dei volumi, o celle, in cui è suddiviso il dominio di calcolo. L'insieme dei nodi e delle celle costituisce la cosiddetta griglia di calcolo. È possibile distinguere tra tre diverse tipologie di griglie:

ƒ Griglie strutturate cartesiane, costituite da famiglie mutuamente ortogonali di rette parallele. Ciò consente di identificare in maniera univoca i volumi di controllo definiti dall’intersezione di tali linee, attraverso una terna di indici (i,j,k). La flessibilità geometrica delle griglie strutturate è molto limitata anche se il ricorso a più blocchi contigui permette di trattare domini costituiti dall’unione di rettangoli, in due dimensioni, e parallelepipedi, in tre dimensioni.

ƒ Griglie strutturate curvilinee, logicamente identiche alle griglie strutturate cartesiane ma più onerose da un punto di vista computazionale. Tali griglie sono caratterizzate da una maggiore flessibilità geometrica rispetto alle precedenti, in particolare utilizzando più blocchi contigui.

ƒ Griglie non strutturate. Sono le griglie più flessibili ed adatte le geometrie complesse di interesse industriale. La griglia non è più definita da famiglie di linee ma, piuttosto, il dominio è suddiviso in elementi di forma arbitraria (tetraedri, esaedri) che possono essere facilmente addensati nelle zone di maggior interesse, anche in modo automatico nel corso della soluzione (griglie adattive). Gli svantaggi di tali griglie sono l’elevato costo computazionale e la maggiore complessità nell’implementazione.

L’accuratezza del calcolo aumenta, generalmente, all’aumentare della risoluzione spaziale adottata, anche se un maggiore numero di celle comporta tempi di elaborazione più

per il buon esito di una simulazione numerica. Infatti, la scelta di una griglia grossolana (coarse) può fornire risultati poco accurati, mentre il ricorso a griglie troppo fini può portare a problemi numerici di convergenza. E’ quindi necessario trovare un compromesso per sfruttare con efficacia le risorse computazionali.

Nel metodo FVM le equazioni differenziali sono risolte in ciascuna cella della griglia di calcolo. Gli integrali di volume sono trasformati in integrali di superficie, utilizzando il teorema della divergenza di Gauss-Green, e le equazioni continue vengono approssimate con funzioni discrete. La collocazione delle variabili nei volumi di controllo può essere di due tipi: ƒ Collocata (Collocated o Unstaggered), se tutte le variabili sono definite nel centro

delle celle.

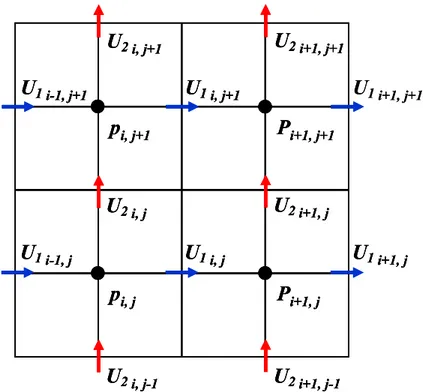
ƒ Sfalsata (Staggered) se nei punti nodali sono definite le variabili relative al bilancio di massa e dell’energia (pressione, temperatura, densità, frazioni massiche delle specie chimiche) mentre le variabili relative al bilancio della quantità di moto sono assegnate ai bordi dei volumi di controllo.

La configurazione sfalsata (Figura 2.5) fornisce, rispetto alla distribuzione collocata, un migliore accoppiamento tra il campo di pressione e di velocità e permette, pertanto, di ridurre le oscillazioni e migliorare la convergenza. Tuttavia, la collocazione staggered della variabili è possibile solo nel caso di griglie strutturate cartesiane e ciò ha contribuito a diffondere la configurazione collocata nella gran parte dei codici CFD commerciali. Inoltre, dagli anni 80 ad oggi, sono state introdotte modifiche nelle tecniche di interpolazione per le griglie collocate (Rhie e Chow, 1982) che riducono il rischio di disaccoppiamento tra velocità e pressione.

p

P

p

P

U

U

U

U

U

U

U

U

U

U

U

U

p

P

p

P

U

U

U

U

U

U

U

U

U

U

U

p

P

p

P

U

U

U

U

U

U

U

U

U

U

U

U

Figura 2.5 – Esempio di griglia sfalsata (staggered) in due dimensioni.

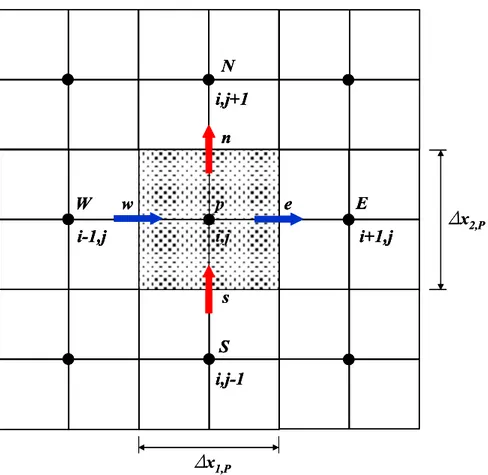
Per illustrare gli schemi di discretizzazione delle equazioni di conservazione facciamo riferimento all’equazione di trasporto del generico scalareϕ (temperatura, componente di velocità, concentrazione): ϕ ϕ ϕ ρ ϕ ρ S x x x u t _{i i} eff _i i ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ Γ ∂ ∂ = ∂ ∂ + ∂ ∂ 2.70

dove Γ è una diffusività efficace e eff S è un termine di sorgente che include i contributi della ϕ pressione e delle forze di volume. Integrando l’equazione 2.70 su un generico volume di controllo e, applicando il teorema di Gauss-Green, si ottiene,:

dV S dA dn x dA dn u dV t V V i A A i eff i i

∫

∫

∫

∫

Nel caso stazionario l’equazione 2.71 diventa:

dV S dA dn x dA dn u V i A A i eff i i

∫

∫

∫

Facendo riferimento al volume di controllo di centro P riportato in Figura 2.6, i termini convettivi che compaiono nell’equazione di trasporto 2.72 possono essere discretizzati come:

∫

_∫

( )

( )

( )

( )

w u x F u x F u x F u x

F = ρ ₁ ∆ _2, = ρ ₁ ∆ _2, = ρ ₂ ∆ _1, = ρ ₂ ∆ _1, 2.74

Per calcolare i termini convettivi è necessario conoscere il valore assunto dalla variabile ϕ sulle facce delle celle, in funzione dei valori che la stessa variabile assume nel centro del volume di controllo.

Lo schema Upwind (UDS) è uno schema numerico del primo ordine in base al quale il valore della variabile ϕ sulla periferia di ciascuna cella è assunto uguale a quello del nodo posto a monte: ⎩ ⎨ ⎧ < > = 0 0 e E e P e F F ϕ ϕ ϕ . 2.75

Oltre allo schema Upwind esistono altri schemi del primo ordine. Tra questi, lo schema alle differenze centrali (CDS) valuta ϕ_e come:

2 E P e ϕ ϕ ϕ = + . 2.76

Lo schema alle differenze centrali è più accurato dello schema Upwind ma non consente di realizzare modelli numerici veloci e stabili. Per questa ragione, esso viene impiegato solo nel caso di flussi a bassa velocità mentre, per quelli ad alta velocità, si preferisce lo schema

Upwind.

È possibile combinare i vantaggi dei due modelli con lo schema ibrido (HDS). Secondo tale schema, il valore di ϕe è dato da:

⎩ ⎨ ⎧ < ≥ = 2 2 , , Pe Pe CDS e UDS e e ϕ ϕ ϕ . 2.77

Il numero di Peclet, Pe, è definito come rapporto tra i flussi convettivo e diffusivo:

eff i F Pe Γ = . 2.78

p W s n w e E N S i,j i,j-1 i+1,j i-1,j i,j+1 Dx_1,P Dx_2,P p W s n w e E N S i,j i,j-1 i+1,j i-1,j i,j+1 p W s n w e E N S i,j i,j-1 i+1,j i-1,j i,j+1 Dx_1,P Dx_2,P

Figura 2.6 – Volume di controllo per una griglia collocata.

Per quanto riguarda i termini diffusivi, viene generalmente ipotizzata una variazione lineare della variabile ϕ tra i nodi:

(

)

dove λ_e,PE è il coefficiente di interpolazione

P E P e PE e x x x x − − = , λ . 2.80

La componente del gradiente normale alla faccia del volume di controllo viene, quindi, approssimata come: P E P e e x ϕ ϕ ϕ ϕ ϕ − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ 1 . 2.81

Infine, il termine di sorgente, S , viene espresso come una funzione lineare della _ϕ

variabile ϕ: ϕ ϕ ϕ ϕ S S P S = _,0+ _, . 2.82

2.5.3 Algoritmo di risoluzione

La trasformazione delle equazioni differenziali dalla forma continua a quella discreta ha come risultato finale l'ottenimento di un sistema di equazioni algebriche aventi per incognite i valori delle grandezze di interesse nei nodi. Il sistema da risolvere può essere indicato come:

b

Aϕ = 2.83

dove A è la matrice dei coefficienti, b è il vettore dei termini noti ϕ è il vettore delle

incognite. Il sistema 2.83 viene risolto con un opportuno metodo iterativo che produce una sequenza di vettori ϕn

convergenti al vettore ϕ del sistema iniziale.

Il sistema di equazioni può essere risolto con due approcci differenti:

ƒ Soluzione sequenziale. Ciascuna equazione viene risolta separatamente, come se contenesse un’unica variabile incognita, quella primaria, e considerando le altre variabili note. Per ottenere la convergenza delle singole equazioni sono necessarie un certo numero di iterazioni, dette iterazioni.interne. Una volta completata la risoluzione sequenziale è necessario realizzare le cosiddette iterazioni esterne, per ottenere la convergenza contemporanea di tutte le equazioni.

ƒ Soluzione simultanea. In questo caso le equazioni discretizzate sono considerate facenti parte di un unico sistema e sono risolte simultaneamente.

2.5.4 Criteri di convergenza

Il metodo più comune per valutare la convergenza di una simulazione numerica consiste nel monitorare l’andamento dei residui, definiti come:

n n

A b

r = − ϕ . 2.84

Generalmente, i criteri di convergenza vengono applicati ai residui normalizzati:

ϕ ∆ = P n n a r r~ 2.85

dove aP è un coefficiente caratteristico del volume di controllo considerato e ∆ indica ϕ l’intervallo di variabilità di ϕ nel dominio. Una soluzione viene, pertanto, giudicata convergente se le componenti del vettore n

r~ risultano tutte inferiori ad un valore prefissato.