APPENDICE A
APPROFONDIMENTI SULLE
FUNZIONI BASE
A.1 DEFINIZIONE DELLE FUNZIONI BASE
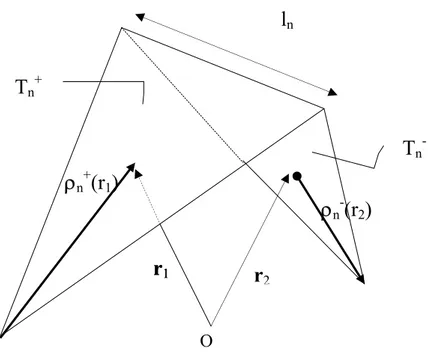
Richiamiamo la definizione di funzione base data nel paragrafo 1.3. Consideriamo l’n-esimo spigolo del modello a piastre triangolari; nell’ipotesi che non si tratti di uno spigolo di bordo, la funzione base sulle due facce Tn± è definita come segue:
altrove 0 ) ( 2 ) ( 2 ) ( n n ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ∈ ∈ = − − − + + + T r r ρ T r r ρ r f n n n n n n n A l A l (A.1) dove:
ln è la lunghezza del generico spigolo (necessariamente non di bordo),
spigolo, spigolo,
An+ e An- sono, rispettivamente, l’area della faccia positiva e l’area di
An+ e An- sono, rispettivamente, l’area della faccia positiva e l’area di
quella negativa, quella negativa,
ρn+ è il vettore che congiunge il vertice libero della faccia Tn+ con il
ρn+ è il vettore che congiunge il vertice libero della faccia Tn+ con il
generico punto di essa, generico punto di essa,
ρn- è il vettore che congiunge il generico punto della faccia Tn- con il
ρn- è il vettore che congiunge il generico punto della faccia Tn- con il
suo vertice libero, suo vertice libero,
O è l’origine del sistema di riferimento. O è l’origine del sistema di riferimento. ρn-(r2) ρn+(r1) r1 r1 O r2 ln Tn+ Tn-
fig. A.1 - Visualizzazione della funzione base fig. A.1 - Visualizzazione della funzione base
A.2 PROPRIETA’ DELLE FUNZIONI BASE
1) La densità di corrente superficiale ha componente normale nulla
ai bordi della regione (Tn+ ∪Tn-).
Per renderci conto del perchè basta osservare la figura A.1, considerando la funzione di base sui bordi della regione suddetta 2) La componente normale della funzione base relativa all’n-esimo
spigolo è costante e continua.
Poichè vogliamo calcolare la componente normale al lato ln,
moltiplichiamo scalarmente entrambi i membri della (A.1) per il versore :
ˆn
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=
⋅
=
=
⋅
=
⋅
− − − − + + + +1
2
2
ˆ
)
(
2
1
2
2
ˆ
)
(
2
ˆ
)
(
n n n n n n n n n n n n n n nl
A
A
l
A
l
l
A
A
l
A
l
n
r
ρ
n
r
ρ
n
r
f
(A.2)ed otteniamo esattamente quanto affermato nell’enunciato della proprietà.
3) La componente normale della densità di corrente superficiale
relativa all’n-esimo spigolo è costante e continua attraverso lo spigolo stesso
Per dimostrare questa proprietà, consideriamo l’espressione della
J(r
ln)=Ι
nf
n(r
ln),
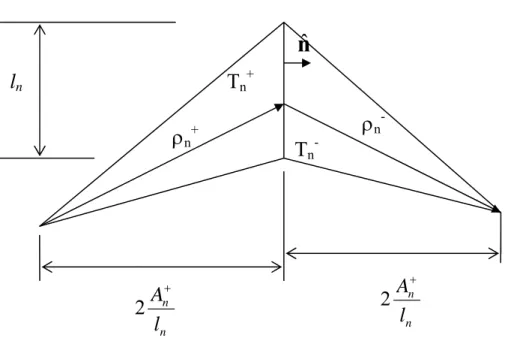
(A.3)dove rln è un generico punto appartenente a ln, come mostrato in
figura A.2. ln
nˆ
ρn -ρn+ Tn+ Tn -n n l A+ 2 n n l A+ 2Fig. A.2: Riferimenti geometrici per la proprietà 2
Nella (A.3) non consideriamo i contributi delle funzioni base relativi ai quattro spigoli che costituiscono i confini della regione (Tn+ ∪ Tn-): questo
perchè, per la proprietà 1, tali contributi risultano nulli.
Poichè siamo interessati alla componente normale al lato n-esimo della
J(rln), dalla proprietà 2) otteniamo:
⎪
⎪
⎩
⎪⎪
⎨
⎧
=
⋅
=
⋅
=
⋅
− − + + n n n n lnI
ˆ
)
(
2
I
I
ˆ
)
(
2
I
ˆ
)
(
n
r
ρ
n
r
ρ
n
r
J
n n n n n nA
l
A
l
(A.4)Da questa proprietà discende immediatamente la seguente:
4) I coefficienti In rappresentano la densità di corrente superficiale
normale al lato n-esimo.
A.3 DEFINIZIONE DI PRODOTTO SCALARE TRA DUE FUNZIONI BASE
Dato uno spazio vettoriale V si definisce prodotto scalare un’applicazione (V x V) → R che gode delle seguenti proprietà:
i. u ,v = v ,u ∀ u, v ∈V; ii.
(
u+v)
,w = u ,w + v ,w ∀ u, v, w ∈V; iii.( )
λu ,v =λ u ,v ∀ u ∈V, λ ∈ R; iv. u ,u ≥0 ∀ u ∈V; v. u ,u =0 ⇔ u=0 ∀ u ∈V.Definiamo dunque il prodotto scalare fra due generiche funzioni base fn(r)
e fm(r) secondo la seguente espressione:
f
n(
r
),
f
m(
r
)
=
∫∫
f
n(
r
′
)
⋅
f
m(
r
′
)
d
r
′
S(A.5)