CAPITOLO 2 IL MODELLO MONODIMENSIONALE PER SCHEMI SEMPLICI DI TRAVI

CAPITOLO 2 41

CAPITOLO 2

IL MODELLO MONODIMENSIONALE PER SCHEMI SEMPLICI DI

TRAVI

2.1 INTRODUZIONE

Allo stato attuale della ricerca non risulta disponibile una formulazione analitica in grado di valutare la tensione nei cavi non aderenti a rottura.

Come si è visto in precedenza, esistono, in letteratura, numerose formulazioni ma si è evidenziato come la maggior parte di esse siano di carattere “sperimentale” ovvero utilizzino coefficienti valutati attraverso prove in laboratorio.

In questo capitolo si intende sviluppare un modello analitico in grado di valutare il carico e la tensione nel cavo a rottura per travi precompresse con cavi non aderenti. In particolare si intende effettuare un confronto tra il comportamento a rottura di schemi semplici a cavi non aderenti ed a cavi aderenti al fine di valutare la convenienza nell’utilizzo di questi ultimi come alternativa alla precompressione tradizionale.

La validità della formulazione analitica sviluppata per i cavi non aderenti verrà confrontata nel Capitolo 3 con le prove sperimentali disponibili in letteratura. Il confronto tra cavi aderenti e non aderenti avverrà a livello analitico e numerico, effettuando modellazioni con il programma agli elementi finiti Atena e sviluppando, inoltre,in questo capitolo, un’indagine parametrica al fine di evidenziare i principali fattori che influenzano la fase di rottura per i due tipi di precompressione.

2.2 I MODELLI ANALITICI

La fase di rottura viene studiata in generale per capire il grado di sicurezza di un’ipotetica struttura rispetto ad una situazione di criticità ovvero per determinare quale coefficiente di sicurezza abbia la struttura in fase di esercizio rispetto alla situazione critica di rottura.

Nel caso di travi precompresse con cavi aderenti la valutazione della deformazione del cavo a rottura viene effettuata valutando tale deformazione nella sezione più sollecitata, sfruttando l’aderenza tra cavo e calcestruzzo secondo la trattazione classica (Giancreco [57], Collins [58]) e pertanto l’incremento di deformazione del cavo ∆ε_ps

,

dovuto al carico esterno, risulta

“section - dependent” ovvero dipende dalla geometria della sezione.

Nel caso dei cavi non aderenti la trattazione classica non è più applicabile perché viene a mancare l’ipotesi fondamentale di aderenza tra cavo e calcestruzzo.

I numerosi test effettuati in laboratorio dai vari ricercatori hanno dimostrato che la rottura di una trave monolitica precompressa a cavi non aderenti, sottoposta ad un carico verticale esterno, è dovuta al raggiungimento del valore critico della deformazione di compressione del

calcestruzzo ovvero la rottura della trave avviene per schiacciamento del calcestruzzo mentre il cavo rimane generalmente in campo elastico e quindi al di sotto del limite di snervamento. Per questo tipo di strutture è quindi importante conoscere il valore della tensione nel cavo nella fase di rottura.

Una delle principali difficoltà che si incontrano quando si intende valutare analiticamente la tensione nel cavo a rottura è il calcolo dell’incremento di deformazione nel cavo ∆ε_ps (figura 2) per effetto del carico esterno (equazione 1.1).

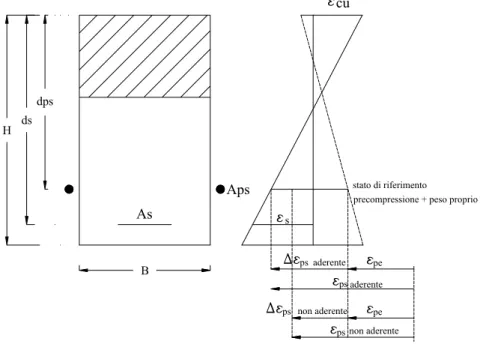
Figura 2. La differenza tra cavi aderenti e cavi non aderenti in termini di deformazioni.

Dal momento che i cavi non sono aderenti essi sono liberi di muoversi in relazione alla deformazione totale della trave. Pertanto la deformazione del cavo è sostanzialmente differente in ogni sezione dalla corrispondente deformazione del calcestruzzo. Per valutare l’incremento di deformazione del cavo ∆ε_ps è necessario, quindi, ricorrere alla congruenza tra cavo e calcestruzzo: ∆ε_ps diventa una funzione della deformazione complessiva della trave valutata alla quota del cavo e pertanto in letteratura viene definito “member – dependent”. Questa caratteristica rende, ovviamente, più complicata l’analisi della trave precompressa con cavi non aderenti e si pone, pertanto, il problema di come modellare la deformabilità globale della trave stessa. Inoltre, dal momento che la forza di precompressione viene trasferita al calcestruzzo attraverso gli ancoraggi o i deviatori, si desta la resistenza dovuta all’attrito.

Per semplicità di modellazione e di calcolo, vengono generalmente considerati due casi estremi: 1. caso di “free slip”(assenza di attrito)

il cavo si muove liberamente in corrispondenza dei deviatori senza incontrare alcuna resistenza dovuta all’attrito. In questo caso si assume che la deformazione del cavo sia costante per tutta la sua lunghezza e l’incremento d deformazione ∆ε_ps viene calcolato secondo la relazione: dz L L c cm ps =∆ =

∫

∆ ∆ 0 1 _ε ε ε (2.a) Aps As cu B H ds dps pe ps ps pe aderente non aderente ps aderente non aderente ps stato di riferimento

precompressione + peso proprio

CAPITOLO 2 43

2. caso “perfectly fixed” (assenza di scorrimento del cavo in corrispondenza dei deviatori). In questo caso il cavo è considerato bloccato in corrispondenza dei deviatori e questo implica che la variazione di deformazione di ciascun tratto di cavo compreso tra due deviatori è completamente indipendente dagli altri tratti. L’incremento di deformazione del cavo dipende, pertanto, esclusivamente dalla deformazione dei due deviatori o dei due ancoraggi ai quali il cavo è fissato. L’incremento di deformazione dell’i-esimo cavo ∆ε_ps,i viene espresso nel seguente modo:

i i i ps _l l ∆ = ∆ε _,

(2.b)

dove ∆l_i

è l

’incremento di lunghezza che si ha nel cavo i-esimo per effetto dei carichi esterni e l_i è la lunghezza iniziale dell’i-esimo cavo.

In questo capitolo si intende illustrare i due modelli analitici sviluppati per valutare la tensione a rottura nei cavi ed il momento ultimo di una trave precompressa sia nel caso di cavi aderenti che nel caso di cavi non aderenti. I due modelli analitici di seguito sviluppati adottano l’ipotesi di cavi “free slip”ovvero di cavi liberi di scorrere in corrispondenza dei deviatori (viene quindi trascurato l’attrito) e sono:

• Il modello semplificato

Questo modello ha permesso di comprendere gli aspetti essenziali del problema e gli ordini di grandezza dei parametri in gioco. E’ stata sviluppata una formulazione adimensionale che, con la richiesta di pochi dati, è in grado di valutare, sia nel caso di cavi aderenti che nel caso di cavi non aderenti, la tensione a rottura del cavo, dell’armatura aderente, il momento ed il carico che determinano la rottura della trave; con tale formulazione si è svolta, inoltre, un’indagine parametrica mirata a valutare l’incidenza di ogni singolo parametro individuato nei confronti della capacità ultima;

• Il modello trave non lineare

si tratta di un modello più affinato rispetto al modello semplificato in quanto tiene conto del comportamento non lineare dei materiali. La trave precompressa viene considerata come una successione di blocchi individuati tra due fessure successive come verrà meglio illustrato di seguito.

Con questa modellazione si intende comprendere, inoltre, la bontà delle approssimazioni introdotte nel modello semplificato in modo da individuare l’errore che si commette nella valutazione del momento ultimo e della tensione del cavo a rottura.

2.2.1 IL MODELLO SEMPLIFICATO

Si consideri una trave appoggiata con sezione trasversale rettangolare sottoposto a differenti tipi di carico e con diversi tipi di tracciato del cavo.

Sono stati considerati i seguenti carichi: • peso proprio e precompressione; • carichi esterni.

L’analisi a rottura è stata svolta con le seguenti ipotesi:

1. per il calcestruzzo compresso si è considerato un diagramma delle tensioni di tipo “stress block” di intensità pari alla tensione ultima e altezza pari a 0.8 volte l’asse neutro.

Figura 2.1: Andamento delle tensioni del calcestruzzo compresso a rottura utilizzato nel modello semplificato.

2. La resistenza a trazione del calcestruzzo è stata trascurata nel calcolo delle tensioni ma è stata portata in conto nella valutazione della deformabilità globale della trave a cavi non aderenti per effetto dei carichi esterni;

3. per il cavo da precompressione e l‘armatura aderente sono stati adottati i legami di tipo elastico perfettamente plastico riportati in figura 2.2 e 2.3;

4. Ai fini della deformabilità globale della trave si è considerata la deformabilità flessionale

g cI

E di tipo elastico dove Ig è l’inerzia dell’intera sezione reagente;

5. l’allungamento del cavo è stato supposto di tipo elastico;

6. nell’analisi dei cavi non aderenti sono stati trascurati gli effetti del secondo ordine legati agli spostamenti relativi tra cavo e trave di calcestruzzo per effetto dei carichi esterni.

Figura 2.2. Il legame costitutivo adottato nel modello semplificato per l’armatura aderente.

Figura 2.3 . Il legame costitutivo adottato nel modello semplificato per il cavo.

As Aps 0.8xc f 'c s f s su sy fy Es Eps py f py pu ps fps

CAPITOLO 2 45

La metodologia è stata applicata a più travi con diversi tracciati dei cavi e differenti carichi applicati. In particolare sono stati analizzati i seguenti 5 casi:

CASO A.

Trave appoggiata con cavo rettilineo ad eccentricità costante soggetta ad una sola forza concentrata di intensità F applicata nella sezione di mezzeria.

CASO B.

Trave appoggiata con cavo rettilineo ad eccentricità costante e soggetta a due forze concentrate di intensità F poste a distanza d dagli appoggi.

CASO C.

Trave appoggiata con cavo rettilineo ad eccentricità variabile soggetta ad un'unica forza di intensità F nella sezione di mezzeria.

F

F F

d d

CASO D.

Trave appoggiata con cavo rettilineo ad eccentricità variabile soggetta a due forze di intensità F a distanza d dagli appoggi.

CASO E.

Trave appoggiata con cavo rettilineo ad eccentricità costante soggetta a carico distribuito costante q.

2.2.1.1 LA FORMULAZIONE ADIMENSIONALE

Si consideri la sezione rettangolare rappresentata in figura 2.4.

Figura 2.4 : Andamento delle deformazioni e delle tensioni nel caso di cavi aderenti

q

ps s dps ds H b Ts Tps C f 'c 0.8xc Aps As aderente ps aderente ps pe s cu

F

F

d d

CAPITOLO 2 47

A rottura l’equazione di equilibrio a traslazione, nella sua forma più generale, è :

C T T

T = _s + _ps =

(2.1)

dove T è la risultante di trazione, T è la trazione nell’armatura aderente, _s T è la trazione nel _ps

cavo e C è la risultante di compressione. L'equilibrio a traslazione (2.1) può essere riscritto nel seguente modo ps ps s s ps s c cb x T T f A f A f C= ' 0.8 = + = + (2.2) dove ' c

f è la tensione del calcestruzzo a rottura, x è la distanza dell’asse neutro dal lembo _c

compresso, f_s e f_ps la tensione, rispettivamente, nell’armatura e nel cavo. Da (2.2) si ricava:

b f T T x c ps s c _' 8 . 0 = + (2.3)

Dividendo entrambi i membri per H si ottiene:

' ' ' 8 . 0 c media c ps ps s s c ps s c f f bH f A f A f bH f T T H x ₌ + ₌ + _{= (2.4)} dove si è posto bH T T

f_media= s+ ps . Sviluppando il termine _'

c media f f _{si ottiene:} ps c ps s c s c ps ps s s c ps s c media f f f f f bH A f A f f bH T T f f _{ρ ρ} ' ' ' ' ' 1 1 ₌ + _{⋅ = +} ⋅ + = (2.5) dove: - s s s _AT

f = è la tensione nell’armatura a rottura;

-

ps ps

ps _A

T

f =

è la tensione nel cavo a rottura

;

-

bH A_ps

ps=

ρ è il parametro adimensionale che tiene conto del rapporto geometrico tra l’area dei cavi e l’area della sezione di calcestruzzo; ρps rappresenta, quindi, la percentuale di

cavi presente rispetto alla sezione di calcestruzzo -

bH A_s

s=

ρ è analogo a ρ_ps ma rapportato all’armatura aderente;

-

' c

f è la tensione ultima del calcestruzzo.

Il momento ultimo, calcolato rispetto al punto di applicazione della risultante a compressione C, è dato da ) 2 8 . 0 ( ) 2 8 . 0 ( ) 2 8 . 0 ( ) 2 8 . 0 ( c ps ps ps c s s s c ps ps c s s u T d x T d x f A d x f A d x M = − + − = − + −

(2.6)

Dividendo e moltiplicando il secondo membro della (2.6) per He ricordando che d_s =H−δ_s e

ps ps H d = −δ si ottiene ) 2 8 . 0 1 ( ) 2 8 . 0 1 ( H x H H A f H x H H A f M_u= _{s s} −δs − c + _{ps ps} −δps − c (2.7)

) 2 1 1 ( ) 2 1 1 ( _{' '} bH f A f A f H H A f bH f A f A f H H A f M c ps ps s s ps ps ps c ps ps s s s s s u + − − + + − − = δ δ (2.8)

Si definisce momento ultimo adimensionale m_u il seguente rapporto:

2 '_bH f M m c u u = (2.9)

Sostituendo nella (2.9) la (2.8) si ottiene la seguente espressione per m_u

2 ' ' ' ₂ ) 1 1 ( ) 2 1 1 ( bH f bH f A f A f H H A f bH f A f A f H H A f m c c ps ps s s p p ps c ps ps s s s s s u + − − + + − − = δ δ (2.10) Effettuando le opportune semplificazioni si ottiene l'espressione del momento ultimo adimensionale in funzione della tensione del cavo, della percentuale di area del cavo e della tensione di rottura del calcestruzzo:

) 2 1 1 ( ) 2 1 1 ( _{' ' '} ' c ps ps s s p ps c ps c ps ps s s s s c s u f f f H f f f f f H f f m = ρ −δ − ρ + ρ + ρ −δ − ρ + ρ (2.11)

A rottura la tensione del cavo f_ps può essere rivista come la somma di due termini:

ps pe

ps f f

f = +∆ (2.12)

dove

- f_pe rappresenta l’effective stress, ovvero la tensione nel cavo per effetto del peso proprio

della trave e della precompressione, avendo già scontato le perdite a breve e a lungo termine;

-

∆fps

l’incremento di tensione nel cavo per effetto dei carichi esterni.

La principale differenza a livello analitico tra cavi aderenti e cavi non aderenti è legata al diverso modo di valutare ∆f_ps

.

In generale, avendo supposto che il cavo abbia un comportamento elastico perfettamente plastico si può dire che

ps ps

ps E

f = ∆ε

∆

(2.13)

dove E _ps è il modulo del cavo e ∆ε_psè l'incremento di deformazione del cavo per effetto dei carichi esterni.

La diversa espressione nei due casi di ∆f_ps dipende dalla differente espressione dell'incremento di deformazione ∆ε_ps.

Nel caso di cavi aderenti ∆ε_ps può essere valutato dal diagramma lineare delle deformazioni, in funzione della deformazione di compressione del calcestruzzo, sfruttando l’ipotesi di aderenza tra cavo e calcestruzzo; nel caso di cavi non aderenti, viceversa, tale ipotesi non sussiste più e

ps

ε

∆ deve essere valutato in un altro modo. Si ricorre alla deformabilità globale della struttura imponendo la congruenza tra l’incremento di deformazione del cavo e l’incremento di deformazione medio della trave, valutato all’altezza della fibra di calcestruzzo in corrispondenza del cavo, per effetto dei carichi esterni.

Di seguito viene illustrato lo sviluppo della formulazione adimensionale per il caso A (trave appoggiata soggetta ad una forza concentrata nella sezione di mezzeria con cavo rettilineo ad eccentricità costante come mostrato in figura 2.5).

CAPITOLO 2 49

F

Figura 2.5. Schema di calcolo su cui si è sviluppata la formulazione adimensionale.

2.2.1.2 LA FORMULAZIONE ADIMENSIONALE PER CAVI ADERENTI

Nel caso di cavi aderenti, come già accennato precedentemente, l'incremento di deformazione dovuto ai carichi esterni, all’altezza della fibra del cavo, può essere ricavato direttamente dal diagramma delle deformazioni sfruttandone la linearità (Figura 2.4). Ne segue che:

(

−

)

= ( −1) = ∆ c ps cu c ps c cu ps _x d x d x ε ε ε (2.14)

dove d_ps e x_c sono le distanze rispettivamente del cavo e dell’asse neutro dal lembo compresso. Moltiplicando e dividendo per H il termine fra parentesi dell’equazione (2.14) e ricordando che d_ps =H−δ_ps, si ottiene ) 1 ( ) 1 ( ) 1 ( − = − = − − = ∆ c ps cu c ps cu c ps cu ps _{H x}H H x H H d x d δ ε ε ε ε (2.15)

invertendo (2.4) e tenendo conto della (2.5) si ricava

ps ps s s c media c c f f f f f x H ρ ρ + = = 0.8 ' 0.8 ' (2.16)

Sostituendo la (2.16) nella (2.15) si ottiene:

] 1 ) 1 ( 8 . 0 [ ' − − + = ∆ H f f bH f ps ps ps s s c cu ps δ ρ ρ ε ε (2.17) Ne segue che: ] 1 ) 1 ( 8 . 0 [ ' − − + = ∆ = ∆ H f f bH f E E f ps ps ps s s c cu ps ps ps ps δ ρ ρ ε ε (2.18) Sostituendo la (2.18) nella (2.11) si ottiene:

] 1 ) 1 ( 8 . 0 [ ' − − + + = ∆ + = H f f bH f E f f f f ps ps ps s s c cu ps pe ps pe ps δ ρ ρ ε (2.19)

Moltiplicando tutti i termini della (2.19) per _'

c ps f ρ si ottiene: ] 1 ) 1 ( 8 . 0 [ ' ' ' ' = + _{f +f} − _H − bH f f E f f f f _ps ps ps s s c cu c ps px ps c pe ps c ps δ ρ ρ ε ρ ρ ρ (2.20)

Lo stesso sviluppo si può ripetere per l’armatura. Dalla linearità del diagramma delle deformazioni, infatti, si valuta la deformazione dell’armatura tesa in funzione della deformazione ultima del calcestruzzo ε_cu:

(

−

)

= ( −1)= ( − −1) = c s cu c s cu c s c cu s _{H x}H H x H H d x d x δ ε ε ε ε (2.21)

sostituendo la (2.4) nella (2.20) si ottiene

] 1 ) 1 ( 8 . 0 [ ' − − + = H f f bH f _s ps ps s s c cu s ε _{ρ ρ} δ ε (2.22)

La tensione nell’armatura tesa f_s, avendo supposto per l’armatura un comportamento elastico

perfettamente plastico, è data da:

] 1 ) 1 ( 8 . 0 [ ' − − + = = H f f bH f E E f s ps ps s s c cu s s s s ε ε _{ρ ρ} δ (2.23)

Moltiplicando entrambi i membri della (2.23) per _'

c s f ρ _{si ottiene:} ] 1 ) 1 ( 8 . 0 [ ' ' ' = _{f + f} −_H − bH f f E f f _s ps ps s s c cu c s s c s s δ ρ ρ ε ρ ρ _(2.24)

Ponendo nelle (2.10), nella (2.20) e nella (2.24)

ps c ps ps f f t = _' ρ

;

ps c pe pe f f t = _' ρ

;

_' c cu ps ps b f E ρ ε µ =

;

s c s s f f t = _'ρ

;

_' c cu s s sb f E ρ ε µ =

,

H c_ps =δps

,

H c s s=δ (2.25)

il momento ultimo, la tensione nel cavo e la tensione nell’armatura assumono rispettivamente, a rottura, le seguenti forme adimensionali :

)] ( 2 1 1 [ )] ( 2 1 1 [ _{s s ps ps ps s ps} s u b t c t t t c t t m = − − + + − − + (2.26) ] 1 ) 1 ( 8 . 0 [ − − + + = _ps s ps b pe ps t _{t t} c t µ (2.27) ] 1 ) 1 ( 8 . 0 [ − − + = s s ps sb s _{t t} c t µ (2.28)

In condizioni di rottura il problema dell’equilibrio, nel caso di cavi aderenti, è pertanto rappresentato dal seguente sistema di equazioni:

          + − − + + − − = − − + = − − + + = )] ( 2 1 1 [ )] ( 2 1 1 [ ] 1 ) 1 ( 8 . 0 [ ] 1 ) 1 ( 8 . 0 [ ps s ps ps ps s s s b u s s ps sb s ps s ps b pe ps t t c t t t c t m c t t t c t t t t µ µ (2.29)

CAPITOLO 2 51

Per rispettare il legame costitutivo del cavo e dell’armatura, ovvero per rispettare la condizione che, superata la soglia di snervamento, la tensione si mantiene costante al crescere delle deformazioni, si definiscono i seguenti parametri adimensionale t_pslimite e t_slimite

' lim c ps py ite ps f f t = ρ

,

lim _' c s y ite s f f t = ρ

(2.30

)

dove fpy e fy rappresentano la tensione di snervamento, rispettivamente, del cavo e

dell’armatura. Ne segue che, per trovare la soluzione del sistema (2.30), si richiede che per valori di tps(o ts

)

maggiori di tpslimite (o tslimite), si ponga tps=tpslimite (o ts =tslimite).

2.2.1.3 LA FORMULAZIONE ADIMENSIONALE PER CAVI NON ADERENTI

Nel caso di cavi non aderenti l’incremento ∆ε_ps viene valutato attraverso la deformabilità globale della trave applicando l’equazione di congruenza

cm

ps ε

ε =∆

∆

(2.31)

dove ∆εcm è l’incremento di deformazione media dell’intera trave valutato alla quota di

calcestruzzo in corrispondenza del cavo; ∆εps risulta, pertanto, dipendente dal tipo di carico

applicato e dal tracciato del cavo, attraverso l'eccentricità. Nel caso in esame (Figura 2.5) ∆εcm è dato da:

            ∆ − ∆ − = ∆

∫

∫

2

∫

0 2 0 2 2 0 2 2 L L g c ci c L g c cm _{E I} e dz N dz A E N zdz I E e F L ε (2.32)

dove L è la luce della trave, A_cie I_g sono, rispettivamente, l’area ed il momento d’inerzia della sezione di calcestruzzo ideale rispetto al baricentro, e è l’eccentricità del cavo, ∆N è l’incremento di trazione nel cavo per effetto della forza esterna F. Per la congruenza nelle sezioni di testata, dove cavo e calcestruzzo sono aderenti, deve valere la (2.31) con

ps ps ps= _E∆N_A ∆ε (2.33) Uguagliando la (2.32) e la (2.33) si ottiene: ps ps L L g c ci c L g c E A N dz e I E N dz A E N zdz I E e F L ∆ =               ∆ − ∆ −

∫

∫

∫

2 0 2 0 2 2 0 2 2 _(2.34)

Risolvendo gli integrali si ottiene :

ps ps L g c L ci c L g c E A N z e I E N z A E N z I E e F L ∆ = ∆ − ∆ − ) 2 2 ( 2 2 0 2 2 0 2 0 2

Facendo le opportune semplificazioni si ottiene:

ps ps g c ci c g c E A N e I E N A E N I E eL F ₋ ∆ ₋ ∆ 2₌ ∆ 8 (2.35)

L’incremento generico di momento ∆M dovuto alla sola forza F è 4

FL M =

∆ (2.36)

Invertendo la (2.36) ,a rottura, si ricava il valore della forza ultima

L M

F_u = 4∆ u (2.37)

Tenendo conto della (2.37), la relazione (2.35), a rottura, assume al seguente forma

ps ps g c ci c g c u A E N e I E N A E N I E e ₋ ∆ ₋ ∆ ₌ ∆ ∆Μ 2 2 (2.38)

Ricordando la (2.9), ∆Μ_u può essere scritto in forma adimensionale nel seguente modo:

2 '_bH f m M_u =∆ _{u c} ∆ (2.39)

Ricordando la definizione di ρs, l’area della sezione ideale è data da: ) 1 ( ) 1 ( s _s s ci bH nA bH n_bHA bH n A = + = + = + ρ (2.40)

Il momento d’inerzia I_g per la sezione rettangolare di figura 2.4 è dato da

2 3 ₎ 2 ( 12 1 H d nA bH I_g = + _{s s}− (2.41)

dove n=E_s/Ec. Per semplificare la formulazione della (2.41) si è supposto, ai fini del calcolo del momento d’inerzia, che il baricentro si trovi a distanza H/2 dal lembo superiore.

Ricordando che d_s=H−δ_s, e facendo gli opportuni passaggi, la (2.41) può essere sviluppata nel seguente modo: 2 2 3 2 3 ₎ 2 1 ( 12 1 ) 2 ( 12 1 H H nA bH H nA bH I_g = + _s −δ_s = + _s −δs (2.42)

Mettendo in evidenza nella (2.42)

12

3

bH _{e ricordando la definizione di}

s

ρ si ottiene la seguente espressione per il momento d’inerzia

] ) 2 1 ( 12 1 [ 12 2 3 H n bH Ig s s δ ρ − + = (2.43)

Sostituendo la (2.39), la (2.40) e la (2.43) nella (2.38) ed effettuando le opportune semplificazioni si ottiene ps ps s s c s c s s c c u A E N H n H e bH N E n E bH N H n H e E f m ₌ ∆ − + ∆ − + ∆ − − + ∆ ] ) 2 1 ( 12 1 [ 1 ) ( 12 ) 1 ( 1 ] ) 2 1 ( 12 1 [ 1 6 2 2 2 ' δ ρ ρ δ ρ (2.44)

Moltiplicando e dividendo il secondo ed il terzo termine del primo membro della (2.34) per

ps A si ottiene ps ps s s ps ps c s c ps ps s s c c u A E N H n H e bH A A N E n E bH A A N H n H E e f m ₌ ∆ − + ∆ − + ∆ − − + ∆ ] ) 2 1 ( 12 1 [ 1 ) ( 12 ) 1 ( 1 ] ) 2 1 ( 12 1 [ 6 2 2 2 ' δ ρ ρ δ ρ (2.45)

CAPITOLO 2 53 Ponendo ps ps = _A∆N ∆σ e ricordando la definizione di bH A_ps ps= ρ , la (2.45) diventa ps ps s s ps ps c s c ps ps s s c c u E H n H e E n E H n H E e f m σ δ µ ρ σ µ µ σ δ ρ ∆ = − + ∆ − + ∆ − − + ∆ ] ) 2 1 ( 12 1 [ 1 ) ( 12 ) 1 ( 1 ] ) 2 1 ( 12 1 [ 6 2 2 2 ' (2.46)

Dalla (2.46), mettendo in evidenza ∆σ_ps

,

si ricava la seguente espressione:

] ) 2 1 ( 12 1 [ 1 ) ( 12 ) 1 ( 1 1 ][ ) 2 1 ( 12 1 [ 1 6 2 2 2 ' H n H e E n E E H n H e E f m s s ps c s c ps ps s s c c u ps δ ρ ρ µ ρ δ ρ σ − + + + + − + ∆ = ∆ (2.47)

Sostituendo la (2.47) nell’espressione (2.11) la tensione nel cavo assume la seguente forma:

] ) 2 1 ( 12 1 [ 1 ) ( 12 ) 1 ( 1 1 ][ ) -2 1 ( 12 1 [ 1 6 2 2 2 ' H n H e E n E E H n H e E f m f f s s ps c s c ps ps s s c c u pe ps δ ρ ρ ρ ρ δ ρ − + + + + + ∆ + =

(2.48)

Moltiplicando ambo i membri della (2.48) per _/ ' c ps f

ρ ,e semplificando dove è possibile per ' c f , si ottiene : ] ) 2 1 ( 12 1 [ 1 ) ( 12 ) 1 ( 1 1 ][ ) 2 1 ( 12 1 [ 1 6 2 2 2 ' ' H n H e E n E E H n H E e m f f f f s s ps c s c ps ps s s c ps u c ps pe c ps ps δ ρ ρ ρ ρ δ ρ ρ ρ ρ − + + + + − + ∆ + = (2.49)

Moltiplicando e dividendo per Eps il secondo termine del membro di destra dell’espressione

(2.49) si ricava: ] ) 2 1 ( 12 1 [ 1 ) ( 12 ) 1 ( 1 ][ ) 2 1 ( 12 1 [ 1 6 2 2 2 ' ' H n H e E E n E E H n H E xe E m f f f f s s ps c ps s ps c ps s s c ps ps u c ps pe c ps ps δ ρ ρ ρ ρ δ ρ ρ ρ ρ − + + + + − + ∆ + = (2.50)

L’incremento di momento adimensionale ∆m_u, dovuto solo al carico esterno F, si può esprimere come differenza tra il momento ultimo adimensionale e il momento adimensionale dovuto al peso proprio m_g così definito.

2 '_bH f M m c g g =

(2.51)

Pertanto, tenendo conto dell’espressione (2.10) ottenuta per il momento adimensionale ed esprimendola in funzione dei parametro t_ps si ricava

g s ps s s s ps ps ps g u unb u m m t c t t t c t t m m −       _{− − + + − − +} = − = ∆ ( )] 2 1 1 [ )] ( 2 1 1 [

(2.52)

Si definisce, inoltre, il seguente parametro adimensionale:

H e E E ps c ps unb ρ µ = (2.53)

da cui si ricava che: H e E E _unb ps c ps _{ρ =} µ (2.54)

Ricordando le (2.25) e sostituendole nella (2.50) , insieme alla (2.52), (2.53) e (2.54) si ottiene

] ] ) 2 1 ( 12 1 [ 1 12 ) 1 ( 1 1 ][ ) 2 1 ( 12 1 [ )] ( 2 1 1 [ )] ( 2 1 1 [ 6 2 2 s s unb s H unb s s g s ps s s s ps ps ps unb pe ps c n H e n e c n m t t c t t t c t t t − + + + + − + −       _{− − + + − − +} + = ρ µ ρ µ ρ µ (2.55)

Il problema dell’equilibrio a rottura nel caso di cavi non aderenti è formulato anch’esso, come nel caso dei cavi aderenti, attraverso un sistema di tre equazioni in tre incognite (rappresentate dai parametri t_ps e t_sdal momento ultimo adimensionale unb

u

m ) così di seguito definito:

                  + − − + + − − = − − + = − + + + + − + −       _{− − + + − − +} + = )] ( 2 1 1 [ )] ( 2 1 1 [ ] 1 ) 1 ( 8 . 0 [ ] ] ) 2 1 ( 12 1 [ 1 12 ) 1 ( 1 1 ][ ) 2 1 ( 12 1 [ )] ( 2 1 1 [ )] ( 2 1 1 [ 6 2 2 s ps s s s ps ps ps unb u s s ps sb s s s unb s H unb s s g s ps s s s ps ps ps unb pe ps t t c t t t c t m c t t t c n H e n e c n m t t c t t t c t t t µ ρ µ ρ µ ρ µ (2.56)

con il vincolo che per trovare la soluzione del sistema (2.56) si richiede che per valori di t_ps (o

s

t ) maggiori di t_pslimite (o t_slimite), si ponga t_ps =t_pslimite (o t_s =t_slimite).

Osservando la (2.38) e la (2.56), e ricordando la (2.24) e la (2.53), si comprende che per determinare la tensione adimensionale nel cavo a rottura t_ps o il momento ultimo adimensionale

u

m è sufficiente valutare i seguenti parametri:

CAVI ADERENTI CAVI NON ADERENTI

pe

t , ρ_ps, ρ_s, c_ps, c_s t_pe, ρ_ps, ρ_s, c_ps, c_s, e /H

CAPITOLO 2 55

2.2.1.4 IL SIGNIFICATO DEI PARAMETRI ADIMENSIONALI

Nella formulazione adimensionale del problema dell’equilibrio a rottura di una trave precompressa con cavi aderenti, rappresentata dal sistema di equazioni (2.28), compaiono otto parametri adimensionali b

u

m , t_ps, t_s, t_pe, µ_b, µ_sb, c_ps

,

c_s.

Il parametro t_pe tiene conto della tensione nel cavo per effetto delle azioni dovute

esclusivamente al peso proprio ed alla precompressione, avendo già portato in conto gli effetti dovuti alle perdite di breve e lungo termine.

Il parametro adimensionale t_ps valuta la tensione totale adimensionale del cavo a rottura,

portando, quindi, in conto anche gli incrementi di trazione dovuti al carico esterno. Il parametro t_s rappresenta, invece, la tensione adimensionale nell’armatura aderente tesa . Il parametro µ_b, definito come

' c cu ps ps b f E ρ ε µ =

(2.57)

è un parametro adimensionale in cui non compare l’armatura aderente e tiene conto sia delle caratteristiche meccaniche della sezione di calcestruzzo e del cavo sia delle caratteristiche geometriche della trave. Le prime vengono valutate, per il calcestruzzo, attraverso la tensione di rottura '

c

f e la deformazione ultima ε_cu mentre, per il cavo, attraverso il modulo di elasticità

ps

E ; le caratteristiche geometriche sono, invece, portate in conto attraverso il parametro

adimensionale ρ_ps definito precedentemente nella (2.5) come il rapporto tra l’area del cavo e l’area dell’intera sezione di calcestruzzo.

Il parametro µ_sb , definito attraverso la (2.58),

' c cu s s sb f E ρ ε µ = (2.58)

in cui si portano in conto le caratteristiche meccaniche (con E_s) e geometriche (con ρ_s)

dell’armatura, è analogo al parametro µ_b: mentre µ_b combina le caratteristiche geometriche del cavo con quelle geometriche e meccaniche del calcestruzzo, µ_sb è il parametro adimensionale che tiene principalmente conto dell’influenza dell’armatura.

I parametri c_ps

e

cs

,

definiti precedentemente in (2.25) rappresentano i copriferri,

rispettivamente del cavo e dell’armatura adimensionalizzati rispetto all’altezza totale H della sezione.

b u

m è il momento ultimo adimensionale nel caso dei cavi aderenti definito nelle espressione (2.9) e valutato attraverso la (2.29).

Nella formulazione del problema dell’equilibrio a rottura per cavi non aderenti compaiono i seguenti parametri adimensionali: unb

u

m , tps, ts, tpe, ρps, ρs, µsb, e /H, µunb, cps, cs.

Il significato dei parametri tpe, tps, ts, µsb, cps, cs è stato già anticipato nella descrizione dei

parametri adimensionali che definiscono il problema dell’equilibrio a rottura dei cavi aderenti. Il parametroµ_unb, definito come

H e E E ps c ps unb ρ µ =

(2.59)

è il parametro in cui si concentrano, maggiormente, le caratteristiche del cavo: compare, infatti, la geometria attraverso il parametro ρps, ovvero l’area Aps, il tracciato del cavo stesso

attraverso la sua eccentricità e, adimensionalizzata rispetto a H, e le caratteristiche meccaniche del cavo attraverso il modulo E_ps .

Il parametro ρ_s è analogo a ρ_ps: rappresenta, infatti, la percentuale di armatura aderente tesa presente nella sezione di calcestruzzo.

Infine unb

u

m è il momento ultimo adimensionale definito nelle espressione (2.9) e valutato attraverso la (2.56).

2.2.1.5 L’ESTENZIONE DELLA FORMULAZIONE ADIMENSIONALE AGLI ALTRI SCHEMI Come è stato accennato nel paragrafo 2.1.1 la formulazione adimensionale è stata sviluppata per altri 4 esempi di cui si riportano in Tabella 2.1 i sistemi di equazioni sia nel caso di cavi aderenti che nel caso di cavi non aderenti.

Come si può notare le formulazioni sono simili tra loro come struttura. In ognuna di esse compare, però, un parametro adimensionale caratteristico dello schema statico e che le distingue una dalle altre. Ad esempio negli Schemi 1 e 3 compare il rapporto adimensionale d /L dove d è la distanza della forza applicata dall’appoggio; gli Schemi 2 e 3 dipendono, invece, dall’angolo α , ovvero dall’inclinazione del cavo rispetto all’orizzontale, e dall’eccentricità del cavo nella sezione di mezzeria e_m.

Il parametro adimensionale * unb

µ definito nel seguente modo

H e E E _m s c s unb µ µ* = _(2.60)

CAPITOLO2 57

Tabella 2.1. La formulazione adimensionale di f per altri schemi di trave. _ps

N. SCHEMA

FORMULAZIONE ADIMENSIONALE PER CAVI ADERENTI

FORMULAZIONE ADIMENSIONALE PER CAVI NON ADERENTI

1 F F ] 1 ) 1 ( 8 . 0 [ − − + + = _ps s ps b pe ps t _{t t} c t µ ] ] ) 2 1 ( 12 1 [ 1 12 ) 1 ( 1 1 ][ ) 2 1 ( 12 1 [ ) 1 ( )]] ( 2 1 1 [ )] ( 2 1 1 [ [ 12 2 2 s s unb s H unb s s g s ps s s s ps ps ps unb pe ps c n H e n e c n L d m t t c t t t c t t t − + + + + − + −       _{− − + + − − + −} + = ρ µ ρ µ ρ µ 2 F ] 1 ) 1 ( 8 . 0 [ − − + + = _ps s ps b pe ps t _{t t} c t µ ] ] ) 2 1 ( 12 1 [ cos 4 ) 1 ( cos 1 ][ ) 2 1 ( 12 1 [ ) )]] ( 2 1 1 [ )] ( 2 1 1 [ [ 4 2 * * 2 * s s m unb s Hm unb s s g s ps s s s ps ps ps unb pe ps c n H e n e c n m t t c t t t c t t t − + + + + − +       _{− − + + − − + −} + = ρ α µ ρ α µ ρ µ 3 F F ] 1 ) 1 ( 8 . 0 [ − − + + = ps s ps b pe ps t _{t t} c t µ ] ] ) 2 1 ( 12 1 [ ) 4 3 ( cos 4 ) 1 ( cos 1 ][ ) 2 1 ( 12 1 [ ) 3 4 1 ( )]] ( 2 1 1 [ )] ( 2 1 1 [ [ 12 2 * * 2 * s s m unb s Hm unb s s g s ps s s s ps p ps unb pe ps c n L d H e n e c n L d m t t c t t t c t t t − + − + + + − + −       _{− − + + − − + −} + = ρ α µ ρ α µ ρ µ 4 q ] 1 ) 1 ( 8 . 0 [ − − + + = _ps s ps b pe ps t _{t t} c t µ ] ] ) 2 1 ( 12 1 [ 1 12 ) 1 ( 1 1 ][ ) 2 1 ( 12 1 [ )]] ( 2 1 1 [ )] ( 2 1 1 [ [ 8 2 2 s s unb s H unb s s g s ps s s s ps ps ps unb pe ps c n H e n e c n m t t c t t t c t t t − + + + + − +       _{− − + + − − + −} + = ρ µ ρ µ ρ µ

2.2.1.6 I PARAMETRI RICORRENTI NELLE FORMULAZIONI ANALITICHE DI f_ps.

La Tabella 2.1, insieme alla (2.56), rappresentano le formulazioni adimensionali proposte, utilizzando il modello semplificato, per valutare la tensione nel cavo a rottura f_ps.

Le formulazioni di t_ps proposte sono equazioni di secondo grado in cui la tensione f_ps risulta

dipendere da:

a. tipo di carico agente sulla trave

Per ogni tipologia di carico l’espressione di t_ps si particolarizza ed assume forme diverse: in

particolare, quando il carico è costituito da due forze concentrate, appare nella formulazione la distanza d della forza dagli appoggi. Tale dipendenza si riscontra anche nelle

formulazioni di Harajli e Kanj [29], Lee Moon Lim [30] (attraverso il coefficientef ,

Naaman Alkhairi [32] (attraverso il coefficiente Ω_u), Ng [37] (attraverso L_s che

rappresenta la distanza della forza dall’appoggio); b. effective prestressing f_pe

Tutte le formulazioni riportano questo termine. Come è stato premesso nel Capitolo 1, in tutte le formulazioni della tensione a rottura nei cavi non aderenti, f_ps viene vista come la

somma di due termini (si veda l’equazione (1.1)); c. tracciato del cavo

Tale dipendenza, nelle formulazioni del modello semplificato proposto, è portata in conto attraverso l’eccentricità del cavo e, nel caso di cavo dritto, e attraverso l’eccentricità nella

sezione di mezzeria e_m e l’angolo di inclinazione α, nel caso di cavo inclinato. Nelle altre formulazioni tale dipendenza non compare esplicitamente: si ritrova, generalmente, la distanza del cavo dal lembo compresso d_ps;

d. il rapporto geometrico dei cavi ρ_ps

Tale parametro compare nell’espressione (2.59) di µ_unb e si rivelerà avere un peso notevole nella valutazione di f_ps come verrà ampiamente illustrato nel prossimo paragrafo.

La dipendenza da questo parametro è comune a tutte le formulazioni sin dagli anni ’60; e. il rapporto geometrico dell’armatura aderente tesa ρ_s

La dipendenza da questo parametro appare esplicitamente nella formulazione adimensionale di tutti i casi illustrati (Tabella 2.1 ed equazione (2.56)) anche se l’incidenza di ρ_s sulla tensione del cavo a rottura si rivelerà di scarsa importanza.

La dipendenza da questo parametro è stata introdotta intorno agli ’80. Le formulazioni che riportano questo parametro sono quella di Tam & Pannell [23], Du & Tao [25], Harajli & Kanj [29], Naaman & Alkhairi [32], Chakrabarti [35]. Nella formulazione proposta da Lee, Moon, Lim [30] compare esplicitamente l’area di armatura non adimensionalizzata;

f. le caratteristiche meccaniche del calcestruzzo

La caratteristiche meccaniche del calcestruzzo che compaiono nelle formulazioni della Tabella 2.1 e nell’equazione (2.56) sono la resistenza del calcestruzzo '

c

f (che entra nelle

CAPITOLO2 59

nella definizione del parametro µ_unb e del coefficiente di omogeneizzazione n). Tutte le formulazioni presentano la dipendenza dalle caratteristiche meccaniche del calcestruzzo: nella maggior parte dei casi compare '

c

f mentre in Naaman & Alkhairi [32]e in Ng [37] appare ε_cu.

g. il copriferro dell’armatura tesa (c_s) e del cavo (c_ps)

Tali dipendenze si manifestano attraverso i parametri adimensionali c_s e c_ps che

implicitamente riportano la dipendenza di fps dai rapporti ds/H, per l’armatura aderente,

e d_ps /H per il cavo (è sufficiente ricordare che δs=H−ds e δps =H−dps).

In letteratura le formulazioni in cui compare la distanza d_s dell’armatura dal lembo compresso sono quelle di Du & Tao [25], Chakrabarti [35]e Lee, Moon, Lim [30]: nelle ultime due, in realtà, la dipendenza di fps è dal rapporto dps /ds. Per quanto riguarda dps,

molte formulazioni presenti in letteratura individuano la dipendenza di f_ps dal rapporto

ps

d

L/ anziché dalla sola grandezza d_ps.

In generale si può dire che nelle formulazioni ricavate dal modello semplificato (riportate in Tabella 2.1 e nell’equazione (2.56)) si ritrovano la maggior parte dei parametri individuati dalle formulazioni presenti in letteratura.

Il modello semplificato non ritrova, però, la dipendenza esplicita dal rapporto L /d_ps che, in letteratura, viene ritenuto un parametro fondamentale ai fini della valutazione della tensione a rottura nei cavi non aderenti. In particolare, la dipendenza esplicita dalla luce della trave, nelle formulazioni ottenute dal modello semplificato, compare solo per gli schemi caricati con due forze concentrate. Questo fatto rientra nel modo in cui si è operato per arrivare a formulare le

cinque espressioni: poiché si sostituisce l’espressione del momento nell’equazione di congruenza (si veda il passaggio per arrivare alla (2.38) nel caso dello schema di trave caricata con una forza concentrata nella sezione di mezzeria) la luce si semplifica e non compare nella formulazione finale.

2.2.1.7 L’ANALISI PARAMETRICA

Per comprendere l’effettivo peso di ciascun parametro nella formulazione adimensionale ottenuta con il modello semplificato, sia nel caso dei cavi aderenti che nel caso di cavi non aderenti, è indispensabile definire l’intervallo di variazione dei valori che può assumere ogni singolo parametro. In questo modo si può effettuare un’analisi di sensibilità con lo scopo di individuare quanto ciascun parametro incida sul comportamento a rottura della struttura e di effettuare, in maniera molto semplice e rapida, un preliminare confronto tra cavi aderenti e non aderenti.

Nella Tabella 2.2 si riportano i campi di variabilità scelti per i parametri della formulazione adimensionale del problema dell’equilibrio a rottura, sia nel caso di cavi aderenti che nel caso di cavi non aderenti.

L’analisi parametrica viene condotta analizzando in un primo momento l’influenza dei parametri di base

(

tpe

,

ρps

,

ρs

)

sul comportamento a rottura della struttura, avendo, però,

fissato i materiali e la posizione del cavo e dell’armatura (parametri c_ps

,

c_s

,

e /H

)

. Questo

permetterà di comprendere i parametri che giocano un ruolo fondamentale nella valutazione del momento e della tensione del cavo a rottura.

Tabella 2.2. Campi di variabilità dei principali parametri della formulazione adimensionale. PARAMETRO CAMPO DI VARIABILITA’ ε_cu 0.0035÷0.0028 ' c f 300÷600 c E 300000÷410000 ps E 2100000 s E 2100000 pe f 10000 ÷14000 ps c 0.1÷0.3 s c 0.01÷0.2 PARAMETRO CAMPO DI VARIABILITA’ H e / 0.1÷0.5 ps ρ 0.001÷0.01 s ρ 0.005÷0.01 b µ 0.009÷0.25 unb µ 0.0005÷0.035 sb µ 0.04÷0.25 pe t 0.015÷0.5 ite ps t _lim 0.02÷0.5 ite s t _lim 0.02÷0.2

Successivamente si analizzerà se e quanto il tipo di calcestruzzo e la posizione del cavo e dell’armatura sono in grado di influenzare la fase di rottura della struttura. Infine si valuterà se esistono campi in cui i due tipi di precompressione (a cavi aderenti e non) possono equivalersi in termini di capacità ultima o se esistono delle condizioni per cui la precompressione a cavi non aderenti risulta più efficace rispetto alla precompressione tradizionale.

Per valutare l’influenza dei parametri sul momento ultimo è stato necessario fissare il valore di alcune grandezze. Si è scelto di assegnare a queste ultime il valore medio del campo di variabilità che è stato precedentemente stabilito.

cu

ε '

c

f E c Eps Es fpy fy e /H cps cs

0.00315 450 355000 2100000 2100000 13500 3750 0.3 0.2 0.105

CASO CAVI NON ADERENTI .

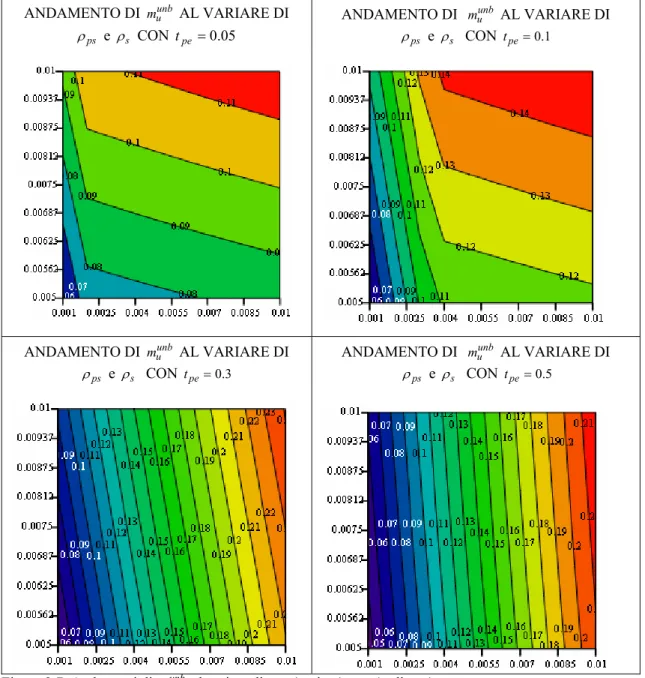
In Figura 2.6 sono riportati gli andamenti del momento ultimo adimensionale unb

u

m in funzione di t_pe (parametro adimensionale che tiene conto del tiro) per assegnati valori diρ_ps. Agli altri 4 parametri sono stati assegnati i valori medi dei campi di variabilità precedentemente definiti ovvero

s

ρ c_ps c_{s e/H}

0.0075 0.2 0.105 0.3 Come si può vedere dai grafici gli andamenti individuano 3 zone: i. zona in cui unb

u

m presenta un andamento lineare crescente con t_pe

;

ii. zona in cui unb

u

m si mantiene costante con t_pe; iii. zona in cui unb

u

CAPITOLO2 61

L’estensione delle 3 zone cambia al variare ρ_ps: l’aumento di quest’ultimo parametro sembra determinare una riduzione della zona a unb

u

m costante che tende a restringersi notevolmente. Questo comportamento trova una spiegazione nel fatto che, aumentando ρps, il cavo tende a

snervarsi dopo, ovvero per limiti di snervamento maggiori (si ricorda infatti che il limite di snervamento adimensionale tpslimite è direttamente proporzionale a ρps), mentre per l’armatura

si riduce la zona iniziale in cui è snervata (figura 2.26a). Sovrapponendo quindi questi due andamenti secondo la (2.56), si ottiene la zona a unb

u

m costante (che è anche la zona a unb

u

m massimo). Tale zona tende a ridursi se ρps aumenta: l’andamento di munbu tende sempre di più

ad un andamento lineare: crescente, per bassi valori di t_pe, decrescente per alti valori di t_pe.

ANDAMENTO DI munb_u AL VARIARE DI t_pe CON 002ρ_ps =0. ANDAMENTO DI munb_u AL VARIARE DI t_pe CON 005ρ_ps =0. ANDAMENTO DI unb u m AL VARIARE DI t_pe CON ρ_ps =0.007

ANDAMENTO DI unb u m AL VARIARE DI t_pe CON 009ρ_ps =0.

Figura 2.6. Andamenti di munb_u al variare di t_pe (ascissa) e ρps.

ANDAMENTO DI t_s AL VARIARE DI t_pe ANDAMENTO DI t_ps AL VARIARE DI t_pe

CAPITOLO2 63

I grafici di Figura 2.7 mostrano gli andamenti di unb u m al variare di ρ_ps

(ascissa)

e ρ_s (ordinata). ANDAMENTO DI unb u m AL VARIARE DI ps ρ e ρs CON tpe =0.05 ANDAMENTO DI unb u m AL VARIARE DI ps ρ e ρ_s CON t_pe=0.1 ANDAMENTO DI unb u m AL VARIARE DI ps ρ e ρs CON tpe=0.3 ANDAMENTO DI unb u m AL VARIARE DI ps ρ e ρs CON tpe=0.5

Figura 2.7. Andamenti di unb u

m al variare diρ_ps (ascissa), ρ_s (ordinata) e t . _pe I grafici di Figura 2.7 mostrano gli andamenti di unb

u

m , al variare diρ_ps (ascissa) e diρ_s(ordinata) per diversi valori di t_pe. In particolare, aumentando t_pe (considerando, quindi, i grafici di Figura 2.7 nel loro insieme), ma mantenendo costante ρ_ps, si nota come l’aumento diρs tenda ad influenzare sempre meno munbu fino ad arrivare alla quasi totale indipendenza di

unb u

m dall’armatura per t_pe =0.5 (gli andamenti tendono a diventare delle rette verticali indici della non dipendenza di unb

u

m da ρ_s). Si osserva, comunque, che l’aumento di armatura (valutato attraverso la variazione del parametro ρs) produce incrementi percentuali di muunb che variano

Il parametro ρ_ps è in grado di incidere notevolmente sul momento ultimo adimensionale unb u

m . In particolare un aumento di ρ_ps comporta incrementi di unb

u

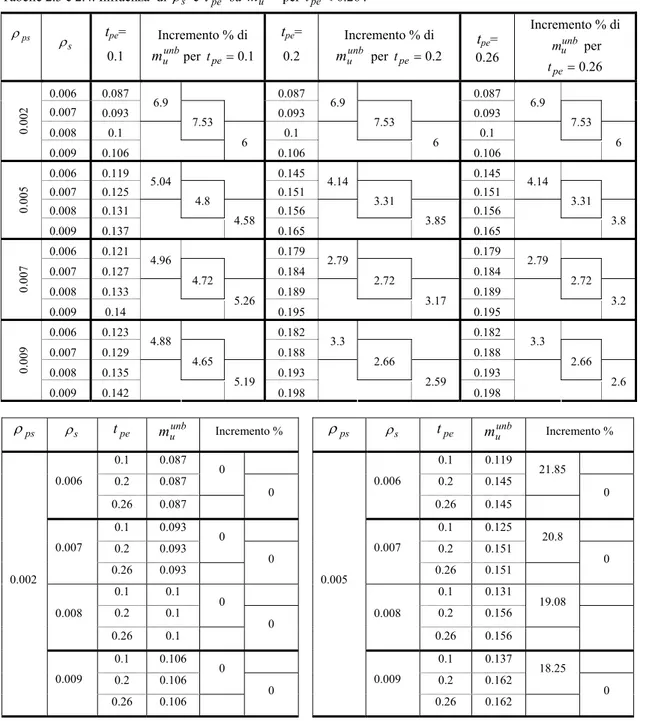
m che si rivelano di entità maggiore se ρ_ps ≤0.005 e t_pe >0.26 (tabelle 2.5, 2.10).

L’aumento di t_pe, avendo fissato ρ_ps e ρs, per valori di tpe<0.26 comporta un incremento di unb

u

m che varia tra il 20% ed il 48% circa se lo si accoppia con ρ_ps >0.002 mentre, per valori di

26 . 0 >

pe

t , comporta una riduzione compresa tra lo 0.5% ed il 21% di unb u

m (tabelle 2.4, 2.6, 2.8, 2.10).

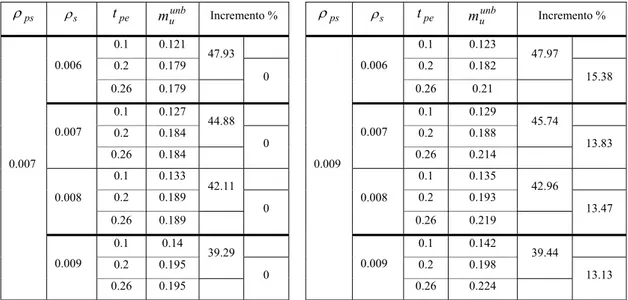
Tabelle 2.3 e 2.4. Influenza di ρ_s e t_pe su m_uunb per t_pe<0.26.

ps ρ s ρ tpe= 0.1 Incremento % di unb u m per 1t_pe=0. tpe= 0.2 Incremento % di unb u m per t_pe=0.2 tpe= 0.26 Incremento % di unb u m per 26 . 0 = pe t 0.006 0.087 0.087 0.087 0.007 0.093 6.9 0.093 6.9 0.093 6.9 0.008 0.1 7.53 0.1 7.53 0.1 7.53 0. 002 0.009 0.106 6 0.106 6 0.106 6 0.006 0.119 0.145 0.145 0.007 0.125 5.04 0.151 4.14 0.151 4.14 0.008 0.131 4.8 0.156 3.31 0.156 3.31 0. 005 0.009 0.137 4.58 0.165 3.85 0.165 3.8 0.006 0.121 0.179 0.179 0.007 0.127 4.96 0.184 2.79 0.184 2.79 0.008 0.133 4.72 0.189 2.72 0.189 2.72 0. 007 0.009 0.14 5.26 0.195 3.17 0.195 3.2 0.006 0.123 0.182 0.182 0.007 0.129 4.88 0.188 3.3 0.188 3.3 0.008 0.135 4.65 0.193 2.66 0.193 2.66 0. 009 0.009 0.142 5.19 0.198 2.59 0.198 2.6 ps ρ ρ_s t_pe unb u m Incremento % 0.1 0.087 0.2 0.087 0 0.006 0.26 0.087 0 0.1 0.093 0.2 0.093 0 0.007 0.26 0.093 0 0.1 0.1 0.2 0.1 0 0.008 0.26 0.1 0 0.1 0.106 0.2 0.106 0 0.002 0.009 0.26 0.106 0 ps ρ ρ_s t_pe unb u m Incremento % 0.1 0.119 0.2 0.145 21.85 0.006 0.26 0.145 0 0.1 0.125 0.2 0.151 20.8 0.007 0.26 0.151 0 0.1 0.131 0.2 0.156 19.08 0.008 0.26 0.156 0.1 0.137 0.2 0.162 18.25 0.005 0.009 0.26 0.162 0

CAPITOLO2 65 ps ρ ρ_s t_pe unb u m Incremento % 0.1 0.121 0.2 0.179 47.93 0.006 0.26 0.179 0 0.1 0.127 0.2 0.184 44.88 0.007 0.26 0.184 0 0.1 0.133 0.2 0.189 42.11 0.008 0.26 0.189 0 0.1 0.14 0.2 0.195 39.29 0.007 0.009 0.26 0.195 0 ps ρ ρ_s t_pe unb u m Incremento % 0.1 0.123 0.2 0.182 47.97 0.006 0.26 0.21 15.38 0.1 0.129 0.2 0.188 45.74 0.007 0.26 0.214 13.83 0.1 0.135 0.2 0.193 42.96 0.008 0.26 0.219 13.47 0.1 0.142 0.2 0.198 39.44 0.009 0.009 0.26 0.224 13.13

Tabella 2.5. Influenza di ρ_ps e t_pe su m_uunb per tpe<0.26

.

s ρ ρ_ps unb u m per tpe=0.1 Incremento % di unb u m per tpe=0.1 unb u m per tpe=0.2 Incremento % di unb u m pertpe=0.2 unb u m per tpe=0.3 Incremento % di unb u m per 26 . 0 = pe t 0.002 0.087 0.087 0.087 0.005 0.119 36.8 0.145 66.7 0.145 66.7 0.007 0.121 1.7 0.179 23.4 0.179 2.3.4 0. 006 0.009 0.123 1.6 0.182 1.7 0.21 17.3 0.002 0.093 0.093 0.093 0.005 0.125 34.4 0.151 62.4 0.151 62.4 0.007 0.127 1.6 0.184 21.8 0.184 21.8 0. 007 0.009 0129 1.6 0.188 2.17 0.214 16.3 0.002 0.1 0.1 0.1 0.005 0.131 31 0.156 56 0.156 56 0.007 0.133 1.53 0.189 21.1 0.189 21.1 0. 008 0.009 0.135 1.5 0.193 2.12 0.219 15.9 0.002 0.106 0.106 0.106 0.005 0.137 29.2 0.162 52.8 0.162 52.8 0.007 0.14 2.19 0.192 20.4 0.192 20.4 0. 009 0.009 0.142 1.4 0.198 1.54 0.224 14.9

Tabella 2.6. Influenza di ρ_ps e t_pe su m_uunb per t_pe<0.26

.

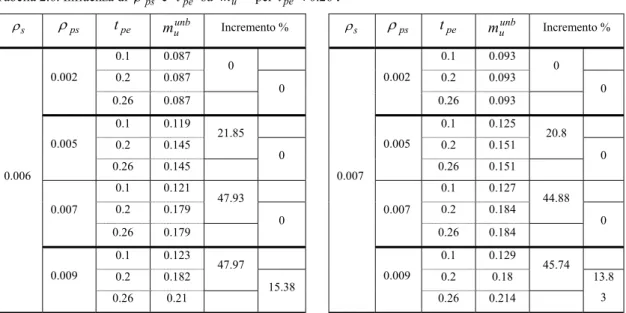
s ρ ρ_ps t_pe unb u m Incremento % 0.1 0.087 0.2 0.087 0 0.002 0.26 0.087 0 0.1 0.119 0.2 0.145 21.85 0.005 0.26 0.145 0 0.1 0.121 0.2 0.179 47.93 0.007 0.26 0.179 0 0.1 0.123 0.2 0.182 47.97 0.006 0.009 0.26 0.21 15.38 s ρ ρ_ps t_pe unb u m Incremento % 0.1 0.093 0.2 0.093 0 0.002 0.26 0.093 0 0.1 0.125 0.2 0.151 20.8 0.005 0.26 0.151 0 0.1 0.127 0.2 0.184 44.88 0.007 0.26 0.184 0 0.1 0.129 0.2 0.18 45.74 0.007 0.009 0.26 0.214 13.8 3 s ρ ρ_ps t_pe unb u m Incremento % 0.1 0.1 0.2 0.1 0 0.002 0.26 0.1 0 0.1 0.131 0.2 0.156 19.08 0.005 0.26 0.156 0 0.1 0.133 0.2 0.189 42.11 0.007 0.26 0.189 0 0.1 0.135 0.2 0.193 42.96 0.008 0.009 0.26 0.219 13.47 s ρ ρ_ps t_pe unb u m Incremento % 0.1 0.106 0.2 0.106 0 0.002 0.26 0.106 0 0.1 0.137 0.2 0.162 18.25 0.005 0.26 0.162 0 0.1 0.14 0.2 0.195 39.29 0.007 0.26 0.195 0 0.1 0.142 0.2 0.198 39.44 0.009 0.009 0.26 0.224 13.13

CAPITOLO2 67

Tabella 2.7. Influenza di ρ_s e t_pe su m_uunb per t_pe>0.26.

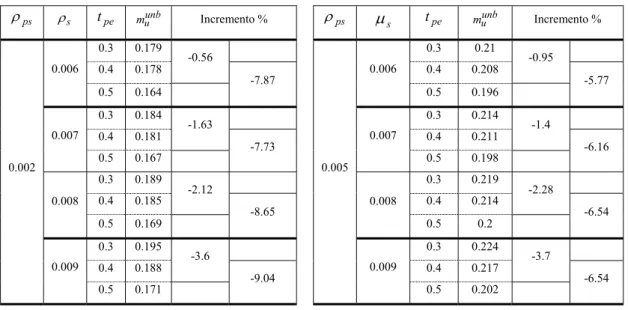
ps ρ s ρ unb u m per tpe=0.3 Incremento % di unb u m per t_pe=0.3 unb u m per tpe=0.4 Incremento % di m_uunb per t_pe=0.4 unb u m per tpe=0.5 Incremento % di m_uunb per tpe=0.5 0.006 0.087 0.087 0.071 0.007 0.093 6.9 0.092 5.7 0.074 4.23 0.008 0.1 7.53 0.096 4.3 0.077 4 0. 002 0.009 0.106 6 0.101 5.21 0.08 3.9 0.006 0.145 0.144 0.13 0.007 0.151 4.14 0.148 2.78 0.132 1.54 0.008 0.156 3.31 0.152 2.7 0.135 2.27 0. 005 0.009 0.162 3.17 0.156 2.63 0.137 1.48 0.006 0.179 0.178 0.164 0.007 0.184 2.79 0.181 1.69 0.167 1.83 0.008 0.189 2.72 0.185 2.21 0.169 1.2 0. 007 0.009 0.195 3.17 0.188 1.62 0.171 1.18 0.006 0.21 0.206 0.196 0.007 0.214 1.9 0.211 1.44 0.198 1 0.008 0.219 2.34 0.214 1.42 0.2 1 0. 009 0.009 0.224 2.28 0.217 1.4 0.202 1

Tabella 2.8. Influenza di ρ_s e t_pe su m_uunb per tpe>0.26. ps ρ ρ_s t_pe unb u m Incremento % 0.3 0.087 0.4 0.087 0 0.006 0.5 0.071 -18.4 0.3 0.093 0.4 0.092 -1 0.007 0.5 0.074 -19.6 0.3 0.1 0.4 0.096 -4 0.008 0.5 0.077 -19.8 0.3 0.106 0.4 0.101 -4.7 0.002 0.009 0.5 0.08 -20.8 ps ρ ρ_s t_pe unb u m Incremento % 0.3 0.145 0.4 0.144 -0.7 0.006 0.5 0.13 -9.7 0.3 0.151 0.4 0.148 -2 0.007 0.5 0.132 -10.8 0.3 0.156 0.4 0.152 -2.56 0.008 0.5 0.135 -11.18 0.3 0.162 0.4 0.156 -3.7 0.005 0.009 0.5 0.137 -12.18

ps ρ ρ_s t_pe unb u m Incremento % 0.3 0.179 0.4 0.178 -0.56 0.006 0.5 0.164 -7.87 0.3 0.184 0.4 0.181 -1.63 0.007 0.5 0.167 -7.73 0.3 0.189 0.4 0.185 -2.12 0.008 0.5 0.169 -8.65 0.3 0.195 0.4 0.188 -3.6 0.002 0.009 0.5 0.171 -9.04 ps ρ µ_s tpe muunb Incremento % 0.3 0.21 0.4 0.208 -0.95 0.006 0.5 0.196 -5.77 0.3 0.214 0.4 0.211 -1.4 0.007 0.5 0.198 -6.16 0.3 0.219 0.4 0.214 -2.28 0.008 0.5 0.2 -6.54 0.3 0.224 0.4 0.217 -3.7 0.005 0.009 0.5 0.202 -6.54

Tabella 2.9 . Influenza diρ_ps e t_pe

su

m_uunb per tpe>0.26

.

s ρ ρps unb u m per tpe=0.3 Incremento % per tpe=0.3 unb u m per tpe=0.4 Incremento % per tpe=0.4 unb u m per tpe=0.5 Incremento % per 5 . 0 = pe t 0.002 0.087 0.0087 0.071 0.005 0.145 66.7 0.144 65.5 0.13 83.1 0.007 0.179 21.4 0.178 23.6 0.164 26.1 0. 006 0.009 0.21 17.3 0.208 16.8 0.196 19.5 0.002 0.093 0.092 0.074 0.005 0.151 62.4 0.148 60.9 0.132 78.4 0.007 0.184 21.8 0.181 22.3 0.167 26.5 0. 007 0.009 0.214 16.3 0.211 16.6 0.198 18.6 0.002 0.1 0.096 0.077 0.005 0.156 52.8 0.152 58.3 0.135 75.3 0.007 0.189 20.4 0.185 21.7 0.169 25.2 0. 008 0.009 0.219 14.9 0.214 15.7 0.2 18.3 0.002 0.106 0.101 0.08 0.005 0.162 52.8 0.156 54.5 0.137 71.2 0.007 0.195 20.4 0.188 20.5 0.171 24.8 0. 009 0.009 0.224 14.9 0.217 15.4 0.202 18.1

CAPITOLO2 69

Tabella 2.10 . Influenza diρ_ps e t_pe su m_uunb per t_pe>0.26.

s ρ ρ_ps t_pe unb u m Incremento % 0.3 0.087 0.4 0.087 0 0.002 0.5 0.071 -18.4 0.3 0.145 0.4 0.144 -0.69 0.005 0.5 0.13 -9.7 0.3 0.179 0.4 0.178 -0.56 0.007 0.5 0.164 -7.87 0.3 0.21 0.4 0.208 -0.95 0.006 0.009 0.5 0.196 -5.77 s ρ ρ_ps t_pe unb u m Incremento % 0.3 0.093 0.4 0.092 -1.08 0.002 0.5 0.074 -19.57 0.3 0.151 0.4 0.148 -1.99 0.005 0.5 0.132 -10.81 0.3 0.184 0.4 0.181 -1.63 0.007 0.5 0.167 -7.73 0.3 0.214 0.4 0.211 1.4 0.007 0.009 0.5 0.198 -6.16 s ρ ρ_ps t_pe unb u m Incremento % 0.3 0.1 0.4 0.096 -4 0.002 0.5 0.077 -19.8 0.3 0.156 0.4 0.152 -2.56 0.005 0.5 0.135 -11.18 0.3 0.189 0.4 0.185 -2.12 0.007 0.5 0.169 -8.65 0.3 0.219 0.4 0.214 -2.28 0.008 0.009 0.5 0.2 -6.54 s ρ ρ_ps t_pe unb u m Incremento % 0.3 0.106 0.4 0.101 -4.72 0.002 0.5 0.08 -20.79 0.3 0.162 0.4 0.156 -3.7 0.005 0.5 0.137 -12.18 0.3 0.195 0.4 0.188 -3.59 0.007 0.5 0.171 -9.04 0.3 0.224 0.4 0.217 -3.13 0.009 0.009 0.5 0.202 -6.91