Capitolo 3 Metodologia numerica

Capitolo 3

Metodologia numerica

Il capitolo descrive le tecniche numeriche utilizzate per la risoluzione del modello matematico associato al problema della dinamica di un cilindro circolare, dotato di uno o più gradi di libertà, immerso in un fluido. La prima parte è dedicata alla scrittura delle equazioni sia per il campo di moto del fluido che per la dinamica del corpo, facendo riferimento alla rispettive discretizzazioni. La seconda e ultima parte, invece, si occupa di caratterizzare il metodo d’interazione fluido – struttura utilizzato nel presente lavoro.

3.1. Le equazioni di Navier Stokes e la loro

discretizzazione

Si consideri il dominio Ω  ⊂  ℝ2  _{dotato di un contorno lipschitziano ∂Ω,}

e si indichi con 𝑡 ∈ 0, 𝑇 , con 𝑇 > 0,  la variabile temporale e con f(x,y,t) un campo di forze esterno, espresso in unità di superficie. Le equazioni di Navier Stokes, scritte per un fluido newtoniano e incomprimibile,

permettono di determinare il campo di velocità

𝒖 𝑥, 𝑦, 𝑡 = 𝑢_! 𝑥, 𝑦, 𝑡 , 𝑢_!(𝑥, 𝑦, 𝑡) ! _{e il relativo campo di pressione}

𝑝 = 𝑝(𝑥, 𝑦, 𝑡), tale che (sistema A):    

𝑑𝑖𝑣  𝒖 = 0 𝑖𝑛  Ω  × 0, T 𝜌_! 𝜕𝒖

𝜕𝑡 + 𝒖 ∙ 𝑔𝑟𝑎𝑑  𝒖 = 𝜌!𝒈 − 𝑔𝑟𝑎𝑑  𝑝 + 𝜇∇𝟐𝒖 + 𝐟 𝑖𝑛    Ω  ×   0, T dove 𝜌_! e 𝜇 sono la densità e la viscosità del fluido e g è l’accelerazione di gravità. Affinché il problema di Navier Stokes sia ben posto è tuttavia necessario che vengano fornite delle condizioni inziali per la velocità:

𝒖 = 𝒖_𝟎 𝑖𝑛   0  ×  Ω

e delle opportune condizioni al contorno, che nel caso presente lavoro sono condizioni di Dirichlet del tipo:

𝒖 = 𝒂 𝑖𝑛   0, 𝑇  ×  ∂Ω!"

𝒖 = 𝒃 𝑖𝑛   0, 𝑇  ×  ∂Ω_!"# 𝒖 = 𝒄 𝑖𝑛   0, 𝑇  ×  ∂Ω_!

(si è indicato con ∂Ω!" il bordo di inflow, con ∂Ω!"# le pareti laterali e con

∂Ω! il bordo relativo al cilindro circolare). Dividendo l’equazione di

bilancio di quantità di moto per la densità 𝜌_! e moltiplicando entrambe le equazioni per un’opportuna combinazione di ℓ𝓁 e U, rispettivamente una lunghezza e una velocità caratteristica del problema, si giunge alla formulazione di Navier Stokes in forma adimensionale (sistema A’):  

𝑑𝑖𝑣  𝒖 = 0 𝑖𝑛   0, 𝑇  ×  Ω 𝜕𝒖 𝜕𝑡 + 𝒖 ∙ 𝑔𝑟𝑎𝑑  𝒖 = − 1 𝐹𝑟!− 𝑔𝑟𝑎𝑑  𝑝 + 1 𝑅𝑒∇𝟐𝒖 + 𝐟 𝑖𝑛   0, 𝑇  ×  Ω 𝒖 = 𝒖_𝟎 𝑖𝑛   0  ×  Ω 𝒖 = 𝒂 𝑖𝑛   0, 𝑇 ×  ∂Ω!" 𝒖 = 𝒃 𝑖𝑛   0, 𝑇 ×  ∂Ω_!"#

dove 𝑝 è la pressione adimensionalizzata attraverso il termine 𝜌𝑈!_{, Re è il}

3.1.1. Discretizzazione spaziale delle equazioni di NS

Per la discretizzazione spaziale del sistema A’, è utilizzato un metodo agli elementi finiti. In primo luogo è necessario passare alla formulazione variazionale delle equazioni, per cui si definiscono due spazi funzionali V e Q come:

• 𝑽!Ω! = 𝒗   ∈ 𝐻! Ω !: 𝒗 = 0  𝑜𝑛  ∂Ω! è lo spazio dei vettori le cui

componenti, insieme alle loro derivate prime, siano a quadrato sommabile1 _{in Ω e che siano nulle sul bordo dove sono imposte le} condizioni di Dirichlet;

• 𝑄 = 𝑞   ∈  𝐿!(Ω) è lo spazio delle funzioni scalari a quadrato sommabile in Ω.

Moltiplicando la seconda equazione per una funzione test 𝒗   ∈   𝑽!Ω! e

integrando sul dominio Ω, si arriva a scrivere: 𝜕𝒖 𝜕𝑡 + 𝒖 ∙ 𝑔𝑟𝑎𝑑  𝒖 ∙ 𝒗  dΩ + 1 𝐹𝑟! 𝒗dΩ + 𝑔𝑟𝑎𝑑  𝑝 ∙ 𝒗  dΩ − 1 𝑅𝑒 ∇𝟐𝒖 ∙ 𝒗  dΩ = 𝐟 ∙ 𝒗  dΩ ∀𝒗 ∈ 𝑽

Sfruttando poi la formula di Green, si ottiene (per i dettagli della procedura si veda (Quarteroni, 2008)):

𝜕𝒖 𝜕𝑡 + 𝒖 ∙ 𝑔𝑟𝑎𝑑  𝒖 ∙ 𝒗  dΩ + 1 𝐹𝑟! 𝒗dΩ − 𝑝  𝑑𝑖𝑣  𝒗  dΩ + 1 𝑅𝑒 𝑔𝑟𝑎𝑑  𝒖  : 𝑔𝑟𝑎𝑑  𝒗  dΩ = 𝐟 ∙ 𝒗  dΩ ∀𝒗 ∈ 𝑽

dove con “:” è indicato il prodotto interno tra i tensori gradiente di u e v. In modo del tutto analogo si tratta l’equazione di continuità, quindi si moltiplica per una funzione test 𝑞 ∈ 𝑄 e si integra in Ω, così da ottenere:

𝑞 𝑑𝑖𝑣  𝒖  dΩ = 0 _{∀𝑞 ∈ 𝑄}

Quindi il sistema A’, nella sua versione variazionale, può essere scritto come segue (si eliminano le tilda dalle variabili sottintendendo comunque di trattare grandezze adimensionali) (sistema B):

trovare 𝒖, 𝑝 ∈ 𝑽×𝑄 tale che: 𝜕𝒖 𝜕𝑡 + 𝒖 ∙ 𝑔𝑟𝑎𝑑  𝒖 ∙ 𝒗  dΩ + 1 𝐹𝑟! 𝒗dΩ − 𝑝  𝑑𝑖𝑣  𝒗  dΩ + 1 𝑅𝑒 𝑔𝑟𝑎𝑑  𝒖 ∶ 𝑔𝑟𝑎𝑑  𝒗  dΩ = 𝐟 ∙ 𝒗  dΩ  ∀𝒗 ∈ 𝑽 𝑞 𝑑𝑖𝑣  𝒖  dΩ = 0 ∀𝑞 ∈ 𝑄 con 𝒖(𝑡 = 0) = 𝒖𝟎, 𝒖 = 𝒂 in ∂Ω!", 𝒖 = 𝒃 in ∂Ω!"# e 𝒖 = 𝒄 in ∂Ω! per ∀𝑡 > 0.

S’introducono poi le seguenti definizioni: ⋅ Forme bilineari

a : 𝑽  ×  𝑽   ↦ ℝ 𝑎(𝒖, 𝒗) =_𝑅𝑒1 𝑔𝑟𝑎𝑑  𝒖 ∶  𝑔𝑟𝑎𝑑  𝒗 𝑑𝛺 b : 𝑽  ×  𝑄   ↦ ℝ 𝑏 𝒖, 𝑞 = − 𝑞  𝑑𝑖𝑣  𝒖 𝑑𝛺

⋅ Forma trilineare

c : 𝑽  ×  𝑽  ×  𝑽 ↦ ℝ 𝑐 𝒖, 𝒗, 𝒘 = 𝒖 ∙ 𝑔𝑟𝑎𝑑  𝒗 ∙ 𝒘  𝑑𝛺 per cui il sistema B può essere riscritto come:

trovare (𝒖, 𝑝) ∈ 𝑽×𝑄 tali che (sistema B’):

𝑏 𝒖, 𝑞 = 0 ∀𝑞 ∈ 𝑄

𝜕𝒖

𝜕𝑡, 𝒗 !!_(!)+ 𝑎 𝒖, 𝒗 + 𝑑(𝒗) + 𝑏 𝒗, 𝑝 + 𝑐 𝒖, 𝒖, 𝒗

= (𝐟, 𝒗)_!!_(!)

∀𝒗 ∈ 𝑽

dove d(v) è il funzionale associato al termine del Fr.

Il sistema B’ è il punto di partenza per arrivare alla formulazione discretizzata agli elementi finiti secondo Galerkin. Si definiscono due famiglie di sottospazi 𝑽_! ⊂ 𝑽 e 𝑄_! ⊂ 𝑄 di dimensione finita, dipendenti dal

passo di discretizzazione spaziale h. La formulazione discretizzata agli elementi finiti assume la seguente forma (sistema C):

trovare 𝒖!, 𝑝! ∈ 𝑽!×𝑄! tale che:

𝑏 𝒖_!, 𝑞_! = 0   _∀𝑞 ! ∈ 𝑄! 𝜕𝒖_! 𝜕𝑡 , 𝒗! _!!_(!),!+ 𝑎 𝒖!, 𝒗! + 𝑑(𝒗!) + 𝑏 𝒗!, 𝑝! + 𝑐 𝒖!, 𝒖!, 𝒗! = (𝐟!, 𝒗!)!!_(!),! ∀𝒗! ∈ 𝑽!

L’esistenza e l’unicità della soluzione del problema discretizzato C sono assicurate dal teorema del Brezzi che, considerando le caratteristiche di continuità e di coercività della forma  𝑎 𝒖!, 𝒖! e la

continuità della 𝑏 𝒖_𝒉, 𝑞_! , è equivalente alla nota condizione di inf-sup

discreta (detta anche condizione LBB, Ladyzhenskaya-Babuška-Brezzi) (Quarteroni, 2008):

∃  𝛽 > 0  t.c.:

inf!!∈!!,!!!!sup𝒗!∈!!,𝒗!!!  

𝑏 𝒖_𝒉, 𝑞_ℎ

𝒖

∙

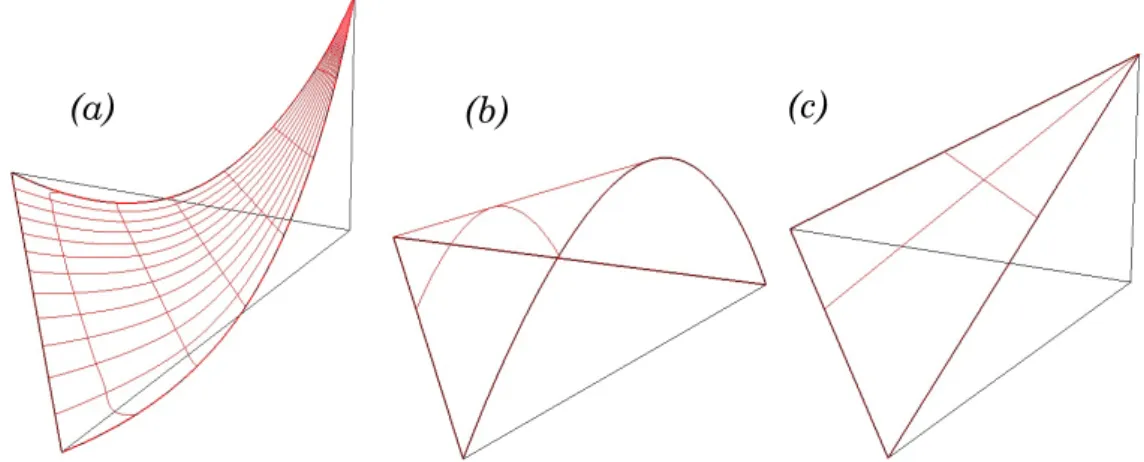
Questa condizione, che è naturalmente verificata nel continuo, nel discreto si traduce nello scegliere coppie di sottospazi Vh-Qh stabili2. In particolare nel presente lavoro si considerano, per mesh triangolari, elementi finiti di Taylor-Hood di tipo P2 – P1, di cui si da una rappresentazione in Figura 3.1.

2 _{Le coppie che non soddisfano la condizione di inf - sup vengono dette coppie instabili, dato che}

la scelta di questi elementi comporta la non unicità della pressione, e per questo le funzioni qh

vengono dette modi spuri di pressione. Un altro metodo per soddisfare la soluzione di inf – sup è quella di stabilizzare il problema a priori o a posteriori (Quarteroni, 2008).

Il sistema C può essere efficacemente rappresentato in forma algebrica

(Quarteroni, 2008). Infatti, indicando le funzioni di base per gli spazi Vh e

Qh come:

𝝋! ∈ 𝑽! 𝜙! ∈ 𝑄!

le funzioni incognite discretizzate si possono scrivere come: 𝒖!(𝑥, 𝑦) = 𝑢!𝝋!(𝑥, 𝑦) ! !!! 𝑝_!(𝒙) = 𝑝_!𝜙_!(𝑥, 𝑦) ! !!!

con N=dimVh e M=dimQh. Il sistema C quindi diventa (sistema C’): 𝐵𝑼 𝑡 = 𝟎 𝑀𝑑𝑼 𝑡 𝑑𝑡 + 𝐴𝑼 𝑡 + 𝐷 + 𝐵!𝑷 𝑡 + 𝐶 𝑼 𝑡 𝑼 𝑡 = 𝑭 𝑡 dove: 𝑀 = [𝑚!"] = 𝝋!∙ 𝝋!𝑑Ω 𝐴 = 𝑎!" = 𝑎(𝝋!, 𝝋!) 𝐵 = 𝑏_!" = 𝑏(𝝋_!, 𝜙_!) 𝐶 = 𝑐_!" = [𝑐 𝑼 𝑡 , 𝝋_!, 𝝋_! ] 𝐷 = 𝑑! = 1 𝐹𝑟! 𝝋!𝑑Ω     𝑼(𝑡) = [𝑢_!(𝑡)]  

Figura 3.1 – Rappresentazione di alcune funzioni di base scelte per la discretizzazione agli elementi finiti: (a)-(b) elemento P2, (c) elemento P1.

𝑃(𝑡) = [𝑝_!(𝑡)]  

3.1.2. Discretizzazione temporale delle equazioni di NS

Per quel che riguarda la discretizzazione temporale si adotta uno schema di ordine 2 nel tempo, basato sulle Backward Differences

Formulas (BDF) (Quarteroni, 2008). In particolare per il termine non

stazionario si può scrivere: 𝜕𝒖 𝑡!!! 𝜕𝑡 ≅ 1 Δ𝑡 3 2𝒖!!!− 2𝒖!+ 1 2𝒖!!! + 𝑜(∆𝑡!)

Questo comporta che, qualora all’interno dell’equazioni si scelga di trattate alcuni termini in modo esplicito o semi-esplicito, sia necessaria un’estrapolazione che mantenga l’ordine di convergenza pari a 2. Questo non è il caso della pressione, che deve necessariamente essere considerata in modo implicito3_{, mentre sul termine convettivo è possibile fare alcune} osservazioni. Quest’ultimo, infatti, può essere trattato in modo esplicito, semi-implicito o puramente implicito. Tutti e tre gli schemi presentano i loro vantaggi e svantaggi. In questo lavoro si sceglie una trattazione esplicita, per cui il sistema da risolvere è lineare e inoltre non c’è la necessità di ri-assemblare a ogni passo la matrice di sistema, come invece accade per gli altri due schemi, riducendo così il costo computazionale dell’intera simulazione. Tuttavia l’utilizzo di un trattamento esplicito necessità di rispettare la condizione di CFL, che collega l’avanzamento temporale a quello spaziale4_{, attraverso la relazione:}

∆𝑡 ≤ ℎ

𝒖! !!

3 _{Il trattamento esplicito del termine di pressione non consente di imporre il vincolo}

dell’incomprimibilità sul campo di moto del fluido.

4  _{La condizione di CFL impone che l’avanzamento temporale della soluzione ( 𝑢}!

!!∙ ∆𝑡) debba essere inferiore al passo di discretizzazione spaziale h, che equivale a dire che il dominio di dipendenza dell’equazione differenziale deve essere completamente incluso nel dominio di dipendenza dello schema numerico.

Quindi, sfruttando tutte le considerazioni appena fatte, si giunge al seguente sistema algebrico (sistema D):

𝐵𝑼!!! _{= 0} 3 2∆𝑡𝑀𝑼!!!+ 𝐴𝑼!!!+ 𝐵!𝑝!!! = 𝐷 + 1 ∆𝑡𝑀 2𝑼! − 1 2𝑼!!!   −2𝐶 𝑼! _𝑼!_{+ 𝐶 𝑼}!!! _𝑼!!!_{+ 𝐅}!

3.2. Modello di dinamica del corpo

Il corpo è un cilindro circolare di diametro D infinitamente rigido e di densità uniforme 𝜌!. Definendo una terna di assi cartesiani (x,y,z),

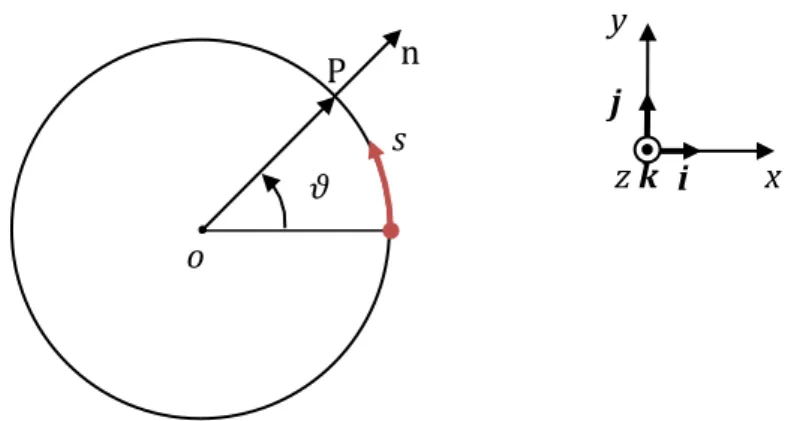
rispettivamente di versori (i,j,k), come mostrato in Figura 3.2, le equazioni che ne definiscono la dinamica sono le seguenti (per comodità di impostazioni delle condizioni al bordo si sceglie di considerare la gravità orientata lungo il versore i) (sistema 1):

  Figura  3.2  –  Definizione  del  sistema  di  coordinate  associate  al  cilindro  circolare.

𝑚𝑑𝑢_𝑑𝑡!(𝑡) = −𝑚𝑔 + 𝒏 ⋅ 𝑻 𝑠, 𝑡 ∙ 𝒊  𝑑𝑠 ! traslazione in x 𝑚𝑑𝑣!(𝑡) 𝑑𝑡 = + 𝒏 ⋅ 𝑻 𝑠, 𝑡 ∙ 𝒋  𝑑𝑠 ! traslazione in y 𝐼_!𝑑𝜗(𝑡) 𝑑𝑡 𝒌 = 𝒓 𝑠 ∧ 𝒏 ⋅ 𝑻 (𝑠, 𝑡)𝑑𝑠 ! rotazione in z 𝜗     n   P   s   x   i   y   j   z  k      x   o  

• m è la massa del corpo (per unità di lunghezza) e 𝐼! è il relativo

momento polare d’inerzia, pari a !_!𝑚𝐷!_;

•  𝑢!, 𝑣! sono rispettivamente la componente x e y della velocità del

corpo e 𝜗 la componente di velocità angolare; • g è il modulo dell’accelerazione di gravità;

• 𝛤 è il dominio di integrazione coincidente con il bordo del cilindro circolare;

• 𝒏 = 𝑛!, 𝑛! è il versore normale al bordo del cilindro nel punto di

coordinata s, Figura 3.25_;

• 𝑻(s, t) è il tensore degli sforzi definito alla coordinata s e al tempo t; • 𝒓 𝑠 è il vettore posizione radiale OP(s);

A questo punto, sostituendo all’interno del sistema 1 l’espressione del tensore degli sforzi e adimensionalizzando tutte le equazioni rispetto alle grandezze di riferimento l e U, si ottiene il seguente sistema (sistema 2):

𝑑𝑢! 𝑑𝑡 = − 1 𝐹𝑟+ 4 𝛼 ∙ 𝜋 −𝑝 + 2 𝑅𝑒∙ 𝜕𝑢 𝜕𝑥 ∙ 𝑛! + 𝑛_! 𝑅𝑒∙ 𝜕𝑣 𝜕𝑥+ 𝜕𝑢 𝜕𝑦 𝑑𝑠 ! traslazione in x 𝑑𝑣_! 𝑑𝑡 = 4 𝛼 ∙ 𝜋 −𝑝 + 2 𝑅𝑒∙ 𝜕𝑣 𝜕𝑦 ∙ 𝑛! + 𝑛_! 𝑅𝑒∙ 𝜕𝑣 𝜕𝑥+ 𝜕𝑢 𝜕𝑦 𝑑𝑠 ! traslazione in y 𝑑𝜗 𝑑𝑡 = 32 𝛼 ∙ 𝜋 ∙ 𝑅𝑒 𝑛!!− 𝑛!! 𝜕𝑢 𝜕𝑦+ 𝜕𝑣 𝜕𝑥 + 2𝑛!𝑛! 𝜕𝑣 𝜕𝑦− 𝜕𝑢 𝜕𝑥 𝑑𝑠 ! rotazione in z

dove si ricorda che 𝛼 è il rapporto tra la densità del corpo e quella del fluido.

3.2.1. Discretizzazione temporale delle equazioni del corpo

Per la discretizzazione temporale delle equazioni della dinamica del corpo, gli schemi considerati nel presente lavoro sono quello di Eulero

5  _{Nel riportare le equazioni in FreeFem è necessario invertire i segni degli integrali per la}

traslazione dato che, nel software, il versore normale è uscente dal dominio di calcolo, e quindi puntato verso il centro del cilindro. Questo non modifica invece l’equazione della coppia, dato che i versori compaiono al quadrato.

esplicito, implicito e quello di Crank-Nicolson. Ad esempio, considerando

la componente in x, i tre schemi forniscono le seguenti 3 espressioni: 𝑢_!!!!_{− 𝑢}

!!

∆𝑡 = 𝑅!! Eulero esplicito (EE)

𝑢_!!!!_{− 𝑢} !!

∆𝑡 = 𝑅!!!! Eulero implicito (EI)

𝑢_!!!!_{− 𝑢} !!

∆𝑡 =

1

2 𝑅!!!!+ 𝑅!! Crank-Nicolson (CN)

Si sottolinea che, mentre l’ultimo schema è accurato al second’ordine nel tempo, i primi due sono accurati solo a prim’ordine. Questo vuol dire che, volendo rimanere in linea con quanto scelto nella discretizzazione temporale delle equazioni del flusso, è necessario innanzitutto sostituire lo schema alle differenze finite al prim’ordine con uno schema alle differenze finite del second’ordine e inserire un’estrapolazione delle forze al second’ordine nello schema di Eulero esplicito, come già visto in precedenza nel caso del termini convettivo delle equazioni di Navier Stokes.

3.3. Schema d’interazione fluido-struttura

Il caso affrontato fa parte della classe dei problemi d’interazione fluido-struttura, dove l’azione che il flusso ha sul corpo, in termini forze e coppie, produce uno spostamento e/o una deformazione che modifica l’evoluzione del flusso stesso. Questo implica che il sistema vada risolto necessariamente con una procedura iterativa.

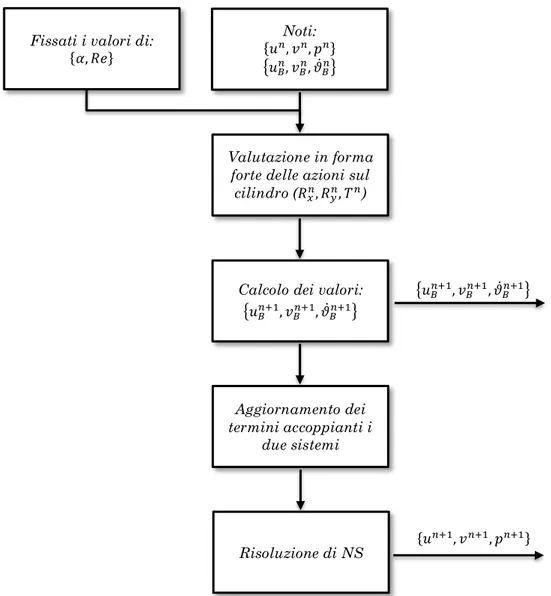
Studiare il caso del cilindro circolare rigido consente di sviluppare un modello di accoppiamento fluido-struttura molto semplice, nel quale i problemi presentati nei paragrafi precedenti sono risolti in modo disaccoppiato. Ammettendo che siano note tutte le grandezze relative al passo temporale n-esimo, uno schema rappresentativo dell’n+1-esimo passo temporale è riportato in Figura 3.3, nel caso venga considerato un

modello esplicito (EE) per la risoluzione del problema della dinamica del cilindro.

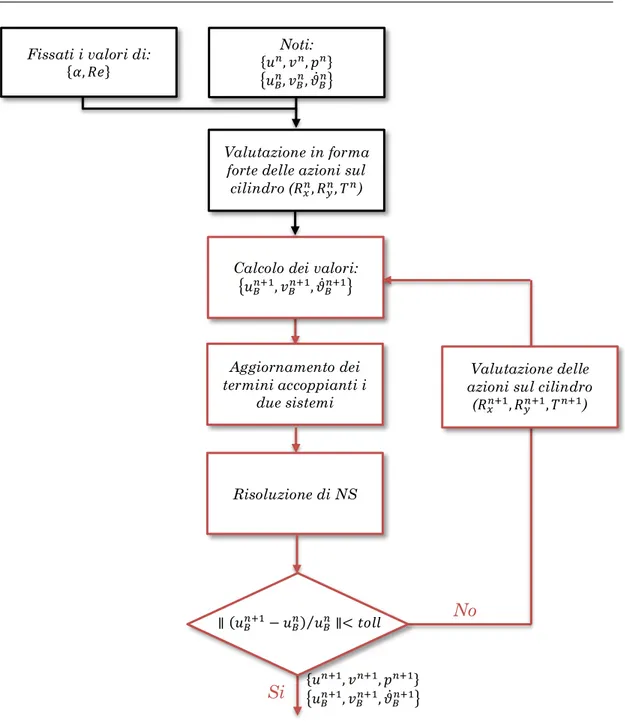
Se invece si sceglie di utilizzare uno schema implicito (EI) o uno di Crank-Nicholson (CN), allora è necessario aggiungere un ciclo interno al precedente, in modo da poter calcolare le forze e i momenti al passo che si sta considerando. Una schematizzazione di questa procedura è riportata in Figura 3.4, dove per la condizione di arresto si usa il valore della velocità del corpo in direzione x.

!𝑢!!!!, 𝑣!!!!, 𝜗̇!!!!!   Noti: {𝑢!_{, 𝑣}!_{, 𝑝}!_} !𝑢!!, 𝑣!!, 𝜗̇!!! Valutazione in forma forte delle azioni sul

cilindro (𝑅!!, 𝑅!!, 𝑇!) Fissati i valori di:

{𝛼, 𝑅𝑒}

Calcolo dei valori:

!𝑢!!!!, 𝑣!!!!, 𝜗̇!!!!! Aggiornamento dei termini accoppianti i due sistemi Risoluzione di NS {𝑢 !!!_{, 𝑣}!!!_{, 𝑝}!!!_}  

Figura 3.3 - Schema rappresentativo dell’n+1-esimo passo temporale relativo al metodo di Eulero esplicito EE

Entrambi i modelli presentano step che sono facilmente riconducibili agli schemi visti nei paragrafi precedenti mentre, per quanto riguarda l’aggiornamento del termine che accoppia i due sistemi, a seconda del caso considerato è necessario sviluppare condizioni diverse, per cui si rimanda ai capitoli successivi l’esplicitazione di tale blocco.

Figura 3.4 - Schema rappresentativo dell’n+1-esimo passo temporale relativo al metodo di Eulero implicito (EI) o di Crank-Nicolson (CN)

Aggiornamento dei termini accoppianti i

due sistemi

Risoluzione di NS Calcolo dei valori:

!𝑢!!!!, 𝑣!!!!, 𝜗̇!!!!! {𝑢!!!_{, 𝑣}!!!_{, 𝑝}!!!_} !𝑢!!!!, 𝑣!!!!, 𝜗̇!!!!!   ∥ (𝑢!!!!− 𝑢!!) 𝑢⁄ !!∥< 𝑡𝑜𝑙𝑙   No Si Valutazione delle azioni sul cilindro

(𝑅!!!!, 𝑅!!!!, 𝑇!!!) Noti:

{𝑢!_{, 𝑣}!_{, 𝑝}!_}

!𝑢!!, 𝑣!!, 𝜗̇!!! Valutazione in forma

forte delle azioni sul cilindro (𝑅!!, 𝑅!!, 𝑇!) Fissati i valori di:

3.4. Freefem++

Il programma utilizzato per l’implementazione dei modelli di calcolo è FreeFem++ (v.3.2), un software open source, scritto in linguaggio c++, sviluppato dai professori O. P´ıronneau, F. Hecht, e A. Le Hyaric presso il Jacques-Louis Lions Laboratory della Pierre and Marie Curie University. FreeFem++ consente, attraverso il metodo agli elementi finiti, di risolvere sistemi di equazioni differenziali alle derivate parziali. Le caratteristiche principali di questo software possono essere riassunte nei seguenti punti (Hecht F., 2011):

a) Descrizione del problema mediante la sua formulazione variazionale, con la possibilità di gestire direttamente i vettori e le matrici;

b) Facile inserimento della geometria attraverso l’uso delle equazioni che ne definiscono il contorno;

c) Uso del generatore automatico di mesh BAMG (Bidimensional

Anisotropic Mesh Generator), basato sull'algoritmo di Delaunay – Voronoi;

d) Vasta scelta sia di elementi finiti (lineari, quadratici, ecc.), sia di solutori di sistemi lineari, sia diretti che iterativi (LU, GMRES, ecc.);

e) Possibilità di utilizzare delle librerie per il calcolo parallelo, basate sullo standard MPI.