CAPITOLO 3 - Teoria di base della CFD

CAPITOLO 3 - Teoria di base della CFD

Dopo la disamina generale ed introduttiva relativa ai motori ad iniezione diretta fatta nei capitoli precedenti, si dà ora un cenno di quella che è la teoria di base del metodo ai volumi finiti (FVM), il quale risulta il più diffuso nel mondo della fluidodinamica computazionale (CFD).

3.1 Generalità

Il FVM si basa su una discretizzazione del continuo, fatta tramite celle (o volumi di controllo) all’interno delle quali si integrano le equazioni generali del moto dei fluidi (note come equazioni di Navier-Stokes).

In questa trattazione, forzatamente semplificata, si prenderanno in considerazione soltanto griglie ortogonali ed uniformi, cioè tali che i segmenti che congiungono i centri di due celle adiacenti siano normali alle superfici esterne delle celle stesse, tutte uguali tra loro da un punto di vista dimensionale.

Si prenda quindi come riferimento un volume di controllo, o control volume (CV), di forma di parellelepipedo, con lati δx, δy, δz. Sia poi P=P x y z

(

, ,

)

il baricentro, o punto centrale, di detto CV. Siano poi le varie proprietà del fluido relative al punto P:

• densità ρ; • pressione p;

• velocità u=

(

u v w, ,

)

; • energia E;

• temperatura T;

• altri (specie chimiche ecc.) che non considereremo.

Tutte queste grandezze dipenderanno sia dal punto che dal tempo.

Siano S, N, E, O, T e B le sei facce del CV (sud, nord, est, ovest, top, bottom) come in figura 3.1. Nella figura 3.2 sono invece riportate le direzioni convenzionalmente positive che saranno considerate per il flusso attraverso la cella.

Fig. 3.1-Volume di controllo

Fig. 3.2-Direzioni convenzionali di flusso di massa positivo

Date le piccole dimensioni di δx, δy, δz, sarà possibile, con buona approssimazione, scrivere le varie proprietà sulle facce con uno sviluppo di Taylor troncato al primo termine. Ad esempio avremo che la pressione p sulla faccia ovest sarà:

1 2 O p p p x x δ ∂ = − ∂ y B z x N O E T S

(

, ,

)

P x y z

CV δy δx δz

( )

1 2 u u x y z x ρ ρ ∂ δ δ δ ⎛ ⎞ − ⎜ _∂ ⎟ ⎝ ⎠

( )

1 2 v v y x z x ρ ρ ∂ δ δ δ ⎛ ⎞ + ⎜ _∂ ⎟ ⎝ ⎠

( )

1 2 w w z x y x ρ ρ ∂ δ δ δ ⎛ ⎞ − ⎜ _∂ ⎟ ⎝ ⎠

( )

1 2 v v y x z x ρ ρ ∂ δ δ δ ⎛ ⎞ − ⎜ _∂ ⎟ ⎝ ⎠

( )

1 2 w w z x y x ρ ρ ∂ δ δ δ ⎛ ⎞ + ⎜ _∂ ⎟ ⎝ ⎠

( )

1 2 u u x y z x ρ ρ ∂ δ δ δ ⎛ ⎞ + ⎜ _∂ ⎟ ⎝ ⎠

E quella relativa alla faccia est sarà invece: 1 2 E p p p x x δ ∂ = + ∂

3.2 Conservazione della massa

Si può senza dubbio affermare (escludendo reazioni nucleari) che il rateo di incremento di massa dell’elemento è uguale al flusso netto di massa entrante (cioè massa entrante meno massa uscente).

Il rateo d’incremento di massa sarà:

( x y z) x y z t t ρδ δ δ _{ρ δ δ δ} ∂ ₌∂ ∂ ∂

essendo il CV fisso (e quindi il volume non dipende dal tempo).

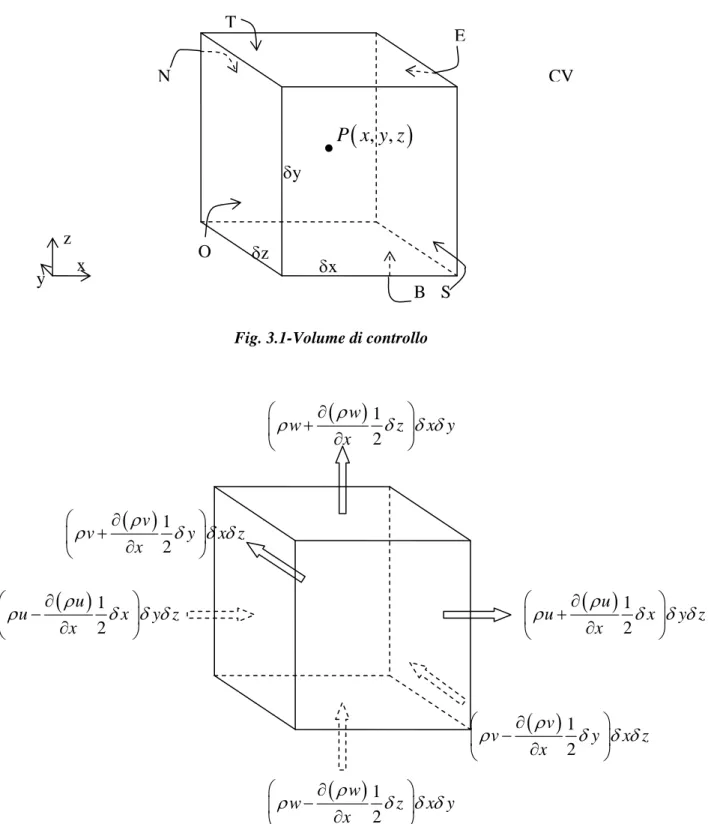
Sommando poi tutti i flussi di massa entranti e quelli uscenti, si ha che il flusso netto è pari a (fig. 3.2):

( )

u

( )

v

( )

w x y z x y z x y z x y z ρ _{δ δ δ} ρ _{δ δ δ} ρ _{δ δ δ} ∂ ∂ ∂ − − − ∂ ∂ ∂

e, in forma compatta, il flusso diviso per il volume Vδ =δ δ δx y z, è pari a ( )

div ρ

− u

In definitiva si può scrivere il bilancio di massa come ( ) 0 div t ρ _ρ ∂ _{+ =} ∂ u

Per un fluido incomprimibile è sempre ρ=costante, per cui l’equazione di conservazione della massa si riduce a 0 divu= Il termine t ρ ∂

∂ descrive il rateo di cambiamento della densità del fluido nel punto P al passare del tempo (vale 0 in tutti i flussi stazionari)

Il termine div(ρu rappresenta invece il termine di flusso attraverso le superfici ed è chiamato ) termine convettivo.

3.3 Derivata materiale

Quantità di moto (momentum) ed energia sono due proprietà che dovranno anch’esse essere regolate da una equazione di continuità. Ciascuna proprietà sarà funzione del tempo e del punto. Sia Φ la generica proprietà relativa all’unità di massa. Si può scrivere allora:

d dt dx dy dz

t x y z

∂Φ ∂Φ ∂Φ ∂Φ

Φ = + + +

∂ ∂ ∂ ∂

Ma è anche dx=udt;dy=vdt; dz=wdt;per cui è anche:

d u v w dt t x y z ⎛∂Φ ∂Φ ∂Φ ∂Φ ⎞ Φ =_⎜ + + + _⎟ ∂ ∂ ∂ ∂ ⎝ ⎠

Dividendo tutto per dt e, per comodità, cambiando simbologia, si ottiene D Dt Φ d dt Φ ⎛_≡ ⎞ ⎜ ⎟ ⎝ ⎠, derivata totale (o sostanziale o materiale) della proprietà Φ rispetto al tempo. Essa rappresenta la variazione complessiva che si ha nella particella, osservandola durante il suo moto (seguendola cioè da un punto di vista lagrangiano). Si deve inserire questa derivata poiché per lo studio di un flusso è molto più comodo usare invece un punto di vista euleriano, cioè vedere come cambiano le proprietà nello spazio, piuttosto che seguire il moto della singola particella. In definitiva si avrà: D grad Dt t Φ ∂Φ_{= + ⋅ Φ} ∂ u

Si ricorda che Φ rappresenta la singola grandezza per unità di massa, mentre per l’analisi che si sta facendo va indicata per unità di volume. Occorrerà allora moltiplicare per la massa e dividere per il volume, cioè moltiplicare per la densità. Si avrà:

D grad Dt t ρ Φ=ρ⎛_⎜∂Φ+ ⋅ Φ⎞_⎟ ∂ ⎝ u ⎠

Questo operatore lega la variazione di Φ rispetto al tempo per una particella (termine a sinistra) con la variazione di Φ all’interno di un elemento fluido stazionario (termine a destra) ed è proprio quello che occorre per passare da un punto di vista lagrangiano a quello euleriano. Partendo dalla (3.1) (che contiene la derivata della massa per unità di volume), è possibile, generalizzandola, applicarla ad ogni proprietà Φ (proprietà per unità di massa) ed avere quindi un termine del tipo:

( ) ( ) div t ρ _ρ ∂ Φ _{+ Φ} ∂ u

dove la prima parte è l’incremento di Φ, mentre la seconda rappresenta il suo flusso netto. Sviluppando il termine precedente si ottiene:

( ) ( ) u v w div u v w t t x y z t x y z ρ _{ρ ρ}⎛ ⎞ ⎛ ρ ρ ρ ρ ⎞ ∂ Φ _{+ Φ =} ∂Φ ∂Φ_{+ +}∂Φ ₊∂Φ _{+ Φ} ∂ ₊∂ ₊∂ ₊∂ ⎜ ⎟ ⎜ ⎟ ∂ u _⎝ ∂ ∂ ∂ ∂ _{⎠ ⎝} ∂ ∂ ∂ ∂ _⎠

D u v w grad t x y z t Dt ⎛∂Φ ∂Φ ∂Φ ∂Φ ⎞ ∂Φ Φ + + + = + ⋅ Φ = ⎜ _{∂ ∂ ∂ ∂} ⎟ _∂ ⎝ ⎠ u

mentre il secondo termine del secondo membro, essendo di fatto la (3.1), è pari a zero. In definitiva si può scrivere:

( ) ( ) D div t Dt ρ _{ρ ρ} ∂ Φ _{+ Φ =} Φ ∂ u

Nella relazione precedente, il primo termine del primo membro rappresenta l’incremento di Φ in un elemento fluido; il secondo termine del primo membro rappresenta il flusso netto di Φ entrante nell’elemento dall’esterno; il secondo membro rappresenta invece l’incremento di Φ nella particella fluida.

3.4 Forme conservative e forme non conservative

Andando a scrivere le equazioni di continuità, la grandezza generica Φ assumerà via via vari significati:

• quantità di moto in direzione x (qmx): Φ diviene u;

• quantità di moto in direzione y (qmy): Φ diviene v;

• quantità di moto in direzione z (qmz): Φ diviene w;

• energia (E): Φ diviene E.

La (3.2) si specializzerà allora nelle forme seguenti: ( ) ( ) Du u div u Dt t ρ ρ =∂ + ρ ∂ u per qmx; ( ) ( ) Dv v div v Dt t ρ ρ =∂ + ρ ∂ u per qmy; ( ) ( ) Dw w div w Dt t ρ ρ =∂ + ρ ∂ u per qmz; ( ) ( ) DE E div E Dt t ρ ρ =∂ + ρ ∂ u per E.

Il primo membro delle forme precedenti è chiamato forma conservativa in quanto in essa è implicita la conservazione della massa; il secondo membro è chiamato invece forma non conservativa, in quanto non la presenta in forma implicita. Entrambe le forme possono essere utilizzate negli sviluppi successivi.

3.5 Equazione della quantità di moto

La seconda legge di Newton (o seconda cardinale della dinamica) dice che la variazione della quantità di moto di una particella fluida è uguale alla risultante delle forze agenti sulla particella stessa. L’equazione è vettoriale: qui sarà considerata nelle sue tre componenti.

L’incremento temporale è dato da:

Du Dt ρ ; Dv Dt ρ ; Dw Dt ρ

Per quanto riguarda le forze agenti sulla particella occorre distinguere tra: • forze di superficie: -forze di pressione

-forze viscose

• forze di volume (o di corpo): -gravità

-forze centrifughe

-forze di natura elettromagnetica -forze di Coriols

-altre

Normalmente gli effetti delle forze di volume vengono introdotti tramite termini di sorgente. Lo stato di tensione di un elemento fluido è dato dalla pressione e dalle nove componenti del tensore delle tensioni. Si indicherà con p la pressione e con τ le tensioni viscose. Si indicherà allora con il termine τij la componente secondo l’asse j della tensione agente sulla faccia

normale all’asse i.

Si consideri, a titolo di esempio, l’equilibrio a traslazione lungo l’asse x:

Fig. 3.3-Componenti di tensione e pressione lungo x

1 2 zx zx z z τ τ −∂ δ ∂ 1 2 yx yx y y τ τ +∂ δ ∂ 1 2 zx zx z z τ τ +∂ δ ∂ 1 2 yx yx y y τ τ −∂ δ ∂ y B 1 2 p p x x δ ∂ − ∂ 1 2 p p x x δ ∂ + ∂ 1 2 xx xx x x τ τ −∂ δ ∂ 1 2 xx xx x x τ τ +∂ δ ∂ z x N O E T S

Da notare che la p è considerata positiva se è effettivamente una pressione (entrante nell’elemento), mentre le τ sono considerate convenzionalmente positive se uscenti dalle superfici. Sommando tutti i termini (di forza, non di tensione: occorre moltiplicare per l’area) si ha: facce N-S: 1 1 2 2 yx yx yx yx y x z yx y x z x y z y y y τ τ τ τ ∂ δ δ δ τ ∂ δ δ δ ∂ δ δ δ ⎛ ⎞ ⎛ ⎞ −_⎜ − _⎟ +_⎜ + _⎟ = ∂ ∂ ∂ ⎝ ⎠ ⎝ ⎠ facce T-B: 1 1 2 2 zx zx zx zx z x y zx z x y x y z z z z τ τ τ τ ∂ δ δ δ τ ∂ δ δ δ ∂ δ δ δ ⎛ ⎞ ⎛ ⎞ −_⎜ − _⎟ +_⎜ + _⎟ = ∂ ∂ ∂ ⎝ ⎠ ⎝ ⎠ facce E-O: 1 1 1 1 2 2 2 2 xx xx xx xx xx p p p x x p x x y z x x x x p x y z x x τ τ δ τ δ δ τ δ δ δ τ _{δ δ δ} ⎡⎛ ₋∂ ⎞₋⎛ ₋∂ ⎞₋⎛ ₊∂ ⎞₊⎛ ₊∂ ⎞⎤ ₌ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎢_{⎝ ∂ ⎠ ⎝ ∂ ⎠ ⎝ ∂ ⎠ ⎝ ∂ ⎠}⎥ ⎣ ⎦ ∂ ∂ ⎛ ⎞ = −_⎜ + _⎟ ∂ ∂ ⎝ ⎠

Per unità di volume si ha allora una risultante pari a:

(

)

yx yx xx zx zx xx p p x x y z x y z τ τ τ ∂ τ _τ ∂ τ ∂ ∂ ∂ ∂ ∂ − + + + = − + + + ∂ ∂ ∂ ∂ ∂ ∂ ∂

Si inserisce poi il termine sorgente all’equazione di conservazione della quantità di moto su x: SMx.

Tutto questo si può ripetere studiando l’equilibrio a traslazione su y e z. Alla fine si ottengono le tre equazioni, dette di Navier-Stokes, relative alla conservazione della quantità di moto di una particella:

(

)

(

)

(

)

yx zx xx Mx xy zy yy My yz xz zz Mz Du p S Dt x y z Dv p S Dt x y z Dw p S Dt x y z τ τ ρ τ τ τ ρ τ τ τ ρ τ ∂ ∂ ∂ = − + + + + ∂ ∂ ∂ ∂ _∂ ∂ = + − + + + ∂ ∂ ∂ ∂ ∂ ∂ = + + − + + ∂ ∂ ∂

Ad esempio, per un campo gravitazionale, è:

0 0 Mx My Mz S S S ρg ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ =_{⎜ ⎟ ⎜}= _⎟ ⎜ ⎟ ⎜₋ ⎟ ⎝ ⎠ ⎝ ⎠ M S (3.3)

3.6 Equazione di continuità dell’energia

Si applica ora il I principio della termodinamica che dice che l’incremento dell’energia di una particella è pari alla somma del calore fornito al fluido e del lavoro fatto sul fluido.

Come al solito, l’incremento di energia sarà pari a: DE

Dt ρ

3.6.1 Lavoro

Il lavoro fatto dalle forze di superficie sulla particella è pari al prodotto delle forze per le velocità secondo l’asse di riferimento considerato.

Si avrà così, seguendo lo stesso ragionamento fatto per ottenere le equazioni della quantità di moto:

(

)

( )

(

)

( )

₍

₎

( )

(

)

( )

₍

₎

su x: su y: su z: yx zx xx xy zy yy yz xz zz u _u u p x y z x y z v v v p x y z x y z w w w p x y z x y z τ τ τ δ δ δ τ τ τ δ δ δ τ τ τ δ δ δ ⎡_{∂ ∂ ∂} ⎤ − + + + ⎢ ⎡_⎣ ⎤_⎦ ⎥ ∂ ∂ ∂ ⎢ ⎥ ⎣ ⎦ ⎡∂ _{∂ ⎡} ∂ ⎤ ⎤ + − + + ⎢ _{⎣ ⎦} ⎥ ∂ ∂ ∂ ⎢ ⎥ ⎣ ⎦ ⎡∂ ∂ ∂ ⎤ + + − + ⎢ ⎡_⎣ ⎤⎥_⎦ ∂ ∂ ∂ ⎢ ⎥ ⎣ ⎦

Il totale del lavoro (per unità di volume) fatto dalle forze di superficie si ha sommando i tre termini e dividendo per il volume δxδyδz.

I tre termini in p possono essere raggruppati:

( )

up

( )

vp

( )

wp

_{( )}

div p x x x ∂ ∂ ∂ − − − = − ∂ ∂ ∂ u

In definitiva il termine di lavoro è pari a:

( ) (

u xx

)

( )

u yx

(

u zx

)

( ) ( ) ( )

v xy v yy v zy

(

w xz

)

( )

w yz

(

w zz

)

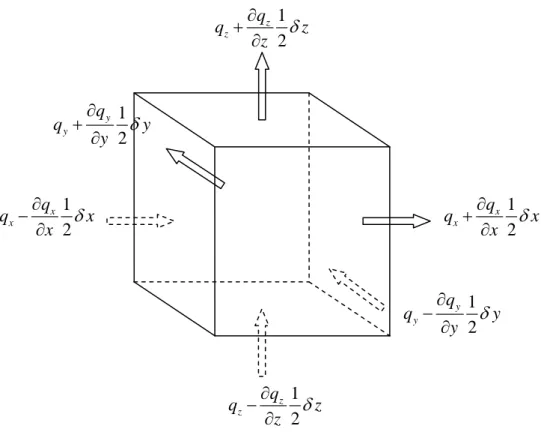
div p x y z x y z x y z τ τ τ τ τ τ ∂ τ ∂ ∂ ∂ τ ∂ τ ∂ ∂ ∂ ∂ − + + + + + + + + + ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ u 3.6.2 Calore

Il flusso di calore q ha tre componenti: qx, qy, qz. Il calore, per convenzione, è ritenuto positivo

Fig. 3.4-flussi di calore in ingresso ed in uscita

Osservando la figura 3.4 e seguendo lo stesso ragionamento visto in presenza, si può scrivere, sommando tutti i contributi e dividendo per il volume:

y x q z q q div x y z ∂ ∂ ∂ − − − = − ∂ ∂ ∂ q

Utilizzando la legge di Fourier, che lega flusso termico e temperatura T, e che ha la forma

( )

k grad T

= − q

il termine di flusso termico netto si può scrivere:

( )

div divk grad T − q= − ⎡_⎣ ⎤_⎦

Da notare che, essendo il coefficiente di conduttività termica k funzione di T, quindi del punto, non può essere portato fuori dall’operatore divergenza.

3.6.3 Equazione generale dell’energia

E’ bene capire cosa si intende per energia E. Normalmente si ottiene sommando l’energia interna i, legata alla temperatura (ossia allo stato di agitazione molecolare), l’energia cinetica macroscopica, che vale 1 2

2U ossia

2 2 2

1

( )

2 u + +v w , e quella potenziale gravitazionale. Qui però conviene considerare l’energia potenziale come un termine sorgente, vedendola come il

1 2 z z q q z z δ ∂ − ∂ 1 2 x x q q x x δ ∂ − ∂ 1 2 z z q q z z δ ∂ + ∂ 1 2 x x q q x x δ ∂ + ∂ 1 2 y y q q y y δ ∂ − ∂ 1 2 y y q q y y δ ∂ + ∂

lavoro fatto da una forza gravitazionale (forza di volume). Inserendo quindi il termine sorgente SE (incremento, nell’unità di tempo e per unità di volume, dell’energia potenziale), si scrive la

forma finale dell’equazione dell’energia:

( )

(

)

( )

(

)

( ) ( ) ( )

(

)

( )

(

)

_{( )}

yx xy yy zy xx zx yz xz zz E u v v v u u DE div p Dt x y z x y z w w w div k grad T S x y z τ τ τ τ τ τ ρ τ τ τ ⎡∂ ∂ ∂ ∂ ∂ ∂ = − +⎢ + + + + + + ∂ ∂ ∂ ∂ ∂ ∂ ⎢⎣ ⎤ ∂ ∂ ∂ + + + ⎥− ⎡_⎣ ⎤_⎦+ ∂ ∂ ∂ _⎥⎦ u dove 1

(

2 2 2

)

2 E= +i u + +v w .

3.6.4 Equazione dell’energia cinetica

Spesso si preferisce separare l’energia cinetica da quella interna, in modo da avere una equazione dipendente da T ed un’altra dipendente dalle variabili meccaniche.

Moltiplicando le tre equazioni della quantità di moto rispettivamente per u, v, w, si ottiene l’equazione dell’energia cinetica:

(

2 2 2

)

( )

1 2 yx xy yy zy yz xx zx xz zz D u v w grad p Dt u v w x y z x y z x y z ρ τ τ τ τ τ τ τ τ τ ⎡ _{+ +} ⎤_{= − ⋅ +} ⎢ ⎥ ⎣ ⎦ ∂ ∂ ∂ ∂ ∂ ⎛∂ ∂ ⎞ ⎛ ⎞ ⎛∂ ∂ ⎞ + _⎜ + + _⎟+ _⎜ + + _⎟+ _⎜ + + _⎟+ ⋅ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ M u u S

3.6.5 Equazione dell’energia interna Si definisce:

i E

S =S − ⋅u S _M

Sottraendo dall’equazione dell’energia quella dell’energia cinetica, si ottiene l’equazione dell’energia interna:

( )

xx yx zx xy yy zy xz yz zz i Di pdiv Dt u u u v v v w w w x y z x y z x y z div k grad T S ρ τ τ τ τ τ τ τ τ τ = − + ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ + + + + + + + + + + ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ + ⎡_⎣ ⎤_⎦+ u

Questa ultima equazione, per fluidi incomprimibili, dove di=cdT (c è il calore specifico), e divu=0, diviene:

(3.4)

(3.5)

( )

xx yx zx xy yy zy xz yz zz i DT c div k grad T Dt u u u v v v w w w x y z x y z x y z S ρ τ τ τ τ τ τ τ τ τ = ⎡_⎣ ⎤_⎦ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ + + + + + + + + + + ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ +

3.6.6 Altre forme dell’ equazione dell’energia

Talvolta l’equazione dell’energia può essere trasformata nell’equazione dell’entalpia. Entalpia specifica (per unità di massa) ed entalpia specifica totale sono così definite:

(

2 2 2

)

0 1 2 p h i h h u v w ρ = + = + + + Si ha che

(

2 2 2

)

(

2 2 2

)

(

2 2 2

)

0 1 1 1 2 2 2 p p h i u v w E u v w u v w ρ ρ = + + + + = − + + + + + + cioè h₀ E p ρ = +

Si ottiene quindi la forma:

( )

(

)

( )

(

)

( ) ( ) ( )

(

)

( )

(

)

0 yx xy yy zy yz xx zx xz zz h Dh p div k grad T Dt t u v v v w u u w w x y z x y z x y z S ρ τ τ τ τ τ τ τ τ τ ∂ = + ⎡_⎣ ⎤_⎦ ∂ ⎡_∂ ∂ _∂ ∂ ∂ ∂ _∂ ∂ _∂ ⎤ +⎢ + + + + + + + + ⎥+ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ⎢ ⎥ ⎣ ⎦ + con Sh=SE.

Da notare è che i tre modi visti di scrivere l’equazione dell’energia nulla aggiungono al sistema, essendo tutti combinabili linearmente tra di loro.

E’ possibile scrivere l’equazione utilizzando anche l’entropia, ma si ritiene opportuno, in questo lavoro, non dilungarci ulteriormente.

3.7 Equazione di stato

Il moto di un fluido è espresso mediante le cinque equazioni alle derivate parziali viste in precedenza. Tra le variabili incognite ci sono ρ, p, i, u e T.

3.7.1 Ipotesi dell’equilibrio locale

Per poter trovare un collegamento tra le variabili tipiche viste sopra, è necessario ricorrere alle equazioni di stato termodinamiche. Occorre però precisare che tali, note, relazioni descrivono

uno stato di equilibrio. Si sa che in un fluido in movimento le grandezze cambiano, anche con gradienti elevati, da punto a punto: il sistema cioè è non in equilibrio. L’ipotesi che si fa è che, dato che un fluido ha una “velocità di aggiornamento” molto elevata, l’adeguamento alle nuove condizioni, in un volume materiale molto piccolo, può essere considerato istantaneo. Ogni elemento, ad ogni istante, si trova cioè in uno stato di equilibrio, diverso dagli elementi adiacenti e da quello dello stesso elemento in un istante diverso. Tale ipotesi consente di utilizzare le note relazioni termodinamiche, permettendo quasi sempre di descrivere bene la fisica del sistema. Solo in caso di onde d’urto molto forti questa ipotesi può portare ad errori, anche se spesso l’approssimazione rimane buona.

3.7.2 Esempi di equazioni di stato

Le equazioni di stato relazionano tra loro due variabili (di stato); ad esempio ρ e T come variabili di stato portano ad avere:

(

,

)

e

(

,

)

p= p ρ T i=i ρ T

Per un gas perfetto tali relazioni sono:

e _v

p=ρRT i=c T

Queste relazioni legano tra di loro da una parte l’equazione dell’energia e dall’altra quantità di moto e massa. Tale legame è dovuto al fatto che le densità variano in conseguenza di variazioni di T e p nel fluido.

Si definisce numero di Mach M il rapporto tra la velocità del fluido e quella della propagazione delle perturbazioni all’interno del fluido stesso (velocità del suono):

U M

a =

Sperimentalmente si osserva che se M è inferiore a 0,3 circa, il fluido può essere considerato, con ottima approssimazione, incomprimibile. Per fluidi incomprimibili, dove ρ=cos t sostituisce p=ρRT, il legame di cui sopra viene a mancare. Questo tipo di problemi, a meno che non compaiano flussi termici, può essere risolto senza l’uso dell’equazione dell’energia.

3.8 Equazioni di Navier-Stokes per fluidi newtoniani

Le componenti del tensore delle tensioni viscose sono, a questo punto della trattazione, incognite: è necessario, pertanto, fornire un modello costitutivo di fluido.

Molti casi di interesse pratico possono essere trattati introducendo un modello in cui le tensioni viscose siano espresse come funzione della deformazione locale. Tale deformazione è composta da una parte lineare e da una volumetrica.

Tutti i gas e moltissimi liquidi sono poi isotropi. Eccezioni sono i liquidi polimerici, dove l’orientazione delle lunghe catene molecolari può dare origine a direzioni preferenziali di deformazione. Tali casi non verranno qui esaminati.

La deformazione lineare ha nove componenti, ma solo sei sono indipendenti nei fluidi isotropi (il tensore è simmetrico). Queste deformazioni si indicano con eij (componente secondo l’asse j

della deformazione relativa alla superficie normale all’asse i). Tre sono le componenti di allungamento: ; ; xx yy zz u v w e e e x y z ∂ ∂ ∂ = = = ∂ ∂ ∂

esistono poi le sei componenti di deformazione a taglio:

1 1 1 ; ; 2 2 2 xy xy xz zx yz zy u v u w v w e e e e e e y x z x z y ⎛∂ ∂ ⎞ ⎛∂ ∂ ⎞ ⎛∂ ∂ ⎞ = = _⎜ + _⎟ = = _⎜ + _⎟ = = _⎜ + _⎟ ∂ ∂ ⎝∂ ∂ ⎠ ∂ ∂ ⎝ ⎠ ⎝ ⎠

La deformazione volumetrica è data dalla somma delle tre componenti di allungamento:

u v w

div

x y z

∂ ₊∂ ₊∂ ₌

∂ ∂ ∂ u

In quello che prende il nome di fluido newtoniano, le tensioni viscose sono proporzionali alle deformazioni.

Si hanno allora, nelle equazioni viscose di Newton, due costanti di proporzionalità, relative rispettivamente alla deformazione lineare (μ, viscosità dinamica) e a quella volumetrica (λ, seconda viscosità). Si può allora scrivere:

2 ; 2 ; 2

xx yy zz

u w

div div div

x y z τ = μ∂ +λ τ = μ ∂ +λ τ = μ ∂ +λ ∂ u ∂ u ∂ u ; ; xy xy xz zx yz zy u v u w v w y x z x z y τ =τ =μ_⎜⎛∂ +∂ _⎟⎞ τ =τ =μ_⎜⎛∂ +∂ _⎟⎞ τ =τ =μ⎛_⎜∂ +∂ ⎞_⎟ ∂ ∂ ⎝∂ ∂ ⎠ ∂ ∂ ⎝ ⎠ ⎝ ⎠

Si sa molto poco circa la seconda viscosità poiché i suoi effetti sono piccoli in moltissimi casi pratici. Si può assumere che per i gas poilatomici essa valga circa 2

3μ. Per i fluidi incomprimibili è divu=0, per cui non compare nelle equazioni.

A questo punto è possibile riscrivere le equazioni di Navier-Stokes, inserendo il legame costitutivo newtoniano appena visto. Rimaneggiando i termini, la forma utile ai fini del FVM può essere così riscritta:

( )

( )

( )

' ' ' Mx My Mz Du p div grad S Dt x Dv p div grad S Dt y Dw p div grad S Dt z ρ μ ρ μ ρ μ ∂ = − + ⎡_⎣ ⎤_⎦+ ∂ ∂ = − + ⎡_⎣ ⎤_⎦+ ∂ ∂ = − + ⎡_⎣ ⎤_⎦+ ∂ u u u dove si è posto S_Mx' =S_M +s_M.

Per quanto riguarda l’equazione dell’energia interna, utilizzando ancora il modello newtoniano, essa può essere riscritta così:

( )

i

Di

pdiv div k grad T S

Dt

ρ = − u+ ⎡_⎣ ⎤_⎦+ Φ +

dove tutti gli effetti dovuti alle tensioni viscose sono descritti dal termine dissipativo Φ che, con alcuni passaggi, si dimostra essere pari a:

(

)

2 2 2 2 2 2 2 2 u v w u v u w v w div x y z y x z x z y μ⎧⎪ ⎡⎛∂ ⎞ ⎛∂ ⎞ ⎛∂ ⎞ ⎤ ⎛∂ ∂ ⎞ ⎛∂ ∂ ⎞ ⎛∂ ∂ ⎞ ⎫⎪ λ Φ = _⎨ ⎢_{⎜ ⎟} +_{⎜ ⎟} +_{⎜ ⎟} ⎥+_⎜ + _⎟ +_⎜ + _⎟ +_⎜ + _{⎟ ⎬}+ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎢ ⎝ ⎠ ⎥ ⎝ ⎠ ⎝ ⎠ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭ u

Tale funzione non può essere negativa, poiché contiene tutti i termini elevati al quadrato. Essa rappresenta una sorgente di energia interna, dovuta al lavoro di deformazione sulla particella fluida. Tale termine è quello di conversione, irreversibile, tra energia meccanica e termica.

3.9 Sistema di Navier-Stokes

Si riscrivono ora tutte le equazioni fin qui ottenute.

( )

( )

₍

₎

_{( )}

( )

₍

₎

_{( )}

( )

₍

₎

_{( )}

( )

₍

₎

_{( )}

' ' ' 0 Mx My Mz i div t u p

div u div grad S

t x

v p

div v div grad S

t y

w p

div w div grad S

t z

i p

div i pdiv div k grad T S

t z ρ _ρ ρ ρ μ ρ ρ μ ρ _{ρ μ} ρ ρ ∂ + = ∂ ∂ _{+ = −}∂ _{+ ⎡ ⎤+} ⎣ ⎦ ∂ ∂ ∂ _{+ = −}∂ _{+ ⎡ ⎤+} ⎣ ⎦ ∂ ∂ ∂ _{+ = −}∂ _{+ ⎡ ⎤+} ⎣ ⎦ ∂ ∂ ∂ ∂ + = − + + ⎡_⎣ ⎤_⎦+ Φ + ∂ ∂ u u u u u u u u u

Ad esse si aggiungono le equazioni di stato

(

,

)

e

(

,

)

p= p ρ T i=i ρ T

(3.8)

L’ipotesi di equilibrio termodinamico locale fornisce queste due ultime equazioni algebriche. Il sistema così ottenuto ha 7 equazioni e 7 incognite; è quindi chiuso ed è possibile darne una soluzione una volta assunte le opportune condizioni al contorno e quelle iniziali.

Come si può osservare, le equazioni sono tutte simili: posta Φ la generica grandezza, infatti, hanno tutte la forma:

( )

₍

₎

_{( )}

div div grad S

t ρ ρ _Φ ∂ Φ + Φ = ⎡_⎣Γ Φ +⎤_⎦ ∂ u

dove si è introdotto il coefficiente di diffusione Γ. Si può provare a scriverla in termini letterali:

L’espressione precedente prende il nome di equazione di trasporto di Φ. Da notare che per far combaciare tale espressione con l’equazione dell’energia interna, occorre scambiare i e T. Ciò può essere fatto utilizzando l’equazione di stato algebrica che lega le due grandezze.

Ponendo quindi Φ pari a 1, u, v, w, i (o T, o h0) e scegliendo i valori appropriati per il

coefficiente di diffusione e per il termine sorgente, è possibile avere facilmente tutte le equazioni che ci servono.

3.10 Integrazione sul CV

Per andare avanti col FVM, occorre ora integrare le forme differenziali viste su di un volume di controllo (CV). Si ottiene:

( )

₍

₎

_{( )}

CV CV CV CV

dV div dV div grad dV S dV

t ρ ρ _Φ ∂ Φ + Φ = ⎡_⎣Γ Φ ⎤_⎦ + ∂

∫

∫

u

∫

∫

Il termine convettivo e quello diffusivo possono essere trasformati in integrali di superficie usando il teorema di Gauss, che per un vettore può essere scritto:

CV A div dV = ⋅ dA

∫

a

∫

n a Quindi:

( )

₍

₎

_{( )}

CV A A CV dV dA grad dA S dV t ρ ρ _Φ ∂ Φ + ⋅ Φ = ⋅ Γ⎡_⎣ Φ ⎤_⎦ + ∂

∫

∫

n u

∫

n

∫

A parole si può scrivere: Incremento di Φ per un elemento fluido Flusso netto di Φ fuori dall’elemento (termine convettivo) Diffusione netta di Φ (termine diffusivo) Incremento di Φ dovuto a sorgenti + + = (3.10) (3.11)

Il primo termine scompare nei problemi stazionari.

In problemi non stazionari è necessario integrare il tutto anche sull’intervallo di tempo considerato. Si arriva pertanto alla forma più generale:

( )

₍

₎

_{( )}

t CV t A t A t CV dV dA grad dA S dV t ρ ρ _Φ Δ Δ Δ Δ ⎡ ∂ Φ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ + ⋅ Φ = ⋅ Γ⎡ Φ ⎤ + ⎢ _∂ ⎥ ⎢ ⎥ ⎢ ⎣ ⎦ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦

∫ ∫

∫ ∫

n u

∫ ∫

n

∫ ∫

3.11 Classificazione dell’ambiente fisico

Ci si occupa ora delle condizioni iniziali e di quelle al contorno.

Occorre distinguere due categorie principali problemi, in relazione all’ambiente fisico: ƒ problemi di equilibrio

ƒ problemi di avanzamento o propagazione 3.11.1 Problemi di equilibrio

Sono problemi stazionari, governati da equazioni ellittiche. Tali equazioni hanno la forma dell’equazione di Laplace che descrive un flusso irrotazionale di un fluido incomprimibile e un trasferimento termico stazionario del tipo (bidimensionale):

2 2 2 2 0 x y ∂ Φ ∂ Φ + = ∂ ∂

Un problema simile si può risolvere fornendo il valore di Φ (e della sua derivata prima) su tutto il contorno.

Questo tipo di problema è anche chiamato problema ai valori di contorno. Una caratteristica importante dei problemi ellittici è che il disturbo all’interno del dominio (ad esempio un termine di sorgente) modifica la soluzione ovunque, propagandosi in ogni direzione. Di conseguenza, anche se le condizioni al contorno sono discontinue, la soluzione al problema sarà sempre continua. Questo fatto favorisce chi progetta metodi numerici: occorre però che la

Incremento di Φ per un elemento fluido Diminuzione di Φ dovuta alla convezione attraverso le superfici di contorno (termine convettivo) Incremento di Φ dovuto alla diffusione attraverso le superfici di contorno (termine diffusivo) Incremento di Φ dovuto a sorgenti interne all’elemento + + = (3.12)

tecnica numerica permetta che gli eventi in ogni punto siano influenzati da ciò che avviene nell’intorno.

3.11.2 Problemi di avanzamento o propagazione

Sono i transitori termici, tutti i flussi non stazionari ed i fenomeni ondulatori. Questi problemi sono governati da equazioni paraboliche o iperboliche e non tutti sono non stazionari. Le equazioni paraboliche descrivono problemi tempo varianti che coinvolgono grosse dissipazioni. Esempi sono flussi viscosi non stazionari e conduzioni di calore non stazionarie. Le equazioni paraboliche hanno la forma (monodimensionale):

2 2

t α x

∂Φ ₌ ∂ Φ

∂ ∂

e per risolverle si ha bisogno delle condizioni al contorno per ogni istante di integrazione del problema e delle condizioni iniziali all’interno del dominio. I problemi di questo tipo sono anche detti problemi ai valori iniziali e di contorno. Disturbi che si originano ad un tempo

0

t> possono influenzare solo la soluzione per tempi successivi. La soluzione evolve nel t tempo e diffonde nello spazio. Anche in questo caso sarà continua anche se le condizioni iniziali presentano delle discontinuità. Per t→ ∞ si arriva all’equilibrio, quindi ad una soluzione stazionaria (ellittica).

Le equazioni iperboliche governano invece i problemi di analisi vibrazionale, problemi cioè non stazionari, ma dove si possono trascurare le dissipazioni. L’equazione tipo, in questo caso, è l’espressione delle onde:

2 2

2 c 2

t x

∂ Φ₌ ∂ Φ

∂ ∂

Occorre anche qui avere le condizioni iniziali e quelle di contorno per ogni istante successivo a t0: anche questi sono problemi alle condizioni iniziali e di contorno. In questo caso però le discontinuità nelle condizioni iniziali non si vedono nella soluzione a causa della mancanza di termini dissipativi: la soluzione infatti è un’onda, esprimibile in serie di Fourier. Una perturbazione si può propagare solo in una certa zona del dominio, ad una velocità non infinita, ma pari alla velocità di propagazione dell’onda. Per analizzare flussi fluidi non viscosi, a velocità prossime o superiori a quella del suono, è necessario ammettere delle discontinuità nella soluzione (onda d’urto).

3.11.3 Condizioni iniziali e al contorno Nella tabella sottostante si riassume quanto fin qui detto.

In pratica, però, molti flussi hanno caratteristiche diverse a seconda del punto. In particolare, ad esempio, si possono avere flussi che, a seconda del punto, siano supersonici o subsonici. Tutto ciò si traduce in complessità nella scelta delle condizioni al contorno.

Si può così schematizzare il problema:

• condizioni iniziali per flussi non stazionari: p (o ρ), u, T devono essere noti per t=0 per

ogni punto del dominio.

• condizioni al contorno per flussi stazionari e non: su parete solida: u u= _wall

wall

T =T oppure k T q_wall n

∂ _{= −} ∂

su contorni fluidi in ingresso: p (o ρ), u, T in funzione del punto su contorni fluidi in uscita: n e t

n t u u p F F n n ∂ ∂ − + = = ∂ ∂

dove t ed n sono il versore tangenziale e normale uscente dalla superficie di contorno. Le ultime sono condizioni riguardo alle tensioni normali o tangenziali sulle superfici, F ed _n F essendo _t valori noti di forze di superficie all’interfaccia. La densità deve essere nota all’ingresso, mentre verrà calcolata all’interno con l’equazione di continuità e non c’è bisogno di specificarla tra le condizioni al contorno. Per flussi incomprimibili non compare affatto.

Normalmente, va detto, i contorni in uscita sono posizionati in posti dove il flusso è approssimativamente unidirezionale e dove le tensioni superficiali sono note. Per flussi ad alti numeri di Reynolds, sia lontano da oggetti solidi (in flussi esterni) che in flussi completamente sviluppati all’uscita di un condotto, abbastanza lontano dalle pareti (getti), non ci sono modifiche in nessuna componente della velocità attraverso la superficie di contorno, per cui è

0 n t u u n n ∂ ₌∂ ₌ ∂ ∂

Generalmente, quindi, le condizioni all’uscita, nelle applicazioni CFD, si riducono a all’imposizione della sola pressione p.

Flusso stazionario Flusso non stazionario Flusso viscoso ellittico parabolico

M<1 ellittico iperbolico

Flusso non viscoso

M>1 iperbolico iperbolico

Qualche problema occorre nel caso di contorni fluidi (tipicamente nell’analisi di flussi esterni). In teoria cioè, in questi casi, occorre fare attenzione a porre un 0

n ∂

=

∂ . Tuttavia, dati la convenienza nell’uso di questa condizione ed i risultati accettabili, essa viene comunque mantenuta.

I codici CFD offrono anche condizioni al contorno per la pressione. Si usano valori fissati, aggiustando con sorgenti e assorbimenti di massa posizionati sul contorno (in ingresso ed in uscita), in modo da avere flussi corretti all’interno del dominio, attraverso ingressi ed uscite a

cos .

p= t

Altre condizioni sono quelle cicliche

(

Φ = Φ_{1 2}

)

(usate se ci sono ripetibilità nel flusso) e simmetriche 0 n ∂Φ ⎛ ₌ ⎞ ⎜ _∂ ⎟ ⎝ ⎠.

Problemi nella scelta delle condizioni al contorno (e dei contorni stessi) nascono allorché si debbano studiare flussi transonici, dove il numero di Reynolds è molto elevato e la zona viscosa nel flusso è molto sottile. La natura iperbolica del problema è la fonte di queste difficoltà: intanto le condizioni di cui sopra sono state ottenute per fluidi viscosi, mentre, come detto, in questo caso il flusso si comporta come se fosse non viscoso in gran parte del dominio. Occorre allora modificare alcune procedure, ma questo discorso non viene qui affrontato.

3.12 La turbolenza

Quando il numero di Reynolds Re UL ν

⎛ ₌ ⎞

⎜ ⎟

⎝ ⎠ supera certi valori, il flusso passa da laminare a turbolento: velocità e pressione cambiano cioè continuamente all’interno del flusso. Finché il flusso è laminare le equazioni viste possono essere risolte, talvolta analiticamente (casi molto particolari), altre volte applicandole direttamente ai codici CFD. Quasi tutti i flussi interessanti da un punto di vista ingegneristico sono, tuttavia, turbolenti: si vedrà come questo complichi le cose.

3.12.1 Cos’è la turbolenza

Il numero di Reynolds indica in pratica il rapporto tra l’inerzia del fluido, associata alla componente convettiva, e le forze viscose.

Per bassi Re (minori di Recr) li flusso è “liscio” e i vari strati di fluido scorrono gli uni sugli altri

in fasci ordinati. Se le condizioni al contorno non cambiano, il flusso è stazionario: si ha un flusso laminare. Per Re>Re_cr avvengono eventi complessi che cambiano radicalmente le

caratteristiche del flusso, portandolo, alla fine, in uno stato caotico e casuale. Il moto diventa intrinsecamente non stazionario, anche se le condizioni al contorno non cambiano. Il flusso si chiama allora turbolento. La natura caotica e casuale del fenomeno turbolento preclude un approccio basato sulla completa descrizione del moto delle particelle.

Quello che si può fare è scomporre la velocità ( )u t (e le altre proprietà v, w, p, T) in una componente media, stazionaria, U ed in una fluttuante sommata ad essa '( )u t .:

( ) '( ) u t = +U u t

Anche in flussi dove la velocità media è mono o bidimensionale, la componente fluttuante assume sempre un carattere tridimensionale. Inoltre, visualizzando un flusso turbolento, si possono osservare moti rotazionali, chiamati vortici turbolenti, che hanno un esteso range di scale di grandezza.

Particelle fluide che erano state inizialmente separate possono essere riportate assieme attraverso i vortici, anche dopo lunghe distanze. Come conseguenza di ciò, calore, massa, quantità di moto, possono scambiarsi molto più facilmente. Si osserva sperimentalmente come, ad esempio, una striscia di colore posta in un punto si rompe velocemente e si disperde. Questo rimescolamento porta ad alti valori dei coefficienti diffusivi.

3.12.2 Interazioni dei vortici

I vortici più grossi interagiscono col flusso medio e gli sottraggono energia tramite un processo chiamato deformazione vorticosa: la presenza di gradienti sulla velocità media provoca cioè la deformazione dei vortici più grandi. La velocità ϑ e la lunghezza A (dimensione preponderante, tipicamente il diametro medio) caratteristica dei vortici più grandi sono dello stesso ordine di grandezza della velocità U e della lunghezza caratteristica L del flusso medio; quindi il numero di Reynolds di un vortice grande ϑ

ν ⎛₌ ⎞

⎜ ⎟

⎝ ⎠

A

sarà grande in tutti i flussi turbolenti

(poiché in essi UL

ν è grande). Si ha allora che l’inerzia, nei grandi vortici, prevale sulla viscosità, che risulta trascurabile. Questi vortici sono in effetti considerati non viscosi: in essi la quantità di moto angolare si conserva durante la deformazione vorticosa, il che comporta un incremento della velocità di rotazione ed una diminuzione del raggio. La conseguenza è la formazione di moti aventi scala minore, sia di lunghezza che di tempo. Il lavoro di deformazione fatto dal flusso medio sui vortici più grandi fornisce ad essi l’energia che permette alla turbolenza di mantenersi.

I vortici più piccoli sono a loro volta fortemente deformati da qualche vortice più grosso e più debolmente dal flusso principale. In questo modo l’energia cinetica è trasmessa dai vortici più grossi a quelli più piccoli, in quella che è definita cascata di energia.

Tutte le parti fluttuanti delle proprietà di un flusso turbolento contengono energia attraverso un ampio range di frequenza o numeri d’onda 2 f

U π

⎛₌ ⎞

⎜ ⎟

⎝ ⎠. La scala di moto più piccola che si può trovare in un flusso turbolento è data dalla viscosità: il Re più piccolo che si può trovare (con velocità υ e lunghezza η) è pari a υη 1

ν = . A queste scale (lunghezze da 0,1 a 0,01 mm e frequenze attorno ai 10kHz in flussi tipici) le tensioni viscose diventano importanti; allora l’energia associata alla vorticità è dissipata dal lavoro viscoso e convertita in energia interna. Questa dissipazione compare come incremento di energia persa associata ai flussi turbolenti. La struttura dei vortici più grandi è fortemente anisotropa (è, cioè, direzionale) a causa della forte dipendenza dal flusso medio. L’azione diffusiva via via più importante della viscosità, tende a far scomparire la direzionalità dei vortici man mano che le scale diminuiscono. Per flussi medi ad alto Re, i vortici più piccoli sono, infatti, isotropi.

3.12.3 Zona di transizione da moto laminare a turbolento

Un problema piuttosto complicato è quello di capire come e dove avvenga il passaggio da flussi laminari a flussi turbolenti. L’origine della transizione è dovuta ad instabilità non viscosa, oppure ad una viscosa, ancora più complessa da descrivere. Fatto sta che, per Re=Re_trans (di transizione laminare-turbolento), disturbi nel flusso provocano degli spot turbolenti che possono annullarsi, ma anche crescere ed unirsi fino a cadere, per Re=Re_crit (critico, turbolento), in moti completamente turbolenti. Attualmente le teorie matematiche non sono ancora complete. L’unico sistema è quello di integrare le equazioni del moto per problemi molto semplici: tale sistema risulta però ancora molto costoso, poiché richiede potenze di calcolo piuttosto elevate.

Normalmente, va detto, le zone di transizione sono piuttosto piccole: questo permette di avere dei risultati accettabili nei calcoli anche se si considera il moto o completamente laminare oppure totalmente turbolento. I codici CFD commerciali, generalmente, seguono questa linea.

3.13 Effetti della turbolenza sulle equazione di Navier-Stokes

Per flussi laminari è abbastanza semplice integrare in CFD e utilizzare i risultati; per flussi turbolenti ci aspettiamo di visualizzare vortici di tutte le scale (si può arrivare fino a 100μm di

lunghezza). Se si prende ad esempio un semplice dominio di flusso turbolento di 10cm di lato, occorrerebbero circa 109÷1012 celle per una corretta visualizzazione. Inoltre la frequenza relativa a vortici piccoli può facilmente arrivare a 10kHz, il che porterebbe alla necessità di integrare su step temporali dell’ordine di 10-9 secondi. Tutto ciò richiede potenze di calcolo molto spinte, ancora oggi appannaggio di pochi cluster, posseduti solo dai grossi centri di ricerca internazionali.

Da un punto di vista ingegneristico, spesso non si è interessati a conoscere ogni singolo piccolo vortice di un flusso, interessando molto di più il flusso medio che, tuttavia, è influenzato dalla turbolenza. Occorre quindi capire che influenza abbiano le fluttuazioni tipiche della turbolenza sui flussi medi.

Sia ϕ una proprietà e Φ il suo valore medio; vale la seguente:

0 1 ( ) t t dt t ϕ Δ Φ = Δ

∫

Il valore di Δt nella relazione precedente dovrebbe essere infinito, ma è sufficiente che sia più grande della scala temporale del vortice più lento. La definizione appena data va bene solo per flussi mediamente stazionari; se invece il flusso è completamente non stazionario, il valore medio è quello ottenuto, dopo un certo tempo t, come la media tra le misure effettuate su numerosi esperimenti tutti uguali tra loro (media d’insieme).

La proprietà ϕ è dipendente dal tempo e può essere ottenuta come somma della componente media Φ e di quella fluttuante '( )ϕ t . Quest’ultima grandezza ha una media temporale nulla:

0 1 '( ) '( ) 0 t t t dt t ϕ = Δϕ ≡ Δ

∫

Si possono avere informazioni anche su valori medi di '( )ϕ t usando il valore rms (root mean square):

( )

2 2 rms 1 ' ' t o dt t ϕ = ϕ = Δ ϕ Δ

∫

I valori rms della velocità sono particolarmente importanti perché possono essere facilmente misurati con una sonda anemometria.

L’energia cinetica k (per unità di massa) associata alla turbolenza è definita come:

(

2 2 2

)

1

' ' '

2

k= u +v +w

L’intensità di turbolenza è legata all’energia cinetica e alla velocità media di riferimento come segue:

1 2 2 3 i ref k T U ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ = 3.14 Equazioni di Reynolds

Si prova adesso ad applicare l’operazione di media al sistema di Navier-Stokes; prima però si elencano brevemente le proprietà di cui godono tali operazioni.

Siano intanto ϕ= Φ +ϕ' e ψ = Ψ +ψ ' due proprietà generiche. Si ha: ' ' 0; ; ; ds= ds ; = ' '; ; ' 0 s s ϕ ϕ ψ ϕ ϕ ψ ϕψ ϕ ψ ϕ ϕ ∂ ∂Φ = = Φ = Φ = Φ ∂ ∂ + = Φ + Ψ ΦΨ + Ψ = ΦΨ Ψ =

∫

∫

Tali uguaglianze discendono tutte dalle operazioni di media viste in precedenza.

Essendo anche le operazioni di divergenza e gradiente delle derivazioni, è possibile estendere anche ad esse le proprietà di cui sopra. Se a è un vettore tale che a A a'= + , possiamo scrivere:

( )

( )

(

)

( )

( )

( )

; ' ' ;

div grad div grad

div div div ϕ div ϕ div div ϕ

ϕ = = = Φ + = Φ ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ a A a a A a

Per osservare l’influenza delle fluttuazioni si consideri, per semplicità, il caso di un flusso incomprimibile e con viscosità costante:

( )

( )

( )

( )

( )

( )

x y z 0 1 qm 1 qm 1 qm div u p

div u div grad u

t x

v p

div v div grad v

t y

w p

div w div grad w

t z ν ρ ν ρ ν ρ = ∂ ∂ + = − + ⎡_⎣ ⎤_⎦ ∂ ∂ ∂ _{+ = −} ∂ _{+ ⎡ ⎤} ⎣ ⎦ ∂ ∂ ∂ ∂ + = − + ⎡_⎣ ⎤_⎦ ∂ ∂ u u u u

Si sostituiscono adesso le seguenti:

'; '; '; '; = + '

u= +U u v= +V v w W= +w p= +P p u U u

E si applica la media temporale alle equazioni.

Per la continuità della massa si ha divu=divU, per cui 0

divU=

( )

( )

( )

( )

( )

; ' ' 1 1 ; u U

div u div U div u

t t

p P

div grad u div grad U

x x ν ν ρ ρ ∂ ₌∂ _{= +} ∂ ∂ ∂ ∂ − = − ⎡_⎣ ⎤_⎦= ⎡_⎣ ⎤_⎦ ∂ ∂ u U u La qmx diviene pertanto:

( )

( )

1

( )

' ' U P

div U div u div grad U

t ρ x ν

∂ _{+ + = −} ∂ _{+ ⎡ ⎤}

⎣ ⎦

∂ U u ∂

Analogamente le qmy e qmz saranno rispettivamente:

( )

( )

( )

(

)

( )

( )

1 ' ' 1 ' ' V P

div V div v div grad V

t y

W P

div W div w div grad W

t z ν ρ ν ρ ∂ _{+ + = −} ∂ _{+ ⎡ ⎤} ⎣ ⎦ ∂ ∂ ∂ _{+ + = −} ∂ _{+ ⎡ ⎤} ⎣ ⎦ ∂ ∂ U u U u

Come si può osservare i primi due termini del primo membro e l’intero secondo membro sono formalmente analoghi a quelli delle equazioni non mediate (nel caso particolare in esame di fluidi incomprimibili e a viscosità costante!). E’ tuttavia importante notare la comparsa del terzo termine al primo membro div u u , conseguenza diretta della mediazione temporale.

( )

' ' Esso coinvolge il prodotto dei termini fluttuanti e costituisce un trasferimento convettivo di quantità di moto, dovuto proprio alla fluttuazione delle velocità. E’ uso porre tale termine al secondo membro, per riflettere il fatto che esso costituisce una ulteriore tensione turbolenta che agisce sui valori medi di U, V, W. Le equazioni divengono pertanto:

( )

( )

( )

( )

(

)

( )

2 2 2 1 ' ' ' ' ' 1 ' ' ' ' ' 1 ' ' ' ' ' U P u u v u w

div U div grad U

t x x y z

V P v u v v w

div V div grad V

t y x y z

W P w u w v w

div W div grad W

t z x y z ν ρ ν ρ ν ρ ⎛ ⎞ ∂ ∂ ∂ ∂ ∂ + = − + ⎡_⎣ ⎤ ⎜_{⎦ ⎜}+ − − − ⎟_⎟ ∂ ∂ _⎝ ∂ ∂ ∂ _⎠ ⎛ ⎞ ∂ _{+ = −} ∂ _{+ ⎡ ⎤ ⎜+ −}∂ ₋∂ ₋∂ ⎟ ⎣ _{⎦ ⎜ ⎟} ∂ ∂ _⎝ ∂ ∂ ∂ _⎠ ⎛ ⎞ ∂ _{+ = −} ∂ _{+ ⎡ ⎤ ⎜+ −}∂ ₋∂ ₋∂ ⎟ ⎣ _{⎦ ⎜ ⎟} ∂ ∂ _⎝ ∂ ∂ ∂ _⎠ U U U

I termini di stress addizionali sono scritti per esteso al fine di mostrarne la struttura. Si ricorda anche il fatto che queste equazioni sono state divise per la densità, essendo essa costante per ipotesi.

Si hanno dunque tre tensioni normali e tre tensioni di taglio addizionali, chiamate tensioni di Reynolds: 2 2 2 ' ; ' ; ' ; ' '; ' '; ' ' xx yy zz xy yx yz zy xz zx u v w u v v w u w τ ρ τ ρ τ ρ τ τ ρ τ τ ρ τ τ ρ = − = − = − = = − = = − = = − (3.13)

Nei flussi turbolenti, le tensioni normali −ρu' , ' , ' ,2 −ρv 2 −ρw2 sono sempre strettamente negative (cioè entranti nella cella: sono pressioni). Le componenti di taglio sono associate alla correlazione turbolenta tra le diverse componenti di velocità. Se, ad esempio, u' e v' fossero statisticamente indipendenti, la media temporale del loro prodotto potrebbe essere nulla; tuttavia anche le tensioni di taglio sono non nulle ed, anzi, generalmente sono molto grandi se confrontate alle tensioni viscose in flussi turbolenti.

Si hanno termini di trasporto aggiuntivi mediando temporalmente anche l’equazione relativa ad uno scalare. Posto infatti ϕ= Φ +ϕ' lo scalare, si ha:

(

)

*

( )

u' ' v' ' w' '

div div grad

t x y z ϕ ϕ ϕ Φ ⎛ ⎞ ∂Φ_{+ Φ = ⎡Γ Φ + −⎤} ∂ ₋∂ ₋∂ ⎜ ⎟ ⎣ ⎦ ∂ U _⎝ ∂ ∂ ∂ _⎠ avendo posto * ρΦ Φ Γ Γ = .

Si è inizialmente assunta la densità come costante. In realtà si sa che anch’essa può variare, sia relativamente al termine medio che a quello fluttuante. Si è però visto sperimentalmente che fluttuazioni non eccessive di ρ non influenzano il flusso in modo significativo: in particolare, se il valore rms della fluttuazione della velocità è inferiore al 5% del valore medio, fluttuazioni di ρ non sono significative in flussi con numero di Mach fino a 3÷5. Spesso però il valore rms della velocità arriva al 20% del valor medio: in tali condizioni le fluttuazioni di ρ non influenzano il flusso fino circa a Mach 1.

3.15 Sistema RANS

Si vedrà adesso quello che è il set di equazioni, mediate temporalemente, che è comunemente usato nei codici CFD commerciali, dove si assume che la densità possa variare, ma si trascura il termine fluttuante. Si indica allora con ρ il termine medio della densità:

( )

( )

₍

₎

_{( )}

( )

₍

₎

_{( )}

(

)

₍

₎

_{( )}

2 2 0 ' ' ' ' ' ' ' ' ' ' ' ' ' ' Mx My div t U P u u v u w

div U div grad U S

t x x y z

V P v u v v w

div V div grad V S

t y x y z

W P w u w v

div W div grad W

t z x y ρ _ρ ρ ρ μ ρ _{ρ μ} ρ ρ μ ∂ + = ∂ ⎛ ⎞ ∂ _{+ = −}∂ _{+ ⎡ ⎤ ⎜+ −}∂ ₋∂ ₋∂ ₊ ⎟ ⎣ _{⎦ ⎜ ⎟} ∂ ∂ _⎝ ∂ ∂ ∂ _⎠ ⎛ ⎞ ∂ ∂ ∂ ∂ ∂ + = − + ⎡_⎣ ⎤ ⎜_{⎦ ⎜}+ − − − ⎟_⎟+ ∂ ∂ _⎝ ∂ ∂ ∂ _⎠ ∂ ∂ ∂ ∂ + = − + ⎡_⎣ ⎤_⎦+ − − ∂ ∂ ∂ ∂ U U U U

( )

₍

₎

_{( )}

2 ' ' ' ' ' ' ' Mz w S z u v w

div div grad S

t x y z ρ _ρ ϕ ϕ ϕ Φ Φ ⎛ _∂ ⎞ − + ⎜ ⎟ ⎜ _∂ ⎟ ⎝ ⎠ ⎛ ⎞ ∂ Φ _{⎡ ⎤} ∂ ∂ ∂ + Φ = _⎣Γ Φ + −_{⎦ ⎜} − − _⎟+ ∂ U _⎝ ∂ ∂ ∂ _⎠

Tale sistema prende il nome di RANS (Reynolds Averaged Navier-Stokes equations).

Come si è detto, attualmente risulta troppo impegnativo un calcolo basato sulle equazioni dirette di Navier-Stokes (DNS: Direct Navier-Stokes) nella loro forma completa. La media temporale permette di concentrarsi sui valori medi del flusso, che più interessano a livello ingegneristico, eliminando però le informazioni sullo stato istantaneo del fluido. Il risultato è l’aggiunta di sei nuove incognite (le tensioni di Reynolds) e altre tre relative alla media dell’equazione di trasporto dello scalare

(

u' ', ' ', ϕ v ϕ w' 'ϕ

)

.

La complessità del fenomeno turbolento non consente di avere forme semplici per esplicitare i termini aggiuntivi: si è reso necessario, quindi, procedere allo sviluppo di procedure computazionali che siano sufficientemente accurate e generali per poter predire i valori di detti termini. Ecco che sono comparsi i modelli di turbolenza.

3.16 Modelli di turbolenza

I modelli di turbolenza altro non sono che procedure di calcolo che servono a chiudere il sistema RANS, in modo da poter calcolare una grande varietà di problemi. Per la maggior parte dei problemi ingegneristici non è importante risolvere nel dettaglio le fluttuazioni tipiche della turbolenza; interessa invece (normalmente) solo l’influenza che la turbolenza ha sul flusso medio. Più in dettaglio, si ha bisogno di relazioni che ci permettano di modellare le tensioni di Reynolds nelle equazioni della quantità di moto mediante il termine di trasporto scalare nella equazione scalare. Un modello di turbolenza, per avere successo come strumento in un codice CFD, deve:

ƒ avere un grosso range di validità (deve cioè essere efficace per numerosi tipi di problemi)

ƒ essere accurato

ƒ essere semplice ed economico (non deve richiedere un tempo di calcolo eccessivo) I modelli più comuni sono:

• modelli classici (basati sulle RANS):

- zero equation model: lunghezza di miscelamento; - two equation model: modellok−ε;

- Reynolds Stress Equations Model (RSM); - Algebraic stress model: Spalart-Allmaras.

• Simulazione di grandi vortici, basato su equazioni generali, filtrate nello spazio (LES: Large Eddies Simulation)

• Simulazione diretta (DNS)

I modelli classici usano la RANS e costituiscono la base del calcolo turbolento nei codici CFD commerciali. Il modello LES invece risolve le equazioni di Navier-Stokes per il flusso medio e per i vortici più grandi, risolvendo la fisica di quelli più piccoli con modelli classici: si è visto infatti come i vortici più grandi influiscano fortemente con il flusso medio e contengano anche molta energia. Questo approccio è quindi buono da un punto di vista fisico, fornendo un modello molto accurato dell’effetto principale della turbolenza, ma richiede elevate potenzialità di calcolo.

Dei modelli classici, quello della lunghezza di miscelamento e quello k−ε sono i più usati e validati. Essi si basano sulla supposizione che esista una analogia tra l’azione delle tensioni viscose e quella turbolenta (tensioni di Reynolds) nel flusso medio. Entrambe le tensioni si trovano a destra delle equazioni della quantità di moto e, nella legge di Newton della viscosità, le tensioni viscose sono considerate proporzionali alle deformazioni degli elementi fluidi. Per un fluido incomprimibile si ha:

j i ij ij j i u u e x x τ =μ =μ⎛⎜_⎜∂ +∂ ⎞⎟_⎟ ∂ ∂ ⎝ ⎠

usando la notazione numerica

(

u₁⇔u u; ; ; ; ; ₂ ⇔v u₃ ⇔w x₁ ⇔x x₂ ⇔ y x₃ ⇔z

)

.

Sperimentalmente si è visto che la turbolenza decade a meno che non ci siano sforzi di taglio. Si è visto, inoltre, che le tensioni turbolente aumentano se aumentano le deformazioni medie. Boussinesq (1877) propose di legare le tensioni di Reynolds con la deformazioni media. Si ha allora la legge di Boussinesq:

' ' i j ij i j t j i U U u u x x τ = −ρ =μ ⎛⎜_⎜∂ +∂ ⎞⎟_⎟ ∂ ∂ ⎝ ⎠ (3.15)

Come si vede, il legame che sussiste è lo stesso delle tensioni viscose, anche se si usano solo i termini medi della deformazione. Ciò che differisce è, logicamente, il coefficiente di proporzionalità: in questo caso esso, per analogia, prende il nome di viscosità dinamica turbolenta

( )

μ_t ed ha le dimensioni di una pressione moltiplicata per un tempo (Pas). Si può anche introdurre una viscosità cinematica turbolenta t

t μ ν ρ ⎛ ₌ ⎞ ⎜ ⎟ ⎝ ⎠.

Il trasporto di calore, massa ed altre proprietà scalari, dovuto alla turbolenza, è modellato in modo simile. L’espressione (3.15) mette in evidenza il fatto che il trasporto della quantità di moto è proporzionale al gradiente medio della velocità. Analogamente il trasporto di uno scalare sarà proporzionale al gradiente della quantità trasportata:

' ' i t i u x ρ ϕ ∂Φ − = Γ ∂

dove si è introdotto il coefficiente di diffusività turbolenta Γ . _t

Siccome i trasporti di quantità di moto, di calore e di massa sono dovuti allo stesso fenomeno, ovvero al rimescolamento del fluido dovuto ai vortici, ci si aspettano valori simili per i due coefficienti turbolenti appena introdotti. Si chiama numero di Prandtl/Schmidt turbolento il rapporto t t t μ σ = Γ

Molti esperimenti hanno dimostrato che questo valore è effettivamente quasi costante e tale è considerato dalla maggior parte dei codici CFD, i quali danno la possibilità all’utilizzatore del software di poterlo modificare nell’intorno del valore 1.

Nei flussi più semplici si può osservare che il livello di turbolenza e le tensioni turbolente possono variare da punto a punto.

Il modello della lunghezza di miscelamento cerca di descrivere le tensioni per mezzo di semplici relazioni algebriche che esprimono μ_t in funzione del punto.

Il modello k−ε è una più sofisticata e generale descrizione della turbolenza, che tiene conto degli effetti del trasporto delle proprietà del flusso medio, della diffusione e di produzione e distruzione della turbolenza. Questo si ottiene risolvendo due equazioni alle derivate parziali aggiuntive: una per l’energia cinetica turbolenta k e l’altra per il rateo di dissipazione dell’energia ε.

Una supposizione che sta alla base di entrambi i modelli è che la viscosità dinamica turbolenta

t

μ sia isotropa, cioè che il rapporto tra le tensioni turbolente e la deformazione sia lo stesso in (3.16)