Capitolo 1
Espressioni Regolari e Automi Finiti
In questo capitolo trattiamo le nozioni fondamentali riguardanti le espressioni regolari che useremo nel seguito della tesi. Presentiamo dei concetti semplici nati nel contesto della teoria dei linguaggi formali e sfruttati in diversi ambienti software con estensioni e variazioni.
In particolare, introduciamo la notazione base delle espressioni regolari (sviluppata dalla teoria dei linguaggi) e ne mostriamo una variazione, sia a livello sintattico che semantico, utilizzata nel database PROSITE [2], il quale contiene dati e informazioni riguardanti sequenze di proteine.
Vedremo qual è la metodologia adottata per costruire una espressione regolare (cioè, come si fa ad ottenere espressioni via via più complicate partendo da istanze semplici) e spiegheremo cosa si intende per stringa (o parola), per alfabeto, per ordinamento lessicografico e per linguaggio, tutti elementi utili a comprendere il lavoro presentato nei capitoli successivi.
1.1 Alfabeto e parole
Indichiamo con il simbolo un insieme finito chiamato alfabeto. In generale i suoi elementi sono chiamati lettere e, per convenienza, le denotiamo con i simboli a, b, c, d e così via.
Una parola o stringa è una sequenza di lettere di lunghezza finita. La lunghezza di una parola u è denotata con |u| ed indica appunto il numero di simboli che compongono la parola u. Indichiamo con u j la j- esima lettera di u.
L’insieme di tutte le parole definite sull’alfabeto è denotato con * , la stringa vuota con e il simbolo + indica l’insieme di tutte le parole escluso la stringa vuota, ovvero l’insieme *
\ { }
.Assumiamo inoltre che esiste un ordinamento sia sull’alfabeto, che sull’insieme di tutte le parole. Rappresentiamo l’ordinamento prescelto nel seguente modo: utilizziamo il simbolo ≤≤≤≤L per dire che una certa lettera o parola è lessicograficamente più piccola di un’altra. Ad esempio, la lettera ‘a’ ≤L ‘c’, così come la parola ‘mare’ ≤L ‘sole’; in poche parole, tanto per intenderci, si assume un tipo di ordinamento lessicografico crescente, per esempio come accade per i cognomi presenti in un elenco telefonico. Ovviamente, la stringa è, secondo l’ordinamento lessicografico ≤L, la più piccola di tutte ed ha lunghezza | | = 0. In realtà, è necessario considerare anche un simbolo che risulti essere il più grande tra tutti quelli presenti nell’alfabeto. Quindi, consideriamo l’alfabeto aumentato con il seguente simbolo $, ovvero ∪ {$}.
Il prodotto (o anche concatenazione) di due parole u e v, denotato con u · v oppure uv, è la parola ottenuta scrivendo sequenzialmente le lettere di u seguite da quelle di v. Data una parola u, il prodotto di k parole identiche ad u è denotato con u k, e considerando k = 0, la parola u0 = .
1.2 I linguaggi
Un linguaggio è un qualunque sottoinsieme dell’insieme * , di conseguenza anche i suoi elementi si considerano ordinati secondo l’ordinamento stabilito ≤L. Il prodotto di due linguaggi U e V, denotato con U · V oppure UV, è il
linguaggio {uv | (u, v) ∈U × V}.
Denotiamo con U k l’insieme di parole ottenute facendo il prodotto di k parole di U. La star di U (stella di Kleene), denotata con U *, è il linguaggio
∪
k≥0 U k.Per convenzione, l’ordine di precedenza tra gli operatori (partendo da quello con priorità più alta), in espressioni in cui gli operandi sono linguaggi, è il seguente: * (o potenza), prodotto e unione.
1.3 Automi finiti: deterministici (DFA) e non deterministici
(NFA)
Un automa finito (FA) consiste di un numero finito di stati e di un insieme di transizioni. Ciascuna transizione parte da uno stato e giunge in un altro a seconda del simbolo, appartenente all’alfabeto , in input all’automa.
Per ciascun simbolo in input è possibile individuare una transizione che parte da uno stato e giunge in un altro (è possibile anche che questa transizione parta da uno stato e ritorni nello stesso stato da cui è partita).
Solitamente denotiamo con s0 lo ‘stato iniziale’ dell’automa e con i termini
‘stato accettante’ e ‘stato finale’ tutti gli altri stati.
A ciascun FA è associato un grafo diretto chiamato diagramma di transizione. I vertici del grafo corrispondono agli stati dell’automa. Se c’è una transizione che parte dallo stato q e giunge nello stato p con simbolo in input a, allora nel grafo c’è un arco etichettato con a che parte dal vertice q e giunge al vertice p. Formalmente denotiamo un automa finito con una 5-tupla (Q, , , s0, F ), dove
Q è un insieme finito di stati, è un alfabeto finito, s0 in Q è lo stato iniziale, F ⊆
Q è l’insieme di stati finali e è la funzione di transizione che mappa Q × in Q,
cioè (q, a) è lo stato in cui si giunge partendo dallo stato q e considerando come simbolo in input a.
L’automa accetta una stringa x se la sequenza di transizioni corrispondente ai simboli di x visita l’automa partendo dallo stato iniziale e proseguendo in uno stato accettante; in poche parole, x è accettata da M = (Q, , , s0, F ) se la
funzione (s0 , x) = p per qualche p appartenente ad F.
Il linguaggio accettato da M, denotato con L(M), è l’insieme di tutte le stringhe {x | (s0 , x) è in F}.
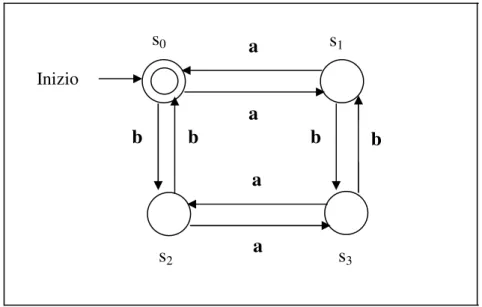
Esempio 1.1. Consideriamo il diagramma di transizione (che rappresenta un
automa M) mostrato in fig. 1.1.
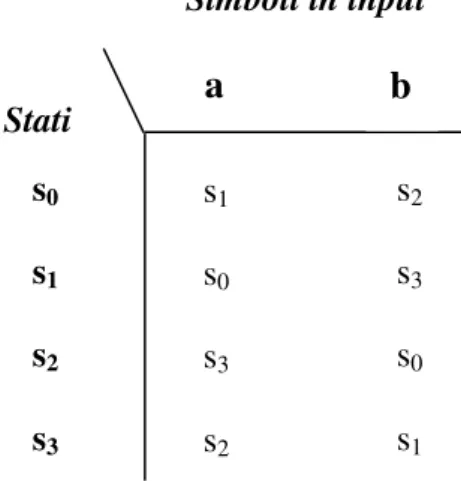
Secondo la notazione formale prima enunciata, l’automa è denotato con M = (Q, , , s0, F), dove Q = {s0, s1, s2, s3}, = {a, b}, F = {s0} e la funzione di
transizione è mostrata in fig. 1.2 della pagina seguente.
s0 s1 s2 s3 a a b b a a b b Inizio
Supponiamo che la stringa ‘aababa’ sia data in ingresso a M. Notiamo che
(s0 , a) = s1 e (s1 , a) = s0. Continuando si ha (s0 , aa) = ( (s0 , a), a) = (s1 ,
a) = s0 ; a questo punto il simbolo in input è ‘b’, quindi (s0 , b) = s2 e (s0 , aab)
= ( (s0 , aa), b) = (s0 , b) = s2. Continuando in questo modo troviamo che (s0 ,
aaba) = s3, (s0 , aabab) = s1 e finalmente (s0 , aababa) = s0. L’intera sequenza
di stati attraversati è: s0 s1 s0 s2 s3 s1 s0 e la stringa ‘aababa’ appartiene ad L(M).
Il tipo di automa di cui abbiamo parlato finora è un tipo di automa
deterministico a stati finiti (Deterministic Finite Automaton, o DFA) e questo è
un caso speciale di un altro tipo di automa: l’automa non deterministico a stati finiti (NFA). Si può dire che ogni DFA è un particolare NFA, per cui è chiaro che la classe dei linguaggi accettata da un NFA include i linguaggi regolari, che sono i linguaggi accettati da un DFA.
In generale, la differenza tra un DFA e un NFA è la seguente: in un DFA, per una data stringa in ingresso w e uno stato q, esiste esattamente, come affermato
Fig. 1.2 Funzione di transizione dell’automa in fig. 1.1.
Simboli in input b Stati s0 s1 s2 s3 s2 s3 s0 s1 s1 s0 s3 s2 a
in precedenza, un cammino etichettato con w che inizia a partire da q. Per determinare se una stringa è accettata da un DFA è sufficiente controllare l’esistenza di questo unico cammino. In un NFA, invece, potrebbero esserci più cammini etichettati con w e tutti devono essere controllati per vedere se uno o più di essi termina in uno stato finale.
Per quanto riguarda la definizione formale di un NFA, possiamo dire che l’unica differenza, rispetto alla definizione di un DFA, è la funzione di transizione che, in questo caso, mappa gli elementi di Q × in 2Q (dove 2Q è
l’insieme di tutti i sottoinsiemi di Q).
1.4 Definizione delle espressioni regolari
I linguaggi (L(M) ) accettati da un automa finito (DFA o NFA) sono facilmente descrivibili da semplici espressioni chiamate espressioni regolari.
Le espressioni regolari e i linguaggi che esse descrivono, appunto i linguaggi
regolari, sono definiti induttivamente, ossia vengono definite prima espressioni
regolari più semplici (questo rappresenta il caso base del principio di induzione) e poi vengono date delle regole di composizione che permettono di costruire delle espressioni regolari via via più complesse (caso induttivo).
Vediamo ora la definizione formale di un’espressione regolare r. Consideriamo l’alfabeto dei simboli . Le espressioni regolari (che indicheremo anche con la sigla RE da ‘regular expression’ ) su e gli insiemi che esse descrivono sono definiti come segue:
a) le RE semplici sono: 0, 1 e a che descrivono rispettivamente l’insieme vuoto
∅, la stringa vuota
{ }
, l’insieme {a} per ogni simbolo a ∈ ;b) due espressioni regolari u e v, che descrivono rispettivamente i linguaggi U e
V, possono essere composte attraverso due regole:
1. (u | v) è l’espressione regolare di alternativa a cui corrispondono le
stringhe rappresentate da u oppure da v e descrive il linguaggio regolare dato dall’unione U
∪
V;2. (u)(v) è l’espressione regolare di concatenazione a cui corrispondono
le stringhe xy ottenute concatenando una qualsiasi stringa x, rappresentata da u, con una qualsiasi stringa y rappresentata da v e descrive il linguaggio regolare U·V;
c) un’espressione regolare u può essere concatenata con se stessa zero, una o più
volte attraverso la seguente regola: (u)* è l’espressione regolare che descrive
il linguaggio regolare U* e consente di concatenare una qualsiasi stringa x, rappresentata da u, con se stessa zero volte, ottenendo la stringa vuota , una volta, ottenendo la stringa stessa, più volte, ottenendo una stringa che è costituita da una sequenza (di lunghezza variabile) di concatenazioni di x stessa.
Seguono alcuni esempi di espressioni regolari formulate correttamente.
Esempio 1.2. L’espressione (c | d) rappresenta sia la stringa ‘c’ che la stringa ‘d’
e quindi l’insieme di stringhe {c, d}. Invece, l’espressione (c)(a) rappresenta la stringa ‘ca’ e l’espressione (c)(b | d) rappresenta l’insieme di stringhe {cb, cd}, (ossia la stringa ‘c’ seguita dalla stringa ‘b’ oppure ‘d’).
Esempio 1.3. L’espressione (b)* rappresenta l’insieme infinito di stringhe { , b,
bb, bbb, bbbb, …}, in cui la stringa vuota sta ad indicare che l’espressione (b)* è stata ripetuta zero volte, ‘b’ che è stata ripetuta una volta, ‘bb’ due volte, ‘bbb’ tre volte e così via.
L’espressione (b)*(a) rappresenta il seguente insieme infinito di stringhe: { a, ba, bba, bbba, bbbba, … }. E’ da notare che in questo insieme ripetendo zero
volte (b)* si ottiene la stringa vuota, che però concatenata con ‘a’ restituisce ‘a’.
Esempio 1.4. Un altro esempio interessante, riguardante sempre la regola esposta
ab, ba, bb, aaa, baa, …, bbb, aaaa, … }, in cui la stringa vuota sta ad indicare
che l’espressione (a | b)* è stata ripetuta zero volte, le stringhe ‘a’ oppure ‘b’ stanno ad indicare che è stata ripetuta una volta, le stringhe ‘aa’ o ‘ab’ o ‘ba’ o
‘bb’ si ottengono ripetendo (a | b)* due volte (ciò corrisponde alla concatenazione (a | b)(a | b)) e così via. Bisogna notare che l’operatore * non è distributivo rispetto all’unione ( | ), ovvero l’espressione (a | b)* ≠ (a* | b*).
Tra tutti gli operatori che vengono utilizzati nelle espressioni regolari, la stella di Kleene * ha priorità più alta, seguono l’operatore di concatenazione (che può essere indicato con · , ma spesso viene omesso) e l’operatore di alternativa (indicato con | ).
Per cambiare la priorità tra gli operatori oppure per non dare adito a situazioni di ambiguità, possono essere utilizzate le parentesi (, ).
Infine, consideriamo un’espressione regolare r e indichiamo con L(r) il linguaggio da essa descritto. Siccome nel capitolo successivo vengono fornite delle nozioni che prendono in considerazione L(M) (ovvero il linguaggio accettato dall’automa M), è interessante, per una migliore comprensione da parte del lettore, far notare che, in base a quanto detto nel paragrafo 1.3, all’inizio del paragrafo 1.4 e nei teoremi 2.3 e 2.4 trattati in [1], fare riferimento ad L(M) è la stessa cosa che fare riferimento ad L(r) e viceversa. Infatti, con il teorema 2.3 in [1], si dimostra l’equivalenza tra L(M) ed L(r), ovvero L(M) = L(r).
1.5 Alcune proprietà delle espressioni regolari
Enunciamo, in questo paragrafo, alcune proprietà interessanti delle espressioni regolari che possono essere utilizzate per semplificare la forma di espressioni che appaiono ostiche e complicate.
In generale, è da premettere che un’espressione regolare r è uguale ad un’altra espressione s se e solamente il linguaggio regolare definito da r è uguale al linguaggio regolare definito da s. Le proprietà più utili sono le seguenti:
1) ( r* )* = r* 2) (ε | r )* = r* 3) (r* s*)* = (r | s)* 4) (r | s) = (s | r) (proprietà commutativa) 5) (rs)t = r (st) (proprietà associativa) 6) (r | s)t = (rt | st) (proprietà distributiva) 7) ((r | s) | t) = (r | (s | t)) (proprietà associativa) 8) r(s | t) = (rs | rt) 9) ∅ * = ε
dove r, s e t sono espressioni regolari.
Facciamo ora degli esempi in cui mostriamo l’applicazione delle proprietà sopra descritte ad alcune espressioni regolari e verifichiamo le uguaglianze tra i rispettivi linguaggi da esse definiti.
Esempio 1.5. Consideriamo l’espressione regolare r = (ε | ab)* e il linguaggio
L(r) da essa definito. L’insieme L(r) è costituito dalle seguenti stringhe: {ε, ab,
abab, ababab, abababab, …}. L’uguaglianza con l’espressione r′ = (ab)* è verificata in quanto il linguaggio definito da r′ è uguale al linguaggio definito da
r. Infatti, l’insieme L(r′) è costituito dalle stringhe {ε, ab, abab, ababab,
abababab, …} che sono le stesse accettate da L(r).
Esempio 1.6. Consideriamo l’espressione regolare r = (a | ab) c* e il linguaggio
L(r) da essa definito. L’insieme L(r) è costituito dalle seguenti stringhe: {a, ab,
ac, abc, acc, abcc, accc, abccc, …}. L’uguaglianza con l’espressione r′ = (
(a)(c)* | (ab)(c)*) è verificata in quanto il linguaggio definito da r′ è uguale al
linguaggio definito da r. Infatti, come si può constatare, l’insieme L(r′) è
costituito dalle stringhe {a, ab, ac, abc, acc, abcc, accc, abccc, …} che sono le stesse accettate da L(r).
Ovviamente, posponendo il membro (a | ab) dell’espressione r e anticipando il
membro (c)*, risulta immediato verificare che c* (a | ab) = ((c)*(a) | (c)*(ab))
(proprietà 8 ).
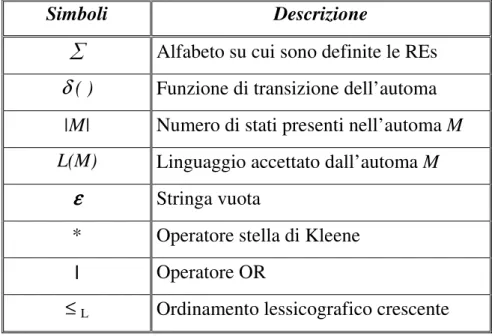
La tabella 1.1 riassume alcune delle notazioni chiave utilizzate finora.
Simboli Descrizione
Alfabeto su cui sono definite le REs
δ ( ) Funzione di transizione dell’automa
|M| Numero di stati presenti nell’automa M
L(M) Linguaggio accettato dall’automa M
εεεε Stringa vuota
* Operatore stella di Kleene
| Operatore OR
≤ L Ordinamento lessicografico crescente
1.6 Le espressioni regolari nel database PROSITE
Le espressioni regolari vengono ampiamente utilizzate nell’ambito della
bioinformatica1 ed in particolare sono sfruttate per l’elaborazione delle proteine. Per esempio, la consultazione del database PROSITE è caratterizzata totalmente dall’immissione di espressioni regolari, di cui forniamo la terminologia.
Il database PROSITE contiene dati e informazioni riguardanti famiglie di proteine. In generale, una proteina è rappresentata da una stringa composta da sequenze di aminoacidi.
1 Ramo dell’informatica che studia e informatizza gli eventi legati alla biologia.
Il database consiste di tre componenti fondamentali: pattern, rule e profile. Senza scendere a fondo nella spiegazione di ciascuno di questi tre elementi (motivi), diciamo subito che il nostro interesse, come spiegato anche nel capitolo introduttivo, è rivolto alla prima componente, i pattern.
Un pattern, descritto utilizzando proprio le espressioni regolari, identifica in maniera succinta un insieme implicito di sequenze di aminoacidi da cercare all’interno delle proteine.
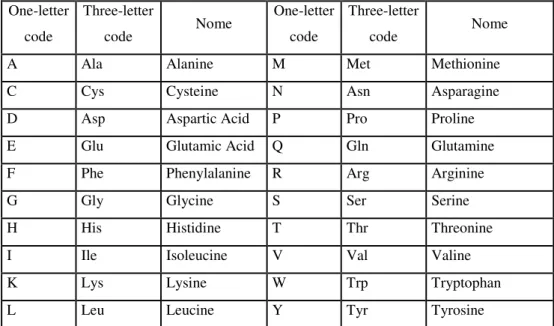
Tali sequenze sono rappresentate da stringhe di lunghezza finita e sono caratterizzate da diverse combinazioni delle venti lettere dell’alfabeto che stanno ad indicare gli aminoacidi comunemente più diffusi nelle proteine. Nella tabella che segue, indichiamo i due tipi di codifica e il nome per esteso di tali aminoacidi. One-letter code Three-letter code Nome One-letter code Three-letter code Nome
A Ala Alanine M Met Methionine
C Cys Cysteine N Asn Asparagine
D Asp Aspartic Acid P Pro Proline
E Glu Glutamic Acid Q Gln Glutamine
F Phe Phenylalanine R Arg Arginine
G Gly Glycine S Ser Serine
H His Histidine T Thr Threonine
I Ile Isoleucine V Val Valine
K Lys Lysine W Trp Tryptophan
L Leu Leucine Y Tyr Tyrosine
La sintassi delle espressioni regolari utilizzate per descrivere un generico
pattern risulta essere molto semplice e la notazione è leggermente diversa da
quella base considerata nelle espressioni trattate nei paragrafi precedenti.
Innanzitutto, diciamo subito che l’alfabeto su cui sono definite tali espressioni è il seguente: = {A, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y}, ovviamente con cardinalità | | = 20.
Ciascun token, che caratterizza un generico pattern, può essere:
1) un aminoacido ben fissato, quindi una A, oppure una C, oppure una D e così
via…;
2) un aminoacido ambiguo che può essere indicato con:
a) x, che rappresenta un qualunque aminoacido;
b) le parentesi [ ], che sostanzialmente esprimono una alternativa (ad
esempio, l’elemento [ST] sta ad indicare che in quella determinata posizione della sequenza può occorrere l’aminoacido Ser oppure Thr); c) le parentesi { }, che indicano qualunque aminoacido eccetto quelli inclusi
nelle parentesi ( ad esempio, il token {AM} sta ad indicare che in quella determinata posizione della sequenza in cui occorre può esserci qualunque aminoacido eccetto gli aminoacidi Ala e Met).
A differenza del significato assunto nella notazione base delle espressioni regolari, le parentesi ( ), in questo tipo di notazione, esprimono la ripetizione di un elemento del pattern, che può essere effettuata o un numero fissato di volte, oppure può variare in un determinato intervallo. Ad esempio il token A(5) sta a denotare che l’aminoacido Ala occorre cinque volte nella sequenza, cioè, esplicitandone il significato, indica che nella posizione in cui occorre si avrà la sottosequenza “AAAAA”. La stessa cosa vale se si è in presenza di una x, di un’espressione di alternativa e di negazione.
Esempio 1.7. Consideriamo il token x(5). Esso indica che nella posizione in cui
occorre si avrà una sottosequenza, di aminoacidi qualsiasi, di lunghezza cinque. Ovvero, esplicitandone il significato, si avrà una sottosequenza del tipo xxxxx (in pratica, x concatenata con se stessa cinque volte). La stessa cosa vale per il token
Esempio 1.8. Consideriamo il token [ST](2). Esso indica che nella posizione in
cui occorre si avrà [ST] ripetuto due volte. Ovvero, esplicitandone il significato, si avrà [S oppure T][S oppure T], che vuol dire ‘SS’, ‘ST’, ‘TS’, ‘TT’.
Esempio 1.9. Consideriamo il token {PQRST}(2). Un modo equivalente di
rappresentarlo è il seguente: [ACDEFGHIKLMN](2), ovvero una espressione di alternativa, che non contiene gli aminoacidi P, Q, R, S, T, ripetuta due volte. Tutto ciò vuol dire [ACDEFGHIKLMN][ACDEFGHIKLMN] e quindi tutte le possibili combinazioni ‘AA’, ‘AC’, ‘AD’,…., ‘CA’, ‘CC’,…, ‘NN’.
Per quanto riguarda la ripetizione di un elemento del pattern un numero variabile di volte, all’interno di un determinato intervallo, possiamo dire che, secondo la notazione sintattica di questo tipo di espressioni, è possibile abbinare le parentesi ( ), contenenti un intervallo, solamente al token x. Ad esempio, all’interno di un pattern è lecito trovare un token x(3,5), che esprime il fatto che il numero di ripetizioni di x può variare fra tre e cinque, ma non A(3, 5), [ST](3, 5), o ancora {PQR}(3, 5). L’elemento x(3, 5), se sviluppato esplicitamente, denota sostanzialmente la seguente espressione di alternativa: (xxx oppure xxxx oppure
xxxxx). Questo vuol dire che nella posizione in cui occorre x(3, 5) si potrà avere
una sottosequenza di aminoacidi qualsiasi, di lunghezza tre, oppure di lunghezza quattro, oppure di lunghezza cinque.
Esempio 1.10. Consideriamo il token x(5, 7). Se sviluppato esplicitamente,
denota la seguente espressione di alternativa: (xxxxx oppure xxxxxx oppure
xxxxxxx). Un altro esempio interessante è x(0, 2). Questo elemento indica che
l’aminoacido ambiguo x può occorrere zero volte, una volta oppure due volte nell’intera sequenza.
Se nella notazione base delle espressioni regolari, la concatenazione fra più token viene espressa con · , in questo tipo di espressioni, ciascun elemento, che compone un generico pattern, è separato dal simbolo - ; per indicare la terminazione del pattern viene utilizzato un punto.
Si noti che l’operatore stella di Kleene, in tale contesto, non viene adottato e per tale motivo le espressioni regolari risultanti vengono talvolta denominate
“network expression”.
Esempio 1.11. Consideriamo un pattern descritto mediante la seguente
espressione regolare r : [AC] - x - V - x(4) - {ED}. Il linguaggio L(r) da essa definito sarà costituito dal seguente insieme implicito di sequenze di aminoacidi: [Ala oppure Cys] - qualunque – Val – qualunque – qualunque – qualunque – qualunque - qualunque ma non gli aminoacidi Glu o Asp.
Esempio 1.12. Consideriamo un pattern descritto mediante la seguente
espressione regolare r : F- [GSTV](3)- P - R - L - G. Il linguaggio L(r) da essa definito sarà costituito dal seguente insieme implicito di sequenze di aminoacidi: Phe – [Gly oppure Ser oppure Thr oppure Val][Gly oppure Ser oppure Thr oppure Val][Gly oppure Ser oppure Thr oppure Val] - Pro – Arg – Leu – Met – Gly.
Esempio 1.13. Consideriamo un pattern descritto mediante la seguente
espressione regolare r : W - x(9,11) - [FYV] - [FYW]- x(6,7) - [GSTNE]. Il linguaggio L(r) da essa definito sarà costituito dal seguente insieme implicito di sequenze di aminoacidi: Trp – (xxxxxxxxx oppure xxxxxxxxxx oppure xxxxxxxxxxx) - [Phe oppure Tyr oppure Val] - [Phe oppure Tyr oppure Trp] – (xxxxxx oppure xxxxxxx) – [Gly oppure Ser oppure Thr oppure Asn oppure Glu].
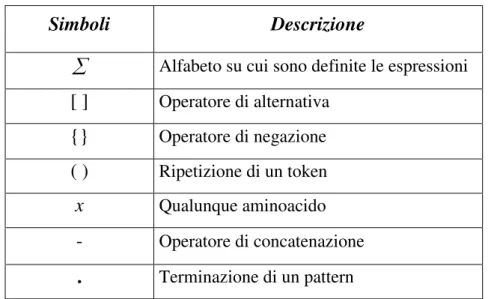
La tabella 1.3 riassume la notazione della sintassi delle espressioni utilizzate nel database PROSITE.
Simboli Descrizione
Alfabeto su cui sono definite le espressioni
[ ] Operatore di alternativa {} Operatore di negazione ( ) Ripetizione di un token x Qualunque aminoacido - Operatore di concatenazione . Terminazione di un pattern
La notazione delle espressioni regolari utilizzate nel database PROSITE può essere trasformata nella notazione delle espressioni trattate nella sezione 1.4. Infatti, l’operatore di alternativa |, utilizzato nella notazione base, corrisponde alle parentesi [] della notazione PROSITE. L’operatore di concatenazione · (che generalmente si omette), della notazione base, corrisponde a -, che nella notazione delle network expression, separa i vari elementi di un generico pattern. Vediamo alcuni esempi di corrispondenza.
Esempio 1.14. Consideriamo il pattern descritto nell’esempio 1.11: [AC] - x - V -
x(4) - {ED}. La corrispondente espressione regolare, secondo la notazione base, è la seguente: (A | C)xVxxxx(A | C | F | G | H | I | K | L | M | N | P | Q | R | S | T | V | W | Y).
Esempio 1.15. Il pattern F - [GSTV](3) - P - R – L - G corrisponde
all’espressione F(G | S | T | V)(G | S | T | V)(G | S | T | V)PRLG.
Esempio 1.16. Consideriamo il pattern descritto nell’esempio 1.13: W - x(9,11) -
[FYV] - [FYW]- x(6,7) - [GSTNE]. L’espressione nella notazione base corrispondente, sarà: W(xxxxxxxxx | xxxxxxxxxx | xxxxxxxxxxx)(F | Y | V)(F |Y | W)(xxxxxx | xxxxxxx)(G | S | T | N | E).