CAPITOLO 4 – ANALISI QUANTITATIVA

(1)

CAPITOLO 4 – ANALISI QUANTITATIVA

4.1 Fase preliminare di inserimento dati

Come già accennato nel capitolo 2 la prima elaborazione operata sui dati di rilievo consiste nell’inserimento delle varie misure eseguite durante la prova in un foglio Excel preparato in maniera tale da poter restituire le varie grandezze geometriche che verranno utilizzate, poi, nelle successive elaborazioni nonché i profili morfologici longitudinali e trasversali che identificano ogni test.

Inserendo tutto il rilievo longitudinale eseguito nei vari intervalli temporali a 5,10,20 e 40 minuti in fase dinamica nonché il rilievo longitudinale effettuato in fase statica (fase dry) il foglio Excel restituisce i vari profili longitudinali rilevati (fig. 4.1).

CR 22 239 NS 75 T1 22,0 27,0 32,0 37,0 42,0 47,0 52,0 270,0 280,0 290,0 300,0 310,0 320,0 330,0 340,0 350,0

Fig. 4.1 Esempio dei profili longitudinali restituiti dal foglio Excel

Nella restituzione grafica del foglio Excel è possibile visionare i vari profili longitudinali rilevati negli intervalli temporali (profili rosso, blu, verde), il profilo rilevato dopo 40 minuti quando ormai la morfologia ha raggiunto una conformazione stabile (profilo nero) e il profilo longitudinale statico in condizioni asciutte rilevato quando i getti non sono più alimentati e l’acqua è completamente defluita dal canale (profilo rosa).

Nel grafico è riportato anche il livello liquido utilizzato nella prova (linea tratteggiata), l’inclinazione dei getti e il livello del fondo inerte (linea marrone).

(2)

In questo modo è possibile renderci conto fin da subito dell’evoluzione temporale del profilo, della conformazione dello scavo e della duna e dell’entità dei depositi avuti a fine prova (fase dry).

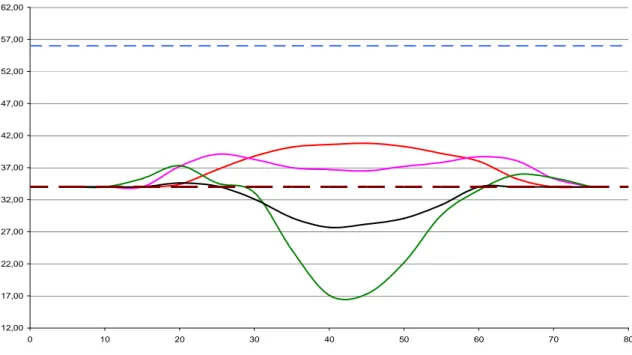
Il foglio di calcolo è impostato in maniera tale da restituire graficamente anche i 4 rilievi trasversali eseguiti in condizioni di equilibrio dopo 40 minuti dall’inizio della prova (fig 4.2). 12,00 17,00 22,00 27,00 32,00 37,00 42,00 47,00 52,00 57,00 62,00 0 10 20 30 40 50 60 70 80

Fig. 4.2 Esempio dei profili trasversali restituiti dal foglio Excel

In questa rappresentazione grafica possiamo notare il profilo trasversale eseguito sull’ascissa X corrispondente alla cresta della duna (profilo rosso), il profilo trasversale eseguito sull’ascissa X corrispondente al punto di massimo scavo (profilo verde) e i profili trasversali eseguiti su ascisse X corrispondenti a punti intermedi (profilo rosa e nero). Nella rappresentazione grafica è anche riportato il livello liquido nel canale (linea tratteggiata celeste) e la quota zero del letto di fondo (linea tratteggiata marrone).

La restituzione grafica della morfologia trasversale di ogni prova è utile per mettere in luce eventuali asimmetrie del punto di massimo scavo e della massima altezza raggiunta dalla duna nonché le particolari conformazioni che la duna assume.

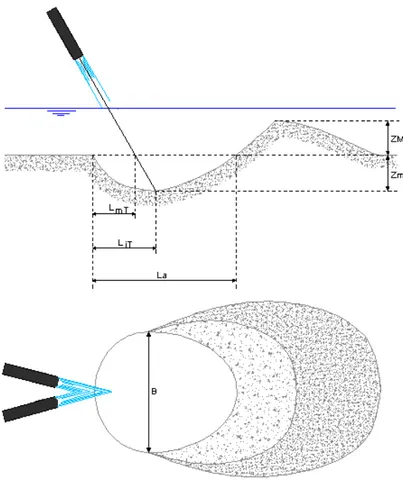
Tuttavia i fogli Excel compilati alla fine di ogni prova ci restituiscono anche tutta una serie di lunghezze geometriche che andremo poi ad elaborare successivamente; queste grandezze sono osservabili in figura 4.3.

(3)

Fig. 4.3 Vista delle lunghezze restituite dal foglio Excel

Le grandezze geometriche restituite sono di seguito descritte:

Zm massima profondità dello scavo in condizioni dinamiche Zm’ massima profondità dello scavo in condizioni statiche

ZM massima altezza raggiunta dalla duna in condizioni dinamiche ZM’ massima altezza raggiunta dalla duna in condizioni statiche B massima larghezza della buca di scavo in condizioni dinamiche B2 massima larghezza della buca di scavo in condizioni statiche La massima lunghezza della buca di scavo in condizioni dinamiche

LiT distanza longitudinale tra il punto di massimo scavo e il punto di inizio scavo

LmT distanza longitudinale tra il punto in cui la traiettoria dei getti interseca il piano a quota zero del fondo e il punto di inizio scavo

Queste grandezze geometriche che caratterizzano le varie prove eseguite in laboratorio sono state raccolte e sono riportate in Appendice A.

(4)

4.2 Analisi del profilo longitudinale dello scavo

Le prime elaborazioni effettuate sui dati a disposizione hanno riguardato il profilo longitudinale che la buca di scavo assume durante lo svolgimento del test e quindi nella fase dinamica, fase nella quale si raggiungono le massime profondità di scavo.

Per poter comparare i profili longitudinali di scavo delle varie prove è stato necessario adimensionalizzare i dati a nostra disposizione.

La adimensionalizzazione è stata realizzata ricercando per ogni punto rilevato del profilo la sua ascissa e la sua ordinata con un valore tale che l’intero profilo risultasse poi compreso in un intervallo (0,1) sia in profondità che in lunghezza; per le ordinate, quindi, è stato ricercato il valore adimensionale:

m ad Z Z Z = 0 dove:

Zad : ordinata adimensionale relativa al generico punto rilevato nello scavo

Z0 : ordinata relativa al generico punto rilevato nello scavo, riferita alla quota zero

individuata sul letto del fondo in materiale inerte (in cm)

Zm : massima profondità dello scavo in condizioni dinamiche (in cm)

L’ascissa adimensionale è invece stata ottenuta come segue:

a ad L X X = 0 dove:

Xad : ascissa adimensionale relativa al generico punto rilevato nello scavo

X0 : ascissa relativa al generico punto rilevato nello scavo, riferita all’origine zero

individuata nel punto di inizio scavo (in cm)

La : massima lunghezza della buca di scavo in condizioni dinamiche (in cm)

Questo procedimento è stato eseguito per le buche di scavo delle prove realizzate senza l’immissione di aria; è stato quindi possibile confrontare i vari profili ottenuti grazie alle 3 elaborazioni grafiche riportate di seguito.

(5)

-1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0 0,2 0,4 0,6 0,8 1 1,2 Xo/La Z o /Z m

Grafico relativo a prove eseguite con un’inclinazione verticale aaav dei getti pari a 60° a

Ο Prove con ac=30° e Tw minimo Ο Prove con ac=75° e Tw minimo Ο Prove con ac=120° e Tw minimo

X Prove con ac=30° e Tw medio X Prove con ac=75° e Tw medio X Prove con ac=120° e Tw medio

∆ Prove con ac=30° e Tw massimo ∆ Prove con ac=75° e Tw massimo ∆ Prove con ac=120° e Tw massimo

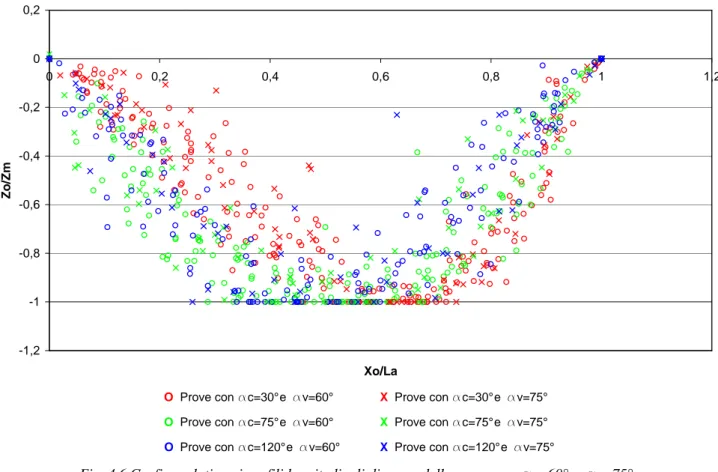
Fig. 4.4 Grafico relativo ai profili longitudinali di scavo delle prove con av=60°

Il grafico della figura 4.4 mostra i profili longitudinali di scavo delle 79 prove effettuate con un’inclinazione verticale av dei getti pari a 60°; i vari profili riportati sono stati

differenziati con colori diversi, a seconda dell’angolazione ac che li caratterizza e con

simboli diversi in relazione al tailwater Tw col quale è stata eseguita ogni prova.

Dagli andamenti riportati salta subito all’occhio come il punto di massimo scavo delle prove eseguite con ac =30° (in rosso) si trovi in una zona abbastanza ristretta e sia

proiettato a maggior distanza dall’origine rispetto alle altre prove; questo è spiegabile se pensiamo che il getto risultante da un ac=30° è compatto e perciò impatta in maniera

decisa sul fondo creando molta turbolenza e portando il punto di massima profondità di scavo nella zona più distante dall’origine. Tali profili di scavo hanno un andamento simile ad una “V” proprio per la quantità di energia che il getto ha sempre al suo interno quando impatta nel letto di fondo.

Da un’attenta osservazione del grafico è possibile notare che la conformazione a “V” degli

scavi ottenuti nelle prove con ac=30° si addolcisce al crescere del Tw; questo

(6)

-1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0 0,2 0,4 0,6 0,8 1 1,2 Xo/La Z o /Z m

energia che si ottiene aumentando il livello liquido hw dello strato d’acqua interposto tra

getti e fondale.

All’aumentare dell’angolo di intersezione tra i 2 getti ac si osserva che i profili assumono

andamenti sempre più dolci a forma di “U” e il punto di massimo scavo si avvicina sempre di più all’origine; ac elevati danno luogo, infatti, a splash molto diffusi nello spazio e

questo fa si che l’erosione operata dal getto non insista in una minima porzione di spazio ma, al contrario, interessi una zona più ampia situata nella zona sottostante i getti stessi.

Per valori alevati di ac come 75° e 120° (in verde e in blu) i profili longitudinali di scavo

non differiscono di molto, tuttavia si può notare che quelli contraddistinti da un ac=120° e

un Tw basso (cerchietti blu) hanno, nella zona di fine scavo a destra del grafico, traiettorie

più alte rispetto alle altre; questo andamento caratteristico è dato dal fatto che in queste prove ho dune molto allungate con un andamento a “scivolo” che degrada fin dentro la buca di scavo quindi, in questi casi, la buca di scavo è allungata e dovendo rientrare nell’intervallo (0,1) delle ascisse assume quell’andamento rialzato.

Grafico relativo a prove eseguite con un inclinazione verticale aaaav dei getti pari a 75°

Ο Prove con ac=30° e Tw minimo Ο Prove con ac=75° e Tw minimo Ο Prove con ac=120° e Tw minimo

X Prove con ac=30° e Tw medio X Prove con ac=75° e Tw medio X Prove con ac=120° e Tw medio

∆ Prove con ac=30° e Tw massimo ∆ Prove con ac=75° e Tw massimo ∆ Prove con ac=120° e Tw massimo

(7)

-1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0 0,2 0,4 0,6 0,8 1 1,2 Xo/La Z o /Z m

Per osservare eventuali differenze è stato ripetuto uno studio per le buche di scavo relative a 24 prove eseguite senza immissione di aria e con un’inclinazione verticale av dei getti

pari a 75°.

In questo secondo grafico in figura 4.5 non si notano significative variazioni rispetto a

quanto è stato già descritto per i test con av=60°, anche in questo caso si osservano profili

più appuntiti per prove caratterizzate da ac=30° e quindi getti compatti mentre per angoli

di intersezione ac maggiori i profili della buca assumono andamenti più addolciti ad “U”.

Anche in questo caso si osserva un avvicinamento del punto di massimo scavo verso

l’origine all’aumentare dell’angolo ac e quindi all’aumentare dello splash generato.

E’ stato infine realizzato un terzo grafico (fig. 4.6) in cui sono stati raccolti tutti i profili di tutte le prove senza immissione di aria eseguite per osservare eventuali differenze degli

andamenti delle buche di scavo al variare dell’inclinazione verticale av.

Ο Prove con ac=30° e av=60° X Prove con ac=30° e av=75°

Fig. 4.6 Grafico relativo ai profili longitudinali di scavo delle prove con av=60° e av=75°

Come è possibile osservare in figura 4.6, i profili di scavo relativi alle prove eseguite con

av=60° non differiscono di molto da quelli ottenuti da prove con av=75° (a parità di ac)

quindi si può concludere che la variazione dell’inclinazione verticale dei getti da 60° a 75° non influisce in modo significativo sull’andamento del profilo longitudinale dello scavo.

(8)

4.3 Analisi sull’evoluzione temporale dello scavo

Lo studio sullo scavo generato da getti multipli incrociati tra loro ha interessato anche l’evoluzione che lo scavo e la duna hanno avuto nel tempo di durata della prova; al fine di poter fare delle considerazioni su questo argomento sono stati eseguiti rilievi del profilo longitudinale dello scavo e della duna in prestabiliti intervalli temporali.

Come già accennato nel capitolo 2, i rilievi temporali sono stati eseguiti al 5°, 10°, 20° minuto durante lo svolgimento della prova oltre al rilievo eseguito al 40° minuto quando ormai la buca di scavo e la duna di valle hanno già assunto una configurazione stabile; un esempio dei risultati ottenuti è osservabile in figura 4.1.

Il rilievo temporale è stato effettuato in alcune delle prove svolte con un’inclinazione verticale av dei getti di 60° mentre è stato eseguito per tutte le prove caratterizzate da un

av = 75° quindi, siccome queste ultime prove sono state scelte selezionando le

combinazioni tra i valori dei parametri Fd90, d e Tw in modo tale da avere rappresentati

tutti i casi possibili (vedi cap.2), allora è stato pensato di studiare le evoluzioni temporali

delle prove senza immissione di aria e con av = 75°.

Lo studio è consistito nell’osservare, per ogni prova, la variazione assunta dalla massima profondità di scavo Zm nel tempo e riportare i dati ottenuti in grafici in maniera tale da poter rilevare, fissando certi parametri e variandone altri, eventuali differenze evolutive nei vari intervalli temporali considerati.

Per poter comparare tra loro le varie evoluzioni temporali registrate nei test è stato necessario, anche in questa elaborazione, adimensionalizzare le ascisse e le ordinate dei punti rilevati; l’ordinata di ogni punto rilevato è rappresentata dalla profondità di scavo misurata, tale valore è stato adimensionalizzato come segue:

eq m ad D Z Z = dove:

Zad : ordinata adimensionale relativa al punto di massimo scavo

Zm : ordinata relativa al punto di massimo scavo ma riferita alla quota zero individuata sul

letto del fondo in materiale inerte (in cm)

(9)

Prove caratterizzate da Fd90=14,47 e dddd compreso tra 3.54 e 6.43 0 1 2 3 4 5 6 7 3 3,2 3,4 3,6 3,8 4 4,2 4,4 4,6 log(tttt) Z m /D e q angolo=30° Tw=0,7 angolo=30° Tw=7,1 angolo=75° Tw=0,7 angolo=120° Tw=0,7

L’ascissa di ogni punto di profondità massima Zm è data dal tempo in cui effettuo il rilevo; i tempi di misura sono al 5°, 10°, 20°, 40° minuto come abbiamo visto ma noi adotteremo un’ascissa adimensionalizzata attraverso il valore log (t) in cui il parametro t è così

definito:

(

)

eq D t d g⋅ ⋅ = ' 90 1/2

τ

dove:

t : ascissa temporale adimensionalizzata

g’ : accelerazione gravitazionale ridotta (in m/s²)

d90 : diametro passante al 90% nella prova di setacciatura effettuata sull’inerte costituente

il fondo incoerente delle prove (in m)

t : intervallo temporale (in s) Deq : diametro equivalente (in m)

Una volta adimensionalizzati i dati rilevati sono stati rappresentati in 6 grafici, ogni grafico è valido per un preciso valore del parametro Fd90 e per determinati valori di d mentre le

varie evoluzioni temporali rappresentate al suo interno sono relative a prove caratterizzate da diversi valori dell’angolo di intersezione tra i getti ac e del tailwater Tw.

I primi 2 grafici di seguito riportati si riferiscono a prove svolte con portate d’acqua Qw alte

(10)

Prove caratterizzate da Fd90=14,47 e dddd=0 0 1 2 3 4 5 6 3 3,2 3,4 3,6 3,8 4 4,2 4,4 4,6 log(tttt) Z m /D e q angolo=30° Tw=0,7 angolo=30° Tw=7,1 angolo=75° Tw=0,7 angolo=75° Tw=7,1 angolo=120° Tw=0,7 angolo=120° Tw=7,1

I 2 grafici di seguito riportati si riferiscono invece a prove svolte con portate d’acqua Qw di

media entità (3.5 l/s) infatti il numero di Froude densimetrico Fd90 ha, in questo caso, un

valore più basso. Come nel caso precedente, anche in questo caso il primo grafico si riferisce a prove eseguite con alti valori di d mentre nel secondo grafico sono

rappresentate evoluzioni temporali di prove svolte con d nullo.

Prove caratterizzate da Fd90=12,06 e dddd compreso tra 4.5 e 6.43

0 1 2 3 4 5 6 3 3,2 3,4 3,6 3,8 4 4,2 4,4 4,6 log(tttt) Z m /D e q angolo=30° Tw=3,5 angolo=75° Tw=3,5

(11)

Prove caratterizzate da Fd90=12,06 e dddd=0 0 0,5 1 1,5 2 2,5 3 3,5 4 3 3,2 3,4 3,6 3,8 4 4,2 4,4 4,6 log(tttt) Z m /D e q angolo=30° Tw=3,5 angolo=75° Tw=3,5 angolo=120° Tw=3,5

Si riportano infine i grafici rappresentanti le evoluzioni temporali che il punto di massimo scavo presenta nelle prove eseguite con basse portate d’acqua Qw (2.5 l/s) e quindi

caratterizzate da parametri Fd90 ridotti.

Prove caratterizzate da Fd90=8,61 e dddd compreso tra 3,54 e 6,43

0 0,5 1 1,5 2 2,5 3 3,5 3 3,2 3,4 3,6 3,8 4 4,2 4,4 4,6 log(tttt) Z m /D e q angolo=30° Tw=0,7 angolo=30° Tw=7,1 angolo=75° Tw=0,7 angolo=120° Tw=0,7

(12)

Prove caratterizzate da Fd90=8,61 e dddd=0 0 0,5 1 1,5 2 2,5 3 3,5 3 3,2 3,4 3,6 3,8 4 4,2 4,4 4,6 log(tttt) Z m /D e q angolo=30° Tw=0,7 angolo=30° Tw=7,1 angolo=75° Tw=0,7 angolo=75° Tw=7,1 angolo=120° Tw=0,7

Da un’attenta analisi delle evoluzioni temporali dei punti di massimo scavo rilevati in fase dinamica notiamo fin da subito che gli andamenti non si discostano molto tra loro,

osservando i grafici non si osservano significative differenze al variare del parametro Fd90,

del d, dell’angolo di intersezione tra i getti ac o del Tw.

Per tutti gli andamenti si nota una tendenza all’aumento della profondità di scavo col passare del tempo, come d’altronde era logico aspettarsi.

Considerando che il tempo adimensionalizzato è riportato in ascissa in forma logaritmica e che l’unità nelle ordinate corrisponde a 3,11 cm non si notano importanti cambiamenti di pendenza delle spezzate riportate e ciò sta a significare che l’evoluzione temporale del massimo scavo ha un ritmo abbastanza omogeneo nel tempo.

(13)

4.4 Elaborazione dei dati sperimentali relativi allo scavo

generato dai getti multipli incrociati

L'osservazione dei risultati delle prove, consente di proporre una trattazione teorica al fine di prevedere, tramite formule analitiche, la profondità, la lunghezza longitudinale e la larghezza di scavo nelle prove eseguite senza immissione di aria, quindi di individuare quelle posizioni dei getti e quei valori dei parametri idraulici che riducono il fenomeno di scavo a valle.

4.4.1 Elaborazione dei dati sperimentali relativi alla profondità di scavo

Zm in condizioni dinamiche

Come abbiamo già visto nei precedenti capitoli, il fenomeno dello scavo è funzione di numerosi parametri idraulici e geometrici quali l’angolazione verticale dei getti av,

l’angolo con il quale si intersecano i due getti ac, il numero di Froude densimetrico Fd90, il

tailwater Tw e il parametro d con il quale viene eseguito il test.

Dato che lo scavo dipende da molte grandezze è stata fatta un’analisi quantitativa del

massimo scavo Zm suddividendo le prove in 6 sottogruppi di seguito riportati:

- Prove eseguite con av = 60° e ac = 30°

In questo modo è stato possibile semplificare le elaborazioni svolte al fine di rendere più semplice e diretta la comprensione dei grafici riportati e delle relazioni analitiche trovate.

(14)

Elaborazione dei dati sperimentali relativi alla profondità di scavo Zm per le prove eseguite con a a a av = 60° e aaaac = 30°

Per le elaborazioni di questi test sono state inizialmente prese in considerazione le prove eseguite con un valore nullo del parametro d; per queste prove sono stati ricercati i valori

Zmcmeas adimensionalizzando la profondità massima Zm (rilevata nella prova in condizioni

dinamiche). La adimensionalizzazione è stata operata dividendo Zm per il diametro equivalente Deq dei getti:

eq meas

D Zm

Zmc =

Una volta ricavata la profondità adimensionale Zmcmeas è stato tracciato un primo grafico

in cui, per test con d = 0, si ricerca l’andamento che la Zmcmeas assume al variare del

numero di Froude densimetrico:

Grafico 1.1 y = 0,2678x + 0,0137 y = 0,3496x - 0,1088 y = 0,4819x - 0,9514 0 4 8 5 11 17 Fd90 Z m c m e a s Tw=1.8 Tw=3.5 Tw=7.1 Tw=1.8 Tw=3.5 Tw=7.1

Dal grafico 1.1 possiamo notare, come era logico aspettarsi, che all’aumentare del numero

di Froude densimetrico Fd90 le profondità di scavo raggiunte aumentano e tali incrementi

differiscono al variare del Tw.

Una volta trovate le linee di tendenza della Zmcmeas al variare di Fd90 è stato necessario

(15)

(

0.04 0.2

)

₉₀

(

0.2 0.44

)

1 = ⋅ w+ ⋅ + − ⋅ w+

calc T Fd T

Zmc

tracciato un secondo grafico in cui ho riportato in ascissa il tailwater Tw e in ordinata i

valori di A e B dove A e B rappresentano il coeff. angolare e l’intercetta delle linee di tendenza viste sopra ed esprimibili, appunto, con la forma generica dell’equazione di una retta y = Ax + B. Grafico 1.2 y = 0,0398x + 0,2019 y = -0,1902x + 0,4373 -1,5 -1,0 -0,5 0,0 0,5 1,0 0,00 1,00 2,00 3,00 4,00 5,00 6,00 7,00 8,00 Tw A e B A B A B

Dal grafico 1.2 ottengo le linee di tendenza che il coefficiente angolare A e l’intercetta B (trovati nel grafico 1.1) assumono al variare del tailwater.

In questo modo è facile comprendere come la massima profondità di scavo dipenda sia dal numero di Froude densimetrico Fd90 sia dal tailwater Tw.

Sostituendo le equazioni delle linee di tendenza, trovate nel grafico 1.2, nella generica equazione y = Ax + B corrispondente alla tendenza che la max profondità di scavo assume al variare di Fd90 riesco ad ottenere una prima equazione analitica (1) che mi consente di

trovare la massima profondità di scavo Zmccalc1 al variare del Tw e di Fd90 ma valida solo

per prove caratterizzate da un parametro d = 0:

(1)

Tuttavia io ricerco una relazione analitica che sia valida per qualunque valore di d quindi

vado a ricercare, in funzione di d, quanto il valore Zmccalc1 si discosta dal valore

(16)

Chiaramente, se la relazione (1) fosse valida per qualunque valore di d allora il rapporto: 1 calc meas Zmc Zmc

verrebbe pari a 1 per ogni valore di d indagato; tuttavia, come possiamo osservare nel

grafico 1.3, ciò non avviene:

Grafico 1. 3 y = 0,05x + 1 0 1 2 -2 0 2 4 6 d Z m c m e a s /Z m c c a lc 1

Come era logico aspettarsi, per d = 0 i punti individuati dal rapporto Zmcmeas/Zmccalc1

tendono a 1 proprio perchè la relazione (1), dalla quale ottengo Zmccalc1,è stata ricercata

per test eseguiti con parametri d nulli tuttavia tale relazione non è attendibile per prove

effettuate con valori d≠0 in quanto, come si nota dal grafico 1.3, il rapporto

Zmcmeas/Zmccalc1 assume valori molto differenti da 1.

Per questo motivo si evince che la massima profondità di scavo è funzione anche del parametro d e quindi c’è bisogno di far comparire nella relazione (1) anche questa

dipendenza da d trovata.

Per far questo vado a moltiplicare la relazione (1) per l’equazione della retta di tendenza osservata nel grafico 1.3, retta che traduce proprio la dipendenza che la massima profondità di scavo ha rispetto a d.

(17)

Con questa elaborazione appena descritta si arriva ad una relazione generale che ci

permette di ottenere analiticamente la massima profondità di scavo Zmccalc2 in funzione del

tailwater Tw, del numero di Froude densimetrico Fd90 e del parametro d:

(

)

(

)

[

0.04 0.2 ₉₀ 0.2 0.44

]

(

0.05 1

)

2 = ⋅ w + ⋅ + − ⋅ w + ⋅ ⋅

δ

+ calc T Fd T Zmc (2)

Chiaramente la relazione (2) è valida per av =60° e ac = 30°.

Per verificare la correttezza della formula analitica (2) trovata è stato tracciato il grafico 1.4 nel quale si confronta, relativamente a tutte le prove eseguite con av =60° e ac = 30° ,

le profondità massime di scavo adimensionali Zmcmeas rilevate in laboratorio con le

profondità massime di scavo Zmccalc2 calcolate con la relazione analitica (2):

Grafico 1.4 0 5 10 0 5 10 Zmc calc2 Z m c m e a s Serie1 25% deviation Perfect agreement

Salvo rare eccezioni si può vedere dal grafico 1.4 che le massime profondità di scavo Zmccalc2 calcolate con la relazione (2) rientrano in una deviazione massima del 25%

rispetto al valore adimensionale Zmcmeas trovato in laboratorio quindi la formula analitica

(18)

Analogamente al procedimento visto precedentemente, anche in questo caso sono state inizialmente prese in considerazione le prove eseguite con un valore nullo del parametro d;

per queste prove sono stati ricercati i valori Zmcmeas adimensionalizzando la profondità

massima Zm (rilevata nella prova in condizioni dinamiche):

eq meas

D Zm

Zmc =

Una volta ricavata la profondità adimensionale Zmcmeas è stato tracciato un primo grafico

in cui, per test con d = 0, si ricerca l’andamento che la Zmcmeas assume al variare del

Grafico 1.5 y = 0,3956x - 0,8944 y = 0,4551x + 0,0598 y = 0,3266x - 1,8542 0 4 8 5 11 17 Fd90 Z m c m e a s Tw=1.8 Tw=3.5 Tw=7.1 Tw=3.5 Tw=1.8 Tw=7.1

Dal grafico 1.5 possiamo notare, anche in questo caso, che all’aumentare del numero di

Froude densimetrico Fd90 le profondità di scavo aumentano e tali incrementi differiscono al

variare del Tw.

indagare sulla dipendenza che questi andamenti hanno manifestato rispetto al Tw quindi ho

(19)

(

0.023 0.48

)

₉₀

(

0.345 0.53

)

1= − ⋅ w+ ⋅ + − ⋅ w+

calc T Fd T

Zmc

valori di A e B dove A e B rappresentano il coeff. angolare e l’intercetta delle linee di tendenza viste nel grafico 1.5.

Grafico 1.6 y = -0,0227x + 0,4873 y = -0,3454x + 0,5308 -2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 0,00 1,00 2,00 3,00 4,00 5,00 6,00 7,00 8,00 Tw A e B A B A B

Dal grafico 1.6 ottengo le linee di tendenza che il coefficiente angolare A e l’intercetta B assumono al variare del tailwater.

Sostituendo le equazioni delle linee di tendenza, trovate nel grafico 1.6, nella generica equazione y = Ax + B corrispondente alla tendenza che la max profondità di scavo assume al variare di Fd90 riesco ad ottenere una prima equazione analitica (3) che mi consente di

trovare la massima profondità di scavo Zmccalc1 al variare del Tw e di Fd90 ma valida solo

per prove caratterizzate da un parametro d = 0:

(3)

Tuttavia, come già visto nella passata elaborazione, io ricerco una relazione analitica che sia valida per qualunque valore di d quindi vado a ricercare, in funzione di d, quanto il

valore Zmccalc1 si discosta dal valore adimensionale Zmcmeas ottenuto in laboratorio

(20)

Grafico 1. 7 y = -0,0109x2 - 0,0758x + 1 0,0 0,5 1,0 1,5 -2 0 2 4 6 d Z m c m e a s /Z m c c a lc 1

Come era logico aspettarsi, per d = 0 i punti individuati dal rapporto Zmcmeas/Zmccalc1

Zmcmeas/Zmccalc1 assume valori molto differenti da 1.

Per questo motivo si capisce come la massima profondità di scavo sia funzione anche del parametro d e quindi c’è bisogno di far comparire nella relazione (3) anche questa

Per far questo vado a moltiplicare la relazione (3) per l’equazione della parabola di tendenza osservata nel grafico 1.7, parabola che traduce proprio la dipendenza che la massima profondità di scavo ha rispetto a d.

Con questa elaborazione appena descritta si arriva alla relazione generale che ci permette

di ottenere analiticamente la massima profondità di scavo Zmccalc2 in funzione del tailwater

Tw, del numero di Froude densimetrico Fd90 e del parametro d:

(

)

(

)

[

0.023 0.48 90 0.345 0.53

]

(

0.01 2 0.076 1

)

2 = − ⋅ w+ ⋅ + − ⋅ w + ⋅ − ⋅δ − ⋅δ +

calc T Fd T

(21)

Chiaramente la relazione (4) è valida, in questo caso, per av =60° e ac = 75°.

le profondità massime di scavo adimensionali Zmcmeas rilevate in laboratorio con le

profondità massime di scavo Zmccalc2 calcolate con la relazione analitica (4):

Anche per questa elaborazione si può vedere dal grafico 1.8 che, salvo sporadiche

eccezioni, le massime profondità di scavo Zmccalc2 calcolate con la relazione (4) rientrano

in una deviazione massima del 25% rispetto al valore adimensionale Zmcmeas trovato in

(22)

Come nelle elaborazioni svolte in precedenza, anche in questo caso sono state inizialmente prese in considerazione prove eseguite con un valore nullo del parametro d; per queste

prove sono stati ricercati i valori Zmcmeas (adimensionalizzando la profondità massima Zm

rilevata nella prova in condizioni dinamiche) ed è stato tracciato un primo grafico in cui,

per test con con d = 0, si ricerca l’andamento che la Zmcmeas assume al variare del numero

di Froude densimetrico: Grafico 1.9 y = 0,3649x - 1,296 y = 0,3362x + 0,1128 y = 0,2122x - 1,5857 0 3 6 5 11 17 Fd90 Z m c m e a s Tw=0.7 Tw=3.5 Tw=7.1 Tw=3.5 Tw=0.7 Tw=7.1

Dal grafico 1.9 possiamo notare, anche nel caso di prove con angolazione ac elevata, che

all’aumentare del numero di Froude densimetrico Fd90 le profondità di scavo aumentano e

tali incrementi differiscono al variare del Tw.

(23)

(

0.02 0.38

)

90

(

0.26 0.044

)

1 = − ⋅ w+ ⋅ + − ⋅ w+ calc T Fd T Zmc Grafico 1.10 y = -0,0205x + 0,3814 y = -0,2568x + 0,0444 -2,0 -1,5 -1,0 -0,5 0,0 0,5 0 4 8 Tw A e B A B A B

Da questo grafico 1.10 ottengo le linee di tendenza che il coefficiente angolare A e l’intercetta B assumono al variare del tailwater.

Sostituendo le equazioni delle linee di tendenza, trovate nel grafico 1.10, nella generica equazione y = Ax + B corrispondente alla tendenza che la max profondità di scavo manifesta al variare di Fd90 riesco ad ottenere una prima equazione analitica (5) che mi

consente di trovare la massima profondità di scavo Zmccalc1 al variare del Tw e di Fd90 ma

valida solo per prove caratterizzate da un parametro d = 0:

(5)

valore Zmccalc1 si discosta dal valore adimensionale Zmcmeas ottenuto in laboratorio

(24)

Grafico 1. 11 y = -0,0669x + 1 0 1 2 0 4 8 d Z m c m e a s /Z m c c a lc 1

Anche in questa elaborazione, per d = 0, i punti individuati dal rapporto Zmcmeas/Zmccalc1

Zmcmeas/Zmccalc1 assume valori diversi da 1.

Per questo motivo si capisce come la massima profondità di scavo sia funzione anche del parametro d e quindi c’è bisogno di far comparire nella relazione (5) anche questa

Per far questo vado a moltiplicare la relazione (5) per l’equazione della retta di tendenza osservata nel grafico 1.11, retta che ci mostra proprio la dipendenza che la massima profondità di scavo ha rispetto a d.

di ottenere analiticamente la massima profondità di scavo Zmccalc2 in funzione del tailwater

(

)

(

)

[

0.02 0.38 ₉₀ 0.26 0.044

]

(

0.067 1

)

2 = − ⋅ w + ⋅ + − ⋅ w + ⋅ − ⋅

δ

+

calc T Fd T

(25)

Per verificare la correttezza della formula analitica (6) trovata è stato tracciato, anche questa volta, il grafico 1.12 nel quale si confronta ancora una volta, relativamente a tutte le prove eseguite con av =60° e ac = 120° , le profondità massime di scavo adimensionali

Zmcmeas rilevate in laboratorio con le profondità massime di scavo Zmccalc2 calcolate con la

relazione analitica (6): Grafico 1.12 0 5 10 0 5 10 Zmc calc2 Z m c m e a s Serie1 25% deviation Perfect agreement

Anche per questa elaborazione, relativa alle prove eseguite con un angolo di intersezione

ac = 120°, si può vedere dal grafico 1.12 che, salvo rare eccezioni, le massime profondità

di scavo Zmccalc2 calcolate con la relazione (6) rientrano in una deviazione massima del

25% rispetto al valore adimensionale Zmcmeas trovato in laboratorio quindi la formula

(26)

Elaborazione dei dati sperimentali relativi alla profondità di scavo Zm per le prove eseguite con a a a av = 75°

Nella elaborazione delle profondità di scavo rilevate nelle prove eseguite con av = 75° è

stato pensato di ricercare il valore Zmccalc2 applicando le relazioni analitiche già trovate per

le prove con av = 60° e verificare se tali relazioni possono ritenersi valide o se necessitano

di correzioni.

Elaborazione dei dati sperimentali relativi alla profondità di scavo Zm per le prove eseguite con a a a a_v= 75° e aaaa_c= 30°.

Per i test eseguiti con un angolo di inclinazione verticale av = 75° e un angolo di

intersezione tra i getti ac = 30° è stato ricercato un valore calcolato Zmccalc2 utilizzando la

formula analitica (2) trovata precedentemente e, per valutare la correttezza di questa formula, è stato tracciato il grafico 1.13 nel quale si comparano i valori Zmccalc2,ottenuti

con la relazione (2), con i valori adimensionali Zmcmeas rilevati in laboratorio:

Grafico 1.13 0 4 8 0 4 8 Zmc calc2 Z m c m e a s Serie1 25% deviation Perfect

Come è possibile osservare dal grafico, i valori Zmccalc2 calcolati utilizzando la formula

analitica (2) rientrano in una deviazione massima del 25% rispetto ai valori adimensionali Zmcmeas rilevati sperimentalmente in laboratorio quindi posso ritenere che la relazione

(27)

Elaborazione dei dati sperimentali relativi alla profondità di scavo Zm per le prove eseguite con a a a av = 75° e aaaac = 75°.

Un procedimento analogo al precedente è stato applicato ai test eseguiti con un angolo verticale av = 75° e un angolo di intersezione tra i getti ac = 75° ; è stato ricercato un

valore calcolato Zmccalc2 utilizzando la formula analitica (4) trovata precedentemente e, per

valutare la correttezza di questa formula, è stato tracciato il grafico 1.14 nel quale si comparano i valori Zmccalc2, ottenuti con la relazione (4), con i valori adimensionali

Zmcmeas rilevati in laboratorio:

Grafico 1.14 0 4 8 0 4 8 Zmc calc2 Z m c m e a s Serie1 Perfect agreement 25% deviation

analitica (4) rientrano approssimativamente in un margine di errore del 25% rispetto ai

valori adimensionali Zmcmeas rilevati sperimentalmente in laboratorio quindi posso ritenere

(28)

Elaborazione dei dati sperimentali relativi alla profondità di scavo Zm per le prove eseguite con a a a av = 75° e aaaac = 120°.

Infine lo stesso procedimento è stato applicato ai test eseguiti con un angolo verticale av

= 75° e un angolo di intersezione tra i getti ac = 120° ; è stato ricercato un valore calcolato

Zmccalc2 utilizzando la formula analitica (6) trovata in precedenza ma la comparazione

degli Zmccalc2 con gli Zmcmeas trovati in laboratorio ha messo in luce differenze sostanziali.

In studi fatti in passato è stato visto che la dipendenza della Zmccalc2 dal tailwater poteva

variare al variare di av quindi è stato tracciato il grafico 1.15:

Grafico 1.15 y = -0,0508x + 0,7247 0,00 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 0,0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 Tw Z m c m e a s /Z m c c a lc 2

In questo grafico si nota come i punti abbiano una linea di tendenza inclinata al variare di Tw quindi la relazione (6) trovata in precedenza necessita di una correzione al fine di

introdurvi anche questa ulteriore dipendenza dal tailwater.. Tracciando la linea di tendenza di questa variazione (vedi grafico 1.15) e moltiplicando la relativa equazione della retta nella relazione (6) ottengo una nuova relazione (7) che mi fornisce la nuova profondità di scavo Zmccalc3 valida per av = 75° e ac = 120°:

(

)

(

)

[

]

(

)

{

0.02 0.38 90 0.26 0.044 0.067 1

} (

0.05 0.72

)

3 = − ⋅ w + ⋅ + − ⋅ w + ⋅ − ⋅ + ⋅ − ⋅ w + calc T Fd T T Zmc

δ

(7)

(29)

A questo punto, per verificare la correttezza della relazione (7), è stato tracciato il grafico

1.16 di comparazione tra i valori calcolati Zmccalc3 e le profondità di scavo adimensionali

Zmcmeas ottenute in laboratorio:

analitica (7) rientrano approssimativamente in un margine di errore del 25% rispetto ai

valori adimensionali Zmcmeas rilevati sperimentalmente quindi posso ritenere che la

relazione analitica (7), corretta aggiungendo la ulteriore dipendenza dal tailwater Tw

(30)

4.4.2 Elaborazione dei dati sperimentali relativi alla lunghezza di scavo

La in condizioni dinamiche

Come abbiamo già osservato precedentemente, il fenomeno dello scavo è funzione di numerosi parametri idraulici e geometrici quali l’angolazione verticale dei getti av,

l’angolo con il quale si intersecano i due getti ac, il numero di Froude densimetrico Fd90, il

tailwater Tw e il parametro d con il quale viene eseguito il test.

Anche in questo caso, dato che lo scavo dipende da molte grandezze, è stata fatta un’analisi quantitativa della massima lunghezza di scavo La suddividendo le prove in 6

sottogruppi di seguito riportati:

(31)

Elaborazione dei dati sperimentali relativi alla lunghezza di scavo La per le prove

eseguite con a a a av = 60° e aaaac = 30°

Lcmeas adimensionalizzando la lunghezza massima La (rilevata nella prova in condizioni

dinamiche). La adimensionalizzazione è stata operata dividendo La per il diametro

equivalente Deq dei getti:

eq meas

D La

Lc =

Una volta ricavata la lunghezza di scavo adimensionale Lcmeas è stato tracciato un primo

grafico in cui, per test con d = 0, si ricerca l’andamento che la Lcmeas assume al variare del

Grafico 2.1 y = 0,2934x + 4,9438 y = 0,65x + 2,8788 y = 1,1121x + 0,8626 0 5 10 15 20 25 5 11 17 Fd90 L c m e a s Tw=1.8 Tw=3.5 Tw=7.1 Tw=1.8 Tw=3.5 Tw=7.1

Dal grafico 2.1 possiamo notare, come era logico aspettarsi, che all’aumentare del numero di Froude densimetrico Fd90 le lunghezze di scavo raggiunte aumentano e tali incrementi

Una volta trovate le linee di tendenza della Lcmeas al variare di Fd90 è stato necessario

(32)

(

0.15 0.06

)

₉₀

(

0.74 5.94

)

1 = ⋅ w+ ⋅ + − ⋅ w+

calc T Fd T

Lc

valori di A e B dove A e B rappresentano il coeff. angolare e l’intercetta delle linee di tendenza viste sopra ed esprimibili, appunto, con la forma generica dell’equazione di una retta y = Ax + B. Grafico 2.2 y = 0,1505x + 0,0631 y = -0,7374x + 5,943 0,0 5,0 10,0 0,00 1,00 2,00 3,00 4,00 5,00 6,00 7,00 8,00 Tw A e B A B A B

In questo modo è facile comprendere come la massima lunghezza di scavo dipenda sia dal numero di Froude densimetrico Fd90 sia dal tailwater Tw.

Sostituendo le equazioni delle linee di tendenza, trovate nel grafico 2.2, nella generica equazione y = Ax + B corrispondente alla tendenza che la max lunghezza di scavo assume al variare di Fd90 riesco ad ottenere una prima equazione analitica (8) che mi consente di

trovare la massima lunghezza di scavo Lccalc1 al variare del Tw e di Fd90 ma valida solo per

prove caratterizzate da un parametro d = 0:

(8)

vado a ricercare, in funzione di d, quanto il valore Lccalc1 si discosta dal valore

(33)

Chiaramente, se la relazione (8) fosse valida per qualunque valore di d allora il rapporto: 1 calc meas Lc Lc

verrebbe pari a 1 per ogni valore di d indagato; tuttavia, come possiamo osservare nel

grafico 2.3, ciò non avviene:

Grafico 2. 3 y = 0,0991x + 1 0 1 2 3 -2 0 2 4 6 d L c m e a s /L c c a lc 1

Come era logico aspettarsi, per d = 0 i punti individuati dal rapporto Lcmeas/Lccalc1 tendono

a 1 proprio perché la relazione (8), dalla quale ottengo Lccalc1, è stata ricercata per test

eseguiti con parametri d nulli tuttavia tale relazione non è attendibile per prove effettuate

con valori d≠0 in quanto, come si nota dal grafico 2.3, il rapporto Lcmeas/Lccalc1 assume

valori molto differenti da 1.

Per questo motivo si evince che la massima lunghezza di scavo è funzione anche del parametro d e quindi c’è bisogno di far comparire nella relazione (8) anche questa

Per far questo vado a moltiplicare la relazione (8) per l’equazione della retta di tendenza osservata nel grafico 2.3, retta che traduce proprio la dipendenza che la massima lunghezza di scavo ha rispetto a d.

(34)

Con questa elaborazione appena descritta si arriva ad una relazione generale che ci

permette di ottenere analiticamente la massima lunghezza di scavo Lccalc2 in funzione del

tailwater Tw, del numero di Froude densimetrico Fd90 e del parametro d:

(

)

(

)

[

0.15 0.06 ₉₀ 0.74 5.94

]

(

0.099 1

)

2 = ⋅ w + ⋅ + − ⋅ w + ⋅ ⋅

δ

+

calc T Fd T

Lc (9)

le lunghezze massime di scavo adimensionali Lcmeas rilevate in laboratorio con le

lunghezze massime di scavo Lccalc2 calcolate con la relazione analitica (9):

Grafico 2.4 0 12 24 0 12 24 Lc calc2 L c m e a s Serie1 25% deviation Perfect

Salvo rare eccezioni si può vedere dal grafico 2.4 che le massime lunghezze di scavo Lccalc2 calcolate con la relazione (9) rientrano in una deviazione massima del 25% rispetto

al valore adimensionale Lcmeas trovato in laboratorio quindi la formula analitica (9) può

(35)

Analogamente al procedimento visto precedentemente, anche in questo caso sono state inizialmente prese in considerazione le prove eseguite con un valore nullo del parametro d;

per queste prove sono stati ricercati i valori Lcmeas adimensionalizzando la lunghezza

massima La (rilevata nella prova in condizioni dinamiche):

eq meas

D La

Lc =

Una volta ricavata la lunghezza adimensionale Lcmeas è stato tracciato un primo grafico in

cui, per test con d = 0, si ricerca l’andamento che la Lcmeas assume al variare del numero

di Froude densimetrico: Grafico 2.5 y = 1,2674x y = 0,9173x y = 1,1523x 0 4 8 12 16 20 24 5 11 17 Fd90 L c m e a s Tw=1.8 Tw=3.5 Tw=7.1 Serie4

Dal grafico 2.5 possiamo notare, anche in questo caso, che all’aumentare del numero di

Froude densimetrico Fd90 le lunghezze di scavo aumentano e tali incrementi differiscono al

variare del Tw.

(36)

(

)

90 1 0.06 T 1.38 Fd

Lc_calc = − ⋅ _w+ ⋅

valori di A dove A rappresenta il coeff. angolare delle linee di tendenza viste nel grafico 2.5. Grafico 2.6 y = -0,0659x + 1,3845 0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 0,00 1,00 2,00 3,00 4,00 5,00 6,00 7,00 8,00 Tw A

Dal grafico 2.6 ottengo la linea di tendenza che il coefficiente angolare A assume al variare del tailwater.

Sostituendo l’equazione della linea di tendenza, trovata nel grafico 2.6, nella generica equazione y = Ax corrispondente alla tendenza che la max lunghezza di scavo assume al variare di Fd90 riesco ad ottenere una prima equazione analitica (10) che mi consente di

trovare la massima lunghezza di scavo Lccalc1 al variare del Tw e di Fd90 ma valida solo per

(10)

valore Lccalc1 si discosta dal valore adimensionale Lcmeas ottenuto in laboratorio

(37)

Grafico 2.7 y = -0,0153x2 + 0,0217x + 1 0,0 0,5 1,0 1,5 -2 0 2 4 6 d L c m e a s /L c c a lc 1

Come era logico aspettarsi, per d = 0 i punti individuati dal rapporto Lcmeas/Lccalc1 tendono

a 1 proprio perché la relazione (10), dalla quale ottengo Lccalc1, è stata ricercata per test

eseguiti con parametri d nulli tuttavia tale relazione non è attendibile per prove effettuate

con valori d≠0 in quanto, come si nota dal grafico 2.7, il rapporto Lcmeas/Lccalc1 assume

valori molto differenti da 1.

Per questo motivo si capisce come la massima lunghezza di scavo sia funzione anche del parametro d e quindi c’è bisogno di far comparire nella relazione (10) anche questa

Per far questo vado a moltiplicare la relazione (10) per l’equazione della parabola di tendenza osservata nel grafico 2.7, parabola che traduce proprio la dipendenza che la massima lunghezza di scavo ha rispetto a d.

Con questa elaborazione appena descritta si arriva alla relazione generale che ci permette di ottenere analiticamente la massima lunghezza di scavo Lccalc2 in funzione del tailwater

(

)

(

)

1 02 . 0 015 . 0 38 . 1 06 . 0 90 2 2 = − ⋅T + ⋅Fd ⋅ − ⋅δ + ⋅δ + Lccalc w (11)

(38)

Chiaramente la relazione (11) è valida, in questo caso, per av =60° e ac = 75°.

le lunghezze massime di scavo adimensionali Lcmeas rilevate in laboratorio con le

lunghezze massime di scavo Lccalc2 calcolate con la relazione analitica (11):

Grafico 2.8 0 12 24 0 12 24 Lc calc2 L c m e a s Serie1 25% deviation Perfect agreement

Anche per questa elaborazione si può vedere dal grafico 2.8 che, salvo sporadiche

eccezioni, le massime lunghezze di scavo Lccalc2 calcolate con la relazione (11) rientrano in

una deviazione massima del 25% rispetto al valore adimensionale Lcmeas trovato in

(39)

Come nelle elaborazioni svolte in precedenza, anche in questo caso sono state inizialmente prese in considerazione prove eseguite con un valore nullo del parametro d; per queste

prove sono stati ricercati i valori Lcmeas (adimensionalizzando la lunghezza massima La

rilevata nella prova in condizioni dinamiche) ed è stato tracciato un primo grafico in cui,

per test con con d = 0, si ricerca l’andamento che la Lcmeas assume al variare del numero di

Froude densimetrico: Grafico 2.9 y = 0,9282x + 0,8365 y = 1,091x + 2,0486 y = 0,6185x + 0,472 0 3 6 9 12 15 18 21 5 11 17 Fd90 L c m e a s Tw=0.7 Tw=3.5 Tw=7.1 Tw=3.5 Tw=0.7 Tw=7.1

Dal grafico 2.9 possiamo notare, anche nel caso di prove con angolazione ac elevata, che

all’aumentare del numero di Froude densimetrico Fd90 le lunghezze di scavo aumentano e

tali incrementi differiscono al variare del Tw.

(40)

(

0.07 1.16

)

90

(

0.24 2.02

)

1= − ⋅ w+ ⋅ + − ⋅ w+ calc T Fd T La Grafico 2.10 y = -0,0744x + 1,1594 y = -0,2396x + 2,0214 -4 -2 0 2 4 0 4 8 Tw A e B A B A B

Da questo grafico 2.10 ottengo le linee di tendenza che il coefficiente angolare A e l’intercetta B assumono al variare del tailwater.

Sostituendo le equazioni delle linee di tendenza, trovate nel grafico 2.10, nella generica equazione y = Ax + B corrispondente alla tendenza che la max lunghezza di scavo manifesta al variare di Fd90 riesco ad ottenere una prima equazione analitica (12) che mi

consente di trovare la massima lunghezza di scavo Lccalc1 al variare del Tw e di Fd90 ma

valida solo per prove caratterizzate da un parametro d = 0:

(12)

valore Lccalc1 si discosta dal valore adimensionale Lcmeas ottenuto in laboratorio

(41)

Grafico 2. 11 y = 0,0402x + 1 0 1 2 0 4 8 d L c m e a s /L c c a lc 1

Anche in questa elaborazione, per d = 0, i punti individuati dal rapporto Lcmeas/Lccalc1

tendono a 1 proprio perché la relazione (12), dalla quale ottengo Lccalc1,è stata ricercata per

test eseguiti con parametri d nulli tuttavia tale relazione non è attendibile per prove

effettuate con valori d≠0 in quanto, come si nota dal grafico 2.11, il rapporto Lcmeas/Lccalc1

assume valori diversi da 1.

Per questo motivo si capisce come la massima lunghezza di scavo sia funzione anche del parametro d e quindi c’è bisogno di far comparire nella relazione (12) anche questa

Per far questo vado a moltiplicare la relazione (12) per l’equazione della retta di tendenza osservata nel grafico 2.11, retta che ci mostra proprio la dipendenza che la massima lunghezza di scavo ha rispetto a d.

di ottenere analiticamente la massima lunghezza di scavo Lccalc2 in funzione del tailwater

(

)

(

)

[

0.07 1.16 ₉₀ 0.24 2.02

]

(

0.04 1

)

2 = − ⋅ w + ⋅ + − ⋅ w + ⋅ ⋅

δ

+

calc T Fd T

(42)

Per verificare la correttezza della formula analitica (13) trovata è stato tracciato, anche questa volta, il grafico 2.12 nel quale si confronta ancora una volta, relativamente a tutte le prove eseguite con av =60° e ac = 120° , le lunghezze massime di scavo adimensionali

Lcmeas rilevate in laboratorio con le lunghezze massime di scavo Lccalc2 calcolate con la

relazione analitica (13): Grafico 2.12 0 12 24 0 12 24 Lc calc2 L c m e a s Serie1 25% deviation Perfect agreement

Anche per questa elaborazione, relativa alle prove eseguite con un angolo di intersezione

ac = 120°, si può vedere dal grafico 2.12 che, salvo rare eccezioni, le massime lunghezze

di scavo Lccalc2 calcolate con la relazione (13) rientrano in una deviazione massima del

25% rispetto al valore adimensionale Lcmeas trovato in laboratorio quindi la formula

(43)

eseguite con a a a av = 75°

Nella elaborazione delle lunghezze di scavo rilevate nelle prove eseguite con av = 75° è

stato pensato di ricercare il valore Lccalc2 applicando le relazioni analitiche già trovate per

le prove con av = 60° e verificare se tali relazioni possono ritenersi valide o se necessitano

di correzioni.

Per verificare l’attendibilità delle relazioni trovate (relazioni (9), (11), (13) che ci

forniscono la lunghezza massima di scavo Lccalc2 rispettivamente per ac =30°, ac =75° e

ac = 120°) è stato tracciato il grafico 2.13 nel quale si osserva come varia il rapporto tra le

lunghezze di scavo adimensionali Lcmeas rilevate sperimentalmente e le lunghezze Lccalc2

calcolate analiticamente al variare del tailwater Tw (variabile scelta in base a studi fatti in

passato): Grafico 2.13 y = -0,0203x + 0,9759 0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60 1,80 2,00 0,0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 Tw L c m e a s /L c c a lc 2

Se le relazioni (9), (11) e (13) fossero valide anche per angolazioni verticali av = 75°

allora il rapporto in ordinata darebbe valori pressoché unitari e indipendenti dal Tw;

tuttavia, come è possibile osservare dal grafico 2.13, i punti hanno una linea di tendenza

leggermente inclinata al variare di Tw quindi le relazioni trovate in precedenza necessitano

(44)

eseguite con a a a av = 75° e aaaac = 30°.

intersezione tra i getti ac = 30° la correzione è stata apportata moltiplicando la relazione

(9), trovata per av = 60°, per l’equazione della linea di tendenza ottenuta nel grafico 2.13:

(

)

(

)

[

]

(

)

{

0.15 0.06 ₉₀ 0.74 5.94 0.099 1

} (

0.02 0.97

)

3 = ⋅ w + ⋅ + − ⋅ w+ ⋅ ⋅ + ⋅ − ⋅ w + calc T Fd T T Lc

δ

(14)

La relazione analitica (14) così ottenuta presenta anche la dipendenza dal tailwater osservata nel grafico 2.13 e ci fornisce la massima lunghezza di scavo Lccalc3 per un

angolazione verticale av = 75° e un angolo di intersezione dei getti ac = 30°.

Per valutare la correttezza di questa formula, è stato tracciato il grafico 2.14 nel quale si

comparano i valori Lccalc3, ottenuti con la relazione (14), con i valori adimensionali Lcmeas

rilevati in laboratorio: Grafico 2.14 0 12 24 0 12 24 Lc calc3 L c m e a s Serie1 25% deviation Perfect

Come è possibile osservare dal grafico, i valori Lccalc3 calcolati utilizzando la formula

analitica (14) rientrano in una deviazione massima del 25% rispetto ai valori adimensionali Lcmeas rilevati sperimentalmente in laboratorio quindi posso ritenere che la relazione

(45)

(

)

[

]

(

)

{

0.06 1.38 90 0.015 2 0.02 1

}

(

0.02 0.97

)

3 = − ⋅ w+ ⋅ ⋅ − ⋅ + ⋅ + ⋅ − ⋅ w+ calc T Fd T Lc δ δ

(15)

rilevati in laboratorio: Grafico 2.15 0 12 24 0 12 24 Lc calc3 L c m e a s Serie1 Perfect agreement 25% deviation

analitica (15) rientrano, salvo rari casi, in una deviazione massima del 25% rispetto ai valori adimensionali Lcmeas rilevati sperimentalmente in laboratorio quindi posso ritenere

(46)

(

)

(

)

[

]

(

)

{

0.07 1.16 ₉₀ 0.24 2.02 0.04 1

} (

0.02 0.97

)

3 = − ⋅ w + ⋅ + − ⋅ w + ⋅ ⋅ + ⋅ − ⋅ w+ calc T Fd T T Lc

δ

(16)

rilevati in laboratorio: Grafico 2.16 0 12 24 0 12 24 Lc calc3 L c m e a s Serie1 25% deviation Perfect agreement

analitica (16) rientrano in una deviazione massima del 25% rispetto ai valori adimensionali Lcmeas rilevati sperimentalmente in laboratorio quindi posso ritenere che la relazione

(47)

4.4.3 Elaborazione dei dati sperimentali relativi alla larghezza di scavo

B in condizioni dinamiche

Come abbiamo già visto in precedenza, il fenomeno dello scavo è funzione di numerosi parametri idraulici e geometrici quali l’angolazione verticale dei getti av, l’angolo con il

quale si intersecano i due getti ac, il numero di Froude densimetrico Fd90, il tailwater Tw e

il parametro d con il quale viene eseguito il test.

Anche in questo caso, dato che lo scavo dipende da molte grandezze, è stata fatta un’analisi quantitativa della massima larghezza di scavo B suddividendo le prove in 6 sottogruppi di seguito riportati:

(48)

Elaborazione dei dati sperimentali relativi alla larghezza di scavo B per le prove eseguite con a a a av = 60° e aaaac = 30°

Bcmeas adimensionalizzando la larghezza massima B (rilevata nella prova in condizioni

dinamiche). La adimensionalizzazione è stata operata dividendo B per il diametro equivalente Deq dei getti:

eq meas

D B

Bc =

Una volta ricavata la larghezza di scavo adimensionale Bcmeas è stato tracciato un primo

grafico in cui, per test con d = 0, si ricerca l’andamento che la Bcmeas assume al variare del

Grafico 3.1 y = 0,8309x - 0,624 y = 0,8309x + 0,9837 y = 0,8309x + 5,8069 0 5 10 15 20 25 5 11 17 Fd90 B c m e a s Tw=1.8 Tw=3.5 Tw=7.1 Tw=1.8 Tw=3.5 Tw=7.1

Dal grafico 3.1 possiamo notare, come era logico aspettarsi, che all’aumentare del numero di Froude densimetrico Fd90 le larghezze di scavo raggiunte aumentano e tali incrementi

Una volta trovate le linee di tendenza della Bcmeas al variare di Fd90 è stato necessario

(49)

(

1.23 3.04

)

83 . 0 ₉₀ 1= ⋅ + ⋅ w− calc Fd T Bc

valori di A e B dove A e B rappresentano il coeff. angolare e l’intercetta delle linee di tendenza viste sopra ed esprimibili, appunto, con la forma generica dell’equazione di una retta y = Ax + B. Grafico 3.2 y = -4E-05x + 0,8305 y = 1,2331x - 3,0411 -1,5 3,5 8,5 0,00 1,00 2,00 3,00 4,00 5,00 6,00 7,00 8,00 Tw A e B A B A B

In questo modo è facile comprendere come la massima larghezza di scavo dipenda sia dal numero di Froude densimetrico Fd90 sia dal tailwater Tw.

Sostituendo le equazioni delle linee di tendenza, trovate nel grafico 3.2, nella generica equazione y = Ax + B corrispondente alla tendenza che la max larghezza di scavo assume

al variare di Fd90 riesco ad ottenere una prima equazione analitica (17) che mi consente di

trovare la massima larghezza di scavo Bccalc1 al variare del Tw e di Fd90 ma valida solo per

(17)

vado a ricercare, in funzione di d, quanto il valore Bccalc1 si discosta dal valore