CCaappiittoolloo VV

C

C

a

a

p

p

i

i

t

t

o

o

l

l

o

o

V

V

Simulazioni e Test del

modello SEM

V.1 Introduzione

L’impianto teorico su cui si basa il SEM, cioè il sistema di equazioni strutturali e i principi su cui si fonda la stima dei parametri del modello, permette un approccio abbastanza immediato con il problema dello studio della connettività effettiva. Tuttavia occorre capire con precisione, attraverso simulazioni e test specifici, quali siano i significati che ogni variabile assume all’interno del modello (con particolare riferimento alla componente di rumore z) e come la stima dei parametri sia influenzata dalle condizioni sperimentali; questo è infatti di fondamentale importanza sia per avere conferma dell’efficacia del metodo di modellizzazione sia per l’interpretazione futura dei risultati che si otterranno dall’analisi dei dati reali. I momenti principali della simulazione sono due: la generazione dei dati e la stima vera e propria.

In fase di generazione si vuole realizzare un set di dati che siano spiegati da un particolare modello di connettività e che abbiano caratteristiche di “rumorosità” determinate.

In fase di stima invece si va ad applicare il SEM ai dati generati precedentemente, cercando di capire come cambiano i risultati in relazione sia al modello di connettività che si va ad applicare ai dati (nel senso che si può usare un modello di stima anche diverso rispetto a quello usato per generare i dati) sia alle condizioni di rumore dei segnali stessi.

V.2 Generazione dei Dati Simulati

L’obiettivo di questa parte del lavoro è quello di capire le potenzialità della modellizzazione SEM e di valutare la bontà della stima ottenuta attraverso il LISREL; il problema da affrontare è come poter effettuare tali valutazioni.

L’idea è quella di generare un set di segnali che descrivano un certo modello di connettività scelto dall’esterno e che sottostiano contemporaneamente alle relazioni di causalità imposte dal modello generativo (tipo SEM) da cui derivano. In questo modo riusciamo a disporre di un insieme di dati che descrive legami di connettività a noi noti e che nasce dallo stesso modello matematico con cui andremo a lavorare in fase di stima; ciò ci permetterà di valutare quanto i parametri stimati divergano dal loro valore reale.

Utilizzando la notazione del LISREL, esplicitiamo il termine

η

dalla equazione descrittiva del modello SEM e otteniamo la relazione necessaria per la generazione dei dati, che indichiamo con il nome di Modello Generativo:

1

(

I

)

(

)

η

_{= −Β ⋅ Γ⋅ +}

−

ξ ζ

Dove l’insieme delle variabili endogene

η

costituisce il vero e proprio set dei dati simulati, mentre le variabili esogene

ξ

e la componente di rumore

ζ

rappresentano le sorgenti da cui nascono i segnali dell’intero modello di connettività. Ai fini della generazione è possibile utilizzare indifferentemente l’una o l’altra sorgente (anche in contemporanea), l’unica cosa che cambia è il significato che esse assumono nel contesto della creazione dei segnali.

La componente di rumore

ζ

rappresenta lo scarto di informazione che non entra nel modello di connettività mentre il termine

Γ ⋅

ξ

riassume i legami attraverso cui le variabili esogene influenzano i segnali del modello. Sicuramente è più semplice e immediato sfruttare come sorgenti le variabili

ξ

piuttosto che la componente

ζ

,

infatti è molto difficile stabilire a priori quale sia lo scarto di informazione legato ad un particolare modello senza conoscere i suoi segnali caratteristici; al contrario nella generazione attraverso le variabili esogene si vanno ad imporre direttamente i segnali sorgente ed i legami attraverso cui essi generano le singole variabili endogene.

Questo tipo di approccio è molto più intuitivo rispetto all’altro infatti consente di vedere il SEM, almeno in questa fase, come un sistema lineare causale in cui le variabili esogene costituiscono i segnali di ingresso al sistema e quelle endogene i segnali d’uscita generati attraverso il modello di connettività imposto. E’ possibile quindi lavorare con delle sorgenti costituite da sequenze temporali vere e proprie e non da innovazioni di rumore (termine

ζ

) che non sono altrettanto facilmente interpretabili.

Modello Generativo

In particolare, avendo eliminato il termine

ζ

dal modello generativo e considerando

ξ

e

η

come vettori colonna contenenti rispettivamente l’insieme delle variabili endogene ed esogene, per delineare con esattezza le caratteristiche del modello generativo, occorre definire:

1. Numero di sorgenti (variabili esogene

ξ

i) attraverso cui si vuol generare

l’intero set di dati:

N

ξ;

1 N_ξ

ξ

ξ

ξ

⎡

⎤

⎢

⎥

= ⎢

⎥

⎢

⎥

⎣

⎦

#

2. Numero di variabili endogene (

η

j) che caratterizzano il modello:

N

η;

1 N_η

η

η

η

⎡

⎤

⎢

⎥

= ⎢

⎥

⎢

⎥

⎣

⎦

#

4. Matrice

B

caratterizzante i legami tra le variabili endogene appartenenti al modello di connettività vero e proprio:

1,2 1, 2,1 ( 1), ,1 ,( 1)

0

0

0

0

N N N N N N

b

b

b

B

b

b

b

η η η η η η − −

⎡

⎤

⎢

⎥

⎢

⎥

= ⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

"

%

#

#

%

"

5. Matrice

Γ

che individua le influenze delle sorgenti sulle variabili endogene del modello: 1,1 1,2 1, 2,1 2,2 ( 1), ,1 ,( 1) , N N N N N N N N ξ η ξ η η ξ η ξ

γ

γ

γ

γ

γ

γ

γ

γ

γ

− −

⎡

⎤

⎢

⎥

⎢

⎥

Γ = ⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

"

"

#

#

#

%

"

V.2.1 Modello di Connettività

L’aspetto fondamentale da tenere in considerazione in questa fase di definizione del modello generativo è la scelta del tipo di modello di connettività che vogliamo realizzare e successivamente testare.

Da un lato sarebbe interessante andare a testare, attraverso le simulazioni, una serie di modelli di connettività tutti diversi tra loro, con lo scopo di capire quali siano stimati meglio o peggio e di avere una panoramica completa delle debolezze e degli errori introdotti dal software LISREL. Dall’altra parte la ricerca che stiamo affrontando è indirizzata verso lo studio e la modellizzazione del sistema olfattivo e quindi sarebbe dispersivo simulare e testare modelli di connettività molto diversi da quello che presumibilmente descrive l’apparato olfattivo stesso.

Per questo motivo si è deciso di utilizzare, anche in questa fase di simulazione, un modello molto simile a quello ipotizzato per la connettività delle varie regioni olfattive (vedi Capitolo II paragrafo II.2.3), così che, quando verrà affrontata l’analisi dei dati reali, sarà più facile interpretarne i risultati avendo a disposizione una valutazione preliminare della bontà della stima di quel particolare modello di connettività in funzione delle condizioni sperimentali (in particolare il rapporto segnale-rumore SNR).

Almeno in prima battuta il modello che andiamo a simulare è costituito da quattro variabili corrispondenti alle quattro principali regioni cerebrali coinvolte nella funzione olfattiva: Bulbo Olfattivo, Corteccia Piriforme, Corteccia Orbito-Frontale e Amygdala.

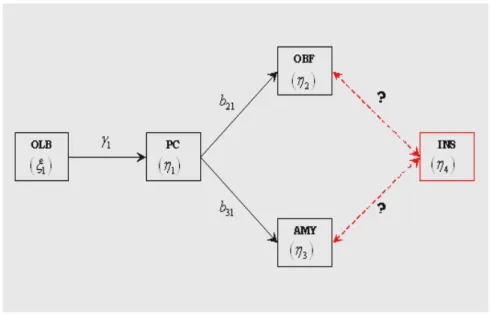
I rapporti di causalità tra le varie aree sono stabiliti dalle connessioni del diagramma riportato di seguito (figura 5.1) che ricalca esattamente il modello di connettività olfattiva presentato nel capitolo II.

Ad ogni regione è associata una variabile, esogena o endogena, a seconda della sua funzione assunta nel modello; nel caso specifico alla regione del Bulbo Olfattivo (OLB) è associata la variabile esogena

ξ

1 poiché quella è l’area sorgente in cui

nascono e da cui si propagano i segnali del sistema; invece alle altre tre zone (Piriform Cortex, OrbitoFrontal cortex e AMYgdala), tra le quali si innescano i veri e propri legami di connettività, sono associate altrettante variabili endogene (

η

1

η

2

3

η

). In sostanza il data-set completo è costituito da un totale di quattro variabili ognuna interpretata come la “variabile osservata” di una regione fisica specifica.

In un secondo momento proveremo ad estendere il modello ed aggiungere la quinta regione dei circuiti olfattivi che abbiamo indicato in precedenza: l’Insula. Questa regione verrà rappresentata nel modello con la variabile endogena

η

4 ma, non

avendo la certezza delle relazioni di causalità tra questa regione e le altre (sia come presenza o meno delle connessioni sia come loro direzionalità), non possiamo dire con certezza quali coefficienti di connettività verranno utilizzati; per il momento

Figura 5.1: modello di connettività preso a riferimento per la generazione dei dati simulati; tale modello rispecchia le regioni anatomiche olfattive e i loro legami di causalità.

possiamo solamente affermare che la scelta avverrà sicuramente tra

b

42,

b

24,

b

43 o 34

b

.

Nel proseguo affrontiamo la messa a punto del modello generativo basandoci sul modello di connettività ridotto a quattro regioni, escludendo per il momento l’Insula, consapevoli che i ragionamenti che riportiamo sono facilmente estendibili al caso in cui siano presenti più regioni cerebrali.

V.2.2 Definizione dei Segnali e dei Parametri del modello

Come si osserva dall’espressione analitica del modello generativo (eq. 5.1), le tre componenti endogene sono variabili dipendenti e rappresentano l’uscita del sistema, mentre la variabile esogena

ξ

1 è l’unica variabile indipendente del sistema

e rappresenta il segnale di ingresso; questa è l’unica variabile che occorre definire esternamente. In altre parole i segnali caratterizzanti le regioni PC, OBF e AMY derivano direttamente dal modello di connettività e dall’input “generato” dalla regione OLB, mentre il segnale caratteristico di quest’ultima regione, nonostante sia anch’esso interpretato come variabile osservata, è definito esternamente e non dipende assolutamente dal modello implementato.

Il segnale di riferimento che associamo alla variabile

ξ

1 e che costituisce la forma

d’onda caratteristica dell’intero set di dati può essere scelto arbitrariamente, tuttavia, per avvicinare la simulazione il più possibile alle condizioni sperimentali reali, si è deciso di utilizzare un segnale che replicasse con buona approssimazione la risposta BOLD del cervello a seguito di un determinato stimolo.

Questo segnale è dato dalla convoluzione della risposta emodinamica cerebrale (HRF) con il segnale task che rappresenta la sequenza temporale dello stimolo cui è stato sottoposto l’ipotetico soggetto. In particolare la risposta emodinamica, secondo la modellizzazione di M. S. Cohen (1997) [33], è descritta attraverso una “funzione gamma” dalla forma:

( )

b _ct

h

t

=

t e

− _con

8 . 6

0 . 5 4 7

b

c

=

⎧

⎨

₌

⎩

Per quanto riguarda invece il task, esso è un onda quadra di periodo T =30s e

duty-cycle pari a 1

3 , con un ritardo iniziale di 20s, che ricalca esattamente il segnale

paradigma dei dati reali di cui presenteremo l’analisi nel capitolo successivo.

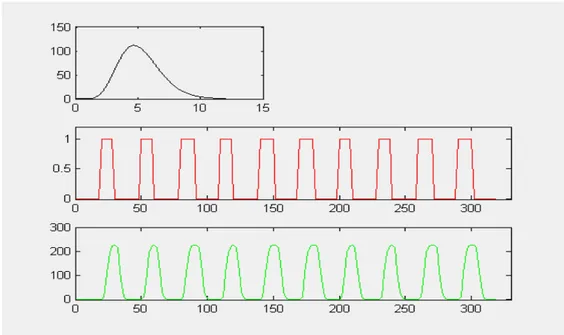
In figura 5.2 sono riportate le due forme d’onda appena descritte ed il risultato della loro convoluzione ovvero il segnale BOLD che prendiamo come forma d’onda di riferimento per la nostra simulazione.

Figura 5.2 : in nero la risposta emodinamica HRF; in

rosso il segnale task; in verde la risposta BOLD ricavata come convoluzione dei due segnali.

Dalla scelta del modello di connettività e dalla definizione delle variabili esogene ed endogene che abbiamo appena concluso, deriva automaticamente anche la caratterizzazione delle matrici di connessione

Β

e

Γ

per quanto riguarda quanti e quali coefficienti descrivono il modello. Nel nostro caso i parametri del modello, come indicato nel diagramma di figura 5.1, sono:

γ

1 appartenente alla matrice

Γ

,

21

b

e

b

₃₁ appartenenti alla matrice

Β

.

In fase di generazione tali coefficienti vengono fissati a priori, così da non avere alcun parametro incontrollato nel modello.

I loro valori sono generati in modo casuale attraverso una funzione random di cui si fissa il range di variazione e la funzione di distribuzione che descrive i valori estratti; la scelta è ricaduta su una funzione di distribuzione uniforme nel range di variazione [0.6 - 1.4], infatti questi sono indicativamente i valori tipici associati ai pesi delle connessioni che si trovano in letteratura [19]. Così riusciamo a creare sets di dati che ci danno la possibilità di simulare modelli di connettività del tutto indipendenti l’uno dall’altro per quanto riguarda il peso delle connessioni.

Per chiarezza riscriviamo il sistema di equazioni del modello in forma matriciale:

1 2 3

η

η

η

η

⎡ ⎤

⎢ ⎥

= ⎢ ⎥

⎢ ⎥

⎣ ⎦

[ ]

1

ξ

=

ξ

3 3

1 0 0

0 1 0

0 0 1

x

I

⎡

⎤

⎢

⎥

= ⎢

⎥

⎢

⎥

⎣

⎦

1 1 3 3 2 1 3 1

0

0

0

0

0

0

0

0

0

x

I

b

b

γ

η

ξ

−

⎡

⎛

⎞

⎤

⎡ ⎤

⎢

⎜

⎟

⎥

⎢ ⎥

=

_⎢

−

_⎜

_⎟

_⎥

⋅

_{⎢ ⎥}

⋅

⎜

⎟

⎢

_⎝

_⎠

⎥

⎢ ⎥

_{⎣ ⎦}

⎣

⎦

Anche se fino ad ora non è stato detto esplicitamente, tutte le variabili definite nel modello generativo sono grandezze continue, descritte da sets di campioni discreti che ne rappresentano le osservazioni nel tempo. Tali campioni possono essere visti come derivanti dal campionamento dei segnali temporali continui associati ad ogni variabile. Quindi per completare la definizione del modello generativo, è necessario andare a stabilire il numero di campioni temporali con cui si vuole descrivere i segnali associati alle singole variabili (

N

c).

I set di segnali reali che abbiamo a disposizione hanno una durata temporale di 320 secondi e sono campionati con TR=2s ovvero hanno una dimensione pari a 160 campioni (nel capitolo successivo affronteremo la loro descrizione con maggiore dettaglio) quindi, per avvicinarci il più possibile alle condizioni dei dati reali, si può prendere questo valore come riferimento e generare sets di dati che abbiano approssimativamente quella lunghezza.

Tuttavia è plausibile che tale parametro (

N

c) influenzi la bontà della stima dei

parametri del modello e quindi si potrebbe pensare di testare, in un secondo momento, sets di dati di lunghezze diverse, in modo da capire l’entità dell’errore introdotto da un numero di campioni limitato.

In forma matriciale, esplicitando i singoli campioni per ciascuna variabile, abbiamo:

1 1 1 1 1 2 2 2 2 2 3 3 3 3 3

(1)

(2)

(3)

(

)

(1)

(2)

(3)

(

)

(1)

(2)

(3)

(

)

c c c

N

N

N

η

η

η

η

η

η

η

η

η

η

η

η

η

η

η

⎡ ⎤ ⎡

⎤

⎢ ⎥ ⎢

₌

⎥

⎢ ⎥ ⎢

⎥

⎢ ⎥ ⎢

⎥

⎣ ⎦ ⎣

⎦

"

"

"

[ ] [

ξ

1

=

ξ

1

(1)

ξ

1

( 2 )

ξ

1

(3)

"

ξ

1

(

N

c

)

]

V.2.3 Inserimento del Rumore: Modello di Misura

L’ultimo aspetto da affrontare per concludere la questione della generazione dei dati è come introdurre la componente di rumore.

Le serie temporali costruite attraverso il modello generativo rappresentano una situazione di idealità nel senso che descrivono un modello di connettività estraneo a qualsiasi componente di rumore: le variabili ideali

η

e

ξ

sono costituite da segnali assolutamente ideali. Per rendere i dati simulati più vicini alla realtà, a tali segnali viene sommata una componente di rumore gaussiano a varianza nota, in modo da fissare il rapporto segnale-rumore (SNR) che caratterizza il set di dati.

Anche in questo caso ci sono due possibili strade: o sfruttare il termine

ζ

oppure attraverso l’impiego dei parametri ε e

δ

.

La prima soluzione è di più difficile interpretazione poiché il termine di rumore

ζ

appartiene a tutti gli effetti al modello generativo; se lo utilizzassimo si riproporrebbe il medesimo problema accennato sopra, cioè come capire a priori quale sarebbe lo scarto di informazione associato ad un particolare modello di connettività, e di conseguenza non saremmo in grado di controllare il rapporto SN del set di dati.

La seconda soluzione invece [28] è di immediata comprensione e più semplice da implementare infatti si tratta di sommare al set di dati prodotto con il modello generativo una componente di rumore gaussiano dalle caratteristiche note che ci permette di imporre l’ SNR desiderato.

In altre parole al modello generativo presentato precedentemente viene affiancato un cosiddetto Modello di Misura che descrive il legame tra le variabili ideali, implicate nella connettività, e le variabili misurate esternamente che costituiscono i veri e propri dati su cui applichiamo la stima del modello:

y

x

η

ε

ξ

δ

=

+

⎧

⎨

₌

₊

⎩

dove y ed x rappresentano dei vettori colonna, di dimensioni pari ai vettori

η

e

ξ

, contenenti gli insiemi delle variabili osservate endogene ed esogene rispettivamente, mentre i termini ε e

δ

rappresentano le componenti di rumore gaussiano a media nulla e varianza nota che si vanno a sommare ai segnali contenuti in

η

e

ξ

.

Le ipotesi che si fanno sono due: la prima è che in ogni istante la componente di rumore mantenga la stessa funzione di distribuzione e che sia indipendente dal rumore presente in altri istanti temporali; la seconda è che tale rumore mantenga le stesse caratteristiche, in termini di funzione distribuzione, media e varianza, in ogni istante della seria temporale. In altre parole si suppone che il rumore sia Indipendente Identicamente Distribuito (I.I.D.) e Omoschedastico.

I termini di rumore ε e

δ

, espressi come matrici, hanno la forma:

(

)

[

]

1 2 3

( )

0,

t 1..

( )

(1)

(2)

(

)

c i i i i c

t

N

N

t

N

ε

ε

_ε

_σ

ε

ε

ε

ε

ε

ε

ε

⎡ ⎤

_⎧

_∈

_{∀ =}

⎪

⎢ ⎥

=

_{⎢ ⎥}

_⎨

=

⎪⎩

⎢ ⎥

⎣ ⎦

"

Modello di Misura 5.2 )

[

]

(

)

1 1 1 1 1

(1)

(2)

(

)

( )

0,

t=1..

c c

N

t

N

_δ

N

δ δ

δ

δ

δ

δ

σ

=

=

∈

∀

"

Essi hanno le stesse caratteristiche e possono essere interpretati come realizzazioni (composte da

N

c campioni) di una stessa variabile aleatoria w a media nulla e

varianza 2 w

σ

(con

σ

w deviazione standard della variabile aleatoria). Ponendo

w ε δ

σ

=

σ

=

σ

_: 1 1 2 2 3 3 1 1

w

w

w

w

w

ε

ε

ε

ε

δ

δ

⎡

⎤

⎡

⎤

⎢

⎥

⎢

⎥

⎡ ⎤

_⎢

_⎥

_⎢

_⎥

=

_{⎢ ⎥}

=

=

⎢

⎥

⎢

⎥

⎣ ⎦

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎣

⎦

[

c

]

( )

( 0 ,

)

t = 1 . . N

(1)

( 2 )

(

)

w i i i i c

w t

N

w

w

w

w

N

σ

∈

∀

=

"

Per semplicità riscriviamo il sistema di equazioni raccogliendo le variabili osservate in un unico vettore colonna denominato v ; otteniamo:

1 1 1 2 2 2 3 3 3 4 1 4

v

y

w

v

y

w

v

s

w

v

y

w

v

x

w

⎡ ⎤

⎡

⎤ ⎡

⎤

⎢ ⎥

⎢

⎥ ⎢

⎥

⎢ ⎥

⎢

⎥ ⎢

⎥

=

= +

=

+

⎢ ⎥

⎢

⎥ ⎢

⎥

⎢ ⎥

⎢

⎥ ⎢

⎥

⎢ ⎥

⎢

⎥ ⎢

⎥

⎣ ⎦

⎣

⎦ ⎣

⎦

Dove le

v

i rappresentano le serie temporali (composte da

N

c campioni) associate

alle variabili osservate ovvero costituiscono il vero e proprio set di dati completo che simula la situazione di connettività effettiva secondo le caratteristiche che abbiamo imposto. Il termine s invece raccoglie le variabili ideali endogene ed esogene (y ed x).

Agendo sulla varianza del rumore è possibile imporre alle serie temporali di v il

valore dell’ SNR desiderato, secondo la relazione:

2 2

10 log

s

20 log

s dB w w

SNR

σ

σ

σ

σ

⎛

⎞

⎛

⎞

=

⋅

_⎜

_⎟

=

⋅

_⎜

_⎟

⎝

⎠

⎝

⎠

dove

σ

w2 e 2 s

σ

sono le varianze rispettivamente del rumore e dei segnali ideali che compongono il set di dati.

Una volta generato il set di segnali ideali (

η

e

ξ

) come descritto precedentemente, attraverso il modello generativo, calcoliamo la varianza di ogni sequenza temporale e ne scegliamo il massimo. Successivamente, fissato il valore massimo dell’ SNR, calcoliamo la varianza

σ

w2 (e quindi la deviazione standard

σ

w ) della

componente di rumore e generiamo i set (di lunghezza

N

c) di campioni di rumore

attraverso una funzione random le cui “estrazioni” abbiano una distribuzione

(

0, w

)

N

σ

.

Le equazioni che usiamo per questo calcolo sono:

m a x

2

2

m a x

|

1 0

2

|

1 0

d B

s

w

S N R

w

w

σ

σ

σ

σ

⎧

=

⎪⎪

⎨

⎪

=

⎪⎩

In questo modo riusciamo ad imporre al nostro set di dati il valore massimo del rapporto segnale-rumore e quindi in fase di interpretazione dei risultati della stima del modello siamo tutelati da eventuali errori dovuti ad una sottovalutazione dell’ SNR. Infatti nella valutazione di quanto il rumore influisca sulla bontà della stima dei parametri possiamo trarre le conclusioni opportune senza il rischio di associarle a dati che in realtà sono caratterizzati da un SNR più elevato di quello supposto, grazie al fatto che abbiamo la certezza che i dati analizzati hanno al più quel rapporto SN.

Oltre al valore massimo dell’ SNR caratterizzante i segnali, si potrebbe pensare di fissare anche quello minimo così da settare un range di variazione a piacere; in realtà studiando più accuratamente il problema si capisce che non è possibile vincolare contemporaneamente i due estremi di tale intervallo senza perdere, almeno in parte, la possibilità di generare coefficienti di connessione in modo casuale.

Per questo motivo, dovendo scegliere dove porre il vincolo di controllo dell’ SNR, abbiamo optato per fissare il limite superiore lasciando libero quello inferiore. L’unica cosa che possiamo fare per avere una valutazione indicativa di questo parametro è quella di calcolare il minimo valore possibile che esso può assumere, in relazione all’

S N R

m a x caratteristico del set di segnali.

Infatti questo valore dipende dall’entità dei coefficienti di connettività e quindi è sufficiente calcolare quale sia il valore minimo tra tutti i possibili rapporti tra coppie di segnali appartenenti allo stesso set di dati per ottenere la relazione tra l’

S N R

_{m a x} ed il minimo possibile

S N R

_{m i n} .

Il range di variazione dei coefficienti di connessione è

[

0.6 1.4÷

]

e poiché

1

0.71

0.6

1.4

=

>

, tenuto conto che nel nostro modello di connettività il numero

massimo di connessioni consecutive equiverse necessarie per collegare due zone è 2, il rapporto minimo tra due segnali appartenenti allo stesso set di dati vale

0.6 0.6

⋅

=

0.36

e quindi:

(

)

(

)

(

)

min max min max

min

20 log 0.36

min

8.87

dB dB dB dB

SNR

SNR

SNR

SNR

dB

= ⋅

+

=

−

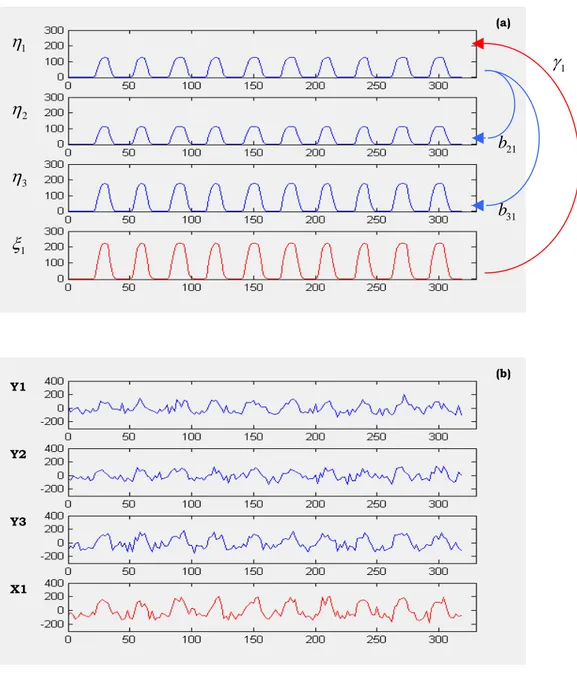
Di seguito (figura 5.3 a-b) riportiamo, a titolo esemplificativo, i grafici dei segnali costruiti attraverso il modello generativo e quelli finali, derivanti dal modello di misura, comprensivi della componente di rumore, in cui abbiamo imposto un

m a x

|

S N R

pari a 15 dB.

Le equazioni per la generazione dei vari set di dati sono implementate con il software Matlab che permette di eseguire con molta facilità il calcolo matriciale.

Y1 Y2 Y3 X1 1

γ

21

b

31

b

1

η

3

η

1

ξ

Figura 5.3 : (a) segnali ideali costruiti attraverso il modello generativo; (b) segnali reali ricavati dal modello di misura.

(a)

(b) 2

Abbiamo realizzato un semplice programma che, ripercorrendo i passi che sono stati appena descritti, riesce a fornire le matrici di connettività del modello e tutte le informazioni relative alla rumorosità dei dati, oltre a costruire la matrice dei dati simulati.

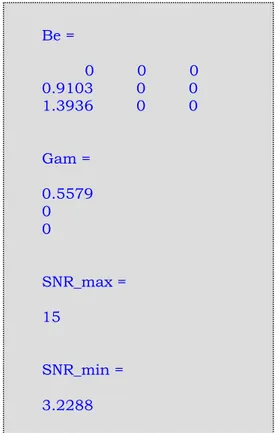
La figura 5.4 mostra come si presenta l’uscita del su detto programma (i dati riportati sono relativi all’esempio precedente).

Be = 0 0 0 0.9103 0 0 1.3936 0 0 Gam = 0.5579 0 0 SNR_max = 15 SNR_min = 3.2288

Figura 5.4 : dati relativi al modello di connettività simulato, ricavati attraverso il software Matlab. Il termine “Be” indica la matrice β, “Gam” il vettore colonna Γ ; Inoltre sono riportati l’SNR massimo (imposto esternamente) e quello minimo derivante dalle caratteristiche dei vari segnali.

V.3 Scelta del Modello di Stima

Riprendiamo il modello di stima completo su cui si basa il programma LISREL (vedi paragrafo IV.3); esso è costituito dalle equazioni:

y x

y

L

x

L

η

η

ξ ζ

η ε

ξ δ

⎧ = Β ⋅ + Γ ⋅ +

⎪ = ⋅ +

⎨

⎪ = ⋅ +

⎩

Tale modello prevede l’utilizzo delle variabili latenti (

η

e

ξ

) a cui sono legate le variabili osservate (

y

e x) attraverso le matrici

L

_x e

L

_y.

Per lo studio di modelli di connettività effettiva, come quello che stiamo affrontando, non è assolutamente necessario l’impiego delle variabili latenti poiché le connessioni tra le varie regioni cerebrali si attuano direttamente tra le variabili osservate.

Occorre quindi settare il programma in modo che implementi un path di connettività adatto a questo scopo; si possono seguire due strade:

1. Dichiarare un numero di variabili latenti pari al numero di variabili osservate ed imporre

L

y

=

I

3 3x

, 1

L

x

=

, associando così ad ogni singola

variabile latente un’unica variabile osservata con coefficiente di regressione pari all’unità. In questo caso la componente di rumore del sistema può essere

introdotta nel modello, alternativamente, o attraverso il termine

ζ

oppure attraverso i parametri

ε

e

δ

.

(

0

)

y

x

η

η

ξ

η

ξ

ε

δ

ζ

= Β ⋅ + Γ ⋅

⎧

⎪

= +

= +

=

⎨

+

⎪

⎩

(

)

(

)

0

0

y

x

ε

ζ

η

ξ

η

δ

η

ξ

⎧ = Β⋅

+

=

+

=

+ Γ⋅ +

⎪

=

⎨

⎪ =

⎩

In blu i vincoli da imporre ed in rosso i parametri che in ognuno dei modelli indicano la componente di rumore.

2. Dichiarare le variabili osservate del modello ma nessuna variabile latente lasciando che il software automaticamente associ ad ogni variabile osservata dichiarata una variabile latente fittizia (non è rappresentabile nel path delle connessioni come se fosse stata dichiarata esternamente) con cui implementare il modello di connettività. In questo caso l’unica possibilità per esplicitare la componente di rumore è attraverso il termine

ζ

, poiché i termini

ε

e

δ

non fanno più parte del modello, infatti l’equazione descrittiva si riduce a:

a)

[

y

= Β⋅ + Γ⋅ +

y

x

ζ

]

dove l’associazione delle variabili osservate alle corrispondenti variabili latenti fittizie avviene in modo implicito senza che tali relazioni entrino a far parte del modello stesso; in pratica il programma imposta autonomamente le relazioni:

L

y

=

I

3 3x

,

L

x

=

1

e

ε

=

0 ,

δ

=

0

senza che queste matrici siano

accessibili o modificabili.

Si osserva subito che il modello c) è del tutto equivalente al modello di stima b); l’unica differenza è che nel c) non sono presenti le variabili latenti, se non in modo fittizio, mentre nel b) (ciò vale anche per a)) esse costituiscono parte integrante del modello.

Dal punto di vista dell’impostazione teorica del SEM quest’ultimo è più fuorviante rispetto al primo poiché il legame di connettività non avviene direttamente tra le variabili osservate, ma attraverso delle variabili latenti che non rappresentano entità realmente esistenti.

Inoltre nei modelli a) e b), vista la presenza di un elevato numero di variabili (latenti e osservate sia endogene che esogene), occorre settare con molta attenzione i coefficienti delle varie matrici se si vuol costruire esattamente il modello di connettività desiderato. Al contrario, da questo punto di vista, il setting del modello c) è molto più facile e lascia margini di errore molto più ristretti; se la scelta si basasse su questo aspetto sarebbe indubbiamente preferibile agli altri due.

L’altro aspetto da tenere in considerazione è che il modello di connettività da noi

proposto è costituito da

N

y

=

3

variabili osservate endogene ed

N

x

=

1

variabili

osservate esogene; questo implica, secondo la relazione 4.4 riportata nel capitolo IV, che il numero massimo di parametri incogniti che può avere il sistema è:

(

) (

)

max ( . .)

1

_{4 5}

10

2

2

y x y x par lib

N

N

N

N

N

D

=

+

⋅

+

+

=

⋅

=

Perciò è necessario valutare preliminarmente il numero di incognite di ognuno dei tre modelli di stima, così da poter eliminare subito quelli che superano il numero massimo consentito di parametri liberi o comunque scegliere il più conveniente. Le matrici

Β

e

Γ

contengono rispettivamente 3 e 1 incognite cui si aggiungono, a seconda del caso, o quelle contenute nelle matrici di covarianza di

ε

e

δ

(

θ

_ε e

θ

_δ ) o quelle della matrice di covarianza di

ζ

(

Ψ

).

Come spiegato nel paragrafo precedente e nel capitolo IV, una delle ipotesi di lavoro del SEM è che la componente di rumore sia I.I.D.; questo implica che le matrici di covarianza

θ

ε ,

θ

δ e

Ψ

hanno la forma di matrici diagonali contenenti

solo i termini di varianza, quindi le incognite contenute in queste tre matrici sono rispettivamente pari a 3, 1 e 3.

Riassumendo il numero di incognite per i modelli a) e c) [=b)] e i loro corrispondenti parametri liberi sono rispettivamente:

var_ var_

8

7

a y x c y x

N

N

N

N

N

N

N

N

N

ε δ ζ

=

+

+

+

=

=

+

+

=

D D _ ( ) _ ( )

2

3

a p a r l i b c p a r l i b

N

N

° °

=

=

5.4 )

Ciò significa che, anche da questo punto di vista, il modello c) è preferibile ad a) poiché ci lascia a disposizione un parametro libero in più che può essere molto utile nel caso si voglia modificare il modello di connettività stimato aggiungendo nuovi elementi incogniti nella matrice

Β

. In conclusione abbiamo scelto come modello di stima il c) che ricalca esattamente l’impianto teorico proposto dal SEM e ci consente un buon margine dal punto di vista del numero di parametri liberi; indicheremo questo modello come Modello di stima standard (nell’equazione abbiamo indicato con il segno

ˆ

i parametri che saranno oggetto della stima di LISREL):

ˆ

ˆ

ˆ

y

= Β⋅ + Γ⋅ +

y

x

ζ

Esso è riferito al caso più generale possibile, ovvero un set di dati composto da quattro variabili osservate tutte affette da rumore, che ricalca esattamente il modello con cui andiamo a generare i segnali delle quattro regioni.

Questa precisazione si è resa necessaria poiché in seguito sorgerà la necessità di modificare la forma del modello (paragrafi V.4.2 e V.4.3), eliminando alcune variabili o caratterizzandole in modo diverso, e quindi sarebbero potute sorgere ambiguità; tuttavia anche in quel caso i modelli che implementeremo deriveranno dal modello standard appena presentato, infatti esso rappresenta il punto di riferimento per qualsiasi variante della stima.

Precisiamo inoltre che nella notazione adottata i termini

y

(3x1), x(1x1) e

ζ

(3x1)

rappresentano dei vettori contenenti rispettivamente le variabili (

y

1

y

2

y

3),

x

1 e i

termini di rumore (

ζ

1

ζ

2

ζ

3); l’equazione 5.5 e tutte le precedenti si riferiscono ad

un singolo istante temporale come si deduce dalle dimensioni dei vari termini,

Modello di Stima Standard

tuttavia con molta semplicità possono essere estese al caso di sequenze temporali di lunghezza a piacere come è stato illustrato nel paragrafo V.2 .

V.3.1 Considerazioni sul significato ed il contenuto del

termine di rumore

ζ

ˆ

Il passo successivo è quello di capire che significato assume il termine di rumore

_ζ

ˆ

in relazione al rumore presente sui dati; ricordiamo che questo è stato aggiunto ai dati ricavati dal modello generativo ideale sommando i contributi

ε

e

δ

.

Andando a confrontare il modello generativo e di misura con quello di stima, otteniamo l’espressione di

_ζ

ˆ

_{in funzione dei termini di rumore}

_ε

_e

_δ

_.

Dal modello di stima:

ˆ

ˆ

ˆ

y

= Β⋅ + Γ⋅ +

y

x

ζ

(

)

(

)

1 1

ˆ

ˆ

ˆ

ˆ

y

=

I

− Β

−

⋅ Γ ⋅ +

x

I

− Β

−

⋅

ζ

Dal modello generativo e di misura:

y

x

η

η

ξ

η

ε

ξ

δ

= Β

+ Γ

=

+

=

+

(

)

1

I

y

x

η

ξ

η

ε

ξ

δ

−

⎧ = −Β ⋅Γ

⎪⎪

_{= −}

⎨

⎪ = −

⎪⎩

Y dal Modello di Stima Standard 5.6 )

(

) (

)

1

(

)

y

− = −Β ⋅Γ⋅ −

ε

I

−

x

δ

(

)

(

)

1 1

y

=

I

− Β

−

⋅ Γ ⋅ −

x

I

− Β

−

⋅ Γ ⋅ +

δ ε

confrontando i due risultati otteniamo:

(

)

₁

( )

1

ˆ

I

−

δ ε

I

−

ζ

− −Β ⋅Γ⋅ + = −Β ⋅

Sotto l’ipotesi che i valori stimati delle matrici di connettività (

_Β

ˆ

_e

_Γ

ˆ

_{) coincidano}

con i loro valori reali (indicando tali matrici genericamente con

Β

e

Γ

) ricaviamo:

(

)

ˆ

_I

ζ

=

− Β ⋅ − Γ ⋅

ε

δ

Quest’espressione ci fa capire come il termine

_ζ

ˆ

_{racchiuda in se quella parte di}

informazione, contenuta nei vari segnali

y

i, che non rientra nei legami di

connettività presenti tra le varie regioni. Infatti nel nostro caso specifico, avendo generato i dati attraverso un modello che escludeva il termine

ζ

, lo scarto

Y dal Modello Generativo Termine di rumore del modello di Stima Standard 5.8 ) 5.7 )

d’informazione rispetto alla connettività portato dal set di segnali, è rappresentato dalle due componenti di rumore

ε

e

δ

, che effettivamente sono la “causa” del termine

_ζ

ˆ

_{del modello di stima come evidenzia la relazione sopra riportata. Se il set}

di dati simulato fosse stato privo di qualsiasi termine di rumore allora nel modello di stima avremmo trovato

_ζ

ˆ

₌

₀

_.

D’altra parte potremmo immaginare di aggiungere nel modello generativo un termine

ζ

che contenga, per ogni variabile

y

i del modello, l’insieme delle

componenti del segnale i-esimo estranee alle interazioni di causalità; in fase di stima lo ritroveremmo tale e quale contenuto in

_ζ

ˆ

_{, sommato alle componenti}

_ε

_e

_δ

_{, a}

dimostrazione del fatto che questo elemento raccoglie appunto tutta l’informazione che esubera dal modello di connettività.

Per verificare attraverso i dati la veridicità di queste considerazioni, in fase di generazione, avendo a disposizione tutte le informazioni sulle componenti

ε

e

δ

, abbiamo calcolato con il Matlab le sequenze associate a

ζ

, sfruttando l’espressione 5.8, e la sua matrice di covarianza; successivamente l’abbiamo confrontata con la

matrice

Ψ

ˆ

(

₌

_cov

( )

_ζ

ˆ

_{) risultante dalla stima di LISREL su quello stesso set di}

segnali.

Il risultato è stato che effettivamente le due matrici di covarianza sono uguali, a meno dell’errore commesso dal LISREL nella stima, a riconferma del fatto che il termine di rumore

ζ

assume effettivamente quel particolare significato (i risultati di queste simulazioni verranno riportati nel paragrafo successivo).

A questo proposito occorre precisare che la matrice

Ψ

, per come è stato costruito il set di dati simulati, non è assolutamente una matrice diagonale come si ipotizza nella modellizzazione del SEM, ma è una matrice simmetrica (per definizione di matrice di covarianza) in cui tutti i termini esterni alla diagonale sono non nulli a causa del fatto che i singoli “segnali” contenuti in

ζ

non sono tra loro incorrelati. In effetti, anche se le componenti di rumore

ε

e

δ

sono I.I.D.,

ζ

nasce dalla loro

combinazione lineare secondo i coefficienti

(

I− Β

)

e

Γ

e quindi è plausibile che si

perda l’incorrelazione tra i singoli

ζ

i.

Questo fatto è legato essenzialmente a come è stato costruito il set di dati simulati (modello generativo e successivamente modello di misura) ed è presumibile che tali condizioni non si ripetano nei dati reali; infatti in quel caso il rumore che affligge i singoli segnali non nasce da un modello di misura a se stante, esterno al modello di generazione, ma è insito all’interno del modello generativo stesso contenuto nel termine

ζ

, e le varie componenti di rumore mantengono, con buona approssimazione, l’indipendenza l’una dall’altra.

In conclusione, in tutti i modelli di stima utilizzati sui dati simulati, continueremo a ipotizzare la matrice di covarianza

Ψ

diagonale, come se il termine di rumore

ζ

fosse costituito da segnali incorrelati tra loro; questo non influenza minimamente la bontà della stima dei parametri del modello e oltretutto ci permette di avere a disposizione più parametri liberi. Semmai, operando sotto questa ipotesi, si tratterà di verificare a posteriori l’eventuale correlazione delle sequenze contenute nel termine

ζ

.

V.4 Simulazioni sul modello di connettività a quattro

regioni

In questo paragrafo vengono presentati i risultati della stima del modello di connettività prodotta da LISREL dandogli come ingresso i set di dati creati secondo il procedimento descritto nel paragrafo V.2 .

Oltre agli indici di bontà (

χ

2

, P-value e RMSEA) forniti automaticamente dal programma, presentiamo gli errori relativi dei parametri stimati rispetto ai loro valori reali che utilizzeremo come indici di valutazione della stima del modello.

In effetti la distribuzione di probabilità dei campioni così generati, come del resto sarà per i dati fMRI reali, non è affatto gaussiana come ipotizza il SEM ma dipende dalla forma d’onda associata ai segnali del modello (risposta BOLD).

E’ quindi prevedibile che in fase di stima i parametri stimati saranno afflitti da un errore causato dalla violazione di questa ipotesi (vedi paragrafo IV.2.3). Tale effetto va ad influenzare soprattutto i parametri di bontà della stima (

χ

2

, p-value e RMSEA), piuttosto che i coefficienti di connettività stimati, rendendoli inutilizzabili per la valutazione del modello.

Per avere a disposizione uno strumento di valutazione che sia indipendente da questo tipo di errore abbiamo pensato di utilizzare appunto l’errore relativo dei coefficienti stimati che costituisce un riferimento più significativo rispetto agli indici di bontà e ci permette di quantificare l’effettivo grado di approssimazione del modello stimato rispetto a quello reale.

V.4 .1 Modello di stima standard: influenza dell’ SNR e del

numero di campioni

Le prime stime che presentiamo sono state realizzate, utilizzando il modello standard descritto nel paragrafo precedente (eq. 5.4), con l’obiettivo primario di valutare come la bontà della stima sia influenzata dal rapporto SN dei dati e dalla lunghezza delle sequenze temporali analizzate.

Inoltre già questi primi risultati ci permettono anche di verificare da un lato l’effetto sulla stima della non gaussianità dei campioni e dall’altro il significato assunto dalla variabile

ζ

del modello, così da avere conferma delle assunzioni fatte durante lo studio dell’impianto teorico del SEM e del LISREL.

Per ciascun valore di

SN R

m ax (0, 5, 10 e 20 dB) e per ogni lunghezza delle

sequenze (120 (240s), 150 (300s) e 180 (360s) campioni) è stato creato, attraverso il Matlab, un gruppo di 30 sets di dati (per un totale di 12 gruppi); ogni set è stato

sottoposto al LISREL da cui abbiamo estratto i parametri di bontà e i valori stimati dei coefficienti di connettività e degli elementi della matrice di covarianza

Ψ

su cui abbiamo calcolato gli errori relativi rispetto ai loro valori reali.

Per completezza riportiamo la definizione dell’errore relativo, in riferimento ad una grandezza generica

x

di cui

ˆx

rappresenta la stima:

ˆ

r

x

x

x

−

Δ =

Per quanto riguarda il rumore, in fase di generazione, per ogni set di segnali è stato calcolato anche il valore minimo del rapporto Segnale-Rumore, così da poter stabilire con precisione il limite inferiore del range di variazione dell’ SNR per quel determinato gruppo di segnali ed averne una descrizione migliore possibile.

Questo varia a seconda della particolare combinazione dei pesi di connettività e come mostra l’equazione 5.3 è sicuramente compreso in un range di 8.87 dB al di sotto dell’

S N R

m a x , tuttavia vale la pena tenere in considerazione il suo valore

reale perché in genere questo è abbastanza al di sopra del suo limite inferiore e ci permette di capire l’effettivo range di variazione del rumore sui nostri dati. Così facendo si mette in evidenza il fatto che non ci sono sovrapposizioni tra gli intervalli di variazione dell’ SNR dei vari gruppi ed i risultati che presentiamo coprono il range tra 0 dB e 20 dB in modo abbastanza continuo ed omogeneo.

Nelle tabelle 5.1 (a-b) sono riportati, per ogni condizione sperimentale, i valori medi

dei parametri

χ

2

, P-value, RMSEA e degli errori

Δ

r , calcolati facendo la media sui

30 set di campioni appartenenti ad ogni gruppo.

SNRmax (dB) 0 dB 5 dB SNRmin (dB) -3.46 -3.67 -2.68 2.35 2.28 0.68 Nc 120 150 180 120 150 180 Gradi di Libertà 3 3 3 3 3 3 2

χ

28.17 35.16 55.63 46.28 61.54 69.12 P-value 0.00105 0.00006 0.00000 0.00000 0.00000 0.00000 RMSEA 0.257 0.263 0.307 0.342 0.359 0.341

( )

1 r

γ

Δ

0.57 0.65 0.59 0.32 0.30 0.33

( )

21 r

b

Δ

0.60 0.64 0.60 0.24 0.27 0.34

( )

31 r

b

Δ

0.56 0.58 0.59 0.25 0.29 0.34 0.19 0.34 0.29 0.20 0.15 0.20 0.35 0.31 0.29 0.05 0.03 0.15

( )

r

Δ Ψ

0.30 0.13 0.40 0.10 0.05 0.06 Tabella 5.1–a : Modello di stima Standard

SNRmax (dB) 10 dB 20 dB SNRmin (dB) 6.69 7.26 6.7 16.72 17.25 15.65 Nc 120 150 180 120 150 180 Gradi di Libertà 3 3 3 3 3 3 2

χ

65.89 82.48 90.25 89.95 125.24 122.46 P-value 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 RMSEA 0.418 0.429 0.404 0.479 0.520 0.469

( )

1 r

γ

Δ

0.05 0.15 0.10 0.02 0.01 0.02

( )

21 r

b

Δ

0.15 0.13 0.12 0.02 0.03 0.02

( )

31 r

b

Δ

0.17 0.13 0.11 0.02 0.03 0.03 0.17 0.10 0.04 0.02 0.01 0.01 0.05 0.02 0.02 0.01 0.01 0.02

( )

r

Δ Ψ

0.06 0.03 0.04 0.01 0.02 0.01

Innanzi tutto andiamo a valutare gli errori relativi dei coefficienti di connettività (

Δ

r

( )

γ

1 ,

Δ

r

( )

b

2 1 e

Δ

r

( )

b

3 1 ); anche se presentano valori abbastanza elevati è

evidente il netto abbassamento in funzione dell’aumento del rapporto segnale-rumore (figura 5.5): si passa da un errore medio (calcolato per ogni fascia di SNR

mediando i valori dell’errore di tutti i parametri ottenuti per i diversi

N

c) del 59.7%

della fascia

[

0dB

]

ad uno del 2.3% della fascia

[

20dB

]

con una diminuzione media

di circa quattro volte.

Al contrario, osservando il diagramma in figura 5.5 il loro andamento in funzione della lunghezza dei segnali, non si rilevano altrettanto forti variazioni ma semplici fluttuazioni che lasciano solo intravedere la tendenza dell’errore a diminuire in modo inversamente proporzionale rispetto ad

N

c stesso. Probabilmente i tre valori

assunti per

N

c sono troppo ravvicinati per poter mettere in evidenza questo

andamento.

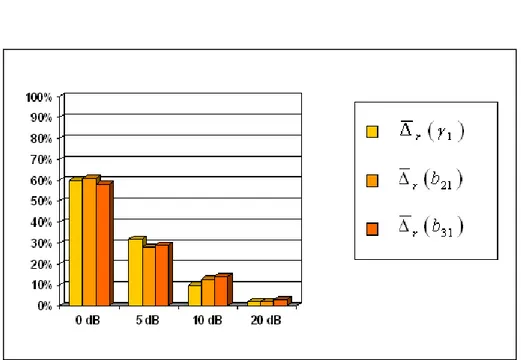
Figura 5.5 : risultati relativi al modello di stima standard. Errore relativo medio dei coefficienti di connettività stimati (

γ

₁,

b

₂₁ e

b

₃₁). I valori riportati nel diagramma sono le medie tra i valori assunti da ogni coefficiente nei tre casi a diversi Nc.

Per quanto riguarda i parametri di bontà del modello osserviamo che in generale i loro valori indicano una scarsa bontà del modello, infatti sia il

χ

2

che l’RMSEA assumono valori abbastanza alti ( 2

28.17

χ

≥

, RMSEA≥0.257) ed il P-value si

aggira quasi sempre su valori al di sotto di 5

10

− , tuttavia è ancora più significativo

osservare il loro andamento in funzione delle condizioni di rumore.

In controtendenza rispetto all’andamento dei valori dei vari

Δ

r , essi mostrano un

peggioramento all’aumentare di

N

c all’interno dello stesso range di SNR, e

soprattutto all’aumentare del l’ SNR a parità di

N

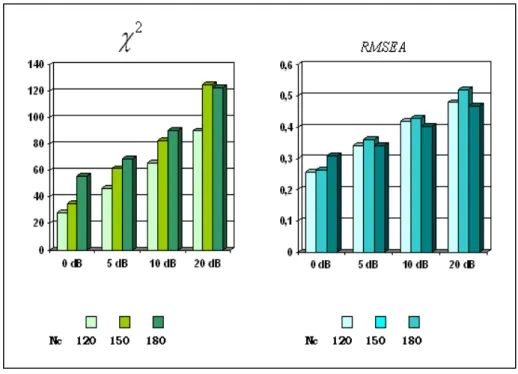
c (figura 5.6).

Figura 5.6 : modello di stima standard; parametri di bontà del modello (χ2

ed RMSEA) per ogni livello di SNR e per ogni lunghezza dei segnali (

N

_c); soprattutto all’aumentare del SNR si riscontra un forte aumento dei due parametri a indicazione che la bontà del modello sta peggiorando.

Ciò significa che secondo tali parametri, anche se la stima dei coefficienti di connettività migliora sensibilmente, i set di dati sottoposti al LISREL si stanno allontanando dalle condizioni ideali ipotizzate dal modello di stima. La spiegazione sta nel fatto che all’aumentare dell’ SNR i campioni del set sono sempre meno distribuiti in modo gaussiano poiché il rumore (gaussiano) che li affligge lascia sempre più spazio alla componente di segnale (tipo BOLD). In sostanza i parametri

2

χ

, P-value, RMSEA ci danno informazioni dal punto di vista delle caratteristiche statistiche dei dati ed evidenziano, già in questa prima simulazione, la scarsa aderenza dei nostri dati con le ipotesi poste dalla modellizzazione tipo SEM.

Questo ci porta a concludere che le stime estratte dalle successive simulazioni e soprattutto quelle che ricaveremo dall’analisi dei dati reali dovranno essere valutate non tanto alla luce dei parametri di bontà forniti dal LISREL, ma piuttosto in funzione dei risultati relativi al legame errore-rumore che riusciamo ad estrarre attraverso le simulazioni stesse.

Come ultimo punto osserviamo che l’errore relativo

Δ

r

( )

Ψ

, calcolato sugli

elementi della matrice

Ψ

, ci da conferma del corretto significato che abbiamo attribuito al termine di rumore

ζ

nel contesto del modello di stima (vedi paragrafo V.3.1).

Infatti tale parametro assume valori relativamente bassi rispetto sia alle condizioni sperimentali che agli altri errori riportati in tabella (riferiti ai coefficienti di connettività); inoltre mostra una chiara tendenza ad annullarsi all’aumentare del rapporto segnale rumore: passa da un valore massimo del 40% , ottenuto nel range di SNR

[

−2.68dB ÷0dB

]

, ad un minimo dell’ 1% ottenuto nella fascia più alta

[

≈

16

dB

÷

20

dB

]

. Per avere una visone d’insieme dell’andamento di questo parametro, in figura 5.7 sono riportate, per ogni valore di

N

c e per ogni classe di

Quindi effettivamente il termine di errore

_ζ

ˆ

_{raccoglie dentro di se lo scarto di}

informazione esterno al modello di connettività contenuto nel set di dati come espresso dall’equazione 5.8.

Potremmo pensare di sfruttare questa informazione per agevolare il LISREL nella stima dei parametri del modello sperando in una riduzione dell’errore relativo. L’idea è quella di fornire al software, oltre al set di dati simulati, anche i valori della matrice di covarianza

Ψ

, così da ridurre il numero di incognite del modello di stima da sei a tre (i soli coefficienti di connettività: Δr

( )

γ

1 , Δr

( )

b21 e Δr

( )

b31 ). A

questo scopo abbiamo ripetuto le stime sugli stessi sets di dati creati

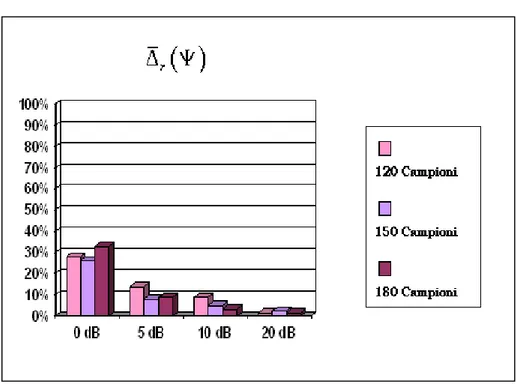
Figura 5.7 : risultati relativi al modello di stima standard. Errore relativo medio dei coefficienti della matrice di covarianza

Ψ

. I valori riportati nel diagramma sono, per ogni Nc, le medie tra gli elementi della matrice per ogni livello di SNR

precedentemente (divisi in 12 gruppi ciascuno contenente 30 sets) dichiarando stavolta anche i valori di

Ψ

. In questo modo è stato possibile confrontare i risultati ricavati precedentemente con quelli attuali e verificare eventuali cambiamenti. La conclusione è che non cambia assolutamente niente nella stima dei coefficienti di connettività, infatti si ottengono gli stessi valori, mentre i parametri di bontà, per altro relativamente significativi per il nostro scopo, aumentano moltissimo a causa del raddoppiato numero di gradi di libertà del modello (si passa da tre a sei). Quindi l’idea è da scartare perché non porta nessuna agevolazione; solamente nel caso in cui avessimo bisogno di un maggior numero di gradi di libertà, per assegnarli a nuove incognite del sistema come per esempio altri coefficienti di connettività, potremmo pensare di operare in questo modo.

Inoltre occorre tenere presente che nel caso di dati simulati è abbastanza facile calcolare il termine di rumore e la sua matrice di covarianza conoscendo a priori tutte le informazioni necessarie, nel caso invece di dati reali la cosa è più complicata perché è necessario valutare la componente di rumore di misura con metodi ad hoc che non sempre danno risultati accettabili.

V.4 .2 Modello di stima senza variabile esogena

Il punto chiave su cui si fondano le nostre simulazioni è l’aver ipotizzato l’esistenza di un modello di connettività composto da quattro regioni, dedicate allo svolgimento dell’attività olfattoria, di cui conosciamo i segnali legati alle loro attivazioni.

In particolare, in base agli studi sull’olfatto trovati in letteratura, abbiamo ipotizzato una struttura di connettività in cui il segnale nasce nel Bulbo Olfattivo per poi propagarsi alla Corteccia Orbitofrontale da cui si divide verso l’Amygdala e la Corteccia

Quindi il modello di stima e i sets di dati che abbiamo preso in considerazione fino ad ora sono costituiti da quattro variabili osservate: tre endogene (

y

1,

y

2 e

y

3),

associate alle ultime tre zone, ed una esogena (

x

1), relativa alla regione da cui nasce

lo stimolo.

In realtà, come approfondiremo meglio nel capitolo successivo, le regioni legate all’olfatto che siamo riusciti ad individuare con la fMRI sono la corteccia Piriforme, l’Amygdala, la corteccia Orbitofrontale e l’Insula; manca la regione del Bulbo Olfattivo che è situata in un punto molto particolare, in prossimità delle interfacce aria-osso osso-tessuto_cerebrale, e che è praticamente impossibile da individuare attraverso la risonanza magnetica.

Questo ci pone di fronte un nuovo problema da affrontare: come impostare il modello di stima tenendo in considerazione che non si hanno informazioni riguardo la regione del bulbo olfattivo e valutare la bontà dei risultati ottenuti attraverso il LISREL riguardo i coefficienti di connettività tra le regioni rimaste in gioco.

Le strade che si aprono sono due: la prima è quella di eliminare del tutto la regione del Bulbo e la variabile osservata ad esso associato (

x

1) operando con un set di dati

composto dalle sole variabili endogene (

y

1,

y

2 e

y

3); la seconda è quella di lavorare

con tutte e quattro le variabili osservate associando alla variabile esogena un segnale ideale (tipo BOLD) che simuli la presenza della regione mancante.

In questo paragrafo presentiamo i risultati ottenuti con la prima soluzione cercando di capire se con questo metodo riusciamo ad ottenere ugualmente una stima accettabile dei parametri di connettività anche lavorando con un modello di stima ridotto rispetto a quello con cui abbiamo generato i dati.

In altre parole, mantenendo lo stesso modello generativo basato sugli stessi legami di connettività e quindi generando sets di dati (

y

1,

y

2,

y

3 e

x

1) con le stesse

caratteristiche di causalità, vogliamo capire quali risultati ci dà il LISREL se lo facciamo lavorare su un set di dati composto dalle sole tre variabili endogene

y

1,

y

2

ˆ

ˆ

y

= Β⋅ +

y

ζ

Avendo eliminato la variabile esogena dal modello di stima, viene a mancare una parte dell’informazione che contribuisce a “spiegare” i segnali associati alle variabili

y

, in particolare per la variabile

y

₁ non è più esplicitato il legame con la variabile

1

x

e quindi non possiamo prevedere se la stima dei coefficienti rimarrà inalterata o

subirà variazioni.

Quello che sicuramente possiamo aspettarci è che cambi il contenuto del termine di rumore

_ζ

ˆ

_{, infatti ricavando la}

_y

_{dal nuovo modello di stima (equazione 5.10):}

(

)

1

ˆ

ˆ

y

=

I

− Β

−

⋅

ζ

e confrontandola con l’espressione 5.7 (il procedimento è il solito esposto nel paragrafo V.3.1 ) otteniamo:

(

)

(

)

ˆ

_I

_x

ζ

=

− Β ⋅ + Γ ⋅

ε

−

δ

Modello di Stima senza Variabile Esogena 5.9 ) Termine di rumore del modello di stima senza variabile esogena 5.11 ) Y dal Modello di Stima senza variabile esogena 5.10 )

La simulazione è stata organizzata come la precedente (paragrafo V.4.1), generando sets di dati caratterizzati da valori crescenti dell’

S N R

m ax suddivisi in quattro fasce

(0dB, 5 dB, 10 dB e 20 dB). Per ognuna di queste sono stati creati 30 sets di dati con cui abbiamo potuto calcolare le medie dei vari indici (

χ

2

, RMSEA, p-value, Δr

( )

b21

e Δr

( )

b31 ) . L’unica differenza è che stavolta non abbiamo diversificato i dati per la

lunghezza dei segnali ma abbiamo scelto un unico valore di

N

c (150 campioni) visto

che non ci sono differenze così marcate variando di poco questo parametro.

Le conclusioni tratte dalla simulazione sul modello di stima standard sono confermate anche in questo caso; infatti sono evidenti sia la forte diminuzione dell’errore relativo che l’aumento dei fattori di bontà (

χ

2

, RMSEA) al crescere del rapporto segnale-rumore.

I risultati sono riportati nella tabella 5.2 (in cui abbiamo omesso i valori relativi ai parametri di bontà (

χ

2

, RMSEA, p-value) perché come abbiamo già verificato nella simulazione precedente sono poco significativi) e visualizzati nel diagramma di figura 5.8 in cui si ha la percezione immediata dell’andamento dei vari parametri.

SNRmax

( )

21 r

b

Δ

Δ

_r

( )

b

₃₁

Δ Ψ

_r

( )

0 dB 0.59 0.64 <10-4 _{0.28 0.26} 5 dB 0.34 0.36 <10-4 _{0.22 0.21} 10 dB 0.14 0.15 <10-4 0.07 0.09 20 dB 0.02 0.02 <10-4 _{0.01 0.03}

Da notare che i valori degli errori relativi si aggirano sullo stesso ordine di grandezza di quelli trovati per il modello di stima standard; l’unico parametro che si discosta sensibilmente dalla media è l’errore relativo del primo elemento di

_Ψ

ˆ

_{, che}

già a partire da valori di SNR piccoli si aggira su valori marcatamente inferiori rispetto agli altri ( 4

10

− ). Ciò significa che l’elemento Ψˆ₁₁ della matrice di covarianza

dell’errore

_ζ

ˆ

_{è stimato praticamente in modo perfetto in ogni condizione di}

rumore.

La variabile esogena è assente dal modello e lo stimatore riesce comunque ad estrapolare in modo esatto la componente di rumore presente nella serie temporale associata ad

y

1, senza aver bisogno di ulteriori informazioni riguardanti la sorgente

da cui si genera il segnale di attivazione.

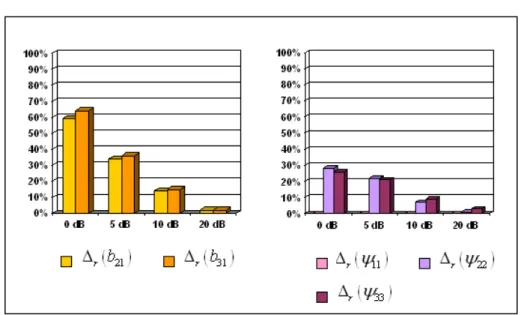
Figura 5. 8 : risultati relativi al modello di stima senza variabile esogena. a) errore relativo degli elementi della matrice di connettività B; b) errore relativo degli elementi della matrice di covarianza

Ψ

. I valori riportati nelle due figure sono le medie degli errori calcolate su 30 set di dati.

E’ possibile dare una giustificazione a questo fatto se riprendiamo l’equazione 5.10, che esprime il legame tra le variabili

y

e la componente di rumore

ζ

, e

esplicitiamo il termine

y

1; il risultato è semplicemente una uguaglianza y1=

ζ

ˆ1, il

che spiega come sia possibile una valutazione di

ζ

1 così precisa: tutta la sua

informazione corrisponde al segnale stesso che noi forniamo allo stimatore come variabile

y

1.

Infatti ricordiamo che il termine

ζ

ha un duplice significato: da un lato rappresenta la componente di informazione esterna alle relazioni di connettività legate alla i-esima regione, dall’altro può essere interpretata come la fonte da cui traggono origine i segnali osservati, secondo il modello previsto dal SEM. In questo caso, poiché la variabile

y

1 non riceve alcun contributo informativo dalle altre regioni

implicate nel modello, è chiaro perché

ζ

contenga esattamente l’intero segnale.

V.4 .3 Modello di stima con variabile esogena ideale

La variante del modello di stima che andiamo a presentare adesso ha la stessa struttura del modello di stima standard, sia per quanto riguarda il numero e la tipologia delle variabili (tre variabili endogene

y

1,

y

2 ed

y

3 e una esogena

x

1) sia

per i legami di connettività imposti (

γ

1,

b

21 e

b

31).

L’unica differenza sta nel fatto che alle tre variabili endogene, come succedeva nel modello standard, sono associati i segnali veri e propri prodotti dal modello generativo, invece alla variabile esogena è associato un segnale ideale, privo di rumore, che rappresenta la sequenza temporale caratteristica del set di dati.

In altre parole alle variabili

y

è attribuito il set di segnali legato alle vere e proprie

attivazioni presenti nelle corrispondenti regioni cerebrali (in questa fase tale set è composto da dati simulati invece durate l’analisi dei dati reali sarà dato dai segnali veri e propri estratti attraverso la fMRI), mentre alla variabile x è associato un

segnale che dovrebbe rappresentare la sequenza temporale ideale generata dall’attività neurale indotta dallo stimolo olfattivo.

La forma d’onda che abbiamo utilizzato come sorgente nella generazione dei dati è la risposta BOLD (vedi paragrafo V.5.2) ed è proprio questo il segnale ideale che associamo alla variabile esogena del modello di stima.

Entrando negli aspetti pratici della realizzazione del set di dati che vogliamo fornire al LISREL, occorre precisare che lo strumento che utiliziamo è sempre il modello generativo descrittivo precedentemente (equazione 5.1), con l’unica differenza che sulla sequenza temporale che attribuiamo alla variabile

x

1 non sommiamo la

componente di rumore

δ

; quindi quello che in realtà andiamo a modificare è il così detto modello di misura:

y

x

η

ε

ξ

=

+

⎧

⎨

₌

⎩

Qui la scelta del tipo di segnale da assegnare a

x

1 sembra scontata, infatti sappiamo

con esattezza qual’è la forma d’onda che caratterizza l’intero set di dati, ma non sarebbe altrettanto banale se lavorassimo sui dati reali; in quel caso non avremmo nessuna certezza e dovremmo scegliere il segnale che meglio approssima l’attività cerebrale indotta da un certo task di stimolazione.

In effetti questo segnale è proprio la risposta BOLD e del resto è lo stesso che abbiamo usato nella realizzazione del modello generativo proprio con lo scopo di avvicinare il più possibile i dati simulati alla realtà. Quindi non dobbiamo stupirci se per questo particolare modello di stima associamo alla

x

1 lo stesso segnale sia in

Modello di Misura modificato