Capitolo 4
Regole di determinazione del massimo e
del minimo in una espressione regolare
In questo capitolo mostriamo un modo alternativo di rappresentare una generica espressione regolare r appartenente ad un insieme R di espressioni regolari. Infatti, l’idea che viene proposta è quella di approssimare l’espressione r con uno o più intervalli disgiunti di stringhe (I1, I2, …, In), dove con il termine
intervallo indichiamo un insieme di stringhe lessicograficamente ordinato e delimitato da due stringhe (gli estremi dell’intervallo), in modo tale che il linguaggio, definito da r, è contenuto nell’unione disgiunta di tali intervalli, ovvero L(r) ⊆ ∪1≤ i ≤n Ii. Di conseguenza, l’insieme R di espressioni regolari viene
rappresentato con un insieme IR di intervalli di stringhe.
La struttura dati indice che meglio si presta alla memorizzazione dell’insieme IR è proprio l’Interval Tree. Mostreremo infatti quanto sia utile, sia in termini di
di intervalli, anche se, come già detto precedentemente, tali intervalli rappresentano insiemi di stringhe e non di interi.
Una volta chiarita la nozione di intervallo, nel corso del capitolo, verranno presentate delle regole per determinare gli estremi dell’intervallo (o degli intervalli) con il quale rappresentiamo una generica espressione r.
4.1 Espressioni regolari ed intervalli di stringhe
Sappiamo che un’espressione regolare definisce un insieme implicito di stringhe. Abbiamo visto che tale insieme, chiamato L(r), contiene tutte le possibili stringhe accettate dall’automa M associato ad r. L’idea di rappresentare un’espressione regolare attraverso un intervallo o l’unione disgiunta di più intervalli è: data una generica espressione r, appartenente ad un insieme R di espressioni, individuiamo la stringa lessicograficamente più piccola e la stringa lessicograficamente più grande (secondo l’ordinamento L) entrambe accettate
dal linguaggio L(r) definito da r. Tali stringhe rappresentano rispettivamente l’estremo sinistro e l’estremo destro dell’intervallo di stringhe con cui rappresentiamo r.
Approssimare un’espressione r con un intervallo di stringhe, delimitato inferiormente dalla stringa lessicograficamente più piccola di L(r) e superiormente dalla stringa lessicograficamente più grande di L(r), dovrebbe assicurare che tutte le stringhe appartenenti al linguaggio definito da r ricadano nell’intervallo. Ovviamente, tale intervallo non solo conterrà le stringhe di L(r), ma anche stringhe (“falsi match”) che non fanno parte del linguaggio definito dall’espressione considerata.
Il problema di stabilire il grado di approssimazione di una espressione con un intervallo di stringhe e l’algoritmo utilizzato per stabilire gli estremi degli intervalli sono rimandati rispettivamente alle sezioni 4.3 e 4.4 del presente capitolo. Ora abbiamo bisogno di spiegare come memorizzare in modo efficiente un’insieme IR di intervalli rappresentate l’insieme di espressioni R.
4.2 Interval Tree per intervalli di stringhe
In questo paragrafo mostriamo come memorizzare un insieme IR di intervalli
di stringhe in un Interval Tree e come ottenere, data una query string qx in
ingresso, tutti gli intervalli, memorizzati all’interno dell’indice, che la contengono.
Consideriamo IR = {[x1:x1], [x2:x2], …, [xn:xn]} un insieme di intervalli finiti
di stringhe, rappresentante un’insieme R di espressioni regolari. In generale, gli estremi xi e xi (1≤ i ≤n) di un intervallo, appartenente all’insieme IR,
rappresentano rispettivamente la stringa minima e la stringa massima del linguaggio L(r) definito da una generica espressione r ∈ R. Indichiamo con xmid la
stringa mediana dei 2n estremi che delimitano gli intervalli contenuti nell’insieme IR. In questo modo, al più la metà degli estremi, appartenenti agli
intervalli in IR, potrà giacere alla sinistra di xmid e al più l’altra metà potrà giacere
alla destra di xmid. Se qx giace alla sinistra di xmid allora gli intervalli collocati
completamente alla destra di xmid , ovviamente, non contengono qx.
Costruiamo un albero binario basato su questa idea. Memorizziamo nel sottoalbero destro dell’intero albero l’insieme Iright degli intervalli collocati
completamente alla destra di xmid e nel sottoalbero sinistro l’insieme Ileft di
intervalli che sono collocati completamente alla sinistra di xmid. Tali sottoalberi
vengono costruiti ricorsivamente allo stesso modo. Ma a questo punto si presenta un problema: come memorizzare gli intervalli che contengono proprio la stringa xmid? Una possibile soluzione sarebbe quella di memorizzare tali intervalli in
entrambi i sottoalberi, ma si potrebbe presentare ricorsivamente la stessa situazione anche per i figli di un generico nodo. Infatti, un intervallo potrebbe essere memorizzato più volte, con conseguente continuo ingrandimento della struttura.
Per evitare la proliferazione degli intervalli possiamo risolvere il problema accennato nel seguente modo: memorizziamo l’insieme IRmid, di intervalli
contenenti xmid , in una struttura separata e associamo tale struttura alla radice del
nostro albero, proprio come mostrato in fig. 4.1.
Sappiamo che tutti gli intervalli in IRmid contengono la stringa xmid.
Supponiamo, per esempio, di considerare qx collocata alla sinistra di xmid , come
mostrato in fig. 4.2. IRmid Ileft Iright xmid Iright Ileft IRmid
Fig.4.1 Classificazione degli intervalli rispetto a xmid
qx xmid
In questo caso sappiamo già che l’estremo destro di tutti gli intervalli in IRmid
giace alla destra di qx. Di conseguenza, sono importanti solo gli estremi sinistri
degli intervalli, per cui si può dire che: qx è contenuta in un intervallo [xj : xj] se e
solamente se xj ≤L qx. Se memorizziamo gli intervalli in una lista ordinata per
estremi sinistri crescenti, allora qx può essere contenuta in un intervallo se e solo
se è contenuta in tutti i suoi predecessori presenti nella lista. In poche parole, possiamo semplicemente muoverci lungo la lista ordinata riportando tutti gli intervalli che contengono qx, fino a quando non incontriamo un intervallo che
non contiene qx. Nel momento in cui incontriamo un intervallo che non contiene
qx ci fermiamo, poiché nessuno degli intervalli rimanenti può contenere qx.
Ovviamente, si verifica una situazione simile a quella appena descritta anche nel caso in cui qx si trova a destra di xmid. L’unica differenza è che in questo caso
ci muoviamo lungo la lista ordinata per estremi destri decrescenti. Nel caso in cui si verifica che qx =L xmid , allora possiamo riportare tutti gli intervalli contenuti in
IRmid .
Diamo ora una descrizione succinta della struttura dati che memorizza l’insieme IR:
• se IR = ∅ allora l’Interval Tree è una foglia;
• altrimenti, indichiamo con xmid la stringa mediana degli estremi degli
intervalli. Sia
Ileft := {[ xj : xj] ∈ IR : xj <L xmid},
Imid := {[ xj : xj] ∈ IR : xj≤L xmid≤ L xj},
Iright := {[ xj : xj] ∈ IR : xmid <L xj}.
L’Interval Tree consiste di un nodo radice V che memorizza xmid. Inoltre si
ha che:
• l’insieme IRmid è memorizzato due volte; una prima volta in una lista
Lleft(V), ordinata per estremi sinistri degli intervalli, una seconda volta
in una lista Lright(V), ordinata per estremi destri degli intervalli,
• il sottoalbero destro di V è un interval tree per l’insieme Iright.
Fatte le dovute osservazioni sulla struttura dell’interval tree, rimane da mostrare l’uso di tale indice per recuperare gli intervalli contenenti la query string qx. L’algoritmo adottato è il seguente:
Algoritmo QUERYINTERVALTREE(V, qx )
Input. La radice V di un interval tree e una query string qx.
Output. Tutti gli intervalli che contengono qx.
1. if V non è una foglia
2. then if qx <L xmid(V)
3. then Ci muoviamo lungo la lista Lleft(V),
e iniziamo dall’intervallo con estremo più a sinistra, riportando tutti gli
intervalli contenenti qx. Ci si ferma
quando si trova un intervallo che non contiene qx.
4. QUERYINTERVALTREE(lc(V), qx )
5. else Ci muoviamo lungo la lista Lright(V),
e iniziamo dall’intervallo con estremo più a destra, riportando tutti gli
intervalli contenenti qx. Ci si ferma
quando si trova un intervallo che non contiene qx.
6. QUERYINTERVALTREE(rc(V), qx )
Analizzare la complessità temporale dell’algoritmo non è complicato. Qualunque nodo v visitiamo, il tempo speso è pari a O(1+kv), dove kv rappresenta
il numero di intervalli restituiti al nodo v. La somma dei termini kv, sui nodi
visitati, è pari a k. Inoltre, visitiamo al più un nodo a qualsiasi profondità dell’albero. La profondità dell’interval tree è O(log n), per cui la complessità risultante è O(|qx| log n+ k |qx|), dove qx è composta da |qx| caratteri.
In realtà, utilizzando la tecnica generale presentata in [11,12], è possibile ottenere, come complessità dell’algoritmo di ricerca, un tempo pari a O(log n + k +|qx|) con qx composta da |qx| caratteri (invece di una complessità pari a O( |qx|
log n + k |qx| )).
4.3 Nozione di densità di una espressione regolare
Una generica espressione regolare r può essere approssimata con uno o più intervalli disgiunti di stringhe, dove il generico intervallo è delimitato inferiormente da una stringa lessicograficamente più piccola e superiormente da una stringa lessicograficamente più grande.
La scelta di queste due stringhe, che rappresentano rispettivamente l’estremo sinistro e l’estremo destro, come delimitatori dell’intervallo assicura che l’insieme L(r) ⊆ ∪1≤ i ≤n Ii, nel caso in cui l’espressione venga approssimata con
l’unione di n intervalli disgiunti (I1, I2, …, In), oppure L(r) ⊆ I, nel caso in cui
l’espressione venga approssimata con un singolo intervallo (I).
La rappresentazione di un’espressione r attraverso un intervallo (o più intervalli) di stringhe comporta, inevitabilmente, l’introduzione di un errore, poiché, nell’intervallo che si costruisce, non vengono incluse solo le stringhe appartenenti ad L(r), ma anche altre stringhe (maggiori dell’estremo sinistro dell’intervallo e minori dell’estremo destro dell’intervallo) che non fanno parte dell’insieme L(r), ovvero non soddisfano l’espressione r. Tali stringhe sono individuate con il nome di falsi positivi o falsi “ match”.
Al fine di stabilire l’entità dell’errore indotto da questo tipo di rappresentazione, introduciamo la nozione di densità di un’espressione regolare r espressa dal rapporto
dove il numeratore, |L(r)|, esprime una misura (o dimensione) del linguaggio definito da r e il denominatore, | ∪1≤ i ≤n Ii |, esprime una misura dell’insieme
∪1≤ i ≤n Ii.
In realtà, se l’espressione è approssimata con un unico intervallo I, il denominatore esprime la misura dell’insieme I, ovvero al denominatore compare la quantità | I |.
Essendo l’insieme L(r) contenuto nel generico intervallo I = [x:x ] (o nell’unione degli intervalli disgiunti I1, I2, …, In), che costruiamo per
rappresentare r, si ha che |L(r)| ≤ |I|. Quindi come si può ben intuire, se la
quantità |L(r)| = |I| allora il rapporto d(r) = 1. Questo vuol dire che nell’intervallo I non sono inclusi falsi positivi, per cui l’espressione r viene approssimata in modo esatto attraverso l’intervallo.
Il caso appena esposto è un caso ottimale poiché in realtà il valore del denominatore è sempre più alto del valore del numeratore. Naturalmente più il rapporto densità tende a 1, ovvero d(r) 1, e migliore è la rappresentazione dell’espressione r attraverso la tecnica degli intervalli di stringhe.
Per determinare il valore numerico delle quantità coinvolte nel rapporto (1), possiamo utilizzare le misure esposte nel capitolo 2, che sono state studiate non solo per stabilire la taglia di un linguaggio regolare (finito o infinito), ma anche per stabilire la dimensione di altri tipi di insiemi di stringhe. Infatti, possono essere facilmente applicate al caso degli intervalli di stringhe.
Per quanto riguarda l’applicazione della misura Max-Count ad un generico intervallo di stringhe, possiamo dire che per stabilire |[x : x ]|, dove [x : x ]
|L(r)| d(r) =
| ∪1≤ i ≤n Ii |
rappresenta l’intervallo di stringhe delimitato inferiormente dalla stringa x e superiormente dalla stringa x , contiamo tutte le stringhe, appartenenti all’intervallo, di lunghezza s, per 1≤ s ≤ , dove il parametro intero rappresenta
la lunghezza massima di una stringa appartenente all’intervallo preso in considerazione. Chiaramente, più grande risulta e maggiori saranno l’efficienza e la precisione con cui la misura Max-Count riflette la taglia dell’insieme [x : x ]. Ad esempio, un possibile valore da assegnare a sarebbe quello relativo alla lunghezza della query string qx in ingresso alla struttura dati Interval Tree.
Invece, per quanto riguarda l’applicazione della misura “Rate-of-Growth” all’intervallo di stringhe [x : x ], possiamo considerare il rapporto (1) del capitolo 2. Infatti, possiamo stabilire |[x : x ]| in modo simile a ciò che è stato fatto per i linguaggi, solo che al numeratore del rapporto (1) poniamo il conteggio di tutte le stringhe di lunghezza s, per ≤ s ≤ + -1, e al denominatore poniamo il
conteggio di tutte le stringhe di lunghezza s, per + ≤ s ≤ + 2( )–1. I
parametri e rappresentano rispettivamente la lunghezza che denota l’inizio della prima finestra e la grandezza della finestra.
Per quanto riguarda la misura MDL, possiamo dire che il generico intervallo che approssima r è rappresentato da un automa M parzialmente completo, per cui è possibile dare una stima della dimensione di I generando prima un campione casuale di stringhe c, appartenente al linguaggio definito dall’automa M (L(M)), e poi calcolando per ogni stringa w ∈ c il costo di decodifica MDL(M, w). Il valore
MDL(M, w) è calcolato nel seguente modo: consideriamo w della forma w = w1.
w2.…. wn ∈ L(M) e la sequenza s0, s1, s2,…, sn l’unica sequenza di stati in M
visitati dalla stringa w. Il valore MDL(M, w) viene calcolato effettuando la sommatoria del numero di bit richiesti per specificare la transizione fuori dallo stato si, per 1≤ i ≤ n. Ottenuto il valore MDL(M, w) si calcola il rapporto tra
MDL(M, w) e la lunghezza di w (|w|) e questo lo si fa per ogni stringa w ∈ c.
Infine, si moltiplica il valore ottenuto per l’inverso della cardinalità del campione c (|c|), come mostrato nell’equazione (2) della sezione 2.5.
4.4 Nozione di stringa maggiorante e minorante di un
insieme L(r)
Consideriamo un’espressione regolare r e il linguaggio L(r) da essa definito. Sappiamo che l’insieme L(r) è un sottoinsieme dell’insieme *, dove * è l’insieme di tutte le parole definite sull’alfabeto , quindi L(r) ⊆ *.
Prima di enunciare le regole utilizzate per determinare gli estremi di un intervallo con cui rappresentiamo r, conviene dare alcune definizioni che ci aiuteranno a comprendere come fare ad individuare le stringhe che delimitano l’intervallo, ovvero la stringa lessicograficamente più piccola (estremo sinistro) e la stringa lessicograficamente più grande (estremo destro) del linguaggio L(r).
Definizione 4.1 Sia r un’espressione regolare e sia L(r)⊆ * il linguaggio da essa definito. Diciamo che l’insieme di stringhe L(r) è limitato superiormente se esiste una stringa s∈ * tale che p ≤L s per ogni stringa p ∈ L(r). La stringa s si dice
maggiorante dell’insieme L(r).
Definizione 4.2 Sia r un’espressione regolare e sia L(r)⊆ * il linguaggio da essa definito. Diciamo che l’insieme di stringhe L(r) è limitato inferiormente se esiste una stringa s∈ * tale che s ≤L p per ogni stringa p ∈ L(r). La stringa s si dice
minorante dell’insieme L(r).
Definizione 4.3 Sia r un’espressione regolare e sia L(r)⊆ * il linguaggio da essa definito. Diciamo che l’insieme di stringhe L(r) è limitato se è sia limitato superiormente sia limitato inferiormente.
E’ chiaro che se l’insieme L(r) è limitato superiormente e la stringa s è un maggiorante di L(r), allora ogni stringa x∈ *, tale che s ≤L x, è ancora un
maggiorante di L(r); analogamente, se L(r) è limitato inferiormente e la stringa s è un minorante di L(r), allora ogni stringa x ∈ *, tale che x ≤L s , è ancora un
minorante di L(r).
Chiariamo questi concetti appena esposti applicando le definizioni date ad alcuni esempi di espressioni regolari.
Esempio 4.1 Supponiamo di avere un alfabeto con i seguenti simboli = {a, b,
c} e consideriamo la semplice espressione regolare r = (a | b)(c).
L’automa associato ad r è esposto in fig.4.4. L’insieme L(r) è costituito dalle stringhe {ab, ac}, dove la stringa ‘ab’ è un minorante di L(r) (infatti si ha che ‘ab’ ≤L ‘ac’ ) e la stringa ‘ac’ ne è un maggiorante; in effetti, l’insieme dei
minoranti è costituito anche da tutte quelle stringhe appartenenti a * che sono
più piccole, secondo l’ordinamento ≤L , della stringa ‘ab’ e tra queste è compresa
anche la stringa vuota ε che, secondo l’ordinamento ≤L , è la più piccola di tutte.
La stessa cosa accade per l’insieme dei maggioranti che è costituito da tutte quelle stringhe appartenenti a * che sono più grandi, secondo l’ordinamento ≤L,
della stringa ‘ac’.
Esempio 4.2 Supponiamo di avere un alfabeto con i seguenti simboli = {b, c,
d} e consideriamo l’espressione regolare r = (b)(c | d | cd) definita sui simboli di
questo alfabeto.
c a, b
L’insieme L(r) è costituito dalle stringhe {bc, bcd, bd} dove la stringa ‘bc’ è
un minorante di L(r) (infatti si ha che ‘bc’ ≤L ‘bcd’ ≤L ‘bd’) e la stringa ‘bd’ ne è
un maggiorante; anche in questo caso, come constatato già nell’esempio precedente, l’insieme dei minoranti è costituito anche da tutte quelle stringhe appartenenti a * che sono più piccole, secondo l’ordinamento ≤L, della stringa
‘bc’ e tra queste è compresa anche la stringa vuota ε che è la più piccola di tutte. La stessa cosa accade per l’insieme dei maggioranti che è costituito da tutte quelle stringhe appartenenti a * che sono più grandi, secondo l’ordinamento ≤L,
della stringa ‘bd’.
Chiariti questi due semplici concetti possiamo introdurre la nozione di massimo e minimo in una generica espressione regolare r.
4.5 Nozione di massimo e minimo
Introduciamo in questa sezione la nozione di stringa massima e stringa minima, rispettivamente indicate con max(L(r)) e min(L(r)), dell’insieme L(r).
Definizione 4.4 Sia r un’espressione regolare e sia il linguaggio da essa definito
L(r) ⊆ * un insieme limitato superiormente. Diciamo che l’insieme di stringhe L(r) ammette stringa massima s, secondo l’ordinamento ≤Lstabilito, se:
1) s è una stringa maggiorante di L(r);
2) s ∈ L(r).
In tal caso, scriveremo s = max(L(r)) .
Definizione 4.5 Sia r un’espressione regolare e sia il linguaggio da essa definito
L(r) ⊆ * un insieme limitato inferiormente. Diciamo che l’insieme di stringhe L(r) ammette stringa minima s , secondo l’ordinamento ≤Lstabilito, se:
2) s ∈ L(r).
In tal caso, scriveremo s = min(L(r)) .
Non è detto che un insieme limitato superiormente ammetta stringa massima. Infatti, il seguente esempio ci mostra come, presa un’espressione regolare particolare della forma r = (r′)*, l’insieme di stringhe L(r) da essa definito (si
noti che si tratta di un insieme infinito) sia limitato superiormente, ma non ammetta la stringa massima, ovvero la stringa più grande che, secondo l’ordinamento delle stringhe ≤L, appartiene al linguaggio L(r).
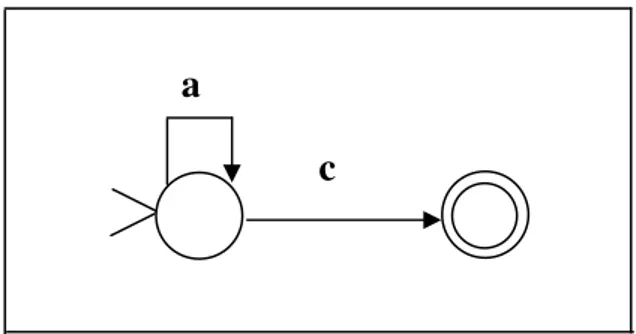
Esempio 4.3 Consideriamo l’espressione regolare r = (b)* definita sull’alfabeto
= {a, b, c} e il linguaggio L(r) da essa definito.
L’insieme L(r), costituito dalle stringhe {ε, b, bb, bbb, bbbb, bbbbb, ..., …}, risulta limitato superiormente poiché esiste una stringa s∈ * tale che p ≤L s per
ogni stringa p ∈ L(r), ma non ammette stringa massima perché l’insieme L(r) è
disgiunto dall’insieme delle sue stringhe maggioranti. Infatti, per esempio, la stringa s = ‘c’ ∈ * risulta essere più grande, secondo l’ordinamento
lessicografico ≤L, di qualsiasi altra stringa appartenente a L(r), ovvero si ha che
per ogni stringa p ∈ L(r) p ≤L s, ma non è la stringa massima perché essa non
appartiene al linguaggio definito dall’espressione r e questo vale anche per tutte le stringhe appartenenti all’insieme delle stringhe maggioranti di L(r) . Tutto ciò
dimostra che per l’insieme L(r) non esiste max(L(r)).
Analogamente, non è detto che un insieme limitato inferiormente ammetta stringa minima. L’esempio che segue ci chiarirà meglio le idee.
Esempio 4.4 Consideriamo l’espressione regolare r = (a)*(c) definita
sull’alfabeto = {a, b, c, d} e il linguaggio L(r) da essa definito.
L’insieme L(r), costituito dalle stringhe {ac, aac, aaac, aaaac, aaaaac, ..., c}, risulta limitato inferiormente poiché esiste una stringa s∈ * tale che s ≤L p per
ogni stringa p ∈ L(r), ma non ammette stringa minima perché l’insieme L(r) è
disgiunto dall’insieme delle sue stringhe minoranti. Infatti, per esempio, la stringa s = ‘a’ ∈ * risulta essere più piccola, secondo l’ordinamento
lessicografico ≤L, di qualsiasi altra stringa appartenente a L(r), ovvero si ha che
per ogni stringa p ∈ L(r) s ≤L p, ma non è la stringa minima perché essa non
appartiene al linguaggio definito dall’espressione r e questo vale anche per tutte le stringhe appartenenti all’insieme delle stringhe minoranti (che ovviamente contiene ε) di L(r). Tutto ciò dimostra che per l’insieme L(r) non esiste min(L(r)).
Notiamo che se l’insieme L(r) ha stringa massima allora max(L(r)) è la stringa più piccola, secondo l’ordinamento lessicografico ≤L, dell’insieme delle sue
stringhe maggioranti. Allo stesso modo, se l’insieme L(r) ha stringa minima allora min(L(r)) è la stringa più grande, secondo l’ordinamento lessicografico ≤L,
dell’insieme delle sue stringhe minoranti.
La definizione della nozione di sup(L(r)) si riferisce proprio al concetto appena esposto: per ogni insieme non vuoto L(r) ⊆ * limitato superiormente, la minima
c
Fig. 4.5 Automa che accetta il linguaggio definito da r = (a)*(c)
tra le stringhe maggioranti di L(r), stabilita secondo l’ordinamento ≤L, si chiama
estremo superiore di L(r) e si indica con sup(L(r)).
Quindi, riassumendo, l’estremo superiore di un insieme L(r) si caratterizza nel seguente modo:
Proposizione 4.1 Sia L(r) il linguaggio definito da un’espressione regolare r
contenuto in *, non vuoto e limitato superiormente. Si ha s = sup(L(r)) se e solo
se s verifica le seguenti due proprietà: 1) p ≤L s per ogni stringa p ∈ L(r);
2) considerando l’ordinamento delle stringhe ≤L , per ogni stringa s più piccola
di s (cioè s ≤L s) esiste una stringa p ∈ L(r) tale che s <L p ≤L s.
Questa proposizione ci dice che s = sup(L(r)) se e solamente se s è la stringa
minima dell’insieme delle stringhe maggioranti di L(r), infatti la 1) dice appunto che s è maggiorante di L(r), mentre la 2) afferma che nessuna stringa più piccola di s può essere una stringa maggiorante di L(r) e ciò significa che s è la stringa minima dell’insieme delle stringhe maggioranti di L(r).
Per simmetria, la proposizione che definisce s = inf(L(r)) dice che s è una
stringa minorante dell’insieme L(r) e nessuna stringa più grande di s è minorante
di L(r), quindi s è la stringa massima dell’insieme delle stringhe minoranti di
L(r).
Esempio 4.5 Riprendiamo in considerazione l’espressione regolare dell’esempio
1, ovvero l’espressione r = (a | b)(c).
Il linguaggio L(r) ⊆ *, definito da r, contiene le stringhe {ac, bc}, quindi alla
luce di quanto detto si ha che inf(L(r)) = min(L(r)) = ‘ac’, sup(L(r)) = max(L(r))= ‘ bc’.
Lo stesso accade per l’espressione r = (b)(c | d | cd) presa in considerazione
stringhe {bc, bcd, bd}, quindi in base a ciò che è stato detto finora si ha che
inf(L(r)) = min(L(r)) = ‘bc’, sup(L(r)) = max(L(r)) = ‘ bd’.
E’ importante far notare che nell’esempio appena fatto, sia nel caso della prima espressione, sia nel caso della seconda, la stringa minima (min(L(r))) e l’estremo inferiore dell’insieme L(r) (inf(L(r))) coincidono. La stessa cosa accade per la stringa massima (max(L(r))) e l’estremo superiore di L(r) (sup(L(r))).
Purtroppo, in generale, non è detto che l’estremo superiore (o inferiore) di un insieme L(r) esistano sempre.
Esempio 4.6 Consideriamo l’espressione regolare r = (a)* definita sull’alfabeto
= {a, b, c} e il linguaggio L(r) da essa definito.
L’insieme L(r), costituito dalle stringhe {ε, a, aa, aaa, aaaa, aaaaa, ..., …}, risulta limitato superiormente poiché esiste una stringa s∈ * tale che p ≤L s per
ogni stringa p ∈ L(r), ma non ammette stringa massima perché l’insieme L(r) è
disgiunto dall’insieme delle sue stringhe maggioranti. Infatti, per esempio, la stringa s = ‘b’ ∈ * risulta essere più grande, secondo l’ordinamento
lessicografico ≤L, di qualsiasi altra stringa appartenente a L(r), ovvero si ha che
per ogni stringa p ∈ L(r) p ≤L s, ma non è la stringa massima perché essa non
appartiene al linguaggio definito dall’espressione r e questo vale anche per tutte le stringhe appartenenti all’insieme delle stringhe maggioranti di L(r). Tutto ciò dimostra che per l’insieme L(r) non esiste max(L(r)).
Contemporaneamente, l’insieme L(r) non ammette estremo superiore, ovvero esiste un insieme di maggioranti di L(r), ma non esiste il minimo, cioè non esiste sup(L(r)).
Invece, l’esistenza della stringa massima implica l’esistenza dell’estremo superiore, poiché se un insieme L(r) ha stringa massima allora questa è la stringa
più piccola dell’insieme delle sue stringhe maggioranti, che è proprio la definizione di estremo superiore di un insieme.
Considerare espressioni regolari che descrivono insiemi che non ammettono stringa massima (o minima), complica la fase di costruzione degli intervalli di stringhe, poiché non ci permette di determinare in modo esatto l’estremo destro (o sinistro) dell’intervallo con cui rappresentiamo una generica espressione e quindi di delimitare l’insieme L(r). Quindi, come si può ben intuire, considerare linguaggi infiniti implica non poter determinare l’intervallo associato all’espressione regolare corrispondente.
Nel paragrafo che segue, mostriamo quale metodo viene adottato per ovviare all’inconveniente che si presenta quando si ha a che fare con un insieme L(r) infinito (che quindi non ammette stringa massima) ed inoltre si fa presente come tale metodo, inevitabilmente, vada a scapito della precisione con cui si costruisce l’intervallo.
4.6 Troncamento di un linguaggio L(r) infinito
Il problema di trattare linguaggi che non hanno stringa massima ci costringe ad introdurre un espediente che in qualche modo consenta di stabilire, seppure in modo approssimato, la stringa che, secondo l’ordinamento ≤L , risulta essere la
più grande (o la più piccola) tra tutte quelle appartenenti al linguaggio.
Abbiamo notato che per linguaggi regolari finiti, cioè costituiti da un numero finito di stringhe, il problema di individuare la stringa massima (o minima) non si pone. Tra tutte le stringhe che costituiscono l’insieme, basta scegliere la più grande (o la più piccola) secondo l’ordinamento ≤L stabilito. Invece, per
linguaggi regolari della forma U* , cioè ∪k≥0 Uk , che sono linguaggi descritti da
espressioni r=(u)*, il problema di individuare la stringa massima (ricordiamo che
la stringa minima è la stringa vuota) si pone poiché, preso un generico elemento appartenente al linguaggio descritto da r, si riesce sempre a determinarne un altro che risulta essere più grande di quello preso inizialmente in considerazione. Di
conseguenza, non si riesce mai ad individuare con esattezza una stringa che risulti essere la più grande di tutte.
Per chiarirci meglio le idee consideriamo l’esempio che segue.
Esempio 4.7 Supponiamo di avere un alfabeto con i seguenti simboli = {a, b,
c} e consideriamo la semplice espressione regolare r = (ab)*.
Sappiamo, dalla definizione base delle espressioni regolari, che in generale un’espressione della forma r* consente di concatenare una qualsiasi stringa x,
rappresentata da r, con se stessa zero o più volte. Quindi considerando (ab)0 otterremmo ε, con (ab)1 otterremmo ‘ab’, con (ab)2 otterremmo ‘abab’, con (ab)3 otterremmo ‘ababab’ e così via fino all’infinito. Come già detto in precedenza e
come si può notare, la stringa ottenuta al passo i risulta essere sempre più piccola (secondo l’ordinamento ≤L ) di quella ottenuta al passo successivo, ovvero al
passo i+1 e questo vale per ogni i ≥ 0. E’ evidente quindi che non esiste una
stringa, appartenente ad L(r), che sia in assoluto la più grande di tutte, a meno che non si considera la stringa costituita da un numero infinito di ‘ab’.
Il concetto trattato nell’esempio appena fatto viene formalizzato nella seguente proposizione:
Proposizione 4.2 Sia r un’espressione regolare della forma r = (r )*. Allora vale:
per ogni stringa x ∈ L(r) esiste una stringa y ∈ L(r) t. c.
x = (r )i ≤L y = (r ) i + 1 ∀ i ≥ 0 .
Dimostrazione: La dimostrazione della proposizione viene fatta per induzione sul
valore del parametro i.
Consideriamo prima il caso base e poi il caso induttivo:
caso base: per i = 0 si ha che x = (r )0 ≤L y = (r ) 1, disuguaglianza che è
palesemente verificata, poiché (r )0 = ε è minore o uguale di qualsiasi altra stringa;
caso induttivo: bisogna dimostrare che se per un generico i vale la proprietà enunciata, ovvero vale P(i), allora questa varrà per i+1, cioè varrà P(i+1), quindi bisogna sfruttare l’ipotesi induttiva per dimostrare che P(i) P(i+1).
Dimostriamo che x = (r ) i +1 ≤L y = (r ) i +2. Sappiamo che (r ) i+2 = (r ) 1(r ) i+1
per cui si ha che: (r ) 1(r ) i
≤L { per Hp. Induttiva: x = (r )i ≤L y = (r ) i + 1}
(r ) 1(r ) i+1 c.v.d.
E’ da notare che la proposizione appena enunciata vale anche per espressioni della forma r = (r )*, dove r = (r1 | r2 ), solo se, al passo i (per i= 0, 1, 2,…), si prende in considerazione la stringa più grande tra quelle possibili. In poche parole, se consideriamo l’espressione regolare r = (a | b)*, al passo i = 1 avremo
che la stringa più grande, tra {a, b}, in base all’ordinamento ≤L, sarà ‘b’, che
sarà minore di ‘bb’ (che è la più grande tra {aa, ab, ba, bb}) ottenuta al passo i = 2, che a sua volta sarà minore di ‘bbb’ ottenuta al passo i = 3 e così via.
Come abbiamo avuto modo di capire fino a questo punto, le espressioni regolari che possono essere definite su un alfabeto sono infinite. Per tale
motivo esistono tantissime espressioni regolari che possono essere ottenute dalla concatenazione di una serie di espressioni della forma suddetta con altre espressioni di diverso tipo e quindi possono risultare così particolari o complicate da non ammettere stringa massima (o minima). Questa riflessione ci porta al seguente risultato:
Proposizione 4.3 Esistono infinite espressioni regolari r per le quali, considerato
L(r) il linguaggio descritto da r, la stringa massima (max(L(r))) e la stringa minima (min(L(r))) non esistono.
Per cui, è chiaro che, considerato un alfabeto di simboli , possono essere formulate infinite espressioni regolari per le quali non è possibile individuare la stringa massima (o minima).
A dimostrazione di quanto affermato nella proposizione 4.3 consideriamo il seguente esempio in cui vengono prese in considerazione più espressioni regolari r per le quali è valida l’affermazione appena fatta.
Esempio 4.8 Supponiamo di avere un alfabeto con i seguenti simboli = {a, b,
c} e consideriamo l’espressione regolare r = (ba)*(aba | b).
Come si può ben notare il linguaggio L(r), costituito dalle stringhe {aba, b, baaba, babaaba, …, bab, babab, bababab, … }, non ha stringa massima, ovvero max(L(r)) non esiste.
La stessa cosa accade per l’espressione r=(ba)*(aba|(ab)*) e per
r=(ba)*(aba)* e per infinite altre espressioni, contenenti la stella di Kleene, che possono essere definite su .
Nell’esempio appena fatto abbiamo visto tre esempi di espressioni regolari, particolarmente annidate, per le quali non esiste stringa massima. Stabilire la stringa minima di queste tre espressioni non è complicato poiché per r=(ba)*(aba|b) la stringa minima corrispondente è ‘aba’, per r=(ba)*(aba|(ab)*)
e per r=(ba)*(aba)* la stringa minima corrispondente è la stringa vuota.
Esistono casi in cui la determinazione della stringa minima di un linguaggio non è immediata come nei tre esempi mostrati sopra. Infatti, consideriamo l’espressione dell’esempio che segue.
Esempio 4.9 Supponiamo di avere un alfabeto con i seguenti simboli = {a, b,
c} e consideriamo l’espressione regolare r = (a*b). Come si può ben notare il
stringa massima, ovvero max(L(r)) = ‘b’, ottenuta al passo i = 0 (cioè considerando a0 b).
Invece, la stringa minima di L(r) non esiste poiché la stringa ottenuta al passo i+1 risulta essere sempre più piccola (secondo l’ordinamento ≤L) di quella
ottenuta al passo precedente, ovvero al passo i-1 e questo vale per ogni i ≥ 0. Ad
esempio, se consideriamo i=2 otteniamo che a2b ≤L a1b, ovvero esplicitando si
ottiene che aab ≤L ab e questo vale per ogni i ≥ 0.
E’ evidente quindi che non esiste una stringa, appartenente ad L(r), che sia in assoluto la più piccola di tutte.
L’esempio appena fatto ci fa capire che non è possibile determinare la stringa più piccola appartenente ad L(r) poiché l’espressione r, presa in considerazione, è caratterizzata dalla concatenazione di un linguaggio infinito (rappresentato da a*) con un linguaggio finito (rappresentato da b). Quindi, in questo caso, la determinazione della stringa minima di L(r) dipende dall’esistenza della stringa massima del linguaggio definito da a*, che, come abbiamo avuto modo di capire finora, non ammette stringa massima.
A questo punto, visto che sono stati messi in chiaro alcuni concetti fondamentali, spieghiamo come individuare, approssimativamente, la stringa massima di un linguaggio L(r) infinito. Questo passo ci aiuterà a risolvere anche i problemi (tipo quello mostrato nell’esempio 4.9) legati alla determinazione della stringa minima.
Introduciamo, con la definizione che segue, la nozione di troncamento di un linguaggio infinito.
Definizione 4.6 Sia r un’espressione regolare della forma r = (r′)*; di
conseguenza il linguaggio L(r) risulta essere infinito. Diciamo che il troncamento di L(r), indicato con trω(L(r)), è la stringa ottenuta dalla ripetizione di r′ un
rappresenta la stringa massima del linguaggio finito L′(r) ottenuto considerando
tutte le stringhe di L(r) tranne la stringa costituita da un numero infinito di concatenazioni di r′, che viene troncata in posizione .
L’idea che c’è dietro la definizione 4.6 è semplice ed intuitiva. Supponiamo di considerare l’espressione regolare r = a*; le stringhe appartenenti all’insieme
L(r) sono le stringhe {ε, a, aa, aaa, aaaa, aaaaa,….}. L’insieme L(r) non ammette stringa massima poiché per ogni stringa x ∈ L(r) si riesce sempre a
determinare una stringa y ∈ L(r) tale che x ≤L y.
Per stabilire un’approssimazione della stringa massima possiamo procedere nel seguente modo: sappiamo che nell’insieme L(r) è presente anche la stringa che è costituita da un numero infinito di ‘a’, per cui quello che possiamo fare è troncare questa stringa in un certo punto, ovvero considerare a , dove è un
intero molto grande fissato a priori. Si ottiene così un linguaggio L′(r), contenuto
in L(r), che ha come stringa massima proprio la stringa ‘a ’, cioè max(L′(r)) =
tdω(L(r)) = ‘a ’, dove ovviamente ‘a ’ sta ad indicare che ‘a’ viene ripetuta
volte.
Naturalmente, il troncamento della stringa infinita ‘aaaaaaa…’ introduce un errore che, come vedremo, andrà ad influire sulle stringhe che faranno parte degli intervalli che andremo a costruire per rappresentare l’espressione r.
Al fine di evitare l’introduzione di un ulteriore errore nella rappresentazione di una generica espressione r che definisce un linguaggio infinito, imponiamo che la lunghezza della query string qx in ingresso, da cercare all’interno di un
generico intervallo, non superi , ovvero assumiamo che | qx | ≤ .
Alla luce della definizione 4.6 mostriamo come individuare il troncamento dei linguaggi infiniti considerati nell’esempio 4.8 e 4.9 e quindi facciamo vedere
come determinare la stringa massima di un linguaggio L′(r)1 ottenuto
considerando la nozione di troncamento di un linguaggio L(r) infinito.
Esempio 4.10 Riprendiamo in considerazione la prima espressione dell’esempio
4.8 illustrato precedentemente.
Utilizzando la nozione di troncamento, precedentemente introdotta, otteniamo un linguaggio L′(r) per il quale possiamo stabilire come stringa massima la
stringa più grande tra ‘(ba) aba’ e ‘(ba) b’. Ovviamente, il valore di deve
essere uguale in entrambe le stringhe, altrimenti risulta difficile stabilire quale delle due è la più grande. Infatti, se il valore di fosse maggiore nella prima stringa, rispetto a quello scelto nella seconda, allora si avrebbe che ‘(ba) b’≤L‘(ba) aba’, altrimenti se il valore di fosse maggiore nella seconda
stringa, rispetto a quello scelto nella prima, allora si avrebbe che ‘(ba) aba’≤L‘(ba) b’. Invece, per valori di uguali (sottintendiamo che sia
sempre così qualunque caso si presenti), la stringa maggiore è ‘(ba) b’ e quindi
si può concludere che max(L′(r)) = ‘(ba) b’.
Per le espressioni r1= (ba)*(aba | (ab)*) e r2 = (ba)*(aba)* la stringa massima
è rispettivamente max(L′(r1)) = (ba) (ab) e max(L′(r2)) = (ba) (aba) .
Esempio 4.11 Consideriamo l’espressione r = (a*b) dell’esempio 4.9 illustrato
precedentemente.
Applicando la definizione 4.6 riusciamo a determinare la stringa minima di L′(r) che è uguale ad a b, ovvero min(L′(r)) = ‘a b’.
4.7 Proprietà dei linguaggi regolari
Nella sezione 4.5 e 4.6, abbiamo fornito tutte le nozioni riguardanti i concetti di stringa massima e stringa minima di un linguaggio regolare ed inoltre abbiamo
1 Indicheremo sempre con il simbolo L′(r) il linguaggio ottenuto dal troncamento di un linguaggio L(r)
affrontato alcuni problemi che potrebbero presentarsi nel caso in cui si prendono in considerazione certe espressioni regolari. Quindi, secondo quanto detto, se il linguaggio è finito riusciamo sempre a determinare la stringa massima e la stringa minima di L(r), invece, se il linguaggio definito dall’espressione è infinito, occorre introdurre un espediente che ci consenta di stabilire approssimativamente una stringa massima (o minima) di un linguaggio finito L′(r) ottenuto considerando la nozione di troncamento di L(r).
Di seguito mostriamo che, se la stringa massima di un linguaggio regolare esiste, allora non deriva da un troncamento. Infatti, abbiamo appena visto che esistono linguaggi infiniti per cui non è possibile individuare la stringa massima o la stringa minima poiché inesistenti.
Il concetto appena esposto viene sintetizzato nella proposizione 4.4.
Proposizione 4.4 Sia r un’espressione regolare e sia L(r) il linguaggio da essa
definito. Se max(L(r)) esiste allora non deriva da una espressione di Kleene. Di seguito mostriamo i passi principali della dimostrazione della proposizione 4.4.
Dimostrazione. La dimostrazione della proposizione viene fatta sfruttando la
struttura sintattica della generica espressione regolare r in ingresso.
Se il max(L(r)) esiste e il linguaggio L(r) è finito, allora non c’è troncamento e la proposizione vale banalmente. Quindi assumiamo che il linguaggio L(r) è infinito (ciò vuol dire che contiene la stella di Kleene).
Assumiamo per assurdo che il massimo esiste ed è un troncamento, ovvero soddisfa un’espressione regolare r′ della forma r′ = α (β)* γ tale che
1) non esistono α′, α′′, γ′, γ′′ per cui r′ = α′ ( α′′ (β)* γ′ )* γ′′;
2) α non contiene *;
4) r′ non contiene espressioni di alternativa.
Una tale forma di r′ può essere sempre trovata.
Posto s = max(L(r)), mostriamo che esiste sempre una stringa s′ ∈ L(r) tale che
s <L s′ ottenendo quindi una contraddizione. Mostriamo come si procede con la
costruzione delle stringhe s ed s′.
Per quanto riguarda s ∈ L(r) abbiamo che risulta essere della forma s = sαsβsγ
tale che sα ∈ L(α), sβ ∈ L(β)*, sγ ∈L(γ), dove sβ = βt, con t ≥ 0.
Per quanto riguarda la costruzione di s′ ∈ L(r), possiamo assumere per ipotesi
di assurdo che max(L(β)*) e max(L(γ)) esistono. Distinguiamo due casi:
1) max(L(β)*) >L max(L(γ)) allora la stringa s′ è della forma s′ =
max(L(α))max(L(β))t+1;
2) max(L(β)*) <L max(L(γ)) allora la stringa s′ è della forma s′ =
max(L(α))max(L(γ)).
Mostriamo che la stringa s <L s′ in entrambi i casi.
Infatti, nel primo caso si ha che sα <L max(L(α))per definizione di stringa
massima e ovviamente s = βt <
L max(L(β))t+1. Nel secondo caso si ha che sα <L
max(L(α))per definizione di stringa massima e sγ <L max(L(γ)) per definizione di
stringa massima.
Per cui, poiché s′ ∈ L(r), siamo giunti ad una contraddizione dell’ipotesi
affermando che il massimo deriva da una stelle di Kleene.
4.8 Regole per determinare max(L(r)) e min(L(r))
Consideriamo una generica espressione regolare r e il linguaggio L(r) da essa descritto. In questo paragrafo forniamo un metodo generale che, applicato all’espressione r, restituisce la stringa massima e la stringa minima dell’insieme L(r) (nel caso in cui esso sia finito) o L′(r) (nel caso in cui L(r) sia infinito).
Come nel caso della definizione formale delle espressioni regolari, è possibile definire la stringa massima e la stringa minima prima per espressioni semplici e poi per espressioni composte ottenute a partire da quelle semplici.
La stringa massima e la stringa minima di una generica espressione regolare r, definita su un alfabeto di simboli , sono formalizzate nel seguente modo:
a) per le RE semplici:
se r = ε allora min(L(r)) = ε e max(L(r)) = ε ;
se r = a allora min(L(r)) = a e max(L(r)) = a per ogni simbolo a ∈ ;
b) per le RE composte dobbiamo distinguere due casi:
1. se consideriamo una espressione di alternativa della forma r = (r1|r2) allora si ha che min(L(r))=MIN(min(L(r1)), min(L(r2))) e max(L(r))=
MAX(max(L(r1)), max(L(r2)));
2. se consideriamo un’espressione di concatenazione della forma r=(r1)(r2)
allora nel calcolo della stringa minima bisogna controllare se (min(L(r1)) è prefisso max(L(r1))). Nel caso in cui tale condizione è
verificata, si stabilisce come stringa minima di L(r) la stringa min(L(r))= MIN(max(L(r1))min(L(r2)), min(L(r1))min(L(r2))), altrimenti
la stringa minima risultante è min(L(r)) = min(L(r1))min(L(r2)).
Nel calcolo della stringa massima bisogna controllare se (min(L(r1)) è
prefisso max(L(r1))). Nel caso in cui tale condizione è verificata, si
stabilisce come stringa massima di L(r) la stringa max(L(r))= MAX(min(L(r1))max(L(r2)), max(L(r1))max(L(r2))), altrimenti la stringa
massima risultante è max(L(r)) = max(L(r1))max(L(r2));
c) per una generica espressione con la stella di Kleene r = (r′)* dobbiamo
distinguere due casi:
1. se r′ non è della forma (r2|r3), ovvero r′ ≠ (r2|r3), allora la stringa minima di L′(r) è min(L′(r)) = ε e la stringa massima è la stringa
2. se r′ è della forma (r2|r3), ovvero r′ = (r2|r3) allora la stringa minima di
L′(r) è min(L′(r)) = ε e per stabilire la stringa massima occorre
verificare la seguente condizione: (max(L(r′))max(L(r′)) ≤L
min(L(r′))max(L(r′))). Se la condizione è verificata assegniamo ad una
variabile stringa temporanea x il valore x = min(L(r′)), altrimenti, se la
condizione non è verificata, x = max(L(r′)). La stringa massima
risultante è la stringa ottenuta concatenando la stringa (x)ω, a sua volta ottenuta dalla concatenazione della stringa x un numero di volte pari a
ω, con max(L(r′)).
Per quanto riguarda il caso 2 descritto nel punto b) occorre fare una precisazione sul modo in cui vengono determinate la stringa massima e minima. Per introdurre tale precisazione mostriamo subito un esempio che evidenzia chiaramente alcuni problemi che si potrebbero presentare per casi particolari di espressioni regolari.
Esempio 4.12 Consideriamo l’espressione regolare r1 = (b | bb | bbb | d) e due
espressioni r2 = a e r′2 = c in modo tale da poter effettuare la concatenazione di r1
sia con r2 sia con r′2. Per cui esaminiamo prima r = (b | bb | bbb | d)a e poi r′ =(b |
bb | bbb | d)c.
Nel primo caso applicando la regola che determina la stringa minima si ottiene, in modo corretto, che min(L(r)) = ‘ba’. Invece, nel secondo caso si ottiene min(L(r′)) = ‘bc’. Quest’ultimo risultato è errato poiché la stringa minima
di L(r′) è ‘bbbc’ e non ‘bc’.
Il problema esposto nell’esempio 4.12 si presenta nel caso in cui nell’espressione di alternativa r1 sono presenti delle stringhe tali che una è
dell’esempio la stringa minima ottenuta è esatta, nel secondo caso questo non succede poiché r′2 è lessicograficamente più grande del min(L(r1)), per cui
concatenando min(L(r1)) con min(L(r′2)) si ottiene, in modo sbagliato, la stringa
‘bc’.
Una situazione identica si presenta anche nel caso in cui l’espressione r assume una forma del tipo r = (a* | b)c (con r1 = (a* | b) ed r2 = c). Infatti, la
stringa minima stabilita secondo le regole esposte nel punto 2 del caso b) risulta essere ‘bc’ anziché ‘a c’. Si noti che ‘a c’ è la stringa minima di L′(r), poiché
L(r) non ha stringa minima. Si può osservare che questo tipo di espressioni possono essere ricondotte ad una forma del tipo ( | a | aa | aaa | aaaa | aaaaa |…|a | b)c, in cui esplicitando il linguaggio rappresentato dall’espressione a* otteniamo un linguaggio L′ costituito dalle stringhe { , a, aa, aaa, …, a }.
Simmetricamente, succede la stessa cosa nel caso della determinazione della stringa massima. Infatti, l’esempio che segue ci mostra come il problema esposto si ripresenti anche nel calcolo della stringa massima.
Esempio 4.13 Consideriamo l’espressione regolare r1 = (c | cc | ccc | a | aa) e due
espressioni r2 = b e r′2 = d in modo tale da poter effettuare la concatenazione di r1
sia con r2 sia con r′2. Per cui esaminiamo prima r = (c | cc | ccc | a | aa)b e poi
r′ = (c | cc | ccc | a | aa)d.
Nel primo caso applicando la regola che determina la stringa massima si ottiene, in modo corretto, che max(L(r)) = ‘cccb’. Invece, nel secondo caso si ottiene max(L(r′)) = ‘cccd’. Quest’ultimo risultato è errato poiché la stringa
massima di L(r′) è ‘cd’ e non ‘cccd’.
Come già visto nel caso della stringa minima, il problema esposto nell’esempio 4.13 si presenta nel caso in cui nell’espressione di alternativa r1
sono presenti delle stringhe tali che una è prefisso dell’altra, ovvero ‘c’ è prefisso di ‘cc’ e di ‘ccc’. Mentre nel primo caso dell’esempio la stringa massima ottenuta
è esatta, nel secondo caso questo non succede poiché r′2 è lessicograficamente
più grande del max(L(r1)), per cui concatenando max(L(r1)) con max(L(r′2)) si
ottiene, in modo sbagliato, la stringa ‘cccd’.
Al fine di stabilire un valore esatto della stringa massima e minima per il caso di espressioni regolari appena esposto, possiamo modificare la regola del punto b) caso 2 nel seguente modo: per il calcolo della stringa minima calcoliamo min(L(r1)$). Per cui la regola viene modificata scegliendo il
MIN(min(L(r1)$)min(L(r′2)), min(L(r1)) min(L(r′2))). In particolare, la nuova
regola è la seguente: se (min(L(r1)) è prefisso max(L(r1))) allora si stabilisce
min(L(r))=MIN(min(L(r1)$)min(L(r′2)),max(L(r1))min(L(r2)),min(L(r1))min(L(r2))
altrimenti min(L(r))=MIN(min(L(r1)$)min(L(r′2)),min(L(r1))min(L(r2))).
Invece, nel caso della stringa massima calcoliamo max(L(r1)$). Per cui la
regola viene modificata scegliendo il MAX(max(L(r1)$) max(L(r′2)), max(L(r1))
max(L(r′2))). In particolare, la nuova regola è la seguente: se (min(L(r1)) è
prefisso max(L(r1))) allora max(L(r)) = MAX(max(L(r1)$)max(L(r′2)),
max(L(r1))max(L(r2)), min(L(r1)) max(L(r2))), altrimenti si ottiene come stringa
massima, la stringa MAX(max(L(r1)$) max(L(r′2)), max(L(r1))max(L(r′2))).
Gli operatori MIN e MAX, utilizzati nella definizione delle regole per
determinare la stringa massima e minima, selezionano rispettivamente la stringa più piccola e la stringa più grande, tra quelle possibili, in base all’ordinamento ≤L
stabilito.
Per individuare la stringa massima e minima di un linguaggio L(r) occorre applicare le regole sopra descritte all’interno dell’algoritmo mostrato nel capitolo successivo.
Seguono degli esempi in cui mostriamo l’applicazione delle regole ad alcune espressioni regolari.
Esempio 4.14 Consideriamo l’espressione regolare r = (c | b | a); in base a quanto
detto precedentemente, abbiamo che min(L(r)) = MIN(min(L(r1)), min(L(r2)),
min(L(r3))) = MIN (‘c’, ‘b’, ‘a’ ) = ‘a’; invece max(L(r)) = MAX(max(L(r1)),
max(L(r2)), max(L(r3))) = MAX (‘c’, ‘b’, ‘a’ ) = ‘c’.
Esempio 4.15 Consideriamo l’espressione r = (b)*; utilizzando le regole
otteniamo che max(L′(r′)) = ‘ b ’e min(L′(r)) = ε.
Esempio 4.16 Consideriamo l’espressione regolare r = (a | b)*. Possiamo subito
dire che min(L′(r)) = ε, mentre per determinare la stringa massima occorre verificare che max(L(r′)) = ‘b’ concatenato con max(L(r′)) = ‘b’ è ≤Lmin(L(r′)) =
‘a’ concatenato con max(L(r′)) = ‘b’. La stringa ‘bb’ non è ≤L della stringa ‘ab’
per cui x = max(L(r′)) = ‘b’ e quindi il valore finale della stringa massima risulta
essere la stringa (b) b. Si ricorda che r′in questo caso corrisponde all’espressione (a | b).
4.9 Correttezza delle regole che determinano max(L(r)) e
min(L(r))
In questa sezione mostriamo la correttezza delle regole esposte nella sezione precedente.
Per quanto riguarda le regole definite per le RE semplici, possiamo dire che dimostrarne la correttezza è abbastanza semplice poiché segue dalla definizione di stringa massima e minima di un linguaggio regolare.
Consideriamo r della forma (r1|r2). Per quanto riguarda la regola che determina la stringa minima di L(r), possiamo dire che se min(L(r1)) e min(L(r2))
quindi basta prendere la stringa più piccola tra min(L(r1)) e min(L(r2)),
dimostrando per assurdo che ne esiste una più piccola di quella che determinano le regole. Nel caso in cui almeno una tra min(L(r1)) e min(L(r2)) derivino da un
troncamento allora si calcola la stringa minima con i linguaggi L′(r1) e/o L′(r2),
che derivano rispettivamente dal troncamento di L(r1) e L(r2). Per dimostrare la
correttezza della stringa massima, considerando r della forma suddetta, si procede in modo identico a quanto visto per la regola che determina la stringa minima.
Consideriamo un’espressione r della forma (r′)*. Se r′ non è della forma
(r2|r3), ovvero r′ ≠ (r2|r3), allora la stringa minima determinata correttamente dalle regole è ε che è, per definizione, la più piccola di tutte. La stringa massima
di L(r) non esiste (come visto nelle proposizioni 4.2 e 4.3) poiché L(r) è un insieme infinito di stringhe. Per cui applicando la nozione di troncamento si ha che la regola determina in modo corretto (e questo lo si dimostra attraverso una semplice dimostrazione per assurdo) max(L′(r)), dove L′(r) è il linguaggio finito
ottenuto dal troncamento di L(r). Lo stesso ragionamento vale anche nel caso in cui r′ è della forma (r2|r3).
Consideriamo r della forma (r1)(r2). Per quanto riguarda la stringa minima
occorre dimostrare che la regola determina in modo corretto come stringa minima una stringa tra le seguenti: min(L(r1)$) min(L(r′2)), max(L(r1))min(L(r2)),
min(L(r1))min(L(r2)). La dimostrazione anche in questo caso viene fatta per
assurdo. Si procede affermando che esiste una stringa più piccola di quella determinata dalla regola e mostrando che si giunge ad una contraddizione dell’ipotesi iniziale.
Anche per la dimostrazione della correttezza della regola che determina la stringa massima si procede in modo simile a quanto visto per la stringa minima, solo che si assume per assurdo l’esistenza di una stringa più grande di quella determinata dalla regola.