Capitolo 5
Cilindro
circolare
non
vincolato
Il capitolo affronta lo studio di un cilindro circolare libero di muoversi in un fluido in quiete al variare del rapporto di massa 𝜶. La prima parte è dedicata alla definizione dei parametri necessari per la discretizzazione numerica per poi passare alla validazione del modello mediante il confronto dei risultati ottenuti con i dati presenti in letteratura. Infine lo schema numerico sviluppato è sfruttato per definire la curva di stabilità neutra del cilindro rispetto al fenomeno di instabilità primaria.
5.1. Parametri di discretizzazione numerica
5.1.1 Dominio di calcolo
Il dominio di calcolo utilizzato in queste simulazioni è il medesimo presentato nel paragrafo 4.2.1, a cui si rimanda per la definizione delle caratteristiche geometriche.
5.1.2 Scelta del metodo di risoluzione del problema
fluido-struttura
Il caso del cilindro circolare, che cade o galleggia in un fluido in quiete partendo da fermo, è un problema che presenta difficoltà di ordine diverso rispetto al caso del cilindro dotato del solo grado di libertà in rotazione. Infatti, affrontare lo studio di un corpo, che parte dalla condizione statica e accelera in funzione della risultante delle forze valutate all’interno del modello numerico, necessita che le stesse forze siano da subito stimate in modo pressoché esatto; si rischia, altrimenti, di compiere errori considerevoli sulla dinamica del corpo. In particolare sul cilindro agiscono la forza peso, la spinta di Archimede, il contributo di massa aggiunta e la resistenza. Tuttavia, nei primi istanti del moto, l’ultimo contributo è trascurabile rispetto agli altri. Questo significa che l’integrale sul bordo del tensore degli sforzi, proiettato lungo la direzione della forza peso, fornisce unicamente il valore della spinta di Archimede e della massa aggiunta. L’insieme delle azioni sul corpo è quindi schematizzabile come in Figura 5.1. Se da una parte la spinta di Archimede ha un valore costante, il termine di massa aggiunta è variabile e del tutto determinante per la corretta definizione dell’accelerazione del corpo nei primi istanti del moto.
Figura 5.1 – Schematizzazione delle forze sul corpo nei primi istanti del moto
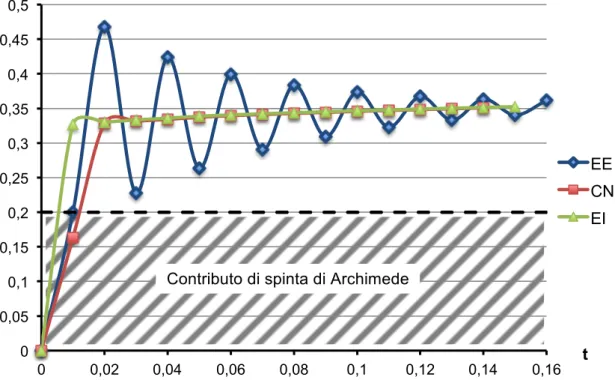
Per un’esatta valutazione della massa aggiunta, dunque, è necessario studiare a priori come i modelli presentati in precedenza, l’EE, l’EI e il CN, riescono a darne una stima. La massa aggiunta ha un effetto non trascurabile per corpi che hanno densità dello stesso ordine di grandezza del fluido nel quale si muovono1. Si analizza, quindi, l’andamento delle forze per il cilindro con valori di α sufficientemente contenuti. Nelle Figure 5.2-5.3 sono riportati gli andamenti dell’integrale dell’azione del flusso sul corpo, considerando α = 4 e α = 3, per i primi istanti di simulazione per i tre schemi considerati: la linea tratteggiata nera fornisce il contributo della spinta di Archimede e quindi la quota oltre tale livello è relativa alla massa aggiunta. Da questi andamenti si nota come, per α = 4, tutti e tre i modelli tendono a convergere verso un unico valore, sebbene l’EE con un andamento periodico smorzato, mentre
1 Ad esempio per valori di αsuperiori a 10 il problema è meno importante dato che
l’effetto della massa aggiunta sull’accelerazione è comunque più contenuto.
𝛼 < 1
Contributo di massa aggiunta Contributo di spinta di Archimede Contributo della forza peso 𝛼 > 1
l’EI e il CN in modo da subito stabile. La differente risposta tra gli schemi numerici è legata alle diverse caratteristiche dei modelli. Infatti, nel modello EE, le forze che sono utilizzate per risolvere la dinamica del corpo al passo n+1 sono valutate mediante le grandezze relative al passo n. Questo, in riferimento ai primi istanti del moto, significa che il modello valuta la dinamica del corpo alla prima iterazione con la soluzione inziale ed è questo il motivo per cui, il valore della forza a 0,01 s, è il solo contributo della spinta di Archimede. Avendo però sottostimato la risultante delle azioni del flusso sul corpo al 1° passo, la relativa accelerazione sarà sovrastimata2 e al passo successivo il contributo di massa aggiunta risulterà invece sovrastimato. Questa sottostima e sovrastima della risultante sul corpo si presenta ad ogni iterazione ed è il motivo per cui si ritrova un andamento periodico per lo schema EE. Un comportamento analogo è presente anche nei modelli EI e CN, ma all’interno del ciclo che itera sull’entità della forza e che ne fornisce una stima solo quando due valori consecutivi non convergono. Il fatto che lo schema EE sia smorzato sta a significare che le grandezze valutate hanno scostamenti sufficientemente contenuti rispetto al valore reale, per cui l’errore tende via via a ridursi. Al contrario può capitare che gli errori iniziali siano grandi, come ad esempio accade per il caso di α = 3. Per questo valore, infatti, il modello EE presenta un andamento periodico amplificato e non consente quindi una corretta definizione della dinamica del corpo. Per quanto riguarda gli altri modelli, invece, la stima è ancora definita correttamente. Infine si sceglie di studiare i casi di α = 1,1 e 0,8, i cui risultati sono riportati nelle Figure 5.4-5.5. Per tali valori di densità anche il modello implicito entra in crisi, non riuscendo a raggiungere la convergenza nel suo ciclo interno. Questo comportamento è indice del fatto che, anche nel ciclo sulla forza, ampi scostamenti dei valori valutati rispetto al valore reale, possono far divergere la soluzione mano a mano
2 L’azione del flusso sul corpo ha un effetto complessivo di resistenza per α > 0 quindi,
che il ciclo itera. Per quanto riguarda il modello EE, si ritrova un andamento fortemente divergente, mentre lo schema CN fornisce una soluzione da subito corretta. Il buon comportamento del modello di Crank-Nicholson è ragionevole poiché, essendo uno schema che media i valori valutati in due passi consecutivi, tende, in questo caso, a compensare le eventuali sovrastime e sottostime delle forze. Quindi, tra gli schemi presentati, l’unico disponibile per le simulazioni a bassi valori di α è il modello di CN.
Figura 5.2 -‐ Risultante dell'azione del flusso sul corpo per i tre schemi di risoluzione considerati per 𝜶 = 4
È infine doveroso sottolineare che lo studio dell’instabilità numerica che nasce per la non corretta valutazione della massa aggiunta è un tema che trova ampio rilievo in letteratura (Prosperetti e Tryggvason, 2006), dove vengono proposte varie soluzioni. La scelta nel presente lavoro di utilizzare uno schema di CN con iterazioni di punto fisso risulta, tuttavia, particolarmente adatta, dato che facilmente implementabile su codici già esistenti.
0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 t EE CN EI
Figura 5.3 -‐ Risultante dell'azione del flusso sul corpo per i tre schemi di risoluzione considerati per 𝜶 = 3
Figura 5.4 -‐ Risultante dell'azione del flusso sul corpo per i tre schemi di risoluzione considerati per 𝜶 = 1.1 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2 t esplicito mediato implicito
Contributo di spinta di Archimede
EE CN EI 56 57 58 59 60 61 62 0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 t EE CN Contributo di spinta di Archimede
Figura 5.5 -‐ Risultante dell'azione del flusso sul corpo per i tre schemi di risoluzione considerati per 𝜶 = 0.8 Infine sono necessarie alcune precisazioni in merito alla scrittura del sistema matematico risolutivo del problema.
Per prima cosa il modello di risoluzione della dinamica del fluido è scritto in un sistema di riferimento non inerziale che trasla in modo solidale con il cilindro circolare rispetto a un sistema di riferimento inerziale. Nell’equazione di Navier Stokes di bilancio di quantità di moto, quindi, devono essere aggiunti i contributi di forza apparente sul corpo. La possibilità di utilizzare un sistema di riferimento che trasla solamente rispetto a un sistema fisso e considerare il problema della rotazione solo nell’imposizione delle condizioni al contorno, in maniera del tutto analoga a quanto fatto nel capitolo precedente, è possibile perché il corpo trattato è un cilindro circolare infinitamente rigido; per cui, qualunque sia il suo spostamento, la forma che esso mostra rispetto al flusso è sempre la stessa. Caso ben diverso sarebbe trattare una geometria generica dato che, volendo usare la stessa procedura, le equazioni dovrebbero essere scritte per un sistema di riferimento che trasla e ruota con il corpo,
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 0 0,05 0,1 0,15 0,2 t EE CN
portando a non banali problemi nella trattazione delle condizioni al contorno.
In secondo luogo, dovendo adimensionalizzare le equazioni, è necessario poter definire da subito una dimensione e una velocità di riferimento. Per il caso del cilindro con il solo grado di libertà di rotazione, trattato nel capitolo precedente, l’adimensionalizzazione non pone problemi, dato che si può sceglie di usare come velocità di riferimento quella di ingresso e come dimensione il diametro D del cilindro. Nel caso affrontato in questo capitolo, invece, non è nota a priori alcuna velocità caratteristica del flusso. Per ovviare a questo è possibile selezionare, come velocità di riferimento U, la velocità terminale del cilindro, ovvero quella raggiunta del corpo una volta che la risultate delle forze si porti a un valore mediamente3 nullo. Tuttavia la sua definizione richiede una procedura iterativa che si articola nei seguenti punti:
1. Si sceglie un valore di primo tentativo del coefficiente di resistenza medio e, risolvendo l’equazione di equilibrio del cilindro nella condizione di moto mediamente stazionario, si ricava una prima stima della velocità terminale UT;
2. Si pone il valore UT stimato in input al modello4 e si esegue la simulazione;
3. La velocità terminale del cilindro, una volta raggiunta la condizione di moto mediamente stazionario, non sarà esattamente pari a quella stimata al punto 1, per cui si deve iterare questa procedura, aggiornando il valore del coefficiente di resistenza medio in modo che le due velocità coincidano. Infine, come già mostrato nel Capitolo 3, nell’equazione di risoluzione della dinamica del cilindro, il termine di forza peso è considerato in direzione orizzontale, per comodità nell’esecuzione delle
3 La presenza del vortex shedding fa si che le forze abbiano fluttuazioni nel tempo, per
cui il cilindro raggiunge una velocità costante solo in termini medi.
simulazioni5. Tuttavia, trattando di corpi che cadono o galleggiano in un fluido in quiete, è più realistico, nell’esposizione dei risultati, fare riferimento alla direzione verticale come quella di avanzamento di un corpo che è soggetto alla forza di gravità.
5.1.3 Condizioni iniziali e condizioni al contorno
La simulazione del flusso attorno al cilindro non vincolato ha inizio dalla condizione stazionaria. Quindi, la condizione iniziale può essere espressa come:
𝒖 = 𝟎 𝑖𝑛 𝟎 × 𝜴
Inoltre, scrivendo le equazioni in un sistema di riferimento che trasla solidalmente con il corpo, è evidente che anche sui bordi laterali si dovranno imporre le condizioni al contorno che consentono al campo di potersi sviluppare correttamente. Definendo, quindi, con 𝒖𝑩 il vettore
velocità del corpo e con 𝜗! la sua rotazione, si arriva a scrivere il seguente set di condizioni al contorno:
𝒖 = −𝒖𝑩 𝑖𝑛 0, 𝑇 × ∂Ω!"
𝒖 = −𝒖𝑩 𝑖𝑛 0, 𝑇 × ∂Ω!"#
𝒖 = −𝑦 ∙ 𝜗!∙ 𝒊 + 𝑥 ∙ 𝜗!∙ 𝒋 𝑖𝑛 0, 𝑇 × ∂Ω!
La relazione sul bordo del cilindro circolare, in analogia a quanto osservato nel capitolo precedente, assicura il rispetto della condizione di non scorrimento del fluido sul corpo, in riferimento al grado di libertà di rotazione.
5.2. Caratteristiche
della
soluzione
e
validazione con i dati di letteratura
La validazione del modello è ottenuta mediante il confronto dei risultati ottenuti con quelli esposti in (Namkoong et al., 2008). Tuttavia è
5 Variando il segno dell’accelerazione di gravità, infatti, è possibile avere sempre una condizione di inflow sul bordo sinistro del dominio e una condizione di outflow sul bordo destro, così da non dover mai modificare le condizioni al bordo.
necessario in primo luogo fornire una descrizione delle caratteristiche della soluzione. Il cilindro, sottoposto alla forza peso e all’azione del flusso, tende a disporsi su una traiettoria di salita o di discesa (rispettivamente per α < 1 e α > 1), con una velocità verticale media costante (si veda paragrafo 5.2.2). La presenza del vortex-shedding, però, conferisce al moto del cilindro una caratteristica di non-stazionarietà, portando a fluttuazioni sia nelle componenti di velocità di traslazione che in quella rotazionale. La velocità in-line presenta fluttuazioni di piccola ampiezza attorno al valore della velocità media, con una frequenza di oscillazione doppia rispetto a quella di vortex-shedding. La componente di crossflow e quella di rotazione, entrambe a media nulla, hanno una frequenza di oscillazione esattamente pari a quella di distacco dei vortici. Un esempio di questi andamenti è fornito nelle Figure 5.6 - 5.7 per il caso di α = 4 e Re = 100.
Figura 5.6 – Andamento della velocità in-‐line per il caso di 𝜶 = 𝟒 e Re = 100
0 0,2 0,4 0,6 0,8 1 1,2 0 20 40 60 80 100 120 140 160 180 u/U tU/D
Figura 5.7 – Andamento della velocità trasversale v ( ) e della velocità di rotazione 𝝑𝑩 ( ) per il caso di 𝜶 = 𝟒 e Re = 100
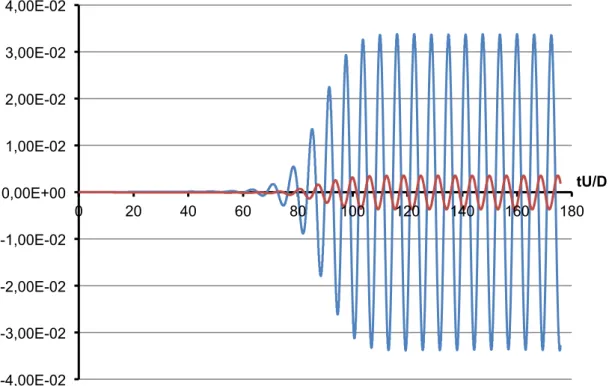
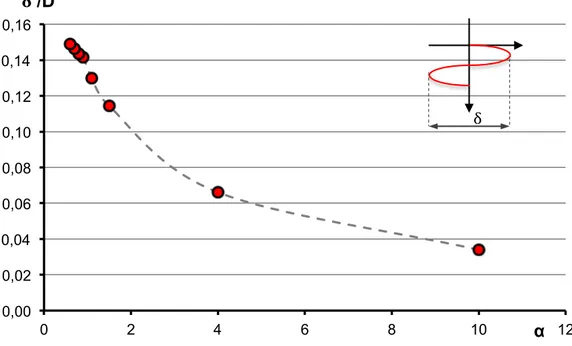
La caratteristica di periodicità delle componenti di velocità del cilindro, porta il corpo a impegnare una traiettoria oscillatoria, come mostrato in Figura 5.8 per il caso di α = 4 e Re=100. Le ampiezze delle oscillazioni trasversali sono tuttavia funzione di α, dato che più basso è il rapporto di massa e più importante è la risposta dinamica del corpo al vortex shedding. Allo scopo di evidenziare tale aspetto, in Figura 5.9 è presentato l’andamento dell’ampiezza di oscillazione trasversale massima raggiunta dal corpo in condizioni di flusso stabile in funzione di α (l’ampiezza è qui definita come lo spostamento trasversale del cilindro dal massimo positivo al massimo negativo, come evidenziato in Figura).
-4,00E-02 -3,00E-02 -2,00E-02 -1,00E-02 0,00E+00 1,00E-02 2,00E-02 3,00E-02 4,00E-02 0 20 40 60 80 100 120 140 160 180 tU/D
Figura 5.8 – Traiettoria del cilindro per il caso di 𝜶 = 𝟒 e Re = 100
Figura 5.9 – Andamento dell’ampiezza di oscillazione del cilindro in condizioni di flusso stabile
per Re = 100 e al variare di 𝜶. -180 -160 -140 -120 -100 -80 -60 -40 -20 0 -3 ,0 0E-0 2 -2 ,0 0E-0 2 -1 ,0 0E-0 2 0, 00 E+0 0 1, 00 E-0 2 2, 00 E-0 2 3, 00 E-0 2 4, 00 E-0 2 5, 00 E-0 2 x/D y/D 0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14 0,16 0 2 4 6 8 10 12 δ /D α δ
Dal punto di vista del flusso, la soluzione presenta delle caratteristiche che lo differenziano rispetto alla soluzione relativa al caso del cilindro circolare fisso. È utile, dunque, studiare come evolve la soluzione in un semiperiodo di distacco dei vortici. Si faccia riferimento alle Figure 5.10-5.11. L’idea di base è che il corpo, al netto della velocità media di avanzamento, percorre una traiettoria a “otto” per effetto della scia di von Karman. Nell’istante in cui inizia a formarsi il vortice antiorario sulla parte destra della scia (punto A), la bassa pressione associata alla formazione del vortice fa sì che il corpo acquisti una velocità laterale, risultando di fatto “aspirato” dal vortice stesso. Tale velocità laterale raggiunge il massimo quando il cilindro passa nel centro della scia (punto B della curva). Infine il vortice si separa e l’allontanamento dal cilindro comporta un recupero di pressione sulla base del corpo, che avanza fino alla posizione C, da dove inizia a formarsi il vortice di segno opposto sull’altro lato della scia.
Figura 5.10 – Traiettoria del cilindro al netto della velocità di discesa per 𝜶 = 𝟒 e Re = 100
-0,0003 -0,00025 -0,0002 -0,00015 -0,0001 -0,00005 0 0,00005 0,0001 0,00015 0,0002 0,00025 0,0003 -0,04 -0,03 -0,02 -0,01 0 0,01 0,02 0,03 0,04 x/D y/D
A
B
C
Figura 5.11 – Visualizzazione del campo di velocità e della vorticità per i tre punti individuati in Figura 5.9
Tale dinamica è ulteriormente confermata dall’analisi delle forze istantanee sul cilindro e dalle relative accelerazioni in un periodo di vortex shedding, mostrate in Figura 5.12 e 5.13 in riferimento agli istanti A,B,C definiti nelle Figure 5.10 e 5.11.
P -0,25 -0,2 -0,15 -0,1 -0,05 0 0,05 0,1 0,15 0,2 0,25 0 1 2 3 4 5 6 7 B A B C C B A A t 1,28 1,285 1,29 1,295 1,3 1,305 0 1 2 3 4 5 6 7 A B C B A t CD CL
Figura 5.12 – Andamento dei coefficienti di forza in un ciclo di vortex shedding per Re = 100 e
𝜶 = 𝟒 : (a) CL , (b) CD.
(a)
Per quanto riguarda i coefficienti di forza medi, l’effetto complessivo è quello di una riduzione, rispetto al caso del cilindro fisso, sia del valore r.m.s del CL che del valor medio nel tempo del CD, come mostrato in Figura 5.14. Tale andamento conferma qualitativamente quanto evidenziato nello studio di (Namkoong et al., 2008), sebbene nel presente lavoro il coefficiente di resistenza risulti lievemente superiore. Questa riduzione dei coefficienti di forza rispetto al caso stazionario è strettamente collegata alla possibilità del cilindro di muoversi nella direzione in-line, che gli consente di avere un maggiore recupero di
-0,04 -0,03 -0,02 -0,01 0 0,01 0,02 0,03 0,04 0 1 2 3 4 5 6 7 -0,0025 -0,002 -0,0015 -0,001 -0,0005 0 0,0005 0,001 0,0015 0,002 0,0025 0 1 2 3 4 5 6 7
Figura 5.13 – Andamento delle accelerazioni istantanee sul cilindro durante un ciclo di vortex shedding per Re = 100 e 𝜶 = 𝟒 : (a) accelerazione trasversale ay , (b) accelerazione in
line ax. A B C A B ay t t ax (a) (b)
pressione nel momento in cui i vortici si staccano dalla base. Qualora invece il cilindro fosse libero di oscillare solo in direzione crossflow, allora i coefficienti di forza sarebbero esattamente pari a quelli del caso del cilindro fisso (si veda Namkoong et al., 2008 e Beretta S.L., 2007).
Figura 5.14 –Valori dei coefficienti CD e CL (r.m.s) a Re =100 e per vari valori di alfa. La linea tratteggiata
rossa indica il valore del coefficiente per il caso del cilindro circolare fisso.
Al fine di validare il modello agli elementi finiti, un ulteriore confronto con lo stesso studio può essere tracciato in merito al numero di Strouhal (di seguito indicato con St). Infatti, la presenza di oscillazioni sul corpo porta a un rallentamento nella dinamica della scia con una conseguente riduzione della frequenza di distacco dei vortici. Si selezioni, quindi, un valore del Re, ad esempio pari a 100, e si faccia variare il valore di α. Per quanto esposto in merito all’ampiezza delle oscillazioni in funzione della densità del corpo, è lecito attendersi che, a più bassi valori di α, l’effetto di riduzione del numero di St sia maggiore. In effetti, tale ipotesi è confermata dall’andamento di Figura 5.15: i risultati del presente lavoro, definiti con gli indicatori discreti, sono qui confrontati con l’andamento mostrato in letteratura, riportato in linea tratteggiata. Si osserva in primo luogo che i due andamenti sono del tutto compatibili, mostrando uno scostamento massimo inferiore all’1%. Questo assicura la validità del modello fin qui utilizzato. In secondo luogo, ricordando che il numero di St per la scia alternata del cilindro fisso è pari a 0,165 per Re = 100 (si veda Figura 4.6 Capitolo 4), si osserva come i valori siano in
0 0,05 0,1 0,15 0,2 0,25 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 CL(rms) 1,2 1,22 1,24 1,26 1,28 1,3 1,32 1,34 0,5 1,5 2,5 3,5 4,5 CD α α
questo caso sensibilmente minori (si arriva ad avere delle variazioni dell’ordine del 10-15%), sebbene l’ampiezza di oscillazione trasversale del cilindro non superi il 15% del diametro.
Figura 5.15 – Andamento numero di Strouhal per Re = 100 in funzione del rapporto tra le densità 𝜶. Si può
notare che i valori determinati nel presente lavoro ( ) sono perfettamente sovrapponibili rispetto a quelli definiti in (Namkoong et al., 2008). (- -)
Infine, allo scopo di avere un’indicazione più completa del comportamento della frequenza di distacco dei vortici, si consideri il caso opposto, ovvero mantenendo costante il valore di 𝛼 e facendo variare il numero di Re. I risultati delle simulazioni sono riportati in Figura 5.16. In questo caso si trova un andamento che ricalca sostanzialmente quello relativo al caso del cilindro stazionario. Tale risultato sta a indicare che, per variazioni modeste del numero di Re, le variazioni delle ampiezze di oscillazioni risultano altrettanto esigue, per cui l’effetto di modifica sulla frequenza di vortex shedding può essere trascurato. In quest’ottica, i dati forniti dalle simulazioni consentono di sviluppare una relazione che valuta il numero di St per ogni coppia (𝛼,Re) selezionata per il caso del
0,1591 0,1528 0,1506 0,1495 0,1489 0,1481 0,1468 0,142 0,144 0,146 0,148 0,15 0,152 0,154 0,156 0,158 0,16 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 St α
cilindro libero di muoversi. In particolare si sceglie di seguire la stessa metodologia utilizzata in Namkoong et al. (Namkoong et al., 2008), ovvero quella di partire dalla relazione che lega l’andamento del numero di St al numero di Re, secondo quanto proposto nel lavoro di Williamson e Brown (Williamson e Brown, 1998), e aggiungere la dipendenza del numero di St al valore del parametro 𝛼. In quest’ottica, interpolando i dati ottenuti dalle simulazioni è possibile ottenere una relazione del tipo6:
𝑆𝑡 = 𝛼 + 𝐷𝛼 + 𝐶 ∙ 𝐴 − 𝐵
𝑅𝑒 (5.1) dove:
A = 0,2660 C = 1,0790 B = 0,9975 D = 1,2930
La variazione del numero di St è collegata, quindi, con la possibilità del cilindro di muoversi trasversalmente rispetto alla direzione di discesa o di salita. Questo significa che, se considerassimo un valore di α molto grande, dovremmo ottenere una soluzione simile a quella del cilindro circolare fisso, dato che l’inerzia del corpo rispetto alle velocità indotte dal distacco dei vortici sarebbe molto grande. La relazione precedente conferma tale affermazione dato che, nel caso di 𝛼 ≫ 1 , l’espressione si riduce a un’equazione del tipo 𝑆𝑡 = 𝑓( !!"), con coefficienti analoghi a quelli presentati nel capitolo 2 dovuti a Willimanson e Brown (Williamson e Brown, 1998).
6 L’interpolazione è eseguita in ambiente MatLab, dove è possibile impostare una forma
della relazione che si vuole sviluppare e determinare i valori delle costanti in modo che la funzione risultate approssimi nel miglior modo possibile il set di dati ottenuti dalle simulazioni.
Figura 5.16 – Andamento numero di Strouhal in funzione di 𝜶 e numero Re (i valori indicati in legenda si riferiscono al valore di 𝜶). Le linee tratteggiate rappresentano l’andamento della relazione 5.1 presentata a
pagina precedente, estrapolata dai dati ottenuti dalle simulazioni, che invece sono riportati con indicatori discreti.
5.3. Mappa di stabilità
Il modello evolutivo d’interazione fluido-struttura fin qui utilizzato è sfruttato, infine, per svolgere un’analisi di stabilità del flusso. Si ricerca, per valori di α selezionati, il valore del Recr d’instabilità primaria per il quale si passa da una soluzione stabile stazionaria a una stabile ma periodica, con la formazione di una scia alternata di vortici. È appena stato mostrato che, al variare del rapporto tra le densità α, l’evoluzione della scia è diversa per il diverso valore del numero di St. Quindi è plausibile aspettarsi che anche il Recr possa essere funzione dello stesso parametro. È possibile fare un’ulteriore osservazione. Si
0,1 0,11 0,12 0,13 0,14 0,15 0,16 0,095 0,105 0,115 0,125 0,135 0,145 0,155 St Re-0.5 4 da relazione 1,5 da relazione 1,1 da relazione 0,9 da relazione 0,7 da relazione 0,6 da relazione 4 da simulazione 1,5 da simulazione 1,1 da simulazione 0,9 da simulazione 0,7 da simulazione 0,6 da simulazione
considerino due cilindri circolari con valori di α simmetrici rispetto a 1, ad esempio 1,1 e 0,9. All’equilibrio, se non si considerasse l’effetto della scia alternata, si dovrebbe avere qualitativamente la stessa dinamica, dato che la forza risultante, che fa cadere il primo e galleggiare il secondo cilindro, risulterebbe la stessa. Tuttavia, la differente risposta inerziale che i due corpi mostrano nei confronti del fenomeno del vortex-shedding, porta alla formazione di scie a frequenze diverse, per cui è possibile che ci sia un diverso effetto rispetto al fenomeno d’instabilità.
Nel paragrafo successivo è brevemente descritto il metodo numerico utilizzato in questa serie di simulazioni, mentre nell’ultimo sono esposti i risultati ottenuti.
5.3.1. Metodo numerico
La definizione delle caratteristiche di stabilità può essere affrontata attraverso varie metodologie. L’idea sviluppata in questa fase è di sfruttare nuovamente il modello evolutivo agli elementi finiti fin qui utilizzato, ma inizializzando la simulazione con la soluzione del problema di Navier Stokes stazionario per il cilindro fisso. Infatti, per ogni valore del Re, la soluzione stazionaria equivale alla soluzione che si avrebbe, allo stesso Re, considerando un cilindro non vincolato, che cade o galleggia secondo il valore di α, una volta che si sia eliminata l’instabilità di vortex shedding. A questo punto, ponendo tale soluzione in input al modello evolutivo, la simulazione può evolvere secondo due direzioni: se il flusso continua a rimanere stazionario, allora significa che, al valore dell’α selezionato, quel determinato numero di Re è al di sotto del Recr; se, viceversa, a partire dalla soluzione stazionaria, il cilindro si porta verso una soluzione periodica di vortex shedding, significa che il valore del Re è questa volta superiore al Recr.
5.3.2. Risultati
Per definire un numero sufficiente di punti nella curva di stabilità neutra, si considerano i seguenti valori di α e di Re:
𝛼 = [0,6 0,7 0,8 0,9 1,1 1,5 2 4 10] 𝑅𝑒 = [37 ÷ 47]
Ovviamente, volendo ridurre il costo computazionale delle simulazioni, non si eseguono le prove per tutte le combinazioni possibili di questi due parametri, ma si cerca da subito di individuare, per ogni valore di α , un più piccolo intervallo di Re all’interno del quale è plausibile aspettarsi di trovare il valore critico e si concentrano poi le prove all’interno di questo, in modo da individuare il valore corretto del Recr con il minor numero di simulazioni possibile.
I risultati ottenuti sono riassunti nelle Figure successive. In Figura 5.17 è riportata la curva di stabilità neutra in un grafico α-Re. Per prima cosa si nota come la diminuzione di densità del corpo comporti un’anticipazione dell’instabilità primaria rispetto al caso del cilindro circolare fisso, per il quale il Recr è pari a 47. L’altro aspetto fondamentale su cui porre attenzione, come già accennato nel paragrafo 5.4, è la non simmetria del grafico per valori di α simmetrici rispetto a 1.
𝛼
Recr
10 46 ± 1 4 45 ± 1 1,5 44 ± 1 1,1 43,5 ± 1 0,9 43 ± 1 0,8 42,5 ± 1 0,7 42 ± 1 0,6 41 ± 1
Figura 5.17 – Mappa 𝜶-‐Re per l’individuazione del margine della zona di instabilità primaria
Questi aspetti possono essere meglio evidenziati introducendo un parametro adimensionale ricavato dal numero di Fr, definito come:
𝐹𝑟! =
𝑈!
𝑔 ∙ 𝐷∙ 𝑈 𝑈
che indica, non solo il rapporto tra la forza inerziale e il peso, ma anche se il cilindro si trova su una traiettoria di salita (il cilindro galleggia e
𝐹𝑟!< 0), o su una traiettoria di discesa (il cilindro cade e 𝐹𝑟!> 0). Rispetto a questo parametro, la curva di stabilità neutra è riproposta in Figura 5.18. 10 4 1,5 1,1 0,9 0,8 0,7 0,6 0 1 2 3 4 5 6 7 8 9 10 11 40 41 42 43 44 45 46 47 48
α
Re Va lo re del R e cr p er il cil in dr o Z is so
Figura 5.18 - Valori del Recr in funzione del Frs
L’andamento evidenzia nuovamente come il parametro 𝛼 influenzi in modo decisivo il valore del Recr, portando a un’accelerazione del fenomeno di instabilità, via via maggiore al diminuire di 𝛼. Questo è spiegabile facendo riferimento all’evoluzione del campo al variare del numero di Re . Si consideri la soluzione del flusso che presenta due vortici stazionari alla base del corpo per Re < Recr. Le perturbazioni che nascono nel campo fluido all’aumentare del numero di Re, agiranno sul corpo che, essendo non vincolato, inizierà a muoversi anche in direzione trasversale7, anticipando la formazione della scia di von Karman rispetto al caso del cilindro vincolato.
7 È evidente che l’accelerazione del corpo in direzione trasversalmente comporta la
nascita di una componente di massa aggiunta che rallenta lo spostamento del corpo e
34 35 36 37 38 39 40 41 42 43 44 45 46 47 -1 -0,5 0 0,5 1 1,5 2 2,5 3 3,5 Re Frs
L’aspetto da rilevare è quello della non simmetria nei numeri di Recr per casi che hanno uguali valori, in modulo, del Frs. Si considerino, infatti, nuovamente i due cilindri con 𝛼 pari a 0,9 e 1,1. La forza propulsiva che fa muovere i due corpi è, a meno del segno, necessariamente la stessa, poiché data dalla differenza tra la forza peso e la spinta di Archimede8. Tuttavia, questo non assicura che la dinamica di formazione della scia alternata di vortici sia la stessa. Infatti, la minore inerzia del cilindro più leggero corrisponde a una maggiore risposta dinamica alle perturbazioni indotte dal flusso, e questo spiega perché l’instabilità avviene a valori del numero di Re via via minori al diminuire di 𝛼.
Infine è doveroso fare una precisazione. Si è detto che casi con valori di 𝛼simmetrici rispetto a 1 presentano uguali valori del Frs. Questo
tuttavia è vero solo in prima approssimazione dato che, per numeri di Re maggiori del numero di Recr, i due corpi hanno CD diversi, a causa della differente instabilità a cui vanno soggetti. Ciò comporta che le velocità a regime saranno, per le varie coppie di corpi, diverse. Tuttavia la variazione del CD è lieve per piccole variazioni di Re e quindi anche le variazioni di velocità saranno modeste.
5.4. Proper orthogonal decomposition
Lo scopo principale della proper orthogonal decomposition (o POD) è quello di rappresentare un fenomeno complesso di grandi dimensioni attraverso un modello di ordine ridotto. La definizione stessa implica che il modello risultante dovrà contenere le componenti significative del problema analizzato. Questa tecnica, estesamente utilizzata in molti ambiti scientifici, in campo fluidodinamico consente, tra i vari usi, di eseguire un’analisi a posteriori dei dati, in modo da identificare le principali strutture vorticose che sono presenti all’interno di un flusso. In
quindi ritarda il vortex shedding rispetto a quello che si potrebbe avere se non ci fosse la massa aggiunta.
8 Valutabile con un’espressione del tipo α − 1 ∙ ρ!∙ V ∙ g, dove con ρ! si è indicata la
questa sede si cerca di delineare gli aspetti fondamentali di questa procedura, mentre per approfondimenti sull’argomento si rimanda alla review dovuta a Luchtenburg et al. (Luchtenburg et al., 2009).
5.4.1. Formulazione analitica della POD
Attraverso la POD, la generica soluzione del campo fluido u(x,t) può essere scritta come una combinazione lineare di una base ortonormale ottimizzata 𝝓 𝒙 = 𝝓𝟏, 𝝓𝟐, … 𝝓𝑵 , secondo la relazione:
𝒖 𝒙, 𝑡 = 𝒂𝒊 𝑡
!
!!!
∙ 𝝓𝒊 𝒙 (1) dove i termini 𝝓𝒊 sono detti anche modi di POD mentre 𝒂𝒊 𝑡 sono i
corrispondenti coefficienti modali, che ne definiscono l’ampiezza in funzione del tempo. La base 𝝓9 è ottimizzata nel senso che, come verrà chiarito al termine del paragrafo, essa rappresenta la migliore approssimazione del campo, corrispondente al massimo tra la media temporale della proiezione del campo reale sulla base 𝝓, ovvero;
𝑚𝑎𝑥 (𝒖, 𝝋)!! !
𝝋 =
(𝒖, 𝝓)!! ! 𝝓 dove 𝝋 è una base generica.
La definizione dell’i-esimo modo di POD si ottiene attraverso la risoluzione del seguente problema agli autovalori sul dominio Ω:
𝑅 𝒙, 𝒚 ∙ 𝝓𝒊(𝒚) !
𝑑𝒙 = (𝑅 𝒙, 𝒚 , 𝝓(𝒚))!! = 𝜆!∙ 𝝓𝒊(𝒙)
dove 𝜆! è l’autovalore associato e 𝑅(𝒙, 𝒚) è il tensore di autocorrelazione
spaziale, definito dall’operatore media temporale10 applicato al prodotto tra la soluzione del campo i due generici punti, ovvero 𝑅 𝒙, 𝒚 = 𝒖 𝒙, 𝑡 ∙ 𝒖 𝒚, 𝑡 . Il tensore è autoaggiunto e semidefinito positivo. La prima
9 Detta anche spazio POD
10 L’operatore media ∙ è definito nel continuo come 𝑎 =!
! 𝑎 𝑑𝑡 !
! . Tuttavia in seguito
viene utilizzata anche la definizione discreta, attraverso l’operatore media d’insieme 𝑎! = lim!→!!! !!!!𝑎!.
proprietà assicura che i modi siano tra loro ortogonali, mentre la seconda che gli autovalori siano non negativi. Dato che l’integrale è esteso sul dominio di calcolo, il problema è di ordine pari al numero di punti in cui è discretizzato il dominio, quindi di solito molto elevato. La relazione (1), tuttavia, può essere letta sia come la combinazione lineare tra i modi spaziali e dei coefficienti temporali, sia come la combinazione lineare tra modi temporali e dei coefficienti spaziali (Luchtenburg et al., 2009).. La scelta di utilizzare quest’ultimo approccio consente di ridurre notevolmente l’ordine del problema, che dipenderà in questo caso dalla discretizzazione temporale. Procedendo in questo senso, nel presente studio si utilizza il metodo delle snapshots, nel quale il problema è discretizzato nel tempo attraverso la costruzione di M campi istantanei11 del tipo:
𝑼! 𝒙 = 𝑢(𝒙, 𝑡 !)
In analogia alla discretizzazione spaziale, l’elemento generico del tensore di autocorrelazione temporale discreto può essere scritto come:
𝑪(𝑡!, 𝑡!) =
1
𝑀 ! 𝑼 ! 𝒙 ∙ 𝑼 ! 𝒙 𝑑𝒙 e il problema agli autovalori diventa:
1
𝑇 𝑪(𝑡!, 𝑡!) ∙ 𝒂𝒊(𝑡!)𝑑𝑡!
𝑻 𝟎
= 𝜇! ∙ 𝒂𝒊(𝑡!)
Gli autovettori della matrice di correlazione C sono icoefficienti temporali 𝒂𝒊 = 𝒂𝒊(𝟏), 𝒂𝒊(𝟐), … 𝒂𝒊(𝑴) e inoltre, la dualità tra il problema spaziale e
quello temporale, fa sì che gli autovalori dei due problemi siano uguali, ovvero 𝜇! = 𝜆!. Sfruttando l’ortonormalità dei modi spaziali e temporali, i
modi di POD possono quindi essere calcolati attraverso la seguente proiezione: 𝝓𝒊(𝒙) = 1 𝑀𝜆! 𝒂𝒊(𝒎)∙ 𝑼! 𝒙 ! !!!
La caratteristica fondamentale dei modi di POD è quella di formare una base che risulti la più simile a tutte le snapshots considerate. Infatti, l’ortogonalità dei coefficienti temporali assicura che:
𝒂𝒊(𝒎)∙ 𝒂
𝒋(𝒎) = 𝜆! ∙ 𝛿!"
Dato che i coefficienti temporali sono la proiezione delle snapshots sui modi (𝒂𝒊(𝒎) = 𝑼! 𝒙 , 𝝓𝒊 𝒙 )!! , allora per il generico autovalore vale la seguente espressione: 𝜆! = 𝒂𝒊(𝒎)∙ 𝒂 𝒊(𝒎) = 1 𝑁 (𝑼! 𝒙 , 𝝓𝒊(𝒙))!!! ! !!! = 𝑼!,! !! !
dove ∙ !! è la norma indotta dal prodotto scalare. Questo risultato assicura che i modi con autovalori maggiori forniscano valori di 𝒂𝒊 più
grandi rispetto a quelli con autovalori minori. Inoltre si dimostra (Berkooz et al., 1993) che la base POD è in questo senso la migliore, essendo quella che fornisce il massimo valore della somma delle proiezioni delle snapshots sui modi stessi. Collegando poi la norma indotta dal prodotto scalare con l’energia cinetica Ec del flusso:
𝐸! = 1
2𝜌 𝑼 !!!
l’autovalore 𝜆! può essere espresso dall’equazione seguente:
𝜆! = 2 𝜌 𝟏 𝟐 𝜴 (𝑼!,! )!𝑑𝒙
Quindi, lo spazio POD è la base di campi che fornisce la migliore rappresentazione delle snapshots in termini di energia cinetica. Infine, se si ordinano i modi in senso decrescente rispetto ai loro autovalori, si ottiene che i primi hanno un contenuto energetico maggiore rispetto ai modi successivi. Dal punto di vista fluidodinamico, questo comporta che analizzando i primi modi si possono avere indicazioni importanti per comprendere quali sono le strutture principali che caratterizzano un flusso.
5.4.2. Analisi POD per il cilindro che cade in un fluido
in quiete
In questo paragrafo sono presentati i risultati dell’analisi POD per il caso del cilindro circolare non vincolato che cade in un fluido in quiete. Si seleziona 𝛼 = 1,1 per Re=45 e si estraggono 100 snapshots in un intervallo temporale 𝑇 = 40 (in unità adimensionali). Calcolando gli autovalori e ordinandoli in modo decrescente, si ottiene l’andamento di Figura 5.19 dove, per chiarezza, sono riportati solo i primi 50 modi. Questo andamento è tipico per il flusso attorno a un cilindro circolare con instabilità di vortex shedding: il modo 1 ha un autovalore molto grande, corrispondente al campo medio12, a cui segue una coppia di punti di pari valore, associati al fenomeno di distacco dei vortici.
Figura 5.19 – Spettro degli autovalori limitato ai primi 50 modi
Come evidenziato in precedenza, gli autovalori sono un indice dell’energia contenuta nei rispettivi modi. È quindi evidente, dal grafico di Figura 5.19, che il contenuto energetico dei primi dovrà corrispondere alla quasi totalità dell’energia del flusso. Escludendo il primo modo associato al
12 Spesso l’analisi POD viene riferita al campo istantaneo fluttuante, ricavato per
differenza tra il campo istantaneo totale e del campo medio. In questa sede invece l’analisi è svolta direttamente sul campo istantaneo quindi, essendo i modi ordinati per contenuto di energia cinetica, il primo modo POD sarà appunto quello del campo medio.
campo medio, infatti, si può dimostrare che i soli modi 2 e 3 contengono il 97% dell’energia totale.
• Modo 1 –Campo medio
In Figura 5.20 è rappresentato il primo modo di POD. Come già accennato, tale modo corrisponde al campo medio del flusso attorno al cilindro. • • • (a) (b) (c) y x y x y x
• Modi 2 e 3
Dall’analisi dello spettro di Figura 5.19 si ricava che gli autovalori di questi due modi sono uguali e quindi che le strutture che essi rappresentano hanno lo stesso contenuto energetico. Le Figure 5.21 e 5.22 mostrano che i modi 2 e 3 presentano andamenti che sono, con buona approssimazione, antisimmetrici rispetto a un piano che contiene l’asse x e quello di simmetria del cilindro.
(a) (b) (c) y x y x y x
Figura 5.11 – Modo 2: (a) Andamento del campo; (b) Componente X; (c) Componente Y.
Figura 5.22 – Modo 3: (a) Andamento del campo; (b) Componente X; (c) Componente Y.
I modi 2 e 3 sono associati, come già evidenziato, al fenomeno del vortex shedding. A dimostrazione di questo, è possibile ricostruire il campo come sommatoria dei primi tre modi di POD, moltiplicati per i rispettivi coefficienti modali, e confrontare il campo così ottenuto con la soluzione reale. Se si sceglie, ad esempio, di rappresentare la soluzione
(a) (b) (c) y x y x y x
alla snapshot 1, questa procedura fornisce i risultati di Figura 5.23: nella colonna di sinistra è riportato il campo reale, mentre nella colonna di destra quello ricostruito con i modi di POD. Dato che il modo 1 è associato al campo medio, allora la perfetta compatibilità tra le due soluzioni permette di confermare che ai modi 2 e 3 è associato il fenomeno del distacco dei vortici.
Gli andamenti di Figura 5.23 mettono anche in luce l’estrema validità dell’analisi POD, che consente di ottenere una buona approssimazione del complesso campo reale attraverso la somma dei soli primi 3 modi.
Figura 5.23 – Confronto tra la snapshot 1 del campo reale (figure nella colonna di sinistra) e il campo ricostruito utilizzando i primi 3 modi POD pesati con i rispettivi coefficienti modali (figure nella colonna di destra). Nelle figure a1 e a2 sono riportate le componenti x, mentre nelle b1 e b2
• Modi 4 e 5
Anche i modi 4 e 5, le cui componenti sono rappresentate nelle Figure 5.24 e 5.25, risultano associati a strutture con un pari contenuto energetico, sebbene inferiore di ordini di grandezza rispetto ai modi 2 e 3.
Figura 2.24 – Modo 4: (a) Andamento del campo; (b) Componente X; (c) Componente Y. (a) (b) (c) y x y x y x
Figura 5.25 – Modo 5: (a) Andamento del campo; (b) Componente X; (c) Componente Y. (a) (b) (c) y x y x y x