Appendice A Equazioni del modello energetico

Appendice A Equazioni del modello energetico

Appendice A Equazioni del modello energetico

In questa appendice vengono riportati tutti i passaggi analitici che permettono di ottenere le equazioni e le relazioni utilizzate nel "modello energetico" elaborato nel capitolo 2, nonché alcuni commenti di supporto.

A.1 Puro rotolamento stazionario su pista

La condizione di puro rotolamento stazionario è alla base di tutto lo studio svolto, in quanto consente di definire un parametro fondamentale: Re, raggio di puro rotolamento.

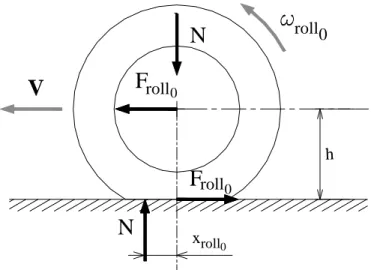
La figura A1 traduce graficamente la definizione riportata nel capitolo 1 nel paragrafo 1.3: la ruota è trainata a velocità costante, in assenza di coppie applicate al mozzo, da una forza tale da compensare l’azione della resistenza al rotolamento.

N

0 roll

F

h x 0 roll roll₀

F

V

0 roll

N

figura A.1 Puro rotolamento stazionario su pista.

Appendice A Equazioni del modello energetico     µ = = − N F 0 Nx h F 0 roll 0 roll 0 roll 0 roll (A.1.1) con 0 roll e V R ω = (A.1.2) Equazione dell’energia V F P₀ = _roll0 (A.1.3)

Il lavoro compiuto dalla forza F_roll0 nell’unità di tempo è tale da compensare la dissipazione dell’energia causata tra il battistrada e la superficie della pista.

A.2 Rotolamento quasi stazionario su pista

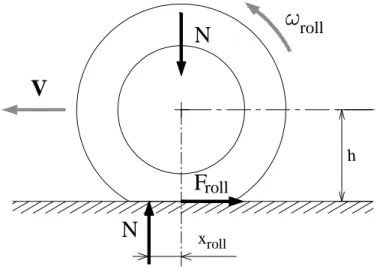
La condizione di puro rotolamento quasi stazionario su pista non prevede l’applicazione di alcun genere di coppie o forze al mozzo della ruota (oltre al carico verticale N). L’interazione tra battistrada e superficie della pista dà come risultato la nascita della forza di rotolamento (

1 roll

F ) che si oppone al moto, determinando una dissipazione di energia non compensata dall’esterno, da cui il rallentamento progressivo della ruota, figura A.2.

Equazioni del moto

    − = µ = − = ω V m N F Nx h F I 1 roll 1 roll 1 roll 1 roll 1 roll & & (A.2.1)

Appendice A Equazioni del modello energetico

N

roll

V

roll x h

F

roll

N

figura A.2 Rotolamento quasi stazionario su pista.

dove con m si indica la somma delle masse del corpo che si immagina collegato al mozzo della ruota e della ruota stessa.

Supponendo di misurare V& e

1 roll ω& :      − =       ω + = V m F V m I h 1 1 N h F x 1 roll 1 roll 1 roll 1 roll & & & (A.2.2) Energia dissipata 1 roll 1 roll I V V m

P =− & − ω& ω (A.2.3)

oppure mettendo in evidenza −m &VVed usando la seconda delle (A.2.1), la si può riscrivere nella seguente forma:

      ω ω + = V m I V 1 V F P roll1 roll1 1 roll _& & (A.2.4)

Appendice A Equazioni del modello energetico

(A.2.4) non serve un gran che perché se si misurano V& e

1 roll

ω& le (A.2.1), (A.2.2), (A.2.3) forniscono tutto, forza braccio ed energia dissipata.

Raggio di rotolamento

La misura sperimentale di V e

1 roll

ω consente di definire il raggio di rotolamento R_e1:

1 roll 1 e V R ω = (A.2.5) con R f(V,N) 1 e = . La 1 roll

ω può essere derivata rispetto al tempo, ottenendo, per N=cost:

( )

( )

_       − =         − = − =         = ω dV dR R V 1 R V R dt d V 1 R V 1 R V R dt d R V R V R V dt d e₁ 1 e 1 e 1 e 1 e 1 e 1 e 2 1 e 1 e 1 e 1 roll & & & & & (A.2.6) infine ponendo: V 1 e 1 e 1 dV dR R V = ε (A.2.7)

la (A.2.6) può essere riscritta come:

(

1

)

1 e 1 roll 1 R V ε − =

ω& & (A.2.8)

Si ricorda che il pedice 1 qui usato, anziché 0 come nel caso precedente, evidenzia che le due situazioni, sebbene vicine dal punto di vista dell’ordine di grandezza delle quantità in gioco, sono a rigore ben distinte.

Appendice A Equazioni del modello energetico

(

)

        ε − + =       ω + = 1 1 e 1 roll 1 roll 1 roll 1 roll 1 R 1 mh I 1 N h F V m I h 1 1 N h F x & &       ω ω + = V m I V 1 V F P roll1 roll1 1 roll _& & da cui ponendo:

(

1

)

2 1 e 1 1 R 1 m I ε − = ξ (A.2.9) si ottiene:       ξ + = 1 1 e 1 roll 1 roll h R 1 N h F x (A.2.10)

(

1

)

1 roll V1 F P = +ξ (A.2.11)

Nota la funzione R_e1 =f₁

(

V,N

)

e calcolata la P tramite la (A.2.3), queste ultime consentirebbero di determinare forza e braccio. Se però si calcolano forza, braccio ed energia dissipata tramite le (A.2.1), (A.2.2), (A.2.3), la (A.2.10) e la (A.2.11) non servono. Tuttavia consentono di calcolare tutto senza dover misurare o stimare ω&_roll1.

A.3 Frenata quasi stazionaria su pista

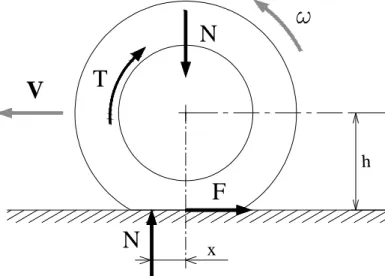
La condizione di frenata su pista prevede l’applicazione al mozzo della ruota di una coppia frenante T, che assieme al piccolo contributo della dissipazione di energia per il rotolamento, determina la progressiva diminuzione della velocità angolare, figura A.3. In particolare si parla di frenata quasi stazionaria nel caso semplificativo in cui s&_x =0, cioè quando l’intensità della frenata si mantiene costante tutto il tempo.

Appendice A Equazioni del modello energetico

T

N

F

h x

V

N

figura A.3 Frenata quasi stazionaria su pista.

Equazioni del moto

   − = µ = − − = ω V m N F T Nx Fh I & & (A.3.1)

oppure supponendo di misurare V& e ω& :

     − =             _ω+ + = V m F V m T I h 1 1 N Fh x & & & (A.3.2) Energia dissipata ω − ω ω − − = mVV I T

P & & (A.3.3)

oppure mettendo in evidenza −m &VVed usando la seconda delle (A.3.1):

            ω+ ω + = V m T I V 1 FV P & & (A.3.4)

Appendice A Equazioni del modello energetico Raggio di rotolamento frenato

La misura sperimentale di V e ω consente di definire il raggio di rotolamento frenato

b e R : ω = V R b e (A.3.5)

mentre l’intensità della frenata è rappresentato dallo slittamento pratico s_x:

b e e e e x R R 1 V R 1 V R V s = −ω = −ω = − (A.3.6)

in cui R è definito come: _e

e roll R 1 V = ω (A.3.7)

essendo ω_roll la velocità angolare che la ruota avrebbe, a pari velocità V, se non fosse frenata.

Conseguente delle relazioni cinematiche

Le relazioni cinematiche ora ricavate possono essere rielaborate per ottenere altre relazioni che sostituite nelle equazioni del moto e dell’energia, permettono di arrivare ad utili espressioni delle forze ed il braccio della risultante delle pressioni al suolo.

Derivando ω_roll rispetto al tempo, in modo analogo a quanto fatto per il puro rotolamento quasi stazionario con la (A.2.8) si ottiene:

( )

−ε = ω 1 R V e roll & & (A.3.8)

Appendice A Equazioni del modello energetico dt dR R V R V R V dt d e_b 2 b e b e b e − =         =

ω& & (A.3.9)

ma dalla (A.3.6):

(

)

(

)

₂ x x e e x x e b e s dt d s 1 R dt dR s 1 1 s 1 R dt d dt dR − + − =       − = (A.3.10)

Il raggio di rotolamento R è funzione dello schiacciamento (o del carico verticale N) e _e della velocità V, quindi in generale vale che

( )

V R V R dt V , dRe e e ∂ ∂ + δ ∂ ∂ δ = δ _{& &} , la quale per il caso specifico di carico verticale costante si riduce a:

V R V dt dR_{e e} ∂ ∂ = & _(A.3.11)

Sostituendo la (A.3.11) nella (A.3.10) e svolgendo i calcoli si ottiene:

(

)

(

)

(

)

(

)

(

)

(

)

      − + − = − + − = − + − = x x e e x e x 2 x e e e e x x 2 x e e x b e s 1 s dV dR R V V V s 1 R s s 1 R dV dR VR VR s 1 V s s 1 R dV dR s 1 V dt dR & _& & & & &

per cui infine:

(

)

      − + ε = x x b e b e s 1 s V V R dt dR & _& (A.3.12)

La (A.3.12) si può ulteriormente modificare come segue:

(

)

( ) (

)

(

x

)

x e x b e x x b e b e b e 2 b e b e b e 1 s s R s 1 V 1 R V s 1 s V V R V R V dt dR R V R V R V dt d − − − ε − =       − + ε − = − =         =

Appendice A Equazioni del modello energetico

( )

x e b e s R V 1 R V & & & = −ε − ω (A.3.13)

che invertita può essere scritta così:

(

)

(

)(

)

V R 1 s 1 V V 1 R V V R s _x e b e e x ω − ε − − =         ω − ε −

= & & & &

& (A.3.14)

Prendendo poi in considerazione la definizione di frenata quasi stazionaria la (A.3.13) diventa:

( )

−ε = ω 1 R V b e & & (A.3.15)

Concludendo, dal rapporto tra la (A.3.8) e la (A.3.15), facendo uso della (A.3.6), si può scrivere:

(

x

)

roll b e e roll 1 s R R − ω = ω =

ω& & & (A.3.16)

Riformulazione dell’equazione dell’energia

Sostituendo la (A.3.5) e la (A.3.15) nella (A.3.3), si ha:

( )

( )

− ω         ε − + − = ω − ε − − − = 1 T R 1 m I 1 V V m T R V 1 R V I V V m P ₂ b e b e b e & & & ponendo poi:

( )

−ε = ξ 1 R 1 m I 2 b e (A.3.17) si ottiene:

Appendice A Equazioni del modello energetico

(

+ξ

)

− ω

=FV1 T

P (A.3.18)

Scomposizione dell’equazione dell’energia in due contributi

L’ipotesi fondamentale che caratterizza il modello energetico è quello di considerare la risultante delle azioni scambiate all’interfaccia pneumatico-suolo, F, come somma di due contributi: quello indicato con F_roll mediante il quale viene dissipata potenza a causa della deformabilità del pneumatico che genera isteresi, aderenza e attrito, e quello F legato _b esclusivamente all’azione della coppia T agente sul mozzo della ruota la quale comporta una diversa ridistribuzione delle pressioni rispetto al caso di puro rotolamento ed un innalzamento dell’intensità delle azioni scambiate. Si assume quindi che valga la seguente:

b roll F

F

F= + (A.3.19)

Sostituendo la (A.3.19) nella (A.3.18):

(

+

)(

+ξ

)

− ω

= F F 1 V T

P _{roll b} (A.3.20)

ed adoperando la divisione dei contributi come indicato sopra, l’equazione della potenza viene divisa in due diverse equazioni:

(

)

V P 1 1 F_roll ξ + = (A.3.21)

(

)

eb b R T 1 1 F ξ + = (A.3.22)

Determinazione del braccio

Sostituendo la (A.3.19) e il T dato dalla (A.3.22) nella prima delle (A.3.1), si ha:

(

1

)

F h Nx h R 1 h F I T Nx h F h F I eb _roll b roll b + −      ξ + − = ω ⇒ − − + = ω& &

Appendice A Equazioni del modello energetico

e nella seconda delle (A.3.1), le (A.3.15) e (A.3.19),si ha:

(

+

)( )

−ε − = ω F F 1 m I R 1 I _{b roll} b e &

Le due equazioni eguagliate tra loro danno:

(

)( )

(

1

)

F h Nx h R 1 h F 1 F F m I R 1 roll b e b roll b b e − +       ξ + − = ε − + −

dalla quale si ottiene l’equazione del braccio in funzione di F_roll e F : _b

        ξ + +       − = h R 1 h N F h R 1 h N F x b eb roll eb (A.3.23)

A.4 Frenata non stazionaria su tamburo rotante

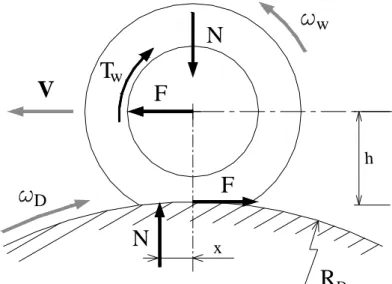
Anche nella condizione di frenata non stazionaria su tamburo rotante la ruota rallenta per effetto della coppia applicata al mozzo e della dissipazione dell’energia. Ma oltre a questi aspetti deve essere preso in considerazione quello legato alla curvatura del tamburo. Infatti il sistema è descritto da due equazioni del moto delle quali la prima, relativa alla ruota, è formalmente identica a quelle del caso precedente, la seconda, relativa al moto del tamburo, presenta il termine −Nx/R_D che rappresenta la coppia di opposizione al moto data dalla risultante delle pressioni all’interfaccia pneumatico-superficie del tamburo agente sul tamburo stesso, figura A.5. Tale coppia, influenzando direttamente la dinamica del tamburo influenza indirettamente anche la ruota, variandone la dinamica rispetto al caso di pista piana.

Inoltre ora la massa m rappresenta la massa del tamburo rotante mentre I rappresenta il _w momento di inerzia rispetto all’asse della ruota dovuta alla massa della ruota stessa, del freno e di tutti gli organo ad essi collegati.

Appendice A Equazioni del modello energetico w D

R

D w

T

N

F

h x

V

N

F

figura A.4 Frenata non stazionaria su tamburo rotante.

Equazioni del moto

     − − = − − = ω D D w w w R x N F V m T Nx Fh I & & (A.4.1) con ₂ D D D R I m = e V=R_Dω_D.

Le equazioni (A.4.1) possono essere manipolate e riscritte in una forma tale da poterle utilizzare per calcolare forza e braccio dalle misure sperimentali. Moltiplicando la seconda delle (A.4.1) per R_D e sottraendo la seconda dalla prima si ottiene:

Nx FR T Nx Fh R V m I Nx FR R V m T Nx Fh I D w D D w w D D D w w w + + − − = − ω ⇒    − − = − − = ω & & & & w D D w w D D w D D D D w w I m VR T R h 1 FR T R h 1 FR R V m I _ = ω − +      + + ⇒ −       + + = −

ω_& & _& &

Appendice A Equazioni del modello energetico

(

)

      + + ω + − = D D w w w D R h 1 R T I V m F & & (A.4.2)

Moltiplicando ora la seconda delle (A.4.1) per h e sommandola alla prima si ottiene:

h R x N Fh T Nx Fh h V m I h R x N Fh h V m T Nx Fh I D w D w w D D w w w − − − − = + ω ⇒      − − = − − = ω & & & & w D w w D w D D w w I m Vh T R h 1 Nx T R h 1 Nx h V m I _=− ω − −      + ⇒ −       + − = +

ω_& & _& &

da cui si può ottenere il braccio x:

(

)

      + + ω − − = D w w w D R h 1 N T I h V m

x & & (A.4.3)

Energia dissipata

In questo caso l’equazione dell’energia dissipata può essere scritta come:

(

w w w

)

w

DVV I T

m

P =− & − ω& + ω (A.4.4)

Relazioni cinematiche

Per quanto riguarda le relazioni cinematiche continuano a valere quelle ricavate nel caso di

frenata quasi stazionaria su pista, (A.3.5), (A.3.6), (A.3.7):

w b e V R ω = ; b e e e e w x R R 1 V R 1 V R V s = −ω = −ω = − ; roll w e V R ω =

Appendice A Equazioni del modello energetico Conseguenze delle relazioni cinematiche

Continuano a valere anche le altre relazioni, derivanti dalle (A.3.5), (A.3.6), (A.3.7):

V R V dt dR_{e e} ∂ ∂ = & _;

(

)

      − + ε = x x b e b e s 1 s V V R dt dR & _& ;

( )

_x e b e w s R V 1 R V & & & = −ε − ω

ma a differenza del caso precedente qui non si ha più l’ipotesi di stazionarietà s&_x ≠0. Manipolando la (A.3.7) il gruppo

(

I_wω&_w +T_w

)

che compare nelle equazioni (A.4.2) (A.4.3) e (A.4.4) assume la seguente forma:

( )

( )

      − + ε − = +         − ε − = + ω x e w w w b e 2 D 2 D w D w x e b e w w w w s R V T I 1 T 1 R R mR I V m T s R V 1 R V I T

I & & & & &

da cui:

( )

D w

(

f

)

b e 2 D w w w m V T 1 u R R 1 T

I ω& + =ς −ε & + + (A.4.5)

in cui ζ e u_f sono dei parametri adimensionali funzioni del tempo definiti come:

D w 2 D D w I I R m I = = ς (A.4.6) x e w w f s R V T I u =− & (A.4.7)

dove u_f viene chiamato fattore non stazionario.

Riformulazione dell’equazione dell’energia

Appendice A Equazioni del modello energetico

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

                    + + ε − ς ω − − =         + + ε − ς − − =       +         + + ε − ς + − =       + ⇒            ω + ω − − = + ω − − =       + + ω + − =       + w f D b e 2 D w D w f D b e 2 D D D w f D b e 2 D D D D w w w w D w w w D D D w w w D D T u 1 V m R R 1 V V m V P T u 1 V m R R 1 h 1 V m R h 1 h Nx T u 1 V m R R 1 R 1 V m R h 1 F V T I V m V P T I h 1 V m R h 1 h Nx R T I V m R h 1 F & & & & & & & & & & & &

(

)

(

)

(

)

(

)

(

)

(

)

                    + + ε − ς − − = + − ε − ς − − =       + + + ε − ς + − =       + w f D b e 2 D b e D w f D b e 2 D D D w D f D b e D D D T u 1 V m R R 1 R 1 V m V P T h u 1 V m hR R 1 V m R h 1 h Nx T R u 1 V m R R 1 V m R h 1 F & & & & & &

(

)

(

)

(

)

(

)

(

)

(

)

             + −         ε − ς + − = + −         ε − ς + − =       + + +         ε − ς − − =       + w b e f D 2 b e 2 D w f D b e 2 D D w D f D b e D D T R u 1 V m R R 1 1 V P T h u 1 V m hR R 1 1 R h 1 h Nx T R u 1 V m R R 1 1 R h 1 F & & &

(

)

(

)

(

)

(

)

           + −         η + − = + −       η + − =       + + + η − − =       + w b e f D b e D w f D D D w D f D D T R u 1 V m R R 1 V P T h u 1 V m h R 1 R h 1 h Nx T R u 1 V m 1 R h 1 F & & & (A.4.8) in cui si è assunto:

( )

b e D R R 1−ε ς = η (A.4.9)

Appendice A Equazioni del modello energetico

Eliminando ora m_DV& tra la prima e la terza delle (A.4.8), si ha:

(

)

(

(

)

)

(

)

(

)

(

(

)

)

(

)

w b e f w D f D b e D w b e f D b e D w D f D D T R u 1 T 1 R u 1 F R h 1 1 1 R R 1 V P T R u 1 V m R R 1 V P T 1 R u 1 F R h 1 1 1 V m + −       η − + +       + η − −         η + − = ⇒        + −         η + − = η − + +       + η − − = & &

(

)

(

)

(

)

(

)

w b e f w D b e D f D b e D T R u 1 T 1 R R R 1 u 1 F R h 1 1 R R 1 V P ₋ + η −         η + + −       + η −         η + = ⇒

(

)

(

)

(

)

w b e f D b e b e D D b e D T R u 1 1 R R R R 1 1 F 1 R h 1 R R 1 V P +               η −         η + + − η −       +         η + = ⇒

(

)

(

)

(

)

w b e f D b e D D b e D T R u 1 1 R R R F 1 R h 1 R R 1 V P +       η − + − η −       +         η + = (A.4.10)

Scomposizione dell’equazione dell’energia in due contributi

Scomponendo poi la forza che compare nella (A.4.10) come già visto nei casi precedenti, nelle componenti "roll" e "b":

(

)

(

)

(

)

(

)

w b e f D b e D b D b e D roll D b e D T R u 1 1 R R R F 1 R h 1 R R 1 F 1 R h 1 R R 1 V P +       η − + − η −       +         η + + η −       +         η + = (A.4.11)

ed assumendo che i fenomeni dissipativi siano imputabili ai termini di tipo "roll" la (A.4.11) si spezza in :

(

)

roll D b e D F 1 R h 1 R R 1 V P η −       +         η + = (A.4.12)

Appendice A Equazioni del modello energetico

(

f

)

w b D b e D b e D b e T u 1 F R R 1 R h 1 R R 1 R + =         +       +         η + (A.4.13)

dalle quali si ricavano rispettivamente i contributi delle forze di contatto F_roll e F : _b

(

)

      +         η + η − = D b e D roll R h 1 R R 1 1 V P F (A.4.12')

(

)

w D b e D b e D b e f b T R h 1 R R 1 R R R 1 u 1 F       +         η +         + + = (A.4.13')

Determinazione del braccio

Eliminando poi m_DV& tra la prima e la seconda delle (A.4.8):

(

)

(

(

)

)

(

)

         + −       η + − =       + η − + + η −       + − = w f D D D w D f D D T h u 1 V m h R 1 R h 1 h Nx T 1 R u 1 1 R h 1 F V m & &

(

)

(

(

)

)

(

)

w f w D f D D D T h u 1 T 1 R u 1 1 R h 1 F h R 1 R h 1 h Nx + −               η − + + η −       + −       η + − =       + ⇒

(

)

(

)

(

)

w

(

f

)

w D D f D D D T h u 1 T 1 R h R 1 u 1 F 1 h R 1 R h 1 R h 1 h Nx + − η −       η + + − η −       η +       + =       + ⇒

Appendice A Equazioni del modello energetico

(

)

(

)

(

(

)

)

w D f D D D D D T R 1 u 1 h R 1 h R 1 F 1 h R 1 R h 1 R h 1 h Nx η − +       η − +       η + − η −       η +       + =       + ⇒

(

)

(

)

(

)

w D D f D D D T R 1 h R 1 u 1 F 1 h R 1 R h 1 R h 1 h Nx η −       + + − η −       η +       + =       + ⇒

e sostituendo le (A.4.12') e (A.4.13'):

(

)

(

)

₍

₎

b D D b e D b e D D b e b D D roll D D D F R 1 R R 1 R h 1 R R 1 h R 1 R F 1 h R 1 R h 1 F 1 h R 1 R h 1 R h 1 h Nx η −         +       +         η +       + − η −       η +       + + η −       η +       + =       +

(

)

(

)

b D D D b e b e D D b e D roll D D D F 1 R h 1 R R R 1 R R 1 h R 1 R h R 1 F 1 h R 1 R h 1 R h 1 h Nx η −       +                       +         η +       + −       η + + η −       η +       + =       + ⇒

(

)

(

)

b D D b e b e D D b e D roll D F 1 1 R R R 1 R R 1 h R 1 R h R 1 F 1 h R 1 h Nx η −                       +         η +       + −       η + + η −       η + = ⇒

(

)

(

)

b D D b e b e D D b e D D b e D roll D F 1 1 R R R 1 R R 1 h R 1 R R R R 1 h R 1 F 1 h R 1 h Nx η −                       +         η +       + −         +       η + + η −       η + = ⇒

(

)

(

)

(

)

b D D b e D b e D b e D D D roll D F 1 1 R R R 1 R R h R 1 R h R 1 R h R 1 F 1 h R 1 h Nx η −                       + η +       + −       η + +       η + + η −       η + = ⇒

Appendice A Equazioni del modello energetico

(

)

(

)

b D D b e D D b e D b e D b e 2 D D roll D F 1 1 R R R 1 R h R 1 R h R 1 R h R R h R R F 1 h R 1 h Nx η −                       + η       + −       + − η + + η + + η −       η + = ⇒

(

)

(

)

b D D b e 2 D D b e D b e b e D b e 2 D D roll D F 1 1 R R R 1 h R R R h R R R h R R h R R F 1 h R 1 h Nx η −                       + η − η − − − η + + η + + η −       η + = ⇒

(

)

(

)

(

)

(

)

(

)

b D b e b e roll D b D D b e b e D D roll D F R R 1 h R 1 F 1 h R 1 h Nx F 1 1 R R R 1 1 R h R 1 R F 1 h R 1 h Nx         +         − + η −       η + = ⇒ η −                       + η − − η − + η −       η + = ⇒

(

)

N F R R 1 h h R 1 N F 1 h h R 1 x b D b e b e roll D         +         − + η −       η + = (A.4.14)

A.5 Frenata non stazionaria su tamburo rotante con coppia

aggiuntiva applicata al tamburo

L’applicazione di una coppia anche al drum consente di fare uno studio del problema in alcune situazioni particolari che vengono analizzate in maniera specifica, ma prima è necessario vedere quali cambiamenti vengono apportati nelle equazioni rispetto ala caso precedente, figura A.5

Equazioni del moto

     − − − = − − = ω D D D D w w w R T R x N F V m T Nx Fh I & & (A.5.1)

Appendice A Equazioni del modello energetico D

T

F

N

V

x h

F

N

T

w D

R

_D w

figura A.5 Frenata non stazionaria su tamburo rotante con momento applicato sul tamburo. con 2 D D D R I m = , V=R_Dω_D e T_D =−F_DR_D.

Le equazioni (A.5.1) possono essere manipolate e riscritte in una forma tale da poterle utilizzare per calcolare forza e braccio dalle misure sperimentali. Moltiplicando la seconda delle (A.5.1) per R_D e sottraendo la seconda dalla prima si ottiene:

D D w D D w w D D D D w w w T Nx FR T Nx Fh R V m I T Nx FR R V m T Nx Fh I + + + − − = − ω ⇒    − − − = − − = ω & & & & D w D D w w D D D w D D D D w w I m VR T T R h 1 FR T T R h 1 FR R V m I _= ω − + −      + ⇒ + −       + = −

ω_& & _& &

da cui può essere ricavata la forza F:

(

)

      + + ω +       + − = D D w w w D D D R h 1 R T I R T V m F & & (A.5.2)

Appendice A Equazioni del modello energetico ottiene: D D D w D w w D D D D w w w R h T h R x N Fh T Nx Fh h V m I R h T h R x N Fh h V m T Nx Fh I − − − − − = + ω ⇒      − − − = − − = ω & & & & D D w D w w D D D w D D w w R h T T h V m I R h 1 Nx R h T T R h 1 Nx h V m I _=− ω − − −      + ⇒ − −       + − = +

ω_& & _& &

da cui si può ottenere il braccio x:

(

)

      + + ω −       + − = D w w w D D D R h 1 N T I R T V m h x & & (A.5.3) Energia dissipata

Oltre ai contributi presenti nei casi precedenti ora si ha anche quello dovuto a TD:

0 T I R V T V V m P T T V V m I P _{w w w w w} D D D D D w w D w w wω ω − − ω − ω ⇒ + + + ω ω + ω = −

= & & & &

da cui:

(

I T

)

0 V R T V m P _{w w w w} D D D  + ω + ω =      +

+ & & (A.5.4)

Relazioni cinematiche

Valgono anche in questo caso le relazioni cinematiche (A.3.5), (A.3.6), (A.3.7) e quelle da esse derivate, ricavate nei casi precedenti:

w b e V R ω = ; b e e e w e w x R R 1 V R 1 V R V s = −ω = −ω = − ; roll e V R ω = ;

Appendice A Equazioni del modello energetico dV dR V dt dR_{e & e} = ;

(

)

      − + ε = x x b e b e s 1 s V V R dt dR & _& ;

(

)

_x e b e W s R V 1 R V & & & = −ε − ω ;

Inoltre anche in questo caso il gruppo

(

I_wω&_w +T_w

)

può essere scritto come indicato nell’equazione (A.4.5) in cui ζ e u_f sono definiti come da (A.4.6) e da (A.4.7)

( )

D w

(

f

)

b e 2 D w w w m V T 1 u R R 1 T I ω& + =ς −ε & + + ; ₂ D D w R m I = ς ; _x e w w f s R V T I u =− & .

Utilizzando poi la (A.4.9):

( )

b e D R R 1−ε ς = η (A.4.9)

la (A.4.5) può essere riscritta come:

(

f

)

w D D w w w T R m V T 1 u

I ω& + =η & + + (A.5.6 )

Riformulazione dell’equazione dell’energia

Sostituendo la (A.5.6) nelle equazioni (A.5.2) (A.5.3) e (A.5.4) si ottiene:

(

)

(

)

(

)

           ω + ω −       + − = + ω −       + − =       + + ω +       + − =       + V T I R T V m V P T I h 1 R T V m R h 1 h Nx R T I R T V m R h 1 F w w w w D D D w w w D D D D D w w w D D D D & & & & & &

(

)

[

]

(

)

[

]

(

)

[

]

         + + η ω −     + − = + + η −       + − =       + + + η +       + − =       + ⇒ w D f w D D D D D D D f w D D D D D D u 1 T V m R T V m P h u 1 T V m R R T V m R h 1 h Nx R u 1 T V m R R T V m R h 1 F & & & & & &

Appendice A Equazioni del modello energetico

(

)

(

)

(

)

(

)

(

)

(

)

(

)

                   − + −         η + − =       + − + −       η + − =       + − + + η − − = ⇒            − + ω − η ω − − = − + − η − − =       + − + + η + − =       + ⇒ D D f b e w D b e D D D D f w D D D D D D f w D D D f w w D D w D D D f w D D D D D D D f w D D D R T u 1 R T V m R R 1 V P R h 1 R T h u 1 T V m h R 1 h Nx R h 1 R T R u 1 T V m 1 F R T u 1 T V V m R V V m V P R T h u 1 T h V m R V m R h 1 h Nx R T R u 1 T V m V m R h 1 F & & & & & & & & &

(

)

(

)

(

)

(

)

                   − + −         η + − =       + − + −       η + − =       + − + + η − − = D D f b e w D b e D D D D f w D D D D D D f w D R T u 1 R T V m R R 1 V P R h 1 N h R T h h u 1 T h V m h R 1 x R h 1 R T R u 1 T V m 1 F & & & (A.5.7)

Eliminando ora m_DV& tra la prima e la terza delle (A.5.7), si ha:

(

)

(

(

)

)

(

)

(

)

⇒          − + −         η + − = η − − η − + + η −       + − = D D w b e f D b e D D D w D f D D R T T R u 1 V m R R 1 V P T 1 R 1 T 1 R u 1 F 1 R h 1 V m & &

(

)

(

(

)

)

(

)

(

)

D D w b e f D D w D f D b e D R T T R u 1 T 1 R 1 T 1 R u 1 F 1 R h 1 R R 1 V P − + −               η − − η − + + η −       + −         η + − = ⇒

Appendice A Equazioni del modello energetico

(

)

(

)

(

)

(

)

(

)

D D w b e f D D b e D w D b e D f b e D D R T T R u 1 T 1 R R R 1 T 1 R R R 1 u 1 F 1 R R 1 R h 1 V P ₋ + ₋ η −         η + + η −         η + + − η −         η +       + = ⇒

(

)

(

)

(

)

(

)

D D b e D w f b e D b e D b e D D R T 1 1 R R 1 T u 1 R 1 1 R R R 1 F 1 R R 1 R h 1 V P               − η −         η + + +               + η −         η + − η −         η +       + = ⇒

(

)

(

)

(

)

(

)

(

)

(

)

D D b e D w f b e D D b e b e D b e D D R T 1 1 R R 1 T u 1 1 R R 1 R R R R 1 F 1 R R 1 R h 1 V P               η − η − −         η + + +               η − η − +         η + − η −         η +       + = ⇒

(

)

(

)

(

)

(

)

D D b e D w f b e D D D D b e b e D D R T 1 1 R R 1 T u 1 1 R R R R R R F 1 R R 1 R h 1 V P             η − η + − η + + +         η − η − + η + − η −         η +       + = ⇒

(

)

(

)

(

)

(

)

D D b e D w D f b e D b e D D T R 1 R R 1 T R 1 u 1 R R 1 F 1 R R 1 R h 1 V P η −         + η + η − +         + − η −         η +       + = (A.5.8)

Scomposizione dell’equazione dell’energia in due contributi

Scomponendo poi la forza che compare nella (A.5.8) come già visto nei casi precedenti, nelle componenti "roll" e "b":

(

)

(

)

(

)

(

)

(

)

D D b e D w D f b e D b b e D D roll b e D D T R 1 R R 1 T R 1 u 1 R R 1 F 1 R R 1 R h 1 F 1 R R 1 R h 1 V P η −         + η + η − +         + − η −         η +       + + η −         η +       + = (A.5.9)

ed assumendo che i fenomeni dissipativi siano imputabili ai termini di tipo "roll" e "D" la

Appendice A Equazioni del modello energetico

(

)

(

)

D D b e D roll b e D D T R 1 R R 1 F 1 R R 1 R h 1 V P η −         + η + η −         η +       + = (A.5.10)

(

f

)

w b D b e D b e D b e T u 1 F R R 1 R h 1 R R 1 R + =         +       +         η + (A.5.11)

dalle quali si ricavano rispettivamente i contributi delle forze di contatto F_roll e F : _b

(

)

D b e D D D b e D b e D D roll T R R 1 R h 1 R R R 1 R R 1 R h 1 1 V P F         η +       +         + η −         η +       + η − = (A.5.10')

(

)

w D b e D b e D b e f b T R h 1 R R 1 R R R 1 u 1 F       +         η +         + + = (A.5.11')

Determinazione del braccio

Eliminando poi m_DV& tra la prima e la seconda delle (A.5.7):

(

)

(

(

)

)

(

)

(

)

         − + −       η + − =       + η − − η − + + η −       + − = D D w f D D D D D w D f D D R T T h u 1 V m h R 1 R h 1 h Nx R T 1 1 T 1 R u 1 1 R h 1 F V m & &

(

)

(

(

)

)

(

)

(

)

D D w f D D w D f D D D R T T h u 1 R T 1 1 T 1 R u 1 1 R h 1 F h R 1 R h 1 h Nx ₋ + ₋               η − − η − + + η −       + −       η + − =       + ⇒

Appendice A Equazioni del modello energetico

(

)

(

)

(

)

(

)

(

)

D D w f D D D w D D f D D D R T T h u 1 R T 1 h R 1 T 1 R h R 1 u 1 F 1 h R 1 R h 1 R h 1 h Nx − + − η −       η + + η −       η + + − η −       η +       + =       + ⇒

(

)

(

)

(

)

(

)

D D D w f D D D D D R T 1 1 h R 1 T u 1 h 1 1 R h R 1 F 1 h R 1 R h 1 R h 1 h Nx             − η −       η + + +             + η −       η + − η −       η +       + =       + ⇒

(

)

(

)

(

)

(

)

D D D w f D D D D D R T 1 1 h R 1 T u 1 h 1 1 R h R 1 F 1 h R 1 R h 1 R h 1 h Nx             − η −       η + + +             + η −       η + − η −       η +       + =       + ⇒

(

)

(

)

₍

₎

(

)

(

)

(

)

D D D D w D f D D D D R 1 T R h 1 1 h R 1 T R 1 u 1 R h 1 h R 1 h R 1 F 1 h R 1 h Nx η −       +       η − −       η + + η − +       +       η − +       η + − η −       η + = ⇒

(

)

(

)

(

)

(

)

h T 1 T R R h 1 1 h R 1 u 1 F 1 h R 1 h Nx _D w D D D f D η − η +       + η −       + + − η −       η + = ⇒

applicando la suddivisione di F nei suoi contributi e sostituendo la (A.5.11):

(

)

(

)

(

)

(

)

(

)

h T 1 T R R h 1 1 h R 1 u 1 F 1 h R 1 F 1 h R 1 h Nx _D w D D D f b D roll D η − η +       + η −       + + − η −       η + + η −       η + =

(

)

(

)

₍

₎

(

)

h T 1 F R R 1 1 h R 1 R R 1 R R F 1 h R 1 F 1 h R 1 h Nx _D b D b e D b e D D b e b D roll D η − η +         + η −       +         η + − η −       η + + η −       η + = ⇒

(

)

(

)

(

)

h T 1 R R 1 R h R 1 R R 1 R h R 1 R R 1 R 1 1 F F 1 h R 1 h Nx _D D b e D D b e D b e D D b e D b roll D η − η +                       +       +         η + −       η +         + η − + η −       η + = ⇒

Appendice A Equazioni del modello energetico

(

)

(

)

(

)

(

)

(

)

h T 1 1 R R 1 R R R h R R R R R h R R R F F 1 h R 1 h Nx _D D b e D D b e D D b e b e D D b e D b roll D η − η +               η −         + η + − η − − + η + + + η −       η + = ⇒

(

)

₍

₎

(

)

h T 1 1 R R 1 R h R R R h R R R h R R h R R F F 1 h R 1 h Nx _D D b e D D D b e D D b e D D D D b roll D η − η +               η −         + η − − η − η + η + + η −       η + = ⇒

(

)

(

)

(

)

(

)

(

)

h T 1 1 R R 1 R 1 R h R 1 R F F 1 h R 1 h Nx _D D b e D b e D D b roll D η − η +               η −         + η − − η − + η −       η + = ⇒

(

)

(

)

N T 1 N F R R 1 h h R 1 N F 1 h h R 1 x b D D b e b e roll D η − η +         +         − + η −       η + = (A.5.12)

La (A.5.12) mostra come il braccio della risultante delle pressioni di contatto pneumatico-suolo sia costituita da tre contributi di cui l’ultimo è dovuto all’applicazione del momento sul tamburo.

Equazioni del moto nelle variabili indipendenti V e sx

Le equazioni del moto (A.5.1) sono in funzione delle variabili indipendenti V e ω_w ma è possibile riscriverle in funzione delle variabili indipendenti V e sx.

Attraverso la (A.5.12) e la:

(

)

x e b e w s R V 1 R V & & & = −ε − ω (A.5.13)

Appendice A Equazioni del modello energetico

(

V,sx

)

Froll

( )

sx Fb

(

V,sx

)

F = + (A.5.14)

(

)

[

( )

]

₍

₎

x b e D x s , V R R V 1 s , V =ς −ε η (A.5.15)

le equazioni del moto possono essere riscritte come segue:

( )

( )

II I      − − − = − − = ω D D D D w w w R T R x N F V m T Nx Fh I & & (A.5.1) Equazione (A.5.1 I)

(

)

(

)

           + = − − − = − − =         − ε − ⇒           + = − − − = − ε − = ω − − = ω b roll D D D D D D w x e b e w b roll D D D D D D x e b e w w w w F F F R m T R m x N m F V T Nx Fh s R V 1 R V I F F F R m T R m x N m F V s R V 1 R V T Nx Fh I & & & & & & & &

( )

       + = − − = − ε −       − − − ⇒ b roll w x e w b e D D D D D D w F F F T Nx Fh s R V I 1 R R m T R m x N m F I &

(

)

(

)

(

)

     + = ε − + ε − + ε − + − − = − ⇒ b roll D b e D D w b e D D w b e D w w x e w F F F T R R m 1 I Nx R R m 1 I F R m 1 I T Nx Fh s R V I &

( )

(

)

(

)

     + = ε − − +         _−ε − +         _−ε + − = ⇒ b roll D b e D D w w b e D D w b e D w x e w F F F T R R m 1 I T Nx R R m 1 I 1 Fh hR m 1 I 1 s R V I &

moltiplicando e dividendo per R i termini 2_D

( )

b e D D w R R m 1 I −ε al secondo membro:

Appendice A Equazioni del modello energetico

(

)

(

)

(

)

      + = ε − − +         _−ε − +         _−ε + − = ⇒ b roll D b e D 2 D D 2 D w w b e D 2 D D 2 D w b e 2 D D 2 D w x e w F F F T R R R m R 1 I T Nx R R R m R 1 I 1 Fh hR R m R 1 I 1 s R V I &

(

)

(

)

(

)

     + = ε − ς − +         _{ς −ε} − +         _{ς −ε} + − = ⇒ b roll D b e D 2 D w b e D 2 D b e 2 D x e w F F F T R R R 1 T Nx R R R 1 1 Fh hR R 1 1 s R V I &

(

)

(

)

(

)

             + = η − η +         +         − + η −       η + = η − + η − +       η + − = ⇒ b roll D b D b e b e roll D D w D x e w F F F T 1 F R R 1 h h R 1 F 1 h h R 1 Nx T T Nx 1 Fh h R 1 s R V I &

(

)

D w D b D b e b e roll D b D roll D x e w F T T T R R 1 h 1 h R 1 h F h R 1 h F h R 1 h F h R 1 s R V I +η + −η         + η −         − +       η + +       ₊η −       ₊η − = ⇒ _&

(

)

w b D b e b e D x e w Fh T R R 1 1 h R 1 h R 1 s R V I +                       + η −         − +       η + − = ⇒ _&

(

)

w b D b e b e D b e D x e w Fh T R R 1 1 h R 1 R R 1 h R 1 s R V I +                       + η −         − +         +       ₊η − = ⇒ _& w b D b e b e b e D b e D D D b e x e w Fh T R R 1 h R h R 1 R R h R h R R R 1 s R V I +                       + η + η − − + η − η − − − = ⇒ _&

Appendice A Equazioni del modello energetico w b D b e D b e D x e w w b D b e b e D D b e x e w Fh T R R 1 h R h R R h 1 s R V I T h F R R 1 h R h R R R s R V I +         +         η +       + − = ⇒ +                       + η + + η + − = ⇒ _{& &} w b D b e b e D D b e x e w Fh T R R 1 R R 1 R h 1 h R s R V I +         +         η +       + − = & ed infine: w b D b e D b e D b e x e w F T R R 1 R h 1 R R 1 R s R V I +         +       +         η + − = & (A.5.16)

Equazione (A.5.1 II)

(

)

(

)

             + = ⇒ η − η +         +         − + η −       η + = − − − = b roll D b D b e b e roll D D D D D F F F T 1 F R R 1 h h R 1 F 1 h h R 1 Nx R T R x N F V m &

(

)

(

)

D D D D b D D b e b e roll D D b roll D R T T R 1 F R R R 1 h h R 1 F R 1 h h R 1 F F V m − η − η −         +         − − η −       η + − − − = ⇒ &

(

)

(

)

      η − η + −                       +         − + −             η −       η + + − = ⇒ 1 1 R T R R R 1 h h R 1 1 F R 1 h h R 1 1 F V m D D D D b e b e b D D roll D&

(

)

(

)

(

)

(

(

−η

)

)

η + η − −         + − + + − η − η + + η − − = ⇒ 1 1 R T R R R 1 R h R R F R 1 R h R R F V m D D D D b e b e b e D b D D D D roll D&

Appendice A Equazioni del modello energetico ed infine:

(

)

(

)

D D D b D b e D D roll D D T 1 R m 1 F R R 1 m R h 1 F 1 m R h 1 V η − −         +       + − η −       + − = & _(A.5.17)

In definitiva il sistema delle equazioni del moto nelle variabili indipendenti V e sx è dato da:

(

)

(

)

             η − −         +       + − η −       + − = +         +       +         η + − = D D D b D b e D D roll D D w b D b e D b e D b e x e w T 1 R m 1 F R R 1 m R h 1 F 1 m R h 1 V T F R R 1 R h 1 R R 1 R s R V I & &

(

)

(

A.5.17

)

16 . 5 . A

Equazioni del moto indipendenti da x

A questo punto le equazioni del moto nelle variabili indipendenti V e ωw possono essere riscritte in funzione delle sole componenti F_roll, F e _b T_D, sostituendo nelle (A.5.1) l’equazione (A.5.12). Effettivamente la seconda delle (A.5.1) è già stata resa indipendente da x, come evidente nell’equazione (A.5.17). Manipolando la prima delle (A.5.1), si ottiene:

(

)

(

)

           + = η − η +         +         − + η −       η + = − − = ω b roll D b D b e b e roll D w w w F F F T 1 F R R 1 h h R 1 F 1 h h R 1 Nx T Nx Fh I &

Appendice A Equazioni del modello energetico

(

)

b

(

)

D w D b e b e roll D b roll w w T T 1 F R R 1 h h R 1 F 1 h h R 1 h F h F I − η − η −         +         − − η −       η + − + = ω&

(

)

(

)

D w D b e b e b D roll w w T T 1 R R 1 h R 1 1 h F 1 h R 1 1 h F I − η − η −                       +         − − +             η −       η + − = ω&

(

)

(

)

D w D b e b e D b e b D roll w w T T 1 R R 1 h R 1 R R 1 h F 1 h R 1 1 h F I − η − η −                       + + − + +             η − η − − η − = ω&

(

)

b

(

)

D w b e D D roll D w w T T 1 F R R 1 h R 1 h F 1 h R 1 h I − η − η −         +       + + η −       + η − = ω& (A.5.18)

La quale attraverso l’equazione (A.5.11') diviene:

(

)

(

)

₍

₎

        + +       +         η + − η − η −         +       + + η −       + η − = ω D b e f D b e D b e b D b b e D D roll D w w R R 1 u 1 R h 1 R R 1 R F T 1 F R R 1 h R 1 h F 1 h R 1 h I &

(

)

(

)

b

(

)

D b e D f D b e D b e D D roll D w w T 1 F R R 1 u 1 h R 1 R R 1 h R R 1 h R 1 h F 1 h R 1 h I η − η −                       + +       +         η + −         +       + + η −       + η − = ω&

Appendice A Equazioni del modello energetico

(

)

(

)

b

(

)

D f b e D f b e D D roll D w w T 1 F u 1 R R u R R 1 h R 1 h F 1 h R 1 h I η − η − +         η −         +       + + η −       + η − = ω& (A.5.18’)

A.6 Equilibrio in condizione stazionaria non frenata con coppia

applicata al tamburo

Applicando un’opportuna coppia al tamburo, e D

T , con T_w =0, si ottiene una condizione stazionaria in cui ruota e tamburo non rallentano, in quanto dall’esterno viene compensata la perdita di energia relativa al rotolamento. La coppia T_De deve essere motrice. In questo caso le componenti F_roll e F , essendo _b T_w =0 e dunque s_x =0,valgono:

• Forza frenante: F_b =0;

• Forza di rotolamento: F_roll =µ_roll0 ⋅N.

mentre le equazioni che descrivono il sistema sono ancora le (A.5.1), (A.5.12) nelle quali i momenti di inerzia vengano assunti nulli:

     = − − − = − 0 R T R x N F 0 Nx Fh D De D (A.7.1)

Sostituendo nella seconda il valore di Nx si ricava il valore e D T : N R h 1 R T D D 0 roll De       + µ − = (A.7.2)

Appendice A Equazioni del modello energetico

A.7 Equilibrio in condizione stazionaria frenata con coppia

applicata al tamburo

La condizione di frenata stazionaria identifica una condizione di equilibrio dinamico rispetto alla quale è possibile analizzare il comportamento del sistema nella risposta a piccoli ingressi. La coppia

0 D

T deve compensare in questo la dissipazione dell’energia per rotolamento e l’azione della coppia frenante applicata alla ruota T_w0. Da tenere presente che si suppone che sia assegnato

0 x

s , quindi le due coppie devono essere tali da mantenere nel tempo una data intensità di frenata. Quindi, assegnato s_x0 sono note:

• Forza frenante: F_b0 =

{

K_µsxs_x0 +

[

C₀

( )

N +C₁V

]

s2_x0

}

⋅N; • Forza di rotolamento: F

(

1 K s2

)

N 0 x r 0 roll 0 roll =µ + ⋅ .

Le equazioni del moto (A.5.1) diventano:

     = − − − = − − 0 R T R x N F 0 T Nx h F D 0 D D 0 0 0 w 0 0 0 (A.7.1)

mentre dalla (A.5.12) il braccio x è:

(

)

(

)

N T 1 N F R R 1 h h R 1 N F 1 h h R 1 x D0 0 0 0 b D 0 b e 0 0 0 b e 0 roll 0 0 0 D 0 0 _−η η +         +         − + η −       η + = (A.7.2)

Per ricavare i valori da assegnare ai momenti T_D0e T_w0 si può utilizzare il metodo di Cramer applicato al sistema (A.7.4), costituito dalle (A.7.1) e (A.7.2), in cui si è indicato con xˆ la porzione di x indipendente da ₀ T_D0.

Appendice A Equazioni del modello energetico

(

)

N F R R 1 h h R 1 N F 1 h h R 1 xˆ b0 D 0 b e 0 0 0 b e 0 roll 0 0 0 D 0 0         +         − + η −       η + = (A.7.3)

(

)

          − =                               η − η − 0 0 0 0 0 0 D 0 w 0 0 D D xˆ F h F x T T 1 N 1 0 R N R 1 0 N 0 1 (A.7.4)

Il determinante della matrice vale:

( ) ( ) ( 0) D 0 D 0 0 D D 0 0 D D R 1 R 1 1 N 1 R N R 1 1 N 1 0 R N R 1 0 N 0 1 η − η + = ∆ ⇒ η − η − − = ∆ ⇒ η − η − = ∆

(

1 0

)

RD 1 η − = ∆ (A.6.5) Quindi il momento 0 w T :

(

)

(

)

(

)

∆ η − η + − η − η + = ⇒                     η − η − − ∆ = R 1 N N h F R 1 xˆ N N 1 NF R 1 h F T 1 N 1 xˆ R N R 1 F N 0 h F 1 T 0 0 D 0 0 D 0 0 0 0 D 0 0 0 w 0 0 0 D D 0 0 0 0 w

Appendice A Equazioni del modello energetico

(

) (

)

(

)

(

)

∆             η − η + η + η − + − = ⇒ ∆         η − η +       η − η + + − = 0 0 0 D 0 0 D 0 0 D 0 0 w 0 0 0 0 D 0 0 D 0 0 w 1 R h 1 R h F R 1 xˆ N T 1 1 1 R h F R 1 xˆ N T

(

0

)

0

(

0 D 0

)

0 0 w Nxˆ 1 F R h T =− −η + η + (A.7.6) mentre il momento 0 D T :

(

0

)

D D 0 0 0 D D 0 0 0 D 0 D 0 0 0 0 D 1 R R N xˆ F T R N xˆ F T 1 xˆ 0 R N F 0 N h F 1 1 T _ −η      − − = ⇒ ∆ − − = ⇒                     − ∆ =

(

0

)

D 0

(

0

)

0 0 D F 1 R xˆ N1 T =− −η − −η (A.7.7)