Capitolo 4 Identificazione con modello energetico e momento motore sul drum costante

(1)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante

138

Capitolo 4

Identificazione con modello energetico

e momento motore sul drum costante

4.1 Introduzione

Le simulazioni realizzate nel capitolo precedente, mediante i valori assegnati dall’ottimizzatore ai parametri che compaiono nelle strutture che definiscono µ_b e µ_roll, hanno permesso di ottenere, per la velocità angolare della ruota e del tamburo, andamenti molto prossimi ai dati sperimentali, dai quali si discostano non più di qualche percento. Inoltre, il confronto tra gli errori percentuali ottenuti mediante simulazione con i parametri identificati tramite la funzione lsqnonlin e quelli ottenuti mediante simulazione coi valori originali, hanno evidenziato la qualità dei valori identificati mediante la procedura manuale descritta nel paragrafo 2.8. Tuttavia bisogna ricordare che le informazioni complete su come le prove sono state svolte non sono disponibili, per cui entrambe le identificazioni sono state realizzate nell’ipotesi che, al momento dell’applicazione del momento frenante, il tamburo fosse messo in folle, in analogia a quanto descritto per test simili disponibili in letteratura. A questo stadio nasce l’esigenza di identificare i parametri presenti nelle strutture suddette nell’ipotesi che il sistema venga forzato da un momento frenante senza che il tamburo sia messo in folle. Tale analisi è stata realizzata considerando il contributo del momento motore sul tamburo, in prima ipotesi come dissipante assieme alla forza di rotolamento, come già valutato nel secondo capitolo, in seconda ipotesi come componente, assieme alla forza longitudinale dovuta al momento frenante sulla ruota, dell’effettiva forza frenante. Le simulazioni mediante i valori identificati del coefficiente K_roll nel primo caso

(2)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante

139 e dei coefficienti K_µ_s_x , C e ₀ C₁ nel secondo hanno permesso di valutare quale delle due formulazioni fosse la più corretta.

4.2 Identificazioni

con

momento

motore

sul

tamburo

considerato dissipante

Non avendo le informazioni complete su come le prove sperimentali siano state compiute bisogna analizzare il caso in cui queste siano state svolte senza che il tamburo sia stato messo in folle. In particolare si suppone che sul tamburo permanga il momento motore necessario a mantenere la ruota in condizione stazionaria non frenata alla velocità di inizio del test di frenata. L’analisi viene dunque realizzata supponendo che il sistema ruota-tamburo sia forzato mediante il momento frenante sperimentale e il momento sul ruota-tamburo

e D

T appena definito.

Le equazioni della dinamica del sistema ruota-tamburo, riferite al caso di frenata non stazionaria con momento applicato sul tamburo, analizzate dettagliatamente nel paragrafo 2.6, vengono riscritte per il caso in esame:

     − − − = − − = ω D e D D D w w w R T R x N F V m T Nx Fh I & & (4.1)

in cui il momento sul tamburo T_D_erisulta:

N R h 1 R T D D 0 roll De       + µ − = (4.2)

La forza longitudinale F viene decomposta nelle due componenti F_roll e F : _b

b roll F F

(3)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante

140 Nel caso in esame in questo paragrafo, il contributo del momento motore sul tamburo viene considerato, nell’equazione dell’energia (2.35), dissipativo assieme alla forza di rotolamento, ossia:

(

)

      +         η +         + η −       +         η + η − = D b e D b e D D e D D b e D roll R h 1 R R 1 R R 1 R T R h 1 R R 1 1 V P F (4.4)

mentre la forza frenante è definita, sempre nell’ equazione (2.35), come il contributo di F che va ad equilibrare il momento frenante:

(

)

      +         η +         + + = D b e D D b e f b e w b R h 1 R R 1 R R 1 u 1 R T F (4.5)

Attraverso tali definizioni il braccio della risultante delle azioni di pressione risulta:

(

)

(

−η

)

η +         +         − + η −       η + = 1 N T R R 1 h R 1 h N F 1 h R 1 h N F x De D b e b e b D roll _(4.6)

Mediante le definizioni date appare evidente che, avendo considerato il contributo del momento sul tamburo come dissipativo, la curva caratteristica del coefficiente di attrito di rotolamento sia caratterizzata da un parametro K_roll di entità diversa da quella identificata mediante la procedura manuale. Le identificazioni effettuate in tale sede sono dunque rivolte all’individuazione dei valori da assegnare al parametro K_roll nel caso in cui sul tamburo sia applicato un momento motore pari a

e D

T .

Per continuare il confronto dei risultati già avviato nel precedente capitolo, si illustrano, nelle figure 4.1-4.3, degli ingrandimenti riferiti alle velocità angolari della ruota e del

(4)

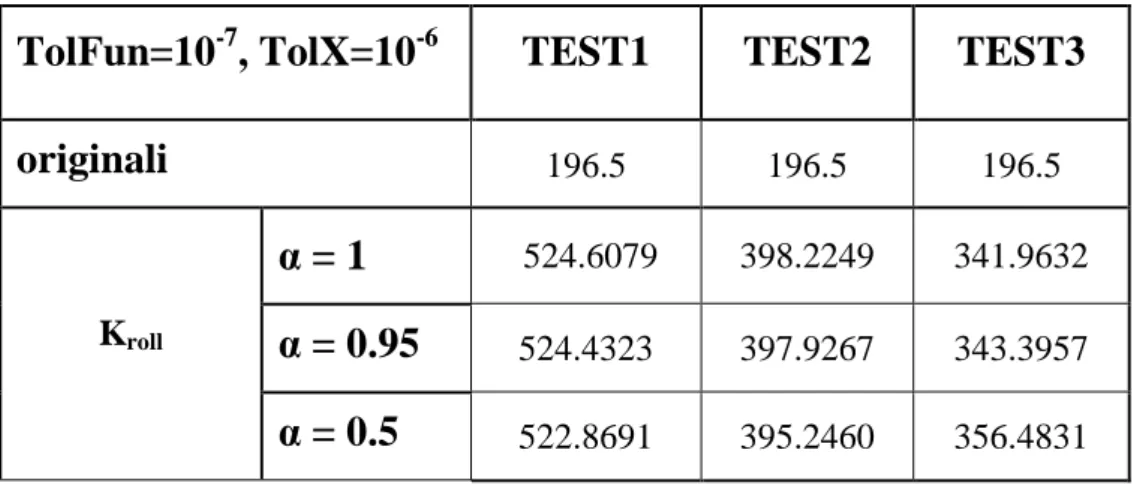
141 tamburo, sperimentali e simulate, nell’ipotesi T_D =T_D_e , coi parametri originali e identificati. Inoltre nelle figure 4.4-4.7 si riportano le distribuzioni degli errori percentuali per i tre test coi tre valori del peso α ed un ingrandimento, riferito al test 3, che esclude il picco presente nel primo secondo di simulazione.

Analizzando le figure si può notare come le velocità angolari simulate con i parametri originali, nell’ipotesi

e D

D T

T = , divergano rapidamente sia per il tamburo che per la ruota mentre, le simulazioni coi parametri identificati comportino un errore percentuale dell’ordine ordine di 1÷2 %.

I valori identificati per il coefficiente K_roll, nell’ipotesi

e D

D T

T = , vengono riassunti nella tabella 4.1 per tutti i test in esame e per ogni valore del peso α. Inoltre la tabella 4.1 riporta i valori delle tolleranze sulla funzione e sui parametri adottati durante il ciclo iterativo di identificazione.

TolFun=10

-7

, TolX=10

-6

TEST1

TEST2

TEST3

originali

196.5 196.5 196.5

α

= 1

524.6079 398.2249 341.9632

α

= 0.95

524.4323 397.9267 343.3957

Kroll

α

= 0.5

522.8691 395.2460 356.4831

tabella 4.1 Riassunto dei valori numerici assunti da K_roll durante le diverse identificazioni.

(5)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante 142 0 0.5 1 95 100 105 110 115 ω W [ ra d /s ] 4 4.5 5 60 65 70 75 7 7.5 8 35 40 45 50 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K roll originale (TD=TDe) K_roll identificato (T_D=T_De) 4 4.5 5 27 28 29 30 31 32 tempo [s] 7 7.5 8 16 18 20 22 tempo [s]

figura 4.1 Ingrandimenti delle velocità angolari della ruota e del tamburo, identificazione

di K_roll, per il test 1 con α = 0.95, nell’ipotesi

e D D T T = . 0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 72 74 76 78 80 82 7 7.5 8 52 54 56 58 60 62 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_roll originale (T_D=T_De) K_roll identificato (T_D=T_De) 4 4.5 5 31 32 33 34 35 tempo [s] 7 7.5 8 23 24 25 26 27 tempo [s]

di K_roll, per il test 2 con α = 1, nell’ipotesi

e D

D T

(6)

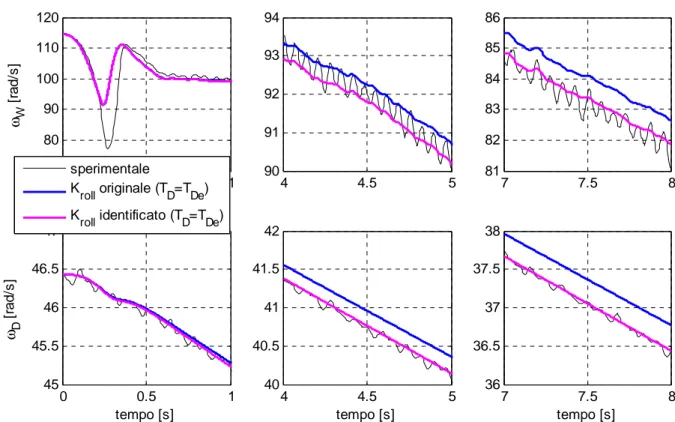
Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante 143 0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 91 92 93 94 7 7.5 8 81 82 83 84 85 86 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale K roll originale (TD=TDe) K roll identificato (TD=TDe) 4 4.5 5 40 40.5 41 41.5 42 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s]

(7)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 4 4 fi g u ra 4 .4 E rr o ri p er ce n tu al i p e r le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i ro ll K , p er il t es t1 a l v ar ia re d el p es o α , n el l’ ip o te si eD D T T = . 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 αααα =1 Test1 =1 Test1 =1 Test1=1 Test1 e % tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 αααα =0.95 Test1 =0.95 Test1 =0.95 Test1=0.95 Test1 tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 tempo [s] α

ααα=0.5 Test1=0.5 Test1=0.5 Test1=0.5 Test1

e% ω_W con parametri originali e% ω_D con parametri originali e% ω_W con parametri identificati e% ω_D con parametri identificati

(8)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 4 5 fi g u ra 4 .5 E rr o ri p er ce n tu al i p e r le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i ro ll K , p er il t es t2 a l v ar ia re d el p es o α , n el l’ ip o te si eD D T T = . 0 2 4 6 8 -2 -1 0 1 2 3 4 αααα =1 Test2 =1 Test2 =1 Test2=1 Test2 e % tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 αααα =0.95 Test2 =0.95 Test2 =0.95 Test2=0.95 Test2 tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 tempo [s] α

(9)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 4 6 fi g u ra 4 .6 E rr o ri p er ce n tu al i p e r le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i ro ll K , p er il t es t3 a l v ar ia re d el p es o α , n el l’ ip o te si eD D T T = . 0 2 4 6 8 -5 0 5 10 15 20 25 30 α

ααα=1 Test3=1 Test3=1 Test3=1 Test3

e % tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 α

tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 tempo [s] α

e% ω_W con parametri originali e% ω

D con parametri originali e% ω

W con parametri identificati e% ω

(10)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 4 7 fi g u ra 4 .7 In g ra n d im en ti d eg li er ro ri p er ce n tu al i d el le v el o ci tà a n g o la ri d el la r u o ta e d el ta m b u ro p er il te st 3 . 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 α

ααα=1 Test3=1 Test3=1 Test3=1 Test3

e % tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 α

tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 tempo [s] α

(11)

148

4.3 Identificazioni

con

momento

motore

sul

tamburo

considerato frenante

4.3.1 Rielaborazione del modello QSTM_08

In questa sede viene descritta la rielaborazione del modello QSTM_08, mediante la quale si valutano gli effetti indotti dal considerare il contributo del momento sul tamburo come aggiuntivo alla componente longitudinale dovuta al momento applicato sulla ruota, per la determinazione dell’effettiva forza frenante. Nel prossimo sottoparagrafo verranno analizzati nel dettaglio i risultati ottenuti per i tre test al variare del peso α.

Il sistema analizzato è quello di figura 4.8, identico a quello analizzato nel paragrafo 2.6. L’analisi iniziale è concorde con quella già svolta, ossia:

Equazioni del moto:

     − − − = − − = ω D D D D w w w R T R x N F V m T Nx Fh I & & (4.7) Equazione dell’energia:

(

_w _w _w

)

_w D D _V _I _T R T V m P _ − ω + ω      + − = & & (4.8)

Procedendo poi in maniera del tutto analoga ai casi analizzati nel capitolo 2 si ottiene per la potenza l’espressione:

(

)

(

) ( )

(

−η

)

        + η + η −         + + − η −       +         η + = 1 R R 1 R T 1 R R 1 u 1 R T 1 R h 1 R R 1 F V P e_b D D D D b e f b e w D b e D _(4.9)

La forza F viene ora decomposta nelle due componenti Froll e Fx, ossia:

x roll F F

(12)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante 149 D

T

F

N

V

x h

F

N

T

w D

R

_D w

figura 4.8 Frenata non stazionaria su tamburo rotante con momento applicato sul

tamburo.

attraverso la quale l’equazione della potenza dissipata diviene:

( ) ( ) ( ) ( ) ( −η)         + η + η −         + + − η −       +         η + + η −       +         η + = 1 R R 1 F 1 R R 1 u 1 R T 1 R h 1 R R 1 F 1 R h 1 R R 1 F V P eb D D D b e f b e w D b e D x D b e D roll (4.11)

Considerando Froll come la parte dissipativa della forza longitudinale F, cioè la responsabile della dissipazione, e Fx , FD come le forze che equilibrano la potenza frenante si ottengono dalla (4.11) le espressioni che definiscono appunto Froll e Fx nota la FD :

(

)

      +       η + η − = D eb D roll R h 1 R R 1 1 V P F (4.12)

(

f

)

w D D D eb eb D D eb x F R T 1 u R R 1 R R 1 R h 1 R F + η = +       +       η +       + ⋅ (4.13)

(13)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante 150

(

)

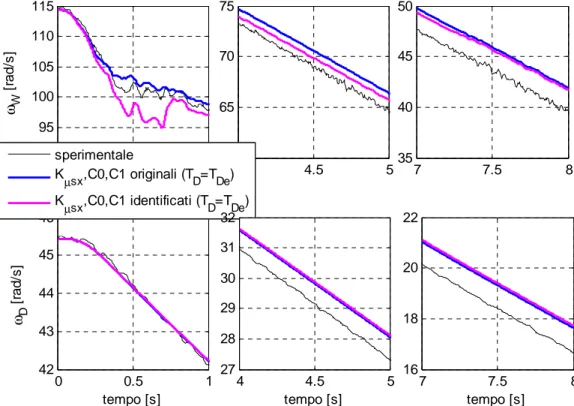
      +       η +       + + +       +       η +       + η − = D eb D D eb f eb w D eb D D eb eb D x R h 1 R R 1 R R 1 u 1 R T R h 1 R R 1 R R 1 R T F (4.14)

Attraverso questa ipotesi la forza frenante effettiva (Fx) risulta minore rispetto al caso precedente (Fb) in quanto è presente un’ulteriore forza longitudinale, dovuta al momento sul tamburo, che tende ad accelerare la ruota. Dalle figure successive si può notare infatti come la ruota, ma soprattutto il tamburo, rallenti meno rispetto ai dati registrati.

E’ da notare come, anche in questo caso, il secondo termine al secondo membro dell’equazione (4.14), ossia il termine dipendente dal momento frenante, possa essere definito come segue:

(

)

      +       η +       + + = D eb D D eb f eb w b R h 1 R R 1 R R 1 u 1 R T F (4.15)

in modo del tutto analogo a quanto fatto sin’ora.

Infine, l’espressione del braccio della risultante delle pressioni all’interfaccia battistrada-pneumatico, risulta:

(

)

      +       − + η −       η + = D eb eb x D roll R R 1 h R 1 h N F 1 h R 1 h N F x (4.16)

equazione del tutto analoga all’equazione del braccio nel modello QSTM_08 in cui si è sostituito F con _b F_x.

L’aver considerato il contributo del momento sul tamburo come componente dell’effettiva forza frenante comporta che l’equazione (2.58), che definisce la struttura del coefficiente di attrito frenato, debba essere riscritta come segue :

(14)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante 151

(

)

    + = + = µ _µ V C C K ) s ( sign s K s K 1 0 2 x 2 x 2 x x s x (4.17)

in cui F_x =µ_xN e K_µ_s_x ,C ,₀ C₁ sono dei parametri, diversi da quelli originali, da identificare con l’ipotesi T_D =T_D_e. Nell’ipotesi poi che T_D =0 si ricade nel caso F_x =F_b.

4.3.2 Risultati

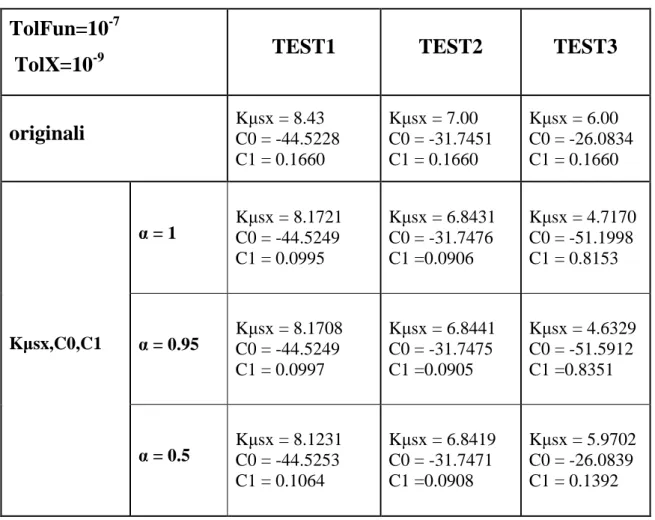
Le figure 4.9-4.15 illustrano le velocità angolari della ruota e del tamburo e i rispettivi errori percentuali simulati mediante i parametri identificati attraverso la rielaborazione del modello energetico analizzata in precedenza. E’ evidente che, aver considerato il contributo del momento motore come componente dell’effettiva forza frenante, comporti uno scostamento delle velocità angolari simulate dai dati sperimentali maggiore rispetto a quanto si ottiene considerandolo dissipativo assieme alla forza di rotolamento. Nella tabella 4.2 vengono riportati i valori identificati per i tre parametri.

0 0.5 1 90 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 60 65 70 75 7 7.5 8 35 40 45 50 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx,C0,C1 originali (T_D=T_De) K_µ_sx,C0,C1 identificati (T_D=T_De) 4 4.5 5 27 28 29 30 31 32 tempo [s] 7 7.5 8 16 18 20 22 tempo [s]

di K_µ_s_x,C ,₀ C₁, per il test 1 con α = 0.95, nell’ipotesi

e D D T

(15)

Capitolo 4 - Identificazione con modello energetico e momento motore sul drum costante 152 0 0.5 1 90 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 72 74 76 78 80 82 7 7.5 8 52 54 56 58 60 62 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx,C0,C1 originali (T_D=T_De) K_µ_sx,C0,C1 identificati (T_D=T_De) 4 4.5 5 31 32 33 34 35 tempo [s] 7 7.5 8 23 24 25 26 27 tempo [s]

di x s

K_µ ,C ,₀ C₁, per il test 2 con α = 1, nell’ipotesi

e D D T T = . 0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 91 92 93 94 7 7.5 8 81 82 83 84 85 86 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx,C0,C1 originali (T_D=T_De) K_µ_sx,C0,C1 identificati (T_D=T_De) 4 4.5 5 40 40.5 41 41.5 42 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s]

di K_µ_s_x,C ,₀ C₁, per il test 3 con α = 0.5, nell’ipotesi

e D D T

(16)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 5 3 fi g u ra 4 .1 2 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i x s K µ , 0 C , 1C , p er il t es t1 a l v ar ia re d el p es o α , n el l’ ip o te si eD D T T = . 0 2 4 6 8 -6 -4 -2 0 2 4 6 8 αααα =1 Test1 =1 Test1 =1 Test1=1 Test1 e % tempo [s] 0 2 4 6 8 -6 -4 -2 0 2 4 6 8 αααα =0.95 Test1 =0.95 Test1 =0.95 Test1 =0.95 Test1 tempo [s] 0 2 4 6 8 -6 -4 -2 0 2 4 6 8 tempo [s] α

e% ω_W con parametri originali e% ω_D con parametri originali e% ω

(17)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 5 4 fi g u ra 4 .1 3 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i x s K µ , 0 C , 1C , p er il t es t2 a l v ar ia re d el p es o α , n el l’ ip o te si eD D T T = . 0 2 4 6 8 -10 -8 -6 -4 -2 0 2 4 αααα =1 Test2 =1 Test2 =1 Test2 =1 Test2 e % tempo [s] 0 2 4 6 8 -10 -8 -6 -4 -2 0 2 4 αααα =0.95 Test2 =0.95 Test2 =0.95 Test2 =0.95 Test2 tempo [s]

e% ω_W con parametri originali e% ω_D con parametri originali e% ω_W con parametri identificati e% ω

D con parametri identificati

0 2 4 6 8 -10 -8 -6 -4 -2 0 2 4 tempo [s] α

(18)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 5 5 fi g u ra 4 .1 4 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i x s K µ , 0 C , 1C , p er il t es t3 a l v ar ia re d el p es o α , n el l’ ip o te si eD D T T = . 0 2 4 6 8 -5 0 5 10 15 20 25 30 35 αααα =1 Test3 =1 Test3 =1 Test3 =1 Test3 e % tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 35 αααα =0.95 Test3 =0.95 Test3 =0.95 Test3=0.95 Test3 tempo [s] 0 2 4 6 8 -40 -30 -20 -10 0 10 20 30 tempo [s] α

e% ω

W con parametri originali e% ω

D con parametri originali e% ω

W con parametri identificati e% ω_D con parametri identificati

(19)

C a p ito lo 4 I d en tif ic a zi o n e co n m o d el lo e n er g et ic o e m o m en to m o to re s u l d ru m c o st a n te 1 5 6 fi g u ra 4 .1 5 In g ra n d im e n ti d eg li er ro ri p er c en tu a li d el le v el o ci tà a n g o la ri d el la r u o ta e d el ta m b u ro p er il te st 3 . 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 αααα =1 Test3 =1 Test3 =1 Test3 =1 Test3 e % tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 αααα =0.95 Test3 =0.95 Test3 =0.95 Test3 =0.95 Test3 tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 tempo [s] α

e% ω_W con parametri originali e% ω_D con parametri originali e% ω

(20)

157

TolFun=10

-7

TolX=10

-9

TEST1

TEST2

TEST3

originali

Kµsx_{C0 = -44.5228} = 8.43 C1 = 0.1660 Kµsx = 7.00 C0 = -31.7451 C1 = 0.1660 Kµsx = 6.00 C0 = -26.0834 C1 = 0.1660 α = 1 Kµsx_{C0 = -44.5249} = 8.1721 C1 = 0.0995 Kµsx = 6.8431 C0 = -31.7476 C1 =0.0906 Kµsx = 4.7170 C0 = -51.1998 C1 = 0.8153 α = 0.95 Kµsx_{C0 = -44.5249} = 8.1708 C1 = 0.0997 Kµsx = 6.8441 C0 = -31.7475 C1 =0.0905 Kµsx = 4.6329 C0 = -51.5912 C1 =0.8351 Kµsx,C0,C1 α = 0.5 Kµsx = 8.1231 _{C0 = -44.5253} C1 = 0.1064 Kµsx = 6.8419 C0 = -31.7471 C1 =0.0908 Kµsx = 5.9702 C0 = -26.0839 C1 = 0.1392

tabella 4.2 Riassunto dei valori numerici assunti da K_µ_s_x ,C ,₀ C₁ durante le diverse identificazioni.