1.6 Modello monotraccia di autoveicolo Prima procedere si riepilogano le equazioni ottenute. Per generalità, si suppone che anche le ruote posteriori possano sterzare, con angolo

1.6 Modello monotraccia di autoveicolo

Prima procedere si riepilogano le equazioni ottenute. Per generalità, si suppone che anche le ruote posteriori possano sterzare, con angolo δ2 (positivo se antiorario). Con δ1 = δ si indica l’angolo di sterzo

anteriore.

Si hanno le seguenti equazioni di equilibrio (cfr. (1.22)) 2 2 1 2 1 ) (u vr F₁ F₂ F₁ F₂ F₂ SC u m &− = _x + _x − _yδ − _yδ + _x − ρ _x 2 1 2 1 ) (v ur F_x F_x F_y F_y m &+ = δ + δ + + (1.23) b F F a F F r J_&=( _x1δ₁+ _y1) −( _x2δ₂ + _y2)

e le equazioni di congruenza per u>0 (cfr.2.5))

u ra v+ − = ₁ 1 δ α (1.24) u rb v− − = ₂ 2 δ α

cui vanno affiancate le equazioni costitutive per un certo modello di pneumatico, ad esempio nel caso non lineare

) ( _i i y Y F i = α

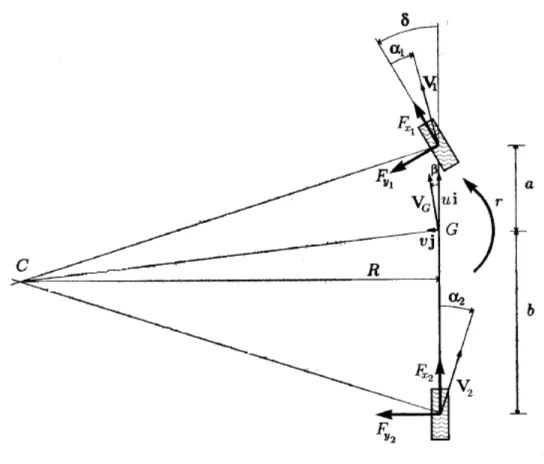
Fig. 1.6: Modello monotraccia di autoveicolo (con δ2 = 0)

Tutte queste equazioni sono alla base del modello monotraccia (single track model), illustrato in Fig. 1.6. Esso è a volte anche detto “modello a

bicicletta”, ma non ha niente della dinamica di un veicolo a due ruote: si

tratta invece della semplificazione ottimale per effettuare calcoli consistenti sulla dinamica degli autoveicoli.

Analogamente alla Fig. 1.4, in Fig. 1.6 è evidenziato anche il legame puramente cinematico fra la posizione del centro di istantanea rotazione

C ed i due angoli di deriva α1 e α2. La posizione di C (e quindi anche la

sua distanza R dall’asse del veicolo) è univocamente determinata dalla direzione delle velocità di due punti del corpo rigido, come, ad esempio, V1 e V2. La velocità di tutti gli altri punti discende di conseguenza.

Una volta fissato il modello non resta che stabilire cosa considerare noto e cosa incognito. Si può ad esempio [20] supporre assegnate le forze

longitudinali Fx1(t), Fx2(t) e gli angoli di sterzo δ1(t) e δ2(t). Nel caso di un

legame costitutivo di tipo algebrico rimangono allora incognite le tre funzioni u(t), v(t) e r(t).

In base alle equazioni di congruenza si possono esprimere gli angoli di deriva come α1 = α1(u,v,r,t) e α2 = α2(u,v,r,t), e quindi anche le forze

laterali Fy1 e Fy2 diventano funzioni di u, v, r, t. Si perviene così ad un

sistema di tre equazioni differenziali del primo ordine in forma normale nelle variabili di stato u(t), v(t) ed r(t)

) , , , ( 2 1 1 1 2 2 1 2 2 1 2 1 F F F F SC u vr f u v r t F m u_&= _ _x + _x − _yδ − _yδ + _x − ρ _x _+ =

[

]

[

]

Nelle funzioni fi(u,v,r,t) compare esplicitamente il tempo e il sistema è

quindi detto non autonomo.

Nel caso si scelga un legame costitutivo dato da un’equazione differenziale (caso linearizzato e non lineare negli esempi di legame costitutivo fatti in precedenza), vanno aggiunte le rispettive equazioni e anche le forze laterali Fy1(t) e Fy2(t) diventano funzioni del tempo,

rendendo il sistema a cinque variabili di stato.

Sistemi di questo tipo non presentano grossi problemi ad essere integrati numericamente (ad esempio mediante le formule di Runge-Kutta). Variando le condizioni iniziali e gli andamenti delle funzioni note (angolo di sterzo, ecc.) si possono simulare manovre di interesse pratico. Una volta note, sia pure in forma approssimata, le funzioni u(t), v(t) e

r(t), può essere interessante conoscere anche il moto del veicolo rispetto

quindi dette di "assi suolo" (Fig. 1.7), che può essere considerato inerziale perché la rotazione terrestre ha influenza trascurabile sul moto dei veicoli.

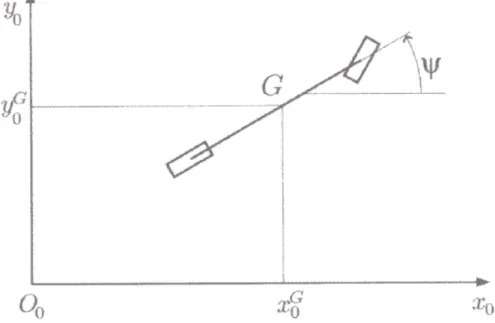
Fig. 1.7: Coordinate del veicolo rispetto ad un sistema di riferimento fisso.

L’angolo di rotazione

ψ

ˆ

∫

Una volta noto l'andamento dell'angolo di imbardata ψ(t), è immediato ottenere le componenti della velocità VG del baricentro nel riferimento

fisso (x0, y0, z0; O0) (Fig. 1.7), le quali mediante una successiva

integrazione nel tempo forniscono le coordinate assolute e della traiettoria del baricentro ad ogni istante t =

G x_{0 y}G 0 tˆ

[

]

∫

∫

0 (ˆ) (0) & ( )cosψ( ) ( )sinψ( )

[

]

∫

∫

0 (ˆ) (0) & ( )sinψ( ) ( )cosψ( )

Purtroppo la conoscenza di un certo numero di soluzioni in funzione del tempo non e molto illuminante del comportamento generale del veicolo. Occorre quindi procedere in modo diverso. Come si vedrà, ciò richiede la formulazione di ulteriori ipotesi semplificative.

1.6.1. Vere coordinate e quasi-coordinate

Per i sistemi olonomi, come quello in esame, le ben note equazioni di Lagrange possono essere esposte nella forma seguente

, k k k Q q L q L dt d = ∂ ∂ −       ∂ ∂ & k=1,...n (1.28)

dove L = T - U è la lagrangiana, data dalla differenza fra l'energia cinetica T e l'energia potenziale U, Qk sono le forze generalizzate non

conservative (o, comunque, non incluse in U) e qk rappresentano le n

coordinate generalizzate.

Queste coordinate qk possono essere considerate come vere coordinate

[7], nel senso che se sono note le velocità , una integrazione in funzione del tempo permette di ottenere le corrispondente coordinate

q

) (t q_&k

k(t).

Nel caso di modello monotraccia si possono utilizzare come vere coordinate le coordinate x0 e y0 del baricentro del veicolo (o di un

qualunque altro punto), e l'angolo di imbardata

ψ

Al contrario, la velocità di avanzamento u e la velocità laterale v, utilizzate abitualmente nella dinamica dei veicoli, non sono esprimibili

come derivate temporali di vere coordinate. In effetti, valgono le relazioni: 0 0 sin cos x y u= ψ_& + ψ_& (1.29) 0 0 cos sin x y v=− ψ_& + ψ_& ψ& = r

in cui la forma differenziale lineare cosψx_&0+sinψy_&0non è un differenziale esatto di una qualche funzione. Lo stesso vale per −sinψx_&0+cosψy_&0.1 Taluni autori, parlano in casi come questo di differenziali di

quasi-coordinate (o di pseudo-quasi-coordinate).

Nel caso del modello monotraccia l'introduzione delle componenti u e v è stato un passo del tutto naturale, che ha addirittura facilitato la stesura diretta delle equazioni di equilibrio, ma quando si vogliono utilizzare modelli di veicolo più complicati può essere utile ricorrere alle equazioni di Lagrange (1.28) che nella forma classica richiedono l'impiego di vere coordinate, poco pratiche in molti altri casi. E' infatti ben noto che anche le tre componenti della velocità angolare Ω = (p, q, r) di u corpo rigido non sono le derivate di vere coordinate.

Fortunatamente si possono generalizzare le equazioni di Lagrange in modo da introdurre direttamente le quasi-coordinate. Per la teoria generale si rimanda a testi di meccanica analitica. Qui ci si limita ad illustrare la procedura per il modello monotraccia.

In definitiva si tratta semplicemente di considerare le equazioni di Lagrange (1.28) per le vere coordinate q = (x0, y0,

ψ

relazione lineare (1.29) fra velocità che qui si riscrive in forma matriciale

q C ω= &

1 _{In entrambi i casi si vede immediatamente che le derivate miste di f non verificherebbero in teorema}

dove ω = (u, v, r). La matrice C è in questo caso una matrice di rotazione ed è quindi ortogonale (CT = C-1). In generale C dipende da tutte le coordinate generalizzate q, anche se qui dipende solo dall'angolo di imbardata

ψ

L'energia cinetica T può essere espressa sia in termini di q_&che di ω

[

]

[

]

T = _{& &} ψ_& = _& + _& + ψ_& = = + + (1.30) Si noti anche che l'energia cinetica non dipende dalle coordinate e quindi

0 /∂ =

∂T q_k e ∂Tˆ/∂q_k =0 per ogni k.

Dato che q , applicando le ben note regole di derivazione delle funzioni composte, si ottengono facilmente le relazioni

ω CT = &                   ∂ ∂∂ ∂∂ ∂ =                   ∂ ∂ ∂ ∂ ∂ ∂ r T v Tu T T y T x T ˆ ˆ ˆ 0 0 T C ψ_& & &

ovvero, in forma più compatta

      ∂ ∂ =       ∂ ∂ ω C q T T T ˆ & (1.31)

Derivando rispetto al tempo la relazione precedente si ottiene

      ∂ ∂ +       ∂ ∂ =       ∂ ∂ ω C ω C q T T T T dt d T dt d ˆ _& ˆ & (1.32) dove ψ ψ ψ ψ ψ & &           − − − = 0 0 0 0 sin cos 0 cos sin T C

Si possono riscrivere ancora le equazioni di Lagrange considerando che nel modello monotraccia di autoveicolo l'energia potenziale U è sempre nulla e l'energia cinetica T (equazione (1.30)) non dipende dalle coordinate generalizzate qk, quindi

Q ω C ω C q T T ₌       ∂ ∂ +       ∂ ∂ =       ∂ ∂ T T dt d T dt d ˆ _& ˆ &

dove Q = (Q1, Q2, Q3) che raccoglie le forze generalizzate.

Se adesso si premoltiplica la precedente equazione per la matrice C, in modo da avere CCT = I, si ottengono le equazioni di Lagrange per quasi-coordinate2 N CQ ω CC ω T _{= =}       ∂ ∂ +       ∂ ∂T T dt d ˆ ˆ _(1.33)

che esplicitate divengono

          =                     − =           3 2 1 0 0 0 0 0 0 0 N N N Jr mv mu r r r J v m u m & & &

Si vede immediatamente che coincidono con le equazioni di equilibrio (1.22) ottenute per via diretta.

1.7 Modello monotraccia classico

Se adesso si suppone assegnata la velocità di avanzamento, e quindi la funzione u(t), si ottiene una nuova e fondamentale semplificazione delle equazioni di equilibrio del modello monotraccia di autoveicolo. Infatti, la

prima equazione in (1.23) diventa un'equazione algebrica nella nuova incognita, che sarà necessariamente una delle forze longitudinali Fzi(t).

Se si considera un veicolo a trazione posteriore con sterzatura solo sulle ruote anteriori (

δ

e nelle restanti due equazioni non compare la funzione incognita Fx2(t)

(1.35) b F a F r J _{y y} 2 1 − = &

In definitiva, il sistema dinamico è governato da due sole equazioni differenziali in v(t) e r(t).

Nel caso di veicoli a trazione anteriore o integrale, la situazione è un po' più complessa perché non si ha più questo disaccoppiamento.

In generale si ha disaccoppiamento solo se la trazione e la sterzatura sono su assali differenti. Per un veicolo a trazione anteriore, ponendo

Fx2 = 0, si ottiene dalla prima equazione delle (1.23)

2 2 1 ) ( ₁ 2 m u vr F SC u F_x = _&− + _yδ + ρ _x (1.36)

in perfetta analogia con la (1.34). Ma la funzione Fx1(t) compare anche

nelle restanti due equazioni di equilibrio che, in base alle precedente relazione, diventano δ ρ δ ] 2 1 ) ( [ ) ( 2 1 2 1 F m u vr F SC u F yr v m _&+ = _y + _y + _&− + _y + _x (1.37) δ ρ δ SC u a F vr u m b F a F r J _{y y y x} ] 2 1 ) ( [ 2 1 2 1 − + − + + = _& &

Anche in questo caso il sistema dinamico è governato da due sole equazioni differenziali in v(t) e r(t), tuttavia, dato che i termini in più sono moltiplicati tutti per l'angolo di sterzo

δ

δ

Inoltre, con u(t) assegnata, le equazioni di congruenza diventano un legame lineare tra (

α1

α2

)] ( ) ( [ δ₁−α₁ + δ₂−α₂ = b a l u v (1.38) )] ( ) [(δ₁−α₁ − δ₂−α₂ = l u r

Si ha quindi la possibilità di scegliere tra (v, r) e (

α1

α2

di stato del sistema. La prima delle (1.36) permette anche di esprimere l'angolo di assetto

β

Il modello monotraccia più classico utilizza le due equazioni di equilibrio (1.35), oltre alle solite due equazioni di congruenza (1.23) e ad un modello di pneumatico. Si tratta quindi di un sistema dinamico a due variabili di stato.

Su questo tipico caso si svilupperà ulteriormente l'analisi, considerando i modelli lineare e non lineare di pneumatico precedentemente esemplificati.

1.8 Modello monotraccia lineare

Si tratta del modello più semplice, ma costituisce la base per modelli più complessi.

Se ci si limita a simulare angoli di deriva molto piccoli (circa 2° per autovetture medie su strada aderente, di meno su strada scivolosa), si può

far uso del modello lineare per i pneumatici. Introducendo le equazioni di congruenza (1.24) si ottengono le seguenti relazioni

) ( 1 1 1 1 u ra v C C F_y = α = δ − + (1.39) ) ( 2 2 2 2 _u rb v C C F_y = α = − −

che legano linearmente le forze laterali alle variabili di stato (v, r). Come già ricordato, le rigidezze di deriva per ciascun assale vanno valutate tenendo conto dell’influenza delle forze aerodinamiche sui carichi verticali agenti sulle singole ruote.

Se si sostituiscono queste espressioni nelle due equazioni di equilibrio (1.35) si ottiene il seguente sistema di due equazioni differenziali lineari del primo ordine, non omogeneo, che descrive completamente il modello di veicolo in esame3 δ m C r u mu b C a C v mu C C v 1 2 1 2 _{ +} 1      − ₊ −       + − = & (1.40) δ m a C r u Ju b C a C v Ju b C a C r 1 2 2 2 1 2 1 ₊       + − −       − − = &

Per inciso, si ricorda che i coefficienti a secondo membro vengono spesso indicati con il termine, tipico in ingegneria aeronautica, di derivate di stabilità (stability derivatives).

Introducendo la notazione matriciale, il sistema di due equazioni differenziali si può riscrivere come

b Aw

w_& = + (1.41)

dove w(t) = (v(t), r(t)) rappresenta il vettore delle variabili di stato, il vettore dei termini noti è dato da b(t) = (C1/m, C1a/J)δ(t) e

            + − + − + − = = Ju b C a C Ju b C a C u mu b C a C mu C C t u 2 2 2 1 2 1 2 1 2 1 )) ( ( A A (1.42)

è la matrice dei coefficienti. E’ importante notare che la matrice A dipende dalla velocità di avanzamento u, ma non dall’angolo di sterzo δ. Il contrario vale per il termine noto b.

Le variabili di stato non sono spostamenti, ma velocità, infatti non è di alcun interesse effettivo la posizione assoluta del veicolo nel piano.

1.8.1 Soluzione generale per velocità di avanzamento

costante

La soluzione generale w di (1.41) è data dalla somma dell’integrale w0

del sistema omogeneo associato e di un integrale particolare wp

Purtroppo, nel caso generale in cui sia u(t) ≠ cost non è possibile ottenere analiticamente queste soluzioni perché il sistema, anche se lineare, ha coefficienti dipendenti dal tempo.

Se invece la velocità di avanzamento u è uniforme (du/dt = 0), il sistema di equazioni differenziali lineari (1.41) diventa a coefficienti costanti, e ciò permette di ottenere la soluzione in forma analitica, almeno per la parte omogenea che verifica w&0 =Aw0. Si tratta quindi di

un’ipotesi di grande rilevanza per i successivi sviluppi.

Come è noto, nel caso di equazioni differenziali lineari a coefficienti costanti si ipotizza una soluzione in forma esponenziale4

t e t r t v t x λ w&₀( )=( ₀( ), ₀( ))= (1.43)

4 _{A rigore solo se A è diagonalizzabile, ma il caso patologico di A non diagonalizzabile ha rilevanza}

da cui segue subito _{w (t)=λxe}λt. Sostituendo ed eliminando e 0

& λt, si

perviene immediatamente ad un classico problema agli autovalori per la matrice A

Ax = λx

Gli autovalori sono dati dalle radici dell’equazione caratteristica

det(A-λI) = 0

che, nel caso di matrici 2x2, diventa

λ2-tr(A)λ+det(A) = 0.

Risolvendo si ottengono i due autovalori λ1 e λ2

2 ) ( 4det ) ( tr ) ( tr 2 2 , 1 A A A ± − = λ (1.44)

Se il discriminante è negativo, ovvero se tr(A)2<4det(A), i due autovalori sono complessi coniugati.

Dalla (2.41) si ricavano la traccia

0 1 ) ( tr 2 2 2 1 2 1 _<       + + + − = J b C a C m C C u A (1.45) e il determinante

[

]

Queste due quantità sono molto importanti perché possono fornire utili informazioni sui due autovalori λ1 e λ2 di A grazie alle relazioni

tr(A) = λ1 + λ2 (1.47)

det(A) = λ1λ2 (1.48)

Le precedenti relazioni si ottengono subito scrivendo l’equazione caratteristica come (λ - λ2)(λ - λ1) = 0.

Una volta noti gli autovalori (che dipendono da u ma non da δ) si possono calcolare i rispettivi autovettori x1 e x2 risolvendo i due sistemi

x è un autovettore lo è anche un qualsiasi suo multiplo. Nel caso di autovalori complessi coniugati (λ1 = λ2*), anche gli autovettori sono a

componenti complesse e possono essere scelti in modo da essere coniugati. (x1 = x2*).

Per la linearità del sistema, l’integrale generale della parte omogenea è dato da t t _e e t 1 2 2 2 1 1 0( ) λ λ _γ γ x x w = + (1.49)

con γ1 e γ2 costanti arbitrarie. In termini di componenti si ha

t t _{x e} e x t v 1 2 12 2 11 1 0( )=γ λ +γ λ (1.50) t t _{x e} e x t r 1 2 22 2 21 1 0( ) λ λ _γ γ + = dove x1 = (x11, x21) e x2 = (x12, x22).

L’integrale particolare wp(t) = (vp(t), rp(t)) dipende dal temine noto b e

quindi dalla funzione δ(t). Il caso più semplice si ha per δ = cost, ma si sanno trattare analiticamente anche i casi in cui δ(t) è una funzione poliniomiale o trigonometrica.

Nel caso di sterzo in posizione fissa (dδ/dt = 0) anche l’integrale particolare sarà costante nel tempo (dwp/dt = 0). Per ottenerlo, basta risolvere il sistema di equazioni -Awp = b, che ha per soluzione (l = a + b è il passo del veicolo)

δ δ ) ( ) ( ) det( ) ( 2 1 2 2 2 1 1 2 2 2 1 2 2 b C a C mu l C C u C mau bl C mJu u C mau bl C v_p − − − = − = A (1.51) δ δ ) ( ) det( 2 2 _{1 2} 2 1 2 1 2 2 1 b C a C mu l C C lu C C mJu lu C C r_p − − = = A

1.8.2 Studio della stabilità di marcia

Analizziamo meglio quanto finora ottenuto.

Le due parti w0 e wp della soluzione generale hanno significati fisici ben

distinti. L’integrale particolare rappresenta la soluzione di regime, ovvero il moto del veicolo dopo un tempo sufficientemente lungo, mentre l’integrale dell’omogenea associata rappresenta la parte transitoria della soluzione, che decade con il passare del tempo, perlomeno fintanto che il sistema è stabile.

Come in ogni sistema lineare, la stabilità del veicolo è determinata dai due autovalori λ1 e λ2, o meglio solo dal segno della loro parte reale

Re(λ1) e Re(λ2): il sistema è asintoticamente stabile se e solo se i due

autovalori hanno parte reale negativa.

Si può ricavare da un qualunque testo di analisi matematica o di tecnica del controllo che affinché entrambi gli autovalori abbiano parte reale negativa occorre e basta che siano verificate le seguenti due condizioni

stabilità ↔ tr(A) < 0 e det(A) > 0 (1.52)

Dalla (1.45) si ricava subito che, per il modello di veicolo in questione, la traccia della matrice è sempre negativa, e, quindi, la prima condizione è sempre verificata. Ciò esclude, fra l’altro, la possibilità di avere entrambi gli autovalori con parte positiva o nulla.

La stabilità è quindi determinata solo dalla seconda condizione in (1.52). Annullando il deteminante (1.46) si ha un’equazione in u che fornisce il valore della (eventuale) velocità critica ucr, oltre la quale si ha

comportamento instabile del veicolo

) ( _{1 2} 2 2 1 b C a C m l C C u_cr − = (1.53)

Si noti che ucr non dipende da J, ma solo dalla sua massa, dalla posizione

del suo baricentro e dalle caratteristiche dei pneumatici. La velocità critica esiste solo se

C1a - C2b > 0 (1.54)

ovvero se la capacità direttiva C1a dell’avantreno è superiore alla

capacità direttiva C2b del retrotreno. In base a questo risultato, è

consuetudine dare le seguenti definizioni (si ricordi però che queste definizioni sono inadeguate, e quindi errate, se applicate a modelli con pneumatici non lineari, come si vedrà in seguito):

1. veicolo sovrasterzante se C1a - C2b > 0

2. veicolo neutro se C1a = C2b

3. veicolo sottosterzante se C1a - C2b < 0

da cui risulta che solo un veicolo sovrasterzante possiede una velocità critica oltre la quale diventa instabile. La posizione del baricentro influenza direttamente a e b, ed indirettamente le rigidezze di deriva perché fa variare il carico statico su ciascun assale. Nell’ambito della validità del presente modello, la ucr non dipende dall’angolo di sterzo δ.

Come mostrato successivamente, se si considerano pneumatici non lineari, oppure si rimuove l’ipotesi di u assegnata, la ucr qui ottenuta

rimane valida solo nel caso di marcia rettilinea.

1.8.3 Tipo di moto durante il transitorio

Ha un certo interesse conoscere quale sia l’evoluzione degli autovalori al crescere di u, anche quando il veicolo ha un comportamento stabile.

A questo scopo, è utile riportare in un grafico tr(A) e det(A), che, in base alle equazioni (1.45) e (1.46), possono essere espressi sinteticamente nel modo seguente5 β α + = ₂ ) det( u A , u tr(A)=−γ

dove α e γ sono sempre positive, mentre β = (C2b - C1a)/J è positiva o

negativa a seconda del carattere sotto o sovrasterzante del veicolo. Si vede subito che entrambe le funzioni sono monotone in u e che

− +∞

→ ( )= 0

limtr A

u , ulim→+∞det(A)=β

Eliminando la velocità u si ottiene il legame β γ α ₊ = 2 2 ( ) ) det(A tr A

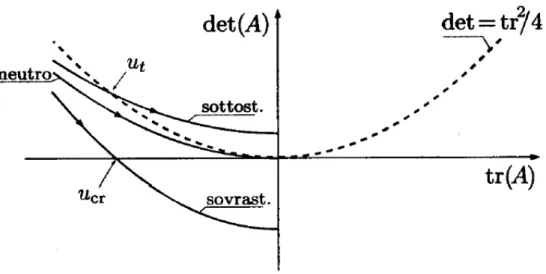
Pertanto, la crescere di u, si percorrono in Fig. 1.8 i rami di sinistra di parabole con vertice nel punto di coordinate (0, β).

In Fig. 1.8 è anche riportata la parabola di equazione det = tr2/4, che, come risulta dalla (1.44), individua i punti per cui si ha λ1 = λ2

(discriminante nullo). questa curva suddivide il piano in due zone: quella inferiore che corrisponde ad autovalori reali e distinti e quella superiore che corrisponde ad autovalori complessi coniugati.

Si può dimostrare che la quantità

[

]

dove si è posto J = mk2, introducendo il raggio di inerzia k. Il valore massimo di 1/4 lo raggiunge per C1a = C2b (veicolo neutro) e J = mab.

Ne segue che tutti i veicoli, a velocità sufficientemente bassa, hanno comportamento stabile con autovalori reali e distinti (tranne il caso di veicolo neutro con k2 = ab che ha sempre autovalori coincidenti).

Fig. 1.8: Evoluzione di det(A) e di tr(A) al crescere della velocità di avanzamento u.

Al crescere della velocità si hanno i seguenti comportamenti.

Un veicolo sovrasterzante ha sempre autovalori reali e distinti. Di questi, uno diventa positivo quando la parabola di Fig. 1.8 attraversa l’asse delle ascisse (det = 0). L’attraversamento si ha per u = ucr e

corrisponde alla perdita di stabilità.

Un veicolo neutro generico (k2 ≠ ab) ha sempre autovalori reali e negativi (Fig. 1.8). Al crescere di u, sia la traccia che il determinante tendono a zero.

Un veicolo sottosterzante ha inizialmente autovalori reali e negativi. Oltre una certa velocità u = ut si trasformano però in complessi coniugati (Fig. 1.8), con parte reale negativa: λ1 = ζ+iω, λ2=ζ-iω, con ζ = tr(A)/2 < 0. Pur avendo sempre comportamento stabile, cambia il

tipo di moto durante il transitorio. A bassa velocità è di tipo aperiodico smorzato (λ1, λ2 ∈ℜ), mentre per u > ut è di tipo oscillatorio smorzato

La velocità ut è quella che annulla il discriminante in (1.44)

[

]

Se J = mab e il veicolo non è neutro, si ha

) /( ) ( 2 / ) (t l C₂b C₁a mab u = − .

Naturalmente può darsi che ut sia una velocità non raggiungibile dal

veicolo. Lo stesso vale per ucr.

Nel caso di autovalori complessi coniugati, la soluzione generale può essere messa in una forma più manipolabile utilizzando le formule di Eulero

[

(t et _z1 t _z2 t _wp t

w = ζ ω + ω

]

Chiaramente, la parte immaginaria degli autovalori determina la pulsazione ω delle oscillazioni, mentre lo smorzamento dell’ampiezza eζt viene dalla parte reale ζ.

Il vettore z1 si ottiene immediatamente scrivendo l’espressione in (1.56)

al tempo t = 0

z1 = w(0) - wp(0) (1.57)

dove w(0) indica le condizioni iniziali imposte.

Per l’altro vettore basta considerare che dw0(0)/dt = Aw0(0). Ma dalla

(1.56) si ottiene che dw0(0)/dt = ζz1 + ωz2, oltre a w0(0) = z1. Pertanto si ha la notevole relazione ζz1 + ωz2 = Az1, da cui

1 2 ( ) 1 z I A z ζ ω − = (1.58)

1.8.4 Comportamento a regime

Come è stato già evidenziato, se il veicolo è stabile l’integrale particolare

wp(t) rappresenta il tipo di moto in condizioni di regime (non

necessariamente stazionarie se dδ/dt ≠ 0).

Verranno esaminati in dettaglio due casi tipici, caratterizzanti numerosi tipi di prove ISO per i veicoli da strada [8, 9, 10,11]. In entrambi i casi il termine noto è costante nel tempo e quindi il veicolo percorre a regime delle traiettorie circolari. Ne segue, fra l’altro, che il centro di istantanea rotazione C rimane fisso nel tempo e viene quindi semplicemente detto centro di rotazione.

Percorso circolare (steering pad)

Nel caso di sterzo in posizione fissa (δ = cost) e velocità di avanzamento uniforme, il veicolo si stabilizza su un percorso circolare e le (1.51) indicano i valori della velocità laterale vp del baricentro e

della velocità di imbardata rp a regime. In questo caso si parla di moto in

condizioni stazionarie perché tutte le grandezze rilevanti sono costanti nel tempo. In base alle norme ISO 4138 e ISO 9816 [9, 11], le prove vengono solitamente condotte con traiettorie di raggio 100m. In alternativa, qualora sussistano problemi di spazio, si possono condurre prove con raggio 40m.

Dalle equazioni di equilibrio (1.55) si ricavano le seguenti utili relazioni

a l F b l F F F mur p y p y p y p y p = 1 + 2 = 1 = 2 (1.59)

che mostrano come, a regime, le forze laterali esercitate dai pneumatici equilibrino la componente laterale delle forze di inerzia6 e diano momento nullo rispetto al baricentro.

La conoscenza di vp e rp permette di ottenere il valore di una serie di altre

grandezze a regime, quali l’angolo di assetto β (equazione 1.6) δ β ) ( ) ( 2 1 2 2 2 1 1 2 2 b C a C mu l C C C mau bl C u v_p p _{− −} − = = (1.60)

la distanza R dell’asse del veicolo dal centro di rotazione C, che in questo caso è anche raggio di curvatura (equazione 1.8)

            − − = = l mu C C b C a C l r u R p p 2 2 1 2 1 1 δ (1.61)

gli angoli di deriva anteriore e posteriore

δ δ α ) ( _{1 2} 2 2 2 1 2 2 1 2 1 b C a C mu l C C b C mu lC R b mu u a r v p p p p = = _{− −} + − = (1.62) δ δ α ) ( _{1 2} 2 2 2 1 1 2 2 2 2 b C a C mu l C C a C mu lC R a mu u a r v p p p p = = _{− −} − − = .

Da queste relazioni si ottiene che, in queste particolari condizioni di prova, il segno di α1p - α2p è concorde con quello di C2b - C1a. Pertanto,

coerentemente con le definizioni date precedentemente, si ha che un veicolo sottosterzante ha, a regime, deriva anteriore maggiore di quella posteriore (α_1p >α_2p ), mentre il contrario avviene in un veicolo sovrasterzante, almeno finché è stabile. Queste relazioni fra gli angoli di deriva, si badi bene, non sono necessariamente rispettate durante il transitorio, oppure se le condizioni di prova sono diverse, come nel caso fosse presente una spinta laterale.

In base alla relazione (1.7), si ha che             − + = − + = 2 1 1 2 2 2 2 1 1 1 ) ( 1 C C a C b C l mu R R_p α p α p _p δ (1.63)

da cui risulta che, per mantenere costante Rp all’aumentare della velocità u, occorre aumentare l’angolo di sterzo δ se il veicolo è sottosterzante, mentre si deve ridurre δ se il veicolo è sovrasterzante (fino ad avere δ = 0 se u = ucr, qualunque sia Rp). Probabilmente, i

termini sovra e sottosterzante sono stati coniati proprio a causa di questo fenomeno.

Utile è anche l’espressione seguente, che discende immediatamente dalla (1.63) introducendo l’accelerazione laterale a regime a~_{y =}u2/R_p

y p y p Ka R l a C C a C b C l m R l + =       − + = 2 1 1 2 δ (1.64)

il coefficiente di ay è, per questo modello, il cosiddetto gradiente di

sottosterzo K       − =         − = 2 1 1 2 ~ _Rl m_l C_Cb_CCa a d d K p y δ (1.65)

Dato che il segno di K è lo stesso di C2b - C1a, le definizioni si possono

dare anche in termine di gradiente di sottosterzo: 1. veicolo sovrasterzante se K < 0

2. veicolo neutro se K = 0

3. veicolo sottosterzante se K > 0

In autovetture europee, K (alle ruote) è dell’ordine di 1.5-2.5 gradi/g (che corrisponde a circa 30-50 gradi/g al volante, supponendo un rapporto di riduzione di 1:20). [7]

Le espressioni di molte delle grandezze di regime si semplificano notevolmente se si introduce il gradiente di sottosterzo K:

) ( 1 _{l Ku}2 R_p + = δ δ 2 Ku l u r_p + = δ α α _      + = − ₂ 2 ₂ 1 1 Ku Ku p p       + = 1 2 ₂ 2 ) det( u Ku l mJ l C C A

da questa ultima espressione si ricava il valore della velocità critica nel caso sia K < 0

K l

u_cr = − (1.66)

Al contrario, nel caso sia K > 0 viene spesso introdotta la velocità caratteristica

K l

u_car = (1.67)

che rappresenta la velocità in cui il rapporto rp/δ (yaw velocity gain)

raggiunge il massimo valore. E’ immediato ricavare che alla velocità caratteristica si ha δ = 2l/Rp, ovvero l’angolo di sterzo è esattamente il

doppio di quello necessario in condizioni di derive nulle. Ovviamente, tutto ciò ha senso purché sia ancora applicabile il modello lineare in esame.

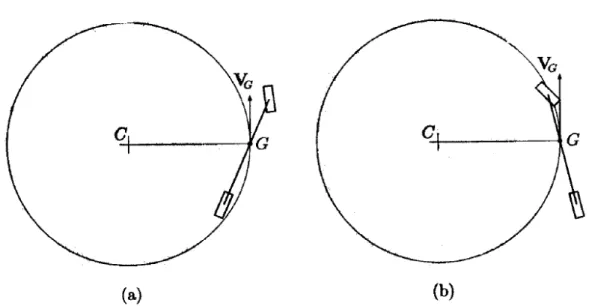
Fig. 1.9: Assetto del veicolo rispetto alla traiettoria del baricentro: a) a bassa velocità (u < uβ) e b) ad alta velocità (u > uβ)

La presenza di una velocità laterale vp a regime non deve sorprendere,

Sta semplicemente ad indicare che la traiettoria del baricentro non è tangente all’asse del veicolo. Come illustrato in Fig. 1.9(a), a velocità prossima a zero (derive nulle ≡ sterzatura cinematica), l’angolo di assetto è concorde con l’angolo di sterzo (si ha βp = bδ/l) e la ruota anteriore

percorre una traiettoria di raggio più grande di quella della ruota posteriore (muso fuori dalla curva). al crescere della velocità di avanzamento u e quindi all’aumentare degli angoli di deriva, l’angolo βp

cala fino ad annullarsi per u = uβ

am bl C

u ₌ 2

β

Oltre questa velocità (Fig. 1.9 b)), βp diventa discorde con δ e, se i due

semipassi sono uguali (a = b), la ruota anteriore percorre una traiettoria di raggio inferiore a quella della ruota posteriore (muso dentro la curva). Ciò accade in ogni caso per velocità sufficientemente alta anche se a ≠ b. Ovviamente, il segno di βp è lo stesso di vp.

Utilizzando l’equazione in (1.34) è anche possibile ottenere la forza di trazione Fx2 sulla ruota posteriore necessaria per mantenere i l veicolo in

moto stazionario

[

]

Si osservi che, nel caso di veicolo sovrasterzante e per δ fisso, si ottiene per u → u ∞ → p x F

2 cr, a meno che non si abbia δ = 0. Esattamente lo

stesso vale per vp e rp. Questi risultati, poco accettabili dal punto di

vista fisico, indicano che il modello è poco realistico e mal si presta a descrive il reale comportamento del veicolo, tranne che in condizione di marcia rettilinea.

La situazione è un po’ diversa se si suppone di tenere fissa la distanza Rp,

facendo variare l’angolo di sterzo secondo la relazione (1.63). In questo caso si ottiene per la forza motrice l’espressione

2 2 2 2 1 2 2 2 1 2 2 1 2 1 ) ( ) ( 2 _{C a C b R} Sc u b C a C l C C F _x p p x ₋ + ρ + =

che si mantiene limitata.

La forza motrice può anche essere ottenuta con considerazioni energetiche. Oltre alle forze aerodinamiche, anche le forze laterali F

p x F₂

yi

agenti sui pneumatici dissipano energia. Infatti, a causa degli angoli di deriva, forza e velocità del punto di applicazione non sono fra loro ortogonali e per mantenere costante l’energia cinetica del veicolo occorre che il motore fornisca energia al sistema. Facendo il bilancio delle potenze in condizioni di moto stazionario, si ottiene

0 ) 2 1 ( ) ( ) ( ) ( 2 2 1 2 2 −F u+F v +r a +F v −r b − Sc u u= F p _{p p x} y p p p y p y p x δ ρ

da cui 2 2 2 2 2 1 1 2 1 2 C C SC u Fp _x x = α p + α p + δ (1.69)

Si può verificare che le due formule (1.68) e (1.69) forniscono lo stesso risultato. In entrambi i casi, l’impostazione del problema ha validità generale, mentre l’ultima riga vale solo per pneumatici dal comportamento lineare.

Spinta laterale

E’ interessante osservare cosa accade se il veicolo è sottoposto ad una spinta laterale Fl, come se fosse soggetto ad una raffica di vento

trasversale. In realtà, si tratta di una simulazione molto grossolana, perché per mantenere il problema lineare si assume che la forza sia costantemente perpendicolare all’asse del veicolo. Più realisticamente si può pensare che la spinta sia dovuta alla forza peso nel caso che il veicolo percorra una strada con pendenza laterale (banked road).

Le equazioni di equilibrio cambiano solo per l’aggiunta della forza laterale e della relativa coppia. Nel caso che la forza laterale Fl abbia

componenti (0, Fl, 0), ovvero spinga da sinistra verso destra e passi a

distanza x dal baricentro del veicolo, si ha

l y y F F F ur v m( &+ )= ₁ + ₂ − (1.70) x F b F a F r J&= _y1 − _y2 − _l

La distanza x è positiva se la retta di applicazione di Fl passa davanti al

Le equazioni del moto sono ancora nella forma (1.41), con la sola differenza che il termine noto è dato da

l F J x m J a Cm C           −           = 1 1 1 δ b (1.71)

Le condizioni di moto a regime wp si ottengono risolvendo come al solito, il sistema -Awp = b, con A data dalla (1.41). Se si suppone che l’angolo di sterzo venga mantenuto costantemente nullo (δ = 0), si hanno le seguenti condizioni di moto a regime

[

]

[

]

dove si è posto x = e+y, con

2 1 2 1 C C b C a C e + − = (1.73)

Se l’angolo di sterzo non è nullo basta aggiungere le (1.49) (sovrapposizione degli effetti).

Si ottiene subito che la velocità di imbardata a regime rp è nulla (y = 0) se la forza laterale Fl passa a distanza e (con segno) dal baricentro del veicolo: a regime gli angoli di deriva anteriore e posteriore sono fra loro uguali e, quindi, il veicolo trasla muovendosi “in diagonale” (Rp = ∞). La distanza e individua il punto sull’asse del veicolo che è spesso

chiamato punto neutro (neutral steer point) per le ragioni appena esposte.

Nel caso di moto traslatorio dell’attuale modello di veicolo, le equazioni (1.70) diventano l F C C + − =( )α 0 _{1 2} e F b C a C − − _l =( )α 0 _{1 2}

che forniscono un altro modo per ottenere la distanza e.

Dalla (1.73) si vede subito che e > 0 in un veicolo sovrasterzante, mentre e < 0 in un veicolo sottosterzante. La quantità adimensionale

e/l è detta margine di stabilità (static margin). In autovetture medie, il

rapporto e/l è dell’ordine di 0.05 - 0.07. E’ interessante osservare che, anche se gli angoli di deriva a regime sono ovviamente influenzati dalla presenza della forza Fl, rimane valida la definizione di gradiente di

sottosterzo K data dalla (1.65). In altri termini, la presenza di Fl non

influenza il valore di K.

Il raggio di curvatura a regime, sempre con δ = 0, è dato da

l p p F C C y b C a C mu l C C r u R ) ( ) ( 2 1 2 1 2 2 1 1 + − − − = =

Dato che il denominatore è sempre positivo (per u < ucr), il segno del

raggio di curvatura a regime è concorde con quello di Fl se y < 0 e

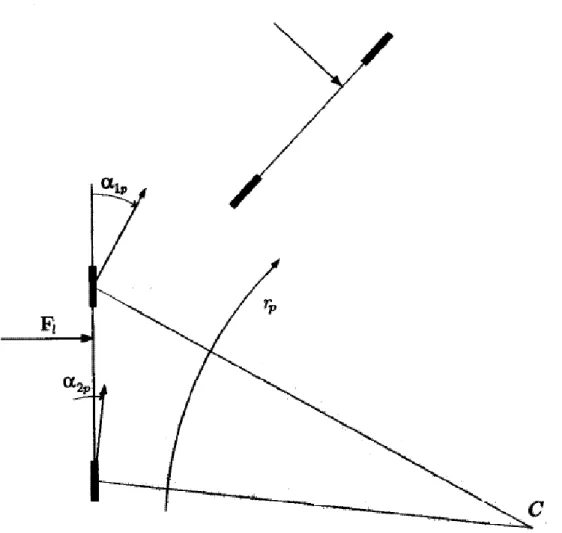
Fig. 1.10: Forza laterale applicata in posizione avanza (x > e)

Se la forza laterale Fl è applicata in posizione sufficientemente avanzata,

come in Fig. 1.10, cioè tale da avere x > e, ovvero y > 0, il veicolo curva dalla parte dove è diretta la forza laterale perché l’angolo di deriva anteriore è maggiore di quello posteriore. Se invece la forza Fl è

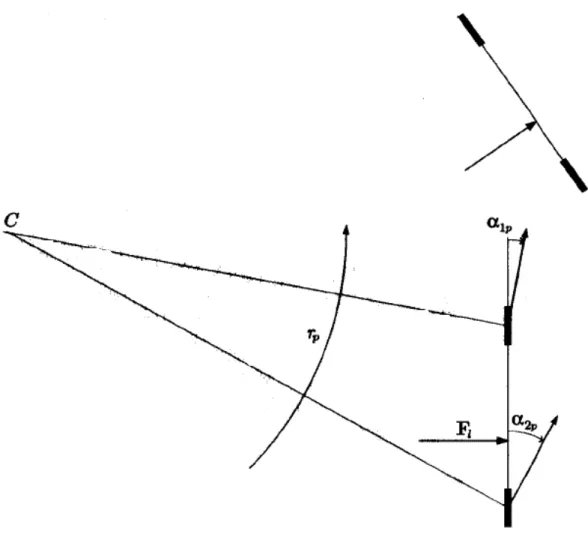
applicata in modo da avere y < 0, ovvero in posizione arretrata (x < e), il veicolo curva dalla parte opposta rispetto a Fl (Fig. 1.11), perché

Fig. 1.11: Forza laterale applicata in posizione arretrata (x < e)

Il valore assoluto del raggio di curvatura Rp dipende dalla velocità di

avanzamento u e dal carattere sovra-sottosterzante del veicolo. Ovviamente, se il veicolo è sottosterzante, il raggio Rp cresce in modulo

al crescere di u, mentre accade il contrario se il veicolo è sovrasterzante. Interessante è anche considerare l’andamento delle forze esercitate dai pneumatici. All’aumentare della velocità u si ha, a regime, una diminuzione della forze sui pneumatici se y > 0, mentre si ha una crescita se y < 0. D’altra parte, nel primo caso il veicolo “cede” alla spinta laterale (Fig. 1.10) e le azioni inerziali concorrono ad equilibrare F

p yi

F

l. Nel secondo caso si ha la situazione opposta, con il veicolo che

inerziali che si sommano a Fl nel caricare i pneumatici. Delle due

situazioni è da preferire la prima, perché allontana il rischio di superare il limite di aderenza.

Queste considerazioni sulle forze dei pneumatici valgono indipendentemente dal carattere sovra - sottosterzante del veicolo, che ha però influenza sul valore di e. Ad esempio, applicare una forza Fl

all’altezza del baricentro G, come accade nel caso di strada con pendenza laterale, equivale ad avere y = -e. Se il veicolo è sottosterzante curva verso la stessa direzione della forza (y > 0), mentre se è sovrasterzante curva dalla parte opposta (y < 0). a parità di punto di applicazione si ha quindi un comportamento totalmente diverso.

Il punto di applicazione della spinta laterale dovuta al vento dipende dalla forma del veicolo e dalla direzione del vento stesso. Avere e < 0 rende più semplice fare in modo che nel caso di vento laterale la forza Fl sia applicata a distanza x > e dal baricentro.

Le condizioni di moto a regime nel caso di angolo di sterzo non nullo si ottengono sommando le equazioni (1.50) alle precedenti espressioni di vp

e rp (sovrapposizione degli effetti). In particolare, si può ottenere quel