Modellazione numerica del comportamento viscoso fessurato di elementi in CCA

(1)

ALMA MATER STUDIORUM - UNIVERSITÀ DI BOLOGNA

FACOLTÀ DI INGEGNERIA - D.I.S.T.A.R.T.

Dipartimento di Ingegneria delle Strutture, dei Trasporti, delle Acque, del Rilevamento e del Territorio

Corso di laurea in Ingegneria Civile

indirizzo

Strutture

Insegnamento:

TECNICA DELLE COSTRUZIONI LS

MODELLAZIONE NUMERICA DEL

COMPORTAMENTO VISCOSO FESSURATO DI

ELEMENTI IN C.C.A.

Tesi di laurea di:

NICOLA FRANZONI

Relatore Chiar.mo Prof. Ing. CLAUDIO MAZZOTTI

Sessione III

(2)

Introduzione Capitolo 1

1

Capitolo 1

Introduzione

Questo studio mira ad affinare modelli numerici a fibre che siano in grado di valutare il comportamento viscoso fessurato di elementi in conglomerato cementizio armato.

Nei prossimi capitoli verrà messo a punto un modello numerico capace di analizzare il comportamento in esercizio di elementi inflessi in cca sottoposti ad un carico differito.

Il modello è stato implementato in Matlab. Sono stati prodotti tre modelli:

a. FIBRA: simula le deformazioni da creep di una singola fibra di cls

b. SEZIONE: riproduce la curvatura di una sezione in cca gettata in due fasi e sottoposta a tre incrementi di momento

c. TRAVE: ricostruisce la deformata di una trave inflessa a quattro punti

Il modello numerico è stato calibrato e raffrontato con due campagne sperimentali che hanno studiato il fenomeno del creep in due travi in ca. Le travi sono state gettate in due fasi e sollecitate in modo da simulare il loro comportamento in esercizio, mantenendo gli incrementi di carico costanti per diverse settimane così che si verificassero le deformazioni a lungo termine. La prima campagna sperimentale è stata svolta nel 2007 da Ylenia Ponzoni, mentre la seconda nel 2008 da Michele Fabiani.

Il modello FIBRA è stato utilizzato per verificare la correttezza delle calibrazioni dei moduli pseudo-elastici.

Il modello SEZIONE è stato creato per valutare la curvatura della sezione in mezzeria nelle due travi che furono oggetto di studio gli anni scorsi. SEZIONE si compone di 3 subroutine:

I. Ipotizza la sezione non fessurata e considera il cls reagente a trazione come a

compressione

(3)

2 III. Utilizza la tecnica del tension stiffening per cercare la soluzione reale, intermedia ai due

casi limite valutati in precedenza.

Il tension stiffening è una pratica consolidata per lo studio di sezioni in c.a. di sezioni gettate in una fase unica. Nel nostro caso, una complicazione è data dal fatto che la sezione in c.a. è gettata in due fasi.

Il modello TRAVE studia il comportamento flessionale a lungo termine di una trave prefabbricata, realizzata per fasi. In esso, la trave viene discretizzata in conci e la curvatura viene integrata fino ad ottenerne la deformata. Data la simmetria dello studio di una trave inflessa a quattro punti, il problema si semplifica allo studio di mezza trave, appoggio-incastro scorrevole.

Capitolo 2

Creep e Ritiro

Vengono qui trattati gli aspetti teorici di ritiro e viscosità ed elencati i fattori che li influenzano. Si potranno cosi inquadrare i problemi delle deformazioni a lungo termine sul calcestruzzo.

Esistono due tipi di modelli: i metodi algebrizzati e i modelli reologici. Questi ultimi si prestano ad una formulazione incrementale implementabile in un modello numerico (basato sullo sviluppo in serie di Dirichlet).

Viene infine descritta la teoria della solidificazione di Bazant ed illustrato, in particolare, un algoritmo di tipo esponenziale risolutore di tale teoria.

Capitolo 3

Sistemi di prefabbricazione

Breve descrizione del sistema costruttivo di cui fanno parte le travi oggetto del confronto.

Capitolo 4

Campagna sperimentale M

In questo capitolo vengono brevemente illustrate le prove di laboratorio per interpretare al meglio i risultati dei confronti tra modello numerico e risultati sperimentali.

Le prove descritte riguardano prove di creep e ritiro effettuate su provini cilindrici ed una prova di carico differito su una trave realizzata in due fasi.

Capitolo 5

Campagna sperimentale Y

Sono riportati i dati e i risultati delle prove differite nel tempo che sono state utilizzate come confronto negli elaborati successivi.

(4)

3

Capitolo 6

Modelli a fibre per l’analisi differita nel tempo

Qui vengono descritti i modelli numerici che, a differente scala, elaborano le deformazioni differite nel tempo di elementi sollecitati da carico variabile nel tempo.

I modelli si chiamano FIBRA, SEZIONE e TRAVE e modellano i rispettivi elementi strutturali. Viene illustrato il metodo del tension stiffening per mediare i due casi limite di sezione fessurata e di sezione interamente reagente.

Capitolo 7

Calibrazione dei parametri riguardanti le proprietà reologiche dei calcestruzzi

In questo capitolo vengono cercati ed ottimizzati i parametri necessari ai modelli. Essi riguardano ritiro e creep e vengono calibrati sulle prove descritte al capitolo 4 e 5. Tali parametri vengono poi verificati ed ottimizzati col modello FIBRA.

Capitolo 8

Risultati dei modelli numerici

Si confrontano i risultati della modellazione numerica con quelli delle prove sperimentali. Si commentano poi gli aspetti non colti dal modello o dalle prove sperimentali in grado di influire sui risultati, e rispettivi metodi per inserirli all’interno del modello.

(5)

Creep e Ritiro Capitolo 2

4

Capitolo 2

Creep e Ritiro

2.1 Generalità

La deformazione totale ε all’istante t di un elemento in calcestruzzo, soggetto a condizioni di carico e temperatura costanti, è la somma della deformazione istantanea 𝜀𝜀₀, della deformazione viscosa 𝜀𝜀_𝜑𝜑 e di quella da ritiro 𝜀𝜀_{𝑐𝑐𝑐𝑐}:

𝜀𝜀 = 𝜀𝜀0 + 𝜀𝜀𝜑𝜑 + 𝜀𝜀𝑐𝑐𝑐𝑐

Nella figura sottostante si mostrano le differenti componenti della deformazione totale per un

Figura 2-1:Deformazione totale del calcestruzzo per effetto di uno stato di tensione costante

(6)

5 elemento soggetto ad uno stato tensionale costante σ0 applicato al tempo t0.

Le deformazioni differite del calcestruzzo sono quelle dovute ai fenomeni del ritiro e del creep e, come si può evincere dalla Figura 2-1, si tratta di deformazioni che si evolvono nel tempo.

Nei paragrafi seguenti si descriveranno sinteticamente le principali caratteristiche del ritiro e del creep del calcestruzzo e si riporteranno le indicazioni in merito ad essi fornite dall’Eurocodice2 e dal CEB-FIP Model Code 90, che propongono modelli attraverso cui è possibile prevedere l’andamento delle deformazioni differite nel tempo.

2.2 Ritiro

Il ritiro è la diminuzione di volume che il calcestruzzo subisce, in assenza di sollecitazioni, a causa di una serie di reazioni chimico-fisiche. La principale di queste è legata all’evaporazione dell’acqua d’impasto durante la fase di maturazione.

Si possono definire cinque differenti tipi di ritiro per il calcestruzzo (Aitcin, 1997):

 il ritiro plastico (plastic shrinkage), chiamato anche ritiro fresco, è dovuto all’evaporazione dell’acqua dalla superficie libera del calcestruzzo quando ancora si trova in condizioni plastiche (non è ancora avvenuto l’indurimento) subito dopo la sua messa in opera. Esso induce fenomeni di fessurazione della suddetta superficie con conseguente calo della durabilità dell’elemento.

 il ritiro termico (thermal shrinkage), è dovuto al fatto che, all’inizio della presa, le reazioni chimiche d’idratazione sviluppano calore; di conseguenza la temperatura aumenta e il calcestruzzo si dilata. Alla fine della presa, le reazioni sono molto rallentate e la temperatura si abbassa progressivamente. Ciò avviene a seguito della dissipazione di calore attraverso le casseforme, le quali non offrono condizioni adiabatiche. A seguito di questo raffreddamento la temperatura del calcestruzzo diventa prossima a quella dell’ambiente esterno e si ha una conseguente contrazione del materiale, indicata appunto come ritiro termico.

 il ritiro autogeno (autogenous shrinkage), chiamato anche ritiro d’idratazione, è dovuto al consumo dell’acqua interna al momento dell’idratazione del cemento, il quale porta ad una riduzione di volume della pasta cementizia. Tale ritiro si sviluppa isotropicamente all’interno della massa del conglomerato e il suo valore aumenta al diminuire del rapporto acqua-cemento. La sua curva d’evoluzione ricalca bene quella dello sviluppo della resistenza meccanica: è molto rapida nei primi giorni e raggiunge a 28 giorni il 60÷90% del suo valore ultimo.

 il ritiro d’essiccamento (drying shrinkage), è dovuto all’evaporazione dell’acqua dai pori capillari presenti nella pasta di cemento idrata. Tale acqua, chiamata acqua libera, è trattenuta

(7)

6 da forze che sono tanto più forti quanto più piccolo è il diametro dei pori. Questo ritiro non è isotropo e si manifesta infatti dall’esterno verso l’interno della massa. Il fenomeno dell’essiccazione si sviluppa molto lentamente e può avere una durata di molti anni, durante i quali la massa di calcestruzzo è soggetta ad una continua, anche se decrescente, riduzione di volume.

 il ritiro di carbonatazione (carbonation shrinkage), si produce quando l’idrossido di calcio Ca(OH)2 reagisce con l’anidride carbonica CO2 per formare il carbonato di calcio CaCO3.

Questo ritiro comincia dalla superficie del conglomerato e si dirige, col passare del tempo, verso il cuore della massa di calcestruzzo.

I vari tipi di ritiro, visti in precedenza, interessano la pasta di cemento idrata; il calcestruzzo, tuttavia, contiene anche gli aggregati, che occupano la maggior parte del volume del conglomerato e che non risentono di alcun tipo di ritiro. Essi svolgono perciò l’azione di resistere alla contrazione indotta dall’idratazione della pasta di cemento. Dunque più elevato è il rapporto aggregati-cemento minori sono le deformazioni differite del calcestruzzo.

Per ridurre lo sviluppo di fessure superficiali è opportuno, subito dopo il getto, coprire la superficie a contatto con l’atmosfera con panni umidi e mantenere bagnato il getto stesso per un periodo di tempo tale da permettere che la resistenza a trazione del calcestruzzo raggiunga valori abbastanza alti, così da resistere alle forze di contrazione della massa. Mantenendo bagnato il getto per i primi sette giorni, si fa in modo che il calcestruzzo raggiunga i 3/4 della sua resistenza a

trazione a lungo termine, cosicché quando si cessa di bagnare l’elemento (e il ritiro d’essiccamento inizia a svilupparsi), il calcestruzzo sarà in grado di resistere all’insorgere dei fenomeni fessurativi dovuti all’essiccamento.

Per la scrittura di tale paragrafo si è fatto in parte riferimento a quanto riportato nell’articolo “Integrated View of Shrinkage Deformation”,1997, di C. Aitcin, A.M: Neville e P. Acke.

2.3 Creep

Il creep (o deformazione viscosa), rappresenta la deformazione che un materiale subisce, in aggiunta a quella elastica, quando viene sottoposto permanentemente ad una sollecitazione.

Il creep è determinato da vari e complessi meccanismi, tra i quali (Merli): scivolamento degli strati colloidali di gel di cemento a contatto con l’acqua libera adsorbita, espulsione dell’acqua libera all’interno della pasta di cemento, sviluppo di microfessure locali coinvolgenti la rottura di legami esistenti.

Da un punto di vista pratico, il calcolo del creep per il calcestruzzo è abbastanza complesso in quanto, oltre che dai parametri composizionali, la deformazione viscosa dipende molto da parametri

(8)

7 ambientali (soprattutto umidità relativa), ma anche da quei parametri geometrici delle strutture (rapporto superficie/volume) che finiscono per influenzare direttamente l’essiccamento del materiale e quindi il suo ritiro e creep.

Tra i fattori che influenzano il creep si ricordano (Barocci, 2002):

 influenza dell’umidità relativa: a parità di carico e per uno stesso calcestruzzo, il creep è tanto più elevato quanto più bassa è l’umidità relativa. L’influenza di questa è invece molto inferiore o addirittura assente se il carico viene applicato dopo che il calcestruzzo ha raggiunto l’equilibrio igrometrico con l’ambiente. Ne segue che il creep di un calcestruzzo caricato dopo tempi relativamente lunghi è poco influenzato dall’umidità dell’ambiente.  influenza del carico applicato: molte prove hanno mostrato che esiste una proporzionalità

diretta tra creep e carico applicato, con la possibile eccezione dei campioni caricati a brevi stagionature (3-7 giorni). E’ noto che il calcestruzzo compresso inizia a subire microlesioni per carichi superiori al 40-60% della resistenza a compressione σ’c e non è sorprendente che,

una volta iniziato tale processo, si verifichino variazioni anche nel comportamento del creep. Sopra il limite di proporzionalità (valutabile come 0.4-0.6 σ’c) la velocità di creep aumenta in

misura superiore all’aumento del carico ed esiste un determinato rapporto carico/resistenza oltre il quale si raggiunge la crisi nel tempo a carico costante (creep terziario). Questo rapporto è pari a circa 0.8-0.9 σ’c. Il creep aumenta infatti la deformazione totale fino al raggiungimento del limite a rottura del materiale.

 influenza dell’età del calcestruzzo all’atto dell’applicazione del carico: più il calcestruzzo è giovane, meno esso avrà sviluppato la propria resistenza meccanica e dunque più risentirà del fenomeno del creep.

 influenza della resistenza del conglomerato: il creep specifico finale, cioè il creep per unità di carico applicato, diminuisce al crescere della resistenza all’atto dell’applicazione del carico.  influenza degli aggregati: l’aggregato normale non ha creep apprezzabile, dunque si può dire

che il creep del calcestruzzo si riduce all’aumentare della frazione dell’inerte. Gli aggregati svolgono un’azione di vincolo nei confronti delle deformazioni.

 influenza delle dimensioni del getto: il creep, al pari del ritiro, diminuisce all’aumentare delle dimensioni del getto di calcestruzzo. Questo può essere dovuto al fatto che il creep, nelle zone prossime alla superficie, avviene nella fase d’essiccamento ed è pertanto maggiore che nelle zone interne, che rimangono in condizioni prossime alla saturazione. Anche se con il passare del tempo l’interno perde umidità, esso avrà certamente raggiunto un elevato grado d’idratazione ed un’elevata resistenza, con conseguente minore effetto del creep. Se la

(9)

8 stagionatura avviene senza scambio di umidità con l’esterno, non si verifica alcuna dipendenza dalle dimensioni del getto.

 influenza della temperatura: il creep cresce al crescere della temperatura fino a circa 50°C, poi inizia a decrescere.

 influenza dei cicli di carico e scarico: il creep cresce a seguito dell’applicazione di carichi ciclici. Generalmente i dati di laboratorio relativi al creep dei calcestruzzi sono stati ottenuti sotto un carico permanente costante e dunque l’utilizzazione diretta di tali risultati ,per il calcolo delle strutture reali, può portare a sottovalutare gli effetti di creep.

2.3.1 Calcolo delle Deformazioni Viscose

Quando un elemento di calcestruzzo subisce fenomeni d’essiccamento mentre si trova sotto l’azione di un carico permanente, si assume generalmente che ritiro e creep abbiano effetti additivi e che quest’ultimo sia valutabile come semplice differenza tra la deformazione totale dell’elemento caricato ed il ritiro osservato in un analogo elemento, non sottoposto a carico, nelle stesse

Figura 2-2:

a) Contrazione da ritiro (S) in ambiente insaturo di vapore (UR < 95%) ed in assenza di sollecitazione; b) Contrazione elastica iniziale (εe) seguita da quelle da creep puro (εc) in presenza di una sollecitazione

a compressione costante σ’c in ambiente saturo di vapore;

c) Deformazione totale (εT) dovuta alla deformazione elastica iniziale (εe), più la deformazione da creep

(10)

9 condizioni fisiche e per lo stesso periodo di tempo.

Si esaminano ora le interazioni tra creep e ritiro (Barocci, 2002), facendo riferimento a 3 casi particolari (Figura 2-2):

a) una struttura in calcestruzzo in assenza di sollecitazioni (σ’c = 0), in ambiente insaturo di

vapore, sottoposta ad un ritiro idrometrico (S) in assenza di vincoli a partire dal tempo di scasseratura (t0), misurato a partire dal momento del getto (t = 0);

b) una struttura in calcestruzzo, in ambiente saturo di vapore (UR = 95÷100%) e quindi priva di ritiro, sottoposta, al tempo t0, ad una sollecitazione σ’c che provoca una deformazione

elastica εecui si somma la successiva deformazione εcda creep (deformazione totale εT= εe

+ εc): il valore di εc misurato in queste condizioni, cioè in assenza di ritiro, prende il nome

di creep puro o basic creep;

c) una struttura in calcestruzzo esposta al tempo t0 in ambiente insaturo di vapore che provoca

un ritiro S e simultaneamente sottoposta alla sollecitazione σ’c: in queste condizioni la

deformazione totale εT risulta maggiore della somma dei singoli contributi alla

deformazione εe, εc, S (come riportato graficamente in Figura 2-2):

𝜀𝜀𝑇𝑇 > 𝜀𝜀𝑒𝑒 + 𝜀𝜀𝑐𝑐

La differenza tra la deformazione totale εT misurata nelle condizioni c) e la somma dei singoli contributi deformazionali prende il nome di creep da essiccamento (drying creep, εd). La deformazione totale diventa pertanto:

𝜀𝜀𝑇𝑇 = 𝜀𝜀𝑒𝑒 + 𝑆𝑆 + 𝜀𝜀𝑐𝑐 + 𝜀𝜀𝑑𝑑

Ciò significa che, sotto la sollecitazione di compressione σ’ c in ambiente insaturo di vapore,

l’evaporazione dell’acqua è maggiore di quella che si registra in assenza di σ’ c e che determina il

ritiro S. La maggiore evaporazione dell’acqua (una sorta di “effetto spremitura” del calcestruzzo a compressione) comporta una maggiore deformazione addizionale (εd) che si somma agli altri

contributi deformazionali. In particolare il contributo del creep totale (εcc) è dato dalla somma del

creep puro (εc) e dal creep da essiccamento (εd):

𝜀𝜀𝑐𝑐𝑐𝑐 = 𝜀𝜀𝑐𝑐 + 𝜀𝜀𝑑𝑑

Pertanto si può anche scrivere:

𝜀𝜀𝑇𝑇 = 𝜀𝜀𝑒𝑒 + 𝑆𝑆 + 𝜀𝜀𝑐𝑐𝑐𝑐

Quando si eseguono prove di creep in un ambiente insaturo si valutano le deformazioni totali εT

subite dai provini e, detraendo da queste le deformazioni da ritiro (valutate su analoghi provini non caricati posti nel medesimo ambiente) e le deformazioni elastiche istantanee, si ottiene il valore del creep totale εcc. Sperimentalmente si vede inoltre che, mantenendo il carico costante, tali

(11)

10

deformazioni evolvono nel tempo e, per t → ∞, possono assumere valori pari a 3÷4 volte le

deformazioni istantanee.

Indicando con t0 l’istante di applicazione del carico sul provino, si riscontra l’andamento delle

deformazioni riportato nella Figura 2-3.

La deformazione totale dell’elemento in cls al generico istante t è: 𝜀𝜀𝑐𝑐(𝑡𝑡, 𝑡𝑡0) = 𝜀𝜀𝑖𝑖𝑐𝑐𝑡𝑡(𝑡𝑡0) + 𝜀𝜀𝑐𝑐𝑐𝑐(𝑡𝑡, 𝑡𝑡0)

La deformazione istantanea è pari a:

𝜀𝜀𝑖𝑖𝑐𝑐𝑡𝑡(𝑡𝑡0) = _𝐸𝐸𝜎𝜎𝑐𝑐(𝑡𝑡0) 𝑐𝑐(𝑡𝑡0)

mentre la deformazione viscosa si può esprimere come (CEB, MC90): 𝜀𝜀𝑐𝑐𝑐𝑐(𝑡𝑡, 𝑡𝑡0) = 𝜎𝜎_𝐸𝐸𝑐𝑐(𝑡𝑡0)

𝑐𝑐,28 ∙ Φ(𝑡𝑡, 𝑡𝑡0)

dove E_c_,₂₈ è il modulo elastico del calcestruzzo a 28 giorni d’età.

Il termine Φ(t,t0) è chiamato coefficiente di viscosità ed è dato dal rapporto tra le deformazioni

viscose e quelle istantanee (valutate facendo riferimento al modulo elastico a 28gg). Φ(𝑡𝑡, 𝑡𝑡0) = _𝜎𝜎𝜀𝜀𝑐𝑐𝑐𝑐(𝑡𝑡, 𝑡𝑡0)

𝑐𝑐(𝑡𝑡0) 𝐸𝐸⁄ 𝑐𝑐,28

Per t = t0 (istante applicazione carico) non si hanno deformazioni viscose. Ne viene che

Φ(t0,t0) = 0.

t

₀

ε

c

(t,t )

0

(t )

0

(t )

0

ε

c c

E

σ

c

(12)

Creep e Ritiro Capitolo 2 11 Si ottiene dunque: 2.2 𝜀𝜀𝑐𝑐(𝑡𝑡, 𝑡𝑡0) =_𝐸𝐸𝜎𝜎𝑐𝑐(𝑡𝑡0) 𝑐𝑐(𝑡𝑡0) + 𝜎𝜎𝑐𝑐(𝑡𝑡0) 𝐸𝐸𝑐𝑐,28 ∙ Φ(𝑡𝑡, 𝑡𝑡0) = 𝜎𝜎𝑐𝑐(𝑡𝑡0) ∙ 1 𝐸𝐸𝑐𝑐(𝑡𝑡0) ∙ �1 + 𝐸𝐸𝑐𝑐(𝑡𝑡0) 𝐸𝐸𝑐𝑐,28 Φ(𝑡𝑡, 𝑡𝑡0)� ponendo: 𝐽𝐽(𝑡𝑡, 𝑡𝑡0) =_𝐸𝐸 1 𝑐𝑐(𝑡𝑡0) ∙ �1 + 𝐸𝐸𝑐𝑐(𝑡𝑡0) 𝐸𝐸𝑐𝑐,28 𝛷𝛷(𝑡𝑡, 𝑡𝑡0)� = 1 𝐸𝐸𝑐𝑐(𝑡𝑡0) + 𝛷𝛷(𝑡𝑡, 𝑡𝑡0) 𝐸𝐸𝑐𝑐,28 si avrà: 𝜀𝜀𝑐𝑐(𝑡𝑡, 𝑡𝑡0) = 𝜎𝜎𝑐𝑐(𝑡𝑡0) ∙ 𝐽𝐽(𝑡𝑡, 𝑡𝑡0)

La funzione J(t,t0) prende il nome di funzione di viscosità ed ha le dimensioni dell’inverso del modulo elastico; il suo andamento in funzione del tempo, per un calcestruzzo caricato ad età differenti ti, è rappresentato nella Figura 2-4 osservando la quale si può dire che:

 la parte elastica istantanea diminuisce all’aumentare dell’età di caricamento; ciò deriva dal fatto che il modulo elastico del calcestruzzo aumenta nel tempo;

 il creep è tanto più elevato quanto più il calcestruzzo viene caricato in giovane età;

 la funzione di creep è una funzione monotona crescente, ma la velocità di sviluppo del creep è una funzione decrescente; la pendenza della curva J(t,ti), infatti, si attenua nel tempo.

Si introduce poi, per concludere, il concetto di deformazione viscosa specifica, che rappresenta la deformazione viscosa al tempo t causata dalla tensione unitaria applicata al tempo t0:

Figura 2-4 Andamento della funzione di creep nel tempo e per varie età di caricamento

J

(t,t1)

(13)

Creep e Ritiro Capitolo 2 12 𝐶𝐶(𝑡𝑡, 𝑡𝑡0) =𝜀𝜀𝑐𝑐𝑐𝑐_𝜎𝜎(𝑡𝑡, 𝑡𝑡0) 𝑐𝑐(𝑡𝑡0) Dato che 𝐽𝐽(𝑡𝑡, 𝑡𝑡₀) =𝜀𝜀𝑖𝑖𝑐𝑐𝑡𝑡(𝑡𝑡0) 𝜎𝜎𝑐𝑐(𝑡𝑡0) + 𝜀𝜀𝑐𝑐𝑐𝑐(𝑡𝑡,𝑡𝑡0) 𝜎𝜎𝑐𝑐(𝑡𝑡0) = 1 𝐸𝐸𝑐𝑐(𝑡𝑡0)+ 𝐶𝐶(𝑡𝑡, 𝑡𝑡0) considerando inoltre che 𝐽𝐽(𝑡𝑡, 𝑡𝑡₀) = 1

𝐸𝐸𝑐𝑐(𝑡𝑡0)+

Φ(𝑡𝑡,𝑡𝑡0)

𝐸𝐸𝑐𝑐,28 si ha, secondo il CEB-MC90: 𝐶𝐶(𝑡𝑡, 𝑡𝑡₀) =Φ(𝑡𝑡,𝑡𝑡0)

𝐸𝐸𝑐𝑐,28

In forma duale, quando ad un corpo viene impressa una deformazione e, assegnata al tempo t0 e successivamente mantenuta costante nel tempo, lo stato tensionale varia secondo la legge:

𝜎𝜎𝑐𝑐(𝑡𝑡) = 𝜎𝜎𝑐𝑐(𝑡𝑡0) − 𝜎𝜎𝑟𝑟(𝑡𝑡, 𝑡𝑡0) = 𝐸𝐸𝑐𝑐(𝑡𝑡0)𝜀𝜀𝑐𝑐(𝑡𝑡0) �1 −_{𝐸𝐸(𝑡𝑡}𝐸𝐸𝑐𝑐,28

0) ∙ 𝜓𝜓(𝑡𝑡, 𝑡𝑡0)�

dove alla tensione istantanea sc(t0) viene detratta la tensione di rilassamento sr(t,t0) e y(t,t0)

rappresenta il coefficiente di rilassamento. L’equazione può essere riscritta nella forma:

𝜎𝜎𝑐𝑐(𝑡𝑡) = 𝜀𝜀𝑐𝑐(𝑡𝑡0) ⋅ 𝑅𝑅(𝑡𝑡, 𝑡𝑡0)

dove R(t,t0) è detta funzione di rilassamento:

𝑅𝑅(𝑡𝑡, 𝑡𝑡0) = 𝐸𝐸𝑐𝑐(𝑡𝑡0)[1 − 𝜓𝜓(𝑡𝑡, 𝑡𝑡0)]

Se lo stato tensionale sc(𝜏𝜏) è variabile nel tempo a partire dal valore iniziale sc(t0), in virtù del

principio di sovrapposizione è possibile ottenere la deformazione totale al tempo t sommando alla (2.2) i singoli contributi dec(t, 𝜏𝜏) dovuti agli incrementi di tensione dsc(𝜏𝜏) relativi agli intervalli

elementari d 𝜏𝜏 con centro in 𝜏𝜏 (Figura 2-5):

t

t to c(to)=cost. r(t,to) c(to) c(t,to) c

(14)

Creep e Ritiro Capitolo 2 13 2.3 𝜀𝜀𝑐𝑐(𝑡𝑡, 𝑡𝑡0) =𝜎𝜎_𝐸𝐸𝑐𝑐(𝑡𝑡0) 𝑐𝑐(𝑡𝑡0) �1 + 𝐸𝐸𝑐𝑐(𝑡𝑡0) 𝐸𝐸𝑐𝑐,28 𝜙𝜙(𝑡𝑡, 𝑡𝑡0)� + � �1 + 𝐸𝐸𝑐𝑐(𝜏𝜏) 𝐸𝐸𝑐𝑐,28 𝜙𝜙(𝑡𝑡, 𝜏𝜏)� ∙ 𝑑𝑑𝜎𝜎𝑐𝑐(𝜏𝜏) 𝐸𝐸𝑐𝑐(𝜏𝜏) 𝑡𝑡 𝑡𝑡0 2.4 𝜀𝜀𝑐𝑐(𝑡𝑡, 𝑡𝑡0) = 𝜎𝜎𝑐𝑐(𝑡𝑡0) ∙ 𝐽𝐽(𝑡𝑡, 𝑡𝑡0) � 𝐽𝐽(𝑡𝑡, 𝜏𝜏) ∙ 𝑑𝑑𝜎𝜎𝑐𝑐(𝜏𝜏) 𝑡𝑡 𝑡𝑡0

che è detta equazione integro-differenziale della viscosità. Come è noto, la (2.3) consente di valutare la deformazione totale all’istante t tramite una semplice integrazione, a patto di conoscere l’evoluzione delle tensioni sc(𝜏𝜏) nel tempo ed il coefficiente di viscosità del materiale, come si

verifica nel caso di strutture isostatiche a vincoli rigidi, omogenee e soggette a sollecitazioni costanti.

Diversamente, qualora per la eterogeneità del cemento armato (ridistribuzione degli sforzi nel tempo tra acciaio e calcestruzzo) o per la iperstaticità delle condizioni di vincolo l’evoluzione delle tensioni dipenda da quella delle deformazioni, la (2.3) si trasforma in una equazione integro-differenziale di Volterra nella incognita sc(t), la cui risoluzione esatta è notevolmente complessa.

La forma duale della (2.3) relativa al rilassamento risulta:

2.5

𝜎𝜎𝑐𝑐(𝑡𝑡, 𝑡𝑡0) = 𝜀𝜀𝑐𝑐(𝑡𝑡0) ∙ 𝑅𝑅(𝑡𝑡, 𝑡𝑡0) + � 𝑅𝑅(𝑡𝑡, 𝜏𝜏) ∙ 𝑑𝑑𝜀𝜀(𝜏𝜏) 𝑡𝑡

𝑡𝑡0

Gli operatori integrali di Volterra che vi compaiono sono operatori di convoluzione e sono lineari nella tensione e nella deformazione, rispettivamente. Le funzioni J(t,t0) ed R(t,t0) nelle (2.3) e (2.5)

sono detti nuclei degli operatori di convoluzione. Essi sono nuclei ereditari e dipendono distintamente dagli istanti t e t0.

Gli operatori di viscosità e rilassamento non sono tra loro indipendenti ma devono soddisfare una

t

to c(t0) t d d c( ) c(t)

(15)

14 relazione integrale, che può essere ottenuta facendo uso della teoria degli operatori lineari:

2.6

𝑅𝑅(𝑡𝑡, 𝑡𝑡0) ∙ 𝐽𝐽(𝑡𝑡, 𝑡𝑡0) − �_{𝜕𝜕𝑡𝑡′′}𝜕𝜕 𝑡𝑡

𝑡𝑡0

𝑅𝑅(𝑡𝑡, 𝑡𝑡′′) ∙ 𝐽𝐽(𝑡𝑡′′, 𝑡𝑡′)𝑑𝑑𝑡𝑡′′ _{= 1}

Tramite la (2.6) è possibile, assegnata una generica funzione di viscosità, ricavare la corrispondente funzione di rilassamento.

2.4 Risoluzione degli integrali di Volterra: serie di Dirichlet

Non è possibile risolvere le equazioni di Volterra in forma chiusa, se non per casi molto particolari di caricamento o di nuclei ereditari che compaiono negli integrali di convoluzione.

I modelli reologici trasformano l’integrale (2.3) in una relazione differenziale introducendo opportune espressioni analitiche per la funzione di viscosità. Il grosso vantaggio consiste nell’eliminazione dell’operatore integrale di convoluzione che compare nelle formulazioni generali (2.3), (2.5), snellendo le procedure di risoluzione.

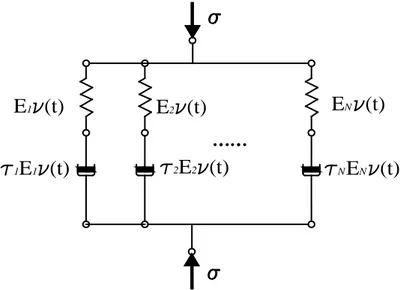
Attraverso questo tipo di approccio, sono stati sviluppati modelli più generali e sofisticati, basati su unità di Kelvin e di Maxwell, che prevedono lo sviluppo in serie di Dirichlet di generiche funzioni di viscosità e di rilassamento, utilizzando come base un insieme di nuclei di forma degenere. Sostituendo la funzione così sviluppata negli integrali di convoluzione che compaiono nelle (2.3), (2.5), si ottengono, come anticipato nei modelli reologici, formulazioni di tipo differenziale. Queste ultime hanno il doppio vantaggio di essere più facilmente risolvibili rispetto ad equazioni integrali (in quanto possono, ad esempio, essere risolte al passo) e di richiedere un minor onere computazionale e di memoria, non essendo più necessaria la registrazione di tutta la precedente storia tensionale.

2.4.1 Funzioni di viscosità

Un nucleo ereditario possiede forma degenere quando costituito da una somma di prodotti di funzioni a variabile singola (t o t’). Una generica funzione di viscosità può essere sviluppata in serie di Dirichlet nel modo seguente:

2.7 𝐽𝐽(𝑡𝑡, 𝑡𝑡′_{) = �} 1 𝐶𝐶𝜇𝜇(𝑡𝑡′) �1 − 𝑒𝑒 �𝑦𝑦𝜇𝜇(𝑡𝑡′)−𝑦𝑦𝜇𝜇(𝑡𝑡)�� 𝑁𝑁 𝜇𝜇=1

dove 𝐶𝐶_𝜇𝜇(𝑡𝑡′) (𝜇𝜇 = 1, . . , 𝑁𝑁) e le 𝑦𝑦_𝜇𝜇(𝑡𝑡′) sono funzioni incognite del tempo. Il vantaggio di utilizzare uno sviluppo in serie del tipo (2.7) consiste, come già anticipato, nel poter convertire

(16)

15 un’equazione integrale in una differenziale. Sostituendo la (2.7) nella (2.3) e dopo alcuni passaggi matematici, si ottiene la deformazione differita totale come somma di termini:

2.8

𝜀𝜀(𝑡𝑡) = � 𝜀𝜀𝜇𝜇(𝑡𝑡) + 𝜀𝜀0(𝑡𝑡) 𝑁𝑁

𝜇𝜇=1

dove le 𝜀𝜀_𝜇𝜇(𝑡𝑡) sono soluzioni del sistema di equazioni differenziali:

2.9 𝜀𝜀̈𝜇𝜇(𝑡𝑡) + 𝐴𝐴𝜇𝜇(𝑡𝑡)𝜀𝜀̇𝜇𝜇(𝑡𝑡) =_𝐵𝐵𝜎𝜎̇(𝑡𝑡) 𝜇𝜇(𝑡𝑡) in cui 𝐴𝐴𝜇𝜇(𝑡𝑡) = 𝑦𝑦̇𝜇𝜇 −𝑦𝑦̈_𝑦𝑦̇𝜇𝜇 𝜇𝜇 𝐵𝐵𝜇𝜇(𝑡𝑡) = 𝐶𝐶𝜇𝜇(𝑡𝑡) 𝑦𝑦̇𝜇𝜇

La (2.9) è un’equazione differenziale del secondo ordine e rappresenta la relazione costitutiva di una catena di unità di Kelvin (Figura 2-7a) a patto di considerare:

𝐴𝐴𝜇𝜇(𝑡𝑡) =_𝐸𝐸 𝜂𝜂𝜇𝜇(𝑡𝑡)

𝜇𝜇(𝑡𝑡) + 𝜂𝜂̇𝜇𝜇(𝑡𝑡) 𝐵𝐵𝜇𝜇(𝑡𝑡) = 𝜂𝜂𝜇𝜇(𝑡𝑡)

dove Em(t) e 𝜂𝜂_𝜇𝜇(𝑡𝑡) sono, rispettivamente, la rigidezza della molla ed il coefficiente di viscosità

del dissipatore di ogni singola unità. Eguagliando queste espressioni con quelle ottenute dallo sviluppo della serie di Dirichlet, si ottiene infine:

𝐸𝐸𝜇𝜇(𝑡𝑡) = 𝐶𝐶𝜇𝜇(𝑡𝑡) −𝐶𝐶̇_𝑦𝑦̇𝜇𝜇(𝑡𝑡)

𝜇𝜇(𝑡𝑡) 𝜂𝜂𝜇𝜇(𝑡𝑡) =

𝐶𝐶𝜇𝜇(𝑡𝑡)

𝑦𝑦̇𝜇𝜇(𝑡𝑡)

Si noti che con queste espressioni è sempre possibile identificare i moduli delle unità di una

EN N E2 2 1 E1 E E1 1 N EN (a) (b)

(17)

16 catena di Kelvin equivalente ad una funzione di viscosità sviluppata in serie di Dirichlet, ma non il contrario. L’identificazione dei coefficienti dello sviluppo di Dirichlet dai parametri di una catena di Kelvin, infatti, conduce ad un sistema di equazioni differenziali non lineari del secondo ordine che non ha, in generale, soluzione in forma chiusa. Solamente nel caso in cui si consideri una catena con moduli costanti nel tempo, e quindi una funzione di viscosità priva del fenomeno dell’invecchiamento, si ha la completa equivalenza tra le varie grandezze corrispondenti.

Un’ opportuna scelta della funzione 𝑦𝑦_𝜇𝜇(𝑡𝑡) (Bazant e Chern, 1984) può essere la seguente:

2.10

𝑦𝑦𝜇𝜇(𝑡𝑡) = �_𝜏𝜏𝑡𝑡 𝜇𝜇�

𝑞𝑞𝜇𝜇

con 𝑞𝑞_𝜇𝜇 esponenti da determinarsi. Per semplicità, nel seguito i coefficienti 𝑞𝑞_𝜇𝜇 sono fissati pari all’unità. I tempi 𝜏𝜏_𝜇𝜇 che compaiono nella (2.10) sono detti tempi di ritardo.

Lo sviluppo della (2.7) descrive una serie di funzioni esponenziali reali. Solitamente il suo primo termine rappresenta la parte istantanea (elastica) della funzione di viscosità. Per fare questo è necessario scegliere un primo tempo di ritardo molto piccolo, ad esempio 𝜏𝜏₁=10-9 giorni. In questo modo il primo termine della serie si riduce a 1 𝐶𝐶⁄ ₁(𝑡𝑡′), che rappresenta quindi la deformabilità istantanea. Per costruire una funzione di viscosità mediante serie di Dirichlet è necessario innanzitutto assegnare il numero N di termini della serie. Successivamente si assegnano i corrispondenti tempi di ritardo 𝜏𝜏_𝜇𝜇 (𝜇𝜇 = 1, . . , 𝑁𝑁), la scelta dei quali non è arbitraria ma deve soddisfare certe condizioni, pena il mal condizionamento del problema. Un criterio usuale (Bazant e Wu, 1973; Bazant, 1988) prevede di scegliere tali tempi 𝜏𝜏_𝜇𝜇 equidistanti nella scala logaritmica del tempo a partire dall’istante di messa in carico (𝑡𝑡 − 𝑡𝑡′), coprendo tutto l’intervallo temporale di interesse. Bazant consiglia di prendere i tempi di ritardo secondo la legge 𝜏𝜏_𝜇𝜇 = 10𝜇𝜇−1𝜏𝜏₁, cioè uno per ogni ordine di grandezza. Infine, l’ultima fase consiste nella scelta delle funzioni 𝐶𝐶_𝜇𝜇(𝑡𝑡′), che devono essere definite per interpolazione dei dati sperimentali, ad esempio con tecniche di minimizzazione quadratica.

2.4.2 Funzioni di rilassamento

Analogamente a quanto appena visto, anche la funzione di rilassamento può essere sviluppata in serie di esponenziali (Dirichlet):

2.11

𝑅𝑅(𝑡𝑡, 𝑡𝑡′_{) = � 𝐸𝐸}

𝜇𝜇(𝑡𝑡′)𝑒𝑒�𝑦𝑦𝜇𝜇(𝑡𝑡′)−𝑦𝑦𝜇𝜇(𝑡𝑡)� 𝑁𝑁

(18)

17 dove 𝐸𝐸_𝜇𝜇(𝑡𝑡′) sono funzioni del tempo e le 𝑦𝑦_𝜇𝜇(𝑡𝑡′) hanno lo stesso significato visto precedentemente, con i 𝜏𝜏_𝜇𝜇 detti ora tempi di rilassamento. Anche in questo caso, scegliendo un tempo 𝜏𝜏₁ prossimo a zero, il primo termine della serie rappresenta la rigidezza istantanea per cui 𝐸𝐸𝜇𝜇(𝑡𝑡′) = 𝐸𝐸(𝑡𝑡′). Scelti a priori i 𝜏𝜏𝜇𝜇, le 𝐸𝐸𝜇𝜇(𝑡𝑡′) sono ottenute per interpolazione dei dati.

Sostituendo la funzione di rilassamento (2.11) nella (2.5) e operando alcune manipolazioni, si ottiene la legge che esprime la variazione della tensione nel tempo, nella forma:

2.12

𝜎𝜎(𝑡𝑡) = � 𝜎𝜎𝜇𝜇(𝑡𝑡) 𝑁𝑁

𝜇𝜇=1

in cui i singoli termini della sommatoria sono soluzioni delle equazioni differenziali del primo ordine disaccoppiate:

2.13

𝜎𝜎̇𝜇𝜇(𝑡𝑡) + 𝑦𝑦̇𝜇𝜇(𝑡𝑡)𝜎𝜎𝜇𝜇(𝑡𝑡) = 𝐸𝐸𝜇𝜇(𝑡𝑡)[𝜀𝜀̇(𝑡𝑡) − 𝜀𝜀̇0(𝑡𝑡)] (𝜇𝜇 = 1, … , 𝑁𝑁)

Appare evidente come la (2.13) sia equivalente all’equazione costitutiva di una catena di unità di Maxwell (Figura 2-7b) in cui le molle hanno rigidezza 𝐸𝐸_𝜇𝜇(𝑡𝑡) e i dissipatori hanno coefficiente di viscosità 𝜂𝜂_𝜇𝜇 = 𝐸𝐸_𝜇𝜇(𝑡𝑡) 𝑦𝑦̇⁄ _𝜇𝜇(𝑡𝑡′), entrambi variabili nel tempo.

Si noti che lo sviluppo della funzione di creep conduce ad una formulazione differenziale del secondo ordine mentre quello della funzione di rilassamento ad una del primo ordine e quindi di più facile risoluzione.

2.4.3 Algoritmi di risoluzione

Come anticipato in precedenza, il vantaggio di operare con formulazioni differenziali risiede nel fatto che non è necessario memorizzare l’intera storia tensionale dell’elemento o, in problemi più complessi, della struttura, bensì è sufficiente memorizzare l’ultimo valore delle variabili di stato prima del passo temporale (finito) successivo.

Tuttavia, in problemi di visco-elasticità, non è possibile adottare i classici metodi di integrazione al passo (Eulero, Rounge Kutta, etc…) che necessitano di ampiezze degli intervalli temporali poco variabili da passo a passo e comunque molto piccoli. Tali metodi richiedono infatti intervalli di ampiezza inferiore al più piccolo tempo di rilassamento impiegato (pertanto dell’ordine di grandezza di pochi secondi), un’ampiezza incompatibile con gli intervalli temporali di interesse nei problemi di viscoelasticità (decine di anni). Per ovviare a ciò, è necessario utilizzare algoritmi ad hoc, quali, ad esempio, il cosiddetto algoritmo esponenziale, inizialmente proposto da Zienkiewicz e Watson (1966) e sviluppato per problemi di visco-elasticità con invecchiamento da Bazant (1971 e Bazant e Wu (1974). Tale algoritmo consente di utilizzare intervalli temporali di ampiezza

(19)

18 variabile senza manifestare problemi di instabilità numerica. Per Dt tendente a zero si dimostra che l’algoritmo esponenziale diventa equivalente al metodo delle differenze centrali e converge alla soluzione con la stessa velocità.

L’idea alla base dell’algoritmo è quella di utilizzare, all’interno del generico passo temporale, l’integrale esatto dell’equazione differenziale (2.13), ottenuto assumendo che il coefficiente 𝑦𝑦̇𝜇𝜇 e il secondo termine dell’equazione rimangano costanti all’interno del passo. In questo modo

l’integrazione esatta della (2.10) al passo r-esimo risulta:

2.14 𝜎𝜎𝜇𝜇,𝑟𝑟 = 𝜎𝜎𝜇𝜇,𝑟𝑟−1𝑒𝑒−Δ𝑦𝑦𝑢𝑢 + 𝐸𝐸𝜇𝜇,𝑟𝑟−1/2⋅ 𝜆𝜆𝜇𝜇,𝑟𝑟(Δ𝜀𝜀𝑟𝑟 − Δ𝜀𝜀𝑟𝑟0) in cui 𝜆𝜆𝜇𝜇,𝑟𝑟 = �1 − 𝑒𝑒 −Δ𝑦𝑦𝜇𝜇� Δ𝑦𝑦𝜇𝜇 Δ𝑦𝑦𝜇𝜇 = Δ𝑡𝑡𝑟𝑟 τ𝜇𝜇 𝐸𝐸𝜇𝜇,𝑟𝑟−1/2 = 1 2 �𝐸𝐸𝜇𝜇,𝑟𝑟−1− 𝐸𝐸𝜇𝜇,𝑟𝑟�

dove l’indice r è quello di passo mentre l’indice 𝜇𝜇 indica la generica unità di Maxwell. Sostituendo la (2.14) nella (2.12) si ottiene una formulazione pseudo-elastica incrementale del tipo:

2.15 Δ𝜀𝜀𝑟𝑟 =_𝐸𝐸1 𝑟𝑟′′ Δσ𝑟𝑟 + Δ𝜀𝜀𝑟𝑟′′ in cui 𝐸𝐸𝑟𝑟′′ = � 𝜆𝜆𝜇𝜇,𝑟𝑟 𝑁𝑁 𝜇𝜇=1 𝐸𝐸𝜇𝜇,𝑟𝑟−1/2 Δ𝜀𝜀𝑟𝑟′′ =_𝐸𝐸1 𝑟𝑟′′ ��1 − 𝑒𝑒 −Δ𝑦𝑦𝜇𝜇� 𝑁𝑁 𝜇𝜇=1 𝜎𝜎𝜇𝜇,𝑟𝑟−1

Ad un generico istante tr, la procedura di risoluzione consiste nel ricavare le costanti

pseudo-elastiche 𝐸𝐸_𝑟𝑟′′ e Δ𝜀𝜀_𝑟𝑟′′ sulla base delle tensioni note al tempo tr-1, risolvere la struttura in campo

elastico utilizzando la (2.15), ed infine ottenere i Δ𝜀𝜀_𝑟𝑟 da utilizzarsi per calcolare in ogni punto della struttura le 𝜎𝜎_{𝜇𝜇,𝑟𝑟}. A questo punto si può procedere all’istante successivo.

Le variabili 𝜎𝜎_𝜇𝜇 ed 𝜀𝜀_𝜇𝜇 prendono il nome di variabili interne (o variabili di stato) e non possono essere misurate direttamente. Contengono ciò nonostante tutte le informazioni necessarie per descrivere l’evoluzione del fenomeno nel tempo. Il valore assunto da queste variabili esprime infatti l’effetto della storia precedente del materiale e rende non più necessario dover risolvere l’integrale di convoluzione. In conclusione si può dire che sia la catena di unità di Maxwell che quella di unità di Kelvin possono, in presenza di invecchiamento, approssimare la legge di creep in forma integrale con qualsiasi precisione.

La determinazione, sulla base dei risultati sperimentali, delle funzioni 𝐸𝐸_𝜇𝜇(𝑡𝑡′), 𝐶𝐶_𝜇𝜇(𝑡𝑡′) (𝜇𝜇 = 1, . . , 𝑁𝑁) che compaiono nelle (2.7), (2.11) è spesso difficoltosa. Pertanto, piccole variazioni dei dati sperimentali inducono grosse alterazioni delle funzioni ricercate e, viceversa, molte

(20)

19 funzioni diverse tra loro sono in grado di ripercorrere con adeguata precisione le curve sperimentali tempo-deformazione. Il mal condizionamento del problema è legato, pertanto, alla mancanza di unicità della soluzione. In taluni casi, inoltre, operando una minimizzazione quadratica sulla distanza tra i valori assunti dalla curve e i dati sperimentali, si ottengono valori negativi di alcune di queste funzioni; sebbene ciò non crei particolari problemi dal punto di vista numerico, è di dubbio significato da un punto di vista termodinamico.

2.5 La teoria della solidificazione di Bazant

2.5.1 Derivazione della funzione di viscosità

I modelli descritti nei paragrafi precedenti, anche se in grado di tenere in conto gli effetti dell’invecchiamento del calcestruzzo, presentano tutti diversi inconvenienti, i principali dei quali sono:

- I modelli più semplici, ad esempio quelli reologici, non possiedono la necessaria attendibilità in presenza delle storie di carico variabili o nel caso di strutture complesse.

- I modelli empirici, si basano su un numero elevato di parametri la cui taratura è spesso complessa.

- Gli sviluppi in serie di Dirichlet hanno coefficienti che sovente conducono, in fase di taratura, a sistemi mal condizionati o si basano su quantità che non possiedono un preciso significato fisico.

La difficoltà nella formulazione di modelli sufficientemente accurati nell’ambito della teoria della visco-elasticità lineare deriva dal fatto che il calcestruzzo ha caratteristiche fortemente variabili nel tempo. In realtà, le caratteristiche fisiche degli aggregati minerali e delle microparticelle di cemento solidificate sono costanti. Al contrario sono variabili nel tempo i legami tra essi e la percentuale di cemento idratato.

La teoria della solidificazione, proposta da Bazant nel 1977 e sviluppata negli anni successivi, si basa sull’ipotesi che il fenomeno dell’invecchiamento sia da imputarsi all’aumento della frazione di volume di materiale solidificato (cemento idratato) e quindi in grado di sopportare carico, le cui caratteristiche sono assunte costanti nel tempo. Pertanto, nella teoria della solidificazione la dipendenza temporale delle proprietà termomeccaniche del calcestruzzo viene considerata come una conseguenza della variazione della composizione dello stesso (rappresentata da 𝜐𝜐(𝑡𝑡)), e non della variazione nel tempo delle caratteristiche meccaniche. In particolare, il fenomeno della solidificazione descrive l’effetto di invecchiamento del calcestruzzo (come frazione di parte di cemento che sopporta il carico), mentre per i singoli costituenti (aggregati e cemento solidificato) sono utilizzati modelli costitutivi non invecchianti.

(21)

20 La variazione di 𝜐𝜐(𝑡𝑡) intende modellare il fenomeno dell’invecchiamento. Pertanto, 𝜐𝜐(𝑡𝑡) non può rappresentare a rigore la frazione di cemento idratato, in quanto l’idratazione termina dopo pochi mesi mentre l’invecchiamento dura per anni. La funzione di solidificazione 𝜐𝜐(𝑡𝑡) deve quindi, più in generale, descrivere la frazione di volume in grado di sopportare il carico. E’ plausibile che la crescita di tale grandezza duri per anni, in quanto i legami fra le particelle idratate continuano ad evolvere per lunghissimo tempo.

Il volume elementare 𝑑𝑑𝜐𝜐(𝑡𝑡) che solidifica all’istante t viene considerato come uno strato infinitesimo che si deposita sulla superficie del materiale già solidificato in precedenza. L’ipotesi ulteriore è che la solidificazione avvenga “in parallelo” rispetto alle modalità di applicazione del carico, così che tutti gli strati ideali sono sottoposti alla medesima deformazione, coincidente con quella totale macroscopica (Figura 2-8).

Caratteristica fondamentale del modello è che prima della solidificazione dello strato, esso non può sopportare carico, e quindi la sua micro tensione corrispondente 𝜎𝜎_𝑔𝑔 è nulla. La deformazione totale e(t) del calcestruzzo viene innanzitutto scomposta in quattro contributi:

2.16

𝜀𝜀(𝑡𝑡) =𝜎𝜎(𝑡𝑡)_𝐸𝐸

0 + 𝜀𝜀

𝑣𝑣_{(𝑡𝑡) + 𝜀𝜀}𝑓𝑓_{(𝑡𝑡) + 𝜀𝜀}0_(𝑡𝑡)

Il primo termine della (2.16), rappresenta la deformazione elastica istantanea, mentre i tre termini successivi costituiscono le deformazioni differite: 𝜀𝜀𝑣𝑣 è il contributo viscoelastico, 𝜀𝜀𝑓𝑓 quello puramente viscoso (termine di flusso), 𝜀𝜀0 è la deformazione indipendente dallo stato tensionale (ritiro, deformazioni termiche, ecc…). Il materiale solidificato sostiene una quantità di carico che

E1 1 N EN 1 2 2 E2 N (t-t') t' t t' t (t-t') 0 1 (t) h(t) f DEFORMAZIONI elastica visco-elastica viscosa (flow) creep ritiro +eff. termici + fessurazione dh(t) d (t) g( ,t) 0 (t-t')

(22)

21 dipende dal tempo trascorso dall’inizio della solidificazione ed è indicato con 𝜎𝜎_𝑔𝑔(𝜐𝜐, 𝑡𝑡). Se si impone l’equilibrio complessivo al tempo t si ottiene:

2.17

𝜎𝜎(𝑡𝑡) = � 𝜎𝜎𝑔𝑔(𝜐𝜐(𝜏𝜏), 𝑡𝑡) 𝑡𝑡

0

𝑑𝑑𝜐𝜐(𝜏𝜏)

La porzione di materiale solidificato, alla micro scala, viene considerata non invecchiante con comportamento viscoelastico lineare. Si può dunque scrivere:

2.18

𝜀𝜀𝑣𝑣_{(𝑡𝑡)−𝜀𝜀}𝑣𝑣_(𝑡𝑡′_{) = � Φ(𝑡𝑡 − 𝜏𝜏) ∙ 𝜎𝜎}

𝑔𝑔(𝜐𝜐(𝑡𝑡′), 𝑑𝑑𝜏𝜏) 𝑡𝑡

0

ove si assume che 𝜎𝜎_𝑔𝑔(𝜐𝜐(𝑡𝑡′), 𝑑𝑑𝜏𝜏) = 0 per 𝜏𝜏 < 𝑡𝑡′; inoltre, 𝜀𝜀𝑣𝑣(𝑡𝑡)−𝜀𝜀𝑣𝑣(𝑡𝑡′) è la deformazione che lo strato infinitesimo subisce a partire dal momento dell’inizio della solidificazione e Φ(𝑡𝑡 − 𝜏𝜏) è detta funzione di viscosità microscopica.

Dal sistema di equazioni integrali (2.17) e (2.18) si ottiene, dopo alcuni passaggi:

2.19

𝜀𝜀̇𝑣𝑣_{(𝑡𝑡) =} 1

𝜐𝜐(𝑡𝑡) � Φ̇ (𝑡𝑡 − 𝜏𝜏)𝑑𝑑𝜎𝜎(𝜏𝜏)

𝑡𝑡 0

dove il punto indica derivata rispetto al tempo t. Operando analogamente per il contributo di deformazione puramente viscoso si ottiene:

2.20

𝜀𝜀̇𝑓𝑓_{(𝑡𝑡) =} 1

𝑝𝑝(𝑡𝑡) � Ψ̇ (𝑡𝑡 − 𝜏𝜏)𝑑𝑑𝜎𝜎(𝜏𝜏)

𝑡𝑡 0

dove ψ(𝑡𝑡 − 𝜏𝜏) è la corrispondente funzione di viscosità microscopica e 𝑝𝑝(𝑡𝑡) ha un significato analogo alla 𝜐𝜐(𝑡𝑡). Essendo 𝜀𝜀𝑓𝑓 una deformazione puramente viscosa, il suo incremento per effetto di una tensione unitaria è pari a 1/𝜂𝜂₀, dove 𝜂𝜂₀ è il coefficiente di viscosità del materiale solidificato. In questo modo si può porre ψ(𝑡𝑡 − 𝜏𝜏) = 1/𝜂𝜂₀ che, sostituita nella (2.20) e risolvendo il successivo integrale, fornisce:

2.21

𝜀𝜀̇𝑓𝑓_{(𝑡𝑡) =}𝜎𝜎(𝑡𝑡)

𝜂𝜂(𝑡𝑡)

dove 𝜂𝜂(𝑡𝑡) = 𝜂𝜂₀∙ 𝑝𝑝(𝑡𝑡) è il coefficiente di viscosità macroscopica; quest’ultimo dipende dalla frazione di materiale solidificato e pertanto possiede caratteristiche variabili nel tempo.

A questo punto, ipotizzando che la tensione applicata all’istante t’ resti costante nel tempo, e definendo opportune funzioni di viscosità e di solidificazione, è possibile pervenire, tramite le (2.20), (2.21) e (2.16), alla formulazione di modelli empirici, come il modello “B3” di Bazant, (Bazant e Baweja, 1995), in cui la funzione di viscosità 𝐽𝐽(𝑡𝑡, 𝑡𝑡′) ricavata, presenta una dipendenza

(23)

22 lineare da un numero di parametri ricavati su base sperimentale (con tecniche di regressione lineare).

2.5.2 Formulazione incrementale

La teoria della solidificazione, illustrata nel paragrafo precedente, può condurre ad una formulazione incrementale, sia in termini di viscosità (storia di carico assegnata), che di rilassamento (deformazione assegnata). In questo modo si evita di risolvere integrali di convoluzione e di dover memorizzare l’intera storia tensionale. Ovviamente l’applicazione della teoria della solidificazione richiede che siano assegnate opportune funzioni di viscosità e rilassamento microscopiche.

2.5.3 Problema di viscosità

Secondo la teoria della solidificazione, la deformazione totale, somma del contributo elastico e di quello viscoso nell’equazione (2.19), si scrive:

2.22

𝜀𝜀̇(𝑡𝑡) =_{𝜐𝜐(𝑡𝑡) �Φ}1 (0)σ̇(t) + � Φ̇(𝑡𝑡 − 𝑡𝑡′)𝑑𝑑𝜎𝜎(𝑡𝑡′)𝑡𝑡

0 �

Si effettui uno sviluppo in serie di Dirichlet della funzione di creep microscopica:

2.23 Φ(𝑡𝑡 − 𝑡𝑡′_{) =} 1 𝐸𝐸 + � 1 𝐸𝐸𝜇𝜇 �1 − 𝑒𝑒 −(𝑡𝑡−𝑡𝑡′)/𝜏𝜏𝜇𝜇� 𝑁𝑁 𝜇𝜇=1

dove E è un modulo elastico convenzionale mentre 𝐸𝐸_𝜇𝜇 e 𝜏𝜏_𝜇𝜇 sono parametri analoghi a quelli introdotti nella risoluzione con serie di Dirichlet, nel caso particolare di grandezze meccaniche costanti nel tempo. La loro determinazione avviene sempre attraverso l’interpolazione di dati sperimentali.

Sostituendo la (2.23) nella (2.22) si ottiene l’incremento di deformazione nella forma:

2.24

𝜀𝜀̇(𝑡𝑡) = 𝜀𝜀̇0(𝑡𝑡) + � 𝜀𝜀̇𝜇𝜇(𝑡𝑡) 𝑁𝑁

𝜇𝜇=1

dove 𝜀𝜀̇₀(𝑡𝑡), 𝜀𝜀̇_𝜇𝜇(𝑡𝑡) (𝜇𝜇 = 0, … , 𝑁𝑁), sono definite come:

𝜀𝜀̇0(𝑡𝑡) =_{𝐸𝐸 ∙ 𝜐𝜐(𝑡𝑡) 𝜀𝜀̇}𝜎𝜎̇ 𝜇𝜇(𝑡𝑡) =_{𝜐𝜐(𝑡𝑡) �}1 _𝐸𝐸1 𝜇𝜇 𝑡𝑡

0

𝑒𝑒−(𝑡𝑡−𝑡𝑡′)/𝜏𝜏𝜇𝜇𝑑𝑑𝜎𝜎(𝑡𝑡′)

In alternativa, le 𝜀𝜀̇_𝜇𝜇(𝑡𝑡) possono essere considerate come la soluzione di una equazione differenziale del tipo:

(24)

Creep e Ritiro Capitolo 2 23 𝜀𝜀̈𝜇𝜇(𝑡𝑡) = �_𝜏𝜏1 𝜇𝜇 + 𝜐𝜐̇(𝑡𝑡) 𝜐𝜐(𝑡𝑡)� 𝜀𝜀̇𝜇𝜇(𝑡𝑡) = 𝜎𝜎̇(𝑡𝑡) 𝜏𝜏𝜇𝜇𝐸𝐸𝜇𝜇𝜐𝜐(𝑡𝑡)

La (2.24) rappresenta l’equazione che governa il comportamento di una catena di unità di Kelvin (Figura 2-7a) con rigidezze delle molle pari a 𝐸𝐸_𝜇𝜇(𝑡𝑡) = 𝐸𝐸_𝜇𝜇𝜐𝜐(𝑡𝑡) e coefficiente di viscosità 𝜂𝜂𝜇𝜇(𝑡𝑡) = 𝜏𝜏𝜇𝜇𝐸𝐸𝜇𝜇(𝑡𝑡). Inoltre, il primo termine della (2.24) può essere interpretato come una molla in

serie (Figura 2-7a) con rigidezza variabile pari a 𝐸𝐸(𝑡𝑡) = 𝐸𝐸𝜐𝜐(𝑡𝑡). Pertanto, la teoria della solidificazione consente di descrivere il fenomeno dell’invecchiamento utilizzando funzioni di viscosità microscopiche a coefficienti costanti nel tempo, moltiplicate per la legge di solidificazione. Il limite della presente formulazione è che la variazione di tutte le caratteristiche meccaniche, rigidezza e coefficiente di viscosità, viene fatta dipendere da una stessa legge 𝜐𝜐(𝑡𝑡).

2.5.4 Problema di rilassamento

Un approccio duale consiste nel formulare la teoria della solidificazione partendo dalla definizione di una funzione di rilassamento microscopico. La formulazione si basa sull’equazione di equilibrio (3.26) e su una equazione costitutiva del tipo:

2.25

𝜎𝜎𝑔𝑔(𝜐𝜐(𝑡𝑡′), 𝑡𝑡) = � Ψ(𝑡𝑡 − 𝜏𝜏)𝑑𝑑𝜀𝜀(𝜏𝜏) 𝑡𝑡

𝜏𝜏=𝑡𝑡′

dove Ψ(𝑡𝑡 − 𝜏𝜏) rappresenta la funzione di rilassamento microscopico e il limite di integrazione inferiore sta ad indicare che solo la deformazione avvenuta dopo l’istante di solidificazione t’ provoca alterazioni dello stato tensionale.

Sostituendo la (2.25) nella (2.17) e integrando opportunamente, si ottiene infine l’equazione corrispondente alla (2.5) nella forma:

2.26

𝜎𝜎(𝑡𝑡) = � Ψ(𝑡𝑡 − 𝜏𝜏)𝜐𝜐(𝜏𝜏)𝑑𝑑𝜀𝜀(𝜏𝜏)𝑡𝑡

𝜏𝜏

da cui si deduce che la funzione di rilassamento macroscopica R può essere espressa come prodotto di una funzione dell’istante di carico 𝑡𝑡′ e di una funzione della durata di tale carico (𝑡𝑡 − 𝑡𝑡′_{), secondo l’espressione:}

2.27

𝑅𝑅(𝑡𝑡, 𝑡𝑡′) = 𝜐𝜐(𝑡𝑡′)Ψ(𝑡𝑡 − 𝑡𝑡′)

Analogamente a quanto esposto nel paragrafo precedente, per ottenere una formulazione differenziale è necessario sviluppare la funzione di rilassamento microscopico in serie di Dirichlet:

2.28

Ψ(𝑡𝑡 − 𝑡𝑡′) = � 𝐸𝐸𝜇𝜇𝑒𝑒−(𝑡𝑡−𝑡𝑡′)/𝜏𝜏𝜇𝜇 𝑁𝑁

(25)

24 La (2.28), sostituita nella (2.26), consente di scrivere la legge della tensione nella forma:

2.29

𝜎𝜎(𝑡𝑡) = � 𝜎𝜎𝜇𝜇(𝑡𝑡) 𝑁𝑁

𝜇𝜇=1

dove 𝜎𝜎_𝜇𝜇 è soluzione dell’integrale differenziale:

2.30

𝜎𝜎̇𝜇𝜇(𝑡𝑡) +𝜎𝜎𝜇𝜇_𝜏𝜏(𝑡𝑡)

𝜇𝜇 = 𝐸𝐸𝜇𝜇𝜐𝜐(𝑡𝑡)𝜀𝜀̇(𝑡𝑡) 𝜇𝜇 = (1, … , 𝑁𝑁)

che risolta fornisce:

2.31

𝜎𝜎𝜇𝜇(𝑡𝑡) = 𝐸𝐸𝜇𝜇 � 𝑒𝑒−(𝑡𝑡−𝑡𝑡′)/𝜏𝜏𝜇𝜇𝜐𝜐(𝑡𝑡′)𝑑𝑑𝜀𝜀̇(𝑡𝑡′) 𝑡𝑡

𝑡𝑡′₌₀

𝜇𝜇 = (1, … , 𝑁𝑁)

Si noti che anche in questo caso, le (2.29) e (2.30) corrispondono alle equazioni che governano una catena di Maxwell con rigidezza delle molle 𝐸𝐸_𝜇𝜇(𝑡𝑡) = 𝜐𝜐(𝑡𝑡)𝐸𝐸_𝜇𝜇 e coefficiente di viscosità 𝜂𝜂𝜇𝜇(𝑡𝑡) = 𝜏𝜏𝜇𝜇𝐸𝐸𝜇𝜇(𝑡𝑡) variabile nel tempo, dove tale dipendenza è espressa mediante un’unica legge 𝜐𝜐(𝑡𝑡)

(Figura 2-9).

2.6 Formulazione incrementale con comportamento asintotico

L’ipotesi che l’invecchiamento dipenda da un solo processo di solidificazione conduce talvolta a risultati non sufficientemente accurati. Bazant ha mostrato, ad esempio, che con una sola legge di solidificazione è difficile cogliere il comportamento a lungo termine di un calcestruzzo caricato pochi giorni dopo la presa.

Inoltre, è facile verificare che, nella sua forma originaria, la teoria della solidificazione di Bazant

E

1

(t)

E

2

(t)

E

N

(t)

1

E

1

(t)

2

E

2

(t)

N

E

N

(t)

Figura 2-9: Serie di Maxwell equivalente al modello di viscoelasticità con invecchiamento della teoria della solidificazione di Bazant

(26)

25 fornisce funzioni di viscosità che prevedono deformazioni illimitate a tempo infinito. Infatti, quando l’intero processo di solidificazione si è concluso e tutti i parametri di rigidezza e di viscosità hanno raggiunto il loro valore finale, il comportamento è governato dallo smorzatore con tempo di ritardo più lungo. Ciò è dunque in contrasto con l’ipotesi del modello del CEB di deformazioni finite a tempo infinito. Pertanto, per riuscire a cogliere questo comportamento asintotico, il modello è stato opportunamente modificato.

Si può generalizzare il problema introducendo diversi processi di solidificazione (governati da leggi temporali indipendenti tra loro), adottando una differente funzione del tempo per ogni singola variabile di stato che compare nello sviluppo di Dirichlet. Ad esempio, sviluppando in serie la funzione di rilassamento, la (2.26) diventa:

2.32

𝜎𝜎𝜇𝜇(𝑡𝑡) = � 𝛹𝛹𝜇𝜇(𝑡𝑡 − 𝜏𝜏)𝜐𝜐𝜇𝜇(𝜏𝜏)𝑑𝑑𝜀𝜀(𝜏𝜏) 𝑡𝑡

𝜏𝜏=0

Arrestando infine lo sviluppo in serie di Dirichlet della 𝛹𝛹_𝜇𝜇(𝑡𝑡 − 𝜏𝜏) nella (2.28) al primo termine, la legge che esprime la tensione totale 𝜎𝜎(𝑡𝑡) è riscrivibile nella forma (2.29), dove ora le 𝜎𝜎_𝜇𝜇(𝑡𝑡) sono soluzione delle equazioni differenziali lineari:

2.33

𝜎𝜎̇𝜇𝜇(𝑡𝑡) +𝜎𝜎𝜇𝜇_𝜏𝜏(𝑡𝑡)

𝜇𝜇 = 𝐸𝐸𝜇𝜇𝜐𝜐𝜇𝜇(𝑡𝑡)𝜀𝜀̇(𝑡𝑡)

L’impiego di un numero elevato di processi di solidificazione ripropone tuttavia i problemi di identificazione dei parametri meccanici già discussi.

Nel presente modello è stata quindi utilizzata una catena di Maxwell, costituita da N-1 elementi completi ed uno (l’N-esimo) degenere, cioè con viscosità nulla, posti in parallelo (Figura 2-10).

Sono state inoltre utilizzate due leggi di solidificazione: la prima, 𝜐𝜐_𝜇𝜇(𝑡𝑡), comune a tutti gli

E

1

(t)

E

2

(t)

1

E

1

(t)

2

E

2

(t)

E

N N

(t)

(27)

26 elementi non degeneri, l’ultima, 𝜐𝜐_𝜇𝜇(𝑡𝑡), per l’elemento degenere, la cui rigidezza è quindi descritta dalla legge 𝐸𝐸_𝑁𝑁(𝑡𝑡) = 𝜐𝜐_𝑁𝑁(𝑡𝑡)𝐸𝐸_𝑁𝑁.

Pertanto, a tempo infinito e quindi a processo di solidificazione concluso, il comportamento è governato dal parametro di rigidezza EN ed ammette pertanto deformazioni finite a tempo infinito in accordo con il Model Code 1990.

2.6.1 Algoritmo esponenziale per l’integrazione nel tempo

La formulazione differenziale (2.33) corrisponde in sostanza alla (2.13) del paragrafo relativo ai modelli reologici; è possibile allora implementare la teoria della solidificazione attraverso un algoritmo di tipo esponenziale (Bazant e Wu, 1974).

Ancora una volta, l’idea alla base dell’algoritmo è quella di utilizzare, all’interno del generico passo temporale, l’integrale esatto dell’equazione differenziale (2.33), ottenuto assumendo che il secondo termine dell’equazione rimanga costante all’interno del passo. L’intervallo di tempo su cui si intende valutare le deformazioni differite viene suddiviso in i intervalli temporali Δ𝑡𝑡𝑟𝑟 = 𝑡𝑡𝑟𝑟 − 𝑡𝑡𝑟𝑟−1 (𝑟𝑟 = 1, … 𝑁𝑁), individuati da N+1 istanti temporali 𝑡𝑡0, … , 𝑡𝑡𝑁𝑁.

Moltiplicando la (2.33) per la funzione di integrazione:

𝑓𝑓𝜇𝜇(𝑡𝑡) = 𝑒𝑒∫

𝑑𝑑𝑡𝑡 ′ 𝜏𝜏𝜇𝜇 𝑡𝑡 𝑡𝑡𝑟𝑟−1 il termine a primo membro può essere così semplificato:

2.34

𝜕𝜕

𝜕𝜕𝑡𝑡 �𝜎𝜎𝜇𝜇(𝑡𝑡)𝑒𝑒𝑓𝑓𝜇𝜇(𝑡𝑡)� = 𝐸𝐸𝜇𝜇𝜐𝜐𝜇𝜇(𝑡𝑡)𝜀𝜀̇(𝑡𝑡)𝑓𝑓𝜇𝜇(𝑡𝑡)

Integrando quindi la (2.34) sull’intervallo temporale generico e portando a secondo membro tutte le grandezze note in quanto determinate al passo precedente, si ottiene l’espressione al tempo t della 𝜇𝜇-esima variabile di stato nella forma:

2.35

𝜎𝜎𝜇𝜇(𝑡𝑡) = 𝑒𝑒−𝑓𝑓𝜇𝜇(𝑡𝑡)�𝜎𝜎𝜇𝜇,𝑟𝑟−1(𝑡𝑡) + � 𝐸𝐸𝜇𝜇𝜐𝜐𝜇𝜇(𝑡𝑡′) 𝑡𝑡

𝑡𝑡𝑟𝑟−1

𝑒𝑒−𝑓𝑓𝜇𝜇(𝑡𝑡)𝑑𝑑𝜀𝜀(𝑡𝑡′)�

dove 𝜎𝜎_{𝜇𝜇,𝑟𝑟−1} rappresenta il valore assunto dalla variabile stessa al passo temporale precedente. Le quantità che compaiono nell’integrale a secondo membro possono essere considerate costanti sul generico intervallo temporale nel caso in cui gli intervalli di tempo siano sufficientemente piccoli oppure quando si abbiano piccole variazioni delle funzioni di invecchiamento 𝜐𝜐_𝜇𝜇(𝑡𝑡). Se risulta verificata almeno una delle due condizioni e ponendo 𝑡𝑡 = 𝑡𝑡_𝑟𝑟, è possibile ottenere la seguente relazione:

(28)

Creep e Ritiro Capitolo 2 27 2.36 𝜎𝜎𝜇𝜇,𝑟𝑟(𝑡𝑡) = 𝜎𝜎𝜇𝜇,𝑟𝑟−1𝑒𝑒−Δ𝑡𝑡 𝑟𝑟 𝜏𝜏𝜇𝜇 + 𝐸𝐸_𝜇𝜇𝜐𝜐_{𝜇𝜇,𝑟𝑟−1/2}∙ 𝜆𝜆_{𝜇𝜇,𝑟𝑟}Δ𝜀𝜀_𝑟𝑟 in cui: 𝜆𝜆𝜇𝜇,𝑟𝑟 = �1 − 𝑒𝑒−Δ𝑡𝑡 𝑟𝑟 𝜏𝜏𝜇𝜇 � 𝜏𝜏𝜇𝜇 Δ𝑡𝑡𝑟𝑟

e 𝜐𝜐_{𝜇𝜇,𝑟𝑟−1/2} rappresenta la media della generica funzione di invecchiamento tra i due valori assunti agli estremi dell’intervallo temporale:

𝜐𝜐𝜇𝜇,𝑟𝑟−1/2 =1_{2 �𝜐𝜐}𝜇𝜇,𝑟𝑟−1+ 𝜐𝜐𝜇𝜇,𝑟𝑟�

Sostituendo la (2.36) nella (2.21) è possibile ottenere una formulazione pseudo-elastica incrementale del tipo:

2.37 Δ𝜀𝜀𝑟𝑟 = _𝐸𝐸1 𝑟𝑟′′ Δ𝜎𝜎𝑟𝑟 + Δ𝜀𝜀𝑟𝑟′′ in cui 𝐸𝐸𝑟𝑟′′ = � 𝜆𝜆𝜇𝜇,𝑟𝑟𝐸𝐸𝜇𝜇𝜐𝜐_{𝜇𝜇,𝑟𝑟−12} 𝑁𝑁 𝜇𝜇=1 Δ𝜀𝜀𝑟𝑟′′ =_𝐸𝐸1 𝑟𝑟′′ � �1 − 𝑒𝑒 −𝛥𝛥𝑦𝑦𝜇𝜇 𝜏𝜏𝜇𝜇 � 𝑁𝑁 𝜇𝜇=1 𝜎𝜎𝜇𝜇,𝑟𝑟−1

Ad un generico istante 𝑡𝑡_𝑟𝑟, l’algoritmo di integrazione numerica consiste nel ricavare il modulo di elasticità pseudo-elastico 𝐸𝐸_𝑟𝑟′′ e la deformazione Δ𝜀𝜀_𝑟𝑟′′ sulla base delle tensioni note al tempo 𝑡𝑡_𝑟𝑟−1, risolvere il problema con una relazione di tipo elastico utilizzando la (2.37), ed infine ottenere gli incrementi di deformazione Δ𝜀𝜀_𝑟𝑟 da utilizzarsi per calcolare i valori aggiornati delle variabili di stato 𝜎𝜎𝜇𝜇,𝑟𝑟.

L’errore che si commette è legato alla validità di almeno una delle due ipotesi che si utilizzano per ottenere l’integrale in forma chiusa della (2.35). Tale procedura consente quindi di utilizzare intervalli temporali di ampiezza anche molto diversi tra loro, ed in particolare molto piccoli nelle prime fasi del caricamento (in quanto invecchiamento e deformazioni viscose progrediscono rapidamente) e molto più lunghi quando il fenomeno dell’invecchiamento si è ormai esaurito.

2.6.2 Taratura del modello

Con l’obiettivo di mettere a punto uno strumento di calcolo coerente con i riferimenti normativi, sono state utilizzate le previsioni formulate dal Model Code 90 (CEB-FIP, 1990), che rappresentano la sintesi di molti dei risultati delle oltre 600 serie di prove sperimentali riportati nel Data Base Rilem (Rilem TC-107, 1998).

(29)

28 Per la taratura del modello proposto devono essere definite due categorie distinte di parametri, riguardanti le proprietà reologiche delle unità di Maxwell (rigidezze e tempi di ritardo) e le leggi di solidificazione.

Per quanto riguarda i primi, seguendo le indicazioni di Bazant, si stabiliscono a priori i tempi di ritardo, presi regolarmente equispaziati nella scala logaritmica dei tempi coprendo tutto l’intervallo da investigare. Ad ogni tempo di ritardo è quindi assegnata una unità di Maxwell. Nella taratura del presente modello sono state utilizzate sei unità di Maxwell più l’unità degenere, con tempi di ritardo variabili da 1·10-3 a 1·105 giorni (t7=1·105).

Per le due leggi di solidificazione, è stata utilizzata la legge di evoluzione temporale del modulo di elasticità longitudinale del calcestruzzo proposta dal Model Code 90:

𝜐𝜐(𝑡𝑡) = �𝑒𝑒𝑐𝑐1�1−�28/𝑡𝑡� 𝜐𝜐_𝑁𝑁(𝑡𝑡) = �𝑒𝑒𝑐𝑐𝑁𝑁�1−�28/𝑡𝑡�

dove s1 e sN sono due parametri da determinarsi ed il tempo è espresso in giorni. La procedura

richiede inoltre la preventiva definizione di parametri quali la resistenza caratteristica a compressione, umidità e perimetro bagnato per i quali sono stati scelti valori di norma (fck=30N/mm2, RH=50%, 2A/u=50÷100mm, T=20°C).

(30)

Sistemi di prefabbricazione Capitolo 3

29

Capitolo 3

Sistemi di prefabbricazione

3.1 Descrizione del sistema costruttivo

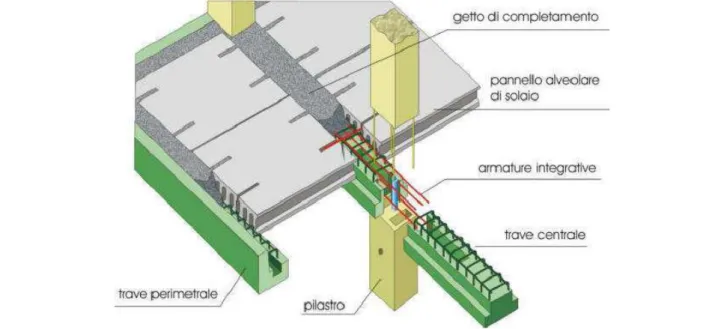
Le travi oggetto di studio di questa tesi fanno parte di un sistema pluriplano iperstatico che viene prodotto dall’azienda APE di Montecchio Emilia (RE). Il sistema consiste in un insieme di componenti strutturali (travi, pilastri, solai ed innesti di fondazione) che coniuga le peculiarità di un sistema prefabbricato industriale autoportante con le prestazioni di una struttura tradizionale realizzata in opera. La caratteristica che contraddistingue il sistema è il nodo di tipo umido, dove la continuità strutturale è garantita dalla sovrapposizione degli elementi e dal successivo getto di solidarizzazione che conferisce iperstaticità ed elevata rigidezza alla costruzione. L’opera finita, pertanto, risulta assimilabile ad una struttura intelaiata ad ossatura portante, realizzata in opera.

Vediamo in sintesi le fasi di montaggio: partiamo da una struttura costituita da fondazioni a trave rovescia in cemento armato, realizzate in opera in due fasi, su cui sono innestati i pilastri prefabbricati del tipo monopiano. I pilastri saranno sostenuti in fase di montaggio da un elemento

(31)

30 tubolare metallico annegato parzialmente in fondazione e messi a piombo tramite l'ausilio di tiranti rigidi; la solidarizzazione della struttura viene ottenuta con il secondo getto della fondazione che incorpora i ferri sporgenti inferiori dei pilastri.

Gli impalcati di solaio sono composti da travi prefabbricate costituite da una parte pregettata ribassata rispetto al solaio e da un traliccio metallico sporgente in ferro tipo FeB44K controllato. Sulle travi sono appoggiati i pannelli alveolari autoportanti in c.a.p. Le travi di bordo e di spina sono autoportanti in prima fase per il peso proprio e l'aliquota di solaio gravante e possiedono una geometria idonea a ridurre al minimo le opere di carpenteria e a rendere quanto più efficace la loro solidarizzazione nel complesso strutturale.

L'unione dei solai con le travi avviene con la messa in opera di idonee armature nella fresatura dei pannelli, di reti metalliche e di un getto di completamento di una soletta collaborante di calcestruzzo, realizzando così una continuità strutturale fra le campate adiacenti.

In definitiva, quindi, le fasi di montaggio possono essere elencate come segue:

1. Posa del trespolo e del pilastro: l’inserto metallico viene annegato in una platea di fondazione ( o in travi rovesce o plinti a seconda della necessità). Tramite appositi tubolari il pilastro viene poi centrato e piombato nella corretta posizione.

2. Posa delle travi: Le travi vengono posate sui pilastri utilizzando gru. Sono anche fornite le armature integrative per realizzare la continuità strutturale.

3. Posa del solaio: le lastre prefabbricato del solaio alveolare in c.a.p. vengono posate utilizzando gru.

4. Getto dei nodi strutturali: I getti integrativi degli impalcati possono essere realizzati con normali calcestruzzi Rck 30 N/mm^2. L’inghisaggio dei pilastri alla fondazione si realizza con malta a ritiro compensato.

Le travi prefabbricate APE sono prodotte in Serie Dichiarata come da Decreto Ministeriale del

Figura 3-2:Posa della trave Figura 3-3:Posa del pilastro

(32)

31

03-12-87, con calcestruzzi di classe 35-40-45-50 N/mm2 ed acciaio tipo FeB44K saldabile

controllato all'origine. Per serie "dichiarata" si intende la produzione in serie eseguita in stabilimento, dichiarata tale dal produttore, conforme alle norme suddette.

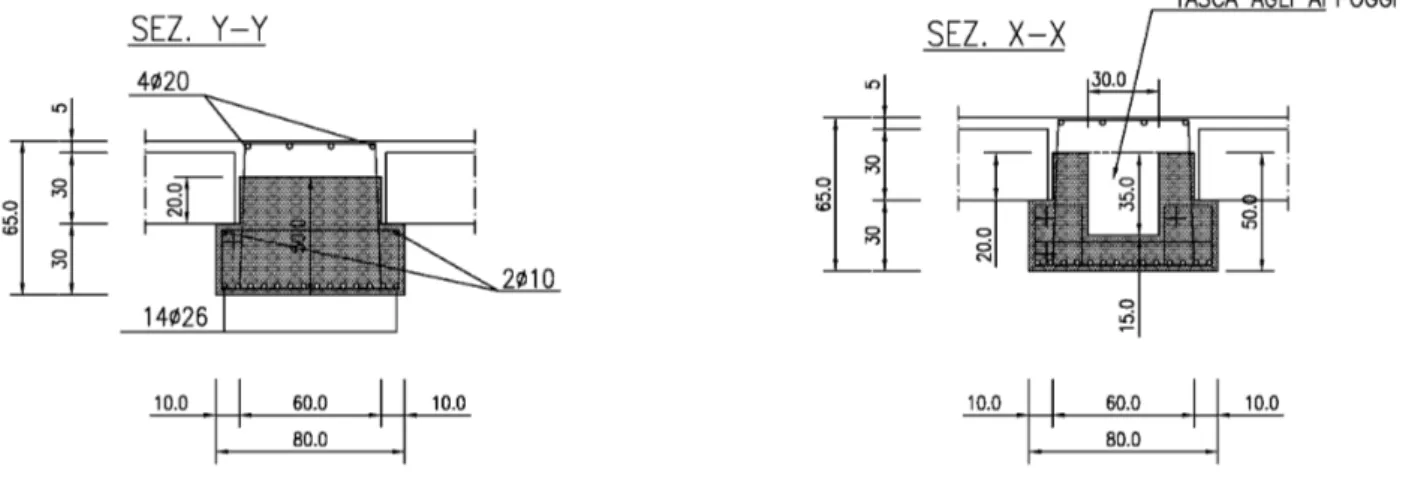
Le tipologie sono suddivise, in funzione della posizione nella struttura, in travi centrali e travi perimetrali.

L'autoportanza iniziale della trave prefabbricata è stata progettata per sostenere in condizioni di semplice appoggio i carichi di montaggio (aliquote dei solai incidenti, getti integrativi e della trave stessa), nonché il personale addetto al montaggio. Il solaio, è un alveolare precompresso.

3.2 Criteri di verifica agli stati limite per travi eseguite in fasi successive

Per stato limite si intende una condizione superata la quale la struttura in esame, o uno dei suoi elementi costitutivi, non soddisfa più le esigenze per le quali è stata progettata.

Esaminiamo i criteri grazie ai quali è possibile condurre le verifiche istantanee di una generica sezione in cemento armato. I collegamenti delle armature delle travi e quello dei pilastri costituiscono due sistemi separati, in quanto l’ordine di grandezza dei momenti di continuità che interessano i due elementi costruttivi risulta abbastanza differente. Per il calcolo delle sollecitazioni, dunque, la trave può essere considerata in qualche modo continua su più campate.

3.2.1 Verifica agli stati limite ultimi

Si definiscono stati limite ultimi (SLU) le condizioni strutturali pari al valore estremo della capacità portante, o altre forme di cedimento strutturale che possono mettere in pericolo la sicurezza delle persone (ad esempio rotture di sezioni critiche, instabilità …). Il superamento di uno stato limite ultimo ha carattere irreversibile e si definisce collasso.

Nella fase I (solo trave prefabbricata), si considerano i pesi effettivamente agenti (e quindi non fattorizzati). Nella II fase si applica invece la rimanente frazione di carichi: il completamento dei