Dinamica ad alta frequenza nei metalli liquidi: spettri IXS e teoria idrodinamica molecolare

(1)

UNIVERSIT `

A DEGLI STUDI DI ROMA

“LA SAPIENZA”

Facolt`

a di Scienze Matematiche Fisiche e Naturali

TESI DI LAUREA IN FISICA

A.A. 2004/2005

Dinamica ad alta frequenza nei

metalli liquidi: spettri IXS

e teoria idrodinamica molecolare

Relatore:

Laureando:

Prof. Giancarlo Ruocco

Stefano Cazzato

Correlatore:

(2)

(3)

Indice

1 Introduzione 7

2 Il linguaggio e gli strumenti 11

2.1 Variabili dinamiche e funzioni di correlazione . . . 11

2.2 Modi longitudinali idrodinamici: diversi formalismi, stessa fisica . 15 2.2.1 Idrodinamica lineare e modi longitudinali . . . 16

2.2.2 L’equazione di Langevin generalizzata . . . 21

La funzione di memoria del secondo ordine e la soluzione idrodinamica . . . 23

Il formalismo GCM . . . 25

Il formalismo GCM e il calcolo dei modi longitudinali idro-dinamici . . . 27

Generalizzare l’idrodinamica: alcuni approcci significativi . 30 2.2.3 Conclusioni . . . 34

2.3 Velocit`a del suono idrodinamica . . . 34

2.3.1 Il caso particolare γ = 1 . . . . 36

2.3.2 Il caso generale . . . 38

Massimi della corrente . . . 38

Massimi del fattore di struttura dinamico . . . 41

Poli . . . 42

2.3.3 Confronto delle diverse definizioni di velocit`a del suono idro-dinamica . . . 42

2.4 Miscele binarie . . . 43

2.4.1 Introduzione . . . 43

2.4.2 Definizioni . . . 44

2.4.3 Lo scattering anelastico da una miscela binaria e i fattori di struttura di Bhatia e Thornton . . . 46

2.4.4 Idrodinamica di una miscela binaria . . . 48

2.4.5 La funzione di memoria del secondo ordine per una miscela binaria . . . 57

2.4.6 L’idrodinamica di una miscela binaria: l’approssimazione markoviana . . . 59

(4)

3 Scattering anelastico di raggi X 67

3.1 IXS . . . 67

3.1.1 La sezione d’urto di scattering anelastico di raggi X . . . . 68

3.1.2 Scattering anelastico di raggi X da una miscela binaria . . 73

3.1.3 IXS e INS nei sistemi disordinati . . . 74

3.2 Layout di uno spettrometro IXS . . . 81

3.2.1 Il potere risolutivo . . . 81

3.2.2 La geometria di backscattering e la scansione in energia . . 84

3.2.3 Gli analizzatori . . . 85

3.2.4 La sorgente e lo stadio premonocromatore . . . 86

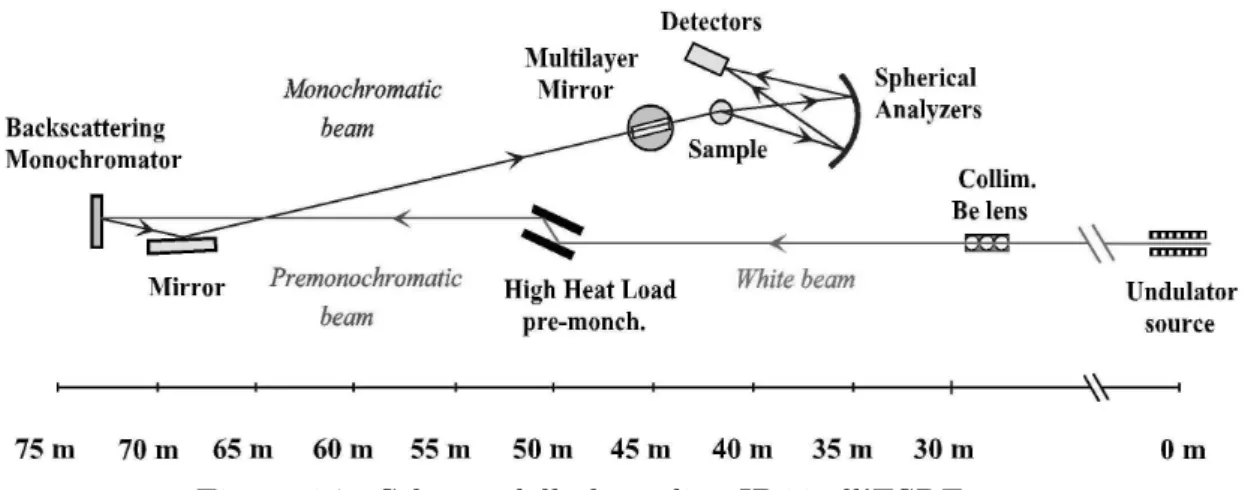
3.2.5 Uno sguardo d’insieme alla beamline . . . 86

4 Modi collettivi nel Nichel liquido 89 4.1 Introduzione . . . 89

4.2 Il Nichel . . . 89

4.3 Perch´e il nichel . . . 91

4.3.1 Il regime isotermo . . . 91

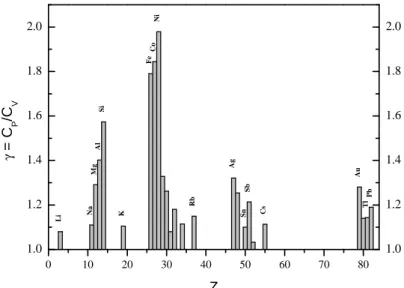
4.3.2 Il rapporto dei calori specifici nei metalli liquidi . . . 92

4.3.3 Una recente indagine INS . . . 94

4.3.4 Un modello semplificato di funzione di memoria . . . 97

4.4 Il setup ad alta temperatura . . . 101

4.4.1 Problematiche legate alla progettazione della cella . . . 101

4.4.2 Descrizione della cella . . . 102

4.5 La S(Q, ω) del nichel liquido . . . 105

5 Studio della dinamica ad alta frequenza in un liquido binario: La Miscela Sodio-Potassio 113 5.1 Introduzione . . . 113

5.2 Caratterizzazione del sistema . . . 113

5.2.1 Generalit`a . . . 113

5.2.2 le propriet`a termodinamiche . . . 114

5.2.3 Le propriet`a strutturali . . . 116

5.2.4 I fattori di forma atomica del sodio e del potassio . . . 119

5.3 L’esperimento IXS . . . 122

5.3.1 Il setup sperimentale . . . 122

5.3.2 Spettri IXS dell’Na-K: la misura e il contributo di cella vuota123 5.4 Risultati . . . 127

5.4.1 Confronto degli spettri di Na-K, Na e K . . . 127

5.4.2 Confronto del modello con i dati sperimentali . . . 131

5.4.3 Tempi caratteristici . . . 140

5.4.4 Coefficienti di trasporto . . . 143

(5)

A Richiami di termodinamica delle miscele 147

(6)

(7)

Capitolo 1

Introduzione

La natura della dinamica microscopica nei sistemi privi di ordine a lungo range (liquidi e vetri) costituisce a tuttoggi uno dei temi pi`u dibattuti nell’ambito dello studio della materia condensata. Una classe particolarmente importante di sistemi disordinati `e costituita dai cosiddetti liquidi semplici, che comprendono tutte le caratteristiche fondamentali dei liquidi reali senza le complicazioni aggiuntive che possono essere presenti in sistemi particolari [1].

L’aggettivo semplice si riferisce dunque alla relativa facilit`a con cui pu`o es-sere descritta la struttura di tali sistemi, per i quali si assumono alcune ipotesi sul comportamento delle forze di interazione tra i loro costituenti; in particolare si assume che il potenziale interatomico sia a simmetria sferica con interazione additiva a due corpi.

Grande interesse ha destato negli ultimi decenni l’evidenza sperimentale riscon-trata in questa classe di sistemi in merito all’esistenza di ben definite eccitazioni collettive a vettori d’onda finiti, cio`e fuori della regione idrodinamica propria-mente detta; in pratica in tali sistemi la propagazione di moti collettivi avviene su distanze spaziali che possono arrivare ad alcune volte la distanza tipica tra i costituenti microscopici [1, 2, 3].

I metalli liquidi in particolare sono riconosciuti ormai come uno dei prototipi di liquido semplice. Questo sembra essere in contrasto con l’ovvia costatazione che un metallo liquido è in realtà un sistema a due componenti e in un approccio rigoroso si dovrebbe estendere il formalismo utilizzato per le miscele binarie. Tuttavia l’investigazione della dinamica atomica di questi sistemi può essere formulata sulla base dello studio delle proprietà ioniche, guardando al fluido come a un sistema di ioni interagenti mediante un potenziale efficace che tiene conto della mediazione dovuta al gas elettronico di conduzione. Risulta in effetti possibile introdurre uno pseudopotenziale di interazione a coppie, dipendente dalla densità. Il concetto di pseudopotenziale è stato largamente sfruttato a partire dagli anni ’60 nella analisi delle proprietà strutturali e dinamiche dei metalli liquidi mediante studi di Dinamica Molecolare divenuti sempre più realiastici grazie all’avvento e alla diffusione dei sistemi di computazione [4].

(8)

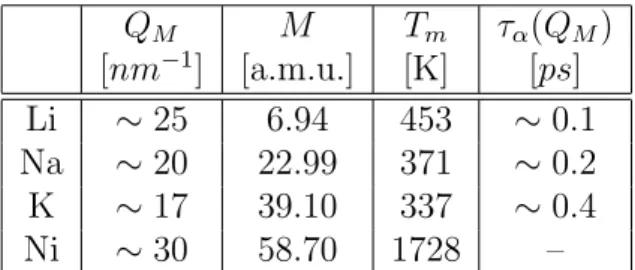
Lo stesso periodo, grazie al compiuto sviluppo delle tecniche di indagine di diffusione anelastica di neutroni (INS), ha visto avviarsi l’investigazione speri-mentale estensiva della dinamica microscopica dei metalli liquidi, sopratutto dei metalli alcalini, dalla prima osservazione pionieristica compiuta sul rubidio liquido [5], fino alle pi`u recenti indagini su cesio [6], sodio [7], litio [8] e potassio [9].

Solo a partire dall’ultimo decennio lo sviluppo della tecnica di Scattering Anelastico di Raggi X (IXS) ha reso possibile il superamento di alcune delle lim-itazioni imposte dalla tecnica IXS all’esplorazione dei modi collettivi nei sistemi disordinati [10, 11, 12]. Infatti l’utilizzo di una sonda non massiva ha rimosso le restrizioni della regione dinamica impulso-energia accessibile allo studio delle eccitazioni collettive, dovute nel caso dell’INS alla cinematica del processo di dif-fusione. D’altra parte la possibilità di una osservazione del contributo puramente coerente della sezione d’urto di diffusione anelastica ha consentito di trarre infor-mazioni limitatamente alla dinamica collettiva dei sistemi disordinati attraverso il fattore di struttura dinamico S(Q, ω) associato alle fluttuazioni della densità atomica. Tale nuova acquisizione ha dischiuso la possibilità di raccogliere in-formazioni sempre più dettagliate sulla dinamica ad alta frequenza nei metalli liquidi estendendo l’esplorazione delle proprietà dinamiche di questi sistemi anche a lunghezze d’onda fino ad ora precluse ad ogni altra tecnica sperimentale. Le potenzialità della spettroscopia IXS sono state ben presto applicate allo studio dei metalli liquidi ([13], [14] [15]) con l’intento di ottenere un riscontro sperimentale diretto di modelli teorici in grado di descrivere il comportamento delle fluttuazioni della densità nella regione mesoscopica.

L’analisi teorica della risposta di un fluido semplice alla perturbazione indotta da una sonda esterna nel limite in cui le lunghezze d’onda sono molto maggiori della distanza interatomica tipica e le frequenze sono molto minori dell’inverso del tempo tipico delle collisioni interatomiche costituisce il campo di applicazione dell’ idrodinamica linearizzata che fornisce un approccio per il calcolo delle correlazioni nel limite del continuo.

Naturalmente ci si aspetta che la descrizione idrodinamica delle fluttuazioni sia destinata a fallire non appena le lunghezze d’onda e le frequenze inverse di-ventano comparabili con le distanze interatomiche e i tempi medi di collisione rispettivamente. Tuttavia nel regime di transizione le deviazioni dal comporta-mento idrodinamico subentrano in modo graduale e le equazioni dell’idrodinamica possono essere ritenute, pur assumendo una dipendenza dalla frequenza e dal mo-mento scambiato dei coefficienti di trasporto e delle grandezze termodinamiche. La formulazione sistematica di una tale generalizzazione procede attraverso l’u-so di un formalismo dedotto nell’ambito della meccanica statistica, noto come formalismo degli operatori di proiezione che porta, in uno sviluppo proposto da Zwanzig e Mori [16], ad una equazione di Langevin generalizzata (ELG).

Il calcolo delle funzioni di correlazione deve tuttavia procedere attraverso tec-niche di approssimazione. In particolare il formalismo della funzione di memoria del secondo ordine deriva da una tecnica di sviluppo in frazioni continue

(9)

del-la ELG, troncato al secondo ordine, e il metodo dei modi collettivi generalizzati (GCM) deriva dalla ELG mediante una approssimazione markoviana.

Vengono riassunti nel seguito i risultati ottenuti in questo lavoro di tesi: 1. Si discute l’equivalenza tra diversi formalismi teorici che consentono il

cal-colo delle funzioni di correlazione in un liquido semplice nel limite idrodi-namico. In particolare se `e ben noto come tutti i risultati dell’idrodinamica linearizzata possono essere formalmente dedotti in un approccio microscop-ico basato sul formalismo della funzione di memoria del secondo ordine, un confronto della soluzione GCM nel limite idrodinamico con i risultati prece-denti manca in letteratura e viene affrontato in questa sede, giungendo a stabilire le relazioni che legano i parametri coinvolti nelle diverse rappre-sentazioni. Si affronta quindi una discussione delle diverse definizioni della velocit`a del suono nel limite idrodinamico.

2. La possibilità di estendere l’idrodinamica linearizzata nella regione meso-scopica porta ad ipotizzare nel caso specifico dei metalli liquidi, in con-seguenza della elevata diffusività termica di questi sistemi, l’esistenza di un regime dinamico isotermo nell’intervallo di impulso scambiato 0.2 . Q . 3nm−1 _{[17]. In tale contesto è nato l’interesse verso lo studio sperimentale}

del nichel liquido. Si discute quindi la progettazione la realizzazione e la procedura di analisi dei dati relativi ad un esperimento IXS su nichel liqui-do, volto ad appurare eventuali violazioni delle predizioni idrodinamiche a piccoli vettori d’onda.

3. Si `e determinata, mediante l’approccio GCM, una espressione analitica per la funzione di memoria del secondo ordine, utilizzata per l’analisi dei dati IXS da una miscela Na-K, ottenuti in un esperimento precedente al pre-sente lavoro di Tesi, fornendo, fra l’altro, l’andamento in Q di coefficienti di trasporto generalizzati, come il coefficiente di interdiffusione fra le due specie e la viscosit`a longitudinale.

Per concludere, il presente lavoro `e organizzato in quattro capitoli.

Nel capitolo 2 vengono introdotti gli strumenti dell’analisi teorica delle corre-lazioni nei liquidi semplici e nelle miscele binarie. Alcuni dei risultati di questo lavoro sono dunque inquadrati nel contesto opportuno in questo capitolo, che costituisce quindi nel suo insieme una premessa fondamentale alla successiva interpretazione dei dati sperimentali.

Il capitolo 3 introduce alla tecnica sperimentale dell’IXS, sviluppandone la teo-ria e dando rilievo alle problematiche sollevate dalla sua implementazione, trac-ciando inoltre un confronto sintetico con la tecnica INS, rivolto specialmente al problema dell’indagine dei sistemi disordinati.

Nel capitolo 4 vengono trattate le motivazioni che hanno destato interesse verso lo studio della dinamica microscopica del nichel liquido. Vengono quindi riportati i risultati dell’indagine sperimentale e dell’analisi dei dati.

(10)

Infine il capitolo 5 descrive i metodi e i risultati dell’analisi dei dati sperimentali ottenuti mediante IXS relativi a una miscela di sodio e potassio.

(11)

Capitolo 2

Il linguaggio e gli strumenti

2.1 Variabili dinamiche e funzioni di correlazione

Ci proponiamo in questo paragrafo di porre le basi del linguaggio che useremo nella nostra indagine della dinamica microscopica di un liquido semplice.

Il nostro sistema comprende N unit`a elementari, atomi o ioni, con posizione ri(t) e impulso pi(t) = mvi(t), i = 1, ..., N , la cui dinamica segue le equazioni del

moto classiche associate alla hamiltoniana H = 1 2 X i p2 i m + VN(r1, ..., rN)

Una variabile dinamica A(pN_{, r}N_{) `e una generica funzione delle 6N}

coordi-nate dello spazio delle fasi Γ. Un ruolo centrale nella descrizione che daremo della dinamica microscopica è rivestito dalle funzioni di correlazione delle vari-abili dinamiche, e nello spazio di tutte le possibili varivari-abili ve ne sono certamente alcune rilevanti per la nostra trattazione. Queste sono la densità numero ρ(r, t), la densità di momento J(r, t) e la densità di energia e(r, t):

ρ(r, t) =. √1 N X i δ(r − ri(t)) J(r, t) =. √1 N X i vi(t)δ(r − ri(t)) e(r, t) =. √1 N X i 1 2mv 2 i(t)δ(r − ri(t)) (2.1)

A partire dalle variabili (2.1) possiamo definire le variabili dinamiche che ne sono le trasformate di Fourier spaziali, come per ogni generica variabile A che sia esprimibile come integrale di una variabile locale ai(t), si pu`o scrivere

A(Q, t) = Z _+∞

−∞

A(r, t)eiQ·r_{dr =}X i

(12)

e questo risulta utile perch´e come vedremo gli esperimenti danno in genere infor-mazioni sullo spazio reciproco Q. Definiamo dunque

ρ(Q, t) = √1 N X i eiQ·ri(t) J(Q, t) = √1 N X i vi(t)eiQ·ri(t) e(Q, t) = √1 N X i 1 2mv 2 i(t)eiQ·ri(t) (2.2)

Veniamo adesso ad introdurre brevemente il concetto di funzione di corre-lazione insieme a qualcuna delle propriet`a peculiari di queste funzioni. Siano A(t) e B(t) due generiche variabili dinamiche; la funzione di correlazione temporale di A e B si scrive

CAB(t, t0) = hδB∗(t0)δA(t)i (2.3)

dove h· · ·i indica la media statistica sull’ensemble h· · ·i =

Z

Γ

dpN_drN_{(· · ·)P(p}N_rN₎

essendo P(pN_rN_{) la distribuzione di probabilit`a del sistema nello spazio delle fasi}

Γ. Nella (2.3) abbiamo posto δA(t) = A(t) − hA(t)i. Vediamo alcune propriet`a di cui gode CAB(t, t0).

• Dalla stazionariet`a di P(pN_rN_{) deriva l’invarianza per traslazione temporale}

delle correlazioni e delle propriet`a statistiche in genere del sistema hA(t)i = hAi

hδA(t)i = hδAi = 0 hδA(t)δB∗_(t0_{)i = C}

AB(t − t0) (2.4)

• Consideriamo il comportamento di CAB(t) rispetto alla trasformazione di

inversione temporale t → −t, o ©rN_{, p}Nª _→©_rN_{, −p}Nª_{. Siano ²}

A,B = ±1

le parit`a delle variabili A, B sotto inversione temporale. Allora CAB(t) = ²A²BCAB(−t)

e ancora

CAB(t) = CBA∗ (−t)

quindi

(13)

In particolare quest’ultima relazione se B = A conduce a

CAA(t) = CAA∗ (t) = CAA(−t) (2.5)

e quindi l’autocorrelazione di una variabile `e sempre reale ed `e una funzione pari del tempo.

• Dalla disuguaglianza di Cauchy-Schwartz discende l’importante propriet`a |CAB(t)| ≤

p

CAA(0)CBB(0)

per cui se A = B

|CAA(t)| ≤ CAA(0) (2.6)

ed `e per questo che spesso si ragiona in termini delle quantit`a ΦA(t) =

CAA(t)/CAA(0) dette correlatori.

• Mediante la scrittura dei valor medi come integrali temporali `e possibile derivare una importante propriet`a delle correlazioni rispetto alla derivata

temporale _D B∗(0) ˙A(t) E = − D ˙ B∗(0)A(t) E che conduce ad esempio alla propriet`a

D

B∗_{(0) ¨}_A(t)E_{= −}D_B_˙∗_{(0) ˙}_A(t)E

Se CAA(t) `e definita come da (2.3), risulta allora possibile definire la sua

trasfor-mata di Fourier temporale CAA(ω), nonch´e la sua trasformata di Laplace ˜CAA(z).

In particolare lo spettro della autocorrelazione di A sar`a una funzione reale e pari di ω, e sar`a esprimibile in termini di trasformata di Laplace da

CAA(ω) =

1

πRe ˜CAA(z = iω) (2.7)

Veniamo alle variabili che avevamo anticipato essere quelle che giocano un ruolo di rilievo nella presente trattazione; in particolare prendiamo la funzione di autocorrelazione della densit`a nello spazio reciproco

F (Q, t) = hρ(Q, t)ρ∗_{(Q, 0)i} _(2.8)

questa si chiama funzione intermedia di scattering, e il suo valore iniziale `e il fattore di struttura statico

S(Q) =|ρ(Q, 0)|2® (2.9)

(14)

Lo spettro della funzione intermedia di scattering, ossia la sua trasformata di Fourier, si chiama fattore di struttura dinamico

S(Q, ω) = Z _+∞

−∞

dte−iωtF (Q, t) (2.10)

ed `e dato in termini della trasformata di Laplace della funzione intermedia di scattering da

S(Q, ω) = 1

πRe ˜F (Q, z = iω) (2.11)

Il fattore di struttura dinamico è come vedremo nel cap.3 ,la grandezza diret-tamente accessibile a un esperimento di diffusione di raggi X o di neutroni, ed è per questo motivo che faremo sempre riferimento nel seguito alla correlazione della densità come all’obbiettivo dei nostri sforzi di indagine della dinamica di un liquido semplice. In questa ottica risulta evidente che il fattore di struttura statico è la quantità accessibile mediante un esperimento di diffrazione di una sonda con momento Q (neutroni, fotoni) sul sistema.

Esaminiamo invece l’autocorrelazione della corrente longitudinale Jl_{(Q, t) =}

ˆ

Q · J(Q, t), definita come la componente lungo ˆQ (il versore di Q) della densit`a di momento J(Q, t) gi`a introdotta.

Cl_{(Q, t) =}D_{Q · J}_ˆ ∗_{(Q, 0) ˆ}_{Q · J(Q, t)}E

In generale la corrente e la densit`a sono legate da una equazione di continuit`a, che esprime la conservazione locale del numero di particelle

∂ρ(r, t)

∂t + ∇ · J(r, t) = 0 (2.12)

portandoci in trasformata di Fourier spaziale questa equazione si scrive ˙ρ(Q, t) + iQ · J(Q, t) = 0

e allora l’autocorrelazione della corrente longitudinale diventa Cl(Q, t) = 1 Q2 h ˙ρ ∗_{(Q, 0) ˙ρ(Q, t)i =} = − 1 Q2 hρ ∗_{(Q, 0)¨}_{ρ(Q, t)i =} 1 Q2F (Q, t)¨ (2.13)

se passiamo poi in trasformata di Laplace ˜ Cl_{(Q, z) =} z2 Q2F (Q, z) −˜ z Q2S(Q) da cui, mediante la (2.7): Cl_{(Q, ω) =} ω2 Q2S(Q, ω) (2.14)

(15)

Nel prossimo paragrafo ci dedicheremo al calcolo delle funzioni di correlazione qui introdotte in merito a un sistema particolare, un liquido semplice monoatomi-co, limitandoci in prima istanza al loro comportamento a Q e ω piccoli, ossia nel limite idrodinamico (specificheremo cosa intendiamo per “piccoli”), ed estendendo successivamente i risultati trovati a una pi`u ampia regione di momento ed ener-gia. Solo nel paragrafo 2.4 tratteremo il caso formalmente pi`u complicato delle correlazioni in un liquido biatomico.

2.2 Modi longitudinali idrodinamici: diversi

for-malismi, stessa fisica

La presente sezione verrà dedicata all’indagine teorica delle fluttuazioni idrodi-namiche in un liquido semplice monoatomico, vale a dire allo studio della risposta di un fluido semplice alla perturbazione introdotta da una sonda esterna nel limite di lunghezze d’onda molto maggiori della distanza interatomica tipica e frequenze molto minori dell’inverso del tempo tipico delle collisioni interatomiche, concen-trando la nostra attenzione sui gradi di libertà rilevanti dal punto di vista di un esperimento di scattering anelastico. Inizieremo facendo riferimento allo scattering nella regione del visibile (scattering di Brillouin), per cui le restrizioni ipotizzate sulla lunghezza d’onda e la frequenza della sonda, e il fatto che una tale tecnica di indagine non sia attuabile trattando di metalli liquidi non sono rilevanti ai fini della nostra trattazione, che deve porre le basi per la successiva estensione dei risultati dell’idrodinamica nella regione mesoscopica, dove le lunghezze d’onda ar-rivano ad essere confrontabili con le distanze tipiche fra i costituenti microscopici. L’informazione che riusciamo a ricavare dal nostro esperimento riguarda il com-portamento della funzione di autocorrelazione della densità, per mezzo del fattore di struttura dinamico che, come mostreremo nel capitolo 3, è la quantità diret-tamente accessibile sperimentalmente. Questo è il motivo per cui ci occuperemo delle fluttuazioni longitudinali idrodinamiche, ovvero, come chiariremo nel seguito, le fluttuazioni nel set di variabili dinamiche accoppiate con la densità nel limite di grandi lunghezze d’onda e piccole frequenze, e responsabili delle caratteristiche principali di uno spettro Raileigh-Brillouin.

Introdurremo tre formalismi differenti e largamente utilizzati capaci di de-scrivere le fluttuazioni longitudinali idrodinamiche. Mostrare l’equivalenza fra questi, derivando le relazioni che intercorrono fra i parametri coinvolti nelle diverse rappresentazioni, costituisce una prima parte di questo lavoro:

• i) L’idrodinamica linearizzata che fornisce una soluzione valida nel limite del continuo, e muove dalla forma delle equazioni fenomenologiche della mecca-nica macroscopica dei fluidi. I parametri coinvolti nell’espressione della fun-zione intermedia di scattering sono quantit`a termodinamiche e coefficienti di trasporto.

(16)

• ii) Il formalismo della funzione di memoria del secondo ordine, che deriva dal quadro teorico dell’equazione di Langevin generalizzata, e si presta all’esten-sione dell’idrodinamica semplice alla regione di piccole lunghezze d’onda e grandi frequenze. La quantit`a centrale in questo approccio `e la funzione di memoria del secondo ordine, che rende conto dei fenomeni di rilassamento rilevanti che influenzano la dinamica collettiva longitudinale. I parametri rilevanti in questo approccio sono le ampiezze e i tempi caratteristici dei diversi canali di decadimento della funzione di memoria.

• iii) Il metodo dei modi collettivi generalizzati (GCM), derivato anch’esso nel contesto del formalismo dell’equazione di Langevin generalizzata, e capace di una estensione nella regione dei grandi vettori d’onda. Il ruolo fonda-mentale in questo approccio `e giocato dalle variabili dinamiche scelte per la descrizione dei modi collettivi, mentre il ruolo di parametri `e assegnato ai valori iniziali e agli integrali nel tempo delle funzioni di correlazione del set di variabili scelto.

2.2.1 Idrodinamica lineare e modi longitudinali

Deriveremo nel presente paragrafo le equazioni dell’idrodinamica lineare con l’in-tento di richiamare lo schema teorico tracciato con maggiore profondit`a ad esempio in [18, 3, 2].

Le variabili fondamentali nel contesto della meccanica dei fluidi sono le densità conservate: la densità numero, la densità di corrente, e la densità di energia. Le leggi di conservazione scritte per le densità nella forma di equazioni di continuità costituiscono il punto di partenza per costruire un sistema di equazioni, la cui chiusura è ottenuta per mezzo di relazioni fenomenologiche. La risposta del sis-tema fluido a piccole perturbazioni esterne è descritta in termini delle fluttuazioni attorno al valor medio delle densità, una volta che sia postulato l’equlibrio ter-modinamico locale, e un set di equazioni che governano dette fluttuazioni può essere derivato dal precedente mediante linearizzazione del sistema.

Se ρ(r, t) è la densità numero locale, J(r, t) è la densità di corrente, e e(r, t) è la densità di energia, le equazioni di continuità, in termini delle densità di corrente associate a ciascuna variabile si scrivono nella forma:

˙ρ(r, t) + ∇ · J(r, t) = 0 (2.15)

˙J(r, t) + ∇ · ˆσ(r, t) = 0 (2.16)

˙e(r, t) + ∇ · Je_{(r, t) = 0} _(2.17)

dove abbiamo definito il flusso di momento ˆσ(r, t), o tensore degli stress, e il flusso di energia Je_{(r, t).}

`

E evidente che abbiamo bisogno di altre due equazioni per risolvere il nostro sistema, esprimendo ˆσ(Q, t) e Je_{(Q, t) in termini di ρ(Q, t), J(Q, t), e(Q, t), vale}

(17)

a dire due relazioni di chiusura. L’equazione che introduciamo per prima concerne la definizione di ˆσ.

La variazione per unit`a di tempo della densit`a di momento dipende dalla forza che agisce sull’elemento di volume, dovuta all’azione del mezzo circostante. Dalla meccanica questa azione risulta in due contributi per un mezzo isotropo, uno scalare dovuto alla pressione idrostatica, e uno dovuto allo shear e alla deformazione dilatazionale.

Sia V un volume fissato ad arbitrio e dS un elemento della superficie S che delimita V . La forza che agisce su dS pu`o essere espressa come dF = ˆσ · dS, dove ˆ

σ `e un tensore simmetrico e, se ˆn `e il versore normale all’elemento di superficie allora1

dFα =

X

β

σαβ(r, t)nβdS (2.18)

Il tasso di variazione della forza agente su V si scrive, se m è la massa di una particella dF dt = m Z V ˙ J(r, t)d3r = −m Z S ˆ σ(r, t) · dS = −m Z V ∇ · ˆσ(r, t)d3r (2.19) che è l’equazione di continuità (2.16).

A questo punto risulta chiaro che l’elemento sulla diagonale σαα del tensore

degli stress produce quella componente della forza dF⊥ che agisce normalmente

all’elemento di superficie dS, e possiamo assegnere alla pressione idrostatica un contributo a questi elementi. Quindi separiamo il contributo della pressione scrivendo

σαβ = −P (r, t)δαβ + ταβ (2.20)

Gli elementi fuori dalla diagonale σαβ (α 6= β) rappresentano componenti della

forza per unità di superficie che agiscono in direzione parallela ai rispettivi piani di riferimento (αβ). Tali componenti del tensore degli stress sono legate ad effetti di tipo viscoso. Si trova sperimentalmente che il flusso dipende dal gradiente della velocità ∇αvβ, che però non è un tensore simmetrico. In realtà due contributi

simmetrici distinti si possono far derivare dal gradiente di un campo vettoriale ∇αvβ, una parte scalare data dalla divergenza del campo vettoriale, e una parte

simmetrica costruita dal tensore simmetrizzato ∇αvβ+ ∇βvα

Quest’ultimo contributo, riscritto in modo da avere traccia nulla, rende conto della forza dovuta alla viscosit`a di shear νs, mentre il primo di quella componente

che deriva dalla viscosit`a di bulk νB.

1_{Si potrebbe ipotizzare una legge pi`}_{u generale per lo stress, che esprima la forza in termini di}

una funzione vettoriale generica di ˆn, dFα= σ(ˆn)αdS, o per mezzo di un tensore non simmetrico.

Tuttavia la legge di conservazione del momento angolare implica, come si pu`o facilmente provare,

la validità della (2.18) e della proprietà di simmetria di ˆσ. Di pi`u: il momento angolare è

automaticamente conservato una volta che ˆσ `e un tensore simmetrico. Questo risultato `e noto

(18)

Il termine di viscosit`a di bulk tiene effettivamente considerazione della parte dissipativa della risposta di un fluido a una compressione. Infatti `e un termine scalare, e quindi contribuisce in modo simile a quanto detto per la pressione, ma genera una forza che si oppone alla creazione di una divergenza di v, quindi a una variazione del volume.

Tutti i contributi che abbiamo visto possono essere sintetizzati come segue σα,β(r, t) = δα,βP(r, t) − νS µ ∂vα(r, t) ∂rβ + ∂vβ(r, t) ∂rα ¶ + δα,β µ 2 3νS − νB ¶ ∇ · v(r, t) (2.21) che `e la prima delle relazioni costitutive di chiusura, e rappresenta in sostanza la definizione della pressione idrostatica P(r, t) e delle viscosit`a di shear e di bulk.

La seconda equazione costitutiva riguarda la variazione nell’unità di tempo della densità di energia. Nel volume fissato V l’energia può cambiare per con-vezione, ma anche a causa del lavoro compiuto dalla porzione di fluido esterno a V , o anche per opera della diffusione del calore.

La variazione di energia in V dovuta alla convezione è data dall’integrale di superficie su S dei singoli contributi dovuti alla quantità di energia dell’elemento di volume che attraversa dS nell’unità di tempo: −e(r, t)v(r, t) · dS.

Il lavoro compiuto su V nell’unit`a di tempo `e l’integrale di superficie dei con-tributi infinitesimi dagli elementi di superficie dS, ciascuno dei quali apporta v · dF = v · ˆσ · dS.

La diffusione del calore è governata dalla legge di Fourier, secondo la quale una quantità di calore fluisce dalle regioni di temperatura maggiore a quelle di temperatura minore, ed è pari a una costante del mezzo, la diffusività termica k, moltiplicata per il gradiente di temperatura : Θ(r, t) = −k∇T (r, t).

Considerando la variazione netta dell’energia in V come la derivata temporale dell’integrale di volume della densit`a di energia, come al solito si trova la corrente di energia da sostituire nell’equazione (2.17)

Je_{(r, t) = e(r, t)v(r, t) − k∇T (r, t) − v(r, t) · ˆ}_{σ(r, t)} _(2.22)

Sostituendo la (2.21) nell’ultima espressione e trascurando termini quadratici nella velocità, che tengono conto degli effetti termici della viscosità, Je_{(r, t) si può}

esprimere in termini della densit`a di entalpia h(r, t) = e(r, t) + P(r, t)

Je(r, t) = hv(r, t) − k∇T (r, t) (2.23) che `e la seconda relazione costitutiva.

Quindi, invocando l’ipotesi di equilibrio termodinamico locale, le deviazioni dal loro valor medio delle variabili termodinamiche locali possono esprimersi mediante un set di variabili indipendenti, come lo sono temperatura e densit`a, e le equazioni di stato termodinamiche possono essere usate per espandere P (r, t) ed e(r, t) al prim’ordine nelle fluttuazioni di ρ e T .

(19)

δP (r, t) = ³ ∂P ∂ρ ´ T δρ(r, t) + ¡_∂P ∂T ¢ ρδT (r, t) δΘ(r, t) = T V ³ ∂S ∂ρ ´ T δρ(r, t) + T V ¡_∂S ∂T ¢ ρδT (r, t) = = −T ρ ¡_∂P ∂T ¢ ρδρ(r, t) + ρCVδT (r, t) (2.24)

dove la densità di energia termica Θ(r, t) si può esprimere in termini della densità di energia e(r, t) per mezzo di argomenti di termodinamica.

Qui CV `e il calore specifico a volume costante, e

³ ∂P ∂ρ ´ T = c2 S γm ¡_∂P ∂T ¢ ρ = − ³ ∂P ∂ρ ´ T ¡_∂ρ ∂T ¢ P = c2 S γαρ (2.25) γ = CP

CV è il rapporto dei calori specifici, cS è la velocità adiabatica del suono,

α `e il coefficiente di espansione termica e m `e la massa di una particella.

Sfruttando l’equazione di stato (2.24) e la seconda relazione costitutiva (2.23), possiamo scrivere una nuova equazione di continuit`a per la temperatura, al posto dell’equazione (2.17) valida per l’energia

˙

T (r, t) − (γ − 1)

αρ ˙ρ(r, t) − γDT∇

2_{T (r, t) = 0} _(2.26)

Dove DT = _ρCk_P `e il coefficiente di diffusione termica.

Le equazioni idrodinamiche si semplificano sostanzialmente ritenendo solo i termini all’ordine dominante nelle deviazioni dal valor medio delle variabili in-dipendenti, e facendo la trasformata doppia di Fourier-Laplace nelle coordinate di spazio e tempo ˜ Aq(z) = Z _∞ 0 dte−zt Z _+∞ −∞ eiQ·rδA(r, t) (2.27)

(A = ρ, J, T). Come ultimo passaggio si separano le parti longitudinale e trasver-sale di ˜Jq con la conseguente scelta di Q lungo l’asse z. Tutti i passaggi che

abbi-amo descritto risultano alla fine in un sistema lineare di equazioni per le densit`a nella rappresentazione di Fourier-Laplace, e la relativa matrice dei coefficienti `e nota come matrice idrodinamica.

Si trova che la matrice idrodinamica T `e diagonale a blocchi, le fluttuazioni nella parte trasversale della corrente risultano completamente disaccoppiate dalle fluttuazioni nelle altre variabili: densit`a, temperatura e corrente longitudinale (d’ora in avanti Jl_{) in termini delle quali il nostro sistema di equazioni si scrive}

(20)

  _γ−1z_c2 iQ 0 SiQ [z + νQ2] γ−1αc2SiQ 0 α−1_{(γ − 1)iQ [z + γD} TQ2]     _Jρ˜˜lq_q(z)_(z) ˜ Tq(z)   =   _Jρql q Tq   _(2.28)

Notiamo che nessuna approssimazione, a parte evidentemente la linearizzazione delle equazioni, `e stata fatta nello scrivere l’equazione (2.28), e la dipendenza da Q degli elementi della matrice idrodinamica deriva dalle propriet`a della trasformata di Fourier (2.27) quando agisce su un sistema di equazioni differenziali.

Come possiamo vedere dalla (2.28) le fluttuazioni di ρ, Jl _{e T , non sono}

in-dipendenti e possiamo parlare di modi longitudinali riferendoci ai meccanismi di decadimento delle fluttuazioni di queste tre variabili.

Infine definiamo i vettori F(Q, t) =¡ρ(Q, t), Jl_{(Q, t), T (Q, t)}¢_{e il suo}

trasfor-mato secondo Laplace ˜F(Q, z) = ³

˜

ρ(Q, z), ˜Jl_{(Q, z), ˜}_{T (Q, z)}´_{che hanno per}

com-ponenti le variabili locali come funzioni del tempo, e le loro trasformate di Laplace. Dato che la (2.28) `e una equazione lineare algebrica con matrice dei coefficienti T (Q, z), risulta immediato esprimere la soluzione per gli elementi di ˜F(Q, z) nella forma ˜ Fi(Q, z) = [detT (Q, z)]−1 X j Pij(Q, z)Fj(Q, t = 0) (2.29)

dove le Pij sono funzioni algebriche (sono gli elementi della matrice dei minori

della T (Q, z)) , e allora la matrice delle funzioni di correlazione delle variabili indipendenti si pu`o calcolare da:

D ˜ Fi(Q, z)Fl∗(Q) E = [detT (Q, z)]−1X j Pij(Q, z) hFj(Q)Fl∗(Q)i (2.30)

La funzione intermedia di scattering relativa alla densit`a si ottiene quindi in maniera semplice dalla (2.28) essendo in realt`a ˜F11(Q, z):

ρq(z)ρ∗q ® ρqρ∗q ® = F (Q, z) S(Q) = z2 _{+ Az + B} z3_{+ Az}2_{+ Cz + D} (2.31) dove A = γDTQ2+ νQ2 B = γDTνQ4+ γ−1_γ c2SQ2 C = γDTνQ4+ c2SQ2 D = DTc2SQ4 (2.32)

Il fattore di struttura dinamico S(Q, ω) si trova secondo la relazione (2.11). In un esperimento tipico di scattering nel visibile Q ∼ 10−4_nm−1 _{mentre in un}

liquido semplice cS ∼ 1nm/ps. Solitamente nel trattare il limite idrodinamico

(21)

scattering ˜F (Q, z), valide se sono piccole le quantit`a DTQ/cS e νQ/cS. In questo

caso i poli della (2.31) si scrivono al prim’ordine nelle quantit`a piccole (ossia fino all’ordine O(Q2_{)) [3]}

z0 = −DTQ2

z± = ±icSQ − 1₂[ν + (γ − 1)DT] (2.33)

Allora il fattore di struttura dinamico `e ottenibile mediante la (2.11) e pu`o essere portato con un po’ di algebra nella forma

S(Q, ω) = NKBT 2πV kT γ · 2(γ − 1)DTQ2 ω2_{+ D}2 TQ4 + + ΓQ 2 (ω + cSQ)2+ Γ2Q4 + ΓQ 2 (ω − cSQ)2 + Γ2Q4 + (2.34) + [Γ + DT(γ − 1)] Q cS µ ω + cSQ (ω + cSQ)2+ Γ2Q4 − ω − cSQ (ω − cSQ)2+ Γ2Q4 ¶¸ dove Γ = 1 2(ν + DT(γ − 1)) e kT = −V1 ¡_∂V ∂P ¢ T `e la compressibilit`a isoterma.

Questa espressione rappresenta la somma di una lorenziana centrata in ω = 0, ed associata perciò alla risposta elastica del sistema alla perturbazione esterna, più due lorenziane centrate in ω = ±cSQ con FWHM pari a ΓQ2, che è il coefficiente

di attenuazione del suono e riceve un contributo dalla viscosit`a longitudinale e uno (piccolo se γ ∼ 1) dai processi di diffusivit`a termica. Gli ultimi due addendi nella (2.34) costituiscono il cosiddetto termine asimmetrico.

L’aprossimazione fatta in Q consente di scrivere il fattore di struttura dinamico nella forma semplice (2.34). La forma esatta dei poli della ˜F (Q, z), nonch´e quella della S(Q, ω) verranno presi in esame nella sezione 2.3 in cui ci occuperemo delle problematiche inerenti le diverse definizioni della velocit`a del suono idrodinamica che vengono spesso date in letteratura, a volte senza troppe distinzioni.

2.2.2 L’equazione di Langevin generalizzata

Introdurremo in questa sezione le basi di un formalismo teorico sviluppato da Zwanzig e Mori [16] con un approccio fondato sulla meccanica statistica, che cos-tituisce il punto di partenza per una estensione dei risultati ottenuti nello studio dell’idrodinamica alla regione di vettori d’onda finiti mediante l’introduzione di una dipendenza dei coefficienti di trasporto dal vettore d’onda e dalla frequen-za (idrodinamica generalizfrequen-zata). Mediante tale formalismo diverse funzioni di correlazione temporali possono essere calcolate opportunamente. Presenteremo successivamente due tecniche di approssimazione diverse frequentemente utiliz-zate in letteratura, che applicheremo nello specifico allo studio delle funzioni di correlazione idrodinamiche, giungendo a mostrare in definitiva l’equivalenza di entrambi i formalismi a quello introdotto nella sezione precedente.

(22)

Richiamiamo dunque i risultati fondamentali lasciando da parte i dettagli della derivazione che possono essere trovati in [1, 2, 3]. Consideriamo una variabile dinamica arbitraria, per esempio – ma non necessariamente – una delle densit`a (2.1). Nella trattazione idrodinamica abbiamo sfruttato le leggi di conservazione derivanti, in definitiva, dalle equazioni generali del moto per un continuo fluido. Ora il punto di partenza `e l’equazione del moto che governa l’evoluzione della variabile dinamica A nello spazio delle fasi, che si scrive

dA(t)

dt = {A, H}P

.

= iLA (2.35)

se H `e l’hamiltoniana del sistema in esame, {·}P denota le parentesi di Poisson, e

L, definito implicitamente dalla (2.35), `e l’operatore di Liouville.

Possiamo definire un prodotto scalare nello spazio delle variabili dinamiche, e per conseguenza un operatore di proiezione P che proietta una data variabile B(t) sul sottospazio generato da A, cio`e dal valore iniziale di A(t) in t = 0. Prendiamo come definizione del prodotto di due vettori A(t) e B(t) semplicemente la loro funzione di correlazione temporale hB(t)A∗_{i, in modo che l’azione di P `e}

PB(t)=. hB(t)A

∗_i

hAA∗_i A (2.36)

Q = 1 − P `e il proiettore sul sottospazio ortogonale ad A. Sfruttando il formalismo degli operatori di proiezione, insieme al formalismo dell’operatore di Liouville (2.35), `e possibile decomporre l’equazione del moto di A in due equazioni che governano l’evoluzione delle componenti di A(t) parallela e ortogonale ad A(0) [2, 1]. La prima di queste equazioni regola l’evoluzione della funzione di autocorrelazione di A(t) come appare chiaro dalla (2.36), e viene riportata di seguito, dove si pone C(t) = hA(t)A∗_i

˙ C(t) −iΩC(t) + Z _t 0 M(t − t0)C(t0)dt0 = 0 (2.37) R(t) = ei(QL)t_{Q ˙}_A M(t) = hR(t)R∗i hAA∗_i

R(t) è la cosiddetta forza random (non un forza nel senso fisico, a parte il caso in cui si scelga il momento come variabile A(t)), essa stessa una variabile dinamica, che rappresenta l’evoluzione, nel senso dell’operatore di Liouville proiettato QL, della componente ortogonale di ˙A. La sua correlazione temporale è la funzione di memoria M(t). La quantità Ω, con le dimensioni di una frequenza, è definita come Ω =< A ˙A∗ _{>< AA}∗ _>−1_{, ed è nulla nel presente caso per le proprietà delle}

funzioni di correlazione temporale.

La soluzione dell’equazione (2.37) risulta di facile espressione se riportata in trasformata di Laplace, in termini del valore iniziale C(0) e della trasformata

(23)

della funzione di memoria ˜M(Q, z), dove introduciamo anche la dipendenza dal momento scambiato

˜

C(Q, z) = C(Q, 0)

z + ˜M(Q, z) (2.38)

Come il formalismo presentato possa essere applicato al calcolo delle funzioni di correlazione idrodinemiche sar`a l’argomento delle prossime sezioni.

La funzione di memoria del secondo ordine e la soluzione idrodinamica In un primo approccio introduciamo una funzione di memoria del secondo ordine M(2)_{(Q, t), e quindi ci riferiremo alla funzione di memoria gi`a introdotta (2.37)}

come alla funzione di memoria del primo ordine M(1)_{(Q, t).}

Supponiamo di segliere una particolare variabile dinamica rilevante. Nel segui-to focalizzeremo la nostra attenzione sulla densità numero, una scelta conveniente se l’obiettivo è quello di descrivere i risultati di un esperimento di scattering anelas-tico (scattering Brillouin nel visibile, scattering anelasanelas-tico di neutroni o raggi X) essendo il fattore di struttura dinamico della densità – ovvero la funzione di auto-correlazione della densità nel dominio dei momenti e delle frequenze – la quantità accessibile sperimentalmente.

Sia F (Q, t) la funzione di autocorrelazione della densit`a nel dominio del tempo, mentre ˜F (Q, z) la sua trasformata di Laplace. Allora

˙

F (Q, t) + Z _t

0

M(1)_{(Q, t − t}0_{)F (Q, t}0_)dt0 _{= 0} _(2.39)

Il problema di risolvere l’equazione (2.39) si riduce al compito di derivare una espressione analitica di M(1)_{(Q, t), compito impossibile se intendiamo partire dalla}

definizione (2.37) di funzione di memoria in terminei della forza random.

In alternativa possiamo ricordarci che M(1)_{(Q, t) `e essa stessa una funzione}

di autocorrelazione, in tale prospettiva siamo in grado di applicare il formalismo gi`a introdotto per cercare di descrivere il suo comportamento per mezzo di una forza random del secondo ordine e una funzione di memoria del secondo ordine. Il processo pu`o essere iterato fino a un arbitrario ordine n, portando a scrivere una serie di equazioni concatenate tutte della stessa forma.

Per i nostri scopi presenti una espansione al second’ordine pu`o bastare, e si traduce in un sistema di due equazioni accoppiate, la(2.39), e

˙

M(1)(Q, t) + Z _t

0

M(2)(Q, t − t0)M(1)(Q, t0)dt0 = 0 (2.40) Passando in trasformata di Laplace entrambe le (2.39) e (2.40) hanno la stessa forma (2.38) in termini dei rispettivi valori iniziali, e in definitiva

˜ F (z) = F (Q, 0) z +_{z+ ˜}M˜_M1(Q,0)2_(Q,z) = S(Q) z + ω20 z+ ˜M2_(Q,z) (2.41)

(24)

dove ω2

0(Q) = M. (1)(Q, t = 0) `e facilmente riconoscibile come il momento

secondo in frequenza normalizzato della S(Q, ω) e S(Q) = F (Q, 0) `e il fattore di struttura statico. L’equazione (2.41) a sua volta come pu`o verificarsi facilmente corrisponde alla singola equazione integrodifferenziale del secondo ordine:

¨

F (Q, t) + ω₀2(Q)F (Q, t) + Z _t

0

M(2)(Q, t − t0) ˙F (Q, t0)dt0 = 0 (2.42) Il procedimento pu`o essere ripetuto agli ordini superiori esprimendo la ˜F (Q, z) nella forma di uno sviluppo in frazioni continue, con coefficienti dipendenti dai valori iniziali delle funzioni di memoria di ordine generico k, fino ad n, che poi sono legati ai momenti del fattore di struttura dinamico fino all’ordie n [1, 2].

Ci potremmo chiedere per quale ragione risulta utile introdurre una fun-zione memoria del secondo ordine e fermarci a questo punto, invece di tentare la soluzione direttamente della (2.37), o andare agli ordini successivi nello svilup-po, trovandoci invece ad affrontare il problema di trovare una espressione analitica per M(2)_.

Una risposta a questa domanda pu`o essere tentata analizzando la forma che assume la funzione di memoria del secondo ordine associata alla soluzione idrod-inamica esatta per la funzione di autocorrelazione della densit`a. Come vedremo la funzione di memoria del second’ordine “idrodinamica” ha una forma analitica semplice, cui corrisponde una interpretazione fisica diretta, e questo costituisce un punto di partenza estremamente utile se ci poniamo nella prospettiva di tentare una estensione della sua dipendenza funzionale allo scopo di trattare l’estensione dell’idrodinamica ad alti Q. Per questo motivo ci volgiamo ora al problema di trovare la forma di M(2)_{(Q, t) tale che, una volta sostituita nella (2.42), conduca}

alla funzione intermedia di scattering idrodinamica (2.31).

Il compito `e pi`u facile se lavoriamo in trasformata e uguagliamo le equazioni (2.41) e (2.31). ˜ F (Q,z) S(Q) = n z + ω02 z+ ˜M2_(Q,z) o₋₁ = n z+ ˜M(2)_(Q,z) z2_{+z ˜}_M2_(Q,z)+ω2 0 o = = z2+(γDTQ2+νQ2)z+(γDTνQ4+γ−1γ c2SQ2) z3_+(γD_T_Q2_+νQ2_)z2_+(γD_T_νQ4_+c2 SQ2)z+(DTc2SQ4) (2.43)

Questo ci conduce a identificare la funzione di memoria del second’ordine idrodinamica come [1, 2, 3] ˜ M(2)_{(Q, z) = νQ}2₊c2S(γ − 1) γ Q2 z + DTQ2 (2.44) che nel dominio del tempo si scrive

M(2)_{(Q, t) = 2νQ}2_{δ(t) +} c2SQ2

γ (γ − 1)e

(25)

Con questa scelta di M(2)_{(Q, t) si ottiene dunque l’idrodinamica semplice.}

L’espressione trovata è valida nel limite di piccoli Q, e la sua interpretazione è immediata. La funzione di memoria del second’ordine evidenzia i due processi rilevanti che regolano il decadimento della funzione di autocorrelazione della den-sità; uno, attivo su una scala di tempo dell’ordine di τth= _γD_T1_Q2 che rappresenta il canale di decadimento delle fluttuazioni termiche, e uno che agisce su scale di tempo molto più piccole di quelle tipicamente sondate nel limite idrodinamico, ascrivibile al rilassamento viscoso. La (2.45) si può facilmente generalizzare in-troducendo ulteriori appropriati canali di decadimento nella forma di contributi istantanei o esponenziali decrescenti con tempi caratteristici propri dei processi di rilassamento della dinamica microscopica del sistema. Diremo di più a questo riguardo nella sezione 2.2.2, tuttavia a questo punto vogliamo presentare un’altra estensione del formalismo dell’equazione di Langevin generalizzata, che ci fornirà uno strumento ulteriore per calcolare le funzioni di correlazione temporale, e fare-mo un confronto del risultato idrodinamico che ne conseguirà direttamente con l’equazione (2.45).

Il formalismo GCM

Anche in questo caso pu`o essere che siamo interessati al comportamento di una variabile rilevante, ma supponiamo di essere in grado di identificare l’insieme delle altre variabili dinamiche indipendenti che sono fortemente accoppiate alla prima, e che ne determinano i meccanismi di decadimento delle autocorrelazioni. Introduciamo una seconda estensione del formalismo discusso nella prima parte del paragrafo, e lo generalizziamo al caso multidimensionale [2, 20, 21, 22, 23].

Sia allora A un set di variabili dinamiche ordinate in un vettore A = {A1, A2,

. . . , An}; possiamo sempre costruire la matrice n×n delle funzioni di correlazione

F= [F. ij] = hAj(t)A∗ii e derivare l’equazione che ne regola l’evoluzione temporale

esattamente nello stesso modo che porta al risultato (2.37) [1] ˙F(t) − iΩ · F(t) +

Z _t

0

M(t − t0_{) · F(t}0_)dt0 _{= 0} _(2.46)

Si noti che ora Ωij =< AiA˙∗j >< AiA∗j >−1 `e una matrice con elementi non

nulli fuori dalla diagonale e non pu`o essere trascurata. Diamo la forma della trasformata di Laplace della (2.46)

˜ F(z) = h zI − iΩ + ˜M(z) i₋₁ F(0) (2.47) dove I `e l’identit`a.

La matrice delle memorie riassume il comportamento rilassamentale delle cor-relazioni temporali della forza random, a sua volta un vettore, ortogonale in ogni istante al set di grandezze A, e se A `e stato scelto in modo tale da comprendere tutte le variabili lente che si accoppiano a quella rilevante possiamo presumere che

(26)

ragionevolmente M decada molto pi`u velocemente delle correlazioni nelle variabili di interesse. Non `e dunque cos`ı arbitrario invocare una approssimazione marko-viana per la matrice delle memorie, vale a dire rappresentare gli elementi di M come funzioni istantanee del tempo, o in trasformata di Laplace funzioni costanti in z.

Allo scopo definiamo la matrice idrodinamica T(Q) come segue

T(Q)= −iΩ(Q) + ˜. M(Q, z = 0) (2.48)

dove gli elementi della matrice delle funzioni di memoria sono rappresentati dal loro valore al tempo zero, per una funzione istantanea del tempo. L’approssi-mazione markoviana risulta dunque nella seguente equazione per la matrice delle correlazioni

˜

F(Q, z) = [zI + T(Q)]−1F(Q, 0) (2.49) Questa equazione ha la stessa forma di quella che governa le fluttuazioni idrodinamiche, la (2.28), a patto di definire T (Q, z) = zI + T(Q).

Possiamo adesso formulare una generalizzazione del concetto di dispersione dato in termini dei poli dell’inversa di T2_{. L’equazione DetT = 0, non `e altro che}

l’equazione agli autovalori per T nella variabile ζ = −z, e la parte immaginaria dei suoi m<n autovalori non reali, come funzione di Q, definisce m relazioni di dispersione ω(k)_{(Q), k = 1,. . . , m. In generale, includendo anche i modi puramente}

rilassamentali, ossia gli autovalori puramente reali, possiamo parlare di n modi collettivi generalizzati [20].

Il problema della risoluzione dell’equazione (2.49), ossia quello di trovare la dipendenza esplicita da z degli elementi di ˜F(z) in approssimazione markoviana, `e di facile soluzione. Siano zα gli autovalori di T, e Xiα la matrice la cui i-esima

colonna `e l’autovettore α-simo di T

n

X

j

Tij(Q)Xjα = zα(Q)Xiα (2.50)

allora X `e la matrice del cambiamento di base da A agli autovettori di T. Siano ˜

F0_{(z) e F}0 _{le matrici che rappresentano ˜}_{F(z) e F nel nuovo sistema di riferimento,}

mentre T0_{`e ovviamente una matrice diagonale con elementi δ}

ijzj(Q). Nella nuova

rappresentazione la (2.49) ha una soluzione immediata ˜ F0 ij(Q, z) = F0 ij z + zi(Q) (2.51)

2_{Come si vedr`a con maggior dettaglio nel §2.3 una definizione della dispersione ω = ω(Q)}

frequentemente adottata in letteratura `e data dalla parte immaginaria dei poli della funzione intermedia di scattering ω(Q) = Im[z(Q)]. Qui le z(Q), come si vede dalla (2.30) sono le radici dell’equazione det T (Q, z) = 0, per cui vengono chiamate anche poli della matrice idrodinamica. Questi poli sono tre nel limite idrodinamico, uno reale e due complessi coniugati, e quindi nel limite idrodinamico la relazione di dispersione ω = ω(Q) `e univoca.

(27)

ma ˜F(Q, z) = X ˜F0_X−1_{, e} ˜ Fij(Q, z) = X αk XiαF˜αk0 £ X−1¤_kj =X αk Xiα P lm[X−1]αlFlmXmk z + zα £ X−1¤_kj = = X α Ã X l Xiα £ X−1¤ αlFlj ! 1 z + zα(Q) = = X α Gα ij(Q) z + zα(Q) (2.52) dove abbiamo definito le ampiezze che descrivono i contributi di ciascun modo zα(Q) [20]. Gα_ij(Q) = n X l=1 Xiα £ X−1¤_αlFlj (2.53)

Nel dominio del tempo la forma markoviana della matrice delle correlazioni `e una combinazione lineare con pesi Gα_{di n termini esponenziali, ciascuno associato}

all’α-simo modo collettivo zα(Q)

Fij(Q, t) = n X α=1 Gα ij(Q)e−zα(Q)t (2.54)

La forma della matrice idrodinamica nella sua approssimazione markoviana si pu`o ottenere fissando Fij(Q, t = 0) =

AiA∗j

®

come la forma corretta delle funzioni di correlazione esatte al tempo zero, e facendo lo stesso per le quantit`a

˜

Fij(Q, z = 0) =

R_∞

0 Fij(Q, t)dt. Quindi dall’equazione (2.49) con z=0 si trova

T(Q) = F(Q, t = 0) · h ˜ F(Q, z = 0) i₋₁ (2.55) Il formalismo GCM e il calcolo dei modi longitudinali idrodinamici Il formalismo GCM appena introdotto `e ampiamente utilizzato in letteratura, spesso con l’obiettivo di guidare l’interpretazione di esperimenti di Dinamica Molecolare (MD) e chiarire il quadro dei processi collettivi dominanti che inter-vengono nel sistema in esame, in un vasto intervallo di vettori d’onda e frequenze, compreso il limite idrodinamico [24, 21, 25, 20, 26]. Scelto un set di variabili di-namiche `e sempre possibile a partire dai risultati di una simulazione MD costruire le funzioni di correlazione i cui valori iniziali sono gli elementi di F(Q, 0) e i cui integrali nel tempo sono gli elementi di ˜F(Q, 0).

Tuttavia non `e stata mai mostrata con un calcolo diretto l’equivalenza, nel lim-ite idrodinamico, dei risultati cui conduce il formalismo GCM con quelli ottenuti

(28)

nell’ambito dei formalismi già introdotti in 2.2.1 e 2.2.2. Questo sarà lo scopo del-la presente sezione. Ci proponiamo dunque di calcodel-lare le funzioni di corredel-lazione idrodinamiche nell’approssimazione markoviana e per tale scopo una scelta ra-gionevole di A può essere il set delle densità conservate A = {ρ, J, e}: densità numero, corrente longitudinale ed energia. Una scelta alternativa ma più conve-niente dal punto di vista algebrico è quella di definire la variabile temperatura locale come combinazione lineare di energia e densità: h(Q, t) = e(Q, t) − hρe_hρρ∗∗i_iρ(Q, t).

Per prima cosa abbiamo bisogno di una forma per la matrice delle correlazioni al tempo zero F(Q, 0), che per`o `e facile da scrivere essendo Jl

q ortogonale sia a

ρq che ad eq in ragione della loro diversa simmetria sotto inversione temporale,

mentre ρq e hq sono ortogonali per costruzione

F(Q, t = 0) =   hρρ ∗_i ₀ ₀ 0 hJJ∗_i ₀ 0 0 hhh∗_i   _(2.56)

Poi dobbiamo calcolare la forma di ˜F(Q, 0), per la qual cosa possiamo us-are, dove possibile, l’equazione di continuit`a che lega la densit`a alla corrente longitudinale, per esempio

˜ FρJ(Q, z = 0) = R_∞ 0 dt ρJl∗_(t)®_{= −}i Q R_∞ 0 dt hρ ˙ρ∗(t)i = = −i Qhρ(0) [ρ∗(∞) − ρ∗(0)]i = Qi hρρ∗i (2.57)

Quando questo non `e possibile definiamo le quantit`a, con le dimensioni di tempi τij(Q) = 1 Fij(Q, 0) Z _∞ 0 Fij(Q, t)dt (2.58)

che sono espresse in termini di funzioni di correlazione esatte. La forma di ˜F si scrive dunque ˜ F(Q, z = 0) =   τρρhρρ∗i _Qi hρρ∗i (τρe− τρρ) hρe∗i i Qhρρ∗i 0 0 (τρe− τρρ) hρe∗i 0 τhhhhh∗i   _(2.59)

La matrice idrodinamica si ottiene infine dalla (2.55). Per rendere la notazione un po’ pi`u compatta notiamo che hJJ∗_{i Q}2_{/ hρρ}∗_{i = K}

BT Q2/mS(Q) = ω02 `e il

momento secondo in frequenza del fattore di struttura dinamico, e ne possiamo esplicitare la dipendenza da Q nel limite idrodinamico notando che in tale limite KBT /mS(Q → 0) = c2T `e la velocit`a del suono isoterma. Poniamo pertanto

hJJ∗_i

hρρ∗_i Q→0

−→ γ−1_c2

(29)

per cui in ultima istanza la matrice idrodinamica si pu`o scrivete nella forma T(Q) =      0 −iQ 0 −iQγ−1_c2 S γ−1c2SQ2 h τρρ−(τρe−τρρ) 2 τhh · hρh∗_i2 hρρ∗_ihhh∗_i i iQγ−1_c2 S (τρe−τρρ) τhh hρe∗_i hhh∗_i 0 iQ(τρe−τρρ) τhh hρe∗_i hρρ∗_i _τ_hh1      (2.61) Riduciamo il problema di mostrare l’equivalenza del risultato ottenuto con entrambi quelli derivati nelle sezioni precedenti fornendo l’espressione della fun-zione di memoria del secondo ordine corrispondente alla matrice delle memorie del primo ordine nelle variabili conservate in approssimazione markoviana; questo vuol dire in sostanza che scriviamo quella funzione di Q e t che sostituita nella (2.42) fornisce la corretta espressone per la funzione intermedia di scattering che si ottiene dalla soluzione (2.52) a partire dalla matrice (2.61),

M(2) m (Q, t) = ω02 Ã τρρ− (τρe− τρρ)2 τhh · hρe∗i 2 hρρ∗_{i hhh}∗_i ! δ(t) + +ω2 0 (τρe− τρρ)2 τhh · hρe∗i 2 hρρ∗_{i hhh}∗_i· µ e−t/τhh τhh ¶ (2.62) che corrisponde come si vede alla forma idrodinamica con un contributo espo-nenziale e uno istantaneo, e deve essere comparata con la (2.45) per stabilire un legame tra quantit`a termodinamiche e coefficienti di trasporto da una parte, e integrali temporali e valori iniziali di funzioni di correlazione dall’altra.

Un confronto diretto mostra che τhh= _hhh1∗_i R_∞ 0 hh(t)h∗i dt = 1 γDTQ2 τρρ = _hρρ1∗_i R_∞ 0 hρ(t)ρ∗i dt = γν c2 S + (γ − 1)τhh τρe = _hρe1∗_i R_∞ 0 hρ(t)e∗i dt = ¯ ¯ ¯ ¯ ³ (γ − 1)hρρ_hρe∗ihhh∗_i2∗i ´1 2 · τhh− τρρ ¯ ¯ ¯ ¯ (2.63)

Il risultato trovato, ovvero la derivazione del corretto comportamento idro-dinamico della autocorrelazione temporale della densit`a in una approssimazione markoviana implica che la matrice delle memorie del primo ordine, scritta nel set di variabili A, assume esattamente la forma markoviana nel limite di gran-di lunghezze d’onda. Questa propriet`a deriva dalla nostra scelta gran-di tre variabili quasi conservate, il che vuol dire variabili che approcciano un regime stazionario nel limite di Q → 0.

(30)

L’equazione di continuit`a per Ai ∈ A si scrive, nel dominio dei momenti

˙

Ai(Q, t) = iQ · Ji(Q, t) (2.64)

Ai si avvicina al limite di una variabile che decade lentamente nel tempo non

appena Q → 0, mentre gli elementi Mij(Q, t) della matrice delle memorie, che

possono riguardarsi come funzioni di correlazione temporale, conservano le pro-prietà di decadimento delle variabili non conservate e la loro variazione per unità di tempo è molto più grande di quella delle Ai, e si spiega come una descrizione

markoviana di Mij diventa esatta quando Q → 0.

Generalizzare l’idrodinamica: alcuni approcci significativi

Nel presente paragrafo abbiamo visto come tutti i risultati dell’idrodinamica lin-earizzata derivati considerando un fluido come un continuo possono essere formal-mente dedotti in un approccio microscopico basato sul formalismo della funzione di memoria. Tale successo, come abbiamo messo in evidenza deriva in ultima analisi dal carattere lento delle variabili idrodinamiche nel limite di Q piccoli, cosa che spiega anche il successo dell’approssimazione markoviana. All’aumentare di Q e ω al di là del limite idrodinamico la validità delle equazioni dell’idrodinam-ica linearizzata (o equazioni di Navier-Stokes linearizzate) comincia a diventare sospetta; infatti difficilmente si può considerare un fluido come un continuo se le scale di lunghezza2π

Q diventano confrontabili con le distanze interatomiche tipiche,

e d’altra parte l’evoluzione delle variabili dinamiche che si conservano nel limite idrodinamico diventa sempre più rapida. In queste condizioni non si può più par-lare di idrodinamica, però si può provare a ritenere formalmente le equazioni di Navier-Stokes, pur assegnando una dipendenza in Q e ω alle proprietà di equilibrio e ai coefficienti di trasporto [1, 3].

Vedremo in questa sezione alcuni approcci che consentono tale estensione. Prendendo per punto di partenza la soluzione idrodinamica, ovvero l’espressione idrodinamica della funzione intermedia di scattering Fhyd(Q, t) valida nel limite

Q → 0, `e possibile interpretare Fhyd nel quadro del formalismo di Mori per

l’e-quazione di Langevin generalizzata, considerando i parametri coinvolti come il limite per Q → 0 di parametri dipendenti da t e Q.

Nel quadro che abbiamo tracciato a proposito della funzione di memoria del secondo ordine possiamo provare ad esplorare la dinamica delle stesse variabili quasi conservate che abbiamo studiato nel limite idrodinamico spingendoci verso valori crescenti del momento scambiato, ossia valori di 2π

Q confrontabili con le

dimensioni atomiche. Vediamo come sia possibile una tale estensione.

Un primo passo consiste nell’applicare semplici criteri fisici che possano aiutar-ci a stabilire una dipendenza da Q almeno per alcuni parametri coinvolti nel-la soluzione idrodinamica. Come esempio di questa procedura consideriamo il momento secondo normalizzato ω2

(31)

ω2 0 = Jl qJql∗ ® ρqρ∗q ® Q2 ₌ KBT Q2 mS(Q) (2.65)

mediante un confronto con la soluzione idrodinamica stabiliamo che ω2 0 Q→0 −→ c2SQ2 γ = c 2 TQ2 (2.66)

Il limite di vettore d’onda nullo del fattore di struttura statico S(0) = ρKBT kT,

insieme con la definizione termodinamica della velocit`a del suono isoterma cT =

q

1

ρkT, ci conducono in modo “naturale” a definire la velocit`a isoterma

generaliz-zata come

c2

T(Q) =

KBT

mS(Q) (2.67)

Una ulteriore generalizzazione dei coefficienti di trasporto riguarda la possibile dipendenza dalla frequenza, e pu`o essere ottenuta guardando alla dipendenza dal tempo della funzione di memoria idrodinamica M(2)_{(Q, t) (2.45). Possiamo}

esten-dere il canale di decadimento legato alla viscosità nel tentativo di descrivere quello che succede quando la frequenza delle fluttuazioni della densità è sufficientemente grande da potersi confrontare con le scale di tempo tipiche del rilassamento strut-turale. Questo può essere ottenuto facendo cadere l’ipotesi sulla natura istantanea (markoviana) del termine viscoso, introducendo nuovi contributi esponenziali pe-sati da una ampiezza totale legata al coefficiente ν, ossia la viscosità cinematica [1, 17]. Ad esempio il modo più semplice di operare in questa direzione, fornendo una prima generalizzazione del limite idrodinamico (2.45), si ottiene estendendo il contributo istantaneo nella M(2)_{(Q, t), quello cioè dovuto alla viscosità,}

sostituen-dolo con un decadimento di tipo esponenziale, introducendo cos`ı una nuova scala temporale caratteristica della dinamica del sistema

M(2)(Q, t) = 2νQ2e−t/τ (Q)+ (γ − 1)ω2₀(Q)e−γDTQ2t _(2.68)

Dove nel limite Q → 0 la forma idrodinamica (2.45) si riottiene facendo la richi-esta che τ (Q → 0) = ν

∆(Q→0) dove ∆(Q) `e l’ampiezza della funzione di memoria.

La dipendenza da Q nei parametri della M(2)_{(Q, t) si pu`o derivare dal confronto}

diretto del nostro modello con i risultati sperimentali, considerando ν, τ , γ e DT

come parametri di fit; si pu`o tentare cos`ı una interpretazione fisica, per esempio, di τ (Q), in termini della dinamica microscopica rilassamentale del sistema sotto indagine.

L’equazione (2.68) definisce il modello viscoelastico, introdoto da Lovesey [27] nel caso γ = 1 trascurando cio`e gli effetti termici. In tal caso

(32)

Il modello viscoelastico, per quanto semplice, è in grado di riprodurre la tran-sizione per un liquido semplice da un regime viscoso ad uno elastico. La legge di decadimento esponenziale per una funzione di memoria è infatti la forma fun-zionale più semplice che contiene sia il limite di risposta viscosa per t À τ che quello tipico di una risposta armonica per t ¿ τ . Nei due casi limite infatti

M(2)(Q, t) ≈ ½

∆(Q)δ(t) per t À τ (Q) ∆(Q) per t ¿ τ (Q)

la funzione di memoria pu`o essere schematizzata con un decadimento istantaneo, o come un termine costante rispettivamente, cosa che indica una istantanea perdita di memoria nel primo caso, e la tendenza a conservare completamente la memoria dei tempi precedenti nel secondo. Allora l’equazione di Langevin generalizzata prende la forma ¨ F (Q, t) + ω2 0(Q)F (Q, t) + ∆(Q) ˙F (Q, t) = 0; per t À τ (Q) ¨ F (Q, t) + [ω2 0(Q) + ∆(Q)]F (Q, t) = 0; per t ¿ τ (Q)

Per tempi grandi riconosciamo l’equazione come quella di un oscillatore armonico smorzato, in queste condizioni il comportamento del sistema si definisce viscoso e la forma funzionale della S(Q, ω) è un DHO. Per tempi piccoli invece l’equazione per F (Q, t) perde il termine di smorzamento, il sistema non riesce più a riarran-giarsi in presenza della perturbazione esterna e al limite si presenta ad essa come congelato, è assente ogni forma di fenomeno dissipativo, perciò diciamo che si tratta di un regime elastico. La transizione fra i due regimi ora descritti è de-terminata evidentemente dall’andamento in Q di ω(Q)τ (Q) dove ω(Q) = 2π

t(Q) `e

legata alla scala di tempo delle fluttuazioni di densità del sistema, ma siccome τ (Q) è un tempo caratteristico della dinamica microscopica si avrà sempre un regime di tipo viscoso nel limite idrodinamico.

Introduciamo anche il contributo termico alla funzione di memoria, riprenden-do quindi in considerazione la (2.68); noi sappiamo che τth(Q) ≈ _D_T1_Q2 `e grande nel limite idrodinamico. In questo caso ωτth À 1 e il tempo di decadimento delle

fluttuazioni termiche è molto più lungo della scala di tempo delle fluttuazioni di densità, cos`ı abbiamo a che fare con un regime adiabatico, e ci aspettiamo di trovare una dispersione lineare ω = cSQ con velocità del suono adiabatica. Il

contributo del termico alla forma dello spettro sar`a dello stesso tipo di quello descritto a proposito del regime elastico.

Invece ad alti Q ωτth ¿ 1 e la scala di tempo delle fluttuazioni di densit`a `e

molto pi`u lenta del tempo di decadimento delle fluttuazioni termiche τth, quindi

la termalizzazione locale è permessa e le fluttuazioni della densità evolvono per-mettendo il trasferimento di calore. In questo limite ci aspettiamo di trovare un regime isotermo , e una dispersione lineare con velocità del suono isoterma. Il contributo del termico alla forma di riga sarà dello stesso tipo a Q alti di quello