+ = + = − = − = R t u t r u V R t u t r u V x x 2 1 2 2 1 2 2 2 2 2 22 21 (4.1)
Si ricorda, come definito in § 1, che la ruota si trova in condizioni di puro rotolamento se Vx =ΩRα0 ossia se la sua velocità longitudinale è
pari al prodotto tra velocità angolare e raggio di rotolamento. Dalla (4.1) risulta evidente che se alle due ruote viene imposto dall’assale rigido la medesima velocità angolare Ω , le ruote non si trovano in condizioni di 2
puro rotolamento ma presentano degli scorrimenti longitudinali non trascurabili (il raggio di puro rotolamento è, con buona approssimazione, uguale per le due ruote).
In generale si può concludere che in condizioni di moto stazionario le due ruote di un assale rigido sono caratterizzate da condizioni di scorrimento combinato indipendentemente dalla coppia motrice applicata all’assale.
In condizioni di scorrimento combinato è conveniente utilizzare lo scorrimento teorico σ per esplicitare le condizioni cinematiche di ciascuna ruota. Lo scorrimento teorico σ=
(
σx,σy)
, come definito in § 1, rappresenta il rapporto tra la velocità di scorrimento Vs e la velocità dirotolamento Vr di ciascuna ruota:
. tan ; 1 0 0 Ω Ω − − Ω Ω = = α α α r V s V σ (1.6)
Tenendo conto delle espressioni delle velocità dei centri ruota definiti in § 2.3, è possibile ricavare le espressione degli scorrimenti teorici delle ruote posteriori:
Ω − − Ω + = Ω − − Ω + = Ω − − Ω − = Ω − − Ω − = 2 2 2 2 2 2 22 22 2 22 22 2 22 2 2 2 2 2 2 21 21 2 21 21 2 21 , 1 2 / , 1 2 / , 1 2 / , 1 2 / R r a v R t r u R r a v R t r u R r a v R t r u R r a v R t r u σ σ (4.2)
Dalla (4.2) emerge che gli scorrimenti laterali (ovvero gli angoli di deriva) delle due ruote di un assale rigido sono rigorosamente uguali; gli
scorrimenti longitudinali, invece, differiscono per il termine legato al prodotto tra la velocità di imbardata e la semicarreggiata.
Per le due ruote anteriori è ancora più semplice perché, trascurando la resistenza al rotolamento, si trovano in condizioni di puro rotolamento, cioè σx =0:
(
)
(
)
(
)
(
)
Ω + − + = − = Ω − − + = − = 1 12 1 1 12 12 1 11 1 1 11 11 2 / , 0 tan , 0 2 / , 0 tan , 0 R t r u r a v R t r u r a v δ α δ α σ σ (4.3)Coerentemente a quanto fatto in § 2.3, è possibile linearizzare le espressioni (4.2) e (4.3) attraverso opportune ipotesi semplificative. Per gli scorrimenti laterali delle due ruote anteriori (in puro rotolamento) è possibile assumere, in campo lineare con a 4m/s2
y ≤ , δα <<1; pertanto risulta:
(
)
(
)
+ ≅ + + + = Ω − ≅ + + − = Ω 2 / 2 / 2 / 2 / 1 1 1 1 12 1 1 1 1 11 t r u r a v t r u R t r u r a v t r u R δ δ (4.4)Per piccoli angoli di deriva è possibile confondere la tangente con l’angolo, pertanto le (4.3) diventano:
(
) (
)
(
) (
)
− + + = − ≅ − = − − + = − ≅ − = δ α α δ α α 2 / , 0 , 0 tan , 0 2 / , 0 , 0 tan , 0 1 1 12 12 12 1 1 11 11 11 t r u r a v t r u r a v σ σ (4.5)Dalla (4.5) emerge che in condizioni di puro rotolamento e per piccoli angoli di deriva, gli scorrimenti laterali (teorico e pratico) e l’angolo di deriva sono legati dalla relazione:
α
σy =sy ≅− (4.6) Assumendo, infine, che sia u>>rt1/2 ovvero t1 <<2R, possono essere assunti uguali gli angoli di deriva ovvero gli scorrimenti teorici delle due ruote anteriori:
− + = = ≅ δ u a r v , 0 1 12 11 σ σ σ (4.7)
Passando agli scorrimenti teorici delle ruote posteriori, il problema si fa più delicato a causa delle condizioni di scorrimento combinato indotto dall’assale rigido. È utile introdurre la posizione:
0 1 / , 2 2 = + << > Ω R u q q u eq (4.8) La quantità q rappresenta il modulo della velocità di scorrimento indotta dalla coppia motrice T trasmessa all’assale rigido.
Dalla (4.8) discendono subito le seguenti identità:
− ≅ Ω ⇒ − ≅ + ⋅ = + = Ω − Ω ≅ Ω − Ω ⇒ − Ω = = − − ≅ + − = + − = Ω − u q u R u q u u q u q u R u u R R u R u u R u q u q u q q u u R u 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 (4.9) Utilizzando le identità (4.9) è possibile ricavare le espressioni degli scorrimenti teorici linearizzati delle due ruote posteriori:
− − − + − ≅ Ω − − Ω + = − − − − − ≅ Ω − − Ω − = u q u r a v u q u rt u q R r a v R t r u u q u r a v u q u rt u q R r a v R t r u 1 , 1 2 , 1 2 / 1 , 1 2 , 1 2 / 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 21 σ σ (4.10) Dalla (4.10) emerge che in condizioni di scorrimento combinato il legame tra scorrimento laterale (teorico e pratico) ed angolo di deriva risulta:
α σ − − ≅ − = u q s u q y y 1 1 (4.11) dalla quale emerge che la quantità q/u rappresenta una sorta di scorrimento teorico longitudinale medio dell’assale posteriore.
Tenendo conto della relazione u=rR che lega velocità longitudinale, velocità di imbardata e la distanza dal centro di istantanea rotazione, è possibile riscrivere gli scorrimenti longitudinali linearizzati nella forma:
R t u q u q R t u q u q u t r u q R t u q u q R t u q u q u t r u q x x 2 1 2 1 2 2 1 2 1 2 2 2 2 2 2 2 22 21 + − ≅ − − − = − − − = − − ≅ − + − = − + − = σ σ (4.12)
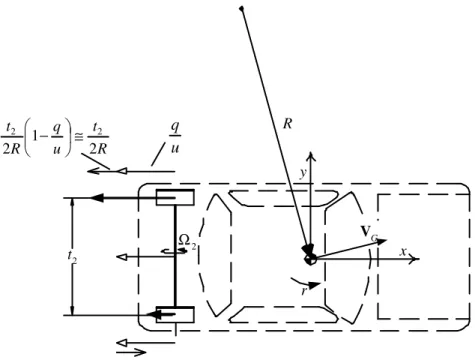
dove le ultime espressioni sono state ottenute coerentemente alla posizione (4.8). u q R t u q R t 2 1 2 2 2 ≅ − x y r G V 2 Ω 2 t R
Le (4.12) mettono in evidenza come lo scorrimento longitudinale di ciascuna ruota posteriore (vedi fig 4.1) possa essere considerato la somma di uno scorrimento medio q/u sempre presente (a causa della trazione) e di uno scorrimento opposto (alternato se fosse una tensione meccanica) che nasce solo nel moto in curva (scompare in rettilineo). In rettilineo gli scorrimenti sono uguali in modulo ed entrambi negativi, mentre in curva hanno ovviamente modulo diverso ma non solo, se la ruota interna è sempre caratterizzata da uno scorrimento negativo, il segno dello scorrimento della ruota esterna non è garantito e, per basse velocità e raggi di curvatura ridotti, può diventare positivo.
4.3
Equazioni costitutive (modello di pneumatico)
Le equazioni costitutive definiscono il legame matematico tra gli scorrimenti della ruota e le forze esercitate dai pneumatici, definendone pertanto il comportamento. Analogamente a quanto fatto in § 2 per la definizione del modello monotraccia classico, si definisce un legame lineare tra la forza (longitudinale e laterale) generata dal pneumatico e lo scorrimento della ruota:
(
)
(
y i)
ij ij ij i x ij y z y x z x F C F F C F σ ς σ ς σ σ σ σ ∆ ± − = ∆ ± − = 0 0 (4.13)La (4.13) definisce un comportamento anisotropo del pneumatico per tener conto dell’evidenza sperimentale secondo la quale la rigidezza longitudinale Cσ0x risulta superiore del 50% ca. rispetto alla rigidezza laterale 0
y
Cσ ; ciò è dovuto principalmente alla flessibilità laterale e torsionale del pneumatico. La quantità ςσ definisce, infine, la sensibilità
della rigidezza al carico verticale.
Nel capitolo dedicato al modello monotraccia classico è stato esplicitato il trasferimento di carico verticale di ciascun assale in condizioni di regime: y i i i i i z h Y B Y Y ma h mg k k h l a l t F i ~ , 1 = = ′ ′ − + − = ∆ φ φ (2.25)
Sostituendo la (2.25) nella (4.13) si ottengono le equazioni costitutive direttamente legate all’accelerazione laterale (a regime):
(
)
(
y)
ij ij ij x ij y y i y x y i x a m D C F a m D C F σ σ σ σ ~ ~ 0 0 ± − = ± − = (4.14) con Di =ςσiBi.Analogamente a quanto fatto nella definizione del modello monotraccia lineare classico, nella presente trattazione verrà trascurata l’influenza dell’angolo di camber. Sperimentalmente, infatti, si ha che il rapporto tra la rigidezza di deriva (cornering stiffness) e la rigidezza di camber (camber thrust) Cγ /Cα è pari a 0.05 ca. per un pneumatico
radiale. Inoltre l’angolo di camber in una autovettura non supera di norma i 2° con spinte di camber dell’ordine dei 100 N, quindi si tratta di forze di modesta entità.
4.4
Equazioni di equilibrio
La stesura delle equazioni di equilibrio richiede due distinte operazioni: il calcolo delle accelerazioni e la valutazione delle forze e dei momenti agenti.
4.4.1 Calcolo delle accelerazioni
Valgono tutte le considerazioni e tutte le relazioni trovate nel paragrafo § 2.4.1.
4.4.2 Forze e momenti
Valgono tutte le considerazioni fatte nel paragrafo § 2.4.2 fino alle tre equazioni generali di equilibrio (2.18) riportate di seguito
(
) (
) (
)
(
)
(
) (
) (
)
(
) (
)
[
]
(
)
(
)
(
)
(
)
2 2 2 2 1 ) ( 1 2 1 2 1 2 12 11 22 21 12 11 22 21 12 11 12 11 22 21 12 11 12 11 22 21 12 11 12 11 t F F t F F t F F a F F a F F F F r J F F F F F F ur v m u SC F F F F F F vr u m y y x x x x y y y y x x y y y y x x x x x y y x x δ δ δ ρ δ − + − − + − + − + + + = + + + + + = + − + + + − + = − & & & (2.18)Anche qui è conveniente sommare i contributi delle due ruote dello stesso assale ponendo
22 21 2 12 11 1 22 21 2 12 11 1 y y y y y y x x x x x x F F F F F F F F F F F F + = + = + = + = (2.19)
in modo da rendere più compatta la notazione.
Come rimarcato in precedenza le ruote anteriori sono folli quindi, trascurando la resistenza al rotolamento, esplicano forze longitudinali nulle, in altri termini si ha
0 0 1 12 11 = x = ⇒ x = x F F F
Ma, a differenza del modello monotraccia lineare classico, la sostituzione sull’assale posteriore (motore) del differenziale ordinario con un assale rigido determina una differenza non trascurabile tra le due forze longitudinali; in altri termini:
22
21 x
x F
F ≠
Da quest’ultima considerazione discende che, a differenza di quanto fatto in § 2.4.2 per il modello monotraccia classico, non più possibile porre uguale a zero il termine
(
)
2 /222
21 F t
Fx − x
− che compare
nell’equazione di equilibrio alla rotazione intorno all’asse z e che verrà indicato con Mz2.
Ripetendo le considerazioni fatte per il modello classico, anche qui è possibile trascurare il termine
(
)
1/212
11 F t
Fy − y δ con il vantaggio di una semplificazione matematica oltre che formale.
In base a quanto detto, si possono scrivere le equazioni di equilibrio nella seguente forma
(
)
(
)
2 2 1 2 1 1 2 2 1 2 2 1 z y y y y x y x M a F a F r J F F ur v m u SC F F vr u m + − = + = + − − = − & & & δ ρ (4.15)in cui compare, come mostrato nella fig. 4.2, oltre alle componenti longitudinali e laterali delle forze esercitate globalmente da ciascun
assale, anche il momento di imbardata Mz2dovuto alla differenza
2
x F
∆ tra le due forze longitudinali posteriori e che caratterizza la formulazione matematica del modello con assale rigido .
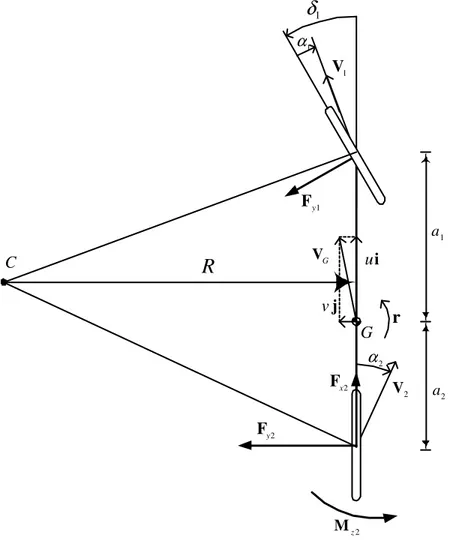
Non resta adesso che esplicitare le forze ed i momenti che compaiono nelle equazioni di equilibrio (4.15) utilizzando le equazioni di congruenza e le equazioni costitutive definite rispettivamente in § 4.2 e § 4.3. Per la forza laterale Fy1 esplicata dall’assale anteriore, si ricava immediatamente: C 1 y F 2 y F 2 x F G i u j v G V 1
δ
1 α 2 α 1 V 2 V 2 z Mr
1 a 2 aR
1 1 1 1 1
C
σσ
C
αα
F
y y y=
−
=
(4.16)dove si è indicato con 1
1 α
σ C
C y = la rigidezza di deriva dell’assale anteriore. Occorre sottolineare che, nel caso di ruota in condizioni di deriva pura, la rigidezza laterale
i y
Cσ coincide con quella di deriva Cαi. Allo stesso modo la forza laterale Fy2 esplicata dall’assale
posteriore assume l’espressione:
2 2 2 2 2 2 σ 1 α α σ σ 43 42 1 C y y u q C C F y y − = − = (4.17)
La (4.17) evidenzia che la rigidezza laterale
i y
Cσ non coincida con la rigidezza di deriva Cαi in presenza di condizioni di scorrimento combinato.
La scrittura delle forze longitudinali posteriori Fx2i risulta più delicata per l’influenza diretta del trasferimento di carico verticale; in particolare risulta:
(
)
(
)
(
)
(
)
− − + = − − + = − + − = − + − = 2 2 2 0 2 2 0 2 2 2 0 2 2 0 ~ 1 2 ~ 1 2 ~ 1 2 ~ 1 2 2 2 22 2 2 21 u a u q t u q a m D C u q u t r u q r u m D C F u a u q t u q a m D C u q u t r u q r u m D C F y y x y y x x x x x σ σ σ σ (4.18) Dall’equazione (4.18) è immediato ricavare le espressioni della forza longitudinale Fx2 e del momento di imbardata Mz2 esplicatedall’assale posteriore: 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 ~ ~ 1 1 2 1 2 2 2 2 2 2 22 21 2 − ≅ − − = − − ≅ Ω ∆ − Ω − = + = u a t m D u q C u a u q t m D u q C r u q t m D u q C R t r F R u C F F F y y z x x x x x x x σ σ σ σ σ ς (4.19)
(
)
y y y z x x z a u q m t D R t C a u t C u q m t D a u q m D u q u t C t t u q ur m D u q u t r C t R u F R t r C t F F M x x x x x ~ 4 ~ 4 ~ 2 1 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 21 22 2 + − = − ≅ + − − = + − − ≅ Ω − ∆ + Ω − = − = σ σ σ σ σ σ ς (4.20) Le espressioni (4.19) e (4.20) sono ingannevolmente semplici: oltre alle variabili di moto del baricentro come la velocità longitudinale u e la velocità di imbardata r compare anche la quantità q/u che, in generale, dipende anch’essa dalle condizioni di moto del veicolo.Tuttavia, le ultime relazioni in (4.19) e (4.20) ottenute con l’ipotesi 1
/u<<
q , mettono in evidenza che sia la forza longitudinale totale dell’assale Fx2 sia il momento di imbardata Mz2 risultano essere la
somma di due termini dal significato ben distinto. Il primo, in cui compare la rigidezza longitudinale dell’assale è un termine prevalentemente cinematico legato principalmente agli scorrimenti longitudinali (vedi fig. 4.3), il secondo è invece un termine prevalentemente elastico legato principalmente alla dipendenza al carico verticale della rigidezza longitudinale del pneumatico.
x
y
r G V 2 Ω 2 t 21 xF
22 x F 0 = σς
Fig. 4.3: Effetto sul momento di imbardata indotto dalla sensibilità del pneumatico al carico verticale.
L’introduzione della variabile q/u rende necessario affiancare, alle tre equazioni di equilibrio del veicolo, l’equazione di equilibrio alla rotazione dell’assale rigido posteriore:
2 2 2−F2R 2 = J Ω&
T x sc (4.21) dove con J2 si è indicata l’inerzia equivalente del sistema ruote – assale
rigido – motore, Rsc2 rappresenta il raggio sotto carico delle ruote posteriori (supposto indipendente dal carico verticale). La quantità T2
rappresenta, infine, la coppia motrice all’assale: è supposta indipendente dalla velocità angolare Ω e costituisce un parametro di manovra gestito 2
direttamente dal driver (attraverso il pedale dell’acceleratore).
Utilizzando le identità (4.9) è possibile ricavare l’equazione di equilibrio dell’assale posteriore in funzione della quantità q/u:
(
u q)
J R F R T − x = 2 &+ & 2 2 2 2 2 (4.22)dove si è assunto per semplicità Rsc2 ≅R2.
4.5
Modello monotraccia di autoveicolo con differenziale
bloccato
In analogia a quanto fatto, in § 2.7, per il modello monotraccia classico è possibile determinare le equazioni di stato del modello di veicolo con assale rigido (o differenziale bloccato) mettendo insieme le equazioni di equilibrio e le espressioni esplicite di forze e momenti.
Svolgendo i vari passaggi si giunge ad un sistema di tre equazioni differenziali (che definiscono le equazioni di moto dell’intero veicolo) nelle tre variabili di stato u , v , ed r ed in cui compare esplicitamente il tempo t : ) , , , ( 1 ) , , , ( 1 ) , , , ( 2 1 1 3 2 1 2 1 2 2 2 1 2 1 1 2 t r v u f u q M a u q F a F J r t r v u f ur u q F F m v t r v u f vr u SC F u q F m u z y y y y x y x = + − = = − + = = + − − = & & & δ ρ (4.23)
Tuttavia, rispetto al modello di veicolo con differenziale ordinario, nelle equazioni di moto del veicolo con differenziale bloccato compare esplicitamente la quantità q/u. Pertanto, alle tre equazioni di moto del veicolo va aggiunta l’equazione di moto dell’assale rigido (o dell’assale con differenziale bloccato) (4.22):
(
u q)
J R F R T − x = 2 &+ & 2 2 2 2 2Una volta fissato il modello non resta che stabilire cosa considerare noto e cosa incognito; si prospettano almeno due scenari di funzionamento:
1. Forse la scelta più naturale è supporre assegnate la coppia motrice T2 e l’angolo di sterzo δ
( )
t . Rimangono incognite le trefunzioni u
( )
t , v( )
t ed r( )
t che definiscono completamente le condizioni di moto del veicolo (ma non quelle delle ruote posteriori) e la funzione q/u( )
t che definisce completamente il moto dell’assale rigido e permette di identificare, insieme con le variabili globali del veicolo, le condizioni cinematiche delle due ruote posteriori.2. Si suppone assegnata la velocità di avanzamento u
( )
t e l’angolo di sterzo δ( )
t . Rimangono incognite le tre funzioni v( )
t ,r( )
t e( )
t uq/ che definiscono completamente le condizioni di moto del veicolo e delle ruote posteriori, e la coppia motrice T2.
In entrambi i casi si è di fronte ad un problema dinamico complesso, non risolvibile in forma chiusa; tuttavia nel secondo caso, se non interessa determinare la coppia motrice T2, è possibile ridurre il
sistema in due equazioni differenziali nelle variabili di stato v
( )
t ed( )
tr , ed in una equazione algebrica non lineare nelle variabile q/u
( )
t . In sintesi si ottiene un sistema di equazioni differenziali lineari in v( )
t ed( )
tr (variabili di stato) e non lineare in q/u
( )
t :( ) ( ) ( ) ( ) ( ) δ δ σ σ σ σ σ σ σ σ σ σ σ J a C r u q J t u m D Ju t u q C Ju a u q C a C v Ju a u q C a C r m C r u mu a u q C a C v mu u q C C v y x y y y y y y y y y 1 2 2 2 2 2 2 2 1 2 1 2 1 1 2 2 1 2 1 1 2 1 2 1 4 / 1 / 1 / 1 / 1 / 1 + − − + − + − − − − = + + − − − + − − = & & (4.24)
con
(
)
2 2 2 2 2 2 2 1 2 1 2 1 r t m D C r t m D vr u m u C S u r a v C u q x y x + + − + + + − = σ σ δ δ ρ & (4.25)Introducendo la notazione matriciale, il sistema di due equazioni differenziali si può riscrivere come
b Aw
w& = + (2.35) dove w
( )
t =(
v( ) ( )
t,r t)
rappresenta il vettore delle variabili di stato, il vettore dei termini noti è dato da(
C( )
t m C a( )
t J)
y y1δ / , σ1 1δ / σ = b e
( )
(
)
(
)
(
)
(
)
(
)
− − + − + − − + − − − + − = = = u q J t u m D Ju t u q C Ju a u q C a C Ju a u q C a C u mu a u q C a C mu u q C C t u q t u x y y y y y y y y 2 2 2 2 2 2 2 1 2 1 2 1 4 / 1 / 1 / 1 / 1 / 1 ), ( 2 2 1 2 1 2 1 2 1 σ σ σ σ σ σ σ σ σ A A (4.26) è la matrice dei coefficienti.Confrontando l’espressione (4.26) della matrice A per il veicolo con differenziale bloccato con l’analoga (2.36) (§ 2.7) relativa al modello monotraccia classico (con differenziale libero) emergono differenze molto nette, considerando le identità formali Cσy1 ≡C1 e Cσy2 ≡C2. La matrice
A di (4.26) dipende dal parametro q/u (oltre che dalla velocità di avanzamento u ) che comporta da un lato la riduzione della rigidezza laterale dell’assale posteriore
2
y
Cσ e dall’altro l’introduzione di un termine aggiuntivo in A
( )
2,2 relativo all’equilibrio ad imbardata. Tuttavia, anche assumendo q/u≅0, non si raggiunge l’identità tra le due matrici A per la presenza in A( )
2,2 del termine legato al momento di imbardata cinematico C rt ux /4
2 2 2
σ indotto dall’assale rigido.
Nessuna differenza, come era da attendersi, nelle espressioni dei termini noti b che dipendono dall’angolo di sterzo imposto δ
( )
t ma non dalla velocità di avanzamento u .Una notevole semplificazione del problema matematico la si ottiene se si assume q/u≅0 con u
( )
t assegnata; infatti la prima equazione in (4.23) diventa un’equazione algebrica nella nuova incognita che sarà necessariamente la forza di trazione Fx2( )
t ma soprattutto siottiene un sistema di equazioni differenziali lineare nelle variabili v
( )
t ed( )
t r : δ δ σ σ σ σ σ σ σ σ σ σ σ J a C r u t C Ju b C a C v Ju a C a C r m C r u mu a C a C v mu C C v y x y y y y y y y y y 1 2 2 2 2 2 1 2 1 1 2 2 1 2 1 1 2 1 2 1 4 + + + − − − = + + − − + − = & & (4.27) L’equazione rimanente serve semplicemente per valutare la forza di trazione Fx2( )
t 2 1 2 1 ) ( 1 2 u SC u ra v C vr u m Fx σy δ δ + ρ x + − + − = &Infine l’equazione di equilibrio alla rotazione dell’assale rigido consente di ricavare la coppia motrice T2
( )
t :u J R F T2 = x2 2 + 2 & 4.5.1 Comportamento a regime
Se il veicolo è stabile, l’integrale particolare wp
( )
t rappresenta il tipo dimoto in condizioni di regime (non necessariamente stazionarie se
( )
t ≠0δ& ). Infatti, la parte transitoria della soluzione decade e, dopo un tempo sufficientemente lungo, diventa del tutto trascurabile.
Nel caso di sterzo in posizione fissa
(
δ =const.)
e velocità di avanzamento uniforme, il veicolo si stabilizza su un percorso circolare.0 ~ 2 2 1 2 1 2 1− + = + = = z y y y y y p M a F a F F F a m mur
dalle quali è possibile ricavare le espressioni delle forze laterali a regime:
(
)
(
)
l u q M g a W l u q M a l a l m F i y z z y i yi / ~ / ~ 2 2 m m = − = (4.28)dove con Wi si è indicato il carico verticale statico agente sul singolo assale.
Tenendo conto delle equazioni costitutive (4.16) e (4.17) si ricavano le espressioni degli angoli di deriva αip:
(
)
(
)
(
)
(
)
(
)
− + − = − = − = = l u q C u q M a l a u q C m u q C F l C u q M a l a C m C F y y y y y y z y y p z y y p / 1 / ~ / 1 / 1 / ~ 2 2 2 2 1 1 2 1 1 1 1 2 2 1 σ σ σ σ σ σ α α (4.29) Tenendo conto della (2.8) si ha che la differenza tra l’angolo di sterzo imposto δ e l’angolo di ackermann δ0 =l/Rp diventa, a regime:(
)
(
)
(
)
+ − − − − = − = − 1 2 2 2 1 1 / 1 1 / ~ / 1 1 2 2 1 y y y y p p l C q u C u q M a u q C a C a l m R l z y p σ σ σ σ α α δ (4.30) Confrontando l’espressione (4.30) della differenza tra gli angoli di deriva ricavata per un veicolo con differenziale bloccato con quella (2.39) relativa al differenziale libero, emergono nette differenze:1. Innanzitutto, accanto al termine classico dipendente dalla differenza capacità direttive dei due assali compare un secondo termine direttamente legato al momento di imbardata generato dalla differenza delle due forze longitudinali posteriori.
2. Anche assumendo trascurabile il termine legato al momento di imbardata Mz2, si ha una differenza tra le due espressioni dovuta al termine
(
1−q/u)
che riduce la capacità direttiva dell’assaleposteriore i cui pneumatici sono caratterizzati da condizioni di scorrimento combinato.
3. La (4.30), a differenza della (2.39), dipende non solo dall’accelerazione laterale a regime ma anche dalle condizioni cinematiche di scorrimento dell’assale posteriore ovvero dal parametro q/u. Questo, come vedremo più avanti, fa sì che il gradiente di sottosterzo di un veicolo con differenziale bloccato dipenda non solo dalle sue caratteristiche costruttive (costanti) ma anche dal tipo di manovra.
Introducendo l’espressione del momento di imbardata Mz2, la (4.30) diventa:
(
)
( ) ( ) ( ) ( ) ( ) + − − + + − − − − = + − − − − − − = = − 1 2 2 1 2 2 1 1 2 2 2 1 1 / 1 1 1 4 ~ 1 / 1 1 / 1 ~ 1 / 1 1 1 4 1 ~ / 1 / , , , ~ 2 2 2 2 1 2 2 2 2 2 2 1 2 y y x y y y y y y x y y C u q C u q R l t C a C u q C t D u q C a C a l m a C u q C u q u t C u q t m D l a u q C a C a l m u q R u a R l y y y y p σ σ σ σ σ σ σ σ σ σ σ σ δ (4.31) La (4.31) può essere semplificata tenendo conto della posizione 1 /u<< q :(
)
R C C l t C a u q C C t D C a C a l m a C C u l t C a u q C C t D C a C a l m u q R u a R l y y x y y y y y y x y y y y y y y y p 1 1 1 4 ~ 1 1 ~ 1 1 4 ~ 1 1 / , , , ~ 1 2 2 1 2 2 1 1 2 2 1 2 2 1 2 2 2 2 1 2 2 2 2 2 2 1 2 + + + − − = + + + − − = = − σ σ σ σ σ σ σ σ σ σ σ σ σ σ δ (4.32) Riprendendo quanto detto in § 2.7.1, si definisce gradiente di sottosterzo η di un autovettura la derivata, rispetto all’accelerazione laterale a regime a~ , della differenza tra l’angolo di sterzo imposto y δ e l’angolo di Ackermann δ0 =l/Rp. Tuttavia, a causa della dipendenza diR l/ −
δ ovvero di α1−α2 non solo dall’accelerazione laterale a~ , ma y anche dalla velocità di avanzamento u o dal raggio di curvatura R , è necessario sostituire il segno di derivata totale della (2.40) con quello di derivata parziale: R l t C C u q l t C mD u l t C C u q l t C mD u l t C C C u q l t C C mD C a C a l m R l a y x y y x y y y x y y y y o o C p y 1 4 ~ ~ 1 4 ~ ~ 1 4 1 1 1 1 ~ 2 2 2 2 2 2 2 2 2 2 2 2 2 ~ 2 1 2 2 2 2 1 2 1 2 0 2 1 σ σ σ σ σ σ σ σ σ σ σ η σ σ η η δ η σ + − ≅ + − ≅ + + + − − ≅ − ∂ ∂ = 4 4 3 4 4 2 1 4 4 4 3 4 4 4 2 1 (4.33) avendo indicato con ηo il gradiente di sottosterzo del veicolo con differenziale ordinario.
La (4.33) evidenzia come il gradiente di sottosterzo di un veicolo con differenziale bloccato (o assale rigido), a differenza di quanto accade per quello dotato di differenziale ordinario, non dipenda esclusivamente dalle sue caratteristiche costruttive (costanti), ma anche dai parametri di manovra quali la velocità di avanzamento u o il raggio di curvatura R .
In particolare, ipotizzando in prima istanza q/u≅cost, nel caso di manovra a velocità costante (Slow Ramp Steer) il gradiente di sottosterzo η diminuisce all’aumentare della velocità; mentre nel caso di manovra a raggio costante η diminuisce all’aumentare del raggio di curvatura.
Non solo ma il gradiente di sottosterzo η, a causa della variazione della rigidezza di deriva col carico verticale, è funzione dello scorrimento medio q/u dell’assale posteriore.
Per definire completamente il comportamento stazionario di un autoveicolo, è necessario considerare, accanto al gradiente di sottosterzo η, il gradiente di assetto ηβ.
Riprendendo la definizione in § 2.7.1, il gradiente di assetto ηβ è
la derivata totale dell’angolo di assetto β rispetto all’accelerazione laterale, in condizioni di regime:
y a~ ∂ ∂ = β ηβ
In § 2.7.1 si è dimostrato che il gradiente di assetto di un autoveicolo dotato di differenziale ordinario sia legato solo alle sue caratteristiche costruttive (costanti); in particolare è dato dal rapporto della massa statica e della rigidezza di deriva dell’assale posteriore:
3 2 1 43 42 1 const R const u C m C m u a = = − = − = 2 2 2 2 2 2 β η (4.34)
Per determinare l’espressione dell’angolo di assetto per un veicolo dotato di differenziale bloccato, si consideri il sistema
2 2 2 2 2 2 2 2 2 2 2 2 1 y y y C F R a C F C u q F R a u r a u r a v y y y σ σ σ β α β β α − = ⇒ ≅ − = + − = + − ≅ − − = (4.35)
costituito dall’equazione di congruenza e da quella costitutiva.
Tenendo conto dell’espressione della forza laterale a regime (4.28) e di quella del momento di imbardata Mz2 (4.20) nell’ipotesi di
1 / 1−q u≅ si ottiene y y a l C m u q t D a u l t C C a a l C m u q t D a R l t C C a y y x y y x ~ 1 4 ~ 1 4 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 1 2 2 2 + − + = + − + = σ σ σ σ σ σ β (4.36)
La (4.36) evidenzia come la presenza del differenziale bloccato determini, relativamente alla manovra di Steering Pad con R=cost, da un
lato un aumento (in assoluto) dell’angolo di assetto cinematico, ossia dell’angolo di assetto a bassa velocità
(
~ ≅ay 0)
; dall’altro, dal momento che risulta per definizione q/u>0, si ha un aumento (in modulo) del gradiente di assetto.Confrontando la (4.34) con la (4.36) si ottiene la relazione tra i gradienti di assetto delle due condizioni estreme, differenziale libero ideale e differenziale completamente bloccato:
4 4 3 4 4 2 1 4 4 4 4 4 4 3 4 4 4 4 4 4 2 1 const R const u u q l t C m D u q t m D u t C l C y o x y o = = − = − + = 2 2 2 2 2 2 2 2 2 2 4 1 σ β σ σ β β η η η (4.37)
Sia l’equazione (4.33) relativa al gradiente di sottosterzo che la (4.37) relativa la gradiente di assetto evidenziano la dipendenza dal parametro q/u; pertanto per completare l’analisi del comportamento a regime del veicolo dotato di differenziale bloccato è necessario indagare il legame tra q/u e le variabili di stato a regime.
Dall’equilibrio longitudinale a regime si ottiene (a partire dalla 4.25): 2 2 2 2 2 2 2 1 2 1 2 1 r t m D C r t m D r v m u C S u r a v C u q x y x + + − + + − = σ σ δ δ ρ
che, tenendo conto delle relazioni u=rR , a~y =ur e β =v/u può essere
riscritta nella forma:
4 4 4 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 4 2 1 4 4 4 4 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 4 4 2 1 const R y x y const u y x y y x x x x C a l t m D R l t C u C S a R t m D l a m C a l t m D u C S a u l t C l a m a u t m D u q = = + + + − + = = + + − + + = 2 2 2 2 ~ 4 2 1 ~ ~ 2 1 ~ 4 ~ 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 σ σ σ σ δ δ ρ β δ ρ β δ (4.38)
Infine, introducendo l’espressione (4.36) relativa all’angolo di assetto β si ottiene per il parametro q/u l’espressione valida a regime:
4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 2 1 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 2 1 const R y y y x y const u y y x y y x y x y x y x y x y x y C a l t m D a l C t m D R l t C a R C S R l t C C a t m D l a m a C m l a C a l t m D a l C t m D u C S a u l t C l a m a u l t C C a t m D C m l a u q = = + + − + + − − + + = = + + − + + + − − + = 2 2 2 2 2 2 2 2 2 2 2 2 ~ ~ 4 ~ 2 1 1 4 ~ ~ ~ 2 1 ~ 4 ~ 1 4 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 σ σ σ σ σ σ σ σ σ σ σ σ δ δ ρ δ ρ δ (4.39) Attraverso la (4.39), che evidenzia il legame polinomiale del 2° ordine rispetto all’accelerazione laterale a regime, è possibile indagare il comportamento del veicolo nelle due manovre classiche a regime: manovra a velocità di avanzamento costante (Slow Ramp Steer) e manovra a raggio di curvatura costante (Steering Pad).
4.5.1.1 Slow Ramp Steer
La manovra consiste nell’aumentare progressivamente l’angolo volante con una rampa sufficientemente bassa
(
δ&sw ≤20deg/sec)
mantenendo costante la velocità di avanzamento. Il veicolo percorre una traiettoria a spirale la cui curvatura aumenta progressivamente dal valore nullo.Negli istanti iniziali della manovra, cioè per ~ ≅ay 0 si ha:
− + = − + = = = ≅ = → = → = → = → 2 2 2 2 2 cost 0 ~ 2 2 2 2 2 cost 0 ~ cost 0 ~ 2 cost 0 ~ 2 2 2 2 2 2 2 2 2 2 1 lim 2 2 ~ lim 0 lim 2 lim u SC C mD u t C l t C u SC C mD u t C l t C M u C SC C F u q x u a x o u a z u a x a u a x x y o y x x y y y x x y ρ η η ρ η η ρ σ σ σ β β σ σ σ σ σ (4.40)
da cui emerge come il parametro q/u sia legato direttamente alla resistenza aerodinamica all’avanzamento e sia inversamente proporzionale alla rigidezza longitudinale dell’assale posteriore. Inoltre è interessante notare come, sebbene in queste condizioni si annulli il momento di imbardata Mz2, i gradienti di sottosterzo e di assetto del veicolo con differenziale bloccato siano diversi da quelli che contraddistinguono il modello monotraccia classico dotato di differenziale ordinario.
In Appendice …. Vengono riportate le espressioni generali dei gradienti di sottosterzo ed assetto per la manovra a velocità di avanzamento costante.
4.5.1.2 Steering Pad
Molto più interessante si presenta l’influenza del differenziale bloccato sul comportamento del veicolo nella classica manovra di Steering Pad.
Infatti per velocità di avanzamento sufficientemente bassa
(
~ ≅ay 0)
, il parametro q/u risulta inversamente proporzionale al raggio di curvatura e direttamente proporzionale all’angolo di sterzo δ:δ lR t u q const R ay 4 lim 2 2 0 ~ ≅ = → (4.41)
Nel modello monotraccia classico l’angolo di sterzo δ che compare nella (4.41) è, per definizione, l’angolo di sterzo cinematico o angolo di Ackermann ed è semplicemente il rapporto tra il passo ed il raggio di curvatura, ossia pari a l/R. Purtroppo, in un veicolo dotato di differenziale bloccato, la differenza tra gli scorrimenti longitudinali delle due ruote posteriori ed il momento di imbardata Mz2 ad essa associata fa sì che l’angolo di sterzo necessario per percorrere un curva di raggio R alla velocità minima (velocità di sostentamento) sia legato anche alle rigidezze, longitudinali e laterali, equivalenti dei due assali. In termini matematici si ha: + ≅ ⇒ − = ≅ + − ≅ − = → 2 2 2 2 2 1 0 ~ 2 ~ 1 4 ~ 1 1 lim 2 2 2 1 2 R t C C R l R l lR t C C C C l M y x y x y y y z const R a σ σ σ σ σ σ δ δ α α (4.42)
Dalla (4.42) è possibile riscrivere la (4.41) in forma esplicita: + = ≅ = → 2 2 2 2 2 2 0 ~ 2 ~ 1 2 4 lim 2 R t C C R t lR t u q y x y const R a δ σ σ (4.43)
La (4.43) mostra che a velocità di avanzamento ridotta, lo scorrimento longitudinale medio dell’assale posteriore è funzione sia di un parametro cinematico quale il rapporto tra la semicarreggiata posteriore ed il raggio di curvatura, sia dei parametri costruttivi del veicolo, in particolare delle rigidezze,longitudinale e laterale, equivalenti dei due assali.
Attraverso la (4.43) è possibile esplicitare i gradienti di sottosterzo e di assetto per valori sufficientemente piccoli dell’accelerazione laterale a regime, ovvero della velocità di avanzamento:
+ − = + + − = = → = → 2 2 2 2 2 2 cost 0 ~ 2 2 2 2 2 2 2 2 cost 0 ~ 2 ~ 1 2 lim 1 4 ~ 2 ~ 1 2 ~ lim 2 2 2 2 R t C C R t l t C mD R l t C C R t C C R t l t C mD y x y o y y x y x y y u a o u a σ σ σ β β σ σ σ σ σ η η η η (4.44) È importante sottolineare come, a differenza del modello monotraccia classico il cui gradiente di assetto ηβo (nella manovra a
raggio di curvatura costante) dipende esclusivamente dalle caratteristiche costruttive del veicolo quali la massa e la rigidezza di deriva dell’assale posteriore, nel modello di veicolo con differenziale bloccato ηβ è funzione del raggio di curvatura stesso ovvero dal
parametro di manovra. Non solo, ma il gradiente di assetto dipende anche dalla rigidezza laterale (e quindi di deriva) equivalente dell’assale anteriore.
4.5.2 Comportamento transitorio
L’introduzione del bloccaggio del differenziale comporta, come detto in precedenza, la risoluzione di un sistema di equazioni differenziali lineare nelle variabili di stato v
( )
t ed r( )
t (essendo la velocità di avanzamento u assegnata) ma non lineare nel parametrou
analitica ed di ottenere una soluzione in forma chiusa. Tuttavia, nel caso di velocità di avanzamento costante e di resistenza all’avanzamento ridotta, è possibile considerare q/u=σx ≅cost ottenendo un modello completamente lineare con il quale studiare il comportamento transitorio del veicolo dotato di differenziale bloccato.
Il primo passo consiste nello studio della stabilità di moto. A questo scopo risulta conveniente riscrivere la matrice dei coefficienti A (eq. 4.26) nella seguente forma, sotto l’ipotesi q/u<<1 ossia 1−q/u≅1:
− + + − + − + − = = u q J t u m D Ju t C Ju a C a C Ju a C a C u mu a C a C mu C C u q u x 2 2 2 2 2 2 2 2 1 1 2 2 1 1 2 2 1 1 2 1 4 , 2 σ A A (4.45) dove 1 1 C y C = σ e 2 2 C y
C = σ sono le rigidezza di deriva dei due assali, mentre
2
x
Cσ rappresenta la rigidezza longitudinale equivalente dell’assale posteriore.
La soluzione generale w
( )
t di (2.35) è data dalla somma dell’integrale wo( )
t del sistema omogeneo associato e di un integrale particolare wp( )
t( )
t wo( )
t wp( )
tw = +
Purtroppo, nel caso generale in cui sia A
( )
t ≠cost non è possibile ottenere analiticamente queste soluzioni perché il sistema, anche se lineare, ha coefficienti dipendenti dal tempo. Se invece è A( )
t =cost il sistema di equazioni differenziali (2.35) diventa a coefficienti costanti, e ciò permette di ottenere la soluzione in forma analitica, almeno per la parte omogenea che verifica w&o =Awo. Si tratta quindi di un’ipotesi di grave rilevanza per i successivi sviluppi.Come noto, nel caso di equazioni differenziali lineari a coefficienti costanti si ipotizza una soluzione esponenziale
( )
(
( ) ( )
)
t o o t r t e v t x λ wo = , = (4.46)da cui segue subito w&o
( )
t =λxeλt. Sostituendo ed eliminando eλt, si perviene immediatamente ad un classico problema agli autovalori per la matrice Ax Ax=λ
Gli autovalori sono dati dalle radici dell’equazione caratteristica
(
)
0det A− Iλ =
che, nel caso di matrici 2× , diventa 2
( )
det( )
02 − Aλ+ A =
λ tr
Risolvendo, si ottengono i due autovalori λ1 e λ2
( )
( )
( )
2 A A A 2 4det 2 , 1 − ± =tr tr λ (4.47)La tr
( )
A ed il det( )
A sono legati agli autovalori dalle relazioni( )
A =λ1+λ2tr (4.48)
( )
1 2det A =λλ (4.49)
Si possono verificare 3 casi:
1. ∆=tr
( )
A 2−4det( )
A <0, allora si hanno due autovalori complessi e coniugati e la soluzione dipende dalla parte reale degli autovalori:• se Re
( )
λ1 <0eRe( )
λ2 <0la soluzione è periodica smorzata con 0lim =
∞ → wo
t ;
• se almeno una parte reale dei due autovettori è positiva allora la soluzione è ancora periodica ma divergente cioè
∞ = ∞ → wo t lim .
2. ∆=0, allora si hanno due autovalori reali e coincidenti e la soluzione dipende dal segno degli autovalori:
• se entrambi gli autovalori sono negativi la soluzione è aperiodica con lim =0
∞ → wo
t ;
• se gli autovalori sono positivi la soluzione è aperiodica con ∞ = ∞ → wo t lim .
3. ∆>0, allora si hanno due autovalori reali e distinti e la soluzione dipende dal segno
degli autovalori:
• se entrambi gli autovalori sono negativi la soluzione è aperiodica con lim =0
∞ → wo
t ;
• se almeno uno degli autovalori sono positivi la soluzione è aperiodica con =∞
∞ → wo
t
lim .
In generale si dice che il sistema è stabile quando, dopo un certo tempo sufficientemente lungo le variabili di stato assumono valori praticamente indipendenti dal tempo. In queste condizioni l’integrale particolare rappresenta la soluzione a regime mentre l’integrale dell’omogenea associata costituisce la parte transitoria della soluzione che decade con il passare del tempo, perlomeno fintanto che il sistema è stabile.
Da quanto appena detto discende subito la definizione matematica di stabilità di marcia:
“Un sistema lineare si dice asintoticamente stabile se e solo se i due autovalori hanno parte reale negativa”
( )
0 e Re( )
0 Re
stabilità ⇔ λ1 < λ2 <
Per fortuna, si può studiare la stabilità anche senza calcolare direttamente i due autovalori ma solo considerando le due relazioni (4.48) e (4.49). Affinché entrambi gli autovalori abbiano parte reale negativa (sistema stabile) occorre e basta che siano verificate le seguenti due condizioni
( )
0 e det( )
0 tr
stabilità ⇔ A < A > (4.50)
A differenza del modello monotraccia classico per il quale la condizione sulla tr
( )
A risulta sempre verificata, per il modello di veicolo con differenziale bloccato la condizione tr( )
A <0 si realizza se(
)
(
)
(
)
2 2 2 2 2 2 2 2 2 2 1 2 1 2 /2 u m t D t C a k C a k C u q + + + + σx < (4.51)dove si è posto J =mk2, essendo k il raggio di inerzia. La condizione sul det
( )
A può scritto in termini di:( )
(
)
(
)
(
)
0 2 / 0 det 2 1 2 2 2 2 2 2 1 2 2 2 1 + + 2 − + < + ⇔ < u q J t D C C u J m t C C C u u l mJ l C C ηo σx A (4.52) che evidenzia come un gradiente di sottosterzo (secondo la definizione classica) positivo non sia sinonimo di stabilità per un veicolo con differenziale bloccato.4.5.3 Esempio numerico
Utilizzando le formule ottenute se ne comprende meglio il valore e l’utilità.
Si consideri il veicolo a trazione posteriore identificato dalle stesse caratteristiche costruttive definite in § 2.7.5, in particolare:
• Massa m=1695kg e momento di inerzia J =3293 kgm2;
• Semipassi a1 =1.032m e a2 =1.668m, da cui l=2.7m;
• Altezza del baricentro hG =0.55m, altezze dei centri di rollio
anteriore e posteriore pari rispettivamente a h1=20mm e
mm h2 =100 ;
• Rigidezze verticali molle anteriore e posteriore, kfm1 =20N/mm e mm
N kfm 20 /
2 = ;
• Rigidezze equivalenti antirollio a terra anteriore e posteriore,
mm N
kfb1 =45 / e kfb2 =15N/mm;
• Variazioni di convergenza in scuotimento anteriore e posteriore,
mm z1=−0.15°/100
ε e εz2 =0.01°/100mm;
• Variazioni di convergenza sotto carico laterale anteriore e posteriore, εfy1=−0.1°/kN e εfy2 =0.1°/kN;
• Rapporto di sterzo ηsw =13.2;
• Rigidezze di deriva dei pneumatici C0 C0 70000N/rad
2
1 = α =
α ;
• Rigidezza allo scorrimento longitudinale del pneumatico
posteriore, C N
x 105000
0
2 = ;
• Variazione della rigidezza di scorrimento in funzione del carico verticale, 26.
2 =
x
σ
ς
Le rigidezze verticali di molla e barra antirollio, le carreggiate e le altezze dei centri di rollio definiscono il gradiente di rollio stazionario,
pari a 4.56 °/g, ed i coefficienti σi (2.25) di ripartizione del trasferimento di carico verticale, rispettivamente σ1=σ2 =0.265.
Le rigidezze di deriva effettive degli assali (2.31) anteriore e posteriore sono, come si è visto, rispettivamente Ceff,1=C1=80778N/rad
e Ceff,2 =C2 =172415N/rad ; tuttavia il fatto che la capacità direttiva
anteriore sia minore di quella posteriore, ovvero C1a1 −C2a2 <0, non è sinonimo, nel caso di veicolo dotato di differenziale bloccato, di gradiente di sottosterzo positivo, in quanto esso è funzione dei parametri di manovra, come la velocità di avanzamento u o il raggio di curvatura
R.
Ad esempio, in una manovra a velocità di avanzamento costante, passando dai 50 ai 100 km/h, il gradiente di sottosterzo (al volante) assume valori compresi tra η50 =104.2°/g e η100=74°/g, entrambi superiori al gradiente di sottosterzo del veicolo con differenziale libero,
g / 3 . 68 0 = °
η . Questo significa che fino alla velocità di 100kmh il termine cinematico nella (4.33) prevale sul termine elastico (legato a q/u) del gradiente di sottosterzo.
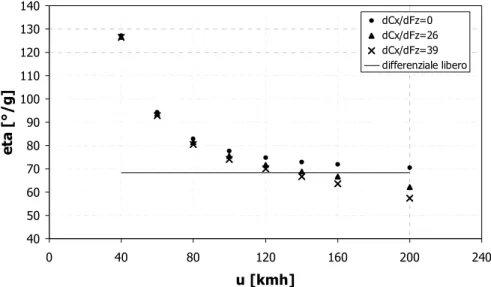
In fig. 4.4 è rappresentato l’andamento del gradiente di sottosterzo per un veicolo dotato di differenziale bloccato in funzione
40 50 60 70 80 90 100 110 120 130 140 0 40 80 120 160 200 240 u [kmh] e ta [° / g ] dCx/dFz=0 dCx/dFz=26 dCx/dFz=39 differenziale libero
Fig. 4.4: andamento del gradiente di sottosterzo in funzione della velocità di avanzamento.
della velocità di avanzamento u e per diversi valori della variazione della rigidezza allo scorrimento del pneumatico rispetto al carico verticale. Si noti come, per / 0
2
2 =dC x dFz =
x σ
σ
ς , ossia per rigidezza di
scorrimento costante, il gradiente di sottosterzo del veicolo con differenziale bloccato risulti sempre superiore a quello del veicolo con differenziale libero (linea continua), coerentemente alla (4.33). La variazione (positiva) della rigidezza allo scorrimento in funzione del carico verticale comporta, invece, una riduzione, per ogni valore di velocità di avanzamento, del gradiente di sottosterzo rispetto al caso in
cui / 0 2 2 =dC x dFz = x σ σ ς . In particolare per u=u ≅140kmh
(
/ 26)
2 dFz = dC xσ si raggiunge l’uguaglianza dei gradienti sottosterzo del
modello di veicolo con differenziale libero e quello con differenziale bloccato. Per u>u l’effetto elastico diventa predominante su quello cinematico ed il gradiente di sottosterzo del veicolo con differenziale bloccato risulta inferiore a quello con differenziale libero e, per valori elevati di ςσx21 e di u , può diventare negativo (veicolo sovrasterzante).
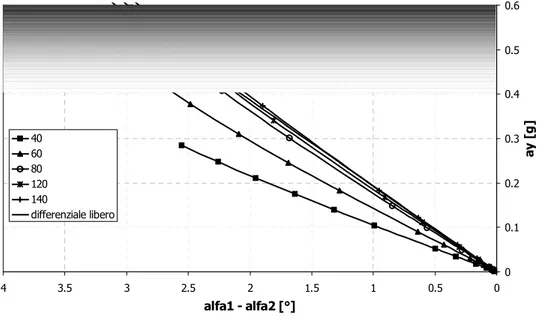
L’handling diagram relativo al modello di veicolo con differenziale bloccato nella manovra a velocità di avanzamento costante,
0 0.1 0.2 0.3 0.4 0.5 0.6 0 0.5 1 1.5 2 2.5 3 3.5 4 alfa1 - alfa2 [°] a y [ g ] 40 60 80 120 140 differenziale libero
e per diversi valori di u è rappresentato in fig. 4.5. Ancora una volta emerge l’impatto della manovra sul comportamento direzionale del veicolo con differenziale bloccato, col gradiente di sottosterzo che diminuisce all’aumentare della velocità di avanzamento.
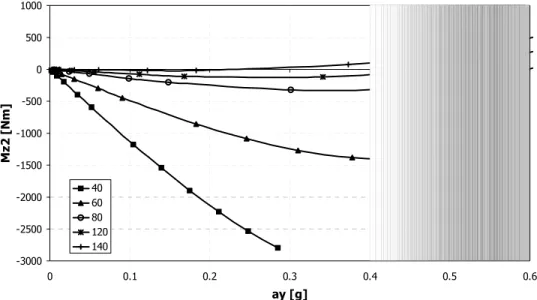
Si noti inoltre la non linearità di comportamento rispetto all’accelerazione laterale. Questo è dovuto principalmente al legame non lineare del momento di imbardata Mz2 rispetto all’accelerazione laterale
e alla velocità di avanzamento, il cui andamento è rappresentato in fig. 4.6.
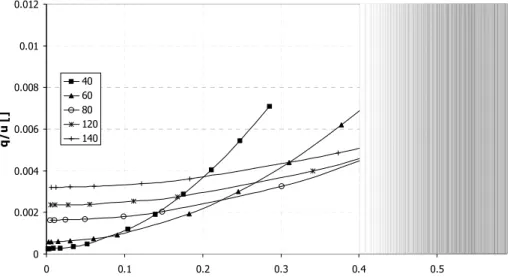
In fig. 4.7, infine, è rappresentato l’andamento del parametro
u
q/ . Si noti che, come ipotizzato in (4.8), si ha 0<q/u<<1.
Si può studiare adesso il comportamento transitorio del veicolo in una idealizzazione della prova di colpo di sterzo. Nella realtà, una volta lanciata la vettura in marcia rettilinea ad una certa velocità (di norma 80 - 100 km/h), si dà una brusca sterzata (con variazione dell’angolo del volante di almeno 250 °/s) e si attende che il moto si stabilizzi mantenendo fisso l’angolo volante per un tempo sufficiente (spesso bastano 3 s). Durante tutta la manovra si tiene fissa l’alimentazione del motore, senza cercare di compensare l’inevitabile calo della velocità di avanzamento. -3000 -2500 -2000 -1500 -1000 -500 0 500 1000 0 0.1 0.2 0.3 0.4 0.5 0.6 ay [g] M z 2 [ N m ] 40 60 80 120 140
Fig. 4.6: Andamento del momento di imbardata in funzione dell'accelerazione laterale.
Per semplicità si suppone in questa sede che il colpo di sterzo avvenga in un tempo nullo (step – steer input) con velocità di avanzamento u costante.
Dal punto di vista matematico, si tratta di risolvere il problema differenziale non lineare (4.25) o 4.26) con angolo di sterzo δ =cost. e con condizioni iniziali nulle w
( )
0 =(
v( ) ( )
0,r 0) ( )
= 0,0 , che corrispondono, appunto, alla marcia rettilinea. Occorre anche fissare la velocità di avanzamento u .In prima istanza assumiamo una velocità di avanzamento pari a
kmh
u=60 (prossima alla velocità caratteristica del veicolo con differenziale libero) con un angolo volante tale da far raggiungere ai due modelli medesimi valori stazionari. Le risposte dei due modelli, con differenziale libero (linea sottile) e bloccato (linea spessa), in termini di accelerazione laterale e velocità di imbardata, è rappresentato in fig. 4.8.
Se l’andamento nel tempo della velocità di imbardata risulta identico per i due veicoli, si registrano, invece, delle differenze significative nello sviluppo dell’accelerazione laterale; in particolare quello del modello con differenziale bloccato è caratterizzato da una minore differenza tra il valore stabilizzato ed il valore minimo (dopo il colpo di sterzo). 0 0.002 0.004 0.006 0.008 0.01 0.012 0 0.1 0.2 0.3 0.4 0.5 ay [g] q / u [ ] 40 60 80 120 140
Fig. 4.7: andamento del parametro q/u in funzione dell'accelerazione laterale.
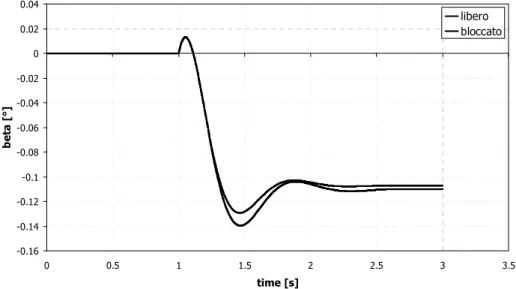
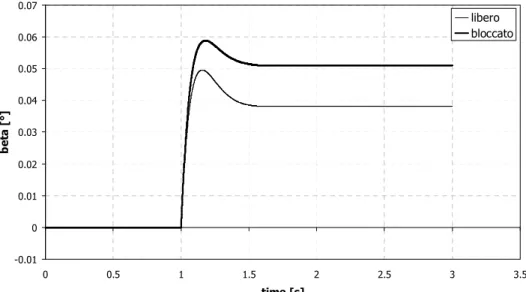
In termini di angolo di assetto, rappresentato in fig. 4.9, il veicolo dotato di differenziale bloccato è caratterizzato da un maggior valore (positivo) stabilizzato ma da un minor rapporto tra primo picco e valore stabilizzato. -2 0 2 4 6 8 10 12 14 0 0.5 1 1.5 2 2.5 3 3.5 time [s] r [d e g / s ] -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 a y [ g ] r ay
Fig. 4. 8: Colpo di sterzo a 60 kmh, andamento della velocità di imbardata e dell'accelerazione laterale. -0.01 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0 0.5 1 1.5 2 2.5 3 3.5 time [s] b e ta [ ° ] libero bloccato
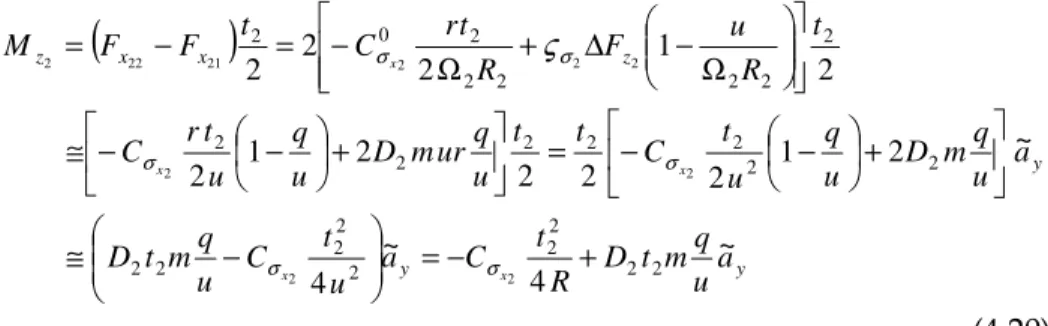
![Fig. 4. 10: Colpo di sterzo a 60 kmh, andamento di forze e momenti.01000200030004000500060007000800000.511.522.53 3.5time [s]Fy [N] -1600-1400-1200-1000-800-600-400-2000 Mz2 [Nm]Fy1Fy2](https://thumb-eu.123doks.com/thumbv2/123dokorg/7233943.78876/32.723.104.614.108.393/fig-colpo-sterzo-kmh-andamento-forze-momenti-time.webp)