Controllo di satelliti in formazione

(1)

A coloro che mi hanno sostenuta nei momenti pi`u bui e che non hanno mai smesso di credere in me.

(2)

Sommario

Il recente incremento dell’ utilizzo di satelliti in formazione in molteplici tipi di missione, rende lo studio di nuovi sistemi di controllo un argomento di grande attualit`a.

L’obiettivo principale del presente lavoro di tesi `e l’implementazione di un sistema di controllo per satelliti in formazione, capace di funzionare per qual-siasi tipo di orbita.

Verr`a presentata una legge di controllo non lineare basata sul metodo di Ljapunov applicabile al posizionamento e allo station keeping di uno o pi`u satelliti forniti di propulsori a bassa spinta.

(3)

Vorrei ringraziare innanzitutto il Prof. Mengali oltre che per i preziosi consi-gli, soprattutto per la grande umanit`a che ha sempre dimostrato nei miei confronti.

Vorrei anche ringraziare tutti coloro che, con la loro disponibilit`a, mi hanno aiutata nella stesura di questa tesi: il prof. Casarosa, Alessandro, i ragazzi del laboratorio di Maccanica del Volo e quelli del laboratorio Fly by wire. I pi`u sentiti ringraziamenti vanno ai miei genitori, per avermi sempre appog-giata, a mio fratello per aver sopportato i miei nervosismi, a mia sorella per il ruolo di fondamentale importanza che ha nella mia vita.

Non posso certo omettere coloro che hanno condiviso con me questo percorso di studi e tra questi in particolare Marco e Lapo, per la profonda amicizia che ci lega.

Grazie anche a Guia, Carlotta, Giulia, Betta, Tizi, Elisabetta, Stella, Fran-ceschina e Roberta per la loro amicizia.

Infine un grazie particolare va a Renato...il pi`u bel regalo che mi ha fatto questa facolt`a!

(4)

1

Introduzione

1.1 Introduzione al concetto di volo in

for-mazione

Un gruppo di satelliti in volo in formazione rappresenta il nuovo modello di riferimento per la sorveglianza dallo spazio e per il rilevamento a distanza. In tale modello, diversi piccoli satelliti volano in formazione, vicini tra loro, e coordinano le loro attività in modo tale che, tramite tecniche basate su raggi di luce artificiali e tecniche interferometriche a ordine sparso, il gruppo di satelliti può operare come se fosse un unico satellite di dimensioni molto più grandi.

La formazione di satelliti funziona come un satellite virtuale con un raggio di copertura effettiva molto grande, senza la necessit`a delle pesantissime infras-trutture che richiederebbe un unico satellite capace di garantire il medesimo raggio di copertura.

Il concetto di formazione di satelliti presenta molti vantaggi rispetto ad un solo grande satellite. I principali sono:

- Ciascun satellite è più piccolo, più leggero, più semplice e di più facile fabbricazione;

- L’economia di scala fa s`ı che la costruzione di molti satelliti sia meno costosa della costruzione di un singolo satellite;

- La formazione pu`o adattarsi all’avaria di uno dei satelliti e il satellite in avaria pu`o essere rimpiazzato;

(5)

- La formazione di satelliti pu`o riconfigurare le orbite dei vari satelliti del gruppo in modo da ottimizzarlo per differenti missioni.

Una costellazione di sotto-gruppi di satelliti permetterebbe una copertura di tutto il pianeta da orbite basse (LEO) e/o una copertura continua nel tempo.

1.2 Obiettivo della tesi

L’introduzione di satelliti in formazione ha reso necessario passare da un sistema di controllo orbitale da Terra (in modo da eseguire manovre a ciclo aperto per permettere di seguire orbite precedentemente pianificate), ad un sistema di controllo a retroazione basato su modelli lineari in grado di af-frontare perturbazioni impreviste e mantenere la traiettoria ottimale.

Il presente lavoro di tesi si pone l’obiettivo di fare un ulteriore passo in avanti, sintetizzando un sistema di controllo non lineare a retroazione dei parametri orbitali equinoziali con matrice di guadagno variabile nel tempo, basato su una dinamica perturbata dagli effetti dello schiacciamento dei poli terrestri, per il posizionamento ed il mantenimento della formazione di satelliti. La principale novità apportata rispetto al simile metodo di controllo basa-to sui parametri orbitali classici, è la possibilità di trattare tutti i tipi di orbite senza incorrere in problemi di singolarità dei parametri orbitali (più chiaramente, si potranno trattare anche orbite equatoriali e/o circolari).

1.3 Organizzazione della tesi

Nel presente lavoro di tesi saranno riportati in primo luogo alcuni richiami di Meccanica del volo spaziale(Capitolo 2), necessari per descrivere il pro-pagatore orbitale sviluppato in (Capitolo 3 ). Poi, dopo un breve excursus sui parametri orbitali equinoziali(Capitolo 4), sarà riportato l’algoritmo di passaggio da elementi equinoziali istantanei ad elementi equinoziali medi ( l’opportunità dell’ utilizzo di questi ultimi sarà precisata nel seguito della tesi )(Capitolo 5 ).

(6)

1 – Introduzione

scopo prefissatoci (Capitolo 6 ), cui faranno seguito alcuni risultati di simu-lazioni al calcolatore compiute con gli strumenti precedentemente descritti (Capitolo 7).

(7)

2

Dinamica della formazione

La dinamica di una formazione di satelliti viene descritta tradizionalmente utilizzando il concetto di moto assoluto e quello di moto relativo. La di-namica di tali moti viene spesso descritta tramite il modello kepleriano dei due corpi, considerando il pianeta attrattore a simmetria sferica. In realtà gli effetti perturbativi dovuti alla non sfericità del pianeta sono sensibili, soprat-tutto se si tratta di formazioni di satelliti in orbita bassa. Nella trattazione seguente, per motivi di semplicità, sono state trascurate le perturbazioni dovute a presenze di altri corpi, alla pressione di radiazione solare ed alla resistenza atmosferica.

In questo capitolo verr`a presentata una rapida descrizione della meccani-ca kepleriana, per soffermarci poi a descrivere nel dettaglio i modelli di perturbazione usati per la creazione del propagatore.

2.1 Sistemi di riferimento

I sistemi di riferimento usati nel seguito sono [1]:

• sistema di riferimento planetocentrico equatoriale (IJK ) (Figura 2.1): terna con origine nel centro del pianeta, ˆI rivolto verso un punto fisso (il primo punto dell’ariete nel caso terrestre) e appartenente al piano equatoriale, ˆK equiverso alla velocit`a di rotazione del pianeta e ˆJ tale da rendere la terna levogira.

(8)

2 – Dinamica della formazione P i a n o e q u a t o r i a l e P o l o N o r d O g g e t t o S f e r a c e l e s t e P i a n o m e r i d i a n o y l d x r z O I^ J^ K^

Figura 2.1: Definizione della terna planetocentrica equatoriale (IJK)

equiverso al momento della quantit`a di moto dell’orbita e ˆQ tale da rendere la terna levogira.

P e r i a s s e W^ Q^ P^ P^ Q^ r n y w x w z w y _w x w

Figura 2.2: Definizione della orbitale (PQW)

• sistema di riferimento locale (RTN ) (Figura 2.3): terna con origine nel baricentro del satellite, îr versore del vettore posizione, ît versore del vettore velocità e în tale da rendere la terna levogira. Questo è comunemente detto sistema di Hill.

Per passare da un sistema di riferimento ad un altro sono state usate le matrici di rotazione definite in [2,1].

(9)

z x y O r

i

_r o r b i t a ^

i

t ^

i

n ^

Figura 2.3: Definizione della terna locale

2.2 Moto kepleriano

Il moto kepleriano [2,1] si riferisce al problema dei due corpi, uno dei quali (il satellite) abbia massa trascurabile rispetto all’altro (il pianeta). Riferendosi alle figure 2.1 e 2.2, l’equazione del moto

¨

r = −µ

r3r (2.1)

ha come soluzione una conica di espressione

r = p

1 + e cos ν (2.2)

A seconda del valore assunto dall’eccentricit`a si ottengono orbite circolari (e = 0), ellittiche (0 < e < 1), o iperboliche (e > 1). Nel moto kepleriano sono presenti due costanti del moto:

• l’energia meccanica specifica:

E , v

2

2 − µ

r (2.3)

• il momento della quantit`a di moto specifica:

h , r ∧ v (2.4)

(10)

2 – Dinamica della formazione

Per orbite ellittiche, determinata l’anomalia eccentrica E, definita l’anomalia media

M , E − e sin E (2.5)

detti t0 l’istante di passaggio dal periasse, M0 l’anomalia media al periasse e

n il moto medio,

n = r

µ

a3 (2.6)

la relazione cercata risulta:

n(t − t0) = 2kπ + M − M0 (2.7)

dove k `e un numero intero che tiene conto del fatto che il satellite pu`o aver compiuto k giri prima del tempo t.

2.2.2 Formule universali per le orbite coniche

Il problema di Keplero `e stato risolto sulla base di una formulazione uni-versale, valida per qualunque tipo di orbita. La dimostrazione dei risultati seguenti `e reperibile in letteratura [2]. Nel seguito si utilizzeranno alcune variabili ausiliarie: √ µ dt dχ = r (2.8) σ , dr dχ (2.9) α , 1 a (2.10) z , αχ2 _(2.11)

Da queste relazioni si ottengono tre equazioni differenziali nelle variabili (χ, z, σ), le cui soluzioni sono

√ µ(t − t0) = χ3S + r0· v0 √ µ χ 2_{C + r} 0χ(1 − zS) (2.12) r = χ2_{C +} r0· v0 √ µ χ(1 − zS) + r0(1 − zC) (2.13) σ = r0√· v0 µ (1 − zC) + (1 − α r0)χ(1 − zS) (2.14)

(11)

in cui C e S sono dati da: C(z) =        1−cos√z z , per z > 0 1/2, per z = 0 1−cosh√−z z , per z < 0 (2.15) S(z) =        √ z−sin_√ √z z3 , per z > 0 1/6, per z = 0 sinh√_√−z−√−z −z3 , per z < 0 (2.16)

In [2] è descritta una tecnica numerica di soluzione che è stata impiegata nell’implementazione del propagatore. Ottenuti i valori delle variabili so-pra definite, vengono valutate posizione e velocità tramite i coefficienti di Lagrange f e g utilizzando le seguenti espressioni:

r = f r0+ gv0 (2.17) v = ˙f r0+ ˙gv0 (2.18) dove f = 1 −χ 2 r0 C(z) ; g = t − t0− χ3 √ µS(z) (2.19) ˙ f = √ µ r0r χ[zS(z) − 1] ; ˙g = 1 − χ2 r C(z) (2.20)

2.3 Variazione dei parametri orbitali

Una volta ottenute posizione e velocit`a nel sistema IJK si passa ai parametri orbitali classici con la metodologia descritta in [1] pp. 48–50 e riassunta nel paragrafo 3.1.1.

2.3.1 Parametri orbitali classici

(12)

pertur-2 – Dinamica della formazione

parametri orbitali come [1]:

˙a = 2a 3 2 p µ(1 − e2₎[e sin ν Fr+ (1 + e cos ν) Ft] (2.21) ˙e = s a(1 − e2₎

µ [sin ν Fr+ (cos ν + cos E) Ft] (2.22) ˙i = s a(1 − e2₎ µ cos u 1 + e cos ν Fn (2.23) ˙ Ω = s a(1 − e2₎ µ sin u (1 + e cos ν) sin iFn (2.24) ˙ω = s a(1 − e2₎ µ · − sin u cot i 1 + e cos νFn + 2 + e cos ν

e(1 + e cos ν) sin ν Ft− cos ν e Fr ¸ (2.25) ˙ M = n − r a µ 1 − e2 e(1 + e cos ν) £

(2e − cos ν − e cos2ν) Fr

+(2 + e cos ν) sin ν Ft] (2.26)

dove Fr, Ft, Fn sono le componenti della risultante delle perturbazioni ris-petto alla terna RTN.

Si noti che le formule citate sono valide solo per orbite ellittiche e non equatoriali. Per tali casi si ottengono singolarit`a, in quanto alcuni parame-tri non sono definibili. Inoltre avvicinandosi a tali casi estremi si trovano sensibili errori numerici confrontando un propagatore orbitale basato sulla formulazione universale con uno basato sulla risoluzione diretta della (2.1).

2.3.2 Parametri equinoziali

Per i motivi sopra descritti risulta necessario definire nuovi parametri che non vadano incontro a singolarit`a. Tali vengono chiamati parametri equinoziali e per la loro trattazione rimandiamo al Capitolo 4

(13)

x z y K r I W J P e r i a s s e n o d o a s c e n d e n t e n i n w W h S a t e l l i t e P

Figura 2.4: Definizione dei parametri orbitali

2.4 Modelli di perturbazione

Per rendere il propagatore adatto a riprodurre “fedelmente” la dinamica del satellite occorre definire alcuni modelli matematici che introducano delle per-turbazioni nella dinamica ideale kepleriana. Nei paragrafi seguenti vengono descritte le perturbazioni dovute alla tridimensionalit`a del campo gravitazio-nale (seguendo la trattazione di [3]).

2.4.1 Perturbazioni dovute alla triassialit`

a del campo

gravitazionale

(14)

2 – Dinamica della formazione y l d x r z O

Figura 2.5: Sistema di riferimento IJK e sferico

U = Gm r " 1 − ∞ X n=2 Jn µ R r ¶_n Pn(sin δ) # (2.27) dove r è la distanza del punto dal centro di massa del corpo, Jn sono delle costanti dette armoniche settoriali, R è il raggio equatoriale del corpo, m è la massa del corpo, δ è la sua declinazione ed infine Pn(sin δ) è il polinomio di Legendre di ordine n in sinδ.

Nel caso generale di un corpo che non ammetta simmetrie, il potenziale pu`o essere espresso mediante una relazione del tipo:

U = Gm r ( 1 − ∞ X n=2 n X m=0 µ R r ¶n

[Cnmcos(mλ) + Snmsin(mλ)] Pnm(sin δ)

)

(2.28)

dove λ `e la longitudine del punto considerato e i termini Pnm(sin δ) sono le funzioni associate di Legendre in sin δ, ovvero:

Pnm(x) = 1 2n_n! ¡ 1 − x2¢m2 d n+m_(x2_{− 1)}n dxn+m (2.29)

Si noti che per m = 0 le funzioni associate di Legendre coincidono con i polinomi di Legendre ed il potenziale si riduce alla (2.27), dove Cn0 = Jn. Il potenziale nel caso pi`u generico della (2.28) comprende anche le cosidette armoniche settoriali (corrispondenti al caso n = m) e tesserali (per n 6= m). Confrontando i valori numerici delle armoniche terrestri [4] si nota come la

(15)

J2 sia di gran lunga la pi`u importante. Pertanto una dinamica basata solo

su essa `e gi`a un importante passo avanti rispetto alla dinamica kepleriana. Gradiente del potenziale

L’accelerazione di perturbazione si ottiene dal gradiente del potenziale gra-vitazionale di perturbazione, ricavato sottraendo dalla (2.28) il potenziale sferico definito dal primo termine della sommatoria:

Up = U − µ r (2.30) da cui Fp = −∇Up = − µ ∂Up ∂x î + ∂Up ∂y ˆj + ∂Up ∂z kˆ ¶ (2.31) Il potenziale è espresso in coordinate sferiche, pertanto è necessario applicare una trasformazione di coordinate:

Fp = ∂Up ∂r µ ∂r ∂r ¶ +∂Up ∂δ µ ∂δ ∂r ¶ +∂Up ∂λ µ ∂λ ∂r ¶ (2.32) I termini dell’equazione (2.32) si dimostrano essere [3]:

∂r ∂r = r r (2.33) ∂δ ∂r = 1 p x2_{+ y}2 µ −zr r2 + ∂z ∂r ¶ (2.34) ∂λ ∂r = 1 x2_{+ y}2 µ x∂y ∂r − y ∂x ∂r ¶ (2.35) Gli altri termini si ottengono per semplice derivazione e non sono qui riporta-ti. Nel toolbox costruito in ambiente Matlabr sono state ottenute le derivate in ambiente simbolico e le espressioni cos`ı ottenute sono state “copiate” in opportune function di veloce richiamo.

2.5 Effetti delle perturbazioni

(16)

dina-2 – Dinamica della formazione

simile tra loro la pressione di radiazione solare, la resistenza atmosferica e l’at-trazione dovuta agli altri corpi, come la Luna, danno contributi differenziali trascurabili rispetto a quelli dovuti all’asimmetria del campo gravitazionale, in special modo per l’armonica J2. Gli effetti principali di tale termine

sul-la dinamica di un singolo satellite consistono in una variazione secosul-lare dei parametri Ω, ω e n, riassumibili in ˙ Ω = −3 2nJ¯ 2 µ R p ¶₂ cos i (2.36) ˙ω = 3 2nJ¯ 2 µ R p ¶₂ µ 1 −5 2sin 2_i ¶ (2.37) ˙n = n · 1 + 3 2J2 √ 1 − e2 p2 µ 1 −3 2sin 2_i ¶¸ (2.38)

(17)

3

Propagatore orbitale

In Appendice B è riportato lo schema a blocchi del propagatore orbitale svi-luppato. Questo è basato sulla rettifica dell’orbita passo-passo, calcolando le derivate dei parametri equinoziali per effetto delle perturbazioni ed assu-mendole costanti per il successivo intervallo d’integrazione. In questo modo, ad esempio, a(i + 1) = a(i) + da/dt δt, in cui δt è il passo d’integrazione.

Il controllo dell’errore procede parallelamente e si basa sul metodo sug-gerito da Encke [1], con la sola differenza che la rettifica viene eseguita ad ogni passo e non solo quando l’errore raggiunge una certa tolleranza. Il su-peramento della tolleranza produce una riduzione di passo d’integrazione, per tornare eventualmente ad aumentarlo in caso di errore sufficientemente piccolo.

Per verificare i risultati `e stato utilizzato un propagatore basato sull’in-tegrazione diretta dell’equazione del moto (2.1) comprensiva dei disturbi (le espressioni sono state ottenute simbolicamente tramite Matlabr_{). Tale}

pro-pagatore è stato usato solo per il confronto dei risultati, in quanto molto più lento, a parità di precisione, a causa dell’irrigidirsi del problema matematico al ridursi dei controlli.

3.1 Il volo in formazione

(18)

3 – Propagatore orbitale

ad esempio la costellazione GPS. Invece “il volo in formazione prevede l’uso di un controllo attivo per mantenere la posizione relativa dei veicoli spaziali” [5]. La differenza, pertanto, risiede nel controllo attivo dello stato relativo. Esistono molti tipi di volo in formazione, tra cui:

Leader-Follower: configurazione base (vedi Figura 3.1) in cui i parametri orbitali sono tutti uguali, tranne l’anomalia vera.

Stessa traccia a terra: in questo caso esiste una differenza imposta ∆Ω e ∆ν tale da far percorrere ai satelliti “slaves” la stessa traccia a terra del master (vedi Figura 3.1).

Orbita relativa ellittica: spesso usata per inviare i dati dai “collectors” al “combiner ” centrale. Su questo tipo di formazione sono state compiute le simulazioni, trattandola nel caso sia presente o meno un reale satellite master (vedi Figura 3.2).

d n

d V

Figura 3.1: Leader-Follower e stessa traccia a terra

S u n

(19)

3.1.1 Definizione dell’orbita di riferimento

Nel caso in cui non sia presente un reale satellite di riferimento, `e necessario definirne uno fittizio in base al quale gli altri satelliti possano controllarsi: `e questo il caso del progetto Laser Interferometry Space Antenna (LISA), formazione di tre satelliti in orbita solare (vedi Figura 3.2). In tal caso occorre che ogni satellite conosca la posizione degli altri per poter calcolare la posizione del virtuale master.

Sono qui presentati due algoritmi per il calcolo dell’orbita del master : il primo è tratto da [6], mentre il secondo è stato utilizzato per le simulazioni i cui risultati sono riassunti nel capitolo 7. Prima di tutto però, è definito l’algoritmo che permette di passare ai parametri orbitali, note che siano la posizione e la velocità.

Algoritmo rv2po

Seguendo [1] si passa dalla posizione e velocit`a (reperibili ad esempio tramite sensori GPS) ai parametri orbitali classici nel modo seguente:

• Calcolo del semiasse maggiore a sfruttando la conservazione dell’energia meccanica specifica (2.3):

a = − µ

2E (3.1)

• Calcolo del momento della quantit`a di moto specifica h:

h = r ∧ v (3.2)

• Calcolo del versore nodale n:

ˆ

n = K ∧ hˆ

| ˆK ∧ h | (3.3)

• Calcolo del vettore eccentricit`a e: e = 1 µ h³ v2₋ µ r ´ r − (r · v)v i (3.4)

(20)

3 – Propagatore orbitale • Calcolo dell’inclinazione i: i = arccos Ã ˆ K · h h ! (3.5)

• Calcolo dell’ascensione retta del nodo ascendente Ω:

Ω = (

arccos(ˆI · ˆn), se ˆn · ˆJ > 0

2π − arccos(ˆI · ˆn), se ˆn · ˆJ < 0 (3.6)

• Calcolo dell’argomento del periasse ω:

ω = ( arccos¡n·eˆ e ¢ , se e · ˆK > 0 2π − arccos¡n·eˆ e ¢ , se e · ˆK < 0 (3.7)

• Calcolo dell’anomalia vera ν:

ν = ( arccos¡e·r er ¢ , se r · v > 0 2π − arccos¡e·r er ¢ , se r · v < 0 (3.8)

• Calcolo della latitudine vera u:

u = ( arccos¡n·rˆ r ¢ , se r · ˆK > 0 2π − arccos¡n·rˆ r ¢ , se r · ˆK < 0 (3.9) Algoritmo po master

1. In [6] `e definito il seguente algoritmo per la determinazione dei parame-tri orbitali del virtuale satellite master. Detto N il numero dei satelliti componenti il cluster, si proceda come segue

• Calcolo del momento totale delle quantit`a di moto hT:

hT = N X

j=1

(21)

• Calcolo del versore totale della linea nodale nT: nT = N X j=1 nj (3.11)

• Calcolo del vettore eccentricit`a totale eT:

eT = N X j=1 ej ⇒ eav = eT N (3.12)

dove eav `e il vettore eccentricit`a media.

• Calcolo dell’inclinazione dell’orbita master im:

im = arccos Ã ˆ K · hT hT ! (3.13)

• Calcolo dell’ascenzione retta del nodo ascendente dell’orbita mas-ter Ωm: Ωm = ( arccos(ˆI · ˆnT), se ˆnT · ˆJ > 0 2π − arccos(ˆI · ˆnT), se ˆnT · ˆJ < 0 (3.14)

• Calcolo dell’argomento del periasse dell’orbita master ωm:

ωm =    arccos ³ ˆ nT·eav eav ´ , se eav· ˆK > 0 2π − arccos ³ ˆ nT·eav eav ´ , se eav· ˆK < 0 (3.15)

• Calcolo dell’anomalia vera dell’orbita master νm:

νm = ( arccos¡eav·rh er ¢ , se rh· vh > 0 2π − arccos¡eav·rh er ¢ , se rh· vh < 0 (3.16)

(22)

3 – Propagatore orbitale

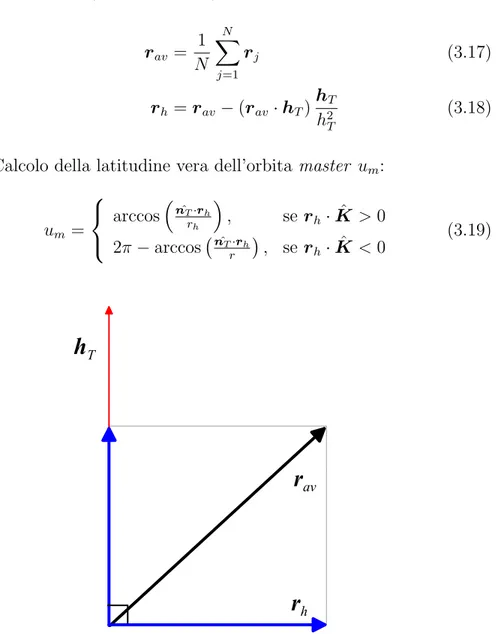
in cui rT `e la componente del vettore posizione medio, rav, orto-gonale a hT (vedi Figura 3.3):

rav = 1 N N X j=1 rj (3.17) rh = rav− (rav· hT) hT h2 T (3.18) • Calcolo della latitudine vera dell’orbita master um:

um =    arccos ³ ˆ nT·rh rh ´ , se rh· ˆK > 0 2π − arccos¡nˆT·rh r ¢ , se rh· ˆK < 0 (3.19)

h

_T

r

_{a v}

r

_h

Figura 3.3: Scomposizione del vettore posizione media

2. Un algoritmo pi`u semplice per la determinazione della posizione del master `e definibile nei seguenti passi:

• Calcolo del centro geometrico della formazione rav dalla (3.17) • Calcolo della velocit`a media vav:

vav = 1 N N X j=1 vj (3.20)

(23)

• Passaggio ai parametri orbitali tramite rv2po (vedi 3.1.1).

Entrambi gli algoritmi sono stati verificati, con il risultato di ottenere mag-giore robustezza dal secondo per la sua magmag-giore semplicit`a. La scelta deve comunque essere compiuta in base alle specifiche della missione.

(24)

4

Parametri orbitali equinoziali

La presenza di singolarit`a nella trattazione del moto dei satelliti, associate all’uso dei parametri orbitali classici, per orbite circolari e/o ad inclinazione nulla, ha spinto all’impiego di parametri alternativi capaci di supplire alle limitazioni di quelli classici.

I parametri che risultano pi`u adeguati a tale scopo sono i cosiddetti parametri orbitali equinoziali.

L’insieme di elementi equinoziali `e definito dai sei elementi seguenti: a → semiasse maggiore

P1 → componente del vettore eccentricit´a

P2 → componente del vettore eccentricit´a

Q1 → componente del vettore nodo ascendente

Q2 → componente del vettore nodo ascendente

λ → longitudine media

Il semiasse maggiore è lo stesso dei parametri orbitali classici. Il vettore eccentricità ha valore assoluto uguale all’ eccentricità e punta dalla terra al perigeo. Gli elementi P1 e P2 sono, rispettivamente, le componenti g e f del

vettore eccentricit`a nel sistema di riferimento equinoziale che verr`a descrit-to nel seguidescrit-to del paragrafo. Il vetdescrit-tore nodo ascendente ha valore assoludescrit-to dipendente dall’inclinazione e punta dalla terra al nodo ascendente. Gli ele-menti Q1 e Q2 sono, rispettivamente, le componenti g e f del vettore nodo

(25)

Andiamo adesso a definire il sistema di riferimento equinoziale.

Per ogni insieme di elementi equinoziali ci sono tre vettori (f,g,w) che defi-niscono il riferimento equinoziale. Questi vettori formano una terna levogira ortonormale con le seguenti propriet`a :

1. I vettori f e g giacciono sul piano dell’orbita del satellite.

2. Il vettore w `e parallelo al vettore momento angolare del satellite . 3. L’angolo tra f e il nodo ascendente `e uguale alla longitudine del nodo

ascendente (Ω).

Dal momento che siamo abituati a lavorare con i parametri orbitali classici `e molto utile, anche per comprendere meglio l’essenza dei parametri equinoziali stessi, vedere come si possono derivare questi ultimi partendo dagli elementi classici (e vice-versa).

4.1 Conversione da elementi orbitali classici

a elementi orbitali equinoziali

Le relazioni da utilizzare sono le seguenti:

P1 = e sin(ω + Ω) (4.1) P2 = e cos(ω + Ω) (4.2) Q1 = [tan µ i 2 ¶ ] sin Ω (4.3) Q2 = [tan µ i 2 ¶ ] cos Ω (4.4) λ = M + ω + Ω (4.5)

Dove M `e l’anomalia media.

Ci sono due longitudini ausiliarie associate con il set di elementi equinoziali: la longitudine eccentrica F e la longitudine vera L.

(26)

4 – Parametri orbitali equinoziali

L = ν + ω + Ω (4.7)

L’utilità di questi due parametri aggiuntivi risulterà evidente nell’algorit-mo di conversione da parametri equinoziali a posizione e velocità e nella modellizzazione degli effetti pertubativi dovuti alla nonsfericità del globo terrestre.

4.2 Conversione da elementi orbitali

equino-ziali a elementi orbitali classici

Per effettuare questa conversione `e in primo luogo necessario introdurre un angolo ausiliario ζ, che `e definito da:

sin ζ = p P1 P2 1 + P22 (4.8) cos ζ = p P2 P2 1 + P22 (4.9) Gli elementi classici sono dunque dati da:

e = q P2 1 + P22 (4.10) i = π 2 + 2 arctan q Q2 1+ Q22 (4.11) sin Ω = p Q1 Q2 1+ Q22 (4.12) cos Ω = p Q2 Q2 1+ Q22 (4.13) ω = ζ − Ω (4.14) M = λ − ζ (4.15)

Anomalia vera ed eccentricit`a vera sono date da:

E = F − ζ (4.16)

(27)

4.3 Conversione da elementi equinoziali a

po-sizione e velocit`

a

Poiché gli elementi equinoziali non hanno un’evidenza fisica immediata, risul-ta necessario determinare l’algoritmo di conversione da elementi equinoziali a posizione e velocità (e vice-versa), per avere una visione più tangibile del moto del satellite lungo la propria orbita.

Il primo passo di questa procedura consiste nell’esprimere i vettori di base del sistema di riferimento equinoziale (f,g,h) tramite le loro componenti nel sistema geocentrico equatoriale (x,y,z).

f = 1 1 + Q2 1+ Q22     1 − Q2 1+ Q22 2Q1Q2 −2Q1     (4.18) g = 1 1 + Q2 1+ Q22     2Q1Q2 1 + Q2 1− Q22 −2Q2     (4.19) w = 1 1 + Q2 1+ Q22     2Q1 −2Q2 1 − Q2 1− Q22     (4.20)

Il secondo passo `e trovare le anomalie eccentrica e media,F e L, rispettiva-mente. Per trovare F bisogna risolvere1 _{la forma equinoziale dell’equazione}

di Keplero:

λ = F + P1cos F − P2sin F (4.21)

Definiamo quindi le due quantit`a ausiliarie n (moto medio Kepleriano) e b: n = r µ a3 (4.22) b = 1 1 +p1 − P2 1 − P22 (4.23)

(28)

L sar`a quindi data da:

sin L = (1 − P22b) sin F + P1P2b cos F − P1

1 − P1sin F − P2cos F

(4.24) cos L = (1 − P12b) cos F + P1P2b sin F − P2

1 − P1sin F − P2cos F

(4.25) La distanza radiale del satellite dalla terra `e data da:

r = a(1 − P1sin F − P2cos F ) =

a(1 − P2

1 − P22)

1 + P1sin L + P2cos L

(4.26) Il terzo passo `e calcolare le componenti della posizione e della velocit`a del satellite, rispettivamente (X,Y ) e ( ˙X, ˙Y ), nel sistema di riferimento equino-ziale:

X = a[(1 − P 2

1 b) cos F + P1P2b sin F − P2] = r cos L (4.27)

Y = a[(1 − P 2

2 b) sin F + P1P2b cos F − P1] = r cos L (4.28)

˙ X = na2 r [P1P2b cos F − (1 − P 2 1 b) − P2] = na(P1+ sin L) p 1 − P 2 1 − P22 (4.29) ˙ Y = na 2 r [(1 − P 2 2 b) cos F − P1P2b sin F ] = na(P2+ cos L) p 1 − P 2 1 − P22 (4.30) Qui i puntini sopra le variabili indicano la differenziazione rispetto al tempo.

Il passo finale `e calcolare i vettori posizione e velocit`a:

r = Xf + Y g (4.31)

˙r = Xf + ˙˙ Y g (4.32)

4.4 Conversione da posizione e velocit`

a in

ele-menti equinoziali

Il primo passo del procedimento consiste nel calcolare il semiasse maggiore a, partendo dalla forma dell’energia nel problema dei due corpi:

a = 1 2 |r| − ˙ |r|2 µ (4.33)

(29)

Il secondo passo `e calcolare i vettori base del sistema di riferimento equino-ziale.

Il vettore w lo otteniamo normalizzando il vettore momento angolare: w = r × ˙r

|r × ˙r| (4.34)

Utilizzando l’equazione (4.20) otteniamo: Q1 = wx 1 + wz (4.35) Q2 = − wy 1 + wz (4.36) Una volta noti gli elementi Q1 e Q2 possiamo ricavare i vettori f e g tramite

le equazioni (4.18) e (4.19).

Il terzo passo `e ricavare i parametri legati al vettore eccentricit`a, facilmente ricavabile :

e = − r |r| +

˙r × (r × ˙r)

µ (4.37)

Quindi ricaviamo P1 e P2 dalla loro definizione:

P1 = e · g (4.38)

P2 = e · f (4.39)

Il passo finale consiste nel calcolare la longitudine media λ. Per fare questo prima ricaviamo le coordinate del satellite nel riferimento equinoziale:

X = r · f (4.40)

Y = r · g (4.41)

Quindi calcoliamo la longitudine eccentrica F : sin F = P1+ (1 − P 2 1 b)Y − P1P2bX ap1 − P 2 1 − P22 (4.42) cos F = P2+ (1 − P 2 2 b)X − P1P2bY ap1 − P 2 1 − P22 (4.43)

(30)

4.5 Variazione dei parametri orbitali

equino-ziali

Le derivate temporali dei parametri equinoziali sono calcolabili come segue: da dt = 2a2 h h (P2 sin L − P1 cos L) Fr+ p rFt i (4.44) dP1 dt = r h n −p r cos L Fr+ h P1+ ³ 1 + p r ´ sin Li Ft −P2(Q1 cos L − Q2 sin L) Fn} (4.45) dP2 dt = r h np r sin L Fr+ h P2+ ³ 1 + p r ´ cos Li Ft +P1(Q1 cos L − Q2 sin L) Fn} (4.46) dQ1 dt = r 2h ¡ 1 + Q2 1+ Q22 ¢ sin L Fn (4.47) dQ2 dt = r 2h ¡ 1 + Q2 1+ Q22 ¢ cos L Fn (4.48) dl dt = n − r h ½· a a + b p r(P1 sin L + P2 cos L) + 2b a ¸ Fr a a + b ³ 1 + p r ´ (P1cos L − P2sin L) Ft+ + (Q1cos L − Q2sin L) Fn} (4.49)

(31)

5

Calcolo dei parametri orbitali

equinoziali medi

Seguendo le indicazioni fornite da [7] , abbiamo deciso di adottare un control-lore basato sui parametri equinoziali medi, in modo da eliminare il problema di controllare oscillazioni di poca rilevanza (in quanto periodiche).

Per ottenere le espressioni da usare per passare dai parametri istantanei a quelli medi abbiamo seguito le indicazioni della SST (Seminalytic Satellite Theory) sviluppata in [8].

La SST rappresenta lo stato orbitale di un satellite con il set di elemen-ti equinoziali, i primi 5 elemenelemen-ti a1,. . . , a5 sono lentamente tempo-varianti,

mentre il sesto elemento, a6 = λ, varia velocemente lungo l’orbita.

La SST scompone gli elementi istantanei âi, negli elementi medi ai più una piccola quantità, ηi, che è 2π periodica nella variabile più ”veloce”:

ˆ

ai = ai+ ηi(a1, . . . ,a6,t) (5.1)

con:

i = 1,...,6 (5.2)

Per motivi di semplicità la nostra analisi si è limitata a variazioni del primo ordine e considerando il disturbo dovuto alla non triassialità del campo gravi-tazionale terrestre limitatamente all’ armonica zonale (in parole più semplici

(32)

5 – Calcolo dei parametri orbitali equinoziali medi

di corto periodo) al primo ordine, possono essere scritte come una serie di Fourier modificata:

ηi = Ci0+ Di(L − λ) +

2N −1_X

j=1

(C_ijcos jL + S_ijsin jL) (5.3)

I coefficienti che compaiono nella (5.3) saranno dati, nel seguito del capitolo, in funzione delle seguenti quantit`a:

1. I coseni direttori (α,β,γ) dell’ asse di simmetria della perturbazione nel sistema di riferimento equinoziale. Per le armoniche zonali il vettore unitario di simmetria zB parte dal centro di massa della Terra e punta verso il polo nord geografico della Terra.

Quindi i coseni direttori risultano: α = zB· f β = zB· g γ = zB· w

Le quantit`a (α,β,γ) non sono indipendenti, ma legate dall’equazione:

α2_{+ β}2_{+ γ}2 _{= 1} _(5.4) Si ha quindi: α = − 2Q1 1 + Q 2 1 + Q22 (5.5) β = 2Q2 1 + Q 2 1 + Q22 (5.6) γ = 1 − Q12− Q22 1 + Q 2 1 + Q22 (5.7) 2. I parametri ausiliari A, B, C, χ:

(33)

A = na2 ₌√_µa _(5.8) B = q 1 − P 2 1 − P22 = 1 b − 1 (5.9) C = 1 + Q 2 1 + Q22 (5.10) χ = p 1 1 − P 2 1 − P22 = 1 B (5.11)

3. La funzione del disturbo dovuto all’effetto J2 , U:

U = J(γ 2₋1 3) a3_{(1 − P} 2 1 − P22) 3 2 (5.12) dove: J = 3µR2J2 4 (5.13)

4. L’operatore derivata in croce:

(34)

5. L’operatore inclusione I :

Is_r(j) = (

1 se r ≤ j ≤ s

0 negli altri casi (5.15)

6. le quantit`a ausiliarie ρj e σj che possono essere ricavate tramite le se-guenti equazioni:

ρj = (1 + jB)(−b)jCj(P1,P2) (5.16)

σj = (1 + jB)(−b)jSj(P1,P2) (5.17)

Dove Sj e Cj si ottengono dalle seguenti formule ricorsive: Cj+1(P1,P2) = P2Cj(P1,P2) − P1Sj(P1,P2) Sj+1(P1,P2) = P1Cj(P1,P2) + P2Sj(P1,P2) con : C0 = 1 S0 = 0 7. La quantit`a (L − λ ): L − λ = ∞ X₂ j(σjcos jL − ρjsin jL) (5.18)

(35)

8. I coefficienti Cj _{e S}j_{, per la cui forma si rimanda all’appendice B.}

Esplicitiamo adesso i coefficienti dell’equazione (5.3):

I termini costanti sono dati da: C_i0 = −

2N −1_X

j=1

(36)

I coefficienti per il semiasse maggiore a sono dati da:

C₁j = I1 1(j) · χ3 n2_a µ 4P2U − P1P2C1+ P 2 2 − P12 2 S 1 ¶¸ + +I₂2(j) · χ3 n2_a ¡ P₂2− P₁2¢U ¸ + +I₁2N −3(j) · χ3 n2_a(j + 2) µ −P2P2Cj+2+ P 2 2 − P12 2 S j+2 ¶¸ + +I 2N −2 1 (j) · 2χ3 n2_a(j + 1) ¡ −P1Cj+1+ P2Sj+1 ¢¸ + +I₁2N −1(j) · 3χ3_{− χ} n2_a jS j ¸ + +I₂2N(j) · 2χ3 n2_a(j − 1) ¡ P1Cj−1+ P2Sj−1 ¢¸ + +I 2N +1 3 · χ3 n2_a(j − 2) µ P1P2Cj−2+ P 2 2 − P12 2 S j−2 ¶¸ S₁j = I1 1(j) · χ3 n2_a µ 4P1U + P1P2S1+ P 2 2 − P12 2 C 1 ¶¸ + +I₂2(j) · χ3 n2_a2P1P2U ¸ + −I 2N −3 1 (j) · χ3 n2_a(j + 2) µ P1P2Sj+2+ P 2 2 − P12 2 C j+2 ¶¸ + −I 2N −2 1 (j) · 2χ3 n2_a(j + 1) ¡ P2Cj+1+ P1Sj+1 ¢¸ + −I₁2N −1(j) · 3χ3_{− χ} n2_a jC j ¸ + −I 2N 2 (j) · 2χ3 n2_a(j − 1) ¡ P2Cj−1− P1Sj−1 ¢¸ + −I 2N +1 3 · χ3 n2_a(j − 2) µ P1P2Sj−2+ P 2 2 − P12 2 C j−2 ¶¸ D1 = 0

(37)

I coefficienti per P1 sono dati da: C₂j = −I1 1(j) h χ 4n2_a2 ¡ P2C1+ P1S1 ¢i −I₂2(j)h χ 2n2_a2P1U i −I₁2N −3(j)h χ 4n2_a2(j + 2) ¡ P2Cj+2+ P1Sj+2 ¢i −I₁2N −2(j)h χ n2_a2(j + 1)C j+1i +I₁2N −1(j) · P2χ n2_a2 ¡ Q1C, αγj − Q2C_{, βγ}j ¢ + 1 χn2_a2 ∂Cj ∂P2 + 3P1χ 2n2_a2jS j ¸ +I 2N 2 (j) h χ n2_a2(j − 1)C j−1i +I 2N +1 3 (j) h χ 4n2_a2(j − 2) ¡ P2Cj−2− P1Sj−2 ¢i S₂j = +I1 1(j) h χ 4n2_a2 ¡ 8U + P2S1− P1C1 ¢i +I 2 2 (j) h χ 2n2_a2P2U i +I 2N −3 1 (j) h χ 4n2_a2(j + 2) ¡ P1Cj+2− P2Sj+2 ¢i −I₁2N −2(j)h χ n2_a2(j + 1)S j+1i +I₁2N −1(j) · P2χ n2_a2 ¡ Q1S, αγj − Q2S_{, βγ}j ¢ + 1 χn2_a2 ∂Sj ∂P2 − 3P1χ 2n2_a2jC j ¸ +I 2N 2 (j) h χ n2_a2(j − 1)S j−1i +I 2N +1 3 (j) h χ 4n2_a2(j − 2) ¡ P1Cj−2+ P2Sj−2 ¢i D2 = 1 χn2_a2 ∂U ∂P2 + P2χ n2_a2(Q1U,αγ − Q2U,βγ)

(38)

I coefficienti per P2 sono dati da:

C₃j = +I1 1(j) h χ 4n2_a2 ¡ 8U + P2S1− P1C1 ¢i +I₂2(j)h χ 2n2_a2P2U i +I₁2N −3(j)h χ 4n2_a2(j + 2) ¡ −P1Cj+2+ P2Sj+2 ¢i +I₁2N −2(j)h χ n2_a2(j + 1)S j+1i −I₁2N −1(j) · P1χ n2_a2 ¡ Q1C, αγj − Q2C_{, βγ}j ¢ + 1 χn2_a2 ∂Cj ∂P1 − 3P2χ 2n2_a2jS j ¸ +I 2N 2 (j) h χ n2_a2(j − 1)S j−1i +I 2N +1 3 (j) h χ 4n2_a2(j − 2) ¡ P1Cj−2+ P2Sj−2 ¢i S₃j = +I1 1(j) h χ 4n2_a2 ¡ P2C1+ P1S1 ¢i +I 2 2 (j) h χ 2n2_a2P1U i −I 2N −3 1 (j) h χ 4n2_a2(j + 2) ¡ P2Cj+2+ P1Sj+2 ¢i −I₁2N −2(j)h χ n2_a2(j + 1)C j+1i −I₁2N −1(j) · P1χ n2_a2 ¡ Q1S, αγj − Q2S_{, βγ}j ¢ + 1 χn2_a2 ∂Sj ∂P1 + 3P2χ 2n2_a2jC j ¸ −I 2N 2 (j) h χ n2_a2(j − 1)C j−1i +I 2N +1 3 (j) h χ 4n2_a2(j − 2) ¡ −P2Cj−2+ P1Sj−2 ¢i D3 = − 1 χn2_a2 ∂U ∂P1 − P1χ n2_a2 (Q1U, αγ − Q2U, βγ)

(39)

I coefficienti per l’elemento Q1 sono dati da : C₄j = I2N −1 1 (j) (1 + Q 2 1 + Q22) χ 2n2_a2 £ −C_{, βγ}j + Q1 ¡ C_{, P1P2}j − C_{, αβ}j − jSj¢¤ C₄j = I2N −1₁ (j)(1 + Q 2 1 + Q22) χ 2n2_a2 £ −S_{, βγ}j + Q1 ¡ S_{, P1P2}j − S_{, αβ}j + jCj¢¤ D4 = − (1 + Q 2 1 + Q22) χU, βγ 2n2_a2

I coefficienti per l’elemento Q2 sono dati da:

C₅j = I2N −1₁ (j)(1 + Q 2 1 + Q22) χ 2n2_a2 £ −Cj , αγ+ Q2 ¡ C_{, P1P2}j − C_{, αβ}j − jSj¢¤ C₅j = I2N −1 1 (j) (1 + Q 2 1 + Q22) χ 2n2_a2 £ −Sj , αγ + Q2 ¡ S_{, P1P2}j − S_{, αβ}j + jCj¢¤ D5 = − (1 + Q 2 1 + Q22) χU, αβ 2n2_a2

(40)

I coefficienti per la longitudine media λ sono dati da: C₆j = −I1 1(j) · χ2 2n2_a2_{(1 + χ)} µ 4P1U + P 2 2 − P12 2 C 1_{+ P} 1P2S1 ¶¸ −I 2 2 (j) · χ2 n2_a2_{(1 + χ)}P1P2U ¸ −I₁2N −3(j) · χ2_{(j + 2)} 2n2_a2_{(1 + χ)} µ P 2 2 − P12 2 C j+2_{+ P} 1P2Sj+2 ¶¸ −I 2N −2 1 (j) · χ2_{(j + 1)} n2_a2_{(1 + χ)} ¡ P2Cj+1+ P1Sj+1 ¢¸ +I₁2N −1(j) · − 2 n2_a ∂Cj ∂a + χ2 n2_a2_{(1 + χ)} µ P1 ∂Cj ∂P1 + P2 ∂Cj ∂P2 ¶¸ +I₁2N −1(j) · χ n2_a2 ¡ Q1C, αγj − Q2C, βγj ¢ − 3 n2_a2C j ¸ +I 2N 2 (j) · χ2_{(j − 1)} n2_a2_{(1 + χ)} ¡ P2Cj−1− P1Sj−1 ¢¸ +I 2N +1 3 (j) · χ2_{(j − 2)} 2n2_a2_{(1 + χ)} µ P 2 2 − P12 2 C j−2_{− P} 1P2Sj−2 ¶¸ S₆j = −I1 1(j) · χ2 2n2_a2_{(1 + χ)} µ 4P2U + P 2 2 − P12 2 S 1_{− P} 1P2C1 ¶¸ −I 2 2 (j) · χ2 n2_a2_{(1 + χ)} P 2 2 − P12 2 U ¸ −I₁2N −3(j) · χ2_{(j + 2)} 2n2_a2_{(1 + χ)} µ −P 2 2 − P12 2 S j+2_{+ P} 1P2Cj+2 ¶¸ −I 2N −2 1 (j) · χ2_{(j + 1)} n2_a2_{(1 + χ)} ¡ P1Cj+1− P2Sj+1 ¢¸ +I₁2N −1(j) · − 2 n2_a ∂Sj ∂a + χ2 n2_a2_{(1 + χ)} µ P1 ∂Sj ∂P1 + P2 ∂Sj ∂P2 ¶¸ +I₁2N −1(j) · χ n2_a2 ¡ Q1S, αγj − Q2S_{, βγ}j ¢ − 3 n2_a2S j ¸ +I 2N 2 (j) · χ2_{(j − 1)} n2_a2_{(1 + χ)} ¡ P1Cj−1+ P2Sj−1 ¢¸ +I 2N +1 3 (j) · χ2_{(j − 2)} 2n2_a2_{(1 + χ)} µ P 2 2 − P12 2 S j−2_{+ P} 1P2Cj−2 ¶¸ D6 = − 2 n2_a ∂U ∂a + 1 n2_a2_{(1 + χ)} µ P1 ∂U ∂P1 + P2 ∂U ∂P2 ¶ + χ n2_a2 (Q1U, αγ − Q2U, βγ)

(41)

Dopo aver verificato l’esattezza dell’algoritmo di passaggio da parametri equinoziali istantanei a parametri equinoziali medi tramite opportune simu-lazioni, siamo potuti passare all’implementazione del sistema di controllo.

(42)

6

Il controllore orbitale

Il fulcro di questo lavoro di tesi `e la creazione di un sistema di controllo non lineare applicabile ad uno o pi`u satelliti.

Schaub e Alfriend [9,10] avevano già mostrato come un controllore basato sul metodo diretto di Lyapunov produceva buoni risultati per manovre di variazione di orbita con motori a bassa spinta. Il loro lavoro aveva però l’inconveniente che le equazioni sviluppate contenevano singolarità per orbite circolari ed equatoriali, da qui l’idea di Naasz [6] di sviluppare una legge di controllo ”alla Lyapunov” usando i parametri equinoziali.

6.1 Metodo diretto di Lyapunov

Il metodo diretto, o secondo metodo, di Lyapunov `e un validissimo strumen-to nell’analisi di sistemi sia lineari che non lineari.

La stabilit`a del sistema

˙z = f(z) (6.1)

dove:

z = x − x∗ _(6.2)

( essendo x il vettore di stato attuale e x∗ _{il vettore di stato target ) `e} ana-lizzata usando l’approccio alla stabilit`a secondo Lyapunov, costruendo una funzione scalare di stato detta potenziale,V (z).

Per tale sistema, il punto di equilibrio x∗ _{`e globalmente asintoticamente} sta-bile se esiste una funzione V (z), continua nella derivata prima, che soddisfi

(43)

le seguenti condizioni: V (0) = 0 (6.3) V (z) > 0 ∀z 6= 0 (6.4) ˙ V (z) < 0 ∀z 6= 0 (6.5) lim||z||→∞V = ∞ (6.6)

La potenza di questo metodo consiste proprio nell’ampia libert`a di scelta della funzione potenziale, ma generalmente si scelgono funzioni quadratiche nelle variabili di stato, in grado di soddisfare le condizioni sopra e di creare un’analogia con l’energia del sistema.

6.2 Controllore basato sui parametri

equino-ziali

Definiamo il vettore di stato istantaneo come:

zist = [a,P1,P2,Q1,Q2,λ]T (6.7)

Scriviamo l’equazione variazionale equinoziale nella forma di Gauss:

˙zist = B(zist)u (6.8)

dove u = [ur,ut,ur]T `e il vettore del controllo espresso nel sistema locale (RTN) e B(zist) `e definita come di seguito:

B =           2a2_(P 2sin L−P1cos L) h 2a2_p hr 0 −p cos L_h r[P1+(1+ p r)sin L] h − P2(Q1cos L−Q2sin L)r h p sin L h r[P2+(1+p_r)cos L] h P1(Q1cos L−Q2sin L)r h 0 0 r(1+Q12+Q22)sin L 2h          

(44)

6 – Il controllore orbitale dove: b = a q 1 − P 2 1 − P22 h = nab p r = 1 + P1sin L + P2cos L r h = h µ (1 + P1sin L + P2cos L)

Si passa adesso al vettore di stato medio:

z = [a,P1,P2,Q1,Q2,λ] (6.9)

ottenibile tramite la trasformazione:

z = ξ(zist) (6.10)

la cui forma `e stata descritta nel precedente capitolo.

Continuiamo adesso scrivendo l’equazione variazionale di Gauss per i pa-rametri medi, includendovi anche gli effetti della perturbazione dovuta a J2: ˙z = A(z) + · ∂ξ ∂zist ¸_T B(zist)u (6.11)

(45)

dove: A =                                    0 3 4µR2J2P2 " _3(1−Q2 1−Q22) (1+Q2_1+Q2₂₎−1+ 2(1−Q2_1−Q2₂₎ (1+Q2_1+Q2₂₎· − 2Q2₁ (1+Q2_1+Q2₂₎− 2Q2₂ (1+Q2_1+Q2₂₎ √µ a2a5(1−P 2 1−P22)2 # −3 4µR2J2P2 " _3(1−Q2 1−Q22) (1+Q2_1+Q2₂₎−1+ 2(1−Q2_1−Q2₂₎ (1+Q2_1+Q2₂₎· − 2Q2₁ (1+Q2_1+Q2₂₎− 2Q2₂ (1+Q2_1+Q2₂₎ √µ a2a 5_(1−P2 1−P22)2 # 3 2 · (−1 − Q21− Q22)µR2J2 · Q2 (1+Q2 1+Q22)2 2(1−Q2 1−Q22) √_µ a2a 5_(1−P2 1−P22)2 ¸ 3 2µR2J2Q1 · (1−Q2 1−Q22) (1+Q2 1+Q22) √_µ a2a 5_(1−P2 1−P22)2 ¸ 3 4µR2J2 1+√1−P2 1−P22 3∗(1−Q2_1−Q2₂₎2 (1+Q2_1+Q2₂₎2 −1 + 2(1−Q2_1−Q2₂₎ (1+Q2_1+Q2₂₎ −2Q2₁ (1+Q2_1+Q2₂₎− 2Q2₂ (1+Q2_1+Q2₂₎ √_µ a2a5(1−P 2 1−P22)2                                   

Sorge per`o adesso un problema.

Nel controllore basato sui parametri orbitali classici, la matrice [∂ξ/∂zist] si dimostrava che era possibile approssimarla con la matrice identit`a avendo la diagonale unitaria e gli altri termini dell’ordine di J2.

Nel caso equinoziale invece la matrice suddetta risulta essere approssimabile con la matrice identit`a solamente per particolari valori dei parametri equi-noziali e pi`u precisamente per [P1 ' 0 e P2 ' 0] e/o

[Q1 ' 0 e Q2 ' 0].

La soluzione più logica a questo problema, è parsa essere quella di implemen-tare un programma che usasse il controllore basato sui parametri equinoziali, solo per valori dei parametri prossimi allo zero, e che poi tornasse ad usare quello già esistente, basato sui parametri classici, una volta usciti dagli in-tervalli di criticità. In questo modo, unendo i due controllori in un unico programma, abbiamo ottenuto un sistema capace di controllare qualsiasi

(46)

ti-6 – Il controllore orbitale

Dopo questo importante inciso, continuiamo a costruire il controllore equi-noziale tenendo, per`o sempre presente che tutto quello che segue ha senso solo quando l’orbita `e quasi circolare ([P1 ' 0, P2 ' 0]) e/o quasi

equato-riale ([Q1 ' 0, Q2 ' 0]) . Approssimiamo, quindi come segue l’equazione

variazionale di Gauss basata sui parametri medi:

˙z ' A(z) + B(zist)u (6.12)

La matrice di influenza del controllo B, ci permette di calcolare il cambia-mento negli elementi orbitali istantanei, dovuto al vettore accelerazione u del controllo. Si assume che questi cambiamenti negli elementi orbitali istanta-nei si riflettano direttamente in eguali variazioni istanta-nei corrispondenti elementi orbitali medi.L`ıerrore introdotto da questa assunzione sar`a dell’ordine di J2.

Inoltre, poich´e la differenza tra gli elementi orbitali istantanei e quelli medi `e relativamente piccola, nel caso della perturbazione dovuta a J2, la differenza

nel calcolare [B] usando o gli elementi istantanei o quelli medi `e sostanzial-mente trascurabile. Noi assumeremo quindi che la matrice [B] sia calcolata usando i parametri medi.

Assegnato per un generico satellite un vettore di stato obiettivo zT si defi-nisce l’errore medio:

δz = z − zT (6.13)

Definiamo quindi la funzione di Lyapunov nel seguente modo: V (δz) = 1

2δz

T_δz _(6.14)

dal momento che `e nostro desiderio che l’orbita target risulti mediamente invariante al J2 , deve valere:

˙

zT = A(zT) (6.15)

cio`e per mantenere l’orbita non `e richiesto alcun controllo. Calcolando la derivata di V ed utilizzando le equazioni (6.12) e (6.14), si ottiene:

˙

(47)

Ponendo ˙V uguale alla quantit`a definita negativa ˙

V = −δzT_Kδz _(6.17)

dove K `e la matrice dei guadagni definita positiva, che sar`a approfondita nella sezione X.

Si ottiene quindi la seguente espressione:

Bu = − [A(z) − A(zT)] − Kδz (6.18) Dal momento che il vettore del controllo ha solo tre componenti, e noi voglia-mo controllare sei elementi, non possiavoglia-mo risolvere in voglia-modo esatto l’equazione (6.18) rispetto a u. Quindi, poich´e il sistema `e sovradeterminato, utilizziamo la pseudo-inversa H di [B] per ricavare u:

u = −H[A(z) − A(zT)] − Kδz (6.19)

H = ¡BT_B¢−1_BT _(6.20)

Se la differenza tra gli elementi orbitali attuali e quelli obiettivo `e piccola, come accade tipicamente per satelliti in formazione e per il caso di station keeping, possiamo dimostrare che la differenza tra A(z) e A(zT) `e molto piccola ed ha un’influenza trascurabile sulla legge di controllo. Linearizzando questa differenza rispetto a zT, otteniamo:

A(z) − A(zT) ' · ∂A ∂z ¸ ¯¯ ¯ ¯ ¯ zT δz (6.21) Da cui, definendo A , · ∂A ∂z ¸ ¯¯ ¯ ¯ ¯ zT (6.22) possiamo esprimere la dinamica dell’errore come segue:

(48)

6 – Il controllore orbitale

La matrice A `e stata ricavata nell’ ambiente simbolico di MAT LAB°c e viene

qui omessa perch´e molto complessa ( il file utilizzato per ottenerla `e presente nel toolbox allegato.)

6.3 Determinazione della matrice dei

guada-gni

Per prima cosa scomponiamo la matrice dei guadagni K in due matrici, in questo modo:

K = ΦK0 (6.24)

La matrice Φ ha lo scopo di concentrare il controllo relativo ad un parame-tro nella zona dell’orbita più favorevole. Ora, mentre nel caso dei parametri classici, è abbastanza semplice trovare la zona dell’orbita nella quale è meglio effettuare il controllo, altrettanto non si può dire per i parametri equinoziali, dato che abbiamo visto che non è facile visulizzarli.

L’idea è, allora, di concentrare il controllo nel punto dell’orbita più favorevole per il parametro classico che ha maggior ”peso” nel parametro equinoziale ( ci rifacciamo cioè alla scrittura dei parametri equinoziali in funzione di quelli classici ).

`

E inoltre necessario precisare in funzione di quale parametro si possa espri-mere l’evoluzione temporale lungo l’orbita.

Se guardiamo l’ equazione (4.7), vediamo che:

ν = L − ˜ω (6.25)

u = L − Ω (6.26)

Distinguiamo tre casi:

(49)

(nella forma L − ˜ω ) visto che Ω in questo caso `e definito: Φ = diag             sinN_{(L − Ω − 2)} cosN (L−Ω−2) 2 cosN (L−Ω−2) 2 cosN_{(L − Ω)} sinN_{(L − Ω)} sinN_λ            

2. Se siamo su un’orbita equatoriale, essendo comunque definita ˜ω, utiliz-ziamo ν (nella forma L − Ω):

Φ = diag             sinN_{(L − ˜}_{ω − 2)} cosN (L−˜ω−2) 2 cosN (L−˜ω−2) 2 cosN_{(L − ˜}_ω) sinN_{(L − ˜}_ω) sinN_λ            

3. Se l’orbita è circolare equatoriale , la velocitá angolare è costante ed è quindi facile, conoscendo l’anomalia vera iniziale, ricavarla per ogni istante: Φ = diag             sinN₍ν 2) cosN ν 2 cosN_ν cosN_{(ν + 1)} sinN_{(ν + 1)} sinN_λ            

In tutte e tre le matrici N `e un numero intero pari (di solito si prende uguale a 4).

(50)

6 – Il controllore orbitale

6.3.1 Determinazione di K

La matrice K contiene i guadagni statici relativi ai singoli parametri. Sosti-tuendo la (6.23) nella(6.16) ed eguagliandola alla (6.17) si ottiene:

K0 = − Φ−1(Aδz + Bu) δzT(δzδzT)−1 (6.27)

L’espressione 6.27 è però molto difficile da ottenere numericamente, è quindi opportuno procedere in un modo alternativo per ottenere la matrice cercata. Dapprima adimensionalizziamo tutti gli errori portandoli in radianti ( per quanto riguarda a lo dividiamo per un semiasse maggiore di riferimento, ad esempio quello del master ). Facciamo poi l’ipotesi di metterci, per ogni elemento, nel caso in cui si abbia il massimo controllo richiesto (possiamo farlo in virtù del disaccoppiamento fornito dalla matrice Φ).

Poniamo inoltre il controllo in direzione radiale uguale a zero, visto che si dimostra essere piuttosto inefficiente.

In virt`u di queste semplificazioni scriviamo un’espressione del tipo:     ur ut un     =     0 KaH21δa + KP1H22δP1 + KP2H23δP2 KQ1H34δQ1+ KQ2H34δQ2+ KλH36δλ     ≤ ¯ T m     1 1 1     (6.28)

dove ¯T è la spinta massima del sistema propulsivo e m è la massa del satellite. Assumiamo che in ogni istante i motori siano allineati con gli assi della terna locale, pertanto la massima spinta disponibile su ogni asse sarà T¯

m.

Invertendo quindi la 6.28 a termine a termine possiamo trovare una limita-zione ai guadagni che ci garantisce di non cadere mai nella saturalimita-zione del comando, cio`e: ut≤ ¯ T m ; un ≤ ¯ T m

(51)

Ka ≤ ¯ T mH21δa (6.29) KP1 ≤ ¯ T mH22δP1 (6.30) KP2 ≤ ¯ T mH23δP2 (6.31) KQ1 ≤ ¯ T mH34δQ1 (6.32) KQ2 ≤ ¯ T mH35δQ2 (6.33) Kλ ≤ ¯ T mH36δλ (6.34) Nelle simulazioni abbiamo scelto i guadagni in questo modo :

• All’interno della tolleranza abbiamo imposto l’uguaglianza nelle (6.29 - 6.34) sostituendo all’errore la tolleranza scelta. Ad esempio:

Ka= ¯ T mH21tola

(6.35) • Al di fuori delle tolleranze abbiamo imposto l’uguaglianza nelle (6.29 - 6.34) mettendo al posto dell’errore, l’errore stesso aumentato di una piccola costante k dell’ordine di 10−3_{. Ad esempio:}

Ka=

¯ T mH21(k + δa)

(52)

7

Simulazioni e risultati

Nel seguente capitolo sono proposti i risultati di alcune simulazioni effettuate utilizzando il propagatore orbitale illustrato nei precedenti paragrafi.

Si `e considerata la perturbazione dovuta allo schiacciamento dei poli terrestri, limitandoci alla seconda armonica del campo gravitazionale terrestre, ovvero J2.

Durante l’elaborazione del presente lavoro di tesi, sono state effettuate nu-merose simulazioni al fine verificare la validità del sistema di controllo pro-gettato. In particolare sono stati studiati posizionamento e station keeping nei casi di orbite di partenza e/o orbite target sia equatoriali che equinoziali. Nel seguito saranno riportati solo alcuni esempi, tra i più significativi. Dato l’esclusivo scopo di verifica del sistema implementato, non è stato ef-fettuato uno studio sistemistico dei satelliti in questione.

`

E stato ipotizzato l’utilizzo piccoli satelliti (uguali tra loro nei casi di volo in formazione), dotati di 4 motori nelle due direzioni normale e tangenziale, assi della terna locale, capaci di modulare la spinta senza limitazioni fino alla saturazione.

Per come `e stato realizzato il calcolo dei guadagni [6.3], siamo certi che non si avr`a la saturazione dei comandi..

La tipologia dei motori utilizzati non è stata ben specificata, si è ipotizzato di utilizzare motori capaci di fornire spinta continua dell’ ordine del Newton. Per uno studio più accurato dei motori di nuova generazione applicabili ai cluster rimandiamo a [11].

(53)

7.1 Posizionamento assoluto

In questo capitolo presentiamo un trasferimento orbitale con successiva ma-novra di station keeping di un satellite le cui caratteristiche sono riassunte in Tabella 7.1. La durata della simulazione `e di 60 ore.

Parametri orbitali Iniziali Obiettivo

a 10000 km 10000 km

e 0.1 0

i 12◦ ₁₅◦

Ω 20◦ ₂₄◦

ω 20◦ ₁₀◦

Spinta max. motore 2 N 2 N

Massa satellite 300 kg 300 kg

CD 1.5 1.5

A 20 m2 _{20 m}2

Tabella 7.1: Parametri orbitale del trasferimanto

In Figura 7.1 `e visualizzata la traiettoria attorno alla Terra. Il piano rosso in semitrasparenza rappresenta il piano equatoriale e la linea evidenziata dall’intersezione dei due diversi colori rappresenta l’asse x della terna IJK.

tolleranze sui parametri orbitali Valori [rad]

tola 10−5 tolP 1 1.5x10−6 tolP 2 10−5 tolQ1 1.5x10−5 tolQ2 5x10−4 tolλ 10−3

(54)

7 – Simulazioni e risultati

Figura 7.1: Traiettoria posizionamento assoluto

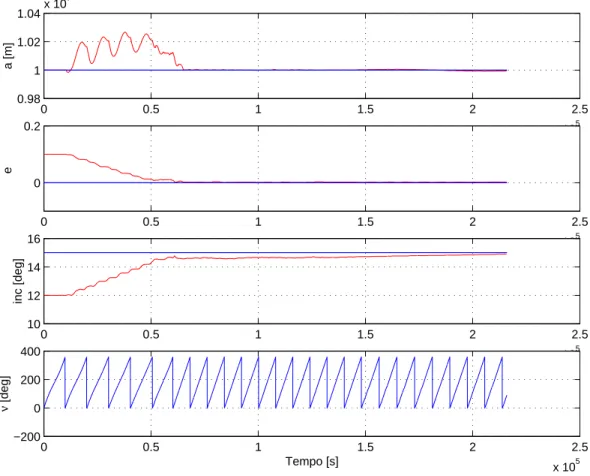
Nelle figure 7.2, 7.3, 7.4, 7.5 sono riportati gli andamenti dei parametri orbitali in funzione dell’anomalia vera. Non tragga in inganno l’andamen-to fortemente oscillal’andamen-torio dell’ argomenl’andamen-to del perigeo ω, dal’andamen-to che in realtà, per orbite a eccentricità nulla come quella in esame, questa variabile non è definita. È invece opportuno notare come gli altri parametri convergano velocemente e si mantengano a lungo entro intervalli di tolleranza ristretti ( vedi tabella 7.2) attorno ai valori target.

Si anche pu`o vedere come il passaggio dal controllo basato sugli elementi orbitali classici, a quello fondato sui parametri equinoziali, avvenga in modo sufficientemente continuo. Alla luce dei risultati ottenuti, siamo quindi au-torizzati a considerare ben riuscito il sistema di controllo realizzato, dato che soddisfa tutte tutte le esigenze di progetto.