CAPITOLO 10 Prova di compressione contenuta

CAPITOLO 10

Prova di compressione contenuta

10.1 Introduzione

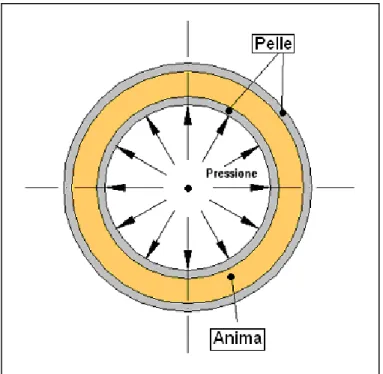
La schiuma sintattica si presta ad essere utilizzata come anima di strutture sandwich aventi forme più complessi rispetti al semplice panello piano. Un esempio , riportato in figura 10.1, schematizza il possibile utilizzo della schiuma sintattica come anima di strutture tubolari, sollecitatati da pressioni agenti sulla parte interna.

Figura 10.1 – Struttura tubolare a sandwich sollecitato da una pressione agente sulla parete interna

Per caratterizzare il comportamento della schiuma sintattica, e valutare la risposta del materiale a sollecitazioni di questo tipo si sono realizzate delle prove di compressione contenuta.

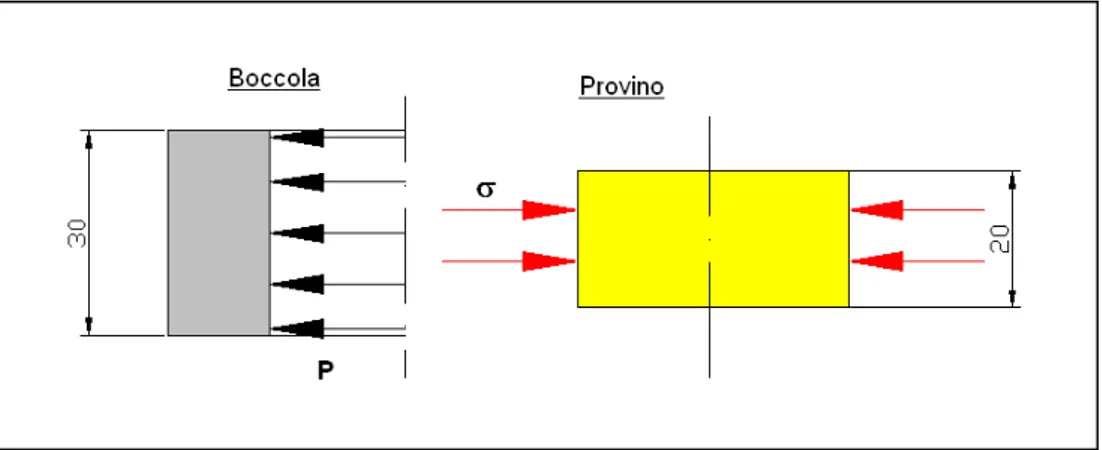
Per compressione contenuta si intende uno stato di sollecitazione indotto da una compressione assiale su un provino vincolato in maniera tale da impedire la sua espansione laterale.

Un provino compresso assialmente, in maniera analoga alla prova descritta nel capitolo 9, sollecitato quindi in maniera uniassiale, tende ad espandersi lateralmente per effetto di Poisson. Se invece viene inserito in una boccola costituita da materiale molto più rigido, rispetto a quello sollecitato in compressione, la sua espansione laterale viene impedita. (Rimane nel campo di deformazione elastica della boccola, e quindi tale da essere trascurabile).

Si realizza quindi all’interno del provino uno stato di tensione pluriassiale, che tende ad essere, aumentando la compressione assiale, quasi idrostatico.

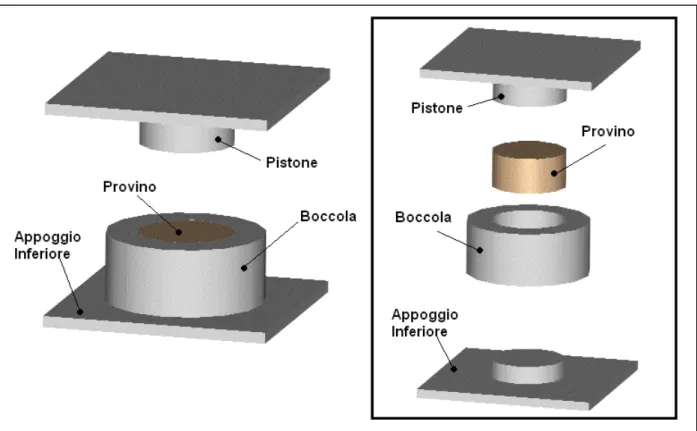
Sono stati ricavati 8 provini della stessa geometria testata nella prova di compressione libera (cilindri aventi diametro di 42.8 mm e altezza di 20 mm), descritti in figura 9.2 ed inseriti in una boccola d’acciaio, con gioco nullo.

Il metodo di preparazione dei provini testati è lo stesso usato per i provini cilindrici della prova di compressione libera, e quindi sono caratterizzati dalla presenza di bolle.

La superficie interna della boccola è stata lavorata in maniera tale da garantire il montaggio dei provini senza gioco praticamente nullo tra le due superfici, ( il gioco massimo misurato è dell’ordine di 0.01 µm, poiché la schiuma sintattica è molto cedevole, viene recuperato in maniera istantanea.

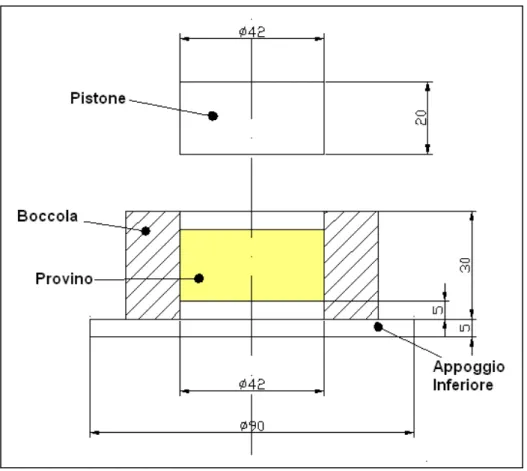
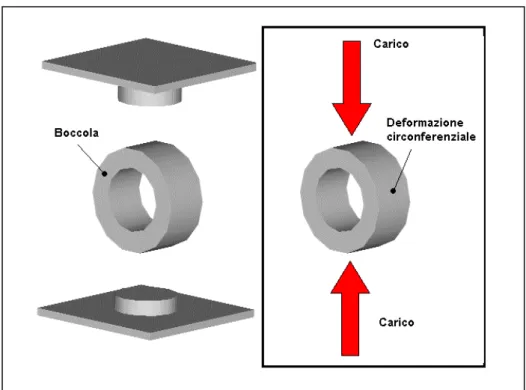
Le figure 10.2 e 10.3 descrivono l’attrezzatura utilizzata:

Figura 10.3 – Geometria dell’attrezzatura di prova per realizzare la compressione contenuta (dimensioni in mm)

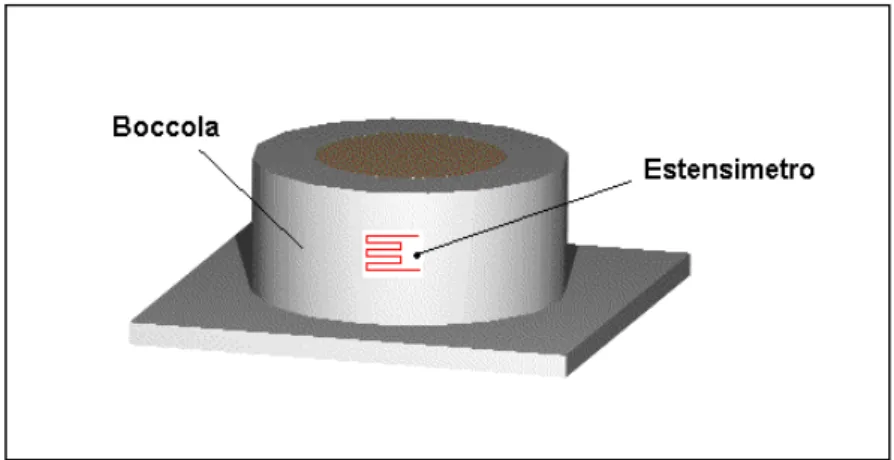
L’attrezzatura di prova è stata montata sulla macchina con cella di carico di 250 kN, cella che fornisce istante per istante il valore del carico di compressione assiale applicato dal pistone sul provino. Sulla superficie esterna della boccola è stato posizionato un estensimetro (figura 10.8), in maniera tale da avere la deformazione elastica circonferenziale della boccola, e quindi il valore della forza radiale esercitata dal provino compresso sulla boccola.

A riassumere, i valori noti dalle misure sono:

o Spostamento del pistone ⇒ Deformazione assiale del provino o Carico di compressione ⇒ Tensione agente sul provino o Deformazione circonferenziale della boccola

10.2 Analisi dello stato di tensione

L’analisi dello stato di tensione può essere effettuata separando i due elementi, boccola e provino, ed andando ad imporre l’equilibrio e la congruenza sulle deformazioni.

o Analisi della boccola di acciaio

La boccola può essere schematizzata come un disco caricato con pressione agente sul bordo interno. ( La figura 10.4 riporta lo schema descritto)

Figura 10.4 – Schema di analisi della boccola

Considerando un sistema di riferimento piano polare, gli andamento delle tensioni radiale σr e circonferenziale σc in funzione del raggio r sono dati dalle seguenti relazioni:

      + ⋅ − ⋅ =       − ⋅ − ⋅ = 2 2 2 2 2 2 2 2 2 2 1 1 r Re Ri Re Ri P r Re Ri Re Ri P c r σ σ (10.1)

Considerando ρ il rapporto tra il raggio esterno e il raggio interno della boccola , indicati con

      + ⋅ − =       − ⋅ − = 2 2 2 2 1 1 1 1 r Re P r Re P 2 c 2 r ρ σ ρ σ

(10.2 Andamento delle tensioni in funzione del raggio)

L’estensimetro è stato posizionato in corrispondenza del bordo esterno della boccola, quindi lo stato di tensione per r = Re risulta noto, e dalle equazioni () è possibile ricavare il valore della pressione che agisce sul bordo interno della boccola:

1 2 0 − = = 2 c r P ρ σ σ

(10.3 Tensioni per r = Re)

Noto lo stato di tensione sul bordo esterno, è possibile ricavare, applicando le equazioni costitutive del materiale elastico lineare omogeneo isotropo (10.4)

(

)

(

)

Sostituendo il valore delle tensioni sul bordo esterno, si determinano i corrispettivi valori delle deformazioni, in particolare il valore della deformazione circonferenziale risulta noto dalla misurazione effettuata dall’estensimetro:

E E c c c r σ ε σ ν ε = ⋅ − =

(10.5 Deformazioni per r = Re)

Dalla misura della deformazione circonferenziale effettuata dell’estensimetro, e della tensione circonferenziale corrispondente, determinata tramite la taratura dell’estensimetro, è possibile ricavare la misura della pressione che agisce sulla superficie interna della boccola:

c 2 2 c c c P P E σ ρ ρ σ σ ε ⋅ − = ⇒ − = = 2 1 1 2

Tramite queste misurazioni risulta completamente determinato anche lo stato di tensione in corrispondenza del bordo interno della boccola. I valori delle tensioni risultano:

1 − = − = ρ σ σ P P c r

(10.7 Tensioni per r = Ri)

Applicando, analogamente a quanto fatto in precedenza, le equazioni costitutive, si determinano le tensioni in corrispondenza del bordo interno:

      ₋ − =       − − − = ν ρ ε ρ ν ε 1 1 1 1 E P E P c r

(10.8 Deformazioni per r = Ri)

o Analisi del provino cilindrico in schiuma sintattica

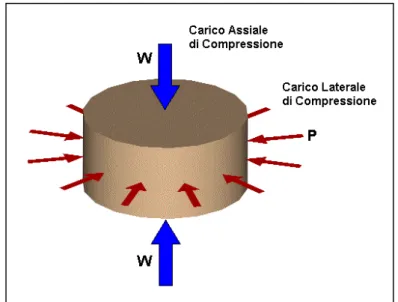
Il provino cilindrico in schiuma sintattica, accoppiato alla boccola di acciaio con gioco nullo, compresso assialmente dal pistone, inizia a deformarsi lateralmente andando a premere sulla boccola. I due corpi si scambiano quindi una pressione laterale P. Isolando il provino dalla boccola lo schema di carico risulta il seguente (figura 10.5)

Figura 10.5 – Schema di carico del provino cilindrico

W: Carico di compressione assiale P: pressione laterale

La pressione laterale non si mantiene costante, ma aumenta all’aumentare della corsa del pistone. Imponendo l’equilibrio tra la boccola e il provino cilindrico, come rappresentato in figura 10.6:

Figura 10.6 – Schema di ripartizione delle pressioni tra boccola e provino

Andando a scrive l’equilibrio all’interfaccia boccola, provino (10.9):

P Hp Hb Hp R P Hb R⋅ ⋅ =− ⋅ ⋅ ⋅ ⇒ = ⋅ ⋅ π σ σ π 2

2 (10.9 Equilibrio all’interfaccia

boccola-provino)

Dove si è indicato:

R : raggio corrispondente all’interfaccia boccola – provino (R = 21.4 mm)

► ► ►

►

Hb : Altezza Boccola (Hb = 30 mm)

Hp : Altezza del Provino ( Inizialmente è di 20 mm, dopo varia in funzione della

compressione imposta dalla corsa del pistone, ed è quindi un valore noto istante per istante)

P : è la pressione media equivalente applicata al bordo interno della boccola, necessaria a

realizzare le tensioni e le deformazioni misurate al punto precedente. Dipende quindi dai valori misurati dall’estensimetro e dalla sua taratura.

► σ: : tensione radiale che si genera sulla superficie laterale del provino cilindrico e deve essere in equilibrio con la pressione P secondo la (10.9)

Le tensioni corrispondenti , considerando un sistema di riferimento cilindrico (r,θ,z) , sono

espresse dalla (10.10). Il provino può essere visto come un cilindro con pressione applicata sul bordo esterno, con il raggio interno uguale a zero.

σ σ σ σ π σ − =       + ⋅ − ⋅ = − =       − ⋅ − ⋅ = ⋅ − = − = 2 2 2 2 2 2 2 2 2 2 2 1 1 4 / r Ri Ri Re Re P r Ri Ri Re Re P D W A W c r z

(10.10 Tensioni agenti sul provino)

Finché lo stato di tensione si mantiene nel campo elastico, le tensioni e le deformazioni sono legate dalle equazioni di Lamè.

Le relazioni costitutive sono espresse dalle (10.11), tenendo presente che risultano incogniti i valori del modulo elastico di Young, e del coefficiente di Poisson della schiuma sintattica:

(

)

[

]

[

]

(

)

[

]

[

(

)

]

Poiché deve essere garantita la congruenza tra boccola e provino cilindrico deve valere la relazione (10.12): int) (r R r Bocc r =ε =

ε (10.12 – Congruenza tra boccola e provino)

Poiché la deformazione radiale della boccola in corrispondenza del bordo interno non è misurata direttamente, occorre determinare il legame tra la questa deformazione e quella misurata dall’estensimetro, in pratica tenendo presente le (10.8) e le (10.11), è sufficiente scrivere il rapporto (10.13):

2 ) 1 ( ) 1 ( − − ⋅ + = ρ ν ρ ε ε EXT c INT r _(10.13)

A questo punto è possibile utilizzare le relazioni costitutive (10.11) per determinare il coefficiente di Poisson della schiuma sintattica, ponendo:

s c r σ σ ε ε = = c r e 2 − ⋅ + − = e s e s e

ν (10.12 - Coefficiente di Poisson del provino)

10.3 Taratura

dell’estensimetro

L’operazione di taratura dell’estensimetro consente di determinare la relazione tra deformazione misurata e carico applicato. In questo caso per effettuare l’estensimetro è stato posizionato sul bordo esterno della boccola, in corrispondenza della mezzeria, in maniera tale da ricavare la deformazione circonferenziale della boccola.

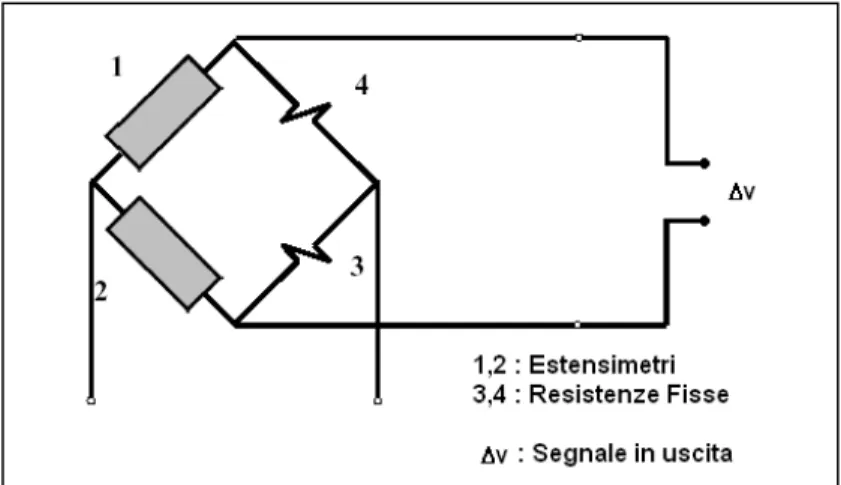
Un secondo estensimetro è stato utilizzato come dummy per compensare gli effetti termici, in pratico è stato incollato su un pezzo di materiale identico alla boccola e collegato al ponte estensimetrico. Gli estensimetri così collegati realizzano una configurazione a mezzo ponte rappresentata dalla figura successiva:

Dalla variazione della tensione in uscita, si ricava la misura della deformazione dell’estensimetro, data dalla relazione (10.13):

5 91 . 1 4 ⋅ ∆ ⋅ = ⋅ ∆ ⋅ ⋅ = G V V G V k n

ε (10.13 – Deformazione misurata dell’estensimetro)

Dove si è indicato:

n = 2 Numero di rami attivi

k = 1.045 Fattore di taratura dell’estensimetro V= 5 Volt Tensione di alimentazione del ponte

G Guadagno di anello del ponte ( Per il provino 16 è stato scelto 1000, per il

provino 16 è stato scelto 1000, per i provini 17,18 è stato aumentato a 2000) Per realizzare la corretta taratura dell’estensimetro, sarebbe stato necessario caricare la boccola con una pressione interna, tuttavia questa modalità comportava una serie di complicazioni non semplici da risolvere.

Si è provveduto alla taratura dell’estensimetro, caricando in flessione la boccola, creando sul diametro della boccola delle deformazioni circonferenziali. Si è misurato il segnale elettrico corrispondente alla deformazione e il corrispettivo valore del carico applicato dalla macchina di prova. Le figure a seguire descrivono le operazioni effettuate:

Figura10.9 – Taratura dell’estensimetro

La determinazione delle tensioni agenti sul diametro esterno della boccola, in corrispondenza del punto di applicazione della boccola è stata compiuta svolgendo un analisi gli elementi finiti, caricando il provino con un carico unitario.

1 X Y Z APR 18 2005 09:46:03 ELEMENTS F

La boccola caricata a flessione ha dato questi risultati:

Carico Applicato 14000 N

Tensione elettrica di squilibrio misurata -1.18 V

Tensioni Circonferenziali Calcolate con Ansys 51.8 MPa

Fattore di Taratura σ /∆V 43.9

Tabella 10.1 – Taratura dell’estensimetro

10.4 Analisi dati sperimentali

I provini montati sulla boccola sono stati posizionati sulla macchina di prova, ( cella di carico da 250 kN) e caricati a compressione imponendo una velocità di deformazione costante, quasi statica, pari a 0,5 mm/min, la stessa usata in modalità di prova ANSI D – 1621 – 94 – Standard

test method for compressive properties of rigid cellular plastics.

Poiché non si sapeva come avrebbe risposto il materiale a questo tipo di sollecitazione, sono state effettuate una serie di prove imponendo alla macchina una lunghezza di corsa sempre maggiore. Si è giunti alla fine ad imporre una corsa di 12 mm, a cui corrisponde un carico applicato di circa 200 kN. Nonostante la deformazione indotta, il provino si presenta deformato, ma ancora compatto, senza la presenza di linee di rottura o cricche, neanche in prossimità delle bolle d’aria presenti come difetto. In totale il numero di prove effettuate sono state 8 di cui 3 utilizzando l’estensimetro per misurare la deformazione circonferenziale della boccola. Le curve ricavate sono riportate in seguito.

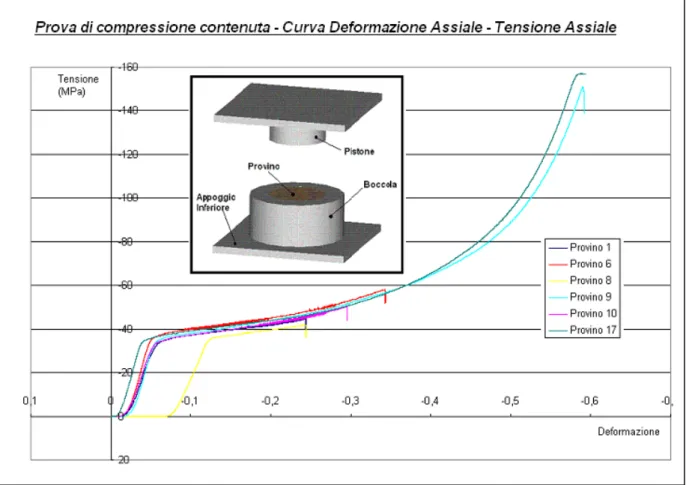
La figura 10.11 riporta le curva tensione assiale – deformazione assiale di 6 degli 8 provini testati. Il primo provino testato è stato l’8, si noti la differenza nell’accostamento iniziale, la corsa è stata aumentata fino ai 12 mm usata per testare i provini 9 e 17.

Le figure 10.12, 10.13, riportano a titolo esemplificativo le curve relative al provino numero 17. La 10.12 riporta la curva carico – spostamento, la figura 10.13 riporta invece, l’andamento delle tensioni agenti sul provino 17 in funzione della deformazione assiale. Si noti come all’aumentare della deformazione i valori della tensione radiale e di quella assiale tendono a convergere. Questo sta a significare, che quando il provino risulta molto compresso (50%), lo stato di tensione agente su di esso è effettivamente idrostatico.

Figura 10.11 – Curve Tensione Assiale – Deformazione Assiale di tutti i provini

Figura 10.13 – Curva Deformazione Assiale – Tensione Assiale e Radiale del provino 17

Dall’andamento delle curve si evidenziano due zone, la prima è la zona dove la compressione rimane in campo elastico. In seguito il materiale raggiunge il carico di rottura, le microsfere iniziano a rompersi, ma il materiale rimane compatto, non si evidenziano linee di fratture e continua a mantenere una certa resistenza alla compressione. Questo probabilmente è dovuto al fatto che con la rottura dei vari strati di microsfere, il materiale va ad occupare il posto precedentemente occupato dai vuoti. C’è in questa fase un andamento tra tensione e deformazione ancora lineare con pendenza minore.

Quando tutti i vuoi sono stati riempiti, ossia è stato raggiunto il massimo livello di densificazione il provino risulta essere una massa compatta, priva di vuoti al suo interno e il carico inizia a crescere bruscamente. Si possono quindi evidenziare almeno tre zone distinte, descritte in figura 10.14:

1. Zona di deformazione elastica 2. Zona di densificazione

Figura 10.14 – Andamento della curva sforzo deformazione nella compressione contenuta

L’andamento tra le tensioni assiali e la deformazione assiale nelle prime due zone risulta lineare, ma con pendenze diverse, la transizione fra le varie zone non è brusca, ma avviene entro un certo intervallo di tensione (Circa 32 – 36). I valori per le tensioni assiali nella tabella 10.2:

Provino Pendenza 1 Pendenza 2 Tensione Max1

1 1078 47 31 – 34 6 1332 51 34 - 36 8 804 47 34 - 36 9 1343 57 32 - 36 10 1082 53 32 - 36 17 1304 48 32 - 36 Media 1157 50,5 Deviazione Standard 193 3.64

Tabella 10.2 – Caratteristiche Curve Deformazioni Assiali – Tensioni Assiali

(dati in MPa)

Figura 10.15 – Curve Deformazione Assiale – Tensione Radiale

Il segnale rilevato risulta meno pulito, ma l’andamento globale risulta simile a quello visto per le tensioni assiale. C’è un infatti una prima zona relativa al campo delle deformazioni elastiche, alla quale segue una zona dove la tensione cresce con pendenza minore, ed è la zona corrispondente alla fase di densificazione e compattazione del materiale, successivamente le curve tendono a perdere l’andamento lineare. I valori delle pendenze misurate risultano più dispersi, e sono riportate nella tabella 10.3

Provino Pendenza 1 Pendenza 2 Tensione Max

16 460 74 18

17 834 103 24

18 1059 57 24

Per quanto riguarda il coefficiente di Poisson, in base alla 10.12, ossia applicando le relazioni costitutive, il valore rilevato nella zona corrispondente alla deformazione elastica risulta:

Provino Coefficiente di Poisson

16 0.38 – 0.40 17 0.35 – 0.38 18 0.38 – 0.43

Tabella 10.4 – Coefficiente di Poisson del Materiale

Nella zona elastica, la deformazione radiale è praticamente nulla, lo stato di tensione può quindi essere ricavato scrivendo le equazioni costitutive in un generico sistema di riferimento 1,2,3, ed imponendo che le deformazioni lungo le direzione 2,3 siano nulle (espressioni 10.14). Si ottiene la relazione (10.15) tra le tensioni 1,2:

(

)

[

]

[

]

(

)

[

]

[

(

)

]

Il tensore di Cauchy scritto in un sistema di riferimento cartesiano, può essere scritto come in figura 10.16: