Sviluppo di un digitalizzatore ottico
Lo scanner 3D sviluppato durante questo lavoro di tesi presso il DIMNP si colloca nel gruppo dei sistemi ottici attivi a triangolazione e più precisamente tra quelli che sfruttano il laser come sorgente di luce [20].
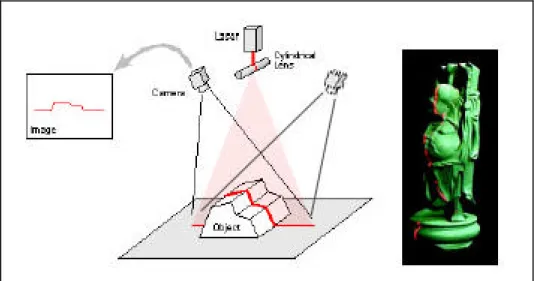
I suoi componenti principali sono due telecamere dotate di sensore CCD, un diodo laser con lente cilindrica, uno stepper motor, una scheda di azionamento per quest’ultimo ed un personal computer per la raccolta ed il processamento dei dati (Figura 3.1).
Per garantire la sicurezza dell’operatore e per rispettare le norme sull’uso delle sorgenti laser, lo stadio di alimentazione del digitalizzatore ed il diodo laser sono racchiusi all’interno di una scatola metallica, da cui la lama laser fuoriesce attraverso un’apertura posta sulla parte anteriore; mentre sul lato è posizionata la presa di corrente di rete e quella per la porta parallela usata per pilotare lo stepper motor.
Tutti gli elementi sono sorretti da una struttura in tubi inox da un pollice, che, con la sua rigidezza, garantisce il reciproco posizionamento delle camere fotometriche e quindi la precisione della misura. Il digitalizzatore viene poi montato su un cavalletto con testa girevole, per facilitare il trasporto e l’inquadratura delle varie scene.
Figura 3.2 Active Stereo con lama laser ed immagine di un oggetto illuminato dalla lama
Il principio di funzionamento si basa sul metodo di rilevazione delle superfici noto in letteratura con il nome di Active Stereo (Figura 3.2): una lama di luce laser viene fatta passare sulla scena e forma, con l’oggetto da acquisire, un’intersezione rappresentata da una linea, che viene poi ripresa dalle due telecamere. Una volta risolto il problema delle corrispondenze (ovverosia identificare sulle due immagini i punti che rappresentano le proiezioni dello stesso punto della scena) con il vincolo epipolare, si sfrutta il principio della triangolazione per ricavare la posizione spaziale dei punti che compongono la curva.
3.1 L’hardware
Il sistema di visione, come anticipato in precedenza, si basa su un metodo di stereopsi attiva e prevede, quindi, un dispositivo di luce strutturata (Structured Lighting) che illumini la scena ripresa dalle telecamere. In questo caso particolare la sorgente di luce è un piano di luce coerente ottenuto facendo passare un raggio laser a bassa potenza, generato da un diodo laser con lunghezza d’onda di 670 nm (Figura 3.3), attraverso una lente cilindrica.
Figura 3.3 Caratteristiche tecniche del diodo laser della Lot Oriel
Per poter “spazzolare” la scena con il piano laser, si è utilizzato uno stepper motor dotato di una propria scheda di azionamento e stadio di alimentazione separato (Figura 3.4).
Figura 3.4 Caratteristiche stepper motor e scheda di azionamento
L’interfaccia tra la scheda di azionamento dello stepper motor ed il personal computer è costituita da una Enhanced Parallel Port (EPP) IEEE1284. Grazie ad un software appositamente
sviluppato in MatLab® presso il DIMNP, è stato possibile pilotare lo stepper motor (ovverosia
muovere il piano laser sulla scena), in maniera sincronizzata all’acquisizione delle immagini da parte delle telecamere e alla loro successiva triangolazione.
Per riprendere la scena sono state utilizzate due telecamere digitali SONY XCD-SX900 in bianco e nero (Figure 3.5 e 3.6), dotate di un sensore CCD che garantisce una risoluzione di 1280x960 pixels (Figura 3.7), con dimensioni del singolo pixel pari a 4,65x4,65 micron.
Figura 3.6 Specifiche tecniche della telecamera Sony XCD-SX900
Figura 3.7 Dimensioni del sensore CCD presente nelle telecamere
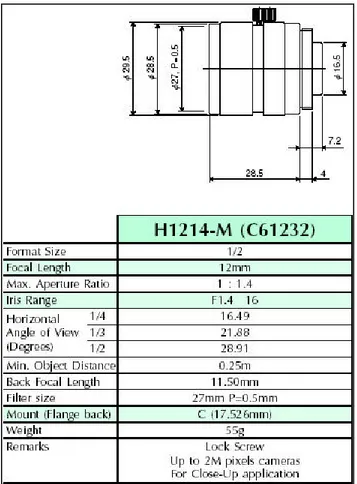
Sulle telecamere sono stati montati due obiettivi da misura COSMICAR/PENTAX modello H1214-M(C61232) (Figura 3.8).
Figura 3.8 Dimensioni e caratteristiche tecniche dell’obiettivo
L’interfaccia tra le telecamere ed il Personal Computer è realizzata attraverso una scheda di acquisizione video digitale, con connessione FireWire IEEE 1394.
IL Personal Computer utilizzato per gestire il sistema di visione e per il post-processing dei dati, è costituito da un PC con processore Pentium®4 a 2,2 GHz, dotato di 1,5 Gbytes di Ram e 40 Gbytes di HardDisk.
Il sistema di visione è montato su un cavalletto Manfrotto modello 117-117X (Figura 3.9), capace di una portata di 18 Kg: esso è dotato di una colonna centrale a cremagliera autobloccante, con crociera inferiore per ottenere una maggiore stabilità e tiranti telescopici che consentono il bloccaggio indipendente di ogni gamba; la testa che collega il cavalletto con la struttura di sostegno del sistema di visione, è orientabile nelle tre direzioni ed è dotata di bolle di livellamento.
Figura 3.9 Testa regolabile e cavalletto Manfrotto
3.2 Calibrazione del sistema
3.2.1 Modello della telecamera
Per poter utilizzare le telecamere come strumenti di misura bisogna calibrarle, cioè effettuare una serie di operazioni che consentano di determinare due gruppi di parametri detti rispettivamente parametri intrinseci e parametri estrinseci: i primi descrivono la geometria interna e le caratteristiche ottiche della telecamera, mentre i secondi descrivono la posizione e l’orientamento della telecamera rispetto ad un sistema di riferimento prestabilito [21,22,23,24].
Nel processo di calibrazione, alla telecamera viene sostituito il suo modello geometrico; il più comune è il cosiddetto modello pinhole o prospettico. Questo nome deriva dal fatto che il modello è costituito da due piani, il primo dei quali presenta un foro di dimensioni infinitesime (pinhole appunto) attraverso il quale passano i raggi luminosi, formando nell’altro piano, che è situato posteriormente al primo rispetto allo spazio di misurazione, un’immagine ribaltata dell’oggetto inquadrato. Geometricamente il modello consiste di un piano R, detto piano di retina, nel quale si forma l’immagine attraverso una proiezione prospettica (Figura 3.10): il punto C, detto centro ottico o fuoco, posto a distanza f (lunghezza focale) dal sistema ottico, è usato per formare l’immagine
m, di coordinate (x,y) nel piano R, del punto tridimensionale M di coordinate (Xc,Yc,Zc), come
punto c (punto principale). Un altro piano di interesse è il piano F (piano focale), passante per C e parallelo ad R: tutti i punti appartenenti a tale piano non hanno immagine nel piano di retina, in quanto i raggi ottici relativi a questi punti sono paralleli al piano R, e quindi non lo intersecano mai.
Figura 3.10 Modello geometrico della telecamera
La relazione che intercorre tra le coordinate immagine di m nel piano R e le coordinate tridimensionali del punto M è data da
c c c Y y X x Z f = − =− , (3.1) ovvero da ⋅ − = ⋅ − = c c c c Z Y f y Z X f x . (3.2)
Spesso, piuttosto che il piano di retina dietro al piano focale, situazione che provoca il ribaltamento dell’immagine (si noti il segno negativo nelle espressioni precedenti), si considera un piano parallelo al piano di retina, sempre distante f dal centro ottico ma davanti a quest’ultimo; in tal caso nelle equazioni (3.2) si può omettere il segno meno.
La trasformazione di coordinate espressa dalle equazioni proiettive (3.2) è non lineare, ma può essere linearizzata facendo uso di coordinate omogenee
⋅ = T Z Y X f f t y x c c c 0 0 0 1 0 0 0 0 0 0 . (3.3)
Si noti che la terza coordinata è stata posta uguale ad un valore generico t, infatti assegnarle un valore unitario avrebbe significato escludere i punti all’infinito.
Il sistema di equazioni (3.3) può essere scritto in forma compatta come m~=P~⋅M~, dove la matrice P~ viene detta matrice di proiezione prospettica.
Purtroppo il semplice modello della pinhole camera non è adatto per i nostri scopi, in quanto la quantità di luce che passa attraverso il centro ottico non è sufficiente per essere rilevata dal CCD; questo problema viene risolto ponendo davanti al piano di retina un altro sistema, composto da un diaframma e da un insieme di lenti.
Il diaframma non è altro che un’apertura variabile che regola la quantità di luce che entra nell’obiettivo. La sua funzione è indispensabile dato che le condizioni di luminosità della scena cambiano molto a seconda delle condizioni operative.
Tuttavia, l’introduzione di un sistema di lenti porta con sé una serie di problemi:
• Necessità della messa a fuoco della scena per ottenere un’immagine nitida
• Inadeguatezza delle equazioni (3.2) del modello della pinhole camera a causa della
distorsione ed aberrazione ottica introdotte dal sistema di lenti
In particolare, il sistema ottico reale si discosta dal modello ideale pinhole a causa dei seguenti fattori:
• Data la limitata apertura delle lenti, la banda ottica del sistema è finita, causando un blur (offuscamento) dell’immagine
• La distorsione geometrica introdotta dalle lenti causa uno spostamento dei punti immagine
• Sfuocamento, dovuto alla non perfetta messa a fuoco dell’immagine ed al fatto che la profondità di campo delle telecamere reali non è infinita, ma è inversamente proporzionale al diametro del diaframma
• Vignetting effect, causato dalla presenza del diaframma, che causa una diminuzione della
luce che entra nell’obiettivo passando dal centro ai bordi
Il processo di formazione di un’immagine da una scena può essere decomposto in quattro fasi principali:
• Moto rigido tra ?w e ?c. La trasformazione di coordinate dal sistema di riferimento solidale
con il mondo ?w al sistema di riferimento ?c solidale con la telecamera, può essere
modellata con una rotazione seguita da una traslazione, ovvero
T R + ⋅ = w w w c c c Z Y X Z Y X (3.4)
I parametri da calibrare sono quelli estrinseci, ovvero la matrice ortonormale di rotazione R ed il vettore di traslazione T.
• Trasformazione di coordinate da ?c a coordinate immagine ideali. La trasformazione tra le
coordinate tridimensionali (Xc,Yc,Zc) nel sistema di riferimento solidale con la camera alle
coordinate immagine ideali (indistorte), è data da
c c u Z X f x = ⋅ , c c u Z Y f y = ⋅ (3.5)
dove il parametro da calibrare è rappresentato dalla lunghezza focale f.
• Trasformazione da coordinate immagine ideali a coordinate immagine reali. Dette dx e dy le
componenti lungo i due assi della distorsione introdotta dalle lenti, la relazione tra le coordinate ideali (xu,yu) e le coordinate reali (xd,yd), si può esprimere come
(
(
)
)
u u y u d u u x u d y x y y y x x x , , ⋅ + = ⋅ + = δ δ . (3.6)I parametri da calibrare sono quelli dei modelli di distorsione, che verranno descritti meglio nel seguito.
• Trasformazione da coordinate immagine reali a pixel. La trasformazione tra le coordinate immagini reali (xd,yd) e le coordinate immagine (u,v) in pixel, è definita da
' u0 d x s u x d + ⋅ = , v0 d y v y d + = (3.7)
dove (u0,v0) sono le coordinate in pixel dell’effettivo centro c del piano immagine, ovvero
del punto di intersezione dell’asse ottico con la matrice di sensori del CCD (punto principale); dx’=dx·(Ncx/Nfx), dove Ncx è il numero di elementi sensibili (fotosensori) nella
direzione x, Nfx è il numero di pixel campionati in una riga dal sistema di acquisizione;
(dx,dy) sono le dimensioni delle celle del CCD. I parametri da calibrare sono le coordinate
del punto principale ed il fattore di scala s; quest’ultimo ha origine dal modo in cui l’immagine viene acquisita dalla telecamera e tiene conto di eventuali imprecisioni o errori di temporizzazione tra l’hardware di acquisizione (PC) e l’hardware di scansione della telecamera.
Riassumendo quanto detto nei punti precedenti, l’algoritmo di calibrazione dovrebbe essere in grado di stimare i sei parametri estrinseci propri del moto rigido descritto dall’equazione (3.4) e l’insieme dei cinque parametri intrinseci. In questo modo si hanno tutte le informazioni necessarie per trovare la relazione che lega le coordinate del punto M nella terna ambiente a quelle del suo punto immagine m nella memoria del PC.
I parametri estrinseci sono gli elementi della matrice R e del vettore T, quindi apparentemente dovrebbero essere dodici, ma in realtà sono sei, perché tra i nove elementi di R ci sono sei relazioni di ortonormalità: in altri termini possiamo scrivere la matrice in funzione dei tre angoli di Eulero (?,f,?) nel modo seguente
+ − + + + − − = ϕ θ ϕ θ γ ϕ γ ϕ θ γ ϕ γ ϕ θ ϕ θ γ ϕ γ ϕ θ γ θ γ θ θ γ θ γ cos cos cos sin sin sin cos cos sin cos sin sin sin cos sin sin sin cos cos cos sin cos cos sin sin cos sin cos cos R . (3.8)
I parametri intrinseci regolano invece il passaggio dalle coordinate 3D dell’oggetto da acquisire, nel sistema della telecamera, a quello relativo al PC: sono la distanza focale f, i coefficienti di distorsione, il fattore di scala s e le coordinate (u0,v0) del centro dell’immagine sul sensore CCD.
3.2.2 Distorsione dell’immagine
Come detto in precedenza, il modello pinhole della telecamera approssima solamente quello che succede nella realtà; infatti il raggio ottico non ha la forma di una retta ideale e questo è dovuto al fatto che l’obiettivo di una telecamera è molto lontano dal concetto di centro ottico.
Cerchiamo di capire meglio come si forma un’immagine fotografica.
Normalmente, il punto M sull’oggetto, il fuoco C ed il punto m’ sul piano immagine non giacciono sulla stessa retta; come vedremo più avanti, distanza della posizione reale di un punto immagine m’ dalla sua posizione ideale m, allineata con il centro ottico C ed il punto M, viene detta distorsione. Ovviamente tutti i punti di un’immagine, anche se in maniera diversa l’uno dall’altro, ne sono affetti. Si possono distinguere due componenti della distorsione, una componente radiale ed una tangenziale, disposta in direzione ortogonale alla prima (Figura 3.11).
Figura 3.11 Distorsione radiale e tangenziale in un punto m dell’immagine
Generalmente la distorsione radiale dr è molto più rilevante di quella tangenziale dt, infatti la letteratura tecnica ci indica che il loro rapporto è di circa 20 a 1.
La distorsione tangenziale è dovuta al non perfetto allineamento assiale di tutte le lenti che compongono l’obiettivo; la distorsione radiale varia invece con la lunghezza focale (Figura 3.12). Si supponga infatti che dr sia la distorsione radiale di un raggio ottico proveniente dal punto M dello spazio; possiamo osservare che esso forma un angolo a con l’asse ottico fino ad incontrare il fuoco
C, dopodiché il raggio devia dalla su direzione originaria formando un angolo a’ con l’asse ottico e
va ad incontrare il piano immagine nel punto m’, distante r dal punto principale c.
Traslando l’immagine lungo l’asse ottico di una quantità df, la distorsione radiale diventa nulla e la lunghezza focale è ora data da f’=f+df; si potrebbe quindi pensare di assumere come nuova lunghezza focale proprio questa f’, ma così facendo può accadere che per un altro punto q, che aveva distorsione radiale iniziale nulla, nasca una nuova distorsione diversa da zero. Da ciò si deduce che per ogni punto di un’immagine esiste una distanza principale per cui la distorsione radiale è nulla.
La distorsione radiale dr è espressa da un polinomio funzione della distanza radiale r dal punto principale ed assume la seguente espressione
... 7 3 5 2 3 1⋅ + ⋅ + ⋅ + =k r k r k r dr (3.9)
dove i coefficienti ki (i=1,…,5) devono essere determinati dal processo di calibrazione; nel sistema
sviluppato al DIMNP si è tenuto conto dei primi quattro coefficienti, anche se in realtà il contributo di quelli successivi al primo è trascurabile.
Si noti infine che, mentre la distorsione radiale è causata dalla forma stessa delle lenti e non può essere in alcun modo eliminata in fase di costruzione dell’obiettivo, la distorsione tangenziale è dovuta al non perfetto allineamento degli assi delle lenti che compongono l’obiettivo.
3.2.3 Teoria della calibrazione
La calibrazione consiste nel misurare con accuratezza i parametri intrinseci ed estrinseci del modello della telecamera. Poiché questi parametri governano il modo in cui punti dello spazio si proiettano sul piano immagine, l’idea è che conoscendo le proiezioni di punti 3D di coordinate note (punti di calibrazione), sia possibile ottenere i parametri incogniti risolvendo le equazioni della proiezione prospettica.
Il processo di calibrazione si basa sulla relazione fondamentale
w B
c= ⋅ (3.10)
dove c rappresenta un vettore contenente le coordinate in pixel degli n punti del provino di calibrazione (Figura 3.13) sul piano immagine della telecamera; w sono lo coordinate degli n punti del provino rispetto ad un sistema di riferimento che chiameremo ambiente, e B è la matrice di trasformazione globale che racchiude in se i parametri intrinseci ed estrinseci da calcolare. Le quantità c e w sono note a priori, in quanto la prima è misurabile direttamente eseguendo un’elaborazione digitale delle immagini acquisite, mentre la seconda è data, poiché è l’insieme delle coordinate dei punti sul provino di calibrazione rispetto al riferimento ambiente, giacente sul provino stesso (si osserva che questi punti hanno tutti coordinata Z nulla essendo appartenenti ad un piano).
Eseguendo una serie di ottimizzazioni sulla soluzione, si riesce ad ottenere come risultato finale la matrice di proiezione B. Siamo quindi in grado di determinare la relazione che intercorre tra la terna di riferimento relativa al piano immagine della camera e quella solidale con il provino.
Analiticamente il processo di calibrazione viene eseguito nel modo seguente: il primo passo consiste nella determinazione dell’orientamento della telecamera e delle componenti x ed y del vettore traslazione T. Invertendo le (3.7) per ogni punto i di calibrazione (i vertici dei quadrati presenti sul provino di calibrazione), si ha
(
0)
' u u s d x i x di = ⋅ − , ydi=dy⋅(
vi−v0)
(3.11)dove con i=1,2,3,…,n si indicano i punti di calibrazione. Noti a questo punto (xdi,ydi), ed anche le
coordinate (Xwi,Ywi,Zwi) degli stessi punti espresse nel riferimento ambiente, si imposta e si risolve il
seguente sistema lineare nelle cinque incognite Ty−1⋅r1, Ty−1⋅r2, Ty−1⋅Tx, Ty−1⋅r4, Ty−1⋅r5
[
]
di y y x y y y wi wi wi di di wi di wi di x r r r r Y X X x y Y y X y = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ − ⋅ − ⋅ ⋅ − − − − − 5 1 4 1 1 2 1 1 1 T T T T T T . (3.12)Questo sistema ha un’unica soluzione se e solo se il rango della matrice dei coefficienti è pieno o, equivalentemente, se tutte le colonne sono linearmente indipendenti; per n>>5 si dimostra che ciò è verificato. Bisogna adesso determinare r1, r2, r3, r4, r5, r6, r7, r8, r9, Tx, Ty a partire da 1
1 r y ⋅ − T , 2 1 r y ⋅ −
T , Ty−1⋅Tx, Ty−1⋅r4, Ty−1⋅r5 calcolati al passo precedente.
Innanzitutto si procede con la determinazione di |Ty|, definendo la matrice C, sottomatrice
superiore sinistra 2x2 della matrice di rotazione R, scalata di 1/Ty
= y y y y r r r r T T T T C 4 3 2 1 (3.13)
l’unicità di |Ty| è assicurata da un lemma e le proprietà di ortogonalità di R permettono di
calcolareT nel modo seguente: y2
se nessuna riga o colonna di C è nulla, allora
(
)
(
')
2 2 ' 4 ' 5 ' 1 2 ' 2 ' 4 ' 5 ' 1 2 2 2 4 r r r r r r r r S Sr r y ⋅ − ⋅ ⋅ ⋅ − ⋅ ⋅ − − = T (3.14) altrimenti( ) ( )
[
2]
1 ' 2 ' 2 = + − j i y r r T (3.15)dove Sr=(r1’)2+(r2’)2+(r4’)2+(r5’)2 ed ri’, rj’ sono gli elementi della riga o colonna di C non nulla.
Dopo aver determinato T , si esegue una ulteriore procedura per ottenere Ty2 y con il segno
corretto. Abbiamo così ricavato le quantità r1, r2, r4, r5, ma a noi interessa conoscere tutta la matrice
R e per determinarla si può scrivere
− − ⋅ − − = 9 8 7 2 5 2 4 5 4 2 2 2 1 2 1 1 1 r r r r r s r r r r r r R (3.16)
dove s=-sgn(r1·r4+ r2·r5) ed r7, r8, r9, sono calcolati come prodotto vettoriale delle prime due righe
di R (si sfrutta la sua proprietà di ortonormalità).
Rimangono ora da determinare la distanza focale f e la Tz; inizialmente se ne determina soltanto
una stima, trascurando la distorsione introdotta dalle lenti: si imposta il seguente sistema per ciascun punto di calibrazione
[
]
i y ci z ci y i w d Y f Y d y = ⋅ ⋅ ⋅ ⋅ − T (3.17)Usando molti punti di calibrazione questo sistema risulta sovradeterminato, ma può comunque essere risolto nelle due incognite f e Tz (usando per esempio il metodo dei minimi quadrati).
L’ultima fase della calibrazione riguarda la determinazione dei valori esatti di f, Tz ed i vari
coefficienti k della distorsione: si imposta un problema di ottimizzazione non lineare, per inizializzare il quale si usano i valori approssimati determinati al passo precedente.
A questo punto, sulla base delle relazioni che descrivono la trasformazione geometrica dai punti oggetto ai punti immagine, è possibile stimare le coordinate della terna ambiente di un qualsiasi punto reale, nota che sia la sua quota Zw e le coordinate in pixel (u,v) della sua immagine nella
memoria del PC. Infatti si ha
(
0)
' u u s d x x d = ⋅ − , yd =dy⋅(
v−v0)
. (3.18)Utilizzando le relazioni (2.6) si possono ora ricavare le coordinate (xu, yu). Successivamente,
invertendo le (2.5), si ottiene f Z x X c u c= ⋅ , f Z y Y c u c = ⋅ . (3.19)
A questo punto, riscrivendo la relazione (3.4) e sostituendovi dentro le espressioni di Xc ed Yc
prima calcolate, si ha T R + ⋅ = ⋅ w w w c u u Z Y X Z f y f x 1 (3.20) ed esplicitando rispetto a
[
Xw Yw Zw]
TT R R ⋅ − ⋅ ⋅ = T c u u T w w w Z f y f x Z Y X 1 . (3.21)
Considerando solo la terza equazione si ha
z y x c u u w r Z r r r f y r f x r Z ⋅ − ⋅T − ⋅T − ⋅T ⋅ + ⋅ + = 3 6 9 3 6 9 (3.22)
da cui si ricava Zc in funzione di grandezze note
9 6 3 9 6 3 r f y r f x r Z r r r Z u u w z y x c + ⋅ + ⋅ + ⋅ + ⋅ + ⋅ = T T T . (3.23)
Mediante le (3.19) si possono quindi calcolare le coordinate del punto oggetto nel sistema di riferimento della camera ed infine, sfruttando le prime due relazioni della (3.21), si ottiene
(
)
(
)
(
)
(
c x)
(
c y)
(
c z)
w z c y c x c w Z r Y r X r Y Z r Y r X r X T T T T T T − ⋅ + − ⋅ + − ⋅ = − ⋅ + − ⋅ + − ⋅ = 8 5 2 7 4 1 (3.24)che permettono di ricavare le coordinate di un punto dell’oggetto rispetto al riferimento ambiente.
3.2.4 Procedura di calibrazione stereo
Il processo di calibrazione si articola nelle seguenti fasi:
• Posizionamento relativo delle telecamere, regolazione della messa a fuoco e dell’apertura
dei diaframmi, stima delle posizioni spaziali del provino, controllo dell’inquadrautra
• Elaborazione delle immagini ed estrazione dei punti di interesse
• Calcolo dei parametri di calibrazione
• Analisi degli errori ed eventuali correzioni.
L’elaborazione digitale delle immagini ed il calcolo dei parametri di calibrazione (delle singole camere e del sistema stereo) sono state effettuati utilizzando delle toolbox precompilate di Matlab® [25]. Per quanto riguarda il provino di calibrazione, è stato necessario utilizzarne uno di notevoli dimensioni, in modo tale da avere un ampio campo di acquisizione per ogni posizionamento del sistema. Da notare che la teoria di calibrazione richiede che tutti i punti estratti dal provino si trovino sul medesimo piano; questo comporta che il provino sia realizzato con un materiale che garantisca una ottima planarità e indeformabilità al variare delle condizioni ambientali ed al trascorrere del tempo. Per questi motivi il provino è stato realizzato mediante una lastra di vetro sulla quale è stato applicato un foglio adesivo in PVC, recante la stampa ad alta definizione di una scacchiera (Figura 3.14).
Prima operazione da effettuare è la scelta della distanza a cui tarare il sistema, questa sarà un compromesso tra le dimensioni della singola inquadratura e la precisione richiesta, ed ovviamente dipenderà dalle dimensioni dell’oggetto da acquisire. Si passa quindi alla messa a punto delle camere; si posiziona il provino di fronte al sistema ad una distanza pari a quella di scansione e con l’aiuto del software di gestione delle camere, che visualizza sullo schermo del PC l’immagine dell’inquadratura, si posizionano le due camere in modo tale che il provino ricada al centro dell’immagine per entrambe.
Figura 3.14 Provino di calibrazione
Questa orientazione relativa tra le camere rimane invariata per tutta la durata dell’acquisizione.
A questo punto si effettua prima la messa a fuoco delle camere, e poi la taratura dell’apertura dei diaframmi, in modo da non avere zone delle immagini che risultino sovraesposte. Entrambe queste operazioni vengono eseguite manualmente agendo sulle ghiere di regolazione presenti sugli obiettivi (le ghiere vengono poi bloccate con delle viti di fermo).
Finita la messa a punto del layout geometrico del sistema, si passa all’acquisizione delle immagini: si effettuano sedici posizionamenti diversi del provino (in modo da definire un volume di calibrazione) e per ognuna delle sedici posizioni si acquisiscono due immagini, una per la camera destra ed una per quella sinistra. Bisogna assicurarsi che la stessa area sia contenuta interamente in entrambe le immagini riprese dalle camere e che tutte le parti del provino siano a fuoco anche nelle posizioni angolate.
Da notare che effettuare più di sedici posizionamenti del provino non porta ad alcun miglioramento della precisione del processo di calibrazione.
Tramite il toolbox Calib_gui di Matlab® (Figura 3.15) si procede alla calibrazione delle singole camere: il software carica in memoria le immagini relative alla singola camera da calibrare (Figura 3.16) ed inizia la loro elaborazione.
Figura 3.15 Camera Calibration Toolbox di Matlab®
L’estrazione dei punti di calibrazione dalle immagini caricate in memoria si basa su una routine del software che, dopo aver definito le dimensioni in pixel di un puntatore rettangolare, ricerca all’interno dello stesso, la massima variazione del livello di grigio dell’immagine. In questo modo, cliccando in maniera approssimata nell’intorno degli spigoli dei quadrati della scacchiera, il sistema individua con ottima precisione la posizione del vertice cercato.
Figura 3.16 Immagini del provino di calibrazione caricate in memoria
Per ognuna delle immagini caricate in memoria è richiesto di ciccare sui quattro spigoli alle estremità della scacchiera (Figura 3.17), definendo così un rettangolo.
Figura 3.17 Selezione dei vertici del rettangolo
L’ordine con cui si clicca per definire i vertici del rettangolo non è casuale, infatti il primo punto su cui si clicca viene riconosciuto come origine del sistema di riferimento associato al provino e questo è particolarmente importante se bisogna determinare i parametri estrinseci di più camere (cioè determinare la loro posizione reciproca). In questo caso il pattern di punti selezionato deve essere lo stesso in tutte le immagini, così come deve essere lo stesso l’ordine con cui vengono selezionati i punti.
Immettendo anche la dimensione del lato dei quadrati stampati sul provino, il programma individua la posizione teorica di tutti gli spigoli dei quadrati presenti all’interno del rettangolo prima definito e visualizza sullo schermo delle crocette sovrapposte all’immagine reale (Figura 3.18).
La posizione dei quadrati individuati dal programma all’interno del rettangolo non tiene conto della presenza della distorsione introdotta dalla lente, per cui se gli spigoli trovati si discostano da quelli reali, l’utente può introdurre un valore iniziale della distorsione radiale e ripetere la procedura appena descritta: tale valore può essere modificato finché non si ottiene una corrispondenza soddisfacente.
Figura 3.18 Estrazione dei punti teorici
Dopo l’estrazione degli spigoli da tutte le immagini, il programma inizia la procedura di calibrazione vera e propria; essa consiste di due steps: first inizialization e non linear optimization. L’inizialization step calcola un set di base di parametri di calibrazione, senza considerare la distorsione delle lenti delle camere: i risultati ottenuti in questa fase preliminare vengono utilizzati nello step della non linear optimization in cui tutti i parametri estrinseci ed intrinseci della camera vengono determinati attraverso un processo che tende a minimizzare iterativamente l’errore di riproiezione (errore tra le coordinate dei punti della scacchiera rispetto al riferimento del provino e le coordinate dei punti riproiettati, cioè ottenuti utilizzando le matrici di proiezione prospettica prima valutate). I risultati forniti dal programma comprendono la distanza focale, la posizione del punto principale, i fattori della distorsione e l’errore nell’estrazione dei punti; tutte le grandezze sono espresse in pixel ed inoltre è possibile visualizzare su di un grafico (Figura 3.19) l’errore di riproiezione, consentendo così di capire quali sono le immagini in cui l’errore è maggiore (ad ogni immagine è associato un colore diverso): per queste è quindi possibile rieffettuare l’estrazione dei punti ed una nuova ottimizzazione o, nel peggiore dei casi, escluderle dal calcolo.
Figura 3.19 Errore di riproiezione
Il programma fornisce anche l’andamento della distorsione, nelle sue componenti radiale e tangenziale (Figura 3.20).
Una volta calibrata la prima camera, si procede in maniera del tutto analoga a calibrare la seconda. Ottenuti i valori dei parametri intrinseci delle due camere, viene effettuata un’ulteriore calibrazione, comunemente detta calibrazione stereo, attraverso l’uso del toolbox Stereo_Gui di Matlab® (Figura 3.21).
Figura 3.21 Stereo Camera Calibration Toolbox di Matlab®
Questo ulteriore processo consente di determinare i parametri estrinseci del sistema; infatti prendendo come riferimento quello relativo ad una delle due camere, il software calcola, sulla base dei parametri intrinseci precedentemente trovati, i valori delle matrici R e T per passare da un sistema di riferimento solidale con la camera di sinistra, a quello relativo alla camera destra. Queste due matrici verranno poi utilizzate nel processo di ricostruzione tridimensionale.
Terminata la procedura di calibrazione è possibile visualizzare su di un grafico tridimensionale la posizione relativa delle due telecamere e la posizione successivamente assunta dal provino di calibrazione; in questo modo si può effettuare una rapida valutazione del volume di spazio effettivamente calibrato (Figura 3.22).
3.3 La visione stereo
La visione stereoscopica consente di ottenere informazioni di profondità da una coppia di immagini, provenienti da due telecamere che inquadrano la scena da differenti posizioni. Il principio è il medesimo su cui si basa il sistema visivo umano: il nostro cervello può fondere (percepire in un’immagine unica) due immagini retiniche che, entro certi limiti si formano su punti retinici lievemente disparati, come ad esempio, quando a causa della distanza tra gli assi visivi, i due occhi osservano lo stesso oggetto sotto due angolazioni diverse. È proprio a causa di questa disparità che avviene la visione stereoscopica, facendoci percepire l’oggetto come “unico” e “solido”.
Con questo tipo di approccio vengono comunemente riscontrati due tipi di problematiche: la determinazione delle corrispondenze e la ricostruzione. Il primo consiste nell’accoppiamento tra punti nelle due immagini che sono proiezione dello stesso punto della scena, generalmente chiamati punti coniugati; il secondo riguarda invece la ricostruzione della posizione nella scena dei punti che sono proiettati sulle due immagini. Questo processo di ricostruzione, come accennato in precedenza, necessita della calibrazione dell’apparato stereo, ovvero del calcolo dei parametri intrinseci ed estrinseci delle due telecamere.
3.3.1 Ricostruzione 3D
Dopo aver risolto il problema delle corrispondenze, argomento che verrà trattato nel paragrafo successivo, vediamo come sia possibile la ricostruzione tridimensionale nel suo caso più generale.
Note dalla calibrazione le coordinate in pixel dei punti coniugati e le due matrici di proiezione prospettica (MPP) relative alle due telecamere, si può facilmente ricostruire la posizione in coordinate assolute del punto di cui entrambe sono la proiezione (Figura 3.23).
Posto m=(u,v)T , e scrivendo P~ nella forma
( )
Pp q q q P~ ~ 34 24 14 3 2 1 = = q q q T T T (3.25) dall’equazione (3.3) si ricava + + = + + = 34 3 24 2 34 3 14 1 q q v q q u T T T T w q w q w q w q (3.26) ovvero(
)
(
)
= − + − = − + − 0 0 34 24 3 2 34 14 3 1 vq q v uq q u T T w q q w q q (3.27) e quindi(
)
(
)
+ − + − = ⋅ − − 34 24 34 14 3 2 3 1 vq q uq q v u T T w q q q q . (3.28)Siano m=(u,v)T ed m’=(u’,v’)T i due punti coniugati che sono riconosciuti come proiezione dello stesso punto dello spazio, si può allora scrivere il sistema lineare sovradimensionato
(
)
(
)
(
)
(
)
+ − + − + − + − = ⋅ − − − − ' 34 ' 24 ' 34 ' 14 34 24 34 14 ' 3 ' 2 ' 3 ' 1 3 2 3 1 vq q uq q vq q uq q v u v u T T T T w q q q q q q q q (3.29)3.3.2 Determinazione delle corrispondenze attraverso la geometria epipolare
Vediamo ora quale relazione lega due immagini di una stessa scena ottenute da due telecamere diverse [26,27,28,29,30,31,32]. In particolare, ci chiediamo, dato un punto m1 nella immagine 1,
quali vincoli esistono sulla posizione del suo coniugato m2 nella immagine 2.
Alcune semplici considerazioni geometriche indicano che il punto coniugato di m1 deve giacere
su di una linea retta nella immagine 2, chiamata retta epipolare di m1 (Figura 3.24).
Figura 3.24 Ai punti marcati con la croce nell’immagine sinistra, corrispondono le rette epipolari tracciate nell’immagine destra
La geometria epipolare è importante anche (e soprattutto) perché descrive la relazione tra due viste di una stessa scena, dunque è fondamentale in qualunque tecnica di visione computazionale basata su più di una immagine.
Si consideri il caso illustrato in Figura 3.24. Dato un punto m1 nella immagine 1, il suo
coniugato m2 nella immagine 2 è vincolato a giacere sull’intersezione del piano immagine R2 con il piano determinato da m1, C1 e C2, detto piano epipolare. Questo poiché il punto m2 può essere la
proiezione di un qualsiasi punto dello spazio giacente sul raggio ottico di m1. Inoltre si osserva che
tutte le linee epipolari di una immagine passano per uno stesso punto, chiamato epipolo, e che i piani epipolari costituiscono un fascio di piani che hanno in comune la retta passante per i centri ottici C1 e C2. Il segmento che unisce i centri ottici C1 e C2 prende il nome di linea di base (o
baseline).
Tutta l’informazione relativa alla geometria epipolare è contenuta in quella che viene chiamata matrice fondamentale, calcolata come funzione delle MPP delle due telecamere.
Fissato un sistema di riferimento assoluto, date due camere 1 e 2, sappiamo che
≅ ≅ w P m w P m ~ ~ ~ ~ ~ ~ 2 2 1 1 . (3.30)
La linea epipolare corrispondente ad m1 è la proiezione secondo 2
~
P del raggio ottico di m1, che
ha equazione + = − 0 ~ 1 ~ 1 1 1 1 P m w c λ , λ∈ℜ. (3.31) Siccome 2 1 1 1 2 2 1 1 1 2 1 2 ˆ ~ ~ 1 ~ ~ 1 ~ e p P P p p P P P = − = − = c − − (3.32) e 1 1 1 2 1 1 1 2 ~ 0 ~ ~ m P P m P P − − = (3.33)
1 1 1 2 2 2 ~ ~ ~ e PP m m ≅ +λ − . (3.34)
Questa è l’equazione, in coordinate omogenee, della retta passante per i punti ~e (l’epipolo) e 2
1 1 1 2P m~
P − . Come è noto, una retta passante per due punti è rappresentata dal prodotto esterno dei due
punti, quindi la retta epipolare di m1 è rappresentata, in coordinate omogenee, dal vettore
[ ]
1 1 1 1 2 2 1 1 1 2 2 ~ ~ ~ ~ ~e ∧P P m = e PP−m =Fm ∧ − (3.35)dove
[ ]
~e2 ∧ è una matrice antisimmetrica che agisce come il prodotto esterno con ~e . La matrice 2[ ]
1 1 2 2 ~ − ∧ = e P P F (3.36)prende il nome di matrice fondamentale.
Il punto coniugato di m1, m2 giace sulla linea epipolare, dunque soddisfa l’equazione seguente,
che viene spesso indicata come Equazione di Longuet-Higgins, e che caratterizza completamente F:
0 ~ ~ 1 2Fm = mT . (3.37)
Dal punto di vista geometrico, Fm~1 definisce la retta epipolare del punto m1 nella seconda
immagine. L’equazione (3.37) dice che il punto corrispondente di m1 nella seconda immagine deve
giacere sulla sua linea epipolare Fm~1.
Una volta determinata la matrice fondamentale, per disegnare la retta epipolare di un punto m=(u,v) che appartiene alla immagine sinistra, basta calcolare F⋅
[
m 1]
T ottenendo così un vettore di tre elementi[
a b c]
, che sono i coefficienti della equazione cartesiana della retta epipolare nella immagine destra: au+bv+c=0.Il problema della corrispondenza risulta, a questo punto, risolto solo in parte; infatti esiste ancora una indeterminazione dovuta al fatto che un punto dell’immagine sinistra avrà come coniugato uno tra gli infiniti punti giacenti sulla sua retta epipolare nell’immagine destra, ma non sappiamo ancora quale.
Per eliminare l’indeterminazione si sfrutta la sorgente di luce laser; infatti, osservando la Figura 3.25, si capisce come il coniugato del punto m1 dell’immagine sinistra (ovverosia il punto m2
dell’immagine destra), debba giacere contemporaneamente sia sulla corrispondente retta epipolare, che sulla immagine destra della linea laser. Dall’intersezione di queste due curve è possibile determinare le coordinate in pixel di m2.
Figura 3.25 Determinazione del coniugato di m1
Da notare che la larghezza della traccia della linea laser sulle due immagini, ha dimensioni finite, cioè la zona di transizione tra pixel scuri e pixel chiari non è netta ma presenta un gradiente che si estende per qualche pixel (Figura 3.26).
Figura 3.26 Ingrandimento dell’immagine della linea laser, con (in verde) la linea estratta con la routine realizzata in Matlab®
inconveniente e per garantire una precisione dell’ordine del subpixel, è stata realizzata una routine in Matlab® che permette di determinare il picco di luminosità della traccia del laser.
Fra le numerose metodologie analizzate [35] (approssimazione gaussiana, stima parabolica, centro di massa, ecc…), è stato implementato il metodo del messo a punto da F. Blais e M. Rioux [33]. Il metodo si basa sul filtraggio del segnale attraverso filtri lineari di quarto e ottavo ordine, con convoluzione del segnale s mediante un operatore g definito da:
∑
+ − = + ⋅ − = n n h n i sign h s i h g () ( ) ( ) (3.38)dove n è l’ordine del filtro. Il filtro agisce come un controllo derivativo sulle frequenze del segnale luminoso, tagliando le zone dove la variazione del segnale è piccola e concentrandosi sul picco del segnale (Figura 3.27).
Figura 3.27 Analisi del segnale luminoso
La posizione del picco di intensità viene definita come:
) ( ) 1 ( ) ( h g h g h g h x − + + = (3.39)
da cui, applicando la (3.38), si ottiene:
) ( ) ( ) (i s i g i t = n (3.40)
Attraverso la (3.40) si può determinare il campo derivativo e, quindi, la traccia voluta (Figura 3.28).
Figura 3.28 Derivata del segnale
Questa analisi non sempre conduce a risultati corretti; infatti il picco di segnale può essere scambiato con un altro presente nello spettro dei profili della scena oppure addirittura il filtro può non “vedere” la traccia laser. Questi errori sono dovuti principalmente alla presenza di componenti luminose esterne (luce solare, fonti di illuminazione artificiale, ecc…).
Per ovviare a questo inconveniente si utilizza un “discriminatore” basato sulla logica Fuzzy; esso si avvale di un modello deduttivo basato sulla logica umana attraverso il quale riesce ad individuare l’effettiva traccia laser anche in presenza di zone ad alta luminosità e di riflessi spuri.
In particolare, il discriminatore prende in esame i valori massimi e minimi di ogni segnale ed esegue le seguenti verifiche:
• distanza tra i valori massimo e minimo del segnale
m M I
I
a= + (3.41)
• simmetria del segnale
m M I
I
b= − (3.42)
• opposizione del segno
m M I
I
c= ⋅ (3.43)
• caratteristica impulsiva del segnale, ovvero la distanza spaziale tra punto di massimo e minimo
• caratteristica luminosa del segnale, con il minimo che precede il massimo (ombra-luce)
m M x
x
e= − (3.45)
La (3.38) e la (3.39) vengono quindi applicate a valle di questo filtro decisionale, ottenendo la posizione (in termini di pixel) del punto di massima intensità del segnale, con precisione del subpixel. Questo consente di ottenere le coordinate del punto nel riferimento immagine di ciascuna telecamera, quindi la matrice dei punti della lama.
A questo punto si determina, attraverso l’uso del vincolo epipolare, la matrice dei coefficienti della retta epipolare e, dalla (3.37), si ricava:
sx T dx tc C FC
R = (3.46)
dove C è la matrice delle coordinate dei centri di massa della linea laser vista dalla telecamera dx
destra e C è l’analoga per la telecamera sinistra. sx
Il punto desiderato, nel riferimento della telecamera destra, si determina analizzando riga per riga la matrice R , in cui (in ogni riga) compaiono i valori ottenuti applicando i coefficienti tc
cartesiani della retta epipolare sinistra a tutti i punti della lama laser destra; per ciascuna riga sarà quindi sufficiente determinare i punti di minima distanza ed interpolarli con i punti della retta epipolare appartenente alla stessa riga (un procedimento analogo viene seguito per i punti della telecamera sinistra).
Si ottengono quindi due matrici che possono essere triangolate con il metodo illustrato nel paragrafo 3.3.1, ottenendo le coordinate tridimensionali dei punti della linea laser.