CAPITOLO 4 Effetti di schermi dielettrici

CAPITOLO 4

Effetti di schermi dielettrici

4.1 Piastre dielettriche

Le piastre dielettriche sono spesso utilizzate come sostegno fisico per schermi sottili (il cui spessore è minore di un centesimo della lunghezza d’onda che, per frequenze dell’ordine della decina di Ghz, corrisponde a circa _{5 10 m}−4 _).

Un altro motivo dell’utilizzo di piastre dielettriche è dato dalla loro peculiarità di stabilizzare la risposta dello schermo al variare dell’angolo di incidenza. In particolare riducono la dipendenza della frequenza di risonanza, alla quale si ottiene un coefficiente di trasmissione unitario, dall’angolo di incidenza. Questo fenomeno risulta particolarmente deleterio per particolari geometrie delle aperture come quelle rettangolari, tra le quali quella considerata in seguito per comprovare la validità delle modifiche apportate al programma presentato. Un altro effetto dovuto all’utilizzo di piastre dielettriche è quello di poter influenzare gli effetti delle Wood’s Anomalies che si manifestano con picchi del coefficiente di trasmissione per

frequenze vicine o superiori alla frequenza di risonanza della struttura. E’ stato dimostrato il letteratura che la frequenza delle Wood’s Anomalies diminuisce all’aumentare dello spessore

dello schermo dielettrico. In questo capitolo valutano gli effetti dello schermo dielettrico in termini di matrice di scattering generalizzata, in analogia a quanto fatto per la superficie selettiva in frequenza.

4.2 Calcolo della GSM totale

La matrice di scattering generalizzata della nuova struttura viene ottenuta dalle matrici relative alle due discontinuità aria-dielettrico ed dielettrico-apertura opportunamente manipolate con le operazioni di spostamento dei piani di riferimento, di trasposta e di connessione descritte nel capitolo 3. Lo schema a blocchi che riassume la procedura utilizzata per il calcolo della GSM di uno schermo con piastre dielettriche è rappresentato il figura 4.1.

Fig 4.1 Schema a blocchi della procedura utilizzata per il calcolo della GSM totale. Nello schema si è indicato con ss/2 la metà dello spessore dello schermo e con sd lo spessore della piastra dielettrica

GSM aria-dielettrico z=0 GSM aria-dielettrico z=sd GSM dielettirico-apertura z=sd GSM aria-apertura z=sd GSM aria-apertura z=sd+ss GSM apertura-aria z=sd+ss GSM TOTALE shift shift connessione connessione trasposta

Nei paragrafi successivi sono ricavate le matrici delle discontinuità aria-dielettrico ed dielettrico-apertura che, come evidenziato dal diagramma, sono il punto di partenza per il calcolo della GSM totale. Si faccia attenzione al fatto che lo schema a blocchi sopra rappresentato è relativo alla configurazione data dallo schermo con piastre dielettriche su entrambi i lati. E’ possibile studiare altresì il caso col piastra dielettrica nella sola zona “d’ombra” (zona in cui avviene la propagazione dell’onda trasmessa) modificando opportunamente lo schema a blocchi precedente e calcolando sia la matrice di scattering generalizzata della discontinuità aria-apertura che quella dielettrico-apertura.

4.3 Discontinuità dielettrico-apertura

Per quanto riguarda il calcolo della matrice di scattering generalizzata che descrive la discontinuità dielettrico-apertura, la trattazione risulta del tutto analoga a quella fatta nei capitoli precedenti per la discontinuità aria-apertura, con la differenza di dover considerare la potenza nel dielettrico e non in aria e quella di sostituire, nel calcolo della matrice di accoppiamento, i coefficienti complessi dello sviluppo modale di Floquet nel dielettrico con

quelli in aria. I coefficienti complessi dello sviluppo modale di Floquet sono calcolati nel

paragrafo successivo

Espansione modale di Floquet nel dielettrico

La trattazione risulta del tutto analoga a quello già fatta per quanto riguarda l’espansione modale di Floquet in aria con la sola differenza che le costanti dielettriche dello spazio libero

sono sostituite con quelle del dielettrico. Alcuni risultati sono comunque di notevole interesse per cui vengono riportati di seguito.

Prima di procedere con il calcolo dei coefficienti moltiplicativi complessi è opportuno ricordare la legge di Snell. La legge di Snell asserisce che, data un'onda piana incidente su di

una discontinuità, esiste una relazione tra l'angolo formato dalla direzione di propagazione con la normale alla stessa superficie data da

1 1 1 1 0 0 sin sin i r r t ε µ θ _{ε µ} θ = ε µ =

La configurazione considerata è rappresentata in figura 4.2.

Θ2

Θ1

Spess dielettrico

Fig 4.2 Onda piana incidente su di uno schermo dielettrico

Applicando la relazione precedente alla (2.3.3) e ricordando che

r r k k= ₀ ε µ si ottiene α π α π θ φ α π α π θ φ π θ φ π θ φ tan 2 sin 2 sin sin tan 2 sin 2 sin sin 2 sin cos 2 sin cos 1 0 2 1 0 2 h h h h D y h h D x a m b n k a m b n k k a m k a m k k i i − + = − + = + = + = (4.3.1)

Si noti che le (4.3.1) risultano equivalenti a quelle trovate per l’espansione in aria e, data la (2.3.2) risultano uguali anche le costanti di propagazione trasverse D

z A zi k i

k = . Questo risultato è particolarmente interessante perché, come viene dimostrato nell’appendice A, si ottiene l’ortonormalità anche tra i coefficienti dei modi nei due mezzi.

0 0 0 0 η ε η µ η η D z r D z TM D i r D z D z TE D i i i i i k k k k Y k k k k Y = = = = (4.3.2)     − − ≥ − = altrimenti k k j k k se k k k i i i t t t D z _{2 2} 2 2 2 2 1 _(4.3.3)

ed applicando quanto sopra ottenuto alla (2.3.1) e (2.3.7) si ottengono

y jk x jk y t y x t x h h TM D i y jk x jk y t x x t y h h TE D i yi xi i i i i yi xi i i i i e e i k k i k k b a E e e i k k i k k b a E − − − −         + =         − = ˆ ˆ sin 1 ˆ ˆ sin 1 α α (4.3.4) y jk x jk y t x x t y h h D z r TM D i y jk x jk y t y x t x h h r D z TE D i yi xi i i i i i yi xi i i i i i e e i k k i k k b a k k H e e i k k i k k b a k k H − − − −         + − =         + = ˆ ˆ sin 1 ˆ ˆ sin 1 0 0 0 0 α η ε α µ η (4.3.5)

4.4 Calcolo della GSM di una discontinuità aria-dielletrico

Per il calcolo della GSM si procede in modo analogo a quanto fatto per la discontinuità aria-apertura. In accordo con il teorema di Floquet è possibile limitare l'analisi alla sola cella elementare che rimane definita come la cella di periodicità dello schermo. Si procede poi facendo il Mode Matching tra i modi di Floquet nello spazio libero e nel dielettrico.

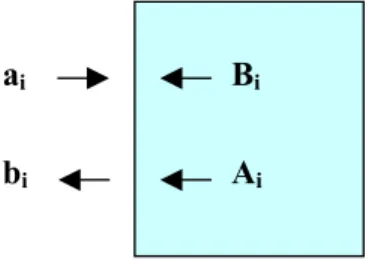
Fig 4.3.3 Coefficienti di modo incidenti e riflessi sul l'interfaccia aria-dielettrico

Consideriamo l'espressione dei campi traversi elettrico e magnetico in aria a z=0

(

)

(

)

∑

∑

∞ = ∞ =

−

=

+

=

1 1 i i i i A t i i i i A t

H

b

a

H

E

b

a

E

(4.4.1)

e nel dielettrico alla stessa coordinata z

(

)

(

)

∑

∑

∞ = ∞ =

−

=

+

=

1 1 i i i i D t i i i i D t

h

B

A

H

e

B

A

E

(4.4.2)

dove si è indicato con Ai , Bi i coefficienti modali associati al modo i-esimo di Floquet nel

dielettrico mentre con ai , bi quelli relativi all'espansione modale in aria.

Imponendo su di esse le condizioni di continuità per il campo elettrico e per il campo magnetico date dalle relazioni

ai bi

Bi Ai

D t A t D t A t H H E E = = _(4.4.3) si ottiene il sistema

(

)

(

)

(

)

_∑

(

)

∑

∑

∑

∞ = ∞ = ∞ = ∞ = − = − + = + 1 1 1 1 i i i i i i i i i i i i i i i i h B A H b a e B A E b a (4.4.4)

utilizzando il prodotto interno già definito nel capitolo 2:

dS z t f t f f f C S ˆ ) ( ) ( , _{2 1 2} 1 >= × ⋅ <

_∫

∗ _(4.4.5) si ottiene:

(

)

(

)

(

)

_∑

(

)

_∫∫

∑

∫∫

∑

∫∫

∑

∫∫

∞ = ∞ = ∞ = ∞ = ⋅       × − = ⋅       _× − ⋅       × + = ⋅       _× + 1 * 1 * 1 0 * * ˆ ˆ ˆ ˆ i S z j i i i i S z j i i i i i _S z j i i i S z j i i i C C C C dS i e h B A dS i e H b a dS i H e B A dS i H E b a (4.4.6)

Il precedente sistema può essere scritto come

(

)

(

)

(

)

(

)

H D H A P B A C b a C B A P b a − = − + = + (4.4.7)

dove, uguagliando membro a membro le due relazioni (4.4.6) e (4.4.7) si ricavano le definizioni

∫∫

∫∫

∫∫

⋅       × = ⋅       × = ⋅       _× = C C C S z j i D S z j i S z j i A dS i h e P dS i H e C dS i H E P ˆ ˆ ˆ * * * (4.4.8)

Si noti che la superficie SC su cui vengono calcolati gli integrali precedenti è quella della cella

elementare imposta dalla periodicità dello schermo. Ricordando che i vettori dei coefficienti modali delle onde riflesse b , possono essere espressi in funzione di quelli B a , tramite la A

matrice S               =       =       A a S S S S A a S B b 22 21 12 11 (4.4.9)

uguagliando membro a membro , dopo alcuni passaggi si ottengono relazioni analoghe alle (1.10) , (1.11) ed (1.12) in cui le (1.11) ed (1.12) vengono modificate come segue:

( )

( )

1 1 1 * 2 A H D

M

P

C

M

P

C

− −

=

⋅

=

⋅

(4.4.10) D jj D ii A jj D ii D jj A ii A jj A ii

P

P

S

S

P

P

S

S

P

P

S

S

P

P

S

S

ij ij ij ij ij ij ij ij 22 22 21 21 12 12 11 11

'

'

'

'

=

=

=

=

(4.4.11)

Nelle relazioni precedenti D ij

P e A

ij

P sono i generici elementi ,i j delle matrici della potenza nel dielettrico ed in aria.

Calcolo della potenza in aria

Il calcolo della potenza in aria è stato affrontato nel capitolo 2 e viene riportato il solo risultato per comodità

     + ≤ = ≤ + ≤ = ≤ = altrimenti n n j i n per Y n j i per Y P ATM _{TE TE TM} i TE TE A i Aij 0 1 1 * * (4.4.12)

Calcolo della potenza nel dielettrico

La trattazione risulta del tutto analoga a quella già effettuata nel capitolo precedente viene quindi riportato solo il risultato finale

     + ≤ = ≤ + ≤ = ≤ = altrimenti n n j i n per Y n j i per Y P DTM _{TE TE TM} i TE TE D i Dij 0 1 1 * * (4.4.13)

Calcolo della matrice di accoppiamento

Ricordiamo la definizione data per quanto riguarda la matrice di accoppiamento C

(

)

∫∫

× ⋅ = C S z j i H i dS e C ˆ (4.4.14)

Conviene, per semplicità, analizzare separatamente le parti della matrice di accoppiamento per i modi TE e per quelli TM nei due mezzi facendo attenzione che la matrice totale è data da

        = _{− −} − − TM TM TM TE TE TM TE TE C C C C C . (4.4.15) Accoppiamento TE-TE

Di seguito si calcola il generico elemento della matrice di indirizzo i,j

∫∫

_ × _⋅ = − C S z TE j TE i TE TE ij e H i dS C * ˆ (4.4.16)

ricordando la formula (2.3.4) ed applicandola alla (4.4.16) si ottiene

∫∫

_⋅      _      × × = − C S z TE j z TE i TE A j TE TE ij Y e i E i dS C * ˆ * ˆ _(4.4.17)

Alla relazione precedente può essere applicata l’uguaglianza vettoriale

(

A C

) (

B A B

)

C

C B

A× × = ⋅ − ⋅ , in cui

(

A B⋅

)

= in quanto prodotto scalare tra vettori con 0 direzioni normali.

∫∫

⋅ = − C S TE j TE i TE A j TE TE ij Y e E dS C * * _(4.4.18)

Ricordando che è stata ricavata l’ortonormalità per i modi nei due mezzi, si ottiene che il generico elemento della matrice di accoppiamento C diviene

   = = − altrimenti j i se Y C TE A j TE TE ij 0 * (4.4.19)

Accoppiamento TM-TM

La trattazione risulta analoga a quella fatta per gli accoppiamenti tra i modi TE nel dielettrico e quelli TE in aria. Partendo dalla definizione

∫∫

_ × _⋅ = − C S z TM j TM i TM TM ij e H i dS C * ˆ (4.4.20)

ricordando la formula (2.3.4) ed applicandola alla (4.4.20) si ottiene

∫∫

⋅      _      × × = − C S z TM j z TM i TM A j TM TM ij Y e i E i dS C * ˆ * ˆ _(4.4.21)

Alla relazione precedente può essere applicata l’uguaglianza vettoriale

(

A C

) (

B A B

)

C

C B

A× × = ⋅ − ⋅ , in cui

(

A B⋅

)

= in quanto prodotto scalare tra vettori con 0 direzioni normali.

∫∫

⋅ = − C S TM j TM i TM A j TM TM ij Y e E dS C * * _(4.4.22)    = = − altrimenti j i se Y C TM A j TM TM ij 0 * (4.4.23)

Accoppiamento TE-TM e TM-TE

Come dimostrato nell’ Appendice A l’ortogonalità tra i modi fa si che gli integrali

∫∫

⋅ = − C S TM j TE i TM A j TM TE ij Y e E dS C * * _(4.4.24) ed

∫∫

⋅ = − C S TE j TM i TE A j TE TM ij Y e E dS C * * _(4.4.25)