IL MODELLO FISICO-MATEMATICO 44

IL MODELLO FISICO-MATEMATICO

4.1 Introduzione

È stato evidenziato in precedenza come il modo operativo del catodo cavo d’interesse per la propulsione spaziale sia lo spot mode. A tal fine si considera questo regime operativo come base d’indagine per lo sviluppo di un modello fisico matematico riguardante il flusso di plasma della regione di scarica del catodo cavo posto in configurazione a diodo.

Per comprendere i meccanismi fisici che governano all’interno della regione in esame è bene dare un breve accenno alla natura fisica del plasma. Come nota a margine, si tiene a precisare che in tutta la trattazione teorica del modello è stato fatto riferimento a [16]. Inoltre, per non appesantire la trattazione, nell’Appendice A vengono riportati alcuni aspetti teorici riguardo al modello adottato.

4.2 Il Plasma

Si definisce plasma un gas ionizzato in cui le concentrazioni di particelle cariche sono sufficientemente elevate che la loro interazione ha come risultato il mantenimento della neutralità macroscopica entro un volume confrontabile con il volume del gas. Infatti qualsiasi variazione di neutralità macroscopica induce un forte campo elettrico che la ristabilisce. Il grado di ionizzazione, X, si può definire come il rapporto tra la concentrazione di ioni e la concentrazione globale di ioni e atomi neutri:

n i i n n n X + =

Per concentrazioni inferiori a si parla di gas debolmente ionizzati mentre per valori superiori si parla di gas fortemente ionizzati. La temperatura T di un plasma viene usualmente espressa in unità energetiche secondo la relazione: 4 10− k bT k T =

dove è la temperatura ordinaria espressa in °K e è la costante di Boltzmann.

k

T kb

Si è detto che la caratteristica principale del plasma è la sua neutralità macroscopica sostenuta dalla reciproca compensazione della carica spaziale degli ioni positivi e degli elettroni. Tuttavia, tale compensazione ha luogo solo in volumi abbastanza grandi ed in intervalli di tempo sufficientemente lunghi. In relazione a questo si dice che il plasma è un mezzo quasi neutro. Le dimensioni e gli intervalli di tempo entro cui la compensazione della carica di volume può anche non avvenire sono detti distanza caratteristica e tempo caratteristico di separazione delle cariche.

È evidente che lo spostamento di uno strato di elettroni può durare soltanto nel caso in cui l’altezza della barriera di potenziale del campo generato dalle cariche di volume sia minore dell’energia del moto disordinato (energia termica) di elettroni e ioni:

i e T

T , <

ϕ

In caso contrario il moto delle particelle sotto l’azione del campo elettrico porta rapidamente al ristabilirsi della neutralità. La distanza caratteristica massima di separazione delle cariche nel plasma è detta lunghezza di Debye: 2 0 e n T l e e De ε = dove è espressa in eV. Te

Se ora si considera il moto degli elettroni dopo la violazione della neutralità, nella regione occupata dallo strato elettronico sugli elettroni

agisce una forza attrattiva da parte degli ioni uguale a EeG. L’equazione del moto degli elettroni è:

r e n E e dt r d m e e G G G 0 2 2 2 ε − = − =

che descrive delle oscillazioni armoniche con frequenza:

0 2 ε ω e e P m e n =

Le oscillazioni non si smorzano dato che non si è considerato né il moto termico né effetti dissipativi. In maniera analoga è possibile assegnare una frequenza naturale a ciascun altro tipo di particella con carica , densità e massa . Le oscillazioni della carica di volume nel caso di violazioni della quasi neutralità sono dette oscillazioni di Langmuir e la corrispondente frequenza è detta frequenza di Langmuir.

α

q

α

n m_α

È evidente che, mediamente su un grande numero di periodi di oscillazione, il plasma si può considerare neutro. Di conseguenza il tempo caratteristico di separazione delle cariche nel plasma è dato da:

P ω τ ≅ 1

Affinché siano soddisfatte le condizioni di quasi neutralità deve essere L>>lDe, t>>τ dove L è la dimensione caratteristica del plasma e t è il tempo caratteristico di variazione dei suoi parametri.

4.3 Descrizione fisica della scarica tra catodo cavo ed anodo

Le condizioni del plasma nella scarica sono lontane dallo stato di equilibrio termodinamico in quanto esso cede continuamente l’energia, in esso immagazzinata, per irraggiamento elettromagnetico e per trasferimento di energia da parte delle particelle cariche e neutre alle pareti dell’anodo. Tuttavia si può considerare il plasma in equilibrio parziale in cui la

distribuzione delle velocità degli elettroni e degli ioni è ancora maxwelliana in cui Ti ≈Tn ma Te ≠Ti (plasma non isotermo).

La geometria non cilindrica dell’anodo coassiale al flusso in uscita dal catodo è causa di una piccola non uniformità del campo elettrico esterno che non permette al flusso un moto perfettamente assialsimmetrico con asse di simmetria la congiungente catodo-anodo.

Inoltre la diminuzione della densità del flusso per via della forte espansione nel vuoto fa si che a una certa distanza dal catodo le condizioni di gas rarefatto prevalgano rispetto a quello di fluido inteso come un continuo, comportando l’utilizzo di una descrizione secondo un modello cinetico.

Tuttavia in condizioni di funzionamento a regime (spot mode) la temperatura del gas è tale da garantire il mantenimento di un plasma fortemente ionizzato, per cui diventa sensibile l’effetto del campo elettrico tra catodo ed anodo sulle particelle cariche dando luogo ad una scarica di plasma sufficientemente densa da giustificare una trattazione secondo un modello fluido (continuo).

Nel moto di particelle cariche in plasmi fortemente ionizzati assumono un ruolo importante le collisioni tra particelle cariche. Ciò è dovuto al fatto che il potenziale coulombiano che determina l’interazione tra particelle cariche diminuisce lentamente con la distanza e quindi l’interazione coulombiana è importante a distanze molto maggiori del raggio atomico. Poiché in una sfera di raggio uguale al raggio di Debye ci sono di solito molti elettroni ed ioni, l’interazione tra particelle cariche non si riduce, a rigor di termini, alle collisioni binarie (collisioni puntiformi tra due particelle). In questo caso è necessario includere l’interazione di ogni particella con molte altre che si trovano nella sfera di Debye.

Nel caso di urti con particelle neutre le collisioni possono considerarsi binarie poiché il raggio d’interazione delle particelle cariche con particelle neutre è molto minore del cammino libero medio.

Tuttavia, la variazione della traiettoria negli urti tra particelle cariche dovuta a interazioni di tipo colombiano può essere, in prima approssimazione, trascurata per la sua irrilevanza. Il risultato globale della variazione della traiettoria di una data particella carica, interagente con le altre particelle cariche, si può rappresentare come la somma delle deviazioni dovute all’interazione con ogni singola particella.

Risulta così possibile usare il concetto di collisioni binarie per la descrizione dell’interazione di particella cariche tra loro nonostante il carattere collettivo di tale interazione.

È uso comune distinguere le collisioni in elastiche, in cui la variazione globale di energia interna delle particelle è nulla, e in anelastiche dove la variazione di energia interna può essere positiva o negativa.

Nel caso di urti anelastici, dalla conservazione dell’energia, si ha che la variazione dell’energia interna della particella pesante Ei,n è uguale alla

variazione dell’energia cinetica dell’elettrone mentre l’energia cinetica della particella pesante non cambia dopo l’urto. Questa conclusione è valida, entro i limiti delle approssimazioni fatte circa le masse degli elettroni, degli ioni e dei neutri (

e K n i e m m m << , ).

Per come nel processo di scarica tra anodo e catodo, le correzioni introdotte, in seguito alle perdite di velocità relativa degli elettroni per urti anelastici con ioni ed atomi nutri, sono piccole. Pertanto ai fini del bilancio in termini di quantità di moto e di energia nel plasma si considerano solo collisioni di tipo elastico tra particelle.

n i

e E

K > ,

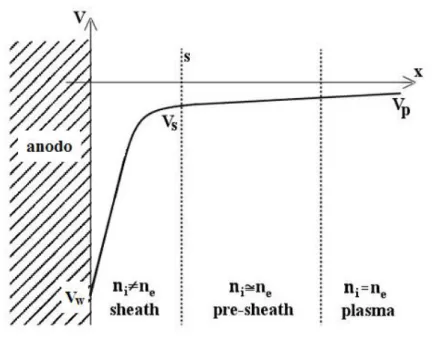
Per quanto riguarda l’interazione del plasma con l’anodo occorre dire che, se il potenziale dell’anodo è diverso da quello del plasma, attorno all’anodo di crea una zona, detta sheath, per effetto dell’attrazione degli elettroni e della repulsione degli ioni, in cui le condizioni di neutralità non vengono più mantenute.

La superficie dello sheath costituisce dunque una superficie di frontiera per il plasma in esame. Le equazioni che saranno utilizzate per la descrizione del plasma in equilibrio parziale sono quindi valide fino alla superficie dello sheath e non al suo interno dove è presente la superficie solida dell’anodo. Si tiene a precisare che è presente anche uno sheath catodico ma questo non viene considerato ai fini del modello in quanto si considerano come condizione al contorno sul catodo quelle allo sbocco dell’orifizio.

Lo sheath anodico si compone, tuttavia, di due regioni: una prossima alla superficie dell’anodo (sheath propriamente detto), ove si ha una forte caduta di potenziale, ed una più esterna (presheath), ove la caduta è assai minore, per cui si può assumere che le condizioni di quasi-neutralità del plasma siano ivi soddisfatte (Figura 4.1).

Figura 4.1 : Andamento del potenziale attraverso lo sheath

4.4 Il modello fisico-matematico

In base alla descrizione della natura dei fenomeni che governano la dinamica del plasma all’interno della regione in esame, si procede alla determinazione del sistema di equazioni da utilizzare nel modello numerico e delle relative ipotesi secondo una descrizione del plasma come un continuo.

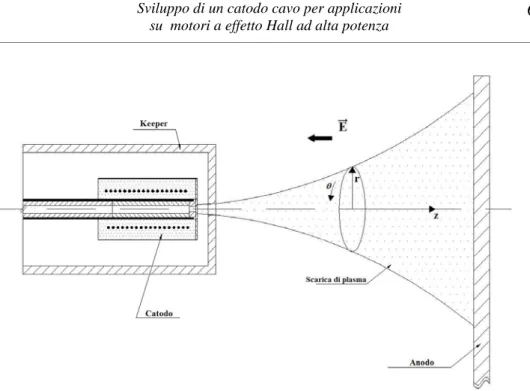
Poiché il funzionamento a regime del catodo è caratterizzato dal fatto che il keeper è spento, vengono trascurate in prima approssimazione le interazioni del plasma con esso (Figura 4.2). Nulla vieta, in seguito, di poter considerare nell’analisi del modello solo la regione tra orifizio e keeper avendo attribuito a quest’ultimo il ruolo di anodo e potendo quindi studiare il comportamento della scarica durante il transitorio di accensione.

Figura 4.2 : Schema della regione di scarica del modello

4.4.1 Descrizione macroscopica del plasma

L’evoluzione del plasma a livello macroscopico (continuo) è descritto da un sistema di equazioni fluidodinamiche, le quali sono derivate dalle equazioni cinetiche, accoppiate alle equazioni di Maxwell.

Nella teoria cinetica lo stato statistico di un plasma a livello microscopico è completamente definito dalla determinazione della funzione di distribuzione delle particelle della specie alfa:

) ; v , (r t f_α G G

dove la quantità f_α(rG,vG;t)dGrdvG rappresenta il numero di particelle della specie alfa situate, al tempo t, in un volume elementare

centrato nel punto di coordinate

3 2 1 3 2 1dr dr dv dv dv dr ) v , r

(G G in fase spazio a sei dimensioni.

Ad ogni funzione dinamica microscopica b_α(rG,vG;xG) corrisponde una funzione dinamica macroscopica B_α( txK, ) (dove xG sono le coordinate di un punto geometrico in tre dimensioni dello spazio fisico) tramite un processo di media statistica:

∫

= ( ,v; ) ( ,v; )drdv ) , (xK t b rG G xG f rG G t G G B_{α α α}

L’equazione sopra fornisce il collegamento base tra la fisica microscopica e quella macroscopica. Le quantità che entrano nel dominio della fisica macroscopica hanno tutte natura di densità locali (densità di massa o di carica, densità di quantità di moto o di carica elettrica). A tali densità macroscopiche corrispondono funzioni microscopiche in spazio fase che hanno una struttura caratteristica comune:

) ( ) v ( ) ; v , (r x r x b_α G G G =β_α G δ G− K

Il valore medio di ogni densità locale microscopica è dato quindi da:

v d ) , ; v ( ) v ( ) , (xK t =

∫

G f G xK t G B_α β_{α α}

La funzione di distribuzione f_α(rG,vG;t) è stata trasformata in una funzione di distribuzione locale della velocità:

r d ) ( ) ; v , ( ) , ; v (G xG t f rG G t rG Kx G f_α =

∫

_α δ −

Si definiscono, quindi, le seguenti quantità per ogni specie alfa di particelle:

Densità locale delle particelle

v d ) , ; v ( ) , (xG t =

∫

f G xG t G nα α

Velocità locale media delle particelle

v d ) , ; v ( v ) , ( 1 ) , (G = _G

∫

G f G xG t G t x n t x u _α α α

Densità d’energia interna delle particelle

v d ) , ; v ( ) , ( v ) , ( 2 ) , (G = G

∫

G−uG xG t 2 f G xG t G t x n m t x _{α α} α α α ε

dove il vettore wK =vG−uG_α(xG,t) rappresenta la velocità disordinata (termica) delle particelle.

Un’altra quantità fondamentale è la temperatura delle particelle. La nozione di temperatura è associata all’equilibrio termodinamico: essa non è la media di una funzione dinamica microscopica (l’idea di temperatura di una singola particella è priva di significato), bensì una proprietà caratterizzante globalmente un particolare stato di equilibrio del sistema.

Per un gas ideale in equilibrio esiste una relazione tra l’energia interna ε_α e la temperatura termodinamica:

α α ε T 2 3 = con k a bT k T_α = °

La condizione sopra può essere estesa al di fuori delle condizioni di equilibrio identificando la temperatura come 1

3 2 −

α

n volte la densità d’energia interna: v d ) , ; v ( ) , ( v 3 1 ) , (xG t = m

∫

G−uG xG t 2 f G xG t G T_{α α α α}

Le quantità , , sono dette variabili plasmadinamiche e costituisco la descrizione multi-fluido del plasma.

α

n u_α T_α

Per ottenere le equazioni macroscopiche plasmadinamiche nelle variabili , , si moltiplicano ambo i membri dell’equazione cinetica successivamente per 1, (r-esima componente del vettore velocità totale della particella alfa),

α n u_α T_α r m v_α 2 v 3 1 α α u m G − G e si integra su vG.

L’equazione cinetica esprime la variazione della funzione di distribuzione dovuta al flusso di particelle φ_α, all’azione di un campo elettrico e magnetico F_α e all’azione di collisioni Kα:

α α α α _φ K + + = ∂ ∂ F t t x f (vG;G, )

Equazione di continuità (bilancio della massa) t n u n t t x n δ δ _α α α α _{=−∇ +} ∂ ∂ ) ( ) , (G G G

Il primo termine al secondo membro indica la variazione di densità dovuta al moto delle particelle di specie alfa, il secondo termine indica la variazione di densità dovuta agli urti accompagnati dalla creazione o dalla distruzione delle particelle di specie alfa.

Equazione di moto (bilancio della quantità di moto)

t n m c t u n m a δ δ π α α α α α α α α α α α α u p B u 1 E n q u u G G G G G G G G G G + ∇ − ∇ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ ×} = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ ⋅∇} ∂ ∂

Il primo membro indica il termine accelerativo delle particelle di specie alfa, il secondo è uguale alla somma delle forze agenti sulle particelle di specie alfa: la forza elettrica, la forza di Lorenz, le forze dovute al gradiente di pressione del gas e dall’azione delle tensioni viscose ed infine la forza di attrito dovuta alle collisioni delle particelle.

Equazione dell’energia (bilancio energetico)

t T n T n T n t T n δ δ π α α α α α α α α α α α α α _∂ + ⋅∇ =− ∇⋅ − ∇⋅ − ⋅∇ + ∂ u 3 2 u 3 2 q 3 2 uG G G G G G G G

Il primo membro indica la variazione lagrangiana della temperatura delle particelle alfa, il secondo membro è uguale al flusso d’energia associato al solo moto termico delle particelle, a quello dovuto al lavoro della pressione e dell’azioni viscose e a quello associato alle collisioni delle particelle.

Queste equazioni sono fortemente accoppiate perché la densità, la quantità di moto e l’energia delle varie specie non si conservano separatamente ma i termini collisionali delle equazioni di bilancio tengono conto dei trasferimenti di densità, quantità di moto ed energia tra le specie.

Il campo elettrico EG che compare nell’equazione di moto è un campo elettrico totale, ossia rappresenta la somma del campo dovuto alla distribuzione spaziale delle particelle cariche nel plasma e di quello esterno.

Per quanto riguarda il campo magnetico B esso è anche un campo magnetico totale costituito dai contributi dovuti al campo magnetico prodotto dal moto delle particelle cariche e di quello esterno.

La trattazione riguarderà un plasma con tre componenti: elettroni, ioni positivi monovalenti ed atomi neutri.

I processi di trasporto in un plasma di questo tipo dipendono dal grado di ionizzazione. Si possono distinguere perciò due casi limite: il caso di un plasma debolmente ionizzato nel quale la frequenza delle collisioni di elettroni e ioni con atomi è molto maggiore della frequenza delle collisioni tra di loro (v_en >>v_ei,v_ee , v_in >>v_ii,(m_e m_i)v_ei) e il caso di un plasma fortemente ionizzato definito da disuguaglianze di segno opposto.

4.4.2 Le equazioni semplificate del modello

Il modello utilizzato è un modello unidimensionale (variazione delle grandezze solo lungo l’asse z), in assenza di campi magnetici e gas fortemente ionizzato.

Inoltre valgono le seguenti ipotesi: - Effetti viscosi trascurabili

Per determinare le condizioni per cui è possibile trascurare gli effetti dovuti alla viscosità nell’equazioni, confrontiamo le componenti del tensore della viscosità, che caratterizza la parte anisotropa della pressione totale, con la pressione scalare (termodinamica):

ν η δ η π _α con nT/ x x _k kl l l k kl ⎟⎟ ≅ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ ∇ − ∂ ∂ − ∂ ∂ − = u 3 2 u u H G

η è detto coefficiente di viscosità. Per cui deve essere:

(

nT

)

u L p nT u L u_TL l

kl = /ν / << = ⇒ <<ν = /

π

dove L è la distanza caratteristica di variazione dei parametri del plasma, uT è la velocità termica e l il cammino libero medio. Le

condizioni l<<L u<<uT sono condizioni generalmente soddisfatte

- Stazionarietà

Il tempo caratteristico di variazione dei parametri del plasma è molto maggiore del tempo tra le collisioni (1/ν). Ciò implica che è possibile trascurare la variazione delle velocità medie nel tempo che intercorre tra due urti.

- Linearità

Nella maggioranza dei casi è possibile trascurare il termine quadratico della velocità nell’equazione di bilancio della quantità di moto. Infatti:

( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ × ∇ × − ∇ = ∇ ⋅ u u 2 u u 2 _K G _G K G G G u n m n m ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∇ = ∇ 2 3 1 T u n m p G G

dove il termine dovuto alla vorticità nel nostro caso è trascurabile ed inoltre vale u<<uT.

La condizione di quasi neutralità si riduce all’uguaglianza delle densità elettronica e ionica in tutto il plasma eccetto che in uno strato, vicino alle pareti conduttrici (anodo), di dimensioni dell’ordine del raggio di Debye: ( ). Per il mantenimento della quasi neutralità è necessario quindi che le variazioni di densità elettronica e ionica siano uguali in ogni elemento di volume infinitesimo:

n n n_e ≅ _i ≅ t n n t n n e e i δ δ δ δ + ⋅ ∇ − = + ⋅ ∇ − K ( uK_i) K ( uK ) (4.1a)

I processi di creazione e distruzione di particelle in un plasma a tre componenti non può portare ad una violazione della quasi neutralità, poiché in questi processi vengono creati o distrutti simultaneamente un elettrone ed uno ione δn_i δt =δn_e δt, per cui:

∇K ⋅

( )

nuK_i =∇K⋅

(

nuK_e

)

⇒ ∇K⋅

(

n(uK_i−uK_e)

)

=0 (4.1b)

La densità di corrente nel plasma dovuta al campo elettrico risulta quindi costante: 0 e i u ) j u ( j G G G G = − = ne (4.1c)

Le equazioni di bilancio della quantità di moto scritte per la specie elettronica e ionica diventano:

( )

0 R R R R E−∇ + _en+ + _e + = − T ei i T en e n nT e K K K K K K (4.2a)

( )

0 R R R R E−∇ + _n+ + + T = ie ie T in i i n nT e K K K K K K (4.2b) dove si è utilizzata la seguente relazione per il termine collisionale

(

∑

+ = β αβ αβ α α _δ

)

δ _T R R uG K K t m (4.3a) I termini

(

α β

)

αβ αβ αβ μ ν u u RG =− K −K (4.3b) αβ αβ αβ αβ αβ αβ αβ αβ T g T dT dv v T T T = ∇K = ∇K K R (4.3c) sono rispettivamente indicati come forza d’attrito e forza termica, [16], e dove β α β α αβ μ m m m m +

= è la massa ridotta delle particelle di specie alfa e beta. La forza d’attrito rappresenta una variazione d’impulso dovuta agli urti mentre la forza termica rappresenta una variazione d’impulso lungo un gradiente di temperatura. noltre per la conservazione dell’impulso negli urti deve essere che:

I T ie T ei R RK =−K .

I termini collisionali vengono esplicitati considerando, per quanto già chiarito nella descrizione fisica della scarica, urti binari di tipo elastico. Per urti elettrone-ione si ha:

) ( _{e i} ei e ei m u u RG =− ν G −G (4.4a) e T T ei g T RG =− ∇G (4.4b)

Nel caso di plasma fortemente ionizzato (ν_ei >>ν_en) si ottiene: ei ei ν ν =0.51 (4.4c) 71 . 0 = T g (4.4d) dove νei e sono rispettivamente la frequenza d’urto efficace (Appendice A) e il coefficiente termico per gli elettroni mentre

T g 2 / 3 2 0 4 ) 4 ( 3 2 4 e e e ei T m L ne πε π ν =

è la frequenza media collisionale.

Per urti ione-neutro la frequenza collisionale vale: in d n

in n e α μ

ν =10 (4.5) dove αd rappresenta la polarizzabilità dell'atomo (Appendice A).

Si nota come in questo caso la frequenza collisionale è indipendente dalla velocità, ciò implica che il coefficiente è nullo per cui questi urti non danno contributo alla forza termica.

T

g

Per urti elettrone-neutro si ha che anche in questo caso la frequenza di collisione è indipendente dalla velocità e può considerarsi costante e la forza termica del termine collisionale è nulla. Perciò come valore per la frequenza collisionale elettroni-neutri viene preso il valore all’orifizio:

0 = = z en en ν ν (4.6) Le equazioni di moto con i termini collisionali esplicitati diventano quindi:

( )

0 ) u u ( u E−∇ − ∇ − _e− − _i = − K K K K K K e ei e en e e T e m m T g n nT e ν ν (4.7a)

( )

0 ) u u ( u E−∇ + T∇ e − in in i− e ei i− e = i m T g n nT e K K K K K K ν ν μ (4.7b)

Elaborando si ha:

(

)

( )

T e e ei e ei e en e g T n nT e m m m + = − −∇ − ∇K K K K K E u u_e ν ν ν _i (4.7c)

(

)

( )

T e i e ei e ei e in in i g T n nT e m m = + −∇ + ∇ + K K K K K _{u E} u μ ν ν ν (4.7d)

da cui si ottengono le velocità medie elettronica ed ionica

( )

ei e e T ei e e ei e i e m T g n m nT m e ν ν ν ∇ − ∇ − − = K K K K K E u u (4.7e)

(

)

n T T n in in i e i _{μ ν} ) ( u =−∇ + K K (4.7f) avendo utilizzato il fatto che meνen <<μinνen.

Queste relazioni possono essere interpretate tenendo conto di fenomeni diffusivi delle particelle cariche all’interno del plasma. Poiché il flusso di diffusione elettronico è molto superiore a quello ionico si tende a creare una regione di separazione di carica. Ciò porta alla formazione di un campo elettrico che accelera il flusso ionico e frena quello elettronico e la cui intensità continua a crescere fino a quando il flusso elettronico e quello ionico si compensano esattamente.

Questo regime di diffusione è detto diffusione ambipolare. Per cui in presenza di campo elettrico esterno la velocità media degli elettroni e degli ioni può essere rappresentata sotto forma di somma della velocità ambibolare e della velocità di corrente associata al campo esterno EG₀:

0 A e u E uG =G −b_e G (4.7g) 0 A E u uG_i =G −b_i G (4.7h) dove

) ( en ei e e m e b ν ν + = ) ( en ei in i e b ν ν μ + =

sono rispettivamente il coefficiente di mobilità elettronico ed ionico.

Poiché il campo elettrico nel plasma è dato dalla somma del campo esterno e di quello ambipolare (EG =EG₀+EG_A), utilizzando le relazioni (4.7e), (4.7f), (4.7g) e (4.7h), si ricava:

(

)

n T T n in in i e i μ ν ) ( u u = _A =−∇ + K K K _(4.7i)

( )

e T g en nTe − T∇ e ∇ − = K K G A E (4.7j) Si vede quindi che la velocità media degli ioni si può assumere pari alla velocità ambipolare in quanto la loro mobilità è molto inferiore a quella degli elettroni. Se ipotizziamo che siano trascurabili i fenomeni di ionizzazione e ricombinazione δne δt =δni δt =0, dalla (4.1a) per ciascuna specie alfa si ricava:

(

)

⎪ ⎩ ⎪ ⎨ ⎧ − = − = ⇒ = ⋅ ∇ dz dn n u dz du dz dn n u dz du n i i e e 0 uK_α K (4.8a) ossia 0 0 e e n u nu = (4.8b) 0 0 i i n u nu = (4.8c) Sostituendo la (4.8c) nella (4.7f) e derivando rispetto a , si ha: z

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ − = dz dT n dz dn T n u e e in in i _{μ ν} 1 (4.9)

dove si è trascurato il termine dovuto alla temperatura ionica essendo .

e

i T

T <<

Poiché la densità di corrente dovuta alle particelle di specie alfa è:

0 0uα α K K en j _o =±

dove il segno positivo vale per gli ioni ed altrimenti per gli elettroni, si ricava dalla (4.9) l’equazione differenziale della densità elettronica ed ionica: e io in in e e eT j dz dT T n dz dn μ ν − − = (4.10) Dall’equazione di bilancio dell’energia per gli elettroni, esplicitando il termine collisionale si ha:

+ − − = ⋅ ∇ + ⋅ ∇ + ∇ ⋅

∑

β β β β ν χ ( ) u 3 2 q 3 2 u T nT n T T ne e e e e e e e e e e G G G G G G

∑

− + β β β ν _{(u u )}2 3 2 G G e e e en m

Sostituendo i termini della frequenza collisionale e del flusso termico ed elaborando si ricava che l’equazione differenziale della temperatura elettronica è: + − + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = _{2 5/2} 1 0 0 2 / 5 1 0 0 2 2 2 3 2 3 ) 5 2 ( 2 5 e e i in in e e e T e e e nT e c j j dz dT eT c j j g dz dT T dz T d μ ν ₄ 1 3 2 4 1 2 _{( )} e i e e cT c T T n T c c _{− −} + (4.11) dove e e q L e m g c e 4 2 0 1 2 ) 4 ( 4 5 π πε = ₂ 0 4 2 ) 4 ( 3 2 8 πε π i e e m L e m c = _{2 0}2 0 2 3 ) 4 ( 9 2 8 51 . 0 j L e m c e e πε π ⋅ =

Dall’equazione di bilancio dell’energia per gli ioni, esplicitando il termine collisionale si ha:

∑

− − = ⋅ ∇ + ⋅ ∇ + ∇ ⋅ β β β β ν χ ( ) u 3 2 q 3 2 u T nT n T T ni i i i i i i i i i i G G G G G G

Trascurando il termine dovuto al flusso termico ed elaborando si ricava che l’equazione differenziale della temperatura ionica è:

) ( 2 ) ( 3 2 3 2 0 2 2 / 3 0 2 0 n i i in e i e i e i i in in e e i i T T j en T T n T j e c enT T j dz dT T T dz dT − − − − − − = μ ν ν (4.12)

Per quanto riguarda i neutri le equazioni di bilancio delle particelle diventano:

Bilancio della massa

0 )

( =

⋅

∇G n_nuG_n (4.13a) Bilancio della quantità di moto

e ne ne n i n ni ni n n n n n n nn u u n T n u u n u m G ⋅∇GG =−∇G( )− μ ν (K −G )+ μ ν G (4.13b) in cui si è trascurata la velocità media dei neutri rispetto a quella degli elettroni. Bilancio dell’energia e i ne n e i n ni n n n n n n n T m n m T T n u T n T u n ν ( ) 2 ν 2 3 2 _{∇⋅ =− − +} + ∇ ⋅G G G G (4.13c) in cui si è trascurato anche in questo caso il termine dovuto al flusso termico e nel secondo termine del secondo membro si è trascurata la rispetto alla

.

n

T

e

Dalla (6.13a) si ha: dz du u n dz dn _n n n n =− _(4.13d) ed integrando 0 0 n n n nu n u n = (4.13e) Dalla (6.13b) e (6.13c), sviluppando i vari termini, si ha:

+ + − − − = 0 0 0 0 0 0 0 0 2 2 n n i in n in n n n i n n n n i n n u n u n n n dz dT u n m n dz dn u n m T dz du ν ν 0 0 0 0 n n i e en e u n m u n mν + (4.13f) 0 0 0 0 2 ) ( 2 3 2 n n i e en e i n n n in n n n n u n m T n m T T u n n dz dn n T dz dT ν ν + − − = (4.13g)

Utilizzando la (4.13d), (4.13f) e (4.13g) si ricavano le equazioni differenziali per la densità e la temperatura dei neutri:

⎜⎜ ⎝ ⎛ + + − − − = ₂ 0 2 0 2 2 0 2 0 2 2 0 2 0 2 0 0 2 2 ) ( 5 3 3 n n i e en n e n n i i n in n n n n n i n n n i n u n m T n n m u n m T T n n n T u n m n u n m dz dn ν ν ⎟⎟ ⎠ ⎞ + − + 0 0 0 0 0 0 2 2 _{i n n} en e e n n in i n in u n e m j m u n e j n nν ν ν (4.13.h) − + ⎜⎜ ⎝ ⎛ + − − − = n in n n i e en n e n n i i n in n n n n n i n n n n i n n n u n m T n n m u n m T T n n n T u n m T n u n m dz dT 2 2 2 ) ( 5 3 2 2 0 2 0 2 2 0 2 0 2 2 0 2 0 0 0 ν ν ν 0 0 0 0 0 0 0 0 0 0 2 2 ) ( 2 _{i n n} e en e n n i n in n n i en e e n n in i u n m T n m u n T T n u n e m j m u n e j ν ν ν ν + − − ⎟⎟ ⎠ ⎞ + − (4.13g)

In ultima analisi si ricava l’espressione del potenziale del plasma utilizzando la (4.7c) con l’approssimazione νen <<νei:

( )

en j m dz dT g dz nT d n eE+1 e + _T e = eνei 0 (4.14a)

ed essendo EG =−∇GV , si ricava l’equazione differenziale per il potenziale del plasma 2 / 3 2 0 0 2 2 0 ) 4 ( 3 2 4 51 . 0 e e e i in in e T T j L e m n e j dz dT g dz dV πε π ν μ ⋅ − − = (4.14b) dove si è sfruttata la (4.10).

Le velocità medie e le pressioni delle tre specie si calcolano tramite le relazioni: ) ( ) ( 0 e0 e z n u n z u = ) ( ) ( 0 0 z n u n z u i i = ) ( ) ( 0 0 z n u n z u n n n n = ) ( ) ( ) ( e z n z T z p = _e ) ( ) ( ) (z n z T z pi = i ) ( ) ( ) (z n z T z p_n = _{n n}