Capitolo 2

(1)

Capitolo 2

Le tecniche di identificazione e di retuning

Al fine di assicurare che le condizioni operative rispettino i valori prefissati è importante avere a disposizione un modello del processo. La conoscenza di un modello del processo è importante non solo in caso di controllo avanzato, ma anche in caso di controllo convenzionale. Nonostante, infatti, i controllori convenzionali (ad esempio i controllori proporzionali-integrali-derivativi) impieghino leggi di controllo non esplicitamente basate sul modello del processo da controllare, quest’ultimo può essere utilizzato nella sintonizzazione di tali controllori.

Per modello di processo si intende una relazione matematica capace di descrivere la dinamica del processo stesso. In un processo, diversi tipi di variabili, dette ingressi, interagiscono tra loro per produrre delle grandezze osservabili dette uscite. Gli ingressi si dividono in variabili manipolate e

disturbi. Questi ultimi si dividono in quelli che possono essere misurati e in quelli che possono

essere osservati solo mediante l’effetto che producono sulle uscite. Le uscite vengono anche dette

variabili controllate.

L’identificazione è ciò che consente l’ottenimento di un modello del processo sulla base dei segnali in ingresso e in uscita dallo stesso. Le varie tecniche di identificazione si differenziano sulla base della tipologia di dati che esse impiegano (dati ottenuti in anello aperto a seguito di perturbazioni a gradino, dati ottenuti in anello chiuso, dati ottenuti in anello chiuso in presenza di un regolatore Relay). Ciascuna tecnica di identificazione ha dei vantaggi e degli svantaggi; la scelta della tecnica di identificazione dipende dagli scopi e dai vincoli eventualmente presenti. Poiché si intende salvaguardare le caratteristiche di non intrusività della PCU, il modulo di identificazione oggetto di questo lavoro di tesi impiega dati acquisiti durante il “normale” funzionamento dell’anello di regolazione, ovvero dati acquisiti in anello chiuso.

Per quanto riguarda la tipologia di modello, vale quanto detto per la tecnica di identificazione e cioè che esistono molte tipologie di modelli, ognuna caratterizzata da una certa struttura; la scelta di quale modello identificare è subordinata alle finalità dell’identificazione stessa, oltre ad essere vincolata dal grado di difficoltà che l’identificazione di un certo modello comporta.

In questo capitolo verranno descritte le tipologie di modelli utili in questo lavoro di tesi facendo particolare riferimento alla tipologia che si è deciso di adottare nella tecnica di identificazione messa a punto (Ljung, 1999). Si descriverà inoltre il metodo matematico adottato al fine di stabilire i parametri del modello scelto. Infine si descriverà la tecnica di retuning scelta per la sintonizzazione del controllore sulla base del modello identificato.

(2)

G(s)

2.1: Modelli nel tempo continuo

Una prima importante classificazione dei modelli nel tempo continuo è quella che distingue i modelli lineari da quelli non lineari. Un modello è detto lineare se l’uscita corrispondente ad una combinazione lineare di ingressi, coincide con la combinazione lineare delle uscite dei singoli ingressi.

Si distinguono inoltre modelli di tipo “input-output” da modelli in variabili di stato. Mentre nei primi compaiono solo le grandezze di ingresso e uscita, nei secondi compaiono anche delle grandezze interne denominate stati. Un’ulteriore classificazione è quella che distingue i modelli tempo invarianti da quelli che non sono tempo invarianti. Un modello si dice tempo invariante se il valore dell’uscita corrispondente ad un certo ingresso è indipendente dal tempo.

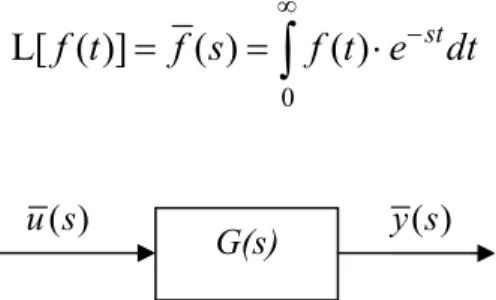
Il modello nel tempo continuo più usato è quello delle trasformate di Laplace, schematicamente riportato in figura 2.1. La definizione di trasformata di Laplace di una funzione f(t) è la seguente:

0 L[ ( )] ( ) ( ) ∞ − = =

_∫

⋅ st f t f s f t e dt (2.1) ( ) u s y s ( )

Figura 2.1: Schema di un modello “input-output” nel dominio di Laplace.

Il modello delle trasformate di Laplace è evidentemente un modello di tipo “input-output”. La funzione G(s) è denominata funzione di trasferimento nel tempo continuo.

La funzione di trasferimento G(s) ha la forma riportata in (2.2), dove il numeratore e il denominatore sono polinomi in s di ordine rispettivamente m ed n.

1 1 1 0 1 1 1 0 .. .. − − − − + + + + = = + + + + m m m m n n n n b s b s b s b N(s) G(s) D(s) a s a s a s a (2.2) Il denominatore di G(s) ha n radici nel piano complesso, dette poli, da cui dipendono le proprietà

asintotiche del sistema, cioè la risposta quando il tempo t→∞. Il numeratore di G(s) ha m radici nel piano complesso, dette zeri, da cui dipendono le proprietà nel transitorio del sistema, cioè la risposta quando il tempo t→0.

Essendo che dai poli dipende la risposta del processo quando t→∞, essi sono strettamente collegati alla stabilità del sistema. Un sistema è stabile se la risposta ad una perturbazione di ampiezza limitata si mantiene limitata per t→∞. In particolare può essere formulato il seguente criterio di stabilità: condizione necessaria e sufficiente perché un sistema sia stabile è che tutti i poli abbiano parte reale negativa.

(3)

2.2: Modelli nel tempo discreto

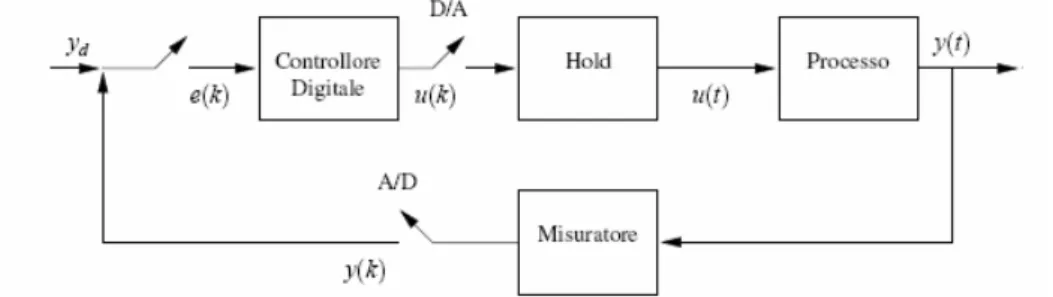
Tutti i controllori moderni, sia convenzionali che avanzati, funzionano nel dominio di tempo discreto. In questi controllori le variabili misurate vengono raccolte ad intervalli regolari. Il tempo che trascorre tra una misurazione e la successiva è noto come “tempo di campionamento”. Per quanto riguarda il segnale di controllo, esso viene generato ad ogni tempo multiplo del tempo di campionamento e viene mantenuto costante per il tempo di campionamento successivo. Un tipico schema di controllo discreto è riportato in figura 2.2.

Figura 2.2: Schema di un loop di controllo nel tempo discreto.

Il processo di conversione dal tempo continuo a quello discreto è detto “campionamento”. Occorre scegliere il tempo di campionamento (Ts) in modo tale che esso sia sufficientemente piccolo da catturare la dinamica del sistema, ma abbastanza grande da evitare costi computazioni elevati e filtrare un eventuale rumore.

Spesso viene suggerita la seguente regola empirica:

(0.1 0.2) min( , )

s

T ≅ ÷ ⋅

ϑ τ

Dove

ϑ

e

τ

rappresentano rispettivamente il ritardo e la costante di tempo dominante del sistema. Per quanto riguarda invece il processo di conversione dal tempo discreto a quello continuo, esso è detto “ricostruzione del segnale” e viene effettuato da un sistema detto “hold”.

Esistono diversi di tipi di “hold” ma quello più comunemente usato è detto di ordine zero; il suo funzionamento è sintetizzato in (2.3).

( ) _k

u t =u , kT_s ≤ ≤t (k+1)T_s (2.3)

L’impiego di schemi di controllo discreti ha indotto all’impiego di modelli nel tempo discreto. Nel seguito si riporterà una descrizione dei modelli nel tempo discreto utili per questo lavoro di tesi.

2.2.1: Il passaggio da continuo a discreto: il campionamento

Come è noto, un sistema lineare, tempo invariante, causale (un sistema si dice causale se l’uscita ad un certo tempo dipende solo dagli ingressi precedenti), può essere descritto mediante la sua riposta all’impulso ( )g τ come riportato in (2.4).

0 ( ) ( ) ( ) y t g u t d τ

τ

τ τ

∞ = =

∫

⋅ − (2.4)

(4)

Ritenendo valida l’espressione riportata in (2.3) e sostituendola in (2.4) si ottiene: ( 1) 1 0 ( ) ( ) ( ) s ( ) ( ) s l T s s _l _T s l y kT g u kT d g u kT d τ τ

τ

τ τ

τ

τ τ

∞ ∞ _⋅ = − ⋅ = = =

∫

⋅ − =

∑

∫

⋅ − (2.5)

{

( 1)

}

1 1 ( ) ( ) s s l T k l T k l l T l l g d u g l u τ

τ τ

∞ _⋅ ∞ − − = − ⋅ = = ⎡ ⎤ = _⎢ _⎥⋅ = ⋅ ⎣ ⎦

∑

∫

∑

Dove si è definito: ( 1) ( ) s ( ) s l T T _l _T g l g d τ

τ τ

⋅ = − ⋅ =

∫

(2.6)

È evidente, dunque, che nota la funzione gT(l) e noto il valore degli ingressi al processo per ogni tempo di campionamento minore di k, è possibile conoscere il valore dell’uscita al tempo di campionamento k.

Il passaggio dal continuo al discreto in caso sia valida l’espressione (2.3) può essere fatto senza alcuna approssimazione.

Definendo ora, un operatore q (forward shift operator) e un operatore q-1 (backward shift operator) tali che: 1 k k q u⋅ =u ₊ 1 1 k k q− ⋅u =u ₋ si può riscrivere l’espressione (2.5) nel modo seguente:

1 1 1 1 ( ) ( ) ( ) ( ) ∞ ∞ ∞ − − − − = = = ⎡ ⎤ = ⋅ = ⋅ ⋅ =_⎢ ⋅ _⎥⋅ = ⋅ ⎣ ⎦

∑

l

∑

l k T k l T k T k k l l l y g l u g l q u g l q u G q u (2.7)

La funzione G(q-1) è detta funzione di trasferimento nel tempo discreto.

Le radici del numeratore e del denominatore della funzione G(q-1) sono dette rispettivamente poli e

zeri del modello nel tempo discreto. Dai poli dipendono le proprietà asintotiche del modello, dagli zeri quelle nel transitorio.

2.2.2: La sovrapposizione di disturbi

Pensare che il valore della variabile controllata al tempo di campionamento k-esimo coincida con quello calcolato in (2.7), è nella maggior parte dei casi non realistico. L’effetto dei disturbi è rappresentato in (2.8), dove ek è rumore bianco, ovvero è una sequenza di variabili casuali, indipendenti, a media nulla e varianza λ.

1 1

( ) ( )

k k k

y =G q− ⋅u +H q− ⋅e (2.8)

La funzione H(q-1) può essere espressa, in analogia a quanto fatto per G(q-1) come:

0 ( ) ∞ ( ) − , = =

∑

⋅ l l H q h l q h(0) 1=

(5)

Da cui: 1 ( ) 1 ( ) l l H q ∞ h l q− = = +

∑

⋅ (2.9)

È utile sottolineare che se si conosce, oltre al valore della variabile manipolata u, anche quello della variabile controllata y, fino al tempo di campionamento (k-1)-esimo, sono automaticamente noti i primi due termini dell’espressione riportata in (2.10).

1 1 ( ) ( ) l k k k k l y G q− u ∞ h l q− e e = = ⋅ +

∑

⋅ ⋅ + (2.10)

Essendo l’unico termine incognito ek ed avendo il rumore bianco media nulla, si può approssimare il valore di yk come: 1 1 ( ) ( ) l k k k l y G q− u ∞ h l q− e = = ⋅ +

∑

⋅ ⋅ (2.11) 1 1 1 1 1 1 ( ) ( ) ( ( ) 1) ( ) ( ( ) 1) ( ) k k k k H q e G q u H q e G q u H q H q − − − − − − ⋅ = ⋅ + − ⋅ = ⋅ + − ⋅ 1 1 1 1 ( ) _k (1 ( )) ( _k ( ) _k) G q− u H− q− y G q− u = ⋅ + − ⋅ − ⋅ 1₍ 1₎ ₍ 1₎ ₍₁ 1₍ 1₎₎ k k H− q− G q− u H− q− y = ⋅ ⋅ + − ⋅

L’espressione riportata in (2.11) non è altro che il valore predetto della variabile controllata y al tempo di campionamento k-esimo noti i valori precedenti della stessa.

(6)

2.2.3: Modello ARX

Il modello più semplice nel discreto di tipo “input-output” è il modello ARX (AutoRegressive model with eXternal input), la cui struttura è riportata in (2.12).

1 1 .. 1 1 .. k k n k n k m k m k y +a y ₋ + +a y ₋ =b u ₋ + +b u ₋ +e (2.12) Definendo: 1 1 1 ( ) 1 .. _n n A q− = +a q− + +a q− (2.13) 1 1 1 ( ) .. _m m B q− =b q− + +b q− si ha: 1 1 ( ) _k ( ) _k _k A q− y =B q− u +e (2.14) 1 1 1 ( ) 1 ( ) ( ) k k k B q y u e A q A q − − − = +

Evidentemente, l’espressione (2.14) coincide con l’espressione (2.8), dove:

1 1 1 ( ) ( ) , ( ) B q G q A q − − − = …. ( 1) 1 ₁ ( ) H q A q − − = (2.15)

Per quanto riguarda l’identificazione di un modello ARX, ponendo ek pari a 0 (trattandosi di rumore bianco questa è la miglior stima che può essere fatta) e sostituendo le espressioni (2.15) nell’espressione (2.11), si ottiene: 1 1 1 1 1 1 ( ) ( ) (1 ( )) ( ) (1 ( )) ( ) k k k k k B q y A q u A q y B q u A q y A q − − − − − − = ⋅ ⋅ + − ⋅ = ⋅ + − ⋅ (2.16)

Introducendo i vettori riportati in (2.17), si ha che il valore predetto della variabile controllata al tempo di campionamento k-esimo può essere espresso come riportato in (2.18).

[

1,..., , 1,...,

]

T k yk yk n uk uk m

ϕ

= − ₋ − ₋ ₋ ₋ (2.17)

[

1, ,.., , , ...,2 1 2

]

T n m a a a b b b

ϑ

= T T k k k y =

ϑ ϕ

⋅ =

ϕ ϑ

⋅ (2.18)

Il fatto che il valore predetto della variabile controllata al tempo k-esimo (y ), possa essere espresso _k

come il prodotto tra un vettore di termini noti (φk) e il vettore dei parametri (ϑ ), è una proprietà molto importante per i modelli ARX, in quanto consente che il vettore delle incognite possa essere determinato con una certa semplicità. Questo argomento verrà approfondito nei prossimi paragrafi. I modelli ARX per questa loro proprietà sono detti modelli a regressione lineare.

(7)

2.2.4: Modello OE

Un ulteriore modello nel discreto di tipo “input-output” è il modello OE (Output Error model structure), la cui struttura è riportata in (2.19).

1 1 .. 1 1 ..

k k n k n k m k m

w +a w ₋ + +a w ₋ =b u ₋ + +b u ₋ (2.19)

k k k

y =w +e

La variabile wk rappresenta il valore della variabile controllata predetto dal modello impiegando gli ingressi al processo e i valori predetti dallo stesso ai tempi di campionamento precedenti.

Definendo: 1 1 1 ( ) 1 .. _n n A q− = +a q− + +a q− (2.20) 1 1 1 ( ) .. _m m B q− =b q− + +b q− si ha: 1 1 ( ) _k ( ) _k A q− w =B q− u (2.21) 1 1 ( ) ( ) k k k B q y u e A q − − = +

Evidentemente, l’espressione (2.21) coincide con l’espressione (2.8), dove:

1 1 1 ( ) ( ) , ( ) B q G q A q − − − = ….H q( −1) 1= (2.22)

Per quanto riguarda l’identificazione di un modello OE, ponendo ek pari a 0 (trattandosi di rumore bianco questa è la miglior stima che può essere fatta) e sostituendo le espressioni (2.22) nell’espressione (2.11), si ottiene: 1 1 ( ) ( ) k B q k y u A q − − = ⋅ (2.23)

Introducendo i vettori riportati in (2.24), si ha che il valore predetto della variabile controllata al tempo di campionamento k-esimo può essere espresso come riportato in (2.25).

[

1 1

]

( ) ( ),..., ( ), ,..., T k wk yk n uk uk m

ϕ ϑ

= − ₋

ϑ

− ₋

ϑ

₋ ₋ (2.24)

[

1, ,.., , , ...,2 1 2

]

T n m a a a b b b

ϑ

= ( ) T k k y =

ϑ ϕ ϑ

⋅ (2.25)

Il modello OE, a differenza del modello ARX, non è un modello a regressione lineare ma un modello a regressione non-lineare in quanto, il valore predetto della variabile controllata al tempo di campionamento k-esimo (y ), è pari al prodotto tra il vettore dei parametri (_k ϑ) e un vettore i cui

(8)

termini sono funzione del vettore dei parametri (

ϕ ϑ

_k( )). Il fatto che un modello sia non-lineare comporta un maggiore difficoltà nella procedura di identificazione.

2.2.5: Modello lineare tempo invariante in variabili di stato

I modelli lineari, tempo invarianti, in variabili di stato, hanno nel discreto la struttura riportata in (2.26). 1 0 k k k k k k x Ax Bu y Cx Du x noto + = + ⎧ ⎫ ⎪ ₌ ₊ ⎪ ⎨ ⎬ ⎪ _→ ⎪ ⎩ ⎭ (2.26) Dove: 1 1 1 p p p p p x A B C D × × × ∈ℜ ∈ℜ ∈ℜ ∈ℜ ∈ℜ

Spesso D, detto “feed through”, non è presente nei modelli in variabili di stato di processi chimico-fisici, in quanto essi sono per la maggior parte strettamente propri e pertanto non si ha un effetto immediato degli ingressi sulle uscite.

La soluzione nel discreto dei sistemi in variabili di stato è molto semplice:

0 1 0 0 2 2 1 1 0 0 1 0 0 1 1 1 0 0 ( ) ... k k k j k j j x noto x Ax Bu x Ax Bu A Ax Bu Bu A x ABu Bu x A x − A − − Bu = → = + = + = + + = + + = +

∑

(2.27)

2.2.6: Stabilità di un modello nel discreto

Considerando di avere a disposizione un modello nel discreto in variabili di stato, la definizione di stabilità asintotica che può essere data è la seguente.

Un sistema lineare, discreto, tempo invariante, del tipo (2.26), è asintoticamente stabile, in assenza di controllo, se e solo se per ogni valore iniziale x0, si ha:

lim _k 0

(9)

Osservando l’espressione (2.27) si ricava che la condizione che deve essere rispettata affinché il sistema (2.26) risulti stabile è quella riportata in (2.28).

lim k 0

k→∞A = (2.28)

Come è noto, la condizione che deve risultare verificata affinché la (2.28) venga rispettata è che il raggio spettrale della matrice A sia minore di 1, ovvero che il modulo di tutti gli autovalori della matrice A sia minore di 1 (2.29).

1 2

( ) max(A _A ; _A ;..; _Ap ) 1

ρ

=

λ

< (2.29)

Gli autovalori della matrice A corrispondono evidentemente ai poli della funzione di trasferimento nel discreto. Un modello stabile è un modello in cui gli zeri del denominatore della funzione di trasferimento nel discreto hanno modulo minore di 1.

È importante ricordare che, dato un modello, è possibile valutare i poli nel discreto (λd) noti i poli nel continuo (λc), sfruttando la relazione riportata in (2.30).

cTs d eλ

λ

₌ ⋅ _(2.30) Posto: , 0 c a ib a

λ

= − ± > si ottiene: ( a ib T) _s a T_s ib T_s d e e e

λ

₌ − ± ⋅ ₌ − ⋅ _⋅ ± ⋅ _(2.31)

Dalla (2.31) si ricava che perchè il modulo di λd sia minore di uno, il segno della parte reale di λc deve essere negativo (2.32).

(

λ

_c = − ± ∪ >a ib a 0)→

λ

_d <1 (2.32)

Si evidenzia il fatto che la presenza di un integratore nel continuo si traduce in un polo unitario nel discreto (2.33).

0 1

c d

(10)

2.3: Modello impiegato nella tecnica di identificazione

Scegliere quale modello impiegare è certamente lo step più delicato nella messa a punto di una tecnica di identificazione. Nel nostro caso si è scelto di impiegare un modello ARX per la motivazione già accennata in precedenza: un modello ARX è un modello a regressione lineare e come tale comporta una certa semplicità nella procedura di identificazione dei suoi parametri. La struttura del modello a cui di seguito si farà riferimento è la seguente:

1 1 n m k j k j j k j k j j y a y ₋ b u ₋ e = = =

∑

− ⋅ +

∑

⋅ + (2.34) Dove:

yk: valore reale della variabile controllata (PV) al tempo k-esimo;

n: numero degli istanti precedenti per i quali il valore della variabile controllata va ad agire sul valore di yk;

uk: valore della variabile manipolata al tempo k-esimo;

m: numero degli istanti precedenti per i quali il valore della variabile manipolata va ad agire sul valore di yk;

j

a : coefficienti della variabile controllata agli istanti precedenti;

bj: coefficienti della variabile manipolata agli istanti precedenti.

ek: errore che si commette nel predire il valore della variabile controllata al tempo k-esimo impiegando i valori misurati della variabile controllata ai tempi di campionamento precedenti e gli ingressi al processo.

La prima ipotesi su cui si basa la tecnica di identificazione è che l’unico ingresso al processo sia costituito dalla variabile manipolata, ovvero che non ci sia alcuna sovrapposizione di disturbi. La seconda ipotesi, intrinseca alla struttura del modello, è che il valore della variabile controllata al tempo k-esimo sia indipendente dal valore della variabile manipolata allo stesso tempo. Questa ipotesi d’altra parte è sempre verificata nei processi fisici, in quanto essi sono dotati di un certa “inerzia” nella risposta. La coppia (n,m) costituisce l’ordine del modello.

Qualora il processo sia caratterizzato da un tempo di ritardo, l’ingresso influenza apprezzabilmente l’uscita dopo un certo numero di tempi di campionamento (L). In tal caso potremmo ritenere i primi

L coefficienti bj nulli e aver cura di scegliere m>L oppure, come si fa nella maggior parte dei casi, modificare la struttura del modello ARX come riportato di seguito:

1 1 n m k j k j j k j L k j j y a y ₋ b u _{− −} e = = =

∑

− ⋅ +

∑

⋅ + (2.35) Dove:

L: numero di tempi di campionamento rappresentativi del ritardo, ovvero rapporto tra il tempo di ritardo e il tempo di campionamento (Ts) del processo.

Se il tempo di campionamento scelto è molto piccolo si ha praticamente la certezza che il tempo di ritardo sia un suo multiplo.

Un’apparente limitazione di quest’ultima formulazione è che il valore del ritardo, ovvero il numero di tempi di campionamento L corrispondenti al ritardo, deve essere noto esplicitamente. Tale limitazione verrà comunque superata come discusso nel seguito.

(11)

2.4: Determinazione dei parametri del modello ARX mediante il

metodo dei minimi quadrati

Per prima cosa occorre specificare che, non avendo a disposizione il valore della variabile manipolata (MV), al suo posto si impiega quello del segnale di controllo (OP), facendo così una terza importante ipotesi relativa al comportamento ideale dell’attuatore.

Sebbene il rispetto di quest’ultima ipotesi, così come il rispetto dell’ipotesi che prevede l’assenza di disturbi sovrapposti, sia fondamentale ai fini di una corretta identificazione, esso potrebbe non essere garantito nella realtà industriale.

Si assuma per il momento che le variabili (n,m) ed L siano note. Il valore predetto dell’uscita al tempo k-esimo, noti i valori delle variabili controllata e manipolata ai tempi di campionamento precedenti è riportato in (2.36). 1 1 n m k j k j j k j L j j y a y ₋ b u _{− −} = = =

∑

− ⋅ +

∑

⋅ (2.36) Dove: k k k y = y −e Posto: max( , ) = + 1 n n m L (2.37)

si assuma di avere e a disposizione una sequenza di ingressi (OP) e la sequenza dei corrispondenti valori delle uscite (PV) per (N+n1) tempi di campionamento. Si valuti quindi il valore predetto dell’uscita dal tempo di campionamento (n1+1)-esimo fino al tempo di campionamento (n1+N) -esimo con riferimento alle espressioni (2.17) e (2.18).

Posto:

{

1 1, 1 1,..., 1 , 1

}

N

n n n N n N

Z = u ₊ y ₊ u ₊ y ₊ (2.38)

il modo più semplice di determinare il vettore delle incognite ϑ, definito in (2.17), è quello di fare in modo, mediante il metodo dei minimi quadrati (LLS: “Linear Least Squares”), che il valore predetto della variabile controllata sia quanto più simile possibile al valore misurato della stessa:

min V_N( ,ZN) ϑ ⎡⎣

ϑ

⎤⎦ (2.39) Dove: 1 1 2 1 1 ( ,

ϑ

) ( ) + = + = n N

∑

− N N k k k n V Z y y N (2.40)

Sostituendo la (2.18) nella (2.40) si ha:

1 1 2 1 1 ( , ) ( ) n N N T N k k k n V Z y N

ϑ

+

ϕ ϑ

= + =

∑

− ⋅ (2.41)

(12)

Poiché VN è quadratica in ϑ è possibile trovare la soluzione semplicemente ponendo il gradiente uguale a zero: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 ( , ) ( ) 0 n N N T N k k k k n n N n N T k k k k k n k n n N n N T k k k k k n k n d V Z y d N y y

ϑ

ϕ

ϕ ϑ

ϑ

ϕ

ϕ ϕ ϑ

ϑ

ϕ ϕ

ϕ

+ = + + + = + = + − + + = + = + = ⋅ − ⋅ = ⋅ = ⋅ ⋅ ⎡ ⎤ =⎢ ⋅ ⎥ ⋅ ⋅ ⎢ ⎥ ⎣ ⎦

∑

(2.42)

Una volta valutato ϑ come riportato in (2.42) è possibile quantificare VN(ϑ,ZN). Esso è rappresentativo dell’errore che si commette nell’identificazione.

È importante che il numero di dati su cui si conduce l’identificazione N sia considerevolmente maggiore del numero di incognite (n+m) per riuscire a ridurre al minimo l’effetto dei disturbi casuali entranti nel processo (ad esempio il rumore di misura della PV).

2.5: Determinazione del tempo di ritardo del processo

Nel paragrafo precedente si è illustrato come determinare i parametri aj e bj del modello ARX supponendo noti i valori di (n,m) ed L.

Per quanto riguarda L, ovvero il numero di tempi di campionamento rappresentativi del ritardo, può essere valutato ripetendo la procedura di identificazione (Lmax+1) volte, cioè per L=0,1, ,K L_max, e individuando il valore di L in corrispondenza del quale si ottiene il minimo scostamento tra il valore predetto della variabile controllata e il valore misurato della stessa (2.43).

min( _N( ))

L V L (2.43)

Essendo che l’errore quadratico medio (V_N) è funzione del numero di dati su cui si conduce l’identificazione (N), è importante che tutte le identificazioni condotte al variare del ritardo L, prevedano lo stesso N, al fine di eseguire un confronto significativo e di identificare correttamente il valore del ritardo.

Proprio per questo si fa in modo che il numero di dati a disposizione sia (N+n1) con n1pari a:

max( , )

= +

1 max

n n m L (2.44)

In questo modo, infatti, N rappresenta il numero di dati su cui si conduce l’identificazione per ogni

L e n1 rappresenta la lunghezza di una finestra di dati da usare, parzialmente o totalmente, per inizializzare il modello sulla base del valore di L supposto.

È importante notare che nella ricerca del ritardo L ottimale si possono incontrare situazioni in cui la matrice 1 1 1 n N T k k k n

ϕ ϕ

+ = + ⎡ ⎤ ⋅ ⎢ ⎥ ⎢ ⎥ ⎣

∑

⎦

ha un numero di condizione molto elevato. Se così è, conviene escludere tale modello in quanto esso risulterebbe molto sensibile al rumore e quindi poco affidabile. In pratica, dalla ricerca del modello che minimizza l’errore quadratico medio vengono esclusi quei

(13)

modelli per i quali la matrice 1 1 1 n N T k k k n

ϕ ϕ

+ = + ⎡ ⎤ ⋅ ⎢ ⎥ ⎢ ⎥ ⎣

∑

⎦

ha un numero di condizione superiore ad un valore di soglia.

Inoltre, dalla ricerca del modello che minimizza l’errore quadratico medio, vengono esclusi quei modelli che risultano instabili in anello aperto, ovvero quei modelli i cui poli hanno modulo maggiore di uno. La maggior parte dei processi tipici delle industrie di processo è infatti stabile in anello aperto.

2.6: Modifiche alla tecnica di identificazione per processi

“integratori”

Sebbene molti dei processi tipici delle industrie di processo siano stabili in anello aperto, un’eccezione abbastanza frequente è rappresentata dai processi “integratori” per i quali a fronte di una variazione a gradino dell’ingresso, l’uscita “diverge”, aumentando o diminuendo linearmente nel tempo.

Poiché i processi che coinvolgono il livello di serbatoi di liquido presentano tale dinamica, da dati provenienti da loops di controllo di livello sarebbe auspicabile ottenere un modello con dinamica integrale.

Come è stato precedentemente detto, dal punto di vista teorico, la funzione di trasferimento discreta di un processo “integratore” presenta un polo in 1; pertanto i coefficienti del denominatore soddisfano la seguente condizione:

1 1 n i i a = = −

∑

(2.45)

Procedendo alla determinazione dei coefficienti del modello da dati sperimentali, come discusso in precedenza, tale condizione difficilmente verrà soddisfatta. I dati di ingresso e uscita utilizzati dalla procedura sono infatti affetti da disturbi (soprattutto rumore di misura) e non determineranno mai l’identificazione di un processo integratore.

Ciò che si può fare nei casi in cui si desideri ottenere una dinamica integrale è andare ad imporre che la condizione precedentemente scritta venga soddisfatta, ovvero andare a risolvere il seguente problema di ottimizzazione quadratica vincolato:

1 2 min ( , ) 1 N N N i i V Z a a ϑ

ϑ

= ⎧ ⎡_⎣ ⎤_⎦⎫ ⎪ ⎪ ⎪ ⎪ ⎨ ⎬ ⎪ = − − ⎪ ⎪ ⎪ ⎩

∑

⎭ (2.46) min ( , ) (1,...,1,0....,0) 1 N N V Z ϑ

ϑ

θ

⎧ ⎡ ⎤ ⎫ ⎪ _⎣ _⎦ ⎪ ⎨ ⎬ ⎪ ⋅ = − ⎪ ⎩ ⎭ 1 1 1 1 1 1 1 1 0 n N n N T T k k k k k n k n y A A ϕ ϕ ϕ ϑ − ₊ + = + = + ⎛⎡ ⎤ ⎞ ⎛ ⎞ ⋅ ⋅ − ⎜ ⎟ ⎛ ⎞₌ ⎢ ⎥ ₊⎜ ⎟ ⎜ ⎟ ⎜_λ ⎣ ⎦ ⎟ ⎜ ⎟ ⎝ ⎠ _⎜ _⎟ _⎜₋ _⎟ ⎝ ⎠ ⎝ ⎠

∑

Dove:

(14)

λ: moltiplicatore di Lagrange il cui valore non ha rilevanza ai fini della procedura di identificazione, A: (1,...,1,0....,0) (vettore ∈ℜn m+ in cui i primi n termini sono uno)

2.7: Esito della tecnica di identificazione

La tecnica di identificazione descritta in questo capitolo consente di minimizzare lo scostamento tra il valore reale della variabile controllata e quello predetto dal modello, se la variabile controllata e il segnale di controllo agli istanti precedenti assumono i valori registrati.

Poiché il nostro scopo non si limita a questo, nel seguito si cercherà di definire degli indici che possano essere significativi della bontà dell’identificazione e possano stabilire ragionevolmente quando questa ha successo.

Nel far questo si terrà conto di due aspetti fondamentali:

1. Lo scopo della tecnica di identificazione è quello di identificare un modello del processo “utile ai fini del controllo”. In altre parole non si richiede che processo e modello siano identici, ma piuttosto che abbiano un comportamento simile in anello chiuso.

2. La tecnica di identificazione si basa su due ipotesi fondamentali: l’assenza di disturbi sovrapposti, il comportamento ideale dell’attuatore. Il venir meno di una di queste due ipotesi potrebbe causare la non somiglianza tra processo reale e modello identificato in anello chiuso.

2.8: Rappresentazione del modello identificato in termini di

funzione di trasferimento

Il modello ARX identificato può essere rappresentato direttamente in funzione di trasferimento nel tempo discreto come riportato di seguito (2.47).

( )

1 2 1 1 2 1 2 1 2 1 m L m k k _n k n b q b q b q y G q u q u a q a q a q − − − − − − − − ⎛ + + + ⎞ = _{= ⎜}_⎜ _⎟_⎟ + + + + ⎝ ⎠ L L (2.47)

Noto il tempo di campionamento, Ts, tale modello può essere convertito, utilizzando ad esempio la funzione di MATLAB “d2c.m”, in funzione di trasferimento continua:

num( ) ( ) ( ) ( ) ( ) den( ) s L T s y s G s u s e u s s − ⋅ ⎛ ⎞ = _{= ⎜} _⎟ ⎝ ⎠ % (2.48)

Può essere utile studiare la corrispondenza tra l’ordine del modello nel tempo discreto e il numero di poli e zeri del modello trasformato nel tempo continuo.

A tal proposito si faccia riferimento all’espressione (2.31) da cui si ricava quanto riportato nella tabella (2.1):

(15)

CONTINUO DISCRETO Polo reale negativo Polo reale positivo (modulo <1)

Polo reale positivo Polo reale positivo (modulo >1) Poli complessi (modulo <1) Poli complessi con parte reale negativa

Poli reali negativi coincidenti (modulo <1) Poli complessi (modulo >1)

Poli complessi con parte reale positiva

Poli reali negativi coincidenti (modulo >1) Tabella 2.1: Corrispondenza tra le caratteristiche dei poli nel continuo e quelle nel discreto.

Dalla tabella 2.1 si deduce che la trasformata di Laplace di un modello che nel discreto ha un polo reale negativo prevede due poli complessi coniugati. D’altra parte infatti, ad un polo reale negativo del discreto corrisponde nel continuo un polo complesso, ma quando è presente un polo complesso è sempre presente anche il suo coniugato.

È evidente allora che un modello ARX con n pari a 2, corrisponde ad un modello in trasformata di Laplace con un numero di poli che può variare tra 2 e 4. Per quanto riguarda il numero di zeri, esso corrisponde al valore di m a patto che il numero di poli nel continuo coincida con quello nel discreto. Se il numero di poli nel continuo viene incrementato a causa di uno o più poli reali negativi nel discreto, il numero di zeri viene incrementato al fine di mantenere costante la differenza tra il grado del numeratore e quello del denominatore.

Nella tabella 2.2 si riportano una serie di esempi significativi.

DISCRETO CONTINUO 1 2 0.25 z z z − − +

Poli reali positivi (modulo<1)

2 0.7726 1.922 1.386 0.4804 s s s + + +

Poli reali negativi

1 2 3 2.25 z z z − − +

Poli reali positivi (modulo>1)

2 0.3781 0.6576 0.811 0.1644 s s s + − +

Poli reali positivi

1 2 0.5 z z z − − +

Poli complessi (modulo<1)

2 0.6931 1.474 0.6932 0.737 s s s + + +

Poli complessi parte reale negativa

1 2 0.7358 0.1354 z z z − + +

Poli reali negativi coincidenti (modulo<1)

2 119.8 5.745 2 10.86 s s s + + +

Poli complessi parte reale negativa

1 2 1.5 1 z z z − − −

Un polo negativo (<1) e un polo positivo (>1)

2 3 2 0.6469 2.085 4.783 0.6931 9.379 7.167 s s s s s + + + + −

Due poli complessi (parte reale negativa) e un polo reale positivo

Tabella 2.2: Esempi di conversione dal discreto al continuo

La funzione di MATLAB “d2c.m” prevede, se non diversamente specificato, l’impiego di un hold di ordine zero, ovvero considera il segnale di controllo costante tra un tempo di campionamento e il successivo.

(16)

2.9: Tecnica di retuning

Come è stato detto all’inizio del capitolo, lo scopo principale dell’identificazione è quello di avere a disposizione un modello del processo sul quale eseguire la corretta sintonizzazione del regolatore. Sebbene le regole di tuning proposte in letteratura per i regolatori convenzionali siano moltissime, il modulo di retuning sviluppato nel corso di questo lavoro di tesi impiega la tecnica SIMC (Skogestad, 2003).

Tale regola consente di valutare i parametri per un regolatore proporzionale-integrale (PI), avendo a disposizione una funzione di trasferimento nel continuo del tipo primo ordine con ritardo e di valutare i parametri per un regolatore proporzionale-integrale-derivativo (PID), avendo a disposizione una funzione di trasferimento nel continuo del tipo secondo ordine con ritardo.

È evidente allora che, indipendentemente da quale sia l’ordine della funzione di trasferimento nel continuo del modello identificato, esso deve essere riportato a quello previsto dalla regola SIMC per la tipologia di controllore di interesse.

La riduzione del modello identificato ad un modello del primo ordine con ritardo viene fatta come descritto di seguito:

1. Si pone il guadagno del modello ridotto (K) pari a quello del modello identificato.

2. Sulla base della risposta del modello identificato ad un gradino unitario, si valuta in prima approssimazione il valore della costante di tempo (τ0) e del ritardo (ϑ₀) del modello ridotto. Come tempo di ritardo si prende il tempo oltre il quale il valore della variabile controllata supera il 5% del valore di stazionario, mentre come costante di tempo si prende il tempo al quale la variabile controllata raggiunge il 63% del valore di stazionario diminuito del tempo di ritardo (2.49). * * 0: |t t t y tsr( ) 0.05 yendsr

ϑ

∀ > → > ⋅ (2.49) * * 0:t 0| t t y tsr( ) 0.63 yendsr

τ

−

ϑ

∀ > → > ⋅ Dove:

ysr: vettore (di lunghezza opportuna) della risposta del modello identificato al gradino unitario;

sr end

y : valore della variabile controllata a stazionario.

3. Si impiegano quindi i parametri τ0 e ϑ₀appena valutati come punto di inizializzazione di una funzione di MATLAB capace di determinare i parametri τe ϑ* che minimizzano le differenze tra la risposta del modello identificato ad un gradino unitario e quella del modello ridotto allo stesso gradino (2.50).

* * * , min[(ysr ysr( , )) (T ysr ysr( , ))] ϑ τ −

ϑ τ

⋅ −

ϑ τ

(2.50) Dove: * ( , ) sr

y ϑ τ : vettore della risposta del modello ridotto (caratterizzato dai parametri ( , )ϑ τ ) al *

(17)

4. Il tempo di ritardo del modello ridotto non viene preso pari a ϑ*, ma a ϑ: * 2 s T ϑ ϑ= + (2.51)

Per quanto riguarda invece, la riduzione del modello identificato ad un modello del secondo ordine con ritardo viene fatta come descritto di seguito:

1. Si pone il guadagno del modello ridotto (K) pari a quello del modello identificato. 2. Si valuta τ0 e ϑ₀ come sopra.

3. Si ricava da τ0 i valori delle due costanti di tempo τ01 e τ02 che insieme a ϑ₀ inizializzano una funzione di MATLAB capace di determinare i parametri τ1, τ2 e ϑ* che minimizzano le differenze tra la risposta del modello identificato ad un gradino unitario e quella del modello ridotto allo stesso gradino (2.52).

* 1 2 * * 1 2 1 2 , , min[ (ysr ysr( , , )) (T ysr ysr( , , ))] ϑ τ τ −

ϑ τ τ

⋅ −

ϑ τ τ

(2.52)

4. Analogamente a quanto fatto per la riduzione del modello ad un primo ordine con ritardo, il tempo di ritardo del modello ridotto non viene preso pari a ϑ* ma a ϑ (2.51).

Una volta valutati i parametri ϑ e τ in caso di regolatore PI e i parametri ϑ, τ1 e τ2 in caso di regolatore PID, le regole di tuning proposte da Skogestad sono le seguenti:

Regolatore PI: 1 2 min( ;8 ) i Kc K τ ϑ τ τ ϑ = ⋅ ⋅ = ⋅ Regolatore PID: se

τ

₁< ⋅8

ϑ

1 2 1 2 2 2 1 0.5 1 i d Kc K τ τ ϑ τ τ τ τ τ _τ τ + = ⋅ = + = + se

τ

₁> ⋅8

ϑ

1 2 2 2 2 0.5 (1 ) 8 8 1 8 i d Kc K τ τ ϑ ϑ τ ϑ τ τ τ _τ ϑ = ⋅ ⋅ + ⋅ = ⋅ + = + ⋅

(18)

Relativamente alla tecnica di retuning appena descritta, è possibile fare le seguenti osservazioni: • Il fatto che la tecnica preveda di impiegare come tempo di ritardo del modello ridotto

almeno la metà del tempo di campionamento, fa si che essa possa essere in generale definita una tecnica robusta. Addirittura in caso di processi privi di ritardo la regola di tuning SIMC risulta piuttosto conservativa.

• In caso di processi con risposta inversa il tuning proposto per regolatori PID potrebbe risultare instabile.

• L’impiego di regolatori PID anziché di regolatori PI, sintonizzati secondo la regola SIMC, è solitamente vantaggioso quando è verificata la seguente disuguaglianza:

2

τ

>

ϑ

• La regola di tuning potrebbe non risulta appropriata per processi instabili in anello aperto, che non siano processi integratori, e per processi oscillanti (presenza di zeri o poli complessi nel continuo).