Capitolo I: DJOSER: sistema di caratterizzazione termica e di ausilio alla progettazione dei dispositivi elettronici di potenza

Capitolo I: DJOSER: sistema di caratterizzazione

termica e di ausilio alla progettazione dei

dispositivi elettronici di potenza

In questo capitolo verranno introdotte le principali problematiche connesse alla simulazione termica di dispositivi elettronici, e verrà presentato il simulatore termico analitico DJOSER di nuova concezione. Sarà affrontato lo studio matematico rigoroso delle equazioni che ne costituiscono la base, e verranno presentati i risultati di procedure di validazione volte a testarne le caratteristiche, sia dal punto di vista teorico che dal punto di vista sperimentale. Descriveremo poi un sistema di simulazione per lo studio dell'insorgenza di singolarità termiche nei transistori cellulari di potenza basato sullo DJOSER. Da ultimo riporteremo alcune applicazioni dello DJOSER allo studio di problematiche reali svolte in collaborazione con industrie del settore elettronico.

I.1 Introduzione alla simulazione termica

Nella fase progettuale dei sistemi elettronici di potenza e dei loro assemblaggi l’aspetto termico è di cruciale importanza per garantire elevate prestazioni ed assicurare un’alta affidabilità del prodotto. Per questa ragione, anche da parte dell’utente dei dispositivi elettronici, è indispensabile l’uso di opportuni strumenti di simulazione che siano in grado di prevedere con sufficiente accuratezza entità e localizzazione delle temperature massime e dei gradienti termici nel sistema. Infatti l’assetto termico interno al dispositivo elettronico dipende anche dalla struttura di assemblaggio che il cliente utilizzatore costruisce come supporto dissipativo, dal numero degli strati da cui è composto, dalla loro geometria, dai materiali e soprattutto dalle condizioni di incollaggio, saldatura o in generale dalla qualità dei

contatti tra gli strati.

L’uso di metodi o strumenti di previsione delle temperature massime inadeguati o troppo semplicistici comporta una incertezza sui reali assetti termici dei dispositivi, che naturalmente si traduce in un eccessivo sovradimensionamento di dispositivi e dissipatori, con conseguente aumento di costi ed ingombri.

Attualmente gli strumenti di calcolo e di simulazione termica più comuni sono basati sul ben noto metodo agli elementi finiti (FEM), adattabile a qualunque tipo di geometria. Esso implica la suddivisione del solido in oggetto in un reticolo tridimensionale composto da un numero molto grande di celle di varie forme e dimensioni. Con la tecnica FEM, il calcolo delle distribuzioni di temperatura interne al sistema viene ricondotto alla risoluzione di un sistema algebrico di grandi dimensioni.

Nonostante siano strumenti molto diffusi sia in ambito scientifico che nella progettazione meccanica, è doveroso notare come nell’ambito della piccola e media industria l’onerosità dei programmi di tipo FEM, il numero eccessivo di variabili da calcolare, il tempo necessario all’implementazione dei modelli e soprattutto la necessità di una specifica competenza da parte dell’operatore favoriscono una certa ritrosia al loro uso. Oltre a ciò, è in generale difficoltoso inserire nei modelli FEM le resistenze termiche di contatto tra due strati diversi che di fatto costituiscono l’elemento di maggiore incertezza nella conoscenza delle reali temperature massime.

Proprio al fine di risolvere il dilemma tra sistemi di calcolo di tipo general purpose ma onerosi e procedimenti troppo semplicistici e inaccurati, stanno prendendo piede, sia in ambito accademico che in quello industriale, alcune tecniche di simulazione termica di tipo analitico, ovvero basate sulla risoluzione esplicita delle equazioni di conduzione del calore [1,2,3,4,5]. L’implementazione di questi codici è resa possibile dalla semplicità delle geometrie dei sistemi di assemblaggio elettronico, consistente per lo più nella sovrapposizione asimmetrica di strati rettangolari omogenei e dalla sostanziale natura bidimensionale delle sorgenti di calore, in generale localizzabili sulla superficie superiore del primo strato oppure all’interfaccia tra strato e strato.

Di fatto i simulatori basati su queste tecniche si pongono in posizione intermedia tra gli strumenti numerici sofisticati e le semplici valutazioni di tipo monodimensionale. Infatti, mediante i codici analitici è possibile ottenere mappe termiche tridimensionali aventi un’accuratezza confrontabile con quelle calcolate dai programmi FEM (entro l’ 1%), ma con un numero di variabili sensibilmente inferiore, con minore tempo di calcolo, con una maggiore semplicità ed automatismo nella costruzione del modello, e soprattutto non necessitano di uno specifico ed approfondito retroterra culturale da parte dell’operatore. In questi programmi analitici si possono inserire tutti i dettagli e le condizioni al contorno

(incluse quelle convettive) che li rendono adatti a simulare dal punto di vista termico una vasta gamma di tipologie di montaggio elettronico, come il flip-chip, il montaggio superficiale dei dispositivi, il naked chip e le strutture ibride a film spesso. Inoltre, proprio grazie alla loro velocità di calcolo, essi sono particolarmente adatti ad essere utilizzati come accurati risolutori termici nei sistemi ciclici di simulazione elettro-termica congiunta dei dispositivi elettronici di potenza [6,7].

I.2 Implementazione del simulatore DJOSER

Alcune strategie di risoluzione analitica per la simulazione termica di assemblaggi elettronici sono state già impiegate per problemi particolari, con condizioni al contorno specifiche, sia in regime statico che dinamico [1,2,3,4,5]. Il software di simulazione che ci accingiamo a presentare, implementato in ambiente MATLAB nella sua forma definitiva presso il LEP (Laboratorio di Elettronica di Potenza) della Facoltà di Ingegneria dell’Università di Pisa, prende il nome convenzionale di DJOSER perché il modello base della struttura di assemblaggio è costituito dalla sovrapposizione di strati di forma parallelepipeda, del tutto simile ad una piramide a gradoni come quella costruita dal noto faraone della III dinastia.

La natura del modello, le mesh bidimensionali alle interfacce utilizzate per la definizione delle funzioni termiche, e una varietà di possibili condizioni al contorno [8] sono caratteristiche che rendono lo DJOSER adatto per una simulazione accurata della maggior parte delle strutture impiegate nell'elettronica di potenza.

I.2.1 Fondamenti teorici

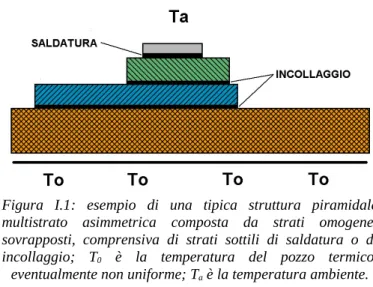
La struttura multistrato in esame, illustrata in Figura I.1, è composta da una pila di elementi prismatici: si tratta di parallelepipedi a facce rettangolari, e di varia altezza, collocati l'uno sull’altro e disposti con spigoli paralleli.

Un generico prisma della pila è fisicamente omogeneo ed ha il rettangolo di base di dimensioni inferiori (al più uguali) di quelle della base del prisma sul quale è appoggiato, e maggiori (al più uguali) di quelle della base del prisma che esso sostiene; ne risulta una sorta di piramide a gradoni di varia altezza, per la quale non sono necessariamente individuabili piani di simmetria.

Prima di cominciare la trattazione matematica rigorosa del problema di conduzione del calore associato alla struttura appena descritta riportiamo in Tabella I.1 l'associazione fra i principali simboli utilizzati, la loro definizione e le loro dimensioni nel sistema MKS. L’analisi termica dell’intera struttura piramidale multistrato si fonda sulla conoscenza della soluzione di un problema di conduzione del calore, in regime stazionario, formulato per un generico elemento prismatico imponendo su tutte le facce opportune condizioni al contorno.

In particolare sulle facce laterali del prisma si ipotizza uno scambio di calore per convezione con un ambiente a temperatura costante in cui è collocata la struttura.

Simbolo Quantità Unità SI

T(x,y,z),

T  x,y,z 



Temperatura ºC

q(x,y,z),

q  x,y,z 



Flusso termico W/m2

R* Resistenza termica di contatto W/ºC m2

ho,…., h5 Coefficienti di convezione ºC m2_/W

Ta Temperatura dell’ambiente esterno ºC

To Temperatura del pozzo termico ºC

F(x,y) Temperatura non unif. del p. termico ºC P(x,y), P*(x,y) Distribuzioni di potenza dissipata W/m2

ki Conducibilità termica W/ºC m

Bi(j) Numeri di Biot

μn, μm Autovalori m-1

Lx, Ly, Lz Dimensioni della lastra m

Tabella I.1: simboli utilizzati nella trattazione matematica, loro descrizione e unità di misura nel sistema MKS.

Per non complicare inutilmente il problema, la temperatura viene valutata assumendo quella dell’ambiente suddetto come zero di riferimento ed, in questo modo, le condizioni al contorno sulle facce laterali risultano lineari omogenee del terzo genere: [9]



q⋅n=h [T x , t−T *]

(I.1)

Figura I.1: esempio di una tipica struttura piramidale multistrato asimmetrica composta da strati omogenei sovrapposti, comprensiva di strati sottili di saldatura o di incollaggio; T0 è la temperatura del pozzo termico,

Anche per le basi dell’elemento prismatico si assume uno scambio di calore per convezione, ma su ciascuna base la temperatura esterna all’interfaccia viene considerata variabile da punto a punto; ne risultano condizioni al contorno ancora lineari del terzo genere, ma non omogenee.

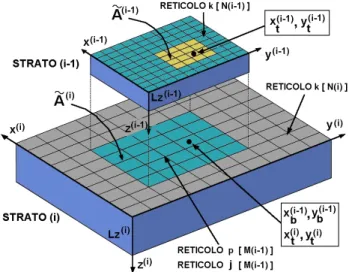
In termini formali, assumendo la terna di coordinate rettangolari indicata in Figura I.2, il problema risulta il seguente:

∇

2

T=0

per

0xL

x ;

0yL

y ;

0zL

z

k

∂

T

∂

x

−

h

1

T=0

per

x=0

;

0yL

y ;

0zL

z k ∂T ∂xh2T=0 per

x=L

x ;

0yL

y ;

0zL

z

k

∂

T

∂

y

−

h

3

T =0

per

0xL

x ;

y=0

;

0zL

z k ∂T ∂yh4T =0 per

0xL

x ;

y=L

y ;

0zL

z

k

∂

T

∂

z

−

h

0

T =-f x,y 

per

0xL

x ;

0 yL

y ;

z=0

k ∂T

∂zh5T =g  x,y  per 0<x<Lx ; 0<y<Ly ; z=Lz (I.2)

dove le funzioni f(x,y) e g(x,y) sono per il momento da considerarsi assegnate sulle due facce.

Il problema può essere risolto identificando due sottoproblemi, ciascuno con condizioni al contorno omogenee, eccetto che per una delle due basi, rispettivamente z=0 oppure z=LZ. Se si applica ai due sottoproblemi il metodo della

separazione delle variabili è facile concludere che essi condividono sia autovalori che autofunzioni. In particolare, una volta introdotte le grandezze adimensionali note come numeri di Biot:

Bi  j= h

_j

L

_j

/ k dove L

₀

= L

₅

= L

_z

, L

₁

= L

₂

= L

_x

, L

₃

= L

₄

= L

_y (I.3) gli autovalori per Bi jBi j1≠0 sono soluzioni della seguente equazione trascendente:

Figura I.2: rappresentazione di un singolo strato: a) e b) mostrano la sezione e la pianta con l'indicazione delle condizioni al contorno; c) mostra la sezione coi termini

ctg ξ =

ξ

Bi jBi  j1 

−

Bi  j⋅Bi  j1

[

Bi  jBi  j1 ] ξ

;

j=1 ξ

_n

=β

_n

L

_x j=

3 ξ

_m=μ_mL_y (I.4) mentre per Bi jBi j1=0 sono invece

ξ=0, π,, 2π , 3π , . .. .. . . n−1  π

Le corrispondenti autofunzioni risultano

X β

_n

x =β

_n

L

_x

cos β

_n

x  Bi  1 sen  β

_n

x 

Y μ_my=μ_mL_ycosμ_my  Bi3 sen μ_my  (I.5)

e le rispettive norme sono: [9]

N 

n

=

1

₂

{

[

 

n

L

x



2

Bi 1

2

]

⋅

[

1

Bi 2

 

_n

L

x



2

Bi 1

2

]



Bi 1

}

N_m=1 2

{

[

mLy 2_{Bi 3}2

_]

_⋅

[

1 Bi4

_mL_y2Bi 42

]

Bi 3

}

(I.6)

A partire dalle autofunzioni, e in accordo con le loro ben note proprietà di ortogonalità, si costruisce una soluzione [4] che contiene una serie doppia relativa allo sviluppo di Fourier della funzione f(x,y) o g(x,y), a seconda della base dove è posta la condizione al contorno non omogenea a cui il sottoproblema si riferisce. La somma delle due soluzioni è infine la soluzione del problema di partenza. Ponendo

υ

_{n, m}

=



β

_n2

μ

_m2

Sn,m =

[

_

υ_{n, m}L_z

_

2Bi 0 ⋅Bi 5 

]

⋅sinh υ_{n, m}L_z 

[

Bi 0Bi5 

]

_

υ_{n, m}L_z

_

⋅cosh υ_{n, m}L_z

(I.7)

T x , y , z= =Lz k ⋅

∑

_n=1 ∞

∑

m=1 ∞ _X nx⋅Ymy  N_n⋅N_m ⋅

⋅

{

n ,mLz

cosh

[n ,mLz−z]Bi

5



sinh

[n ,mLz−z ]

Sn , m  ⋅ ⋅

1

L_xL_y

∫

₀ Lx

∫

0 Ly f x ', y '⋅X_nx '⋅Y_my 'dx 'dy ' n ,mLz

cosh

n ,mzBi 

0



sinh

n ,mz

Sn , m  ⋅ ⋅

1

LxLy

∫

₀ L_x

∫

0 L_y g x ' ,y '⋅Xnx '⋅Yny 'dx 'dy '

}

(I.8) Per trasferire nell’analisi termica della struttura piramidale il risultato relativo ad un elemento, innanzitutto si devono individuare le funzioni f(x,y) e g(x,y) a partire dalla schematizzazione fisica della struttura. Mentre sulle facce laterali di un generico elemento prismatico si ha scambio termico convettivo con l’ambiente esterno, sulle basi possono in generale essere presenti:

sulla base z=0: una sorgente piana di generazione di calore per unità di superficie e di tempo dovuta ad esempio all’effetto Joule; il flusso termico specifico che, attraversando l’interfaccia di contatto Ã, proviene dall’elemento sovrapposto a quello in esame; lo scambio convettivo di calore presente solo sulla parte

 A− A  della superficie di base a diretto contatto con l’ambiente esterno; sulla base z=LZ : lo scambio di calore per conduzione verso l’elemento sottostante

con l’eventuale presenza di una resistenza di contatto tra i due elementi; in presenza della suddetta resistenza di contatto una ulteriore sorgente piana di generazione di calore per unità di superficie e di tempo.

Dal punto di vista analitico la maggiore difficoltà sorge sulla base superiore z=0 dell’elemento prismatico dove, in accordo a quanto abbiamo detto, si hanno condizioni al contorno miste: una del secondo genere su x,y ∈ A , l’altra del terzo genere su q  x,y  [5].

• P(x,y) la generazione piana di calore dovuta ad esempio all’effetto Joule connesso al passaggio di corrente in giunzioni tra semiconduttori o a cadute ohmiche su piste metallizzate;

• q x,y  il flusso termico proveniente dall’elemento sovrastante, nullo per

x,y ∈ A− A  ;

• T(x,y,0) la temperatura sulla base superiore dell’elemento prismatico in esame;

allora la funzione f(x,y) sulla base z=0 sarà data da

f  x,y =P x,y  q x,y h

₀

T  x,y,0 

per



x,y ∈ A

, z=0

f  x,y =P x,y 

per



x,y ∈ A− A 

; z =0 (I.9)

In questo modo per h₀≠0 la condizione al contorno relativa alla faccia z=0 implicherà uno scambio convettivo identicamente nullo sulla parte x,y ∈ A e non nullo con l’ambiente a temperatura zero sulla parte restantex,y ∈ A− A  . Ovviamente la posizione fatta non risolve di per sé la difficoltà connessa all’esistenza di condizioni al contorno miste. Infatti, anche ipotizzando che le funzioni P(x,y) e q  x,y  siano assegnate, la temperatura T(x,y,0) rimane del tutto incognita e ciò implica che nello sviluppo in serie doppia di Fourier si presenti un’equazione integrale.

Sulla base inferiore dell’elemento z=LZ la situazione è più semplice ed indicando

con:

• P*(x,y) la ulteriore generazione piana di calore dovuta ai fenomeni sopracitati;

• T  x,y la temperatura dell’interfaccia dell’elemento prismatico

sottostante;

• R* la resistenza termica di contatto tra l’elemento in esame e il sottostante; la funzione g(x,y) risulta:

g  x,y =P*  x,y 

Tx,y 

R *

per



x,y ∈ A

, z =LZ (I.10)

Si noti che la resistenza termica di contatto comporta uno scambio termico lineare come quello convettivo e che dunque risulta:

R *=1/h₅ (I.11) Dalla schematizzazione fisica della struttura con cui sono state individuate le funzioni f(x,y) e g(x,y) emerge con chiarezza che, mentre i termini di generazione piana di calore P(x,y) e P*(x,y) sono funzioni assegnate, i termini 0xLx e

T  x,y , relativi rispettivamente all’interfaccia superiore ed a quella inferiore dell’elemento in esame, non sono affatto noti, ma anzi dipendono dai campi termici dell’elemento sovrastante e quello sottostante.

Per procedere nell’analisi termica della struttura piramidale, sostituiamo nella soluzione T(x,y,z), e nella sua derivata rispetto a z, le funzioni f(x,y) e g(x,y) con le I.9 e I.10, quindi operiamo in modo da esprimere la temperatura in z=0 ed il flusso termico in z=Lz nella forma seguente:

T  x,y,0 =Bi  0 

_∬

 A

T x ' , y ',0  G

₁₁



x ' , y '∣x,y d x 'd y '



L

z

k

∬

_A

[

P  x ' , y ' q  x ' , y '

]

G

11



x ' , y '∣x,y  d x ' d y '



∬

A

[

R * P * x ' , y '  T x ' , y ' 

]

G

₁₂



x ' , y '∣x,y d x ' d y '

(I.12a)

---q  x,y,L

_z

=h

₀

_∬

 A

T  x ' , y ' ,0 G

₂₁



x ' , y '∣x,y  d x ' d y '



∬

A

[

P x ' , y ' q x ' , y '

]

G

₂₁



x ' , y '∣x,y d x ' d y '

-−

k

L

_z

∬

_A

[

R * P * x ' , y ' T x ' , y '

]

G

22



x ' , y '∣x,y  d x ' d y '

(I.12b)

dove le grandezze Gij(x’,y’|x,y) sono le funzioni di Green così di seguito

strutturate, per il caso presente:

G₁₁x ' , y '∣x,y =1 L_xL_{y n=1}

∑

∞

∑

m=1 ∞ _D 11n,m S n,m  ⋅ X β_nx '⋅Y μ_my '  N β_n⋅N μ_m ⋅

⋅

X β

_n

x ⋅Yμ

_m

y 

(I.13a)

G

₁₂

x ' , y '∣x,y =

1

L

_x

L

_{y n=1}

∑

∞

∑

m=1 ∞

υ

_n,m

L

_z

⋅

Bi 5 

S n,m

X β

_n

x ' ⋅Y μ

_m

y '

N β

_n

⋅

N μ

_m



⋅

⋅

X β

_n

x ⋅Y μ

_m

y 

(I.13b)

---G

₂₁



x ', y '∣x,y =G

₁₂



x ' , y '∣x,y 

(I.13c)

---G

₂₂

x ' , y '∣x,y =

1

L

_x

L

_{y n=1}

∑

∞

∑

m=1 ∞

υ

_n,m

L

_z

⋅

D

22



n,m

S n,m

⋅

⋅

X β

n

x ' ⋅Y μ

m

y '

N β

n

⋅

N μ

m



⋅X β

_n

x ⋅Y μ

_m

y 

(I.13d) avendo posto

D

₁₁



n,m=υ

_n,m

L

_z

cosh

_

υ

_n,m

L

_z

_

Bi  5 sinh

_

υ

_n,m

L

_z

_

D

₁₁



n,m=υ

_n,m

L

_z

cosh

_

υ

_n,m

L

_z

_

Bi  5 sinh

_

υ

_n,m

L

_z

_

(I.14) Si osservi che, come già accennato in precedenza, la I.12a risulta essere un’equazione integrale lineare del tipo di Fredholm di seconda specie [10] con la temperatura T(x,y,0) nel ruolo di funzione incognita e la funzione di Green G11 in

quello di nucleo. Comunque è immediato riconoscere che, anche nel caso fosse Bi(0)=0, la natura integrale dell’equazione non scomparirebbe, anzi entrambe le I.12 hanno tale natura dal momento che negli integrali dei loro secondi membri risultano incognite le funzioni q x,y  e T x,y  .

Adottiamo un indice numerico per indicare il generico elemento prismatico della pila, da 1 per quello di sommità fino ad n per quello di base; l’indice comparirà a pedice delle varie grandezze oppure tra parentesi, come apice. Con queste notazioni sulle interfacce del generico “iesimo” elemento la conservazione del flusso di calore e la continuità della temperatura si traducono nelle relazioni



q  x,y :=q

_i-1



x,y =P

_i-1¿



x,y q

_i-1

x,y,L

_zi-1 



per z=0 (I.15a)



T  x,y := T

_i1



x,y =T

_i1



x,y,0

per z= (i) z

L (I.15b)

equazioni integrali lineari nelle seguenti quattro funzioni: q_i−1x, y  ;



q_ix, y  ; Tix, y ; Ti1x , y , dalle quali discende un sistema di

equazioni integrali lineari che risultano in numero pari al numero delle funzioni incognite.

Se indichiamo con n il numero degli strati della struttura, si potrebbe frettolosamente concludere che 2n sono il numero di coppie di equazioni e altrettante sono le coppie di funzioni flusso e temperatura. In realtà ad un conteggio più attento il numero di equazioni e di funzioni incognite risulta pari a 2(n-1). Infatti, poiché il parallelepipedo collocato alla sommità della pila non sostiene alcun altro elemento, la sua faccia superiore è priva della parte A su cui sono da calcolare gli integrali della temperatura T(x,y,0); ne segue che la suddetta temperatura scompare dal secondo membro della coppia di equazioni relative al primo elemento e ciò esclude dal sistema, come inessenziali, sia la funzione stessa che l’equazione ad essa corrispondente. Anche per il flusso termico che attraversa la faccia inferiore dell’elemento posto alla base della pila si giunge alla medesima conclusione, dal momento che è immediato riconoscere che tale flusso non compare al secondo membro della coppia di equazioni di nessun altro elemento. Grazie a queste osservazioni diminuisce di due unità sia il numero di funzioni che di equazioni.

Infine si deve osservare che, se per il parallelepipedo collocato alla sommità della pila il flusso q  x,y  è ovviamente nullo, per l’elemento posto alla base della pila la funzione T  x,y all’interfaccia inferiore è la temperatura stessa del pozzo termico sul quale poggia la pila medesima, ovvero una funzione F(x,y) assegnata. Sulla base di quanto abbiamo detto, il sistema di equazioni integrali lineari risulta:



q

₁



x,y = P

₁

* x,y 

_∬

A 1

P

₁



x ' , y '  G

₂₁1 



x ' , y '∣x,y d x ' d y ' 

−

k

1

L

1_z

∬

A 1 

[

R

₁

* P

1

* x ' , y '  T

2



x ' , y ' 

]

G

221 



x ' , y '∣x,y d x ' d y '

(I.16a)

---

T

_i



x , y =Bi

_i

0

_∬

A i−1



T

_i



x ' , y '⋅G

₁₁j



x ' , y '∣x , y dx ' dy '



L

z i

k

i

∬

A i

[

P

_i



x ' , y '  

q

_i−1



x ' , y ' 

_]

⋅

G

₁₁i



x ' , y '∣x , y  dx ' dy '



∬

A i

[

R

i

* P

i

* x ' , y '  

T

i1



x ' , y '

]

G

12i



x ' , y '∣x , y dx ' dy '

(I.16b)

 q_ix,y =P_i* x,y h₀i 

∬

Ai-1 T_ix ', y '  G₂₁i x', y'∣x,y d x'd y'

∬

A  i

[

P_ix ' , y '  q_i-1x ' , y' 

]

Gi _{21x ', y '∣x,y d x ' d y '−}

−

k

i

L

_zi

∬

A  i

[

R

_i

* P

_i

*

x ', y '  T_i1x ' , y ' 

_]

G

₂₂i 



x ' , y '∣x,y  d x ' d y '

(I.16c)

---

T

_n



x , y =Bi n 0

_∬

A n −1 



T

_n



x ' , y ' G

n ₁₁

x ', y '∣x , y dx ' dy '



L

z n 

k

_n

∬

_{A n }

[

P

n

x ' , y ' q

n −1



x ' , y '

]

⋅

G

11 n

x ' , y '∣x , y dx ' dy '



∬

A n 

[

R

_n*

_P

n *



x ' , y 'T

₀



x ' , y '

]

G

₁₂n



x ' , y '∣x , y dx ' dy '

(I.16d)

dove si deve tenere presente che ogni equazione si riferisce ad una base di un elemento e che nelle equazioni relative ad elementi diversi le coordinate x,y non sono in genere identiche, essendo riferite a sistemi con assi tutti paralleli, ma con origini non necessariamente coincidenti.

In linea di principio, la soluzione del sistema fornisce le funzioni flusso e temperatura alle interfacce; dalla loro conoscenza si hanno le funzioni f(x,y) e g(x,y) per ogni elemento prismatico, e ciò rende utilizzabile la soluzione del problema conduttivo con condizioni convettive al contorno e quindi calcolabile, elemento per elemento, il campo termico in tutta la struttura.

Dal momento che non è pensabile di risolvere in modo analitico il sistema di equazioni integrali, si rende necessaria una soluzione approssimata. Mediante il ricorso al calcolo numerico degli integrali il sistema integrale può essere trasformato in un sistema algebrico lineare e risolto con l’aiuto dei consueti strumenti di calcolo elettronico.

I.2.2 Formulazione Algebrica

Una singola equazione lineare integrale di Fredholm, dal momento che è formulata su un intervallo finito, può essere ridotta ad un sistema di equazioni algebriche richiedendo che sia verificata in un numero finito di punti e quadrando, in modo approssimato, l’integrale definito mediante i valori assunti nei medesimi punti dalla funzione incognita [5]. Questo metodo è direttamente estendibile ai sistemi di

equazioni integrali lineari ed in particolare è applicabile al sistema I.16 di cui fornisce una soluzione approssimata.

Come primo passo si noti che gli integrali che compaiono nelle equazioni del sistema sono tutti del medesimo tipo e per una generica funzione Φ possono essere così espressi:

∬

A

Φ  x ' , y ' ⋅G

_{i j}



x ' , y '∣x,y  d x ' d y '=

=

∑

n=1 ∞

∑

m=1 ∞

C

_{i j}

n,m X  β

_n

x Y  μ

_m

y ⋅

⋅

1

L

_x

L

_y

∫

₀ Lx

∫

0 Ly

Φ x ' , y '  X  β

_n

x ' Y  μ

_m

y ' d x ' d y '

(I.17)

Scelto il tipo di tecnica di quadratura approssimata in due dimensioni, ed identificato sul dominio A un opportuno reticolo di N punti in cui calcolare la funzione Φ, si ha:

1

L

_x

L

_y

∫

₀ Lx

∫

0 Ly

Φ x ' , y '  X  β

_n

x ' Y  μ

_m

y ' d x ' d y '≃

≃

∑

k=1 N

B

_n,m



x

_k

,y

_k

⋅

Φ  x

_k

,y

_k



(I.18)

dove i coefficienti Bn,m dipendono dal tipo di quadratura adottata, oltre che dai

valori assunti nei punti del reticolo dalle primitive delle autofunzioni.

Ad esempio, nella tecnica di quadratura parallelepipeda su di un rettangolo di lati 2a e 2b si approssima la funzione Φ col valore assunto da essa nel punto di intersezione delle diagonali ottenendo:

B

_n,m



x

_k

,y

_k

=

4⋅sen β

_n

a sin μ

_m

b [cos  β

_n

x

_k





Bi 1 

β

_n

L

_x

sin  β

n

x

k

]⋅[

cos  μ

m

y

k



Bi 3 

μ

_m

L

_y

sin μ

m

y

k

 ]

(I.19)

φ

_ij



x

_k

,y

_k

∣x,y =

_∑

n=1 ∞

∑

m=1 ∞

C

_ij



n,m⋅B

_n,m



x

_k

,y

_k

⋅

X  β

_n

x Y  μ

_m

y 

(I.20) potremo sempre scrivere

∬

A

Φ x ' , y ' ⋅G

_ij



x ' , y '∣x,y  d x ' d y '≃

∑

k=1 N

φ

_ij



x

_k

,y

_k

∣x,y  Φ x

_k

,y

_k



(I.21) Per introdurre questa approssimazione nel sistema di equazioni integrali I.16 dobbiamo fare una importante precisazione: ogni elemento della pila ha un proprio unico sistema di coordinate a cui sono riferiti i punti delle facce z=0 e z=Lz(i), ma

sulle due facce, geometricamente identiche, i reticoli individuati per le quadrature sono in genere diversi per dimensioni della maglia e numero di punti, (vedi Figura I.3). È invece necessario che, sulle interfacce di contatto, due elementi contigui abbiano reticoli identici, perfettamente sovrapponibili.

Naturalmente le coordinate di un punto pensato come appartenente alla superficie dell’elemento superiore ha in generale coordinate diverse da quelle del medesimo punto, pensato sulla superficie dell’elemento sottostante.

Figura I.3: rappresentazione degli indici degli strati, delle coordinate e delle griglie utilizzate nella trattazione

In conformità a quanto abbiamo detto, poiché ogni equazione del sistema I.16 vale per tutti punti della faccia a cui l’equazione è riferita, tanto più deve essere verificata per i soli punti del reticolo adoperato per la quadratura, dando origine ad un pari numero di equazioni algebriche; l’insieme di tutte le equazioni algebriche originate dall’insieme delle equazioni integrali costituisce il sistema algebrico lineare a cui è ricondotto il sistema integrale.

Le notazioni x(i)_{, y}(i) _{si riferiscono alle coordinate di un generico elemento della pila}

per mettere in evidenza che in genere non sono identiche; xt(i), yt(i) per i punti

appartenenti alla faccia superiore z=0 dell’elemento iesimo; xb(i), yb(i) per i punti

appartenenti alla faccia inferiore z=Lz(i) dell’elemento iesimo. Inoltre, per

evidenziare che le sommatorie si riferiscono a reticoli di integrazione generalmente diversi, sono stati usati i simboli k e p per gli N(i) e M(i) punti dei reticoli tracciati, rispettivamente, sulle facce z=0 e z=Lz(i) dell’elemento iesimo, mentre il simbolo j è

stato impiegato per l’interfaccia A di contatto tra due elementi contigui: si tratta di M(i-1) punti dal momento che, sui complessivi N(i) punti del reticolo tracciato sulla faccia z=0 dell’elemento iesimo, l’intero reticolo della faccia z=Lz(i-1)

dell’elemento sovrastante si sovrappone in genere solo in parte, ma esattamente per tutti i suoi M(i-1) punti. Le notazioni sono riassunte in Figura I.3.

Facendo uso delle notazioni suddette ed utilizzando le equazioni I.20 e I.21 per la conversione degli integrali doppi, il sistema di equazioni I.16 viene trasformato in un sistema algebrico formato da 2[M(1)+M(2)+....+M(n-1)] equazioni in altrettante incognite. La sua forma normale, scritta in modo conciso ed in cui si sono isolate a sinistra le variabili incognite, è la seguente:

∑

p=1 M 1

ω

1 pb

⋅

T

2p



q

b1

=

P

b

*

1 



∑

k=1 N 1 

φ

kb1 

⋅

P

k1 

−

∑

p=1 M 1 

ω

pb1

⋅

R

1

*⋅P

p

*

1 con b =1,2,3...M(1); (I.22a) ---T_ti −

∑

j=1 M  i-1 

hi₀ ψi _{j t}⋅Ti_j 

∑

p=1 M i  φ_{p t}i ⋅Ti1_p −

∑

j=1 M  i-1 ψi_{j t}⋅qi-1 _j =

=

∑

k =1 N i 

ψ

_{k t}i

⋅

P

_ki



∑

p=1 Mi 

φ

i_{p t}

⋅

R

_i

* P *

_pi

−

∑

j=1 M  i-1

h

₀i 

φ

i_{j b}

⋅

T

_ji



∑

p=1 M i 

ω

_{p b}i

⋅

T

i1_p

−

∑

j=1 M  i-1 

φ

_{j b}i

⋅

q

_ji-1 



q

_bi

=

=

P

_b

*

i



∑

k=1 N i 

φ

_{k b}i 

⋅

P

_ki 

−

∑

p=1 M i 

ω

_{p b}i 

⋅

R

_i

* P

_p

*

i

con b =1,2,3...M(i); (I.22c)

---T

n _t

−

∑

j=1 M n-1

h

₀n

ψ

n _{j t}

⋅

T

n_j

−

∑

j=1 M n-1

ψ

_{j t}n 

⋅

q

n-1_j

=

=

∑

k=1 N  n

ψ

n_{k t}

_⋅

_P

k n 

_

_∑

p=1 M  n

φ

_{p t}n 

_⋅

[

R

_n

* P

_p

*

n 



F

_p

_]

con t=1,2,3...M(n-1)  N(n); (I.22d)

dove si è indicato con

T_ki ≡ T_ix_ki,y_ki; q_ki≡q_ix_ki,y_ki  ; P_ki≡P_ix_ki ,y_ki

P

∗i_p

≡

P

_i

* x

i_p

,y

i_p



;

P

_p

*

i

≡

P

_i

* x

i_p

,y

i_p



;

F

_p

≡

F x

_p

,y

_p



(I.23) e con

ψ

_{k t}i

≡

L

z

i 

k

_i

φ

11 i



x

_ki 

,y

_ki

∣

x

_ti

,y

_ti



φ_{p t}i≡φ₁₂i x_pi,y_pi∣x_ti,y_ti=φ₂₁ix_pi,y_pi∣x_ti,y_ti

φ

_kbi

≡

φ

₂₁i



x

i _k

,y

i_k

∣

x

_bi

,y

_bi

=

φ

₁₂i 



x

i_k

,y

_ki

∣

x

_bi

,y

_bi



ω_pbi ≡ki L_ziφ22 i x_pi ,y_pi ∣x_bi  ,y_bi   (I.24)

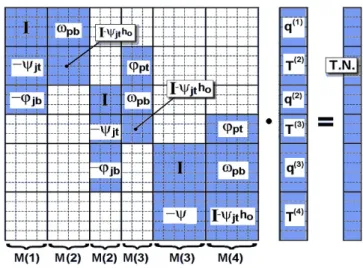
Le quantità definite dalle I.24 costituiscono i coefficienti dei singoli aggiunti rettangolari della matrice principale del sistema algebrico, organizzata come in Figura I.4. La risoluzione del sistema consente la conoscenza delle griglie di valori di flusso e temperatura su tutte le interfacce interne della struttura. Con questi dati è possibile infine calcolare il flusso e la temperatura in ogni punto dell’assemblaggio ottenendo una mappatura tridimensionale completa.

Figura I.4: rappresentazione di un sistema algebrico a quattro strati. I è la matrice identità; T.N. È il vettore colonna dei termini noti. Le sottomatrici bianche

I.3 Validazione teorica e sperimentale del software

Dopo l’esposizione dei presupposti teorici e degli algoritmi di risoluzione del metodo DJOSER, verranno ora presentati alcuni esempi di simulazione di campioni virtuali, con la potenza dissipata sulla sommità della struttura piramidale ed in presenza o assenza di convezione verso l’ambiente [11,12]. Queste prove hanno evidenziato come le distribuzioni di temperatura calcolate siano pienamente sensibili alla conformazione degli strati componenti il package sottostante e/o alle condizioni al contorno. I risultati delle simulazioni ottenute mediante il programma DJOSER sono stati confrontati con quelli ricavati utilizzando un simulatore agli elementi finiti in modo da verificarne la congruenza. Le sorgenti di errore o inaccuratezza del metodo analitico sono state enucleate e valutate sempre assumendo come riferimento i risultati ottenuti con il simulatore FEM. Infine gli andamenti di temperatura calcolati sono stati validati mediante opportune misure di tipo elettrico e termografico su strutture reali appositamente assemblate.

I.3.1 Validazione teorica tramite simulazione di campioni virtuali

I.3.1.1 Struttura dei campioni virtuali e mappe termiche

Il simulatore analitico DJOSER, implementato in Matlab 7, è stato applicato ad una serie di strutture virtuali multistrato appositamente progettate al fine di rappresentare un tipico assemblaggio di un circuito elettronico integrato sul proprio substrato, comprensivo della ricopertura plastica superiore. Questi test sono stati effettuati al fine di fornire le seguenti informazioni:

• le mappe termiche calcolate dal programma di simulazione;

• la sensibilità delle mappe termiche a differenze geometriche e strutturali nei livelli posti sotto allo strato dove viene generato il calore;

• l'influenza della variazione delle condizioni al contorno convettive imposte sulle superfici sulle mappe termiche;

• un termine di paragone per effettuare un confronto fra i profili termici ottenuti dallo DJOSER coi profili termici ottenuti da un programma tradizionale agli elementi finiti sulla medesima struttura.

è composta da una alternanza di strati ad alta e bassa resistenza termica, il che da una parte è rappresentativo, come già accennato, di un tipico montaggio per l'elettronica di potenza di tipo IMS (Insulated Metal Substrate), dall'altra ci consente di testare gli effetti sulla distribuzione del flusso di calore indotti da differenti valori di conducibilità termica degli strati. Le sue caratteristiche termiche e geometriche sono riportate in Tabella I.2, unitamente alla densità delle mesh bidimensionali (nx·ny) e al numero di autovalori strato per strato (Nnm).

.

Strato K (W/m°C) Lx·Ly (mm2_{) Lz (μm) nx·ny Nnm}

Plastica 0,3 3x2 800 12x8 60x60

Silicio 135 3x2 500 28x18 60x60

Allumina 24 4x3 300 32x24 55x55

Rame 386 6x4 1500 32x24 55x55

Tabella I.2: caratteristiche di ciascuno strato dei campioni virtuali D ed A: nome del materiale, conducibilità termica k, dimensioni laterali Lx·Ly, densità delle mesh nx·ny,

numero di autovalori utilizzati (Nnm).

Lo strato principale è un die rettangolare di Silicio di 600um di spessore, ricoperto da 800um di resina epossidica. La potenza viene dissipata da una serie di isole rettangolari disposte sulla superificie superiore del Silicio per un totale di 20W; ciascuna isola ha una densità di potenza uniforme e pari a 10,77W/mm2_{. La}

superficie del Silicio è suddivisa in una griglia di 28x18 celle quadrate. Al di sotto troviamo 300um di isolante elettrico (Allumina) e uno strato più spesso di Rame (1500um) che svolge la funzione di heat-spreader. Tutte le facce laterali e superiori sono in contatto termico con l' ambiente esterno che si trova a una temperatura di 0°C, ad eccezione della faccia inferiore del Rame, che si suppone alloggiato su un pozzo termico ideale che impone una temperatura costante di 20°C. La differenza fra la temperatura ambiente e la temperatura del pozzo termico è stata scelta al fine di evidenziare gli effetti degli scambi convettivi sui risultati della simulazione. L'altra struttura di prova, chiamata “A”, è stata ottenuta a partire dalla struttura “D” introducendo delle asimmetrie geometriche nella disposizione degli strati, ovverosia facendo coincidere le proiezioni sull'asse verticale delle estremità sud-ovest di ciascuno strato. Le altre caratteristiche della struttura sono state lasciate invariate; in questo modo è stato possibile osservare gli effetti della variazione di layout sul campo di temperatura simulato. In Figura I.5 è mostrata la conformazione delle isole di dissipazione di potenza e la disposizione geometrica

degli strati sia per ”A” che per “D”.

I.3.1.2 Risultati delle simulazioni termiche

Nella Figura I.7 sono mostrati i risultati delle simulazione termiche per la struttura “D” con condizioni al contorno adiabatiche per le superfici laterali e superiori: sopra abbiamo la mappa termica della faccia superiore del Silicio, a metà le distribuzioni di temperatura lungo gli assi X e Y tratteggiati in Figura I.5, e sotto la mappa del flusso termico che attraversa la superficie superiore del Silicio. È interessante notare come in quest'ultima raffigurazione ci troviamo in presenza di un flusso termico con valori sia positivi (dal basso verso l'alto) che negativi (dall'alto verso il basso). In particolare, i flussi negativi sono collocati in corrispondenza della isole dove viene dissipata la potenza, mentre i flussi positivi dai valori più elevati sono collocati nelle celle adiacenti ai contorni delle isole. Questo comportamento è causato dalla compresenza di tre fattori:

• la dissipazione non uniforme sulla superficie del Silicio;

• le condizioni al contorno laterali e superiori adiabatiche;

• la presenza di uno spesso strato di resina epossidica a bassa conducibilità termica al di sopra delle zone dissipative.

In Figura I.6 è mostrato il confronto fra gli andamenti di temperatura sul Silicio e sulla resina per il campione simmetrico “D” e per quello asimmetrico “A”, calcolati sugli assi X e Y evidenziati in Figura I.5, scelti in modo da intersecare i Figura I.5: in alto: isole di generazione della potenza; in basso: sezione e pianta dei campioni virtuali

punti dove il valore di temperatura risulta massimo.

È evidente la differenza esistente fra i due grafici, malgrado siano stati ottenuti da campioni che presentano una identica geometria delle isole di dissipazione della potenza e identica natura degli strati; questa differenza è consistente con la differente disposizione geometrica reciproca degli strati sottostanti al Silicio, e cioè l'isolante elettrico costituito dall'Allumina e l'heat spreader costituito dal Rame.

Il campione asimmetrico “A” mostra non solo temperature più elevate ma anche un andamento leggermente deformato del profilo termico; una tale distorsione è maggiormente evidente nella metà sinistra dei grafici del campione “A” tanto per il Silicio quanto per la resina, ed è dovuta alla deviazione del flusso termico sottostante indotta dalla distribuzione asimmetrica degli strati. Nello specifico, l'impilamento degli strati superiori lungo un angolo dell'heat-spreader inibisce la distribuzione laterale del flusso con un conseguente aumento della temperatura totale, causata dalla maggiore concentrazione del flusso medesimo in un volume ridotto.

Con questo primo esempio abbiamo voluto dimostrare come il simulatore DJOSER sia pienamente sensibile alle variazioni di layout dei progetti elettronici. Nel prossimo ci proponiamo di indagare sugli effetti di differenti condizioni al contorno di tipo convettivo: il campo di temperatura dei campioni è stato infatti

Figura I.6: confronto dei grafici di temperatura del Silicio e della plastica fra i campioni virtuali D ed A lungo gli assi X e Y mostrati in Figura I.5. I grafici sono stati calcolati con condizioni al contorno laterali adiabatiche.

calcolato al variare del coefficiente di convezione hv. Nella struttura simmetrica “D” è stato imposto uno scambio convettivo su tutte le superfici esposte laterali e superiori, mentre nella struttura asimmetrica “A” ciò è stato fatto solo sui lati sud e ovest. In Figura I.8 sono mostrati gli andamenti di temperatura sul Silicio e sulla resina per entrambi i campioni calcolati sui soliti assi orizzontali e verticali e parametrizzati per differenti valori di hv, a partire dal caso adiabatico (hv=0 W/°Cm2_{) fino a valori di}

convezione particolarmente elevati (hv=10000 W/°Cm2_{) quali si possono}

ottenere in condizioni di ghiaccio in fusione. Come già accennato in precedenza, la temperatura ambiente è stata impostata a 0°C, cioè a un valore inferiore rispetto a quella del pozzo termico (20°C), al fine di evidenziare gli effetti della convezione. Sempre nella Figura I.8, i grafici di sinistra sono relativi alle cross-section orizzontali dei campioni, mentre quelli di destra sono relativi alle cross-section verticali. I valori di hv utilizzati nelle simulazioni sono riportati nei grafici come parametro. Sia per “D” che per “A” è possibile vedere come gli effetti della convezione sulle temperature superiori dello strato di Silicio siano relativamente modesti e comincino a diventare apprezzabili (con il fattore di scala utilizzato) solamente a partire da valori di hv particolarmente grandi. Questo accade perché, con bassi valori del coefficiente convettivo, il percorso di smaltimento del calore per via conduttiva che passa per gli strati inferiori e termina nel pozzo termico ideale è più vantaggioso, anche in presenza dello strato di Allumina a bassa conducibiltà, e pertanto una buona parte della potenza elettrica dissipata viene

Figura I.7: campione D: dall'alto: mappa termica della superficie del Silicio; distribuzione di temperatura sulle superfici superiori di tutti i livelli lungo gli assi di simmetria x e

smaltita attraverso questa via. In ogni caso, confrontando l'andamento delle temperature sul Silicio per i due campioni al crescere di hv, gli effetti delle differenti condizioni al contorno sono distintamente discernibili: mentre nella struttura “D” si osserva un abbassamento regolare ed uniforme delle temperature dovuto ad un accoppiamento più stretto con la temperatura ambiente, nella struttura “A” l'abbassamento è accompagnato da una distorsione progressiva del profilo di temperatura, poiché la convezione è applicata soltanto alle facce laterali esposte a sud e a ovest.

Figura I.8: grafici di temperatura per i campioni D ed A sulla sommità del Silicio (prima e seconda riga) e della plastica (terza e quarta riga) per diversi valori del coefficiente di scambio termico convettivo (hv) applicato a tutte le facce esposte (campione D) o solamente alle facce sud ed ovest (campione A). I grafici di sinistra sono calcolati lungo le

I grafici della terza e quarta riga di Figura I.8 sono relativi alle superfici della resina epossidica dei due campioni. Qui i valori di hv utilizzati come parametro sono di un ordine di grandezza inferiore rispetto a quelli del Silicio; gli effetti della convezione sono molto più accentuati per queste superfici, anche in presenza di scambi convettivi assai modesti. Questo è dovuto al piccolo valore di conducibilità termica associato alla resina epossidica, che isola piuttosto efficacemente lo strato di Silicio rispetto a quanto avviene al di sopra di esso. Inoltre, i profili di temperatura del campione “A” lungo l'asse X scelto, col loro andamento decrescente all'aumentare di hv, rappresentano efficacemente l'effetto dello smaltimento del calore qualora esso avvenga selettivamente su alcune superfici.

I.3.1.3 Confronto con la tecnica agli elementi finiti

Al fine di stabilire un riferimento con cui valutare le prestazioni del simulatore DJOSER, gli assetti termici dei modelli “A” e “D” sono stati calcolati utilizzando un diffuso software commerciale basato sugli elementi finiti, il COMSOL Multiphisics (già Femlab). Il fine di questa operazione consiste nel confronto di due differenti metodologie di simulazione, entrambe affette da limiti di accuratezza nelle soluzioni fornite, una delle quali però già affermata e generalmente ritenuta utile ed affidabile, piuttosto che ottenere una validazione di tipo assoluto del software DJOSER. In particolare, i risultati forniti dallo DJOSER non possono essere considerati esenti da errore per le seguenti motivazioni:

• le mesh 2D uniformi per la definizione delle temperature e dei flussi alle interfacce hanno densità finita

• l'utilizzo di un metodo di quadratura rettangolare per risolvere gli integrali bidimensionali delle funzioni utilizzate in luogo del più accurato, ma maggiormente complesso, metodo di Cavalieri-Simpson;

• il troncamento della serie di Green a un numero finito di autovalori x e y. D'altra parte, anche l'accuratezza dei sistemi agli elementi finiti dipende da diversi fattori, quali ad esempio:

• la densità delle mesh; • la loro forma;

• la presenza di singolarità;

• la presenza di strati molto sottili alternati a strati spessi; • la scelta del metodo numerico di risoluzione;

Lo DJOSER, per le sue caratteristiche costitutive, è esente dalle ultime tre limitazioni relative agli elementi finiti; in particolare, come già accennato, può gestire senza particolari problemi la presenza di strati molto sottili (saldature, incollaggi, ecc. . .) alternati a strati spessi senza incorrere in instabilità computazionali e difficoltà nella definizione delle mesh.

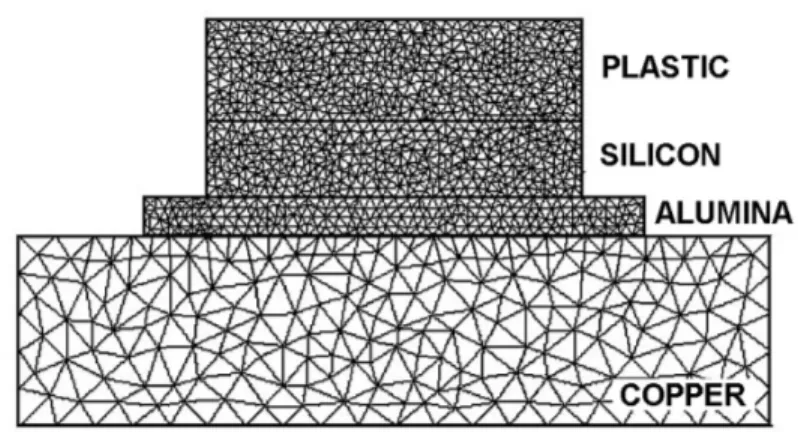
Per i nostri fini, il confronto fra le due metodologie risolutive è stato effettuato impiegando una distribuzione tridimensionale estremamente fitta (con più di 300000 elementi) e non uniforme delle mesh per il programma FEM, con una densità accresciuta in corrispondenza delle interfacce, in modo tale da ottenere un riferimento il più possibile accurato. Giusto per dare un'idea, la superficie superiore dello strato di Silicio è stata modellizzata con un numero di nodi nove volte maggiore rispetto a quello impiegato dallo DJOSER. In Figura I.9 è mostrata la sezione laterale del campione “D” con le relative mesh generate automaticamente dal programma .

Il confronto fra le temperature ottenute coi due diversi metodi è mostrato in Figura I.10 per la struttura simmetrica “D” e in Figura I.11 per la struttura asimmetrica “A”, in termini di errore relativo percentuale dello DJOSER rispetto al FEM, riferito alla temperatura massima calcolata dal FEM sull'intera mappa termica; il profilo è stato campionato lungo l'usuale asse X di riferimento indicato Figura I.5, in condizioni dapprima adiabatiche e poi per due differenti valori del coefficiente di scambio convettivo. Come si può vedere, l'errore percentuale relativo massimo

Figura I.9: vista laterale delle mesh tridimensionali generate dal simulatore agli elementi finiti per il campione D.

si attesta entro l'1% per tutte le condizioni al contorno scelte, il che costituisce appunto l'obiettivo di accuratezza desiderato per il nostro risolutore termico analitico.

È interessante notare come la forma dei profili dell'errore ottenuto per lo strato di Silicio, ovverosia una serie di picchi positivi e negativi accoppiati, sia rappresentativa della strategia di risoluzione adottata dallo DJOSER: in effetti Figura I.10: errore percentuale relativo

delle simulazioni DJOSER rispetto alle FEM lungo l'asse X per il campione D, per la sommità del Silicio (sopra) e della plastica (sotto), per condizioni adiabatiche e due diversi valori del coefficiente di

scambio convettivo hv.

Figura I.11: errore percentuale relativo delle simulazioni DJOSER rispetto alle FEM lungo l'asse X per il campione A, per la sommità del Silicio (sopra) e della plastica (sotto), per condizioni adiabatiche e due diversi valori del coefficiente di

l'errore si rivela minore nei pressi dei massimi e dei minimi locali della temperatura, in corrispondenza dei centri delle isole di dissipazione di potenza o dei centri delle zone di separazione dove non viene dissipata potenza, mentre è massimo in presenza di gradienti improvvisi di temperatura, sia positivi che negativi. Questo comportamento è causato sia dalla densità finita delle celle bidimensionali alle interfacce, sia dal massimo numero di autovalori x e y al quale sono troncate le sommatorie nelle funzioni di Green I.13 (già riportato nella Tabella I.2). Questi valori sono stati scelti operando un compromesso fra accuratezza della risoluzione e tempo impiegato per il calcolo, come dimostrato in [13]. Risultati migliori con una minore percentuale di errore possono essere ottenuti incrementando la densità delle celle, specialmente negli strati in cui la potenza viene dissipata, e incrementando il numero di autovalori della sommatoria; in entrambi i casi, il tempo che lo DJOSER impiega a risolvere il sistema può crescere con legge quadratica.

Per i risultati delle presenti simulazioni sono stati necessari 1050 secondi di computazione su di un laptop dalla prestazioni non particolarmente performanti (1,6Ghz di clock e 512MB di memoria ram), l'80% dei quali dedicato al calcolo dei coefficienti della matrice, che per una data struttura può essere salvata e riutilizzata successivamente per differenti entità e dislocazioni della potenza dissipata, le informazioni relative alla quale sono invece contenute nel termine noto utilizzato per la risoluzione del sistema. Anche tenendo in considerazione questo fatto, tuttavia, l'implementazione software del sistema DJOSER può considerarsi tutt'altro che ottimizzata sotto il profilo della velocità; successivi miglioramenti sotto questo punto di vista, ottenuti ad esempio con l'adozione del linguaggio C al posto del Matlab per le routine di calcolo più onerose, fanno sperare in un ulteriore aumento della appetibilità di questo sistema rispetto ai tradizionali metodi agli elementi finiti.

I.3.2 Validazione sperimentale

I.3.2.1 Analisi termica di strutture multistrato reali

L'accuratezza dello DJOSER è stata testata anche dal punto di vista sperimentale. L'obiettivo di questo tipo di ricerca è di verificare il grado di concordanza dei dati sperimentali rispetto a quelli calcolati, non solo per quanto concerne le temperature minime e massime, ma anche per i profili relativi alla distribuzione spaziale del campo di temperatura.

Le prove sono state effettuate su alcune strutture piramidali appositamente costruite assemblando diversi strati di differenti materiali e dimensioni. Lo strato superiore, di cui in Figura I.12 riportiamo una foto, consiste in una resistenza rettangolare a film spesso di 18x13 mm2 _{di valore pari a 1,1Ω, capace di sopportare una}

dissipazione Joule massima di 40W, deposta per evaporazione su di un substrato di allumina. A causa del tipo di misure effettuato, e al solo scopo di rivelare la temperatura della sorgente di calore, la potenza generata in questa resistenza sulla sommità della struttura rappresenta l'unica sorgente di dissipazione termica.

Figura I.12: fotografia dello strato superiore dei campioni utilizzati nelle

prove.

Figura I.13: a sinistra: fotografia del campione A1; a destra: fotografia del

campione A2.

Figura I.14: sezione e pianta dei campioni A1 e B1 utilizzati per le termografie. Il resistore di potenza è rappresentato dal

Tutti i diversi strati di differenti spessori e materiali, isolanti e conduttori, di conducibilità termica nota ottenuta dai data sheet del produttore, sono stati incollati con una pasta speciale ad alta conducibilità specifica per il packaging dei sistemi elettronici.

In Figura I.14 sono mostrate la pianta e la sezione dei due campioni utilizzati nelle misure, di cui possiamo vedere una foto in Figura I.13. In Tabella I.3 è riportata la sequenza degli strati e la potenza dissipata nella resistenza.

Campione A1 Campione B1

Strato Materiale Lx*Ly

mm2 _mmLz Materiale Lx*Ly_mm2 _mmLz 1 Al2O3 23x23 1.0 Al2O3 23x23 1.0 2 Al 24x24 6.4 Vetro 55x26 1.0 3 Vetro 42x26 1.0 Al 57x58 6.0 4 Cu 42x38 3.6 5 Al 58x56 6.4 Potenza 18.73 W 10.86 W

Tabella I.3: caratteristiche dei campioni A1 e B1 utilizzati nei test.

Il coefficiente di emissività di tutte le superfici è stato reso uniforme e pari a 0,97 tramite una procedura di annerimento con nerofumo. Per questo tipo di misure, la conoscenza dei valori di resistenza termica di contatto fra strati, dovuta alla pasta incollante fra strato e strato e alla pasta termica utilizzata per alloggiare il campione sulla base termostatata di rame, è di importanza fondamentale per il confronto coi dati provenienti dalle simulazioni. Questi parametri, la cui predizione a livello teorico è possibile solo con un elevato grado di approssimazione, dipendono da numerosi fattori, quali:

• la conducibilità dello strato di pasta e il suo spessore; • il grado di ruvidezza delle due superfici poste a contatto; • i materiali da cui sono composte le superfici messe a contatto;

• la pressione che due strati adiacenti esercitano l'uno nei confronti dell'altro; ma possono tuttavia essere ben rappresentati da un valore espresso per unità di superficie (mm2_{/°C W) considerato uniforme sull'intera area di contatto; questo è}

giustificato dal fatto che lo spessore dello strato di interfaccia fra strati è all'incirca due ordini di grandezza inferiore rispetto allo spessore tipico degli strati massivi e

tre ordini di grandezza inferiore rispetto alle dimensioni laterali degli strati stessi. Per rimediare all'elevato grado di incertezza con cui può essere noto a priori il valore di resistenza termica di contatto, sono state condotte delle misure preliminari per ottenerlo sperimentalmente, sia per quanto riguarda la pasta incollante fra strati, sia per quanto riguarda la pasta posta fra il campione e il pozzo termico di riferimento. Per fare ciò, in parallelo alle strutture piramidali sono state costruite delle strutture di tipo parallelepipedo, composte dagli stessi strati delle altre, di area pari al primo strato di allumina contenente la resistenza a film spesso. In questi campioni, per ragioni costruttive, il flusso termico conduttivo è praticamente uniforme e parallelo all'asse verticale; pertanto la resistenza termica di contatto può essere calcolata facilmente a partire da misurazione standard di resistenza termica, sottraendo ai valori complessivi ottenuti i contributi di ciascuno strato massivo, che in questo caso può essere calcolato facilmente con una formula analoga a quella impiegata per ricavare il valore di resistenze elettriche parallelepipede:

R

_TH

=

1



⋅

L

A

(I.25)

dove σ è la conducibilità nota del singolo strato, L il suo spessore ed A la sua area. La base di queste strutture è stata posta in contatto con un pozzo termico alla temperatura di 20°C, mentre la temperatura ambiente misurata è risultata pari a 24°C. I valori di resistenza termica totale sono stati ottenuti dal rapporto fra la differenza tra la temperatura media misurata sullo strato dissipativo superficiale e la temperatura del pozzo, e la potenza dissipata; le misure sono state condotte in tre modi:

• con l'impiego di una termocoppia;

• con l'impiego di un termometro a infrarossi;

• sfruttando la dipendenza dalla temperatura del valore di resistenza a film spesso ottenuto con una calibrazione preliminare.

I valori medii di resistenza termica di contatto dovuta al processo di attach fra strato e strato e alla pasta termica fra campione e substrato sono risultati essere pari a 105 e 123 mm2_{°C/W, rispettivamente, con una dipendenza dal tipo di materiali}

posti a contatto del tutto trascurabile. Questi dati sono stati introdotti nello DJOSER come parametri costitutivi dei modelli da simulare per il raffronto.

Per i campioni piramidali, necessitando di una misura non di temperatura media ma di temperatura puntuale sull'intera superficie dello strato superiore di Allumina, è stata impiegata una videocamera a infrarossi AVIO Neo Thermo TVS-600, che può

visualizzare a display un'immagine a falsi colori dell'oggetto in esame e inviare i dati quantitativi di temperatura sulla sua griglia di misura ad un PC. La scala di temperatura delle termo-immagini è stata accuratamente calibrata sulla superficie di un sistema termostatico capace di una accuratezza di 0,1°C. Le misure sono state effettuate con due differenti gradi di risoluzione: la prima con una lente a 35mm a bassa risoluzione, la seconda con una lente da 70mm a risoluzione più elevata ma di campo più ristretto. Il coefficiente di convezione fra i campioni e l'aria è stato stimato nel range 4-8 W/°C, poiché i test sono stati condotti in condizioni di aria ferma. Anche per queste prove, la temperatura del termostato è stata posta a 20°C, mentre la temperatura ambiente misurata si è rivelata essere di circa 23-24°C. La Figura I.15 mostra il confronto fra i dati ottenuti sperimentalmente e i risultati delle simulazioni ottenuti dallo DJOSER utilizzando i materiali, le caratteristiche degli strati interfacciali e le condizioni al contorno menzionate in precedenza (convezione superiore e laterale in aria ferma; scambio termico conduttivo fra base del campione e termostato ideale attraverso una resistenza termica di contatto).

Le immagini superiori sono relative al campione A1, quelle inferiori al campione B1. Si possono vedere:

Figura I.15: sinistra: termografia dei dispositivi reali; centro: mappa termica simulata; destra: confronto fra profili di temperatura reali e