I Capitolo 1: Considerazioni teoriche sul metodo TRAIT

Capitolo 1: Considerazioni teoriche sul metodo

TRAIT

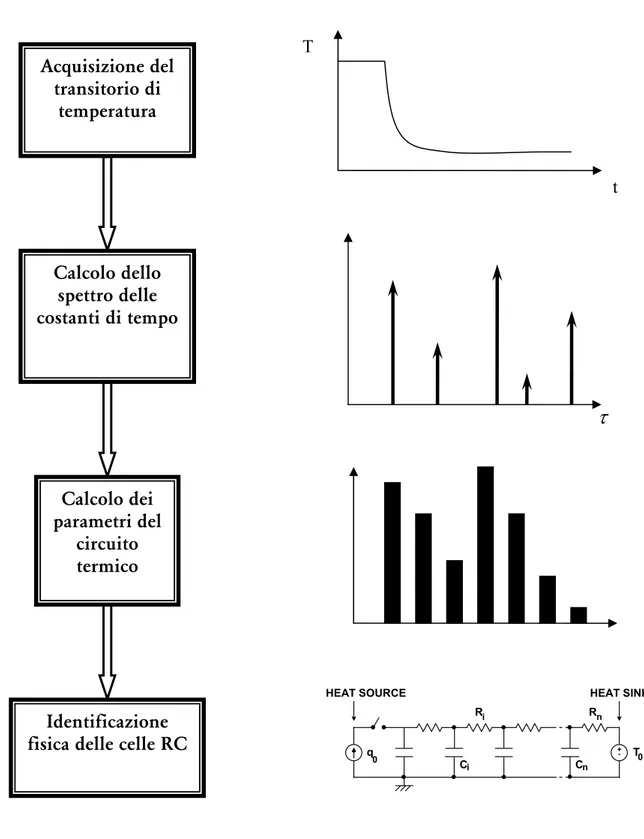
l metodo TRAIT (Thermal Analisys by Induced Transient) permette di caratterizzare spazialmente le proprietà termiche di conduzione del calore dei sistemi fisici, e fornisce un modello in base al quale poter prevedere la variazione di temperatura a cui sono soggetti in risposta a un qualsiasi regime di dissipazione di potenza (continua, sinusoidale, impulsiva, eccetera). Questi risultati vengono ottenuti grazie all’analisi dell’andamento temporale della temperatura dei sistemi stessi, sotto particolari condizioni e in risposta ad opportune sollecitazioni. Il metodo, dopo aver elaborato i dati in ingresso, fornisce i parametri di un circuito elettrico, costituito da resistenze e capacità, le cui equazioni descrittive sono analoghe a quelle del sistema termico. Può essere suddiviso in quattro fasi fondamentali (figura 1.1):

1. acquisizione del transitorio di temperatura della sorgente di calore in seguito alla commutazione a gradino della potenza dissipata;

2. estrazione numerica delle costanti di tempo dalla somma di esponenziali costituenti il transitorio;

3. calcolo dei valori delle resistenze e capacità del circuito equivalente;

4. eventualmente, possono essere adottati varie tecniche volte ad identificare l’estensione delle porzioni del sistema termico corrispondenti alle singole celle RC.

In questo capitolo esporremo i fondamenti teorici matematici e fisici su cui si basano questi passaggi. Malgrado siano stati già trattati in precedenti lavori di tesi incentrati su tematiche analoghe alla nostra ([1] e [2]), noi torneremo sull’argomento con maggiore ricchezza di dettagli, secondo l’approccio proposto in [3] e [4], da un lato con lo scopo di comprendere appieno l’implementazione software del metodo, esposta nel capitolo 2, dall’altro per spiegare le ragioni sottese a molte scelte pratiche di progetto nella

realizzazione dell’apparato di misura, che saranno spiegate dettagliatamente nel capitolo 4, e infine per una corretta interpretazione dei risultati finali degli esperimenti, presentati nel capitolo 5.

Acquisizione del transitorio di temperatura Calcolo dello spettro delle costanti di tempo Calcolo dei parametri del circuito termico Identificazione fisica delle celle RC

t T

τ

+ -q 0 R_i T₀ Ci R_n Cn

HEAT SOURCE HEAT SINK

1.1: Equazioni della conduzione del calore

L’evoluzione della temperatura in un solido con proprietà termiche assegnate, se consideriamo il solo meccanismo della conduzione del calore, è determinata dall’equazione di Fourier e dalle condizioni iniziali e al contorno. L’equazione di Fourier per un mezzo isotropo e omogeneo può essere scritta come:

2

T

T

t

α

∂

_{= ⋅∇}

∂

(1.1)

dove T è la temperatura, t il tempo, e α la diffusività termica così definita:

p

k

c

α

ρ

=

⋅

(1.2)

con k conduttività termica, c capacità specifica a pressione costante, e _p ρ densità del materiale. Il problema differenziale risultante dall’unione dell’equazione di Fourier con le condizioni iniziali e al contorno può essere risolto analiticamente solo per corpi di forma molto semplice e composti da pochi strati di materiali differenti [5]. Questa è la ragione principale del largo successo ottenuto dai software per lo studio e la caratterizzazione termica, sia in regime continuo sia in regime transitorio, basati sull’implementazione dei metodi numerici approssimati alle differenze finite o agli elementi finiti, che consentono l’analisi di sistemi con geometrie e composizioni di qualsivoglia complessità.

In ambito elettronico, che è quello di nostro principale interesse, le strutture formate dal chip, dal package, dal substrato ed eventualmente dal dissipatore possono essere considerate tridimensionali dal punto di vista termico. Questo vuol dire che il campo di temperatura e le linee di flusso, che partono dalle regioni dove la potenza viene dissipata per dirigersi verso il pozzo termico (che possiamo con buona approssimazione

identificare al dissipatore), dipendono da tutte e tre le variabili spaziali. In un sistema monodimensionale, che non esiste nella pratica ma può costituire una modellizzazione fedele di alcune situazioni reali, queste grandezze dipendono da una coordinata spaziale soltanto: è evidente che la trattazione ne risulterà notevolmente semplificata. In seguito mostreremo i limiti e gli inconvenienti derivanti dall’assimilazione delle strutture che esamineremo a sistemi monodimensionali, purtuttavia necessaria per poter applicare gli algoritmi di analisi.

Da un punto di vista generale, le pubblicazioni che trattano di questo argomento sono assai numerose; per avere una conferma, indiretta ma molto significativa, al nostro approccio e ai nostri risultati, ci riferiremo al lavoro di Kadambi e Abuaf [6] sul comportamento termico dei package dei chip di potenza. Questi autori hanno analizzato i fenomeni di conduzione stazionari e transitori di solidi omogenei (cilindri e parallelepipedi) con condizioni al contorno conduttive sulla faccia inferiore, pareti adiabatiche e con la sorgente di calore sulla faccia superiore.

Particolarmente significativo il caso in cui il package è modellizzato da un cilindro omogeneo con raggio di base r , altezza d, coefficiente di convezione h, sorgente di _b

calore circolare di raggio r_c ≺ e flusso uniforme q (figura 1.2). Assumendo che la r_b

potenza dissipata si annulli istantaneamente, il transitorio di temperatura a cui è sottoposta la sommità della struttura è esprimibile come:

2 2 2 0 2 2 2 2 1 2 1 2 2 2 1 ₀

[

cos(

) (

)sin(

)]

( )

2

[

(

) (1

)

(

)

(

) 2

(

)

(

)

n m v t c n n n n b n n t m c n c b m _{n m m b m b}

qd r

v d

v d

hd k

v d

T t

T

e

k r

v d

v d

hd k

hd k

J

r

v

e

r r

v

r J

r

α λ α

_λ

λ

λ

λ

∞ − = − ∞ =

+

= + ⋅

⋅ ⋅

⋅

⋅

⋅

+

⋅ +

⎡

_{+ ⋅}

⋅

_⋅

⎤

⎢

₊

_⋅

⎥

⎣

⎦

∑

∑

(1.3)

dove T(t) è la temperatura della sorgente di calore, T la temperatura del pozzo termico, ₀

m

λ sono gli autovalori del problema differenziale costituito dalle seguenti equazioni trascendentali:

tan(

)

n n

v d

v d

=

hd k

(1.4) 1

(

m b

) 0

J

λ

r

=

(1.5)

Le radici di queste due equazioni sono due sequenze infinite crescenti di valori reali e maggiori di zero, di indice n e m. E’ opportuno osservare che questo insieme di autovalori è composto da elementi infiniti e numerabili, a causa delle dimensioni finite del corpo; solo nel caso di un corpo spazialmente illimitato, cioè col pozzo termico posto a distanza infinita dalla sorgente di calore, avrebbero la potenza del continuo [5].

sorgente di calore pareti adiabatiche Coefficiente di convezione h b r c

r

d flusso di calore uniforme q

Figura 1.2: modellizzazione di un package di potenza secondo la trattazione di Kadambi e Abuaf [5]

La 1.3 sotto particolari condizioni può ridursi a una singola serie di funzioni esponenziali: è il caso di un sistema termicamente monodimensionale. Questo accade quando r_c → , cioè quando la superficie di dissipazione coincide con l’intera faccia r_b

superiore del solido: dalla 1.5 si può ricavare che tutti i termini della serie contenuta fra parentesi quadre nell’espressione 1.3 sono trascurabili per qualunque valore di t.

Abbiamo dunque 0 0 1

( )

_i

exp(

_i

)

i

T t

T

q

∞

A

t

τ

=

= + ⋅

_∑

⋅

−

(1.6) (con

τ

_i+1

≺

τ

_i

∀

i

)

dove q è la potenza termica totale dissipata, le ₀ τ_i sono le costanti di tempo relative a ciascun esponenziale nella prima sommatoria in 1.3, e le A sono le ampiezze associate. _i

Questo risultato può essere ottenuto come caso particolare di un altro approccio, descritto in [5] e [7], in cui però l’ipotesi di monodimensionalità viene fatta dall’inizio, per semplificare il problema e ottenere, così, soluzioni analitiche per sistemi non omogenei. La temperatura in ogni punto di un solido generico multistrato, spazialmente limitato, con la sorgente di calore situata ad una generica ascissa, è data da

0 0 1

( , )

_i

( ) exp(

_i

)

i

T x t

T

q

∞

A x

t

τ

=

= + ⋅

∑

⋅

−

(1.7) (con

τ

_i+1

≺

τ

_i

∀

i

)

Le costanti di tempo τ_i, relative a ciascun esponenziale nella sommatoria, regolano il comportamento termico dinamico di qualsiasi punto del sistema, e non dipendono dall’ascissa x, mentre al contrario le ampiezze associate A sono funzione di x, ovvero _i

variano al variare del punto di cui ci interessa conoscere la temperatura. Possiamo ottenere una sorta di “rappresentazione spettrale” delle proprietà termiche di qualsiasi

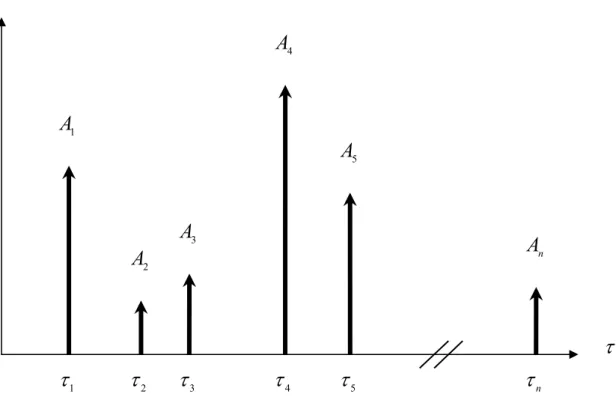
punto xdel nostro corpo, semplicemente andando a costruire un grafico dove associamo alle ascisse le costanti di tempo τ_i, e alle ordinate corrispondenti un segmento proporzionale all’ampiezza A x (figura 1.3). _i

( )

Sotto le ipotesi considerate otterremo uno spettro di valori τ_i e A x composto da un _i

( )

numero di linee infinito e numerabile, a causa della limitatezza del corpo, i cui valori sono determinati dalle condizioni al contorno e dalle proprietà termiche dell’intero sistema, che può essere composto da uno o più strati eterogenei. Se facessimo tendere le dimensioni del corpo all’infinito, assisteremmo a una sorta di “passaggio al continuo” di questo spettro: ritorneremo su questa osservazione nei capitoli successivi.

A partire dalle considerazioni appena esposte, possiamo ora spiegare come il metodo TRAIT riesca a estrarre informazioni sulle proprietà termiche “locali” dei sistemi basandosi sulla osservazione del comportamento termico dinamico degli stessi.

1

τ

τ

₂

τ

₃

τ

₄

τ

₅

τ

_n 1

A

2

A

3

A

4

A

5

A

n

A

τ

1.2: Approssimazione del transitorio termico

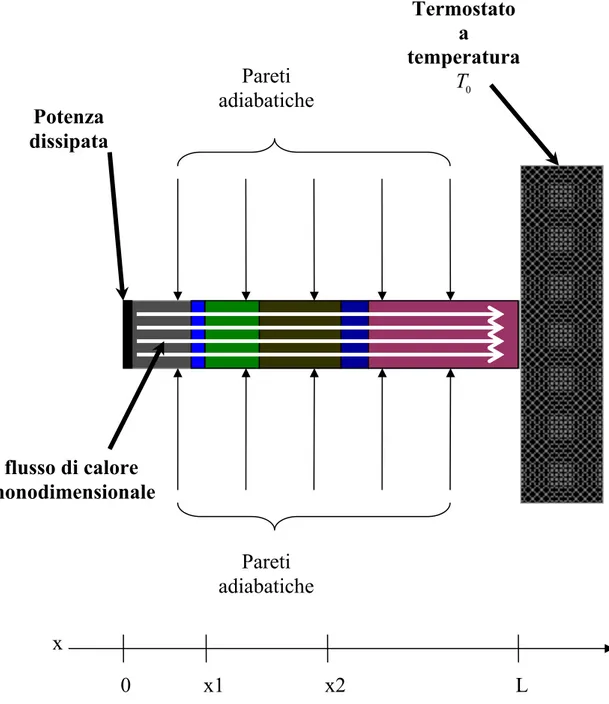
La figura 1.4 mostra lo schema di un solido termicamente monodimensionale, composto da strati di materiali diversi, con una sola sorgente di calore, collocata in x=0, e un pozzo termico o termostato a temperatura costante in x=L. I contributi convettivi e di irraggiamento sono considerati nulli, perciò le pareti laterali sono adiabatiche: sono due condizioni necessarie per trattare il problema come 1-D.

Termostato

a

temperatura

0

T

Potenza

dissipata

x

0

L

Pareti

adiabatiche

Pareti

adiabatiche

flusso di calore

monodimensionale

Figura 1.4: schema di solido multistrato termicamente monodimensionale

In figura 1.5 sono riportati i transitori di temperatura che si ottengono in diverse ascisse del corpo facendo andare bruscamente a zero la potenza dissipata; li abbiamo ottenuti col metodo di simulazione analitica per sistemi monodimensionali multistrato descritto in [7]. Queste curve sono esprimibili matematicamente tramite l’espressione 1.7, e sono tutte caratterizzate dallo stesso insieme di costanti di tempoτ_i, mentre le ampiezze corrispondentiA variano al variare della ascissa considerata. In particolare, i _i

coefficienti A sono tutti positivi solo nel caso in cui x=0, ossia se osserviamo la _i

temperatura nel punto esatto in cui è collocata la sorgente di calore: si noti che la curva ha la concavità sempre rivolta verso l’alto. La somma di tutti gli (0)A_i converge a un valore finito, che coincide con differenza di temperatura fra 0 e L prima della commutazione diviso la potenza dissipata q : ₀

0 1 ₀

(

0,

0)

(0)

i i

T x

t

T

A

q

∞ =

=

=

−

=

∑

(1.8)

Figura 1.5: andamento della temperatura in varie ascisse del corpo di figura 4 a seguito della commutazione della potenza dissipata

che non è altro che l’espressione della resistenza termica totale del corpo fra 0 e L, secondo la definizione: 0 1 0

(

0,

0)

(0)

TH i i

T x

t

T

R

A

q

∞ =

=

=

−

=

=

∑

(1.9)

dove

T

₀ è la temperatura del pozzo termico.

Notiamo che al crescere dell’indice i le costanti di tempo τ_i divengono sempre più piccole, dunque abbiamo a che fare con esponenziali sempre più veloci; e anche le ampiezze relative (0)A_i decrescono rapidamente, a causa della convergenza della sommatoria, che è composta di soli termini positivi, a un valore finito. Pertanto, poiché la funzione T x( =0, )t − è composta da un numero infinito di esponenziali T₀

decrescenti, grazie alla affermazione precedente possiamo pensare di approssimarla prendendo in considerazione solamente i primi n termini della sommatoria:

0 0 1

(

0, )

n _i

(0)exp(

_i

)

i

T x

t

T

q

A

t

τ

=

=

≈ + ⋅

∑

−

(1.10)

L’errore commesso decresce al crescere di n ed è esprimibile in funzione del tempo come: 0 0

( )

_i

(0)exp(

_i

)

_i

(0)

i n i n

Err t

q

∞

A

t

τ

q

∞

A

= =

= ⋅

∑

−

≤ ⋅

∑

(1.11)

Figura 1.6: rete di Foster

1.3: Circuito Termico Equivalente

Un generico sistema in cui operino i fenomeni fisici di conduzione e convezione, ma non di irraggiamento, può essere schematizzato dal punto di vista termico con un circuito passivo a parametri concentrati, composto di resistenze e capacità, dove le tensioni corrispondano alle temperature e le correnti ai flussi di calore. Un termostato (detto anche pozzo termico) è un corpo la cui capacità termica, definita come δQ dT, può essere considerata infinita agli effetti pratici, come l’ambiente esterno o, nel nostro caso, lo scambiatore di calore. Pertanto la sua temperatura non varia (dT =0) qualunque sia il flusso di calore a cui è sottoposto (δQ≠ ) ; nel circuito equivalente 0 sarà quindi rappresentato da un elemento la cui tensione rimane costante (dV =0) qualunque sia la corrente che lo attraversa (dI ≠0) , ossia da un generatore ideale di tensione. Una potenza iniettata in una certa parte del sistema sarà rappresentata da un generatore ideale di corrente che insiste sul nodo circuitale corrispondente.

Stabilite queste analogie, è importante considerare che l’andamento della temperatura nell’ascissa in cui è situata la sorgente di potenza, approssimato come somma di n esponenziali decrescenti (1.10), coincide con la risposta in tensione di un circuito termico, composto di n gruppi RC, in seguito alla commutazione a gradino della corrente q . Si dimostra facilmente che le costanti di tempo ₀ τ_i coincidono con i poli di questo circuito. Le configurazioni circuitali che godono di questa proprietà sono in

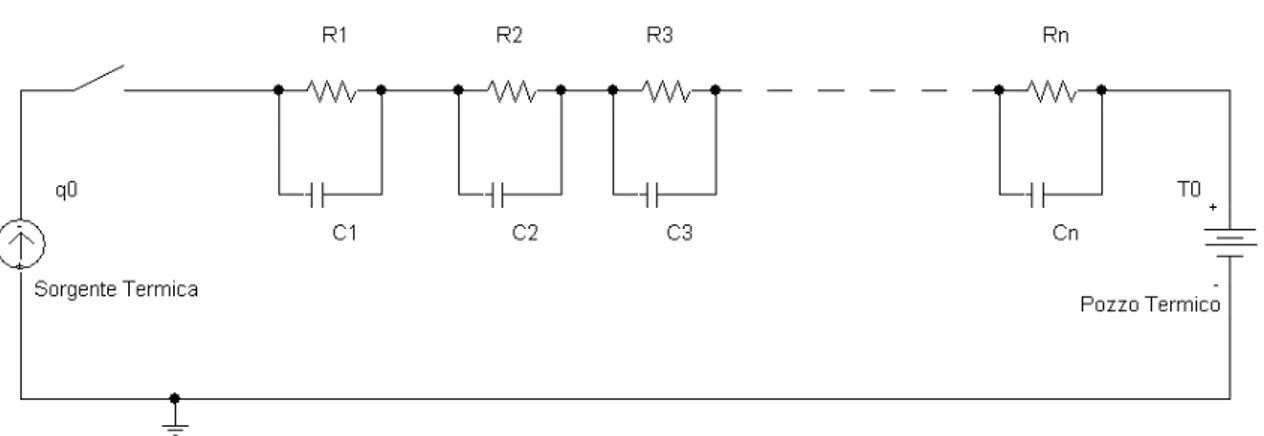
Figura 1.7: rete di Cauer

realtà due; ci riferiremo ad esse come “rete di Foster” (figura 1.6) e “rete di Cauer” (figura 1.7) secondo la nomenclatura adottata da Szekely in [8] e [9].Il generatore di corrente q corrisponde alla potenza dissipata dalla sorgente, il generatore di tensione ₀

0

T al pozzo termico. L’interruttore fa commutare a gradino la potenza, mentre la massa

rappresenta la temperatura ambiente.

Entrambi i circuiti modellizzano un solido termicamente monodirezionale, ovvero con una sola sorgente di calore e un solo pozzo termico: l’energia fluisce dall’uno all’altro lungo un’unica direzione sia in regime statico che in regime dinamico. Questa condizione è soddisfatta nei sistemi elettronici reali se le “perdite” del flusso energetico dalle pareti e dalla sommità del dispositivo verso l’ambiente, dovute a fenomeni di convezione e irraggiamento, sono trascurabili rispetto al flusso termico monodimensionale dovuto ai fenomeni di conduzione.

Sulla base di queste considerazioni, se il transitorio di raffreddamento della temperatura viene approssimato dalla somma di n esponenziali decrescenti (1.10), allora il sistema può essere rappresentato da un circuito formato da n gruppi di resistenze e condensatori. Nella rete di Foster, ciascuna costante di tempo è calcolabile semplicemente col metodo della resistenza vista e pari al prodotto della R e della C di ciascuna cella; nella rete di Cauer le cose sono più complesse perché il valore di ogni costante di tempo dipende da tutte le resistenze e da tutte le capacità del circuito. Da questo punto di vista l’utilizzo di una delle due potrebbe apparire indifferente; ma la rete di Foster, utilizzata da alcuni autori ([12] e [13]), presenta il grande svantaggio di rivelarsi fisicamente sensata solo se la adottiamo per interpretare il comportamento dinamico della sommità della struttura

(corrispondente all’ascissa x=0 di figura 1.4). Questo perché in un circuito elettrico la corrente di spostamento che in regime transitorio attraversa le armature di un condensatore provoca l’accumularsi simmetrico di cariche negative e positive sulle sue facce. Ora, in un circuito termico la quantità di carica accumulata corrisponde all’ energia accumulata da un corpo: Q dt dE• = , ma se nell’analogia considerassimo entrambe le armature del condensatore, poiché la variazione di carica è simmetrica e quindi globalmente nulla, troveremmo che anche l’energia accumulata dE è pari a zero. E’ necessario quindi considerare quello che avviene su una armatura soltanto, pena la perdita del significato fisico (e dell’utilità) di questa rappresentazione.

Questo implica che l’analogia termico-elettrica è valida interamente solo se tutte le capacità del circuito hanno una armatura a massa, come nella rete di Cauer. Nella rete di Foster, in regime transitorio, ciascun nodo mediano è attraversato dalla corrente che proviene dalla resistenza che lo precede e dall’armatura destra del condensatore che si trova in parallelo alla resistenza stessa; quest’ultima componente non ha significato dal punto di vista termico, e pertanto non è possibile mettere in corrispondenza i nodi interni al circuito con i punti interni al sistema. La rete di Cauer non presenta questo inconveniente: possiamo ritenerla topologicamente adatta a rappresentare il comportamento termico del sistema nella sua interezza. Se il corpo può essere considerato monodimensionale, può essere idealmente diviso in n settori i cui volumi siano non sovrapposti, secondo procedure che accenneremo in seguito, seguendo una procedura di discretizzazione spaziale non dissimile da quella impiegata dai metodi che implementano le differenze finite. A ciascuna porzione, che generalmente NON coinciderà a partire dalla sorgente di calore fino al pozzo termico, sarà associato uno degli n gruppi RC della rete.

A causa della particolare struttura del circuito, composto da una serie di celle RC passa-basso, la rete di Cauer genera una serie di poli reali, distinti e negativi, tanti quante sono le celle. Ricordiamo ancora che non esiste alcuna corrispondenza fra i poli/costanti di tempo τ_i e i parametri elettrici delle singole celle, perché ogni costante di tempo dipende da tutte le resistenze e le capacità presenti, e ogni fattore preesponenziale (le ampiezze Ai) è funzione di tutte le resistenze. Perciò non è affatto corretto stabilire una

corrispondenza diretta tra una certa τ_idella curva e le proprietà termiche di una certa porzione del sistema ([10][11][12]) Invece, possiamo assegnare un significato fisico ben determinato a ciascun gruppo RC: esso rappresenterà il contributo all’impedenza termica totale di una certa parte dell’intero sistema, che d’ora innanzi chiameremo “dominio termico”. Più in particolare, il valore di ogni singola Ri è determinato dalla conduttività termica e dall’estensione della porzione di solido in questione, mentre le Ci sono correlate alla massa e al calore specifico della porzione stessa.

Adesso descriveremo la procedura che abbiamo utilizzato per il calcolo dei parametri della rete di Cauer.

1.4: Calcolo dei parametri del circuito

Una volta che il transitorio di temperatura sia stata acquisito sperimentalmente in forma numerica (tramite convertitore A/D o scheda di acquisizione), la curva deve essere analizzata tramite un metodo di fitting, che riesca a scomporla nella somma degli esponenziali di cui è costituita. Supponiamo di riuscire a ottenere una lista di n costanti di tempo e degli n fattori preesponenziali associati [4].

Grazie alla conoscenza della resistenza termica totale R , facilmente ricavabile dalla _TH

1.9, e dei parametri A e _i τ_i, possiamo esprimere il transitorio di raffreddamento della temperatura nel dominio della trasformata di Laplace:

0 0 0 1 1

(

0, )

(

0)

(0)exp(

)

( )

1

n n Laplace _{i i} i i c i i _i

T x

t

T

A x

q

A

t

q

T s

s

τ

τ

τ

= =

=

− ≈

= ⋅

⋅

−

⋅

= ∆

+

∑

∑

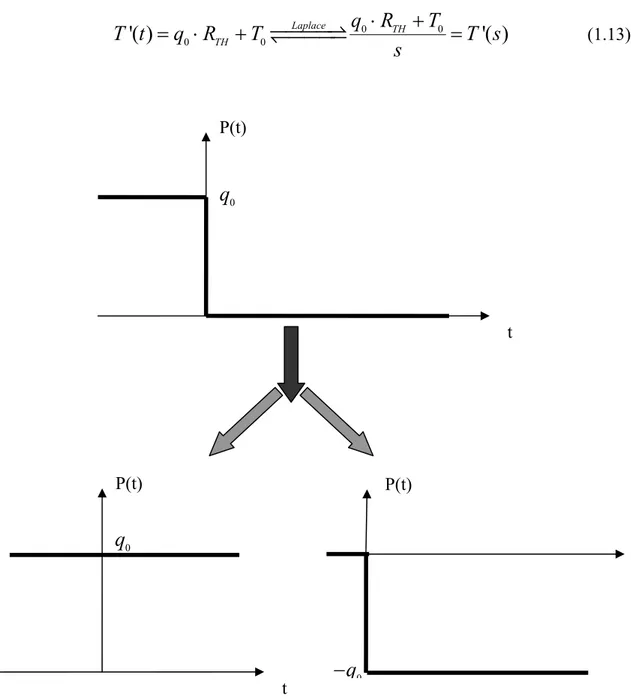
(1.12)

Questo transitorio è esprimibile anche in altra maniera. Scomponiamo l’andamento della potenza dissipata nella somma di una componente costante q e di un gradino ₀

negativo − ⋅q u t₀ ( )(figura 1.8), e procediamo calcolando T x( =0, )t − col metodo T₀

della sovrapposizione degli effetti nel circuito termico equivalente di figura 1.7. Dapprima facciamo agire il generatore T e la parte costante ₀ q della potenza. Poiché ₀

siamo in regime stazionario, dalla 1.9 si trova facilmente che

0 0 0 0

'( )

Laplace _TH

'( )

TH

q R

T

T t

q R

T

T s

s

⋅

+

= ⋅

+

=

(1.13) P(t) t 0

q

P(t) 0

q

−

P(t) t 0

q

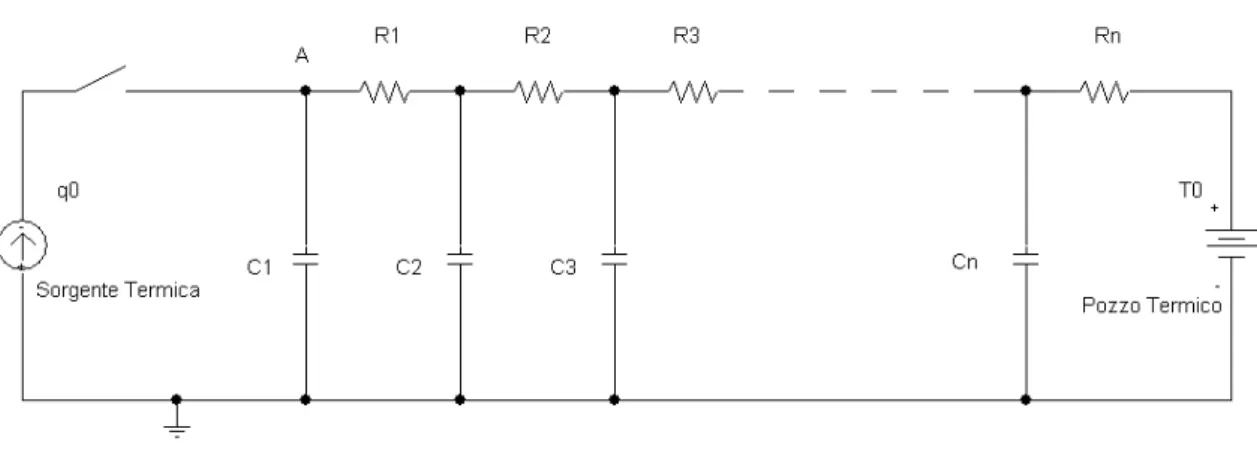
Adesso applichiamo la sollecitazione − ⋅q u t₀ ( ), e osserviamo che il circuito è ora quello di figura 1.9; chiamiamo Z(s) l’impedenza vista dal generatore di corrente. Tramite la definizione stessa di impedenza termica ( ) ( )

( )

T s Z s

P s

= ricaviamo facilmente la risposta del circuito al gradino negativo, la cui trasformata è q0

s − : 0

''( )

( )

( )

( )

q

T s

Z s P s

Z s

s

=

⋅

= −

⋅

(1.14)

Sommando la 1.13 alla 1.14 e togliendo il termine T s otteniamo l’andamento della ₀

temperatura cercato:

[

]

0 0

( )

( )

Laplace

(

0, )

c TH

q

T s

R

Z s

T x

t

T

s

∆

=

−

=

−

(1.15)

A questo punto dall’eguaglianza fra la 1.12 e la 1.15 possiamo esprimere la Z(s) come

1

(0)

( )

1

n i i TH i _i

A

Z s

R

s

s

τ

τ

=

⋅

=

−

+

∑

(1.16) 0 ( ) q u t − ⋅ ( ) Z s

Il calcolo di tutte le R e le C di cui è composta quest’impedenza, nell’ordine fisicamente corretto, a partire dalla sorgente di calore fino al pozzo termico, può essere svolto a partire dall’espressione della Z(s) appena trovata e applicando il metodo di Cauer per la sintesi delle reti passive. Questa tecnica consiste in 2xn divisioni polinomiali fra

impedenze e ammettenze secondo questo algoritmo:

1,...,

i

=

n

1

( )

( )

Z s

=

Z s

1

1

( )

( )

sC

i

Y s

i

Z s

=

+

1

1

( )

( )

i i i

R

Z

s

Y s

=

+

+ 1

( ) 0

n

Z

₊

s

≡

0

q

1

( )

Z s

Y s

₁

( )

Z s

₂

( )

Figura 1.10: illustrazione circuitale dell’algoritmo di calcolo dei parametri della rete di Cauer

Così, abbiamo infine dimostrato che dalla conoscenza del transitorio di raffreddamento della sorgente di potenza possiamo ricavare tutti i parametri di un circuito termico equivalente, e basandoci su questo caratterizzare completamente il comportamento del sistema. Grazie a programmi di simulazione circuitale come SPICE, infatti, possiamo simulare la risposta in temperatura del corpo a sollecitazioni di potenza comunque complesse (sinusoidali, a onda quadra, impulsive, eccetera). Inoltre, possiamo ricavare la temperatura stazionaria lungo i nodi del circuito, per una potenza statica dissipata q , ₀

dal momento che tutte le R sono note; ci basterà applicare questa relazione: _i

0 0 n i j j i

T T

q

R

=

= + ⋅

∑

(1.17)

dove T è la temperatura dell’i-esimo nodo della rete di Cauer. _i

1.5: Identificazione dei contributi

Come abbiamo già avuto modo di accennare, ogni cella RC rappresenta il contributo termico conduttivo di un settore fisico di cui è composto il sistema. Per un numero di celle dato e pari a n, la suddivisione in “dominii termici” e lo spettro delle costanti di

tempo dipendono criticamente dalle struttura del sistema: modificare, anche localmente, le proprietà del solido, implica un cambiamento in tutte le righe dello spettro, e di conseguenza, delle dimensioni (e della forma, se la conduzione non è rigorosamente monodimensionale – vedi oltre) di ciascuna porzione fisica a cui sono associate le celle . In generale, non vi è alcuna corrispondenza fra i dominii termici e gli strati di diversi materiali che compongono il solido: il contributo termico di ogni strato può essere incluso in uno o più dominii, o, viceversa, ciascun dominio può rappresentare il contributo di uno o più strati. Il metodo TRAIT non consente, per ora, di identificare spazialmente i confini dei dominii, anche se l’implementazione di questa funzionalità è prevista in futuro; pertanto dovremo appoggiarci a tecniche “esterne”.

Una di queste consiste nell’esame comparato tra i risultati di una simulazione (analitica o agli elementi finiti), che fornisca il campo di temperatura stazionaria lungo il corpo, e le temperature stazionarie ai nodi ricavate col metodo TRAIT (applicato al corpo stesso) grazie alla relazione 1.17 [14]. In condizioni statiche, questa relazione ci fornisce le temperature T delle superfici isoterme che coincidono coi bordi dei settori. _i

Nell’esempio di figura 11 le superfici di separazione sono piane, parallele fra loro e perpendicolari all’asse del solido, perché il flusso di calore è rigorosamente monodimensionale. Ogni singola ascissa x , che identifica il confine fra il dominio i-_i

esimo e l’i+1esimo, è ricavabile impostando una eguaglianza fra la temperatura del nodo i ricavata dall’analisi TRAIT, e il campo di temperature in funzione di x fornitoci

dal programma di simulazione: il valore che soddisfa l’equazione è quello cercato. Questa procedura è esemplificata visivamente in figura 1.11: il grafico (b) riporta le temperature ai nodi, mentre il grafico (a), che ha la stessa scala verticale di (b), riporta la distribuzione simulata di temperatura lungo l’asse del corpo.

Un altro metodo di identificazione, di carattere più sperimentale, consiste nell’applicare l’analisi TRAIT a due campioni, originariamente identici, che differiscano per un singolo difetto localizzato (non importa se incidentale o provocato ad arte) [15], [16]. Il campione standard deve essere esente da difetti nelle interfacce e negli strati massivi,

poiché deve fungere da riferimento; possiamo sincerarcene con varie tecniche, fra cui l’analisi al SEM, ai raggi X, eccetera. Confrontando i risultati delle analisi, possiamo ottenere informazioni sull’incremento di resistenza termica causato dal difetto, e stabilire quale a quale cella RC corrisponde lo strato interessato.

1.6: Considerazioni sulla tridimensionalità del flusso

In questo paragrafo ci proponiamo di fornire una giustificazione intuitiva ad un fenomeno che condiziona i risultati della maggior parte delle misure TRAIT su strutture reali. Questo fenomeno consiste nell’allargamento dell’area interessata al flusso di calore a mano a mano che ci allontaniamo dalla sorgente di potenza per avvicinarci al pozzo termico, e non è previsto a rigore dalle ipotesi alla base del metodo, perché non è riducibile ad una trattazione monodimensionale, bensì interessa le tre coordinate spaziali.

Come esempio prenderemo un solido omogeneo, schematizzato in figura 1.12, con una sorgente di calore q in x=0, un pozzo termico in x=L, linee di flusso sempre

perpendicolari alle sezioni del solido ortogonali a x, conducibilità termica σ , e area A la cui superficie è dipendente solamente dalla variabile x. Questo sistema presenta una sezione di flusso coincidente con l’area, che è sempre crescente nel verso delle x positive; pertanto, pur essendo monodimensionale, ci permette di descrivere la situazione che si presenta nella pratica, quando la sezione del flusso aumenta a causa dell’allargamento o “spreading” tridimensionale del flusso di calore.

Possiamo scrivere l’incremento di resistenza termica dR relativa alla generica ascissa x del sistema come:

( )

dx

_{( )}

dR x

A x

σ

=

⋅

(1.18)

( )

p

( )

dC x

=

c A x dx

⋅

(1.19)

Si nota immediatamente che al crescere dell’area A il valore di

dR

diminuisce, mentre il valore di

dC

aumenta. Adesso immaginiamo di suddividere la struttura in otto dominii termici, di ampiezza non troppo dissimile fra loro, i cui confini sono segnati in blu sull’asse delle ascisse. Per trovare la resistenza e la capacità termica di ciascun dominio dobbiamo integrare le espressioni 1.18 e 1.19 sulla porzione di solido corrispondente. Il risultato di questa operazione è mostrato in figura 1.13.

Figura 1.12 A(0), σ

q

x=0 x=L A(x), σ A(L), σ x

Figura 1.13

Procedendo da sinistra (sorgente di calore) a destra (pozzo termico) gli istogrammi delle resistenze hanno valori sempre crescenti, gli istogrammi delle capacità sempre decrescenti, nonostante il solido abbia una conducibilità termica omogenea in ogni sua parte. Questo dipende dal progressivo allargarsi dell’area interessata al flusso termico, come possiamo capire considerando i valori di resistenza e capacità elementari 1.18 e 1.19.

Nella misure reali avremo a che fare con strutture più complesse di quella ora esaminata, formate da molti strati di materiali differenti; tuttavia questo fenomeno si manifesterà con regolarità, e dovremo sempre tenerne conto nella interpretazione dei risultati.

Figura 1.14

1.7: Considerazioni sulla ridistribuzione dei dominii

La cosiddetta “failure analysis”, o analisi delle difettosità, è una applicazione del metodo TRAIT di grande utilità e interesse: consiste nel confronto fra i valori di

Strato di materiale aggiuntivo

a)

b)

TH

R

resistenza e capacità termica fra due strutture, una delle quali funge da riferimento rispetto all’altra, che presenta un valore di resistenza termica globale molto più grande, e di cui ci proponiamo di investigare le cause per mezzo dell’analisi spaziale. Spesso però un confronto diretto, dominio per dominio, dei valori di resistenza e capacità fra le due strutture, può rivelarsi fuorviante a causa della differente distribuzione dei confini dei dominii fra l’una e l’altra, dovuto proprio alla presenza del difetto che ci proponevamo di individuare.

Per avere una idea di cosa può succedere in questi casi e cautelarci da una interpretazione erronea dei relativi risultati, consideriamo cosa comporta, a livello della distribuzione spaziale dei dominii, l’introduzione di uno strato altamente resistivo in una struttura monodimensionale simulata, situazione questa molto frequente nella pratica, come avremo modo di vedere nel capitolo 5.

In figura 1.14a è mostrata la struttura di riferimento, composta da quattro strati di materiali differenti, mentre in figura 1.14b possiamo vedere la struttura difettosa, caratterizzata rispetto all’altra dalla presenza di uno strato aggiuntivo altamente resistivo; per entrambe è riportata la suddivisione in dominii termici e l’ampiezza degli istogrammi resistivi relativi a ciascun dominio. Notiamo come nei due casi si abbiano delle suddivisioni parecchio differenti; in particolare nel secondo si è verificato una sorta di “collasso” dei confini dei dominii in corrispondenza dello strato aggiuntivo. Così, se andiamo a confrontare gli istogrammi resistivi ottenuti (figura 1.15), non dobbiamo dimenticare che, se i primi quattro si riferiscono a dominii spazialmente coincidenti, i quattro restanti si riferiscono a porzioni di solido differenti per dimensioni e per materiali compresi.

La figura 1.16, a titolo solamente esemplificativo, mostra cosa accadrebbe, invece, se le ampiezze dei dominii fossero invarianti al variare della struttura: ogni coppia di istogrammi si riferirebbe a una stessa sezione di solido, e ci sarebbe lecito confrontarle senza adottare particolari accorgimenti; accorgimenti a cui invece saremo tenuti a ricorrere quando, nel capitolo 5, esamineremo delle strutture reali che manifestano un comportamento analogo a quello del sistema simulato di figura 1.14.

Figura 1.15: confronto fra istogrammi resistivi per ciascuno degli otto dominii dei sistemi di figura 1.14a (giallo) e 1.14b (rosso)

Figura 1.16: confronto fra istogrammi resistivi nel caso, che non si verifica mai nella pratica, di suddivisione coincidente dei dominii nella struttura di riferimento e nella struttura difettosa

TH

R

Il contributo della

difettosità va ad alterare tutti questi istogrammi

Nel caso di invarianza dei dominii le differenze sono localizzate in questi due