4. IMPLEMENTAZIONE DEL MODELLO DI EFFLUSSO ATTRAVERSO UN CONDOTTO ASSIALE-RADIALE

90

4.

IMPLEMENTAZIONE DEL MODELLO DI EFFLUSSO

ATTRAVERSO UN CONDOTTO ASSIALE-RADIALE

L’analisi teorica realizzata al Cap.3 ha mostrato i limiti di una trattazione volta a descrivere in maniera generale il flusso che si sviluppa all’interno di un Bernoulli gripper. Si è infatti osservato come il porsi in una condizione più generica implichi una maggior conoscenza degli stati del sistema. Non solo, ma le equazioni così ottenute, di formulazione piuttosto complessa e quindi poco pratica da utilizzare, possono fornire solo una stima del comportamento del fluido in ampie zone del meato, come quelle di transizione o quelle soggette alla vena contracta, all’interno delle quali non è possibile, con le nozioni in possesso fino ad oggi, compiere una trattazione rigorosa.

Un’analisi accurata del problema attraverso un modello ai volumi finiti si richiede quindi, per consentire di valutare i complessi fenomeni fluidodinamici che avvengono all’interno delle porzioni del condotto mal rappresentate dai modelli teorici e per fornire una misura quantitativa dei loro limiti, oltre cui la formulazione teorica acquista nuovamente piena validità.

Un modello ai volumi finiti che ben rappresenti la trasformazione reale subita dall’aria compressa in evoluzione all’interno del Bernoulli gripper costituisce, infatti, un potente aiuto nell’approfondimento del fenomeno, consentendo sia di ottenere stime più accurate dello stato del fluido sia di comprendere quali miglioramenti apportare al sistema per incrementarne l’efficienza. Attualmente sono disponibili diversi codici che permettono di risolvere numericamente problemi di CFD (Computational Fluid Dynamics). Per i nostri scopi è stato utilizzato il codice Ansys Fluent®.

Le fasi attraverso cui è passata la risoluzione numerica del problema dell’efflusso di aria compressa attraverso il meato radiale del Bernoulli gripper sono riportate in Fig. 4.1.

91

4.1. Modello fisico

In generale, il passaggio più critico della risoluzione numerica di un problema di efflusso è sicuramente l’individuazione del modello fisico più appropriato.

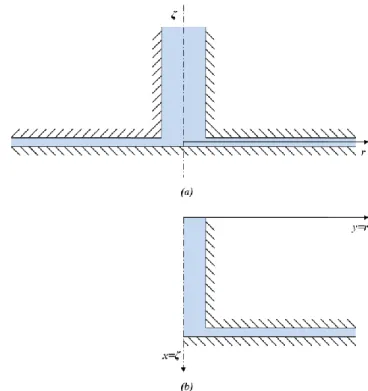
Nel caso specifico in esame, con riferimento alla Fig. 4.2, una simmetria di tipo assiale rispetto all’asse del condotto verticale si presenta sia nella geometria che nelle condizioni al contorno per cui, con riferimento alla prassi, secondo cui il migliore tra i modelli che forniscono risultati adeguati è quello più semplice possibile, è stato scelto di sfruttare la assialsimmetria del problema reale per realizzarne un modello bidimensionale.

In particolare, il modello geometrico deve presentare l’asse di simmetria ζ coincidente con l’asse x del sistema di riferimento del programma.

Figura 4.2 Modello geometrico del Bernoulli gripper (b) realizzato sfruttando la simmetria assiale rispetto a ζ del condotto reale secondo un sistema di riferimento cilindrico (ζ, r, θ), rappresentato in (a) tramite una sua sezione lungo il piano (ζ, r).

4.2. Modello matematico

Per qualsiasi tipo di efflusso, Ansys Fluent® risolve le equazioni di conservazione della portata massica e della quantità di moto. Vengono aggiunte poi, per flussi che ipotizzano la comprimibilità, un’equazione di conservazione dell’energia, mentre per flussi in regime turbolento le equazioni di trasporto.

92 4.2.1 Relazioni costitutive

Il problema viene approssimato come stazionario. Si ipotizza inoltre che il fluido evolvente nel condotto si trovi solo nella fase aeriforme e sia assimilabile ad un gas caloricamente perfetto, per cui i calori specifici sono costanti come la conducibilità termica e la viscosità dinamica μ, il cui valore è stato imposto pari a 1,79·10-5

[Pa·s].

Per quanto concerne infine il regime di efflusso, si è ipotizzato che esso sia turbolento pienamente sviluppato e gli effetti della viscosità molecolare siano trascurabili.

4.2.2 Equazioni di bilancio

Nel caso in esame si è scelto di utilizzare un approccio basato sulla pressione

(pressure-based), sviluppato originariamente per flussi incomprimibili e mediamente comprimibili a

medio-bassa velocità, tramite il quale il campo di velocità è ottenuto dalle equazioni di conservazione della quantità di moto (come, del resto, avviene anche con l’approccio

density-based basato sulla densità) mentre il campo di pressione è calcolato da un’equazione della

pressione ottenuta da quelle di continuità e della quantità di moto. Per un modello 2D assialsimettrico si hanno le seguenti equazioni:

equazione di conservazione della massa o equazione di continuità, (continuità

equation) risulta data da

dove x è la coordinata assiale, r la coordinata radiale e, corrispondentemente, ux ed ur

saranno le componenti assiale e radiale della velocità.

equazione di conservazione della quantità di moto (momentum equation) lungo l’asse

x ed il raggio r sono date dalle

93 4.2.3 Modello di turbolenza

Nelle ipotesi sopra fatte riguardo al flusso turbolento, può essere adottato come modello per la turbolenza il (κ-ε), il quale consente di determinare l’energia cinetica turbolenta κ ed il suo coefficiente di diffusività ε da due equazioni di trasporto separate:

dove Gk rappresenta la generazione di energia turbolenta dovuta ai gradienti di velocità, YM

rappresenta il contributo fluttuante della dilatazione, C1ε, C2ε e C3ε sono costanti. σk e σε sono i

numeri di Prandtl turbolenti per k ed ε, rispettivamente, mentre Sk ed Sε sono termini di

sorgente.

Dalle (4.3’) e (4.3’’) viene calcolata la viscosità turbolenta di Boussinesq, μt

dove Cμ è una costante.

Mentre la (4.3’) è solo di origine teorica, i valori di C1ε, C2ε e C3ε e dei numeri di Prandtl σk e

σε nella (4.3’’) sono determinati sperimentalmente, per cui il modello (κ-ε) è semi-empirico.

Tale modello, che proprio in virtù della formulazione sopra riportata risulta essere semplice e di rapida soluzione, garantisce robustezza ed ragionevole accuratezza per un’ampia gamma di flussi turbolenti.

Poiché con la simulazione si vuole indagare a fondo il comportamento del fluido, considerando che il flusso, sviluppandosi tra due pareti molto vicine tra loro, sarà influenzato dalle stesse, si sceglie di impiegare un metodo di modellazione in prossimità della parete detto

Enhanced Wall Treatment. Tale metodo combina un approccio a due strati con funzioni di

parete di tipo avanzato per essere in grado di valutare bene il sottostrato laminare. Per fare ciò, la discretizzazione geometrica, detta mesh, in prossimità delle pareti interessate dovrà essere particolarmente fine, per cui tipicamente si devono ottenere valori del parametro di riferimento y+ ≈ 1, contro valori generalmente accettati per esso negli altri casi compresi nell’intervallo [ 30 ; 200 ].

Tale parametro valuta in maniera adimensionale la distanza del flusso dalla parete e risulta espresso dalla

94 è la velocità d’attrito alla parete più vicina, definita come radice quadrata del

rapporto tra la tensione di taglio alla parete e la densità del fluido;

y è la distanza del centro della cella rispetto a tale parete; ν è la viscosità cinematica locale del fluido.

L’approccio a due strati consiste nel dividere il dominio prossimo alla parete in due regioni: una dominata dai fenomeni viscosi e l’altra da flusso turbolento pienamente sviluppato. La separazione tra queste due regioni è definita dal numero di Reynolds Rey, definito come

dove y è la distanza tra il centro della cella e la parete, misurata normalmente ad essa. In base a tale valore si distinguono quindi le due zone sopra definite:

Rey > Rey*, Rey*=200 nella regione turbolenta pienamente sviluppata per la quale

viene impiegato il modello (κ-ε);

Rey < Rey*, Rey*=200 nella regione viscosa.

4.2.4 Condizioni al contorno

La corretta definizione delle condizioni appropriate alla natura fisica del problema è fondamentale per poter ottenere un modello matematico ben posto.

Il problema in questione presenta tre tipi di contorni del dominio di calcolo, di seguito riportati in riferimento alla Fig. 4.3.

1) Contorni con flusso entrante di fluido (inflow boundaries):

in corrispondenza dell’ingresso si impone un flusso di massa entrante in direzione normale alla sezione del contorno. Riguardo alla turbolenza, viene imposta l’intensità (5%) in tale sezione ed il diametro idraulico Dh nella stessa.

2) Contorni senza passaggio di fluido:

le pareti del condotto verticale (condotto) e del meato (piattello, jet e piastra) vengono ipotizzate senza scorrimento (no slip boundaries).

3) Contorni con flusso uscente di fluido (outflow boundaries):

nella sezione di uscita si impone una pressione pari al valore atmosferico misurato a valle, con temperatura pari a 300K.

95

Figura 4.3 Definizione dei contorni del dominio geometrico del problema.

4.3. Modello numerico

Il modello matematico sopra creato viene successivamente calcolato a livello locale in maniera globale per un numero elevato, ma comunque finito, di volumi costituenti la geometria.

4.3.1 Discretizzazione spaziale

Il dominio geometrico continuo del problema viene suddiviso, tramite la mesh, in un numero finito di sottodomini detti volumi.

In generale, tale mesh può essere di due tipi: strutturata o non strutturata. Per il problema in esame, considerando che il suo dominio geometrico è piuttosto semplice, possiamo adottare il primo tipo il quale, definendo univocamente le celle tramite una terna di indici (i, j, k), semplifica notevolmente la programmazione.

Le esigenze dettate dal modello di turbolenza definito al Pgrf. 4.3.3, ed in particolare il metodo Enhanced wall treatment, richiedono che le celle in prossimità delle pareti di interesse (condotto, piattello, jet e piastra in Fig. 4.3) siano di dimensioni molto piccole. Per questo, l’esigenza di contenere il più possibile il numero globale dei volumi rende necessario creare una griglia non uniforme ma variabile secondo un opportuno rapporto. Tale variabilità viene sfruttata anche nella definizione del numero dei volumi lungo il raggio r del meato e l’asse x del condotto, ottenendo così una mesh del tipo riportato in Fig. 4.4, molto fitta in corrispondenza della parete jet per poi allungarsi nella direzione del raggio r e dell’asse x muovendosi, rispettivamente, lungo il meato e lungo il condotto.

96

Figura 4.4 Variabilità della dimensione delle celle all’interno del condotto. Graficamente, avvicinandosi alle pareti si osserva un elevato infittimento della mesh fino a perdere la distinzione tra volumi contigui. Si nota anche un ulteriore infittimento realizzato in corrispondenza dello spigolo formato dal condotto con il piattello.

Una volta creata la mesh, nei punti nodali vengono definite le proprietà del fluido mentre le variabili delle equazioni di bilancio sono date sui bordi dei volumi di controllo: tale configurazione, detta staggered, presenta i vantaggi di eliminare alcuni problemi di convergenza e di oscillazione nei campi di pressione e velocità e di localizzare le componenti delle velocità e delle variabili scalari rispettivamente sulle facce dei volumi di controllo e sui punti nodali.

4.3.2 Discretizzazione delle equazioni

Una volta realizzato il meshing, le equazioni discretizzate sono ottenute integrando le espressioni differenziali riportate ai Pgrff. 4.3.2 e 4.3.3 sopra ciascun elemento.

4.3.3 Risoluzione delle equazioni discretizzate

Le equazioni ottenute in forma discretizzata sono nominalmente equazioni lineari. In realtà, però, i coefficienti della generica equazione dipendono solitamente da una variabile dipendente relativa a quella particolare equazione ed, alcune volte, anche da altre variabili dipendenti relative alle restanti equazioni.

Per tenere conto di questi legami esistenti tra le varie equazioni e delle non linearità sono quindi richieste soluzioni ripetute delle forme nominalmente lineari. In particolare, utilizzando un metodo di soluzione sequenziale, ciascuna equazione viene trattata come se in essa fosse presente una sola variabile incognita e quindi risolta, a causa dell’elevata dimensione del sistema, mediante un metodo iterativo al fine di ottenere la sua convergenza

97 (iterazioni interne). Una volta risolte sequenzialmente le varie equazioni di bilancio, è poi necessario ripetere il ciclo per ottenere la convergenza contemporanea di tutte le equazioni (iterazioni esterne). Uno schema che illustra tale processo iterativo è riportato in Fig. 4.4.

Figura 4.4 Schema a blocchi del metodo di soluzione sequenziale delle equazioni di bilancio [fonte 14].

4.3.4 Controllo del parametro y+

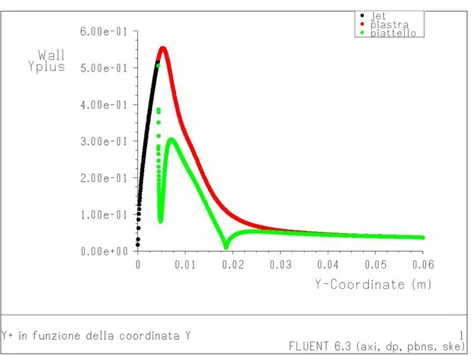
Al Pgrf. 4.3.3 si è visto come la bontà del modello realizzato per il calcolo del flusso in prossimità delle pareti sia strettamente dipendente dal valore assunto dal parametro y+. Poiché esso dipende, oltre che dalla dimensione delle celle alla parete, anche dal campo di velocità, dalla viscosità μ e dalla densità ρ locali del fluido, la sua valutazione si rende possibile solo una volta raggiunta la convergenza della soluzione. Per questo, i modelli finali per ciascuna configurazione sono stati ottenuti solo dopo una serie di soluzioni di prova, susseguitesi affinando e modificando il meshing a livello locale. Essendo di particolare interesse per questo studio la zona dell’efflusso radiale all’interno del Bernoulli gripper, con particolare attenzione alla zona in corrispondenza del cambio di direzione del fluido, il parametro y+ è stato valutato solo in corrispondenza delle pareti di piattello, jet e piastra, per le quali esso è risultato sempre cautelativamente dell’ordine di 10-1

98 L’andamento tipicamente ottenuto è riportato a titolo esemplificativo in Fig. 4.5, che mette in evidenza, come del resto era prevedibile, la maggior criticità della modellazione per piccoli valori del raggio nel meato.

Figura 4.5 Andamento del parametro y+ in funzione del raggio(rappresentato in Fluent dalla coordinata y), per le pareti piattello(in verde), jet(in nero) e piastra(in rosso).