5. Analisi della stabilità di una rampa in massi. 5.1 Meccanismi di rottura di una rampa in pietrame.

5. Analisi della stabilità di una rampa in massi.

5.1 Meccanismi di rottura di una rampa in pietrame.

I meccanismi di distruzione di una rampa in massi possono distinguersi principalmente in: 1 erosione diretta dei massi ad opera della corrente;

2 eccessiva erosione del materiale alla base della rampa e successivo scivolamento dei massi nello scavo che si viene a formare;

3 erosione del materiale tra i massi e conseguente scivolamento di questi ultimi su uno strato sottostante

Il primo meccanismo di crisi avviene quando la corrente è sufficientemente forte da strappare i massi dalla formazione della rampa favorendo anche altri meccanismi di rottura Infatti dopo lo scalzamento di alcuni massi si può avere la scopertura del sottofondo, per cui può sopraggiungere anche la distruzione per erosione dello strato sottostante.

Inoltre è possibile che, dopo le prime partenze dei massi, gli altri si trovino più esposti alla corrente e scivolino via più facilmente.

Figura 5.1 : rottura per erosione diretta.

L’asportazione del materiale d’alveo situato sotto la rampa può avvenire quando i massi vengono posati in opera non molto vicini tra loro . Questo tipo di crisi sopraggiunge anche se i massi rimangono tutti al loro posto e può essere influenzata dalla dimensione dei massi, dalla granulometria del materiale di fondo, dalla compattezza del rivestimento.

La distruzione dovuta all’eccessiva erosione del materiale a valle del piede della rampa è uno dei meccanismi più pericolosi ed è causato proprio dall’insufficiente protezione del materiale d’alveo. In questo caso la struttura si indebolisce inizialmente in basso per scalzamento della prima fila di massi e successivamente anche nella parte alta fino ad arrivare ad una distruzione totale.

Figura 5.2 : rottura per scalzamento al piede.

Nel presente studio si sono analizzate principalmente le rotture per erosione diretta dei massi e per formazione eccessiva di una buca di scavo alla base della rampa.

Questi meccanismi di rottura sono stati studiati per varie tipologie di rampe a posa irregolare dei massi:

• a piede fisso • a piede allungato • a piede libero o mobile

Figura 5.3. : rampa a piede fisso.

Figura 5.4 :rampa a piede mobile.

La tipologia a piede fisso si differenzia da quella a piede mobile per la presenza di un supporto rigido posto alla base il quale impedisce alla prima fila di massi di scivolare nella buca di scavo che si viene a formare in quella zona. Di conseguenza per questa tipologia di rampa la rottura non potrà mai avvenire per eccessivo scavo alla base .

Questo meccanismo di rottura viene evitato anche costruendo la rampa prolungando il piede ad una profondità maggiore rispetto allo scavo massimo che si può riscontrare nel bacino di dissipazione.

Invece, a differenza delle altre, la tipologia a piede mobile, per scavi alla base di una cerca entità può andare incontro ad una instabilità che, inizialmente, interessa la parte media inferiore e successivamente, anche quella superiore della rampa.

5.2 Modalità svolgimento delle prove e descrizione del

fenomeno di crisi

Come già detto precedentemente,le esperienze sono state condotte su vari modelli di rampe • a piede fisso

• a piede allungato • a piede libero o mobile

Ciascuna tipologia di rampa è stata realizzata con materiali di granulometrie diverse, le cui caratteristiche principali sono specificati in tabella:

Materiali utilizzati per realizzare la rampa

Materiali D50 [mm] D90 [mm] D16 [mm] D84 [mm] σ [−] γs[kg/m3] Mr1 14,2 16,4 12,7 15,66 1,11 2533 Mr2 17,5 19 16.3 18.9 1,08 2428 Mr3 22,9 24,7 21 24,1 1,07 2450 Mr4 26 28,7 25,1 27,6 1,05 2528 Mr5 35,9 42,1 34,4 41 1,09 2620 Mr6 40,7 45,1 36,3 44,2 1,1 2546 MATERIALI D[mm] γs[kg/m3] massi di piombo 8,2 10780

Inoltre sono riportate nella tabella seguente le caratteristiche dei materiali utilizzate per il fondo mobile del canale posto a valle della rampa:

Materiali utilizzati per il fondo mobile del canale.

Materiali d50 [mm] d90 [mm] d16 [mm] d84 [mm] σ [−] γs[kg/m3i]

mc1 1,36 1,87 0,93 1,79 1,39 2561

mc2 1,95 2,72 1,35 5,55 1,39 2658

mc3 3,8 5,72 2,97 5,55 1,37 2241

mc4 6,56 8,49 5,63 8,11 1,2 2632

Figura 5.7 : materiali utilizzati per il canale.

M

r

,D

i

,σ,γ

s

m

c

,d

i

,σ,γ

s

Figura 5.8: simbologia adottata.

Sono state analizzate diverse pendenze [1/3,1/4,1/6,1/8 ] e per studiare il fenomeno di rottura sono state prese misure di portata, di altezze liquide e di andamento altimetrico del modello, in corrispondenza di vari livelli di crisi .

Per una comprensione del risultato sperimentale si ritiene opportuno riportare una descrizione dettagliata dell’evoluzione del fenomeno di rottura della rampa a cui si è assistito durante l’esecuzione dei test sperimentali.

Inizialmente in ogni prova è stata fatta defluire nel canale una portata minima. Il deflusso è caratterizzato prevalentemente da un moto di filtrazione tra i massi e il fondo; il tirante.

idrico sulla rampa è praticamente nullo. Successivamente la portata è stata incrementata gradualmente, mediante step successivi di circa 0.2-0.3 l/sec.

Ad ogni incremento di portata è seguito un tempo di attesa prefissato ∆t, alla fine del quale è stata misurata la portata attraverso l’idrometro posto a valle nel canale 1 D e quindi mediante la rispettiva scala di deflusso, oppure nel canale 1 C, grazie a un misuratore di portata. L’intervallo di tempo ∆t tra step successivi di portata è stato scelto in cinque minuti tenendo conto del tempo necessario per la stabilizzazione del flusso sulla rampa ed analizzando i risultati di alcuni test specifici che sono stati svolti.

Infatti in queste particolari prove , per una stessa tipologia di rampa ( rampa a piede fisso)e materiale (massi con D50=22.9 mm ), sono stati presi in considerazione diversi tempi di

attesa ( 1minuti,5 minuti,10 minuti,20 minuti e 30 minuti ) e sono state misurate le portate di crisi della stessa.

Queste portate sono riportate adimensionalmente, rapportandole nei diagrammi seguenti a quelle corrispondenti a un ∆t pari a 1min [q0] , e correlate con i rispettivi tempi di attesa .

0,5 0,6 0,7 0,8 0,9 1 1,1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 ∆T [minuti] qi.mis/qi.0.mis[−] dt=1min dt=5min dt=10 min dt=20 min dt=30 min

Figura 5.9: portate specifiche adimensionalizzate a inizio movimento in funzione del tempo di attesa tra ogni incremento di portata per rampa a piede fisso.

0,5 0,6 0,7 0,8 0,9 1 1,1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 ∆T [minuti] ql.mis/ql.0.mis[−] dt=1min dt=5min dt=10 min dt=20 min dt=30 min

Figura 5.10: portate specifiche adimensionalizzate a rottura locale in funzione del tempo di attesa tra ogni incremento di portata per rampa a piede fisso.

0,5 0,6 0,7 0,8 0,9 1 1,1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 ∆T [minuti] qg.mis/qg.0.mis[ −] dt=1min dt=5min dt=10 min dt=20 min dt=30 min

Figura 5.11: portate specifiche adimensionalizzate a rottura globale in funzione del tempo di attesa tra ogni incremento di portata per rampa a piede fisso.

0,5 0,6 0,7 0,8 0,9 1 1,1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 ∆T [minuti] qu.mis/qu.0.mis[ −] dt=1min dt=5min dt=10 min dt=20 min dt=30 min

Figura 5.12: portate specifiche adimensionalizzate a rottura ultima in funzione del tempo di attesa tra ogni incremento di portata per rampa a piede fisso .

Analizzando i diagrammi precedenti è stato possibile osservare come la stabilità di una rampa è sovrastimata, considerando tempi di attesa tra una variazione di portata e l’altra troppo piccoli e come il fenomeno si stabilizzi considerando intervalli ∆t a partire da 5 minuti. Quindi,procedendo per step di portata nelle modalità e nei tempi (∆t= 5 minuti ) che sono state precedentemente descritti, sono stati osservati vari livelli di rottura della rampa. Il primo sintomo di instabilità è rappresentato dal leggero e quasi impercettibile vibrare di alcuni elementi costituenti la rampa

.

Dopo piccoli incrementi di portata ( 1 o 2 step di portata ) alcuni elementi isolati abbandonano la loro posizione e percorrono , rotolando o saltellando , il corpo della rampa arrestandosi a valle di questa. Questo fenomeno viene definito come inizio del movimento

Figura 5.13: inizio movimento ( vista frontale).

Procedendo ancora con step successivi di portata si arriva alla rottura locale della rampa. Il fenomeno si verifica nella parte inferiore ed è costituito dalla partenza di una decina di elementi tra loro contigui che lasciano sulla rampa un’impronta circolare o semicircolare ( figura 5.14 ).

Aumentando ancora la portata , nelle modalità precedentemente descritte, si verificano varie rotture locali in diverse zone della rampa: esse risultano molto più estese e irregolari delle precedenti crisi e di forma allungata in direzione dell’asse del canale .Questa crisi viene definita come rottura globale e può essere ritenuta quella più significativa, in quanto viene modificata la sua funzionalità e quindi necessita di un intervento di riparazione.

La rampa, comunque, raggiunge una nuova configurazione di equilibrio( figura 5.15 ).

Figura 5.15: rottura globale (vista laterale).

La nuova configurazione di equilibrio prodotta dalla predente crisi rimane stabile per piccoli incrementi successivi di portata ( 1 o 2 step ). Successivamente si assiste a un drastico e rapido cambiamento dell’assetto della rampa in quanto si verifica la scopertura del fondo in più punti e a una variazione della sua geometria. Infatti si verifica un incremento di pendenza nella parte superiore della rampa e a un contemporanea diminuzione della pendenza nella parte inferiore. Questa nuova configurazione viene definita come configurazione ultima e precede il collasso della rampa ( figura 5.16 ).

Figura 5.16: rottura ultima (vista laterale).

In definitiva, per ogni tipologia di rampa prese in esame, si sono analizzate quattro livelli di crisi :

• inizio del movimento • rottura locale

• rottura globale • rottura ultima

5.3 Inizio movimento per rampa a piede fisso.

5.3.1 Definizioni di incipiente moto in letteratura.

Vari ricercatori hanno usato differenti definizioni di condizione critica di moto delle particelle. Shields (1936) determina la tensione tangenziale critica corrispondente alla condizione ”zero” del trasporto dei sedimenti. Esperimenti di Taylor e Vanoni (1972) indicano che la curva di Shields non corrisponde alla condizione “zero” del trasporto ma a un piccolo trasporto.

Altri lavori definiscono tale condizione come “primo movimento di una singola particella” [Neil, 1967];”primo movimento dei sedimenti in un letto orizzontale” [White, 1970] “movimento sparso di particelle” [Rathburn and Guy , 1967];”incipiente trasporto”[Martz, 1977] “debole movimento” [Chiew and Parker, 1994] e infine “un movimento generale sul letto”[Misriet al.,1983].

Inoltre diverse definizioni quantitative di inizio movimento forniscono una oggettiva identificazione di questa condizione limite.

Da simili considerazioni Neil e Yalin (1969 ) e Yalin (1972) hanno trovato un criterio basato nella determinazione del numero di particelle mobilitate per unità di area e di tempo. Questo criterio non è stato molto adoperato, probabilmente per la difficoltà di adoperarlo nelle applicazioni pratiche.

Day (1980 ) e Parker (1982) e altri hanno trovato delle relazioni tra l’inizio di movimento delle particelle e alcune misure pratiche di trasporto solido. Parker e altri (1982 ) introduce il parametro W*: 2 / 3 * * * τ s q W = [5.1] Per W*=0.002 si ha la condizione limite.

Il parametro di Eistein qs* [Eistein, 1942] è pari a:

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₋ ⋅ = 1 * ρ ρ ρ s s s s q q [5.2]

Questo criterio di individuazione dell’incipiente moto è stato usato anche da altri ricercatori [ Wilcock 1993 ;Wilcock e altri 1996; Wilcock e McArdell 1997; Kuhnle 1992 ] Comunque la natura turbolente del fluido e le variabili della geometria dei grani introducono un elemento casuale e quindi si è reso necessario un approccio probabilistico al problema.

Shvidchenko e Pender (2000) nei loro studi hanno legato la condizione limite per il trasporto alla probabilità di movimento della particelle attraverso la intensità di movimento dei sedimenti, espressa come il numero relativo di particelle che si muovono nell’unità di tempo: T N m I ⋅ = [5.3] dove m è il numero di particelle che si sono mosse durante l’intervallo di tempo T nell’area A del letto mobile, e N è il numero di particelle nell’area A e può essere stimato con la seguente formula: 6 ) 1 ( 3 d a d A N ⋅ − ⋅ ⋅ = π [5.4]

dove a è la porosità e d è il diametro della particella.

Quindi attraverso analisi di Einstein (1942 ) l’intensità I può essere interpretata come la probabilità che una particella in un letto di area A con lunghezza L e di larghezza unitaria inizia a muoversi in alcuni prestabiliti secondi.

Considerando la condizione limite di incipiente moto secondo Day (1980 ) e Parker (1982) (W*=0.002 ) è stato dimostrato che il parametro I corrisponde circa al valore 3⋅10-5 _sec-1_.

Nel diagramma seguente, considerando particelle di diametro pari a 3.4 mm, viene riportata la relazione tra il parametro di Shields, l’intensità I e la pendenza dell’alveo.

Figura 5.17: relazione tra il parametro di mobilità di Shields e l’intentcsità I di movimento dei sedimenti.

5.3.2 Analisi dell’incipiente moto con approccio deterministico e

sperimentale in letteratura.

La condizione d’incipiente movimento (c.i.m.) esprime quella d’equilibrio limite tra la stabilità dei granelli e il loro spostamento per effetto della spinta idrodinamica esercitata dalla corrente. Essa è ben definita per materiali incoerenti mentre per quelli coerenti , limi ed argille, dipende dalle forze molecolari di coesione ,le quali sono molto variabili in funzione del grado di compattazione.

La c.i.m. può ricavarsi attraverso un approccio deterministico, con supporto sperimentale oppure con una ricerca solo sperimentale, condotta, razionalmente , sulla base dei risultati di una preliminare analisi dimensionale.

L’approccio deterministico è stato introdotto da White (1940), mentre quello sperimentale da Shield (1936), il quale stabilì il noto diagramma fra le grandezze dimensionali che definiscono la condizione limite.

La condizione di incipiente movimento con approccio deterministico . può essere ricavata da quella di equilibrio limite delle varie forze che sollecitano una particella sul fondo. L’analisi può essere condotta considerando i valori medi della forza esercitata dalla corrente, prescindendo dalle fluttuazioni turbolente, oppure mettendo in conto le

caratteristiche turbolente della corrente, arrivando a definire la probabilità del movimento dei grani, piuttosto che una soglia limite.

Tale approccio ha i suoi limiti nella necessità di ipotizzare una certa disposizione della particella esaminata e di quelle circostanti e nelle difficoltà di esprimere correttamente le forze di resistenza idrodinamica di portanza che sollecitano la particella .

Figura 5.18: schematizzazione di una particella posta sul fondo di un corso d’acqua.

La particella si muove quando il momento della forza attiva, FD+G⋅senα, rispetto al punto

di contatto con la particella posta a valle è maggiore del momento resistente della forza G⋅cosα−FL-B:

(

F_D +G⋅senα

)

⋅R⋅cosϕ ≥

(

G⋅cosα −F_L −B

)

⋅R⋅sinϕ [5.5] essendo:

FD→ spinta idrodinamica esercitata dalla corrente nella direzione del moto

FL→ forza di portanza esercitata dalla corrente

G→ peso della particella

B→ forza di galleggiamento avente la direzione normale al moto ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{⋅ ⋅} 3 6 D π γ

R⋅cosϕ→ braccio della forza attiva R⋅sinϕ→ braccio della forza resistente ϕ→ angolo di attrito

Quindi la condizione di equilibrio alla traslazione nella direzione del moto risulta:

(

)

ϕ γ γ α α G F tg sen G F _L s D ⎟⎟⋅ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⋅ = ⋅ + cos 1 [5.6] La forza idrodinamica FD ha l’espressione:

2 2 2 2 4 b D D u D p c F = ⋅ ⋅π⋅ ⋅ρ⋅ [5.7] dove cD è il coefficiente di resistenza funzione del numero di Reynolds al fondo

ReB=uB⋅D/ν, uB la velocità media che investe la particella e il termine

(

p2⋅π ⋅D2

)

/4 è

l’area investita dalla corrente, con p2<1, poiché tale area è minore della sezione trasversale

della particella per la presenza di grani a monte. La forza di portanza FL può essere espressa come:

2 2 2 2 4 b L L u D p c F = ⋅ ⋅π⋅ ⋅ρ⋅ [5.8] dove cL è il coefficiente funzione del numero di Reynolds al fondo.

Dalla [5.6] si ottiene: ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⋅ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⋅ ≥ ⋅ + α ϕ α ρ ρ ϕ G tg sen tg F F s L D 1 cos [5.9] Sostituendo l’ espressioni di FD e G e dividendo entrambi i termini per ∆=(ρs-ρ)/ρ, si

ottiene: ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⋅ ⋅ ⋅ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ + ⋅ ⋅ ≥ ⋅ ⋅ ∆ ϕ ρ ρ ρ α α ϕ ϕ tg tg tg p tg F F c D g u s s D L D b _{cos 1} 1 3 4 2 2 [5.10]

La velocità al fondo ub si ricava dalle distribuzioni di velocità diverse a seconda che il

fondo del canale sia assimilabile, idrodinamicamente, ad una parete liscia o scabra, oppure intermedio.

Indicando con Φ il rapporto ub/u*, fra la velocità del fondo ub che investe il grano e la

⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⋅ ⋅ ⋅ ⋅ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ + ⋅ ⋅ ≥ ⋅ ⋅ ∆ ϕ ρ ρ ρ α α ϕ φ ϕ tg tg tg p tg F F c D g u s s D L D 1 cos 1 3 4 2 2 2 * _[5.11]

Il termine Φ è una funzione del numero di Reynolds di grano ReD. o Re*.

ν D u R R eB eD ⋅ = Φ = * _[5.12]

Il coefficiente di resistenza idrodinamica cD e i rapporto FL/FD dipendono

da ReB=uB⋅D/ν=Φ⋅u*⋅D/ν= Φ⋅ReD, nonché la disposizione delle particelle, ma ,nel campo di

regime di parete scabra sono dipendenti da ReD stesso ossia dalla viscosità . Si può

concludere che la soglia limite, per una particella sferica isolata, dal termine a destra dell’equazione [5.11)] dipende in generale da :

1. numero di Reynolds di grano ReD (parete liscia e transizione);

2. forma, disposizione e uniformità dei grani sottostanti; 3. angolo d’attrito ϕ;

4. pendenza del corso d’acqua α

Quindi, in condizioni di incipiente movimento,il termine adimensionale u*2/(g⋅∆⋅D), ha un

limite che dipende dalle suddette grandezze. Esso è denominato parametro di Shields (θ) o indice di mobilità(Y) o sforzo tangenziale adimensionale (τ*).

L’approccio deterministico consente di determinare l’influenza di certe grandezze sulla condizione di incipiente movimento, integrando difficili indagini sperimentali .

L’approccio puramente sperimentale è stato analizzato da Shields, il quale ha condotto una estesa indagine in una cabaletta di laboratorio usando quattro tipi di sedimenti : ambra tagliuzzata, lignite, granito e barite frantumati, avente diametro compreso tra 0,36 e 3,44 mm e densità variabile da 1060 a 4300 kg/m3_.

I sedimenti avevano forma più o meno spigolosa e il materiale usato non era del tutto uniforme, presentando una deviazione geometrica σ compresa fra 1,12 e 1,75.

In ogni esperimento, condotto a moto uniforme con valori crescenti di portata, Shields ha misurato, dopo il raggiungimento di una condizione di equilibrio fra portata solida immessa a monte e misurata a valle, il tirante, la pendenza del profilo idrico e la portata solida.

Ha quindi ricavato lo sforzo tangenziale critico di incipiente movimento τ_ocr =γ ×R_b×i , come il valore limite corrispondente all’annullamento della portata solida qs.

Inoltre ha integrato i suoi dati sperimentali con quelli ottenuti da altri ricercatori ( Gilbert, Kramer,Casey), relativi a prove sperimentali con sabbia di quarzo, di diametro compreso fra 0.17e 7 mm.

Ha poi calcolato il numero di Reynolds di grano ReD=u*×D50/ν e lo sforzo tangenziale

critico adimensionale τ*:

(

)

50 * _D s ocr ⋅ − = γ γ τ τ [5.13] Le coppie di valori ReD e τ* relative ai vari esperimenti sono stati riportati in forma

grafica tracciando soltanto una fascia indicativa della relazione di inizio movimento.

Successivamente Rouse e Henderson hanno tracciato differenti linee di interpolazione dei punti sperimentali.

Figura 5.19 : diagramma di Shields.

La curva presente nel diagramma separa la zona di mobilità delle particelle da quella di immobilità: per i punti che giacciono sotto la curva , la corrente d’acqua non è in grado di provocare il moto dell’acqua, mentre i punti al di sopra della curva rappresentano condizioni di movimento delle particelle.

Inoltre il diagramma di Shields è diviso in tre zone:

• zona per ReD ≤ 2 di moto viscoso per pareti idraulicamente lisce

• zona di transizione per 2 ≤ReD ≤ 200

• zona per ReD >200 di moto turbolento per pareti scabre.

Per ReD ≤ 2 la velocità critica è indipendente dal diametro delle particelle e il letto si

comporta come una parete liscia ,essendo i grani completamente immersi nello spessore δ del sottostrato laminare.

Nell’ultimo tratto della curva di Shields, per ReD >200, la dimensione dei grani supera

abbondantemente quella del sottostrato laminare e il parametro di mobilità assume valori pressoché costanti :

( )

057 . 0 2 * _≈ ∆ ⋅ ⋅ = D g u _cr cr θ [5.14] Lo sforzo tangenziale d’incipiente movimento che si ricava dal diagramma di Shields va considerato relativo a sedimenti di diametro uniforme posti su un fondo poco inclinato. Nel caso di una particella giacente su un fondo inclinato questa è mossa dalla corrente più facilmente rispetto alla stessa posta su fondo piano o poco inclinato. Infatti ,il contributo della componente del peso nella direzione della corrente è tanto maggiore quanto più grande è la pendenza. Quindi in questo caso lo sforzo tangenziale d’incipiente movimento è minore di quello di Shields e per determinare il coefficiente correttivo del parametro di mobilità si considerano le condizioni limite nei due casi.

Le condizioni di equilibrio limite di una particella posta su un fondo orizzontale e inclinato risultano rispettivamente:

(

W F

)

tgϕ F_D0 = − _Lo ⋅ [5.15]

(

α

)

ϕ α α G sen G F B tg F_D + ⋅ = ⋅cos − _L0 − ⋅ [5.16]

essendo il peso sommerso per fondo poco inclinato , _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ − = γ γ γ_s W G / il peso della

particella, ϕ l’angolo di attrito e _B=γ _⋅

(

π_⋅D3/6

)

_⋅cosα _{la forza di galleggiamento , la}

quale ha la direzione del gradiente della pressione del fluido.

Il rapporto fra le spinte idrodinamiche esercitate dalla corrente nella direzione del moto,

FDα/FD0 nell’ipotesi che sia

α α D L D L F F F F = 0 0 _vale: ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ − − ⋅ = ϕ α γ γ γ α α tg tg F F s s D D _{cos 1} 0 [5.17]

Esso è uguale al rapporto fra gli sforzi tangenziali:

0 2 0 * 2 * 0 τ τ_α α α _{= =} u u F F D D _[5.18] Dunque lo sforzo tangenziale critico su fondo inclinato ταcr risulta:

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⋅ ⋅ = ϕ α γ γ γ α τ τ_α tg tg s s cr cr 0 cos 1 [5.19]

essendo τ0cr il parametro di mobilità riferito a fondo orizzontale.

Nei casi pratici questo coefficiente correttivo assume valori significativamente minori di 1 solo per pendenze assai elevate.

Considerando, erroneamente, la forza di galleggiamento verticale, invece che normale al fondo, si ottiene la formula di Lane:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⋅ ⋅ = ϕ α α τ τ_α tg tg cr cr 0 cos 1 [5.20]

che fornisce valori praticamente uguali alla formula [5.19] per pendenze minori di 0.01. Un altro fattore che ha un’influenza significativa sulla condizione d’incipiente movimento è il tirante relativo o sommergenza relativa Z=h/D, specialmente per valori piccoli di Z.

Risultati sperimentali hanno mostrato che il valore critico del parametro di Shields aumenta al diminuire della sommergenza.

Armanini (1990) , considerando dati sperimentali con valori di sommergenza relativa Z variabili da 1.1 a 16, ha stabilito la seguente relazione:

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + ⋅ = D h cr 67 . 0 1 06 . 0 * τ [5.21]

Molti ricercatori hanno ripreso lo studio di Shield e tra questi Yalin e Karahan (1979) considerando tutte le fonti note, nonché i risultati di prove sperimentali da loro appositamente condotte in moto laminale e turbolento, hanno prodotto il grafico di figura [5.10] che si può considerare quello più aggiornato e completo.

Il diagramma si differenzia da quello di Shields in quanto la zona di transizione è definita da seguenti limiti : 40 5 . 1 _{≤ =} ⋅ * _≤ ν u D X_cr

Inoltre per Yallin e Karahan (1979) per Xcr>40 l’indice di mobilità critico nel campo

5.3.3 Definizioni di inizio del movimento nel presente studio

.

Nel presente studio si parla di inizio movimento quando uno o più elementi isolati ( da 1-4 elementi) della rampa abbandonano la loro posizione originaria e percorrono, rotolando o saltellando, il corpo della rampa arrestandosi a valle di questa.

Questo fenomeno è il primo sintomo di instabilità della rampa e precede le altre crisi alle quali sono legate.

Figura 5.23: inizio movimento per una rampa in massi.

In genere l’inizio del movimento è preceduta da una fase in cui alcuni massi della rampa cominciano a vibrare in equilibrio instabile con la spinta idrodinamica e proprio questi elementi per piccoli aumenti della portata ( uno o due piccoli step di portata ), iniziano a muoversi provocando appunto la prima rottura della rampa.

Per fornire una oggettiva definizione di questo tipo di rottura è stato valutata l’intensità di movimento I dei massi della rampa con la seguente relazione di Shvidchenko e Pender (2000) : T N m I ⋅ = [5.3]

dove m è il numero di particelle che si sono mosse durante l’intervallo di tempo T nell’area A del letto mobile e N è il numero di particelle nell’area A e può essere stimato con la seguente formula: 6 ) 1 ( 3 d a d A N ⋅ − ⋅ ⋅ = π [5.4]

dove a è la porosità e d è il diametro della particella.

L’intensità I, come accennato nel paragrafo 5.3.1 può essere interpretata come la probabilità che una particella, in un letto di area A con lunghezza L e di larghezza unitaria inizi a muoversi in alcuni prestabiliti secondi.

Il valore del parametro I, così determinato, in tutte le esperienze di laboratorio del presente studio e in corrispondenza dell’inizio movimento della rampa, è risultato essere pari a 10-6÷10-7 _sec-1_{. Questi valori assunti dall’intensità I, anche se differiscono da quello critico}

proposto da Shvidchenko e Pender (2000) (I=10-4sec ), possono essere considerati attendibili in quanto le dimensioni dei massi della rampa risultano essere notevolmente maggiori dei sedimenti utilizzati nei test da questi ultimi ricercatori e quindi il loro numero e la probabilità che si muovono risulta essere inferiore.

5.3.4 Analisi dei dati sperimentali nel presente studio per tipologia di

rampa a piede fisso.

Le variabili che entrano in gioco nell’incipiente movimento di materiale incoerente su rampe inclinate i0 sono variabili di fluido (densità “ρ”,viscosità “ν”), variabili di gravità

(accelerazione di gravità “g”, inclinazione rampa “i0”), grandezze caratterizzanti la

corrente ( altezza liquida h), variabili caratterizzanti il materiale di trasporto ( densità dei massi “ρs”,diametro corrispondente al 50% della curva granulometrica dei massi

costituenti la rampa“D50”).

ρ

,

υ

D50,

ρ

s h

i0

Figura 5.24: grandezze che influenzano l’incipiente movimento di materiali incoerente su rampe inclinate.

Quindi il fenomeno dell’incipiente moto nelle rampe in massi, qui studiato, può essere rappresentato dalla seguente legge funzionale:

F=f (ρ,ν,g, i0, h, ρs-ρ, D50)

Dall’analisi dimensionale e sfruttando il teorema di Buckingam, utilizzando le variabili ρ, D50, g per le iterazioni, dopo alcuni passaggi si trovano 4 grandezze dimensionali, che si

utilizzano per la caratterizzazione del fenomeno:

50 1 D h Z = = Π [5.22] 0 2 =i Π [5.23]

3 1 2 50 * 50 5 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⋅∆ ⋅ = = Π ν g D D [5.24] 50 0 6 D i h ⋅ ∆ ⋅ = = Π θ [5.25] dove: → Z sommergenza relativa [─] → h altezza liquida [m] → 50

D diametro corrispondente al 50% della curva granulometrica dei massi costituenti la rampa [m]

→

0

i pendenza della rampa [─]

→ * 50

D diametro caratteristico o di attrito calcolato con il D50 [─]

→ − = ∆ ρ ρ ρ_s

densità relativa del grano immerso [─]

→

ν coefficiente di viscosità cinematica [m2/sec] →

g accelerazione di gravità [m/sec2]

→

θ parametro di mobilità di Shields [─]

Questi parametri, che caratterizzano l’inizio movimento dei massi, sono stati valutati per ogni test svolto del presente studio ( con rampa a piede fisso ) e riportato nella tabella di figura 5.25:

PROVE n° tipologia rampa i0 [-] ∆ [-] D50 [m] qi [m2/sec] misurate h [m] Z=h/d [-] θ [-] Re* [-] D50* [-] 24 piede fisso 0,250 1,5 0,0175 0,0078 0,011 0,631 0,105 2850,43 425,88 13 piede fisso 0,250 1,5 0,0229 0,0082 0,012 0,507 0,084 3822,59 557,29 29 piede fisso 0,250 1,5 0,026 0,0120 0,015 0,566 0,094 4886,38 632,74 35 piede fisso 0,167 1,5 0,0175 0,0095 0,014 0,783 0,087 2591,79 425,88 33 piede fisso 0,167 1,5 0,0229 0,0106 0,015 0,651 0,072 3537,6 557,29 34 piede fisso 0,167 1,5 0,026 0,0119 0,016 0,620 0,069 4177,19 632,74 44 piede fisso 0,333 1,5 0,0175 0,0059 0,009 0,500 0,111 2928,31 425,88 45 piede fisso 0,333 1,5 0,0229 0,0064 0,009 0,407 0,09 3956,18 557,29 46 piede fisso 0,333 1,5 0,026 0,0088 0,011 0,439 0,098 4973,19 632,74 67 piede fisso 0,250 1,5 0,0175 0,0070 0,010 0,591 0,099 2758,88 425,88 66 piede fisso 0,250 1,5 0,0229 0,0084 0,012 0,515 0,086 3853,17 557,29 65 piede fisso 0,250 1,5 0,026 0,0110 0,014 0,537 0,09 4761,56 632,74 71 piede fisso 0,333 1,5 0,0175 0,0055 0,008 0,479 0,106 2867,55 425,88 72 piede fisso 0,333 1,5 0,0229 0,0068 0,010 0,423 0,094 4033,75 557,29 73 piede fisso 0,333 1,5 0,026 0,0080 0,011 0,413 0,092 4823,74 632,74 60 piede fisso 0,167 1,5 0,026 0,0132 0,017 0,660 0,073 4309,23 632,74 50 piede fisso 0,333 1,5 0,0175 0,0056 0,008 0,484 0,108 2882,83 425,88 51 piede fisso 0,333 1,5 0,0229 0,0075 0,010 0,449 0,1 4156,08 557,29 52 piede fisso 0,333 1,5 0,026 0,0080 0,011 0,416 0,092 4838,84 632,74 78 piede fisso 0,125 1,5 0,0175 0,0124 0,017 0,980 0,082 2511,94 425,88 80 piede fisso 0,125 1,5 0,0142 0,0090 0,014 0,983 0,082 1838,43 345,57 83 piede fisso 0,167 1,5 0,0407 0,0349 0,032 0,776 0,086 9152,69 990,48 87 piede fisso 0,333 1,6 0,0142 0,0047 0,008 0,529 0,11 2203,02 353,09 89 piede fisso 0,250 1,6 0,0142 0,0061 0,009 0,662 0,103 2133,71 353,09 91 piede fisso 0,167 1,6 0,0142 0,0078 0,012 0,846 0,088 1969,13 353,09 92 piede fisso 0,333 1,6 0,0359 0,0133 0,015 0,416 0,087 7849,76 892,66 93 piede fisso 0,250 1,6 0,0359 0,0149 0,017 0,477 0,075 7280,83 892,66 94 piede fisso 0,167 1,6 0,0359 0,0199 0,022 0,623 0,065 6796,43 892,66

Figura 5.25: tabella dei parametri che caratterizzano il fenomeno per rampa a piede fisso.

Nella tabella di figura 5.25 sono riportate anche le portate specifiche qi [m2/sec] in

corrispondenza dell’inizio movimento della rampa e il numero di Reynolds di grano ReD o

Re*[-].

L’altezza liquida h è stata valutata con la formula [5.26] di Manning relativa al moto uniforme: 0 3 2 1 i R A n Q= ⋅ ⋅ b ⋅ [5.26]

dove: →

Q portata defluente [m3/sec]

→

A area della sezione trasversale di deflusso [m2] →

b

R raggio idraulico [─]

→

n coefficiente di scabrezza [sec/m1/3] →

0

i pendenza della rampa [─]

Il raggio idraulico Rb per piccoli tiranti idrici rispetto alla larghezza del canale ( b ) può

essere posto uguale all’incirca ad h:

h h b h b C A R_b ≈ ⋅ + ⋅ = = 2 [5.27] Sostituendo la [5.27] nella [5.26] e considerando la portata q unitaria ( q=Q/b) si ottiene:

0 3 5 1 i h n q= ⋅ ⋅ [5.28] In letteratura ci sono diverse formule sperimentali che stimano il coefficiente di Manning n [sec/m1/3]; Anderson [1990], utilizzando canali sperimentali di pendenza inferiore a 0.01 [m/m ] e materiale d’alveo di forma angolare e arrotondata, di dimensioni comprese da 1.64mm (0.0005 ft) a 304.8 mm (1 ft), determina la seguente relazione:

( )

6 1 50 0395 . 0 D n= ⋅ [5.29] dove il diametro D50 viene espresso in ft (1ft=0.3048m).

Invece Codell [1990] conducendo test sperimentali con pendenze comprese da 0.01 a 0.20 [m/m ] e usando pietre di dimensioni di 26,56,104,130,e 157mm, trova la seguente formula per valutare n:

(

)

6 1 0 50 0456 . 0 D i n= ⋅ ⋅ [5.30] dove il diametro D50 viene espresso in inch (1 inch=25.4mm).

Un’altra formula per calcolare il coefficiente di Manning è stata proposta da Abt Rice e Robinson e vale per 0.1≤i0≤0.4 e 52mm≤D50≤278 mm:

(

)

0.147 0 50 029 . 0 D i n= ⋅ ⋅ [5.31] dove il diametro D50 viene espresso in mm.

Nel presente studio il coefficiente di scabrezza n è stato valutato con la formula di Pagliara-Chiavaccini [2004]:

(

) (

)

0.11 0 50 1 064 . 0 D i n= ⋅ +Γ e⋅ ⋅ [5.32] dove: → ⋅ ⋅ ⋅ ⋅ = Γ L W D N_{B B} 4 2 π

concentrazione dei boulders ( = 0 per rampe senza bouders)

→

B

D dimensione media dei boulders espessa in m

→

B

N numero dei boulders

→

W larghezza rampa [m]

→

L lunghezza rampa [m]

→

e parametro dipendente dalla distribuzione dei boulders ( figura 5.26) →

50

D diametro corrispondente al 50% della curva granulometrica espressa in m →

0

i pendenza della rampa

Coefficiente eq. [5.32] Randon disposition Rounded Surface Rows disposition Rounded Surface Randon disposition Crushed Surface Rows disposition Crushed Surface e 1,00 1,20 1,80 2,30

Figura 5.26: coefficiente e della formula [5.32] in funzione della distribuzione e della superficie dei dei boulders.

La formula [5.32] deriva da analisi di prove sperimentali condotti presso il Dipartimento di Ingegneria Civile dell’Università di Pisa e riguardanti la dissipazione di energia di

rampe in massi rinforzate mediante elementi di dimensioni notevolmente maggiori ( boulders.) rispetto a quelli costituenti il fondo della rampa.

Nella figura seguente viene mostrato un profilo tipico del modello sperimentale utilizzato per questo tipo di studio:

q

Broad crested weir

Boulders

Base material

Filter layer

Stable toe

Figura 5.27: schema del modello sperimentale utilizzato da Pagliara-Chiavaccini [2004].

Figura 5.28: sezione del modello sperimentale utilizzato da Pagliara-Chiavaccini [2004].

Questi test sono stati svolti in tre diversi canali di larghezza rispettivamente pari a 0.25m, 0.35m e 0.5m. Sono state analizzate varie pendenze della rampa [0.08≤ i0 ≤0.40] e per

realizzare lo strato di base della rampa sono stati utilizzati materiali naturali di granulometria uniforme e di varie dimensioni [2mm ≤D50≤ 21.7mm.]. I boulders posti

sopra lo strato di base sono stati realizzati mediante semisfere di metallo di 29mm e 38mm di diametro oppure con massi naturali con D50 pari a 34.2mm e 59.1 mm.

Le semisfere utilizzate erano lisce o rese artificialmente scabre mediante fogli di alluminio oppure con uno strato di sabbia di diametro medio di 2mm incollato sulla superficie.

In questo studio sono state prese in considerazione diverse percentuali di ricoprimento [0%≤Γ≤30%] e diverse disposizione dei boulders:

• Disposizione a random. • Disposizione a fila.

Figura 5.29: disposizione a random e a fila dei boulders.

Nella tabella seguente sono riportati i range sperimentali riguardati le relazioni per valutare il coefficiente n trovate in letteratura :

Autore Formula i0 [-] D50 [mm]

Anderson [1990] [5.29] <0,01 1,64-304,8

Codell [1990] [5.30] 0,01-0,2 25; 56; 104; 130; 157

Robinson [5.31] 0,1-0,4 52-278

Pagliara-Chiavaccini [2004] [5.32] 0,08-0,40 2-21,7

Figura 5.30: campi di validità delle precedenti formule per valutare il coefficiente di Manning n.

La formula [5.32] di Pagliara Chiavaccini [2004] per Γ=0% ( rampa senza boulders di rinforzo) si semplifica:

(

)

0.11 0 50 064 . 0 D i n= ⋅ ⋅ [5.34]

Valutate tutte le grandezze che influenzano l’inizio movimento dei massi di una rampa a piede fisso si è analizzato nel presente studio, in particolare modo, la relazione esistente tra il parametro di mobilità Π4=θ=h⋅i0/∆⋅D50, la sommergenza relativa Z=h/D50 e il

diametro di attrito o caratteristico D50*. Quindi si sono riportate nel diagramma di figura

[5.31] le coppie di valori θ e Z parametrizzati per D50*:

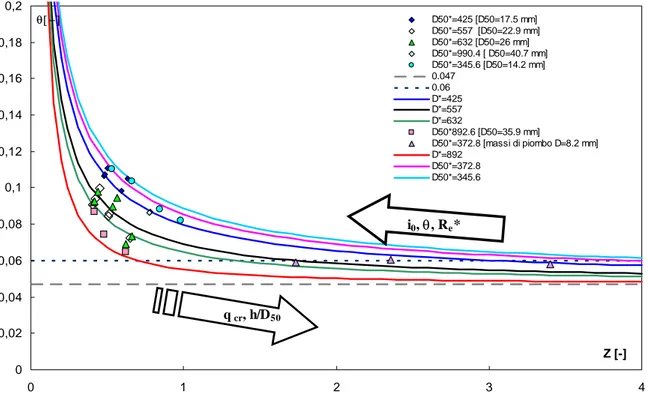
0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2 0 0,5 1 1 Z [-] θ[-] ,5 D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D50*=892.6 [D50=35.9 mm]

Figura 5.31: coppie di valori di θ e Z ,misurati nel presente studio e parametrizzati per D50*.

Nella tabella di figura [5.32] vengono riportati i valori del diametro caratteristico D50* per

ogni ∆ e D50 corrispondenti, considerando la viscosità cinematica ν a 20°C pari a 1x10-6

D50 [mm] γs [kg/m3] ∆ [-] D50*[-] 14,2 2600 1,6 345,57 17,5 2500 1,5 425,88 22,9 2500 1,5 557,29 26 2500 1,5 632,74 35,9 2600 1,6 892,66 40,7 2500 1,5 990,48

Figura 5.32: valori del diametro caratteristico D50*per ogni ∆ e D50 corrispondenti.

Per studiare il fenomeno anche in condizione di alta sommergenza (Z>1) con elevate pendenze della rampa, sono state svolte prove mirate di inizio movimento utilizzando come materiale costituente la rampa sfere di piombo ,opportunamente deformate per avere un comportamento simile ai massi naturali, di peso specifico γ =10780 kg/m^3 e diametro 8.2 mm. In questi test per la rampa sono state scelte le pendenze 1H:3V ; 1H:4V ; 1H:6V . Inoltre per interpretare questi particolari dati sono state fatte diverse foto e filmati in vari istanti della prove. Inoltre si sono conteggiate le sfere che si sono mobilitate per ogni step di portate.

I risultati. di queste prove sperimentali vengono riportati nella tabella di figura [5.33].

Prova n° n° sfere io [-] _[m2q_/sec] i Qi [L/s] h [m] θ [−] Z=h/D50 [-]

86 3 0,333333 0,011279 2,82 0,0123 0,0510 1,497 13 0,333333 0,01439 3,60 0,0142 0,0591 1,733 30 0,333333 0,022719 5,68 0,0187 0,0777 2,279 88 4 0,25 0,016611 4,15 0,0166 0,0516 2,020 7 0,25 0,02152 5,38 0,0193 0,0603 2,359 38 0,25 0,034068 8,52 0,0255 0,0795 3,108 90 4 0,166667 0,026838 6,71 0,0243 0,0505 2,962 15 0,166667 0,033799 8,45 0,0279 0,0580 3,401 33 0,166667 0,036784 9,19 0,0293 0,0610 3,578

dove:

→

n numero di sfere mobilitate corrispondenti alla portata specifica qi .

Figura 5.34: rampa con i massi di piombo .

Figura 5.35: primi movimenti dei massi di piombo .

Nel diagramma (θ ; Z=h/d ) di figura [5.36] vengono riportati questi punti sperimentali indicando anche il numero di massi mobilitati corrispondenti.

0 0,05 0,1 0,15 0,2 0,25 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 Z [-] θ[-] 0.047 0.06 D50*=372.8 [ D=8.2 mm n=7-13 massi di piombo] D50*=372.8 [D=8.2 mm n=30-38 massi di piombo] D50*=372.8 [D=8.2 mm n=3-4 massi di piombo] n° m assi=13 n° m assi=30 n° massi=38 n° m assi=33

n° m assi=3 n° massi=4 n° m assi=4

n° m assi=7

n° massi=12

Figura 5.36: punti sperimentali in condizioni di alta sommergenza.

Poiché la sfericità delle sfere di piombo è maggiore rispetto ai massi naturali ( anche se deformate mediante battitura) si è ritenuto più opportuno considerare come fase di crisi di incipiente moto per tale materiale l’istante in cui il numero di sfere che hanno abbandonato la loro posizione originaria siano un numero maggiore rispetto alle precedenti definizioni di inizio movimento.

Quindi in questo caso ,per tale fase di crisi, si è ritenuto opportuno analizzare solo i valori che assumevano θ e Z corrispondenti ad un numero di 7÷15 sfere mobilitate e questi sono stati riportati nel diagramma di figura [5.37] assieme a tutti gli altri precedentemente discussi.

0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2 0 1 2 3 4 Z [-] θ[-] D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D50*=892.6 [D50=35.9 mm] D50*=372.8 [piombini D=8.2 mm]

Figura 5.37: coppie di valori di θ e Z ,misurati nel presente studio e parametrizzati per D50*.

L’analisi dei dati raccolti nel presente studio ha permesso di fornire l’andamento del parametro di mobilità Π6=θ=h⋅i0/∆⋅D50 in funzione della sommergenza Z=h/D50 e con il

parametro D50*. La relazione θ=f(Z, D50*), osservando l’andamento dei punti sperimentali

in condizioni di bassa sommergenza e l’indipendenza del parametro di mobilità da Z per valori di quest’ultimo maggiori di 1 , è stata posta nella forza:

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⋅ = _{LIM B} Z A 1 θ θ [5.35] dove: A=f1 (D50*) B=f2 (D50*) → LIM

θ parametro di mobilità limite

Nella relazione [5.35] θLIM ,analizzando i dati in condizione di alta sommergenza,è stato

posto uguale a 0.047 e questo valore coincide con quello del parametro di mobilità critico proposto da Yallin e Karahan (1979) per Xcr>40 (nel campo d’indipendenza da ReD).

Per esprimere la relazione tra i coefficienti A e B con D50*è stato scelto un legame di tipo

esponenziale. Questo ha permesso di estendere, con buoni risultati,la validità della relazione tra 7 mm≤D50≤50 mm e pendenze comprese tra 1/3≤S≤1/40.

Nella tabella di figura[5.38] e nel diagramma di figura [5.39] sono riportati i valori assunti dai coefficienti A e B trovati, per vari D50*, tracciando gli andamenti delle curve

corrispondenti nel diagramma (θ ; Z=h/d ).

Regressione esponenziale D50 [mm] D50*[-] A misurato [-] B misurato [-] 8,2 373 14,2 346 0,85 0,8 17,5 425 0,65 0,9 22,9 557 0,42 1,1 26 632 0,36 1,15 35,9 893 0,15 1,55 40,7 990

Figura 5.38: valori dei coefficienti A e B della formula[5.35] per vari D50*.

0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2 0 1 2 3 Z [-] θ[-] 4 D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D50*=892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo] D50*=425 D50*=557 D50*=632 D50*=345.6 D50*=892.6

0 0,5 1 1,5 2 0 400 800 1200 D50* [-] A,B A B A esponenziale B esponenziale

Figura 5.40: andamenti dei coefficienti A e B della formula[5.35] in funzione di D50*.

Quindi le relazioni: A=f1 (D50*)e B=f2 (D50*) che sono state scelte risultano:

( 0.003 50*) _[5.36] 494 . 2 _e D A= ⋅ − ⋅ * 50 001 . 0 543 . 0 _e D B= ⋅ ( ⋅ ) [5.37] Sostituendo la [5.36] e la [5.37] nella [5.35] si ottiene il parametro di mobilità critico [5.38]: ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ + ⋅ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _⋅ ∗ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− ⋅} ∗ 50 001 . 0 543 . 0 50 50 003 . 0 494 . 2 1 047 . 0 D e D D h e θ [5.38]

L’andamento delle curve calcolate con l’eq [5.38] ,per i vari D50* analizzati ,sono riportate

nel diagramma (θ ; Z=h/D)di figura [5.41] insieme ai punti sperimentali del presente studio.

0 0,05 0,1 0,15 0,2 0 1 2 3 Z [-] θ[-] 4 D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D*=425 D*=557 D*=632 D*=1078 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 D50*=345.6

Figura 5.41: andamenti delle curve calcolate con l’eq.[5.38] per vari D50*.

Nel diagramma di figura [5.42] sono inoltre indicati il verso di crescita di alcune grandezze che influenzano il fenomeno ( qi , Re*, i0, θ, Z=h/D)

0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2 0 1 2 3 Z [-] θ[ −] 4 D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D*=425 D*=557 D*=632 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 D50*=372.8 D50*=345.6 i0, θ, Re* q cr, h/D50

Per verificare ed estendere la validità della relazione [5.38] per 7 mm≤D50≤50 mm e

pendenze comprese tra 1/3≤i0≤1/40, si è reso necessario raccogliere ed analizzare altri dati

sperimentali di inizio movimento forniti da altri autori.

Tra questi, sono stati presi in esame i dati derivanti da test di stabilità di rampe in massi eseguiti presso il Dipartimento di Ingegneria Civile dell’Università di Pisa e condotti da Serra[2005], D’Elia [2005],Chines [2004].

Serra , D’Elia e Chines hanno analizzato diversi livelli di rotture di una rampa in massi a piede fisso:

• Inizio movimento • Rottura locale • Rottura globale

Inoltre hanno valutato gli effetti stabilizzanti sulle rampe dei boulders, variando la percentuale di ricoprimento, le dimensioni e le disposizione di questi.

Le disposizioni dei boulders prese in esame sono quelle random, a righe e ad arco e le percentuali di ricoprimento sono comprese tra 0% ≤ Γ≤ 49% . Inoltre le dimensioni dei materiali costituente lo strato di base ,quelle dei boulders e le pendenze della rampa utilizzati nei loro test, sono comprese rispettivamente tra 11.25mm≤D50≤34.2mm ,

26.45mm≤DB50≤88.7mm e 1/4≤i0≤1/12. Nella tabella di figura [5.43] sono riportati i valori

dei parametri di mobilità forniti da Serra , D’Elia e Chines per rampa a piede fisso e per Γ=0%.

Autore i0 [-] [-]∆ D50 [m] qi [m2/sec] misurate h [m] Z=h/D50 [-] [-]θ Re* [-] D50* [-] D'Elia [ 2005 ] 0,125 1,6 0,0115 0,0064 0,011 0,977 0,076 1336,15 285,95 D'Elia [ 2005 ] 0,125 1,6 0,01775 0,0070 0,012 0,689 0,054 2151,7 441,36 D'Elia [ 2005 ] 0,250 1,6 0,0115 0,0041 0,007 0,634 0,099 1521,63 285,95 D'Elia [ 2005 ] 0,250 1,6 0,01775 0,0050 0,008 0,478 0,075 2533,41 441,36 Serra [ 2005 ] 0,125 1,6 0,01775 0,0114 0,016 0,920 0,072 2485,79 441,36 Serra [ 2005 ] 0,250 1,6 0,0115 0,0048 0,008 0,699 0,109 1598,33 285,95 Serra [ 2005 ] 0,250 1,6 0,01775 0,0066 0,010 0,563 0,088 2749,88 441,36 Serra [ 2005 ] 0,125 1,6 0,0115 0,0087 0,014 1,176 0,092 1465,78 285,95 Serra [ 2005 ] 0,083 1,6 0,0115 0,0095 0,016 1,358 0,071 1286,13 285,95 Chines [ 2004 ] 0,250 1,6 0,01125 0,0053 0,009 0,757 0,118 1609,59 279,73 Chines [ 2004 ] 0,250 1,6 0,02205 0,0127 0,015 0,683 0,107 4194,5 548,28 Chines [ 2004 ] 0,250 1,6 0,0342 0,0167 0,018 0,533 0,083 7157,23 850,39 Chines [ 2004 ] 0,125 1,6 0,01125 0,0081 0,013 1,151 0,09 1402,83 279,73 Chines [ 2004 ] 0,125 1,6 0,02205 0,0116 0,017 0,759 0,059 3127,18 548,28 Chines [ 2004 ] 0,125 1,6 0,0342 0,0163 0,021 0,618 0,048 5448,59 850,39 Chines [ 2004 ] 0,083 1,6 0,01125 0,0129 0,019 1,672 0,087 1380,62 279,73 Chines [ 2004 ] 0,083 1,6 0,02205 0,0286 0,032 1,437 0,075 3512,35 548,28 Chines [ 2004 ] 0,083 1,6 0,0342 0,0259 0,031 0,898 0,047 5362,83 850,39

Figura 5.43: tabella dei parametri di mobilità forniti da Serra,D’Elia e Chines per rampe a piede fisso.

Molto utili sono risultati gli studi di stabilità e i dati di inizio movimento dei massi di una rampa condotti da Martin Jaggi. Quest’ultimo ha analizzato rampe a posa regolare e irregolare dei massi e vari meccanismi di rottura (erosione diretta dei massi, erosione al piede della rampa, affondamento nel sottostrato degli elementi costituente la rampa).

Le dimensioni dei materiali costituente le rampe e le pendenze della rampa utilizzati nei suoi test sperimentali sono comprese rispettivamente tra 13.2mm≤D50≤23.5mm e

0.05≤i0≤0.20.

Nella tabella di figura [5.44] sono riportati i valori dei parametri di inizio movimento di Martin Jaggi per rampa a posa irregolare e riferiti a rotture per erosione diretta dei massi.

Autore i0 [-] ∆ [-] D50 [m] qi [m2/sec] misurate h [m] Z=h/D50 [-] θ [-] Re* [-] D50* [-] Jaggi 0,150 1,6 0,0132 0,0112 0,015 1,154 0,108 1955,65 328,22 Jaggi 0,100 1,6 0,0132 0,0103 0,016 1,207 0,075 1632,92 328,22 Jaggi 0,123 1,6 0,0235 0,0126 0,018 0,756 0,058 3404,4 584,33 Jaggi 0,100 1,6 0,0235 0,0273 0,030 1,262 0,079 3967,23 584,33 Jaggi 0,150 1,6 0,0235 0,0215 0,023 0,995 0,093 4313,72 584,33 Jaggi 0,200 1,6 0,0235 0,0143 0,017 0,729 0,091 4262,49 584,33

Figura 5.44: Tabella dei parametri di mobilità di Martin Jaggi per rampe a posa irregolare.

Inoltre dalla bibliografia raccolta sono stati analizzati dati sperimentali di inizio movimento di Graf e Suszka [1987],Bathurst [1984]e Gareth Pender. Nella tabella di figura [5.45] sono riportati i range delle condizioni idrauliche e di trasporto dei sedimenti presi in esame da questi ricercatori.

Autore pendenza _[-] ∆ [-] D50 [mm] σ [-] h [m] _[m/sec] V Fr [-]

Bathurst [1984] 0,005-0,07 1,54-1,77 11,5 ; 22,2 ; 44,3 1,24-1,27 0,044-0,254 0,75-2 0,79-2,21 Pender [2000] 0,0019-0,029 1,6-1,65 1,5 ; 2,4 ; 3,4 ; 4,5; 7,15; 12 1,08-1,26 0,006-0,136 0,06-1,07 0,17-1,17 Graf e Suszka[1987] 0,005-0,025 1,73 12,2 ; 23,5 1,23-1,24 0,094-0,245 0,92-1,54 0,77-1,26

Figura 5.45: Range delle condizioni idrauliche edi trasporto di vari ricercatori.

Nella figura [5.46] sono riportati i dati di inizio movimento di questi autori e che sono stati analizzati nel presente studio:

Autore i0 [-] ∆ [-] D50 [m] h [m] Z=h/D50 [-] θ [-] Re* [-] D50* [-] Pender [2000] 0,0065 1,6 0,00715 0,0815 11,4 0,046 510,148 177,79 Pender [2000] 0,0083 1,6 0,00715 0,0686 9,6 0,05 529,008 177,79 Pender [2000] 0,0115 1,6 0,00715 0,0536 7,5 0,054 550,385 177,79 Pender [2000] 0,0143 1,6 0,00715 0,0458 6,4 0,057 566,951 177,79 Pender [2000] 0,0237 1,6 0,00715 0,03 4,2 0,062 591,27 177,79 Pender [2000] 0,0115 1,6 0,012 0,084 7 0,05 1156,11 298,38 Pender [2000] 0,0141 1,6 0,012 0,0732 6,1 0,054 1195,02 298,38 Pender [2000] 0,0178 1,6 0,012 0,06 5 0,056 1215,61 298,38 Pender [2000] 0,0287 1,6 0,012 0,0432 3,6 0,065 1309,76 298,38 Bathurst [1984] 0,07 1,774 0,0443 0,0709 1,6 0,063 9672,59 1140 Bathurst [1984] 0,05 1,774 0,0443 0,0886 2 0,056 9139,74 1140 Bathurst [1984] 0,03 1,774 0,0443 0,1329 3 0,051 8670,72 1140 Graf e Suszka [1987] 0,015 1,732 0,0235 0,1363 5,8 0,05 3293,74 600 Graf e Suszka [1987] 0,02 1,732 0,0235 0,1105 4,7 0,054 3423,69 600 Graf e Suszka [1987] 0,025 1,732 0,0235 0,094 4 0,058 3531,26 600 Bathurst [1984] 0,01 1,54 0,0222 0,1665 7,5 0,049 2807,94 545 Bathurst [1984] 0,03 1,54 0,0222 0,0755 3,4 0,066 3274,6 545 Bathurst [1984] 0,05 1,54 0,0222 0,0488 2,2 0,071 3400,59 545 Bathurst [1984] 0,07 1,54 0,0222 0,0377 1,7 0,077 3536,97 545 Bathurst [1984] 0,005 1,669 0,0115 0,1403 12,2 0,037 944,148 290 Bathurst [1984] 0,0075 1,669 0,0115 0,1093 9,5 0,043 1020,39 290 Bathurst [1984] 0,01 1,669 0,0115 0,0932 8,1 0,049 1087,97 290

Figura 5.46: Tabella dei parametri di trasporto di altri ricercatori. Nella tabella seguente sono confrontati i range sperimentali dei dati utilizzati nella elaborazione. Autore pendenza _{[-] [-]}∆ D50 [mm] Bathurst [1984] 0,005-0,07 1,54-1,77 11,5 ; 22,2 ; 44,3 Pender [2000] 0,0019-0,0287 1,6-1,65 1,5 ; 2,4 ; 3,4 ; 4,5; 7,15; 12 Graf e Suszka[1987] 0,005-0,025 1,73 12,2 ; 23,5 D'Elia-Serra-Chines 0,25-0,0833 1,6 11,25-34,2 Presente studio 0,333-0,125 9,78-1,5 8,2-40,7

Tutti i dati di incipiente moto di questo studio e dalla bibliografia raccolta sono riportati nel diagramma (θ ; Z=h/D) di figura [5.48]:

0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0 1 2 3 4 5 6 7 8 9 10 11 12 Z [-] θ[-] D50*=425 [D50=17.5 mm] D50*=441 [D50=17.75 mm] Serra D'Elia D50*=548.3[D50=22.05 mm] Chines D50*=545 [D50=22.2 mm] Bathurst D50*=557 [D50=22.9 mm] D50*=584.33 [D50=23.5 mm] Jaggi D50*=600 [D50=23.5 mm] Graf D50*=632 [D50=26 mm] D50*=850.4 [D50=34.2 mm] Chines D50*=990.4 [ D50=40.7 mm] D50*=1078 [D50=44.3 mm] Bathurst D50*=279.7 [D50=11.25 mm] Chines D50*=285.9 [D50=11.5 mm] Serra D50*=300 [D50=12 mm] Pender D50*=328.2 [D50=13.2 mm] Jaggi D50*=345.6 [D50=14.2 mm] D50*=174 [D50=7.15] Pender 0.047 0.06 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm]

Figura 5.48: coppie di valori di θ e Z e parametrizzati per D50*.

Per valutare la validità della relazione trovate anche per i punti sperimentali degli altri ricercatori precedentemente menzionati, nei diagrammi di figura [5.49] e [5.50] sono riportati anche gli andamenti delle curve calcolate con l’equazione trovata [5.38] riferite a vari D50*: Poiché il parametro di mobilità ,per sommergenze bassissime ( Z<0.2), non può

crescere infinitamente nel paragrafo 5.3.7 , viene fissato un limite di validità alla teoria appena descritta, analizzando alcune condizioni limite .

0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Z [-] θ[-] D50*=425 [D50=17.5 mm] D50*=441 [D50=17.75 mm] Serra D'Elia D50*=548.3[D50=22.05 mm] Chines D50*=545 [D50=22.2 mm] Bathurst D50*=557 [D50=22.9 mm] D50*=584.33 [D50=23.5 mm] Jaggi D50*=600 [D50=23.5 mm] Graf D50*=632 [D50=26 mm] D50*=850.4 [D50=34.2 mm] Chines D50*=990.4 [ D50=40.7 mm] D50*=1078 [D50=44.3 mm] Bathurst D50*=279.7 [D50=11.25 mm] Chines D50*=285.9 [D50=11.5 mm] Serra D50*=300 [D50=12 mm] Pender D50*=328.2 [D50=13.2 mm] Jaggi D50*=345.6 [D50=14.2 mm] D50*=174 [D50=7.15] Pender 0.047 0.06 D*=174 D*=425 D*=557 D*=632 D*=300 D*=1078 Eq.Armanini D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 h/D50=1.1 h/D50=16 D50*=372.8

Figura 5.49:andamenti delle curve calcolate con l’eq.[5.38] per vari D50*.

0 0,05 0,1 0,15 0,2 0 1 2 3 4 Z [-] θ[-] D50*=425 [D50=17.5 mm] D50*=441 [D50=17.75 mm] Serra D'Elia D50*=548.3[D50=22.05 mm] Chines D50*=545 [D50=22.2 mm] Bathurst D50*=557 [D50=22.9 mm] D50*=584.33 [D50=23.5 mm] Jaggi D50*=600 [D50=23.5 mm] Graf D50*=632 [D50=26 mm] D50*=850.4 [D50=34.2 mm] Chines D50*=990.4 [ D50=40.7 mm] D50*=1078 [D50=44.3 mm] Bathurst D50*=279.7 [D50=11.25 mm] Chines D50*=285.9 [D50=11.5 mm] Serra D50*=300 [D50=12 mm] Pender D50*=328.2 [D50=13.2 mm] Jaggi D50*=345.6 [D50=14.2 mm] D50*=174 [D50=7.15] Pender 0.047 0.06 D*=174 D*=425 D*=557 D*=632 D*=300 D*=1078 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 D50*=372.8 D50*=345.6

5.3.5 Calcolo iterativo della portata specifica di inizio movimento per

una rampa in massi a piede fisso

.

Dalle considerazioni precedenti, per massi con 7 mm≤ D50 ≤50 mm e pendenze della

rampa comprese tra 1/3≤i0≤1/40 e inoltre nel rispetto del limite di validità valutato nel

paragrafo 5.3.7 in condizioni di bassissima sommergenza ( Z<0.2), il parametro di mobilità risulta: ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ + ⋅ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _⋅ ⋅ ∗ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− ⋅} ∗ 50 001 . 0 543 . 0 50 50 003 . 0 494 . 2 1 047 . 0 D e D D h e θ [5.38]

Ma il parametro di mobilità di Shields è pari anche :

50 0 D i h ⋅ ∆ ⋅ = θ [ 5.39 ] Infatti :

(

)

(

)

(

(

)

)

50 0 50 0 50 2 50 0 D i h D i h g D u D _{s s} s ∆⋅ ⋅ = ⋅ − ⋅ ⋅ ⋅ = ⋅ − ⋅ = ⋅ − = ∗ γ γ ρ γ γ ρ γ γ τ θ dove: 2 0 =ρ⋅u∗

τ → tensione tangenziale al fondo

0 2 i h g u∗ = ⋅ ⋅ → velocità di attrito

Quindi avendo come dati di progetto il D50 , il ∆ dei massi e la pendenza con la quale si

vuole realizzare la rampa è possibile calcolare la portata di inizio movimento attraverso il seguente procedimento iterativo.

Partendo da un’altezza del moto uniforme di tentativo h1 si risolve l’equazione [5.38]. Il

parametro di mobilità così trovato θ1 viene sostituito a quello dell’ eq [5.39] trovando

un’altezza h2. Possono verificarsi due casi:

• h2≠h1

Nel primo caso è necessarioripetere il procedimento con una nuova altezza h1’ di tentativo

fino a quando non si ottiene l’uguaglianza di quest’ultima con l’altezza calcolata con l’eq. [5.39] .Quindi se h1=h2 l’iterazione può ritenersi conclusa.

Trovato h definitiva dopo varie iterazioni con il precedente procedimento si ricava la portata di incipiente moto con la formula di Manning [5.28].

0 3 5 1 i h n q= ⋅ ⋅ [5.28]

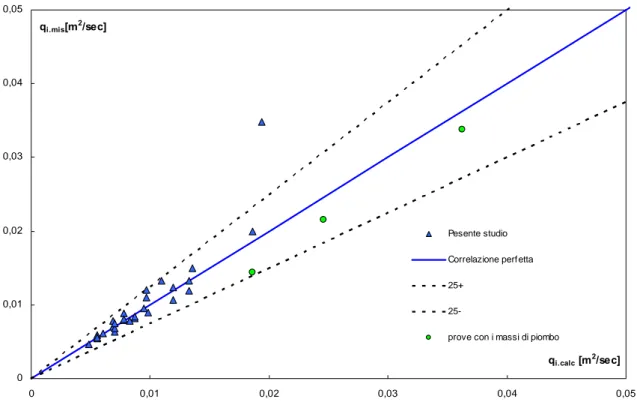
Nelle figura 5.51 e 5.52 viene fatto il confronto fra la portata misurata in corrispondenza dell’inizio movimento e quella calcolata con il precedente procedimento iterativo.

0 0,01 0,02 0,03 0,04 0,05 0 0,01 0,02 0,03 0,04 0,05 qi.calc [m2/sec] qi.mis[m2/sec] Pesente studio Correlazione perf etta 25+

25-prove con i massi di piombo Jaggi Bathurst Graf Chines Serra D'Elia

0 0,01 0,02 0,03 0,04 0,05 0 0,01 0,02 0,03 0,04 0,05 qi.calc [m2/sec] qi.mis[m2/sec] Pesente studio Correlazione perf etta 25+

25-prove con i massi di piombo

Figura 5.52: confronto fra le portate misurate nel presente studio e quelle calcolate.

5.3.6 Esempio numerico di calcolo della portata di inizio movimento per

una rampa a piede fisso.

Si ritiene opportuno eseguire un esempio di calcolo della portata critica di inizio movimento, per una rampa a piede fisso, utilizzando le relazioni trovate nel presente studio. Si consideri, ad esempio, una rampa di pendenza pari a 1V:4H e massi di dimensioni e peso specifico noti (D50= 26 mm e γs=2500 kg/m3).

Quindi i dati iniziali sono: • i0=1/4

• D50=26 mm

• γs=2500 kg/m3

La densità del grano immerso ∆ [-]e il diametro di attrito D50*[-], considerando una

viscosità cinematica ν a 20°C pari a 1x10-6 _m2_{/sec, per il materiale in esame risultano}

rispettivamente: 5 . 1 = − = ∆ ρ ρ ρ_s

3 1 2 50 * 50 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⋅∆ ⋅ = ν g D D =633.7

L’altezza liquida h rispondente a moto uniforme si determina considerando l’equazioni [5.38] e [5.39]: ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ + ⋅ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _⋅ ⋅ ∗ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− ⋅} ∗ 50 001 . 0 543 . 0 50 50 003 . 0 494 . 2 1 047 . 0 D e D D h e θ [5.38] 50 0 D i h ⋅ ∆ ⋅ = θ [5.39] Uguagliando queste ultime relazioni ( eq. [5.38] e [5.39] ) e procedendo iterativamente si determina l’incognita h. Quindi prendendo diversi valori di tentativo di altezza liquida e dopo alcuni passaggi iterativi si trova:

h=0.0147 m

La portata specifica viene calcolata utilizzando l’equazione di Manning.:

0 3 5 1 i h n q= ⋅ ⋅ [5.28] dove il coefficiente n viene valutato con la formula di Pagliara Chiavaccini (2004):

(

)

0.11 0 50 064 . 0 D i n= ⋅ ⋅

Quindi n risulta essere pari a :

(

0.026 0.25

)

0.368 064 . 0 ⋅ ⋅ 0.11= = n

In conclusione la portata specifica di una rampa con pendenza pari a 1V:4H e massi di dimensioni e peso specifico noti (D50= 26 mm e γs=2500 kg/m3 risulta:

(

0.015

)

0.25 0.0097 0368 . 0 1 3 5 = ⋅ ⋅ = q m2/sec

5.3.7 Valutazione del limite di validità delle relazioni trovate.

L’equazione [5.38] è stata elaborata considerando massi con 7 mm≤ D50 ≤50 mm e

pendenze della rampa comprese tra 1/3≤i0≤1/40 e inoltre con sommergente relative Z >0.4.

In questo paragrafo è stato ricercato un limite di validità delle relazioni trovate in quanto il parametro di mobilità, per sommergenze bassissime ( Z<0.2), non può crescere infinitamente. Inoltre, per questi valori di sommergenze, alcune curve calcolate per vari D50* con l’eq. [5.38] tendono ad intersecarsi. Il limite di crescita del parametro di mobilità

è stato valutato analizzando delle condizioni limite: sono state ricercate le coppie di valori Zlim e θlim corrispondenti a rampe con inclinazioni, rispetto al piano orizzontale,

coincidenti con gli angoli di attrito dei massi con cui sono state realizzate.

Servendosi del diagramma di Lane [1953] e classificando i massi presi in esame come moderatamente spigolosi sono stati valutati gli angoli di attrito corrispondenti.

Figura 5.53: angolo di attrito dei diversi materiali secondo Lane [1953].

Conoscendo le dimensioni dei massi e quindi l’angolo teorico della rampa corrispondente , attraverso la [5.38] è stata valutata la portata e il parametro di mobilità per questa condizione limite.

Le coppie di valori Zlim e θlim, così trovati, sono stati riportati nei diagramma di figura

[5.54] e in quello di figura [ 5.55] sono stati interpolati con una curva di equazione: Z

e ⋅ ⋅ =_0.064 2.64

0 0,05 0,1 0,15 0,2 0 1 2 Z [-] θ[-] D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D*=425 D*=557 D*=632 D*=1078 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 D50*=345.6 valori limiti teorici

Figura 5.54: andamenti delle curve calcolate con l’eq.[5.38] per vari D50*e inserimento

delle coppie Zlim e θlim corrispondenti alle condizioni limite e teoriche analizzate.

0 0,05 0,1 0,15 0,2 0 1 Z [-] θ[-] 2 D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D*=425 D*=557 D*=632 D*=1078 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 D50*=345.6 valori limiti teorici curva teorica limite

Figura 5.55: inserimento della curva limite che interpola le coppie Zlim e θlim

Nei diagrammi seguenti sono riportati gli andamenti delle curve calcolate con l’equazione [5.38] e limitate dalla curva limite valutata con la relazione [5.40]

0 0,05 0,1 0,15 0,2 0 1 Z [-] θ[ −] 2 D50*=425 [D50=17.5 mm] D50*=557 [D50=22.9 mm] D50*=632 [D50=26 mm] D50*=990.4 [ D50=40.7 mm] D50*=345.6 [D50=14.2 mm] 0.047 0.06 D*=425 D*=557 D*=632 D*=1078 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 D50*=345.6 curva teorica limite

Figura 5.56: andamenti delle curve calcolate con l’eq.[5.38] per vari D50*

0 0,05 0,1 0,15 0,2 0 1 2 3 4 h/D50 [-] θ[-] D50*=425 [D50=17.5 mm] D50*=441 [D50=17.75 mm] Serra D'Elia D50*=548.3[D50=22.05 mm] Chines D50*=545 [D50=22.2 mm] Bathurst D50*=557 [D50=22.9 mm] D50*=584.33 [D50=23.5 mm] Jaggi D50*=600 [D50=23.5 mm] Graf D50*=632 [D50=26 mm] D50*=850.4 [D50=34.2 mm] Chines D50*=990.4 [ D50=40.7 mm] D50*=1078 [D50=44.3 mm] Bathurst D50*=285.9 [D50=11.5 mm] Serra D50*=300 [D50=12 mm] Pender D50*=345.6 [D50=14.2 mm] D50*=174 [D50=7.15] Pender 0.047 0.06 D*=425 D*=557 D*=632 D*=300 D*=1078 D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 D50*=372.8

D50*=345.6 limite critico inferiore

Figura 5.57: andamenti delle curve calcolate con l’eq.[5.38] per vari D50*

e limitate dalla curva teorica limite [5.40].

0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Z [-] θ[-] D50*=425 [D50=17.5 mm] D50*=441 [D50=17.75 mm] Serra D'Elia D50*=548.3[D50=22.05 mm] Chines D50*=545 [D50=22.2 mm] Bathurst D50*=557 [D50=22.9 mm] D50*=584.33 [D50=23.5 mm] Jaggi D50*=600 [D50=23.5 mm] Graf D50*=632 [D50=26 mm] D50*=850.4 [D50=34.2 mm] Chines D50*=990.4 [ D50=40.7 mm] D50*=1078 [D50=44.3 mm] Bathurst D50*=279.7 [D50=11.25 mm] Chines D50*=285.9 [D50=11.5 mm] Serra D50*=300 [D50=12 mm] Pender D50*=328.2 [D50=13.2 mm] Jaggi D50*=345.6 [D50=14.2 mm] D50*=174 [D50=7.15] Pender 0.047 0.06 D*=174 D*=425 D*=557 D*=632 D*=300 D*=1078 Eq.Armanini D50*892.6 [D50=35.9 mm] D50*=372.8 [massi di piombo D=8.2 mm] D*=892 h/D50=1.1 h/D50=16 D50*=372.8 curva limite teorica

Figura 5.58: andamenti delle curve calcolate con l’eq.[5.38] per vari D50*e limitate dalla