4 Analisi dimensionale. 4.1 Analisi dimensionale per la stabilità delle rampe in massi.

4 Analisi dimensionale.

4.1 Analisi dimensionale per la stabilità delle rampe in massi.

Il fenomeno idraulico oggetto del presente studio è influenzato da diverse variabili che devono essere opportunamente individuate al fine di descrivere in modo completo il processo di scavo a valle di rampe in pietrame.

Il fenomeno è studiato in un modello a scala ridotta utilizzato per potere predire il comportamento del sistema reale in relazione ad alcune caratteristiche.

Il concetto alla base della realizzazione di modelli atti a predire fenomeni reali è la similitudine che può essere limitata solo a determinate grandezze meccaniche (similitudine geometrica, cinematica, dinamica) o, preferibilmente, può estendersi a tutte le grandezze a seconda della complessità che ne deriva.

Il fenomeno qui analizzato, come ogni altro fenomeno reale, è caratterizzato da una serie di parametri (variabili indipendenti o di controllo) attraverso i quali è possibile esprimere ogni altra grandezza di interesse.

Il teorema di Buckingham costituisce il fondamento teorico dell’analisi dimensionale. Esso permette di scegliere parametri tra loro indipendenti, atti a rappresentare una base di un sistema di unità di misura, ed esprimere ogni altra variabile come prodotto di potenze delle grandezze base del sistema di unità scelto.

Se un fenomeno è funzione di n variabili e se le n variabili possono essere descritte da m grandezze fondamentali, allora è possibile raggruppare le n variabili in n-k termini adimensionali che descrivono il fenomeno stesso; k può essere minore o uguale a m ma in genere k=m.

Nella maggior parte dei casi in idraulica si pone m=3.

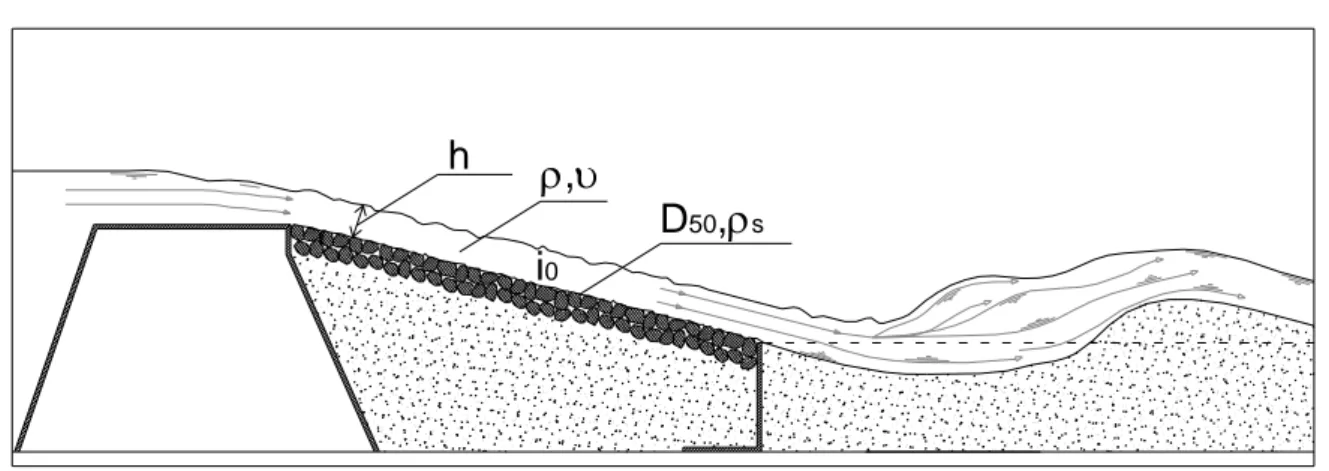
Le variabili che entrano in gioco nell’incipiente movimento di materiale incoerente su rampe inclinate i0 sono variabili di fluido (densità “ρ”,viscosità “ν”) variabili di gravità

(accelerazione di gravità “g”, inclinazione rampa “i0”), grandezze caratterizzanti la

corrente ( altezza liquida h), variabili caratterizzanti il materiale di trasporto ( densità dei massi “ρs”,diametro corrispondente al 50% della curva granulometrica dei massi

ρ

,

υ

D

50

,

ρ

s

h

i

0

Figura 4.1: grandezze che influenzano l’incipiente movimento di materiali incoerente su rampe inclinate

Il fenomeno dell’incipiente moto nelle rampe in massi ,qui studiato, può essere rappresentato dalla seguente legge funzionale:

F=f (ρ,ν,g, i0, h, ρs-ρ, D50)

dove:

r→ densità dell’acqua [M⋅L-3]

g→ accelerazione gravitazionale [L⋅T-2

] i0→ pendenza della rampa [-]

h→ tirante liquido sulla rampa [L]

D50→ diametro corrispondente al 50 % di passante della curva granulometrica [L]

ρs: → densità del materiale [M⋅L-3]

ν→ viscosità dell’acqua [L2_⋅T-1

]

Si sceglie come terna di riferimento la seguente: (ρ, D50, g)

Siano:

7 =

n numero delle variabili da cui dipende il fenomeno

3 =

I gruppi adimensionali, in numero pari a n-m=4, sono i seguenti:

(

D g h

)

f₁ , ₅₀, , 1 = ρ Π

(

50 0

)

2 2 = f ρ,D ,g,i Π

(

ρ ρ −ρ

)

= Π₃ f₃ ,D₅₀,g, _s

(

ρ, ₅₀, ,ν

)

4 4 = f D g Π

Ricerchiamo, ad esempio, il gruppo funzionale P1:

P1= ρa⋅D50b⋅gg h1

Sostituendo le unità di misura di ciascuna variabile: P1= [M⋅L-3]a⋅[L]b [L⋅T-2]g⋅[L]1

Essendo P1 un gruppo adimensionale, i valori numerici delle costanti α, β, γ si deducono

risolvendo il sistema di tre equazioni in tre incognite che deriva dalla precedente equazione: ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − = + + + − = = γ γ β α α 2 0 1 3 0 0

⇒

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ = − = = 0 1 0 γ β α Da cui: 50 1 D h = Π

Analogamente,ripetendo la procedura per il gruppo funzionale P2 si ottiene:

P2= ρa⋅D50b⋅gg i01

P2= [M⋅L-3]a⋅[L]b [L⋅T-2]g⋅[-]1

I valori numerici delle costanti α, β, γ si deducono risolvendo il sistema di tre equazioni in tre incognite che deriva dalla precedente equazione:

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − = + + − = = γ γ β α α 2 0 3 0 0

⇒

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ = = = 0 0 0 γ β α Da cui: P2= i0

Per il gruppo funzionale P3 si trova: P3= ρa⋅D50b⋅gg ρs1 P3= [M⋅L-3]a⋅[L]b [L⋅T-2]g⋅[ M⋅L-3]1 ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − = − + + − = + = γ γ β α α 2 0 3 3 0 1 0

⇒

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ = = − = 0 0 1 γ β α Da cui: ρ ρ ρ − = Π s 3

Infine analizzando il gruppo funzionale P4:

P4= ρa⋅D50b⋅gg ν1 P4= [M⋅L-3]a⋅[L]b [L⋅T-2]g⋅[ L2⋅T-1]1 ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − − = + + + − = = 1 2 0 2 3 0 0 γ γ β α α

⇒

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − = − = = 2 / 1 2 / 3 0 γ β α Da cui: g D ⋅ = Π 3 50 4 ν

Sfruttando un’altra particolarità del teorema di Buckingham si posso ricavare nuovi raggruppamenti combinando adeguatamente quelli gia determinati.

Tra questi, è risultato essere di notevole importanza nel presente studio la combinazione dei gruppi P3 e P4 e quella con i gruppi P2, P1 e P2 :

[ ]

[ ]

∗ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⋅∆ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = Π Π = Π 50 3 1 2 50 3 2 3 50 3 1 3 2 4 3 1 3 5 D g D g D s ν ν ρ ρ ρ

50 0 3 2 1 6 D i h ⋅ ∆ ⋅ = Π Π ⋅ Π = Π

Quest’ultima combinazione coincide con il parametro di mobilità di Shields:

(

)

(

)

(

(

)

)

50 0 50 0 50 2 50 0 D i h D i h g D u D _{s s} s ∆⋅ ⋅ = ⋅ − ⋅ ⋅ ⋅ = ⋅ − ⋅ = ⋅ − = ∗ γ γ ρ γ γ ρ γ γ τ θ dove: 2 0 =ρ⋅u∗

τ → tensione tangenziale al fondo

0 2 i h g u∗ = ⋅ ⋅ → velocità di attrito

In conclusione, i gruppi funzionali utilizzati nell’analizzare la stabilità delle rampe sono:

Z D h = = Π 50 1 → sommergenza relativa

P2= i0 → pendenza della rampa

∗ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⋅∆ = Π 3 ₅₀ 1 2 50 5 D g D

ν → diametro caratteristico o di attrito.

50 0 6 D i h ⋅ ∆ ⋅ = Π → parametro di Shields.