Ellissoide di rotazione APPENDICE A

APPENDICE A

Ellissoide di rotazione

Il tensore di diffusione può essere visualizzato mediante un ellissoide i cui assi principali hanno le direzioni coincidenti con quelle della base di autovettori della matrice associata al tensore stesso. Tale ellissoide viene chiamato “ellissoide di rotazione” ed indicato con ER. In un caso generale l’ellissoide viene visualizzata come segue:

Figura A.1: Ellissoide di rotazione associato ad un tensore in un caso generale.

.

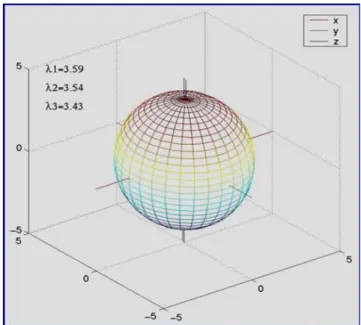
Figura A.2: Ellissoide di rotazione associato ad un tensore in caso di isotropia.

Una rappresentazione più completa, in cui per ogni voxel abbiamo il corrispondente ellissoide di rotazione, assume la seguente forma:

Figura A.3: Rappresentazione del tensore di diffusione mediante ellissoide di rotazione in una regione di

L’ellissoide di rotazione associato al tensore di diffusione ottenuto in ambito DTI può fornire non solo una misura quantitativa della diffusione ed indipendente dalla direzione di acquisizione, ma anche la direzione predominante del moto delle molecole d’acqua in ogni voxel dell’immagine.

APPENDICE B

Indici di anisotropia C

L

, C

P

, C

S

Come visto finora un tensore di diffusione D è un tensore di ordine 2 che può essere rappresentato con una matrice 3x3 contenente le sue 32 = 9 componenti. Se, inoltre, tale tensore è simmetrico la matrice ad esso associata assume la seguente forma:

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 33 23 13 23 22 12 13 12 11 D D D D D D D D D D (B. 1)

Sappiamo che è possibile ricavare gli autovalori λ del tensore risolvendo l’equazione:

( D – λI ) e = 0 (B. 2)

dove e rappresenta un possibile autovettore del tensore e I è la matrice identità di ordine 3.

Se l’equazione sopra ha soluzioni per e ≠ 0 allora dobbiamo imporre:

Det (D – λI ) = | D – λI | = 0 (B. 3)

Scrivendo in forma estesa il determinante al primo membro otteniamo il cosiddetto “polinomio caratteristico” della matrice:

(

)

0 33 23 13 23 22 12 13 12 11 33 23 23 22 33 13 13 11 22 12 12 11 33 22 11 2 3 _{− =} ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + λ + + + λ − λ D D D D D D D D D D D D D D D D D D D D D D D D (B. 4)

Essendo gli autovalori λ scalari ed indipendenti dalla scelta del sistema di riferimento, anche i coefficienti: I₁ =

(

D₁₁+D₂₂+D₃₃

)

(B. 5) 33 23 23 22 33 13 13 11 22 12 12 11 2 _{D D} D D D D D D D D D D I = + + (B. 6) 33 23 13 23 22 12 13 12 11 3 D D D D D D D D D I = (B. 7)

sono tali e rappresentano infatti degli “invarianti” del tensore.

Utilizzando la conoscenza dei suoi autovalori ed autovettori possiamo scrivere la matrice associata al tensore nel seguente modo:

D=

(

e~₁ e~₂ ~e₃

)

−1diag

(

λ₁,λ₂,λ₃

)(

e~₁ ~e₂ ~e₃

)

(B. 8)

e nel caso di tensore simmetrico (i cui autovalori hanno tutti valori reali) si ha:

ottenendo la cosiddetta “decomposizione ai valori singolari” della matrice (B. 1).

Facendo riferimento a questa espressione possiamo dividere il processo di diffusione molecolare in tre casi basilari:

1) lineare ( >>λ₁ λ2 ≅ λ3) : il fenomeno diffusivo si ha principalmente lungo la direzione individuata dall’autovettore associato all’autovalore di valore massimo λ₁; in questo caso si può scrivere:

D≅λ₁D_L =λ₁e~₁e~₁T (B. 10)

2) planare (λ₁≅ λ2>>λ3): il fenomeno diffusivo si ha principalmente nel piano individuato dai due autovettori associati ai due autovalori di valore

maggiore λ₁ e λ₂; in questo caso possiamo scrivere:

D≅2λ₁D_P =λ₁

(

e~₁~e₁T +~e₂e~₂T

)

(B. 11)

3) sferica (λ₁≅ λ2 ≅ λ3) : il fenomeno diffusivo è isotropico e si può scrivere:

D≅3λ₁D_S =λ₁

(

e~₁e~₁T +~e₂e~₂T +e~₃e~₃T

)

(B. 12)

Un qualsiasi processo diffusivo può essere pensato come combinazione dei tre precedenti casi ed un qualunque tensore di diffusione può essere ottenuto da una combinazione lineare dei tre tensori relativi ai tre casi precedenti. A livello algebrico abbiamo infatti:

T 3 3 3 T 2 2 2 T 1 1 1~e ~e ~e ~e ~e ~e D=λ +λ +λ = = ) ~ ~ ~ ~ ~ ~ ( ) ~ ~ ~ ~ )( ( ~ ~ ) ( T 3 3 T 2 2 T 1 1 3 T 2 2 T 1 1 3 2 T 1 1 2 1−λ e e + λ −λ e e +e e +λ e e +e e +e e λ = =(λ1−λ2)DL +(λ2−λ3)DP+λ3DS (B. 13)

dove (_λ1−λ2), (λ₂ −λ₃) e λ3 rappresentano le coordinate di D rispetto alla base di

riferimento formata dai tensori D_L, D_P e D_S.

Si introducono a questo punto i tre seguenti parametri, che sono invarianti del tensore di diffusione in quanto funzioni soltanto dei suoi autovalori:

1 2 1 λ λ − λ = L C (B. 14) 1 3 2 P C λ λ − λ = (B. 15) 1 3 S C λ λ = (B. 16)

Chiaramente vale la seguente relazione:

C_L +C_P +C_S =1 (B. 17)