121 CAPITOLO 4 L’ intrusione di acqua salata nelle falde a seguito della realizzazione di darsene

(1)

CAPITOLO 4

L’ intrusione di acqua salata nelle falde a seguito della realizzazione di darsene

La realizzazione di una darsena interna al litorale può provocare l’entrata di acqua salata proveniente dal mare in zone dell’entroterra dove prima non era presente, con il conseguente probabile inquinamento delle falde da acqua salmastra .

Il problema diventa particolarmente grave laddove l’acqua salata raggiunge zone del terreno dove in precedenza l’acqua di falda non risultava contaminata dall’acqua di mare, pregiudicando l’utilizzo della falda per scopi irrigui e potabili.

Nasce quindi la necessità di valutare il fenomeno per poter in qualche misura prevedere il rischio di inquinamento delle falde, nel quadro di una sempre maggiore attenzione nella progettazione ai problemi ambientali, problemi che possono pregiudicare la reale bontà ed utilità dell’opera proposta, nonostante gli altri aspetti progettuali possano essere stati affrontati in maniera accurata.

Le varie istituzioni, siano esse nazionali o regionali ed gli stessi enti locali, stanno puntando sempre più l’attenzione su tale tipo di problematiche, prescrivendo uno studio attento dell’intrusione salina in previsione della realizzazione di darsene, come si può facilmente constatare consultando gli atti e le delibere dei vari organi preposti (Piani di indirizzo territoriale, Piani territoriali di coordinamento paesistico, Piani strutturali comunali ecc…).

D’altra parte, il fenomeno dell’intrusione salina è sempre più rilevante negli acquiferi costieri; esso è un fenomeno naturale ed è dovuto alla maggiore densità dell’acqua del mare rispetto a quella delle falde: questa differenza è tale da creare un “cuneo” di acqua salata che avanza verso l’entroterra a partire dagli strati più bassi dell’acquifero, fenomeno aggravato dalle modificazioni antropiche come il sovrasfruttamento delle risorse idriche, ovvero dall’emungimento spinto e generalizzato di acqua di falda a scopo irriguo, potabile e talvolta industriale e dagli scavi di terreno; la conseguenza è un richiamo del cuneo salino verso le zone più lontane dalla linea di costa ed una contaminazione delle acque dolci di falda anche nelle zone più interne dell’acquifero; i risultati negativi possono essere sia per l’uomo che per l’ambiente, infatti se da una parte il rischio per l’uomo è quello di pregiudicare

(2)

l’utilizzo irriguo e potabile a causa dell’ emungimento di acqua con elevate percentuali di cloruri, quello per la risorsa naturale è di una salinizzazione spinta degli acquiferi con risalita di acqua salata verso la superficie del terreno, con conseguenze negative facilmente immaginabili sia per le colture che per la vegetazione costiera ( es. pinete).

Gli interventi fino ad oggi più utilizzati per arrestare l’entrata del cuneo salino nelle falde si riassumono in poche tipologie:

- Interventi tesi a ‘rinforzare la falda idrica’, mediante ravvenamento della stessa

con pozzi di ricarica opportunamente ubicati nel territorio, nell’intento di aumentare il carico di acqua dolce gravante sul cuneo salino in entrata dalle zone più profonde della falda.

- Interventi strutturali veri e propri, caratterizzati dalla costruzione di barriere

sommerse, generalmente in calcestruzzo gettato in opera o prefabbricato, oppure costituite da getti continui di argilla-bentonite, che hanno la funzione di bloccare letteralmente l’avanzata del cuneo salino nell’area di interesse. E’ un intervento invasivo che necessita di una conoscenza approfondita del sottosuolo, per l’individuazione dei substrati impermeabili e l’eventuale raggiungimento da parte delle opere. Tra i tipi di barriere utilizzabili vi è anche la membrana ad osmosi inversa, utilizzata finora negli U.S.A., atta a creare una impossibilità di diffusione dell’acqua salata nella falda.

- Interventi tesi a bloccare la risalita dell’acqua salata nei fiumi. I fiumi, infatti,

rappresentano un importante veicolo di risalita per l’acqua salata nell’entroterra, a causa dell’entrata attraverso le foci, per questo impedire l’avanzamento dal mare dell’acqua salata attraverso il corso d’acqua può essere importante. A tale scopo sono state finora utilizzate barriere in acciaio autobloccanti durante il riflusso dell’alta marea (Po, Adige),e barriere sommerse in terra (U.S.A.), mentre è in fase di studio l’utilizzo di particolari getti d’aria verticali (barriere d’aria, Giappone), tali da creare un moto vorticoso che arresti l’avanzata del cuneo salino ( ipotesi valida nel solo caso di velocità non nulla della corrente d’acqua dolce ).

Di seguito riportiamo uno studio del fenomeno teso ad individuare le leggi che ne governano il funzionamento, nell’intento di una utilizzazione delle stesse per l’applicazione a casi reali, che verranno in seguito esaminati.

(3)

Lo studio dell’ avanzamento del cuneo salino al di sotto delle opere previste per la darsena in esame si può eseguire basandosi su due tipi diversi di approccio allo studio del fenomeno:

-Studio del fenomeno dal punto di vista idrostatico -Studio del fenomeno dal punto di vista idrodinamico

Senza dubbio il secondo aspetto è quello che descrive più accuratamente il fenomeno dell’intrusione del cuneo nella falda idrica, tuttavia necessita di un maggior numero di dati iniziali.

Non si può quindi prescindere da un’analisi del fenomeno dal punto di vista statico, infatti essa rappresenta un punto di partenza per un successivo e più accurato studio di tipo dinamico, nonché una base per un confronto dei risultati nei due schemi di valutazione. In entrambi i casi sono state formulate notevoli ipotesi semplificative, che potrebbero essere avvalorate solo da indagini più accurate nella zona in esame e quindi da un maggior numero di dati di campo.

4.1. Studio del fenomeno dal punto di vista idrostatico

Questo approccio si basa essenzialmente sull’ applicazione del principio di eguaglianza delle pressioni tra acqua dolce e salata sull’ interfaccia, ovvero del principio di Ghyben-Herzberg. In altre parole si suppone di studiare il caso in condizioni idrostatiche, una volta che si è raggiunto l’ equilibrio tra l’acqua salata in avanzamento dal mare e l’acqua dolce di falda già presente, senza tenere di conto che quest’ultima rappresenta una massa d’acqua in avanzamento verso la linea di costa. La relazione che regola il fenomeno è il noto principio di seguito riportato:

(

s

)

f

s s f

s

p

h

H

p

=

⇒

⋅

γ

=

+

⋅

γ

(1) dove

p

_s = pressione acqua salata

p

_f = pressione acqua dolce alla

(4)

L.M.M.

Livello di falda

g

s

h

s

Strato impermeabile

Interfaccia acqua dolce/salata

H

h

s

g

f

Acqua salata

Acqua dolce

Fig.4.1. Cuneo salino: caso generale

Da questa, dopo una serie di passaggi, si arriva alla relazione: H h f s f s =

_γ

₋

_γ

⋅

γ

(2) Supponendo 3

000 .

1 m

tonn

f

=

γ

e 3

025 .

1 m

tonn

s

=

γ

si ottiene la forma semplificata:

H

h

_s

≅ 40

⋅

(3)

La stessa relazione (2) si può scrivere anche così, dividendo num. e den. per

g

:

H

h

f s f s

=

_ρ

₋

_ρ

⋅

ρ

(4)

(5)

4.2. Studio del fenomeno dal punto di vista idrodinamico

Come fu osservato da M.K.Hubbert (1940), a causa del deflusso dell’acqua dolce nella falda acquifera verso il mare, l’interfaccia tra acqua dolce e salata si trova ad una profondità maggiore di quella valutabile in condizioni statiche. E’ quindi necessario studiare il fenomeno dell’intrusione salina da un punto di vista idrodinamico ipotizzando la presenza di una portata q=cost di acqua dolce per unità di larghezza della falda diretta verso il mare. In altre parole, quindi, dobbiamo imporre un andamento lineare della piezometrica, che peraltro non si discosta molto dall’andamento ricostruito dalla carta delle isopieze nel precedente paragrafo.

In un analisi di tipo idrodinamico compaiono quindi altre variabili, quali appunto la portata q, ma anche la permeabilità del terreno alle varie profondità, dipendente dalla stratigrafia e da altre caratteristiche del terreno. Dobbiamo anche in questo caso formulare delle ipotesi semplificative, ottenendo però dei risultati più accurati rispetto ad una schematizzazione idrostatica del problema. Infatti a rigor di logica, nello schematizzare l’intrusione dell’acqua salata nei vari strati del terreno non si può prescindere dalla natura di questi e dal fatto che l’acqua di falda sia in movimento verso il mare.

4.2.1 Relazione tra la pendenza della piezometrica e quella dell’interfaccia

Lo studio della relazione che lega la pendenza della piezometrica a quella della linea di separazione acqua dolce-salata parte dall’analisi delle linee di flusso della corrente di falda e delle relative linee equipotenziali ( Fig. 4.2)

Se vogliamo calcolare la profondità dell’interfaccia acqua dolce-salata sulla verticale passante per il punto A, la legge di Ghyben-Herzberg (3) ci fornisce la profondità

GH

H del punto

P

'

, che si trova sulla retta passante per O, punto dove la linea

(6)

Linee equipotenziali

Acqua dolce

Interfaccia HGH HR P P' O Linee di flusso

Mare

A Substrato impermeabile

Acqua salata

(cuneo salino)

Fig.4.2. Differenza tra la profondità reale dell’interfaccia e quella calcolata con la relazione di Ghyben-Herzberg

Tuttavia, nella realtà, il punto

P

'

si deve trovare sulla linea equipotenziale che passa

per A e quindi si ha che H_R >H_GH.

La relazione tra pendenza della piezometrica e dell’interfaccia può essere messa in luce partendo dalla legge di Darcy scritta in forma differenziale:

ds dH K

V = P (5)

dove

ds

è la distanza tra 2 linee

equipotenziali infinitamente vicine (Fig.4.3)

La stessa può essere scritta nella forma:

δ

sin = = ds dH K V _P

(6) _{Fig.4.3. Relazione tra le pendenze della}

(7)

Analizzando la fig.4.3, si può scrivere:

ds

dH

_i

=

ε

sin

(7)

Sostituiamo nella (7) il valore di

H

_i ricavabile dalla relazione di Ghyben-Herzberg

(4):

ds

dH

_P f s f

ρ

ε

−

=

sin

(8)

Sostituendo la (6) nella (8) si ricava la relazione:

K

V

f s f

ρ

ε

−

=

sin

(9)

Le relazioni (6), (8) e (9) mostrano che l’angolo

ε

formato dalla tangente

all’interfaccia in un punto generico con l’orizzontale varia al variare di quello

della tangente alla piezometrica e che

sin

ε

è circa 40 volte più grande di

δ

sin

.

Inoltre, siccome la piezometrica e l’interfaccia acqua dolce-salata convergono verso il mare in uno stesso punto, a parità di portata, in questa direzione aumenta la velocità V ( infatti diminuisce la sezione disponibile al deflusso dell’ acqua dolce

): da questo si evince che sia

ε

che

δ

aumentano avvicinandosi al mare e

che nel tratto in cui è presente l’ interfaccia acqua dolce-salata, la piezometrica non ha più un andamento lineare.

4.2.2 La legge di Todd

Nel punto in cui la linea piezometrica della falda di acqua dolce raggiunge la superficie

libera del mare si ha

H

_P

=

0

; sostituendo questo valore nella relazione di

Ghyben-Herzberg (4), si ottiene che anche

H

_i

=

0

; questo dimostra che pelo libero del

mare, linea piezometrica ed interfaccia acqua dolce-salata si incontrano in un unico punto O.

In definitiva, si potrebbero presentare le due situazioni riportate schematicamente nella figura 4.4.

(8)

Nel caso dell’ immagine 4.4.a il deflusso dell’ acqua dolce verso il mare avverrebbe lungo la stessa linea di costa e quindi , attraverso una sezione di

dimensione nulla; poiché la portata

q

=

V

×

A

=

cost ( dove V è la velocità di

deflusso dell’ acqua dolce ed A la sezione totale dei vuoti del terreno attraversata dall’ acqua stessa ), se fosse A = 0 si

avrebbe che

V

=

∞

, il che è

naturalmente assurdo.

Per questo il caso che si deve ammettere nella realtà è quello della fig.4.4.b, in cui una parte di acqua dolce fuoriesce dal terreno anche al di sopra del livello del mare.

Sperimentalmente si è constatato che l’altezza t sul livello del mare del punto d’intersezione fra piezometrica e superficie del terreno è di solito molto piccola (dell’ ordine di qualche decina di centimetri). Quindi, per avere una semplificazione nei successivi calcoli teorici, si

potrà fare riferimento al caso ideale della figura 4.4.a.

Per calcolare la portata di acqua dolce q che si versa in mare, la cui superficie è situata al livello h al di sopra di un ipotetico strato impermeabile del terreno, adottiamo lo schema reale di fig. 4.5 , in cui abbiamo fissato un sistema di riferimento cartesiano [ O; s,Hp ] nel quale l’origine O coincide con il punto d’intersezione tra pelo libero del mare, linea piezometrica ed interfaccia acqua dolce-salata.

Lungo l’asse delle ascisse s si misurano le distanze da O delle sezioni parallele alla costa, mentre lungo l’asse delle ordinate Hp si misurano le altezze della linea piezometrica. O t O

b

a

Fig.4.4. Intersezione tra superficie del mare,piezometrica ed interfaccia

(9)

Il valore h rappresenta la quota del pelo libero del mare rispetto al livello impermeabile inferiore della falda ( o ad un generico piano di riferimento che ci permetta di definire l’avanzamento L del cuneo salino verso l’entroterra ).

In altre parole tutti i calcoli seguenti verranno eseguiti ipotizzando l’esistenza di un livello impermeabile inferiore del terreno ad andamento orizzontale, che può essere schematicamente sostituito con un piano di riferimento orizzontale ad una generica distanza h dalla superficie libera del mare.

O

H

p

L

H

_H

p

B

h

s

A

H

i

Fig 4.5. Schema di riferimento per la dimostrazione della legge di Todd

Partiamo ancora dalla relazione di Darcy (5) scritta in forma differenziale:

ds dH K

V = P (10)

Separiamo le variabili e moltiplichiamo entrambi i membri per Hi:

ds

K

H

V

dH

H

_i

⋅

_p

=

⋅

i

⋅

(11)

nella relazione precedente poniamo

q

=

V

⋅

H

_i

=

cost; essa rappresenta la portata di

acqua dolce che defluisce in mare per unità di larghezza della falda.

Sostituiamo poi la relazione di Ghyben-Herzberg (4) al posto di Hi presente al primo membro della relazione:

(10)

ds

K

q

dH

H

_p _p f s f

_⋅

₌

_⋅

−

ρ

(12)

Se osserviamo la fig.1.14 si vede che mentre in A risulta s = 0 e Hp = 0 , in B abbiamo s = L e Hp = H.

Con le condizioni al contorno suddette, integriamo la (12) tra le sezioni s = 0 e s = L

:

ds

K

q

dH

H

L p p H f s f

∫

⋅

=

⋅

−

ρ

₀ ₀

ρ

(13)

Svolgendo il calcolo risulta:

K

L

q

H

f s f

⋅

=

⋅

−

2

1 ρ

ρ

(14)

Applicando nuovamente la relazione (4) di Ghyben-Herzberg alla sezione s = L si ha:

h

H

f f s

−

_⋅

=

ρ

(15)

Sostituendo infine la (15) nella (14) si ottiene:

(

)

K

L

q

h

f f s f s f

_⋅

−

₌

⋅

−

2 2 2

2

1 ρ

ρ

(16) e quindi:

L

h

K

q

f f s 2

2

1 _⋅

−

_⋅

⋅

=

ρ

(17)

Questa è la formula proposta da D.K.Todd nel 1959, che ne ha dimostrato solo sperimentalmente la validità. Essa può essere applicata anche alle falde artesiane, sostituendo la grandezza h con lo spessore b della falda.

La (17) fornisce anche la lunghezza L di avanzamento del cuneo salino nell’entroterra.

Questa lunghezza, vista la piccola entità dell’altezza sul livello del mare del punto d’intersezione della piezometrica con la superficie del terreno, può essere confusa con

(11)

4.2.3 Equazione dell’ interfaccia acqua dolce-salata

Nel paragrafo successivo sarà illustrato il procedimento analitico per la ricerca di relazioni che descrivano l’andamento della linea di separazione tra acqua dolce e salata, in presenza di uno o più strati geologici, ognuno caratterizzabile dal suo valore di permeabilità K.

Inoltre la dimostrazione sarà svolta nell’ipotesi che la portata di acqua dolce per unità di larghezza della falda q si mantenga costante.

Unico strato geologico avente coeff. di permeabilità K

Per la ricerca di una relazione che descriva l’andamento dell’interfaccia acqua dolce-salata, si fa riferimento alla figura 4.6, in cui è stato fissato un sistema di riferimento cartesiano [ O; x,y ] in cui l’ origine O coincide con l’intersezione tra pelo libero dell’acqua marina, linea piezometrica e linea d’interfaccia.

L

H

i

h

A

O

y

Q

P

y

(H

i

)

x

(s)

x

Fig.4.6. Schema di riferimento per il calcolo dell’equazione che descrive l’interfaccia

Misuriamo la distanza s del generico punto P dell’interfaccia lungo l’asse x e la sua profondità Hi rispetto al livello del mare lungo l’asse y.

(12)

K

V

ds

dH

f s f i

⋅

−

=

ρ

(18)

Separiamo le variabili e moltiplichiamo entrambi i membri per Hi:

ds

K

q

dH

H

f s f i i

⋅

=

_ρ

₋

_ρ

⋅

ρ

(19)

dopo aver posto , analogamente a quanto fatto nella dimostrazione della legge di Todd,

=

⋅

=

V

H

_i

q

cost.

Integriamo la (19) tra la generica sezione s = x e la generica sezione s = L, tenendo presente che :

a. Per 0 < x < L si ha 0 < y < h ( generico punto P ) b. Per x = L si ha y = h ( punto Q )

ds

K

q

dH

H

L x f s f i i h y

∫

⋅

−

=

⋅

ρ

(20) Si ottiene così:

(

)

(

L

x

)

K

q

y

h

f s f

_⋅

₋

−

=

−

ρ

2 2

2

1

(21) e quindi:

(

)

2 2

2 h

x

L

K

q

y

f s f

_⋅

₋

₊

−

⋅

=

ρ

(22)

La legge (17) di Todd è la seguente:

q

h

K

L

f f s 2

2

1 _⋅

−

_⋅

⋅

=

ρ

(23)

(13)

Sostituendola nella (22), si trova l’equazione:

x

K

q

y

f s f

_⋅

−

⋅

=

ρ

2

(24)

Questa è l’ equazione di una parabola del tipo 2

y

a

x

=

⋅

e quindi passante per

l’origine O e con la concavità rivolta nel verso positivo dell’asse x.

La concavità della parabola, secondo la stessa equazione, è legata alla portata q di acqua dolce per unità di lunghezza della falda, al coefficiente di permeabilità K e alle densità dell’ acqua salata e dell’acqua dolce.

Si può quindi introdurre, per semplificare l’equazione, il parametro di concavità:

K

q

A

f s f

_⋅

−

⋅

=

ρ

2

(25) avente dimensioni

[ ]

L

T

L

T

L

=

⎥

⎦

⎤

⎢

⎣

⎡

3

, vale a dire quelle di una distanza.

Inserendo A nella (24) l’ equazione diventa:

x

A

y

=

⋅

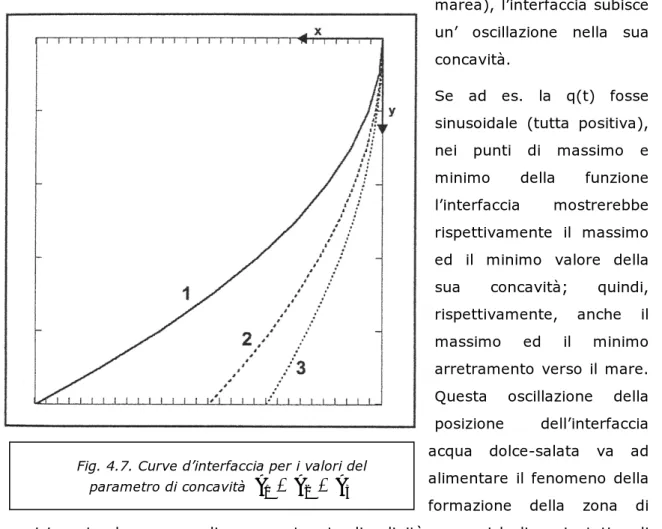
(26)

La relazione precedente ci permette di tracciare una diversa linea d’interfaccia a seconda del valore assunto dal parametro di concavità A, cioè dalle diverse grandezze dalle quali dipende.

Ad esempio, tracciamo le parabole relative a tre valori

q

₁

<

q

₂

<

q

₃ di portata e

quindi relativi a tre valori

A

₁

<

A

₂

<

A

₃ del parametro di concavità. Le linee

(14)

Se vogliamo interpretare i risultati da un punto di vista fisico, si può affermare che la rappresentazione precedente è avvalorata, in quanto un aumento di portata genera un aumento dei carichi che si oppongono all’avanzamento del cuneo salino.

Sempre analizzando il grafico si può osservare che, se la portata è variabile nel tempo con legge q(t) , a parità di altre condizioni ( supponendo ad esempio che , mentre q varia, il livello del mare si mantenga costante, vale a dire che il periodo di una eventuale oscillazione della funzione q(t) sia minore di quello della funzione di marea), l’interfaccia subisce un’ oscillazione nella sua concavità.

Se ad es. la q(t) fosse sinusoidale (tutta positiva), nei punti di massimo e minimo della funzione l’interfaccia mostrerebbe rispettivamente il massimo ed il minimo valore della sua concavità; quindi, rispettivamente, anche il massimo ed il minimo arretramento verso il mare. Questa oscillazione della posizione dell’interfaccia acqua dolce-salata va ad alimentare il fenomeno della formazione della zona di transizione tra le acque a diverso contenuto di salinità, per cui la linea ipotetica di separazione tra acqua di falda ed acqua marina non è netta, ma diventa una zona estesa in cui la salinità varia gradualmente.

Le stesse parabole illustrate nella figura 4.7 possono anche essere disegnate per tre

valori

K

₁

>

K

₂

>

K

₃ del coefficiente di permeabilità o per tre valori

ρ

_s₁

>

ρ

_s₂

>

ρ

_s₃

della densità dell’acqua salata, per cui si ha ancora

A

₁

<

A

₂

<

A

₃.

Infatti un coefficiente di permeabilità maggiore provoca una maggiore facilità del

moto dell’acqua salata nel terreno, mentre un valore maggiore di

ρ

genera spinte

Fig. 4.7. Curve d’interfaccia per i valori del parametro di concavità

A

₁

<

A

₂

<

A

₃

(15)

Allo stesso tempo si può, quindi, valutare l’andamento dell’interfaccia in condizioni

limite, come ad esempio in un terreno infinitamente permeabile: se

K

→

∞

la (25) ci

dice infatti che

A

→

∞

e quindi, per la (26),

y

→

0

per ogni valore di x.

L’interfaccia, in questo caso, è una retta orizzontale passante per l’origine.

Il caso di terreno impermeabile (

K

→

0

) non è valutabile, in quanto in questo modo

si esclude la presenza di porosità nel terreno, quindi anche la presenza di acqua salata e di acqua dolce. ( Dalla (25) si vede che non ha senso parlare di portata q ). Osservazione 1:

L’ ordinata y del generico punto dell’interfaccia è la profondità Hi dello stesso punto rispetto al l.m.m.. Se sostituiamo la (26) nella relazione (4) di Ghyben-Herzberg si trova che:

x

A

x

A

H

f f s P

⋅

≅

⋅

−

=

40

1 ρ

ρ

(27)

Si è così dimostrato che lungo il tratto dove è presente l’interfaccia anche la piezometrica è una parabola ed ha una concavità 40 volte più piccola di quella dell’interfaccia stessa.

Quanto detto è anche in accordo con la legge di Darcy P

_H

_i

dx

dH

K

q

=

⋅

.

Infatti, poiché Hi è variabile con legge parabolica, q è costante solo se la piezometrica varia anch’essa con legge parabolica.

A monte della zona dove è presente l’interfaccia, invece, la piezometrica continua ad essere rettilinea ( o per meglio dire un piano inclinato ), poiché la portata q di acqua dolce scorre attraverso sezioni che si mantengono in teoria costanti.

Osservazione 2:

E’ importante notare che, imponendo il passaggio dell’ interfaccia per il punto Q (L,h), si ottiene ancora la legge (17) di Todd.

Infatti, se sostituiamo nella (24) i valori y = H e x = L si ottiene:

L

K

q

h

f s f

⋅

−

⋅

=

ρ

2

2 ₍₂₈₎

(16)

Due strati geologici orizzontali sovrapposti di coeff. di permeabilità K1 e K2

Analizziamo ora il caso di due strati geologici orizzontali caratterizzati da due coefficienti di permeabilità K1 e K2 , che si sovrappongono in un terreno coinvolto dal fenomeno dell’intrusione salina ( Fig. 4.8).

K

1

L

TOT 2

x

P

y

h

2

h

1

L

1

L

2

x

_O

K

2

Q

y

(H

i

)

Fig.4.8 Schema di riferimento per il calcolo dell’equazione dell’interfaccia per 2 strati geologici orizzontali sovrapposti

L’equazione dell’ interfaccia acqua dolce-salata per

y

≤

h

₁ è la stessa già

precedentemente trovata nello studio di un terreno con un solo strato litografico (equaz. 26).

Nella trattazione seguente, al parametro A caratterizzante questo strato geologico, verrà aggiunto il pedice “1”. Lo stesso dicasi per il coeff. di permeabilità K.

Il calcolo dell’equazione dell’interfaccia per

h

₁

≤

y

≤

h

₁

+

h

₂ è lo stesso di quello

svolto in precedenza per

y

≤

h

₁: si eseguono quindi gli stessi integrali della (20),

inserendo dei nuovi indici di integrazione e sostituendo il coefficiente K con K2. Analogamente alla dimostrazione precedente, si può quindi scrivere:

(17)

ds

K

q

dH

H

x L f s f i i y h

∫

⋅

−

=

⋅

1 1

ρ

2

ρ

(29)

ricordando che L1 è ricavabile dalla (23). Svolgiamo gli integrali:

(

)

(

1

)

2 2 1 2

2

1 L

x

K

q

h

y

f s f

_⋅

₋

−

=

−

ρ

(30)

da cui, sostituendo la legge (23) di Todd al posto di L1, si ricava:

2 1 2 1 1 2 2

2

2 h

h

q

K

x

K

q

y

f f s f s f

₊

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

⋅

−

⋅

=

ρ

(31) Effettuando i calcoli:

(

)

2 1 2 1 1 2 2

2

2 h

q

h

K

x

q

K

q

y

f f s f f s f

₊

⎥

⎦

⎤

⎢

⎣

⎡

⋅

−

⋅

−

⋅

=

ρ

(32) 2 1 2 1 2 1 2 2

2 h

K

h

x

K

q

y

f s f

_⋅

₋

_⋅

₊

−

⋅

=

ρ

(33)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⋅

−

⋅

=

2 1 2 1 2 2

1

2 K

K

h

x

K

q

y

f s f

ρ

(34)

La (34) rappresenta l’equazione dell’interfaccia per

h

₁

≤

y

≤

h

₁

+

h

₂.

In essa si può inserire il parametro di concavità:

2 2

2 K

q

A

f s f

_⋅

−

⋅

=

ρ

(35)

(18)

relativo alla nuova parabola che rappresenta l’interfaccia nello strato “2”. L’ equazione (25) diventa quindi:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⋅

=

2 1 2 1 2 2

1 K

K

h

x

A

y

(36)

La (36) descrive l’andamento di una parabola che ha il vertice sull’asse delle ascisse x, concavità ( determinata dal parametro A2 ) diversa rispetto alla parabola che descrive l’interfaccia nello strato sovrastante e traslata orizzontalmente rispetto a questa.

Vogliamo ora esplicitare la x:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

−

=

⋅

−

⋅

2 1 2 1 2 2

1

2 K

K

h

y

x

K

q

f s f

ρ

(37)

q

K

h

y

q

K

x

f f s f f s 2 2 1 2 2 1 2 2

2

2 ⋅

−

⋅

−

⋅

−

⋅

−

=

ρ

(38) 2 1 2 2 1 1 2 2

2

2 q

h

K

h

q

K

y

q

K

x

f f s f f s f f s

−

_⋅

₊

−

_⋅

₋

_⋅

−

_⋅

=

ρ

(39)

Se inseriamo nell’ultima equazione i parametri di concavità definiti nelle relazioni (25) e (35), si ottiene:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

=

2 1 2 1 2 2

1

1 A

A

h

A

y

x

(40) per

h

₁

≤

y

≤

h

₁

+

h

₂

Il vertice di questa parabola si può trovare ponendo y = 0 nella (40):

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

=

2 1 2 1

1

1 A

A

h

x

_V (41)

(19)

La (41) rappresenta la traslazione lungo l’asse delle ascisse x di tutta la parabola. Al fine di ricavare delle relazioni utili ad una più speditiva rappresentazione delle curve che descrivono il fenomeno, imponiamo il passaggio della curva per alcuni punti notevoli. Inizialmente si impone il passaggio per il punto P ( figura 4.8 ) e cioè per il punto in cui la parte d’interfaccia acqua dolce-salata che si trova nello strato di coeff. di permeabilità K1, incontra la linea di separazione tra i due strati esaminati. A tale

scopo inseriamo il valore

x

=

L

₁ nella equazione (34), con

L

₁ calcolato con la nota

legge di Todd (23):

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⋅

−

⋅

−

⋅

=

2 1 2 1 2 1 1 2 2

1

2

2 K

K

h

q

K

q

y

f f s f s f

ρ

(42) Semplificando si ottiene: 2 1 2 1 2 1 2 1 2 1 2

1 h

K

h

K

y

_⎟⎟

=

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⋅

=

(43)

Imponendo, invece, il passaggio della linea di interfaccia per il punto Q, ( fig. 9) il quale rappresenta l’intersezione della curva d’interfaccia presente nello strato con coeff. di permeabilità K2, con la superficie del sottostrato impermeabile, si ottiene la

lunghezza totale

L

_TOT₂ di avanzamento del cuneo salino nell’entroterra.

Poniamo, nella relazione (40),

x

=

L

_TOT₂ e

y

=

h

₁

+

h

₂:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

=

2 1 2 1 2 2 2 1 2

1

1 )

(

A

h

A

h

L

_TOT (44) Svolgendo i calcoli: 2 2 1 1 2 1 2 2 1 2 2 2 2 2 1 2

2 A

h

A

h

A

h

A

h

A

h

L

_TOT

=

+

⋅

+

−

(45)

(20)

2 2 1 2 2 2 1 2 1 2

2 A

h

A

h

A

h

L

_TOT

=

+

⋅

(46)

Quest’ultima è analoga all’espressione (23) di Todd in cui è stata esplicitata la lunghezza L del cuneo salino (

A

h

L

2

=

).

Infine, calcolando la differenza tra

L

_TOT₂ e

L

₁, si ottiene la lunghezza

L

₂ della

porzione di cuneo salino presente nel solo strato del suolo di permeabilità

K

₂:

1 2 1 2 2 1 2 2 2 1 2 1 1 2 2

2 A

h

A

h

A

h

A

h

L

=

_TOT

−

=

+

⋅

−

(47) 2 2 1 2 2 2 2

2 A

h

A

h

L

=

+

⋅

(48)

Vari strati geologici orizzontali sovrapposti

Andiamo ora ad analizzare il caso di un terreno formato schematicamente da una serie di i strati litografici orizzontali sovrapposti, caratterizzati da coeff. di

permeabilità

K

₁ ,

K

₂ ,

K

₃ , …..,

K

_i. Per trovare l’equazione dell’interfaccia acqua

dolce-salata, ad esempio, nello strato 3, si esegue la stessa integrazione (29) con i nuovi indici di integrazione:

ds

K

q

dH

H

x L f s f i i y h h TOT

∫

⋅

−

=

⋅

+ 2 2 1

ρ

3

ρ

(49) con

L

_TOT₂ fornito dalla (46).

Dopo aver svolto i calcoli analogamente a quanto fatto per gli altri strati, si ottiene l’equazione dell’ interfaccia acqua dolce-salata nello strato 3:

(21)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

=

3 2 2 1 3 2 2 2 3 1 2 1 3 2

1

2

1

1 A

A

h

A

h

A

h

A

y

x

(50)

che rappresenta una parabola con vertice lungo l’asse x, concavità definita dal parametro A3 e traslata orizzontalmente rispetto alla parabola dello strato 2.

O

L

2

L

1

L

i

L

3

x

K

1

L

TOT 2

L

TOT i

K

2

K

i

K

3

h

2

h

1

h

3

h

i

y

Fig. 4.9. Schema di calcolo dell’equazione dell’interfaccia acqua dolce-salata per più strati geologici orizzontali sovrapposti

Analogamente a quanto già eseguito per il secondo strato, si calcola

L

_TOT₃ imponendo

il passaggio della parabola ( equaz. 50 ) per il punto il cui la parabola dello strato 3 incontra la retta di separazione tra questo e lo strato 4. Omettendo i calcoli, si ottiene: 3 3 2 3 3 1 2 2 1 3 2 3 2 2 2 1 2 1 3

2

2 A

h

A

h

A

h

A

h

A

h

A

h

L

_TOT

=

+

⋅

+

⋅

+

⋅

(51)

(22)

che rappresenta la lunghezza totale di avanzamento del cuneo salino al di sopra dello strato impermeabile, ottenuta dalla somma delle lunghezze delle parabole degli strati 1, 2 e 3.

Si può analogamente anche calcolare la lunghezza della sola porzione di parabola

compresa nello strato 3, facendo la differenza tra

L

_TOT₃ e

L

_TOT₂:

3 3 2 3 3 1 3 2 3 3

2

2 A

h

A

h

A

h

L

=

+

⋅

+

⋅

(52)

Se ripetiamo tutti i ragionamenti finora fatti anche per lo strato 4, si ottiene:

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

=

4 2 2 1 4 3 2 3 4 2 2 2 4 1 2 1 4 2

1

2

1

1 A

A

h

A

h

A

h

A

h

A

y

x

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

4 3 3 1

1

2 A

A

h

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

4 3 3 2

1

2 A

A

h

(53) 3 3 2 3 3 1 2 2 1 4 2 4 3 2 3 2 2 2 1 2 1 4

2

2 A

h

A

h

A

h

A

h

A

h

A

h

A

h

L

_TOT

=

+

⋅

+

⋅

+

⋅

4 4 1

2 A

h

⋅

+

+ 4 4 3 4 4 2

2

2 A

h

A

h

⋅

+

⋅

+

(54) 4 4 2 4 4 1 4 2 4 4

2

2 A

h

A

h

A

h

L

=

+

⋅

+

⋅

4 4 3

2 A

h

⋅

+

(55)

A questo punto, per analogia con quanto visto finora, possiamo scrivere le relazioni

generali che forniscono x,

L

_TOT_i e

L

_i per il generico strato geologico i del terreno:

(

)

i

h

y

x

=

+

⎜

⎛

−

⎟

⎞

⋅

+

⋅

−

∑

1 2 2

2

1

(56)

(23)

+

=

∑

= i i i j TOTi

A

h

L

2 1

+

⋅

− − =

∑

j j j i j

A

h

₁ 1 1

2

i i j i j

A

h

⋅

− =

∑

1 1

2

(57)

+

=

i i i

A

h

L

2 i i j i j

A

h

₋

⋅

=

∑

1 1 (58) dove

h

₀

=

0

, j f s f j

K

q

A

⋅

−

⋅

=

ρ

2

e i f s f i

K

q

A

⋅

−

⋅

=

ρ

2

.

Queste relazioni sono valide per

L

_TOT₍_i₋₁₎

≤

x

≤

L

_TOTi e

∑

= − =

≤

i j j i j j

y

h

1 1 1

L’ equazione (57) è analoga alla formula (23) di Todd in cui è esplicitata la lunghezza

(24)

4.2.4 Influenza della presenza di ostacoli sotterranei sul fenomeno dell’ intrusione salina

Andiamo ad affrontare il caso della presenza di un ostacolo immerso nella falda acquifera, il quale influisce sull’equilibrio pre-esistente tra acqua salata ed acqua dolce, facendo muovere l’interfaccia di separazione. Questa analisi è utile per capire quali possono essere i benefici dell’inserimento di una barriera sommersa nel terreno dove è presente l’interfaccia di separazione, ad es. una palancolata od un getto verticale in calcestruzzo.

In particolare, prima studieremo la relazione tra i movimenti dell’interfaccia e quelli della linea piezometrica, per poi andare a valutare quantitativamente tali movimenti.

Relazione tra i movimenti dell’interfaccia e della piezometrica di falda

c

d

L.M.

P

H

p

H

i

H

p

+

c

H

i

+

d

NUOVA PIEZOMETRICA INTERFACCIA

Fig.4.10. Schematizzazione della relazione tra movimenti dell’interfaccia e della piezometrica in presenza di ostacolo sommerso

In riferimento alla figura, siano Hi ed Hp rispettivamente la profondità di un punto dell’interfaccia e l’altezza della piezometrica, rispetto al livello del mare, quando non sia presente alcun ostacolo.

(25)

Supponiamo che, una volta inserito l’ostacolo, dopo un certo periodo di tempo, la piezometrica si abbassi localmente di una quantità d e contemporaneamente la piezometrica si innalzi di una quantità pari a c. Per ora c e d sono valori ignoti dei quali vogliamo sapere solo la relazione che li lega.

Per l’equilibrio idrostatico del punto P, deve risultare:

(

H

_i

+

d

)

⋅

ρ

_s

⋅

g

=

(

H

_P

+

c

)

⋅

ρ

_f

⋅

g

+

(

H

_i

+

d

)

⋅

ρ

_f

⋅

g

(59)

dove g è l’accelerazione di gravità.

Esplicitando

(

H

_i

+

d

)

si ottiene:

(

H

c

)

d

H

_p f s f i

+

=

_ρ

₋

_ρ

+

ρ

(60)

Poiché Hi ed Hp sono i due valori in assenza dell’ostacolo, essi sono legati tra loro dalla relazione di Ghyben-Herzberg:

p f s f i

H

ρ

−

=

(4)

Se sostituiamo la (4) nella (60) si ottiene:

c

d

f s f

_⋅

−

=

ρ

(61)

Analizzando la precedente, si ricava l’importante conclusione che ogni volta che l’interfaccia acqua dolce-salata si abbassa di una quantità d, la piezometrica si innalza di una quantità

40 d

(26)

Calcolo dei valori di c (innalzamento della piezometrica) e d (abbassamento dell’interfaccia) INTERFACCIA

L.M.

H

p

H

i

c

d

PIEZOMETRICA

q

a

H

i

+

d

-

a

Fig. 4.11. Calcolo dei valori di c e di d

Supponiamo che l’ostacolo arrivi ad una profondità a sotto il livello medio del mare e che Hi ed Hp siano ancora la profondità di un punto generico dell’interfaccia e l’altezza della piezometrica, rispetto al livello del mare, in assenza dell’ostacolo ( vedi figura 4.11 ).

Dal punto di vista idrostatico, l’intromissione dell’ostacolo nella falda non cambierebbe l’equilibrio dell’interfaccia, che rimarrebbe immutata: entra però in gioco il fattore idrodinamico a governare il problema.

Per la legge di Darcy, la portata di acqua dolce q = cost per unità di larghezza della falda è data da:

i P

_H

dx

dH

K

q

=

⋅

(62)

(27)

Per mezzo della presenza dell’ostacolo, la sezione di deflusso dell’acqua dolce si riduce in altezza da Hi a Hi+d-a, mentre la piezometrica si alza da Hp a Hp+c.

Supponiamo, come prima ipotesi, che sia c che d rimangano costanti in ogni sezione verticale ortogonale al piano di figura passante per l’ostacolo. Dimostreremo poi la validità di questa ipotesi in un momento successivo.

Se applichiamo nuovamente la legge di Darcy alla situazione in esame, si ottiene:

(

)

₍

₎

a

d

H

dx

c

H

d

K

q

i p

+

_⋅

₊

₋

=

(63)

Analizziamo ora il termine differenziale della relazione precedente nella quale c= cost. Si ha:

(

)

dx

dH

dx

dc

dx

dH

dx

c

H

d

_p _P _P

=

+

=

+

(64)

Se sostituiamo la (64) nella (63), si ricava:

(

H

d

a

)

dx

dH

K

q

i P

⋅

+

−

=

(65) Poiché il rapporto

K

q

è costante, il confronto tra la (62) e la (65) ci permette di scrivere:

(

H

_i

+

d

−

a

)

=

H

_i (66)

e quindi:

a

d

=

(67)

Dalla precedente si ricava l’importante conclusione che, per la presenza dell’ostacolo, l’interfaccia subisce un abbassamento localizzato uguale alla profondità dell’ostacolo stesso sotto il livello del mare.

(28)

Inoltre, per la (61):

40

40 a

d

c

f f s

−

_⋅

_≅

₌

=

ρ

(68)

Ciò significa che la piezometrica si innalzerà di una quantità pari ad 1/40 dell’affondamento dell’ostacolo al di sotto del livello del mare.

Costanza dei valori di c e d sui piani verticali passanti per l’ostacolo

Supponiamo, in linea generale, che l’innalzamento della piezometrica vari, sopra

l’ostacolo, secondo una funzione generica yp , mentre l’abbassamento dell’interfaccia

secondo una funzione yi ( vedi figura 4.12 ).

H

i

+

y

i

-

a

INTERFACCIA

y

i

H

i PIEZOMETRICA

H

p

y

p L.M.

a

(29)

Queste due funzioni sono sicuramente legate dalla (61), quindi: p f s f i

y

⋅

−

=

ρ

(69)

Siano ancora Hi ed Hp la profondità di un punto generico dell’interfaccia, posto sotto l’ostacolo e l’altezza della piezometrica, rispetto al livello del mare.

Applichiamo la legge di Darcy in una sezione trasversale passante per un punto qualsiasi posto sotto l’ostacolo:

(

)

₍

₎

a

y

H

dx

y

H

d

K

q

i i p p

+

_⋅

₊

₋

=

(70)

Svolgendo i prodotti si ricava:

(

−

)

+

⋅

=

⋅

−

y

a

dx

dH

H

dx

dH

K

q

i p i p

(

)

a

y

H

dx

dy

i i p

_⋅

₊

₋

(71)

Dal confronto tra la (71) e la (62) si ricava che il primo membro della (71) è nullo. Quindi, la (71) diventa:

(

y

_i

−

a

)

⋅

dH

_p

+

(

H

_i

+

y

_i

−

a

)

⋅

dy

_p

=

0

(72)

Sostituendo la (4) e la (69) nella (72) si ricava:

+

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

−

p p f s f

dH

a

y

ρ

0 =

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

−

+

⋅

−

p p f s f p f s f

dy

a

y

H

ρ

(73)

Mettiamo in evidenza il rapporto tra le densità e semplifichiamo, ottenendo:

+

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

−

_p f f s p

a

dH

y

ρ

0 =

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

−

+

_p f f s p p

y

a

dy

H

ρ

(74)

(30)

Semplifichiamo l’equazione introducendo il rapporto tra le densità delle acque dolce e salata :

40 a

a

A

f f s

_≅

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

=

ρ

(75)

La (74) diventa in questo modo:

(

y

_p

−

A

)

⋅

dH

_p

+

(

H

_p

+

y

_p

−

A

)

⋅

dy

_p

=

0

(76)

la precedente è un differenziale esatto del tipo:

( )

x

,

y

⋅

dx

+

N

(

x

,

y

)

⋅

dy

=

0 M

(77)

in cui nel caso in esame:

x

=

H

_p ,

y

=

y

_p ,

M

( )

x

,

y

=

y

_p

−

A

,

( )

x

y

H

y

A

N

,

=

_p

+

_p

−

.

Infatti deve essere:

x

N

y

M

∂

=

∂

(78) e nel nostro caso risulta:

(

) (

)

1 =

∂

−

+

∂

=

∂

−

∂

p p p p p

H

A

y

H

y

A

y

(79)

Scelto un qualsiasi punto (

x

₀

, y

₀) nel dominio delle

M

( )

x

,

y

e

N

( )

x

,

y

, si ha:

(

,

₀

)

(

₀

,

)

0

0 0

=

⋅

+

⋅

_∫

∫

M

x

y

dx

N

x

y

dy

y y x x (80)

(31)

Nella dimostrazione precedente abbiamo mostrato che esiste almeno una sezione

dove

y

_p

=

A

0 : quindi, come punto (

x

0

,

y

0) prendiamo (

H

P0

,

A

), dove

H

P0 è

l’altezza della piezometrica senza l’ostacolo nella sezione in cui

y

_p

=

A

0 .

Integriamo tra questa sezione e la sezione generica in cui si ha (

H

_P

,

y

_P):

(

,

)

(

₀

,

)

0

=

⋅

+

⋅

_∫

∫

P P P y A P P H H

dy

y

H

N

dH

A

H

M

P P P (81) Essendo

M

=

y

_p

−

A

e

N

=

H

_p

+

y

_p

−

A

, si ha:

(

)

(

₀

)

0

=

⋅

−

+

⋅

−

_∫

∫

P P P y A P H H

dy

A

y

H

dH

A

P P P (82)

Il primo addendo è nullo, il secondo addendo fornisce:

0

2

1

2 0

⋅

+

⋅

−

⋅

=

P y A P P P P

y

A

y

H

(83)

Svolgendo i calcoli, si ottiene l’equazione di 2° grado:

(

)

2

0

2

₀ 2 ₀ 2

₊

_⋅

₋

_⋅

₊

₋

_⋅

₌

A

H

A

y

A

H

y

_P _P _P _P (84)

che risolta fornisce i seguenti valori:

A

y

_P₁

=

(85) 0 2

2

P P

A

H

y

=

−

⋅

(86)

(32)

Dato che, per la (75), A è molto più piccolo rispetto a

H

_P₀, la (86) ci dà un valore

negativo di

y

_P. La soluzione accettabile è quindi quella fornita dalla (85).

Questo significa che per la sezione trasversale generica che taglia l’ostacolo, ortogonale alla direzione di deflusso della falda, si ha:

40 a

A

y

_P

=

≅

(87) e per la (69) è:

=

⋅

−

=

_p f s f i

y

ρ

a

f f s f s f

=

−

⋅

−

ρ

(88)

In definitiva, si può affermare che sotto l’ostacolo l’abbassamento dell’interfaccia è costante e pari alla sua profondità a rispetto al livello medio del mare.

Sopra l’ostacolo, la piezometrica si innalza localmente di una quantità costante pari ad

40 a

_{, per tutto lo sviluppo longitudinale dell’ostacolo stesso.}

Osservazione 1:

E’ doveroso sottolineare che l’andamento spigoloso della curva d’interfaccia mostrato nelle figure 4.11 e 4.12 è puramente teorico, in quanto, nonostante l’abbassamento al di sotto dell’ostacolo sia fortemente localizzato, al posto degli spigoli nella realtà si hanno delle piccole curve; ciò avviene grazie a numerosi fattori, come ad es. la viscosità; l’abbassamento stesso dell’interfaccia si farà quindi sentire in una piccola zona a monte ed a valle dell’ostacolo stesso.

(33)

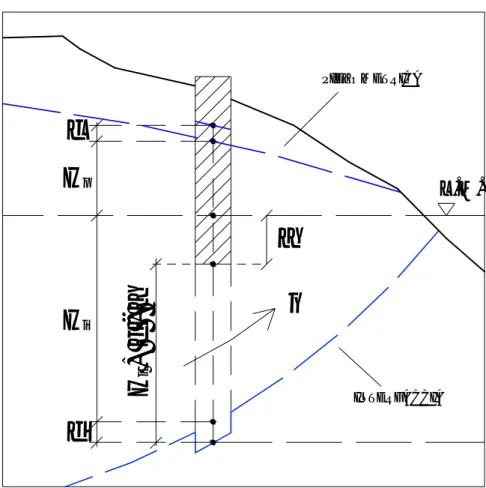
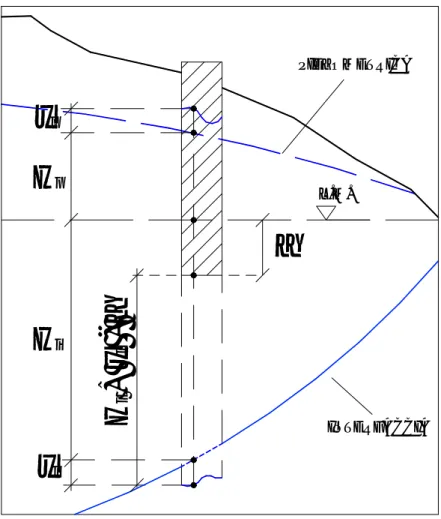
Profondità utile di uno sbarramento

Uno dei metodi utilizzabili per combattere l’intrusione salina negli acquiferi costieri è quello della realizzazione di sbarramenti trasversali al senso di deflusso della falda, costituiti in genere da colonne in calcestruzzo gettato o da palancole, che raggiungano l’eventuale substrato impermeabile del terreno sotto l’acquifero. Questo per evitare totalmente la risalita della falda verso l’entroterra da parte del cuneo salato.

Tuttavia, grazie a ciò che è stato finora dimostrato, è possibile affermare che, per evitare che l’intrusione si spinga oltre lo sbarramento, non importa che quest’ultimo sia talmente profondo da intaccare lo strato impermeabile del terreno.

Infatti esiste un valore utile a* della profondità a rispetto al livello del mare della barriera, per cui l’interfaccia si abbasserà localmente fino ad incontrare lo strato impermeabile, con evidenti benefici a monte della barriera.