A
FLUSSO UNIDIMENSIONALE IN UN CONDOTTO
CONICO
A.1 Introduzione
Il classico modello unidimensionale per lo studio dei flussi comprimibili nei condotti è basato su equazioni che legano i differenziali logaritmici delle variabili aerodinamiche ai parametri indipendenti attraverso opportuni coefficienti di influenza, funzioni di M2 e del rapporto tra i calori specifici γ ([1]). Supponendo che
il gas sia monofase, e abbia calori specifici e peso molecolare costanti è conveniente adottare come parametri indipendenti
A dA , 0 0 T dT , D dx c 4 F e m m d & &
Il termine dA A è relativo alla variazione di area della sezione del condotto,
0 0 T
dT è la variazione di temperatura totale del flusso ed è dovuto essenzialmente a due contributi: calore scambiato con l’esterno attraverso le pareti del condotto e lavoro eventualmente scambiato con parti mobili immerse nel flusso. Il termine dovuto all’attrito viscoso 4cFdx D è quello che in idraulica viene definito fattore di perdita (generalmente indicato con k) e corrisponde alla perdita di pressione del fluido a causa del passaggio in un condotto circolare di diametro D e lunghezza dx (spesso si definisce la quantità f = 4cF fattore di attrito). Infine l’ultimo parametro
m m
d& & prende in considerazione possibili variazioni di flusso di massa nel condotto ad esempio per suction o blowing attraverso le pareti.
Per ognuna delle variabili dipendenti M2, ρ, V, T, p, etc. è possibile scrivere
un’equazione del tipo:
(
)
(
)
(
)
(
)
m m d , M C D dx c 4 , M C T dT , M C A dA , M C X dX 2 4 i F 2 3 i 0 0 2 2 i 2 1 i i i & & γ + γ + γ + γ = (A.1)dove il generico Cij è il coefficiente di influenza della j-esima variabile
La (A.1) può essere scritta in forma matriciale
[ ]
C F X X d = ⋅ (A.2) dove X={M2,V,T,ρ,p} e F={dA A, 0 0 TdT ,4cFdx D,dm& m& } sono i vettori
contenenti rispettivamente le variabili dipendenti e indipendenti e [C] è la matrice dei coefficienti di influenza.
[ ]
( )
(
)
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +γ− γ − − − γ + γ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + γ− γ − − γ − + γ − − γ − − − γ + − − − − γ γ + − − − γ γ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +γ− γ − − − γ − γ + − γ − − γ + − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +γ− γ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + γ− γ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +γ− γ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + γ− − = 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 M 1 M 2 1 1 M 2 ) M 1 ( 2 M ) 1 ( 1 M M 1 M 2 1 1 M M 1 M M 1 M ) 1 ( ) M 1 ( 2 M M 1 M 2 1 1 M 1 M M 1 M ) 1 )( M 1 ( ) M 1 ( 2 M ) 1 ( M 1 M 2 1 1 ) M 1 ( M 1 M ) 1 ( M 1 M 1 ) M 1 ( 2 M M 1 M 2 1 1 M 1 1 M 1 M 2 1 1 ) M 1 ( 2 M 1 M 2 1 1 M M 1 M 2 1 1 ) M 1 ( M 1 M 2 1 1 2 CN.B. generalmente si assume come variabile dipendente il quadrato del numero di Mach poiché risulta conveniente dal punto di vista analitico.
A.2 Modello ad un grado di libertà
Soluzioni in forma chiusa della (A.2) sono ottenibili nei casi particolarmente semplici in cui sia diversa da zero solo una delle quattro variabili indipendenti. Nei casi più generali è necessario procedere per via numerica risolvendo il problema con un procedimento passo-passo.
Tuttavia è possibile, in molti problemi pratici, operare delle semplificazioni che consentono di risolvere analiticamente le equazioni (A.2) anche in presenza di attrito e scambio di calore. In particolare il metodo descritto è applicabile nell’ipotesi di:
• condotto conico;
In questo caso è possibile esprimere i tre parametri dA A,dT0 T0e4cFdx D
come prodotto del termine dx/D per una costante. Per quanto riguarda il termine viscoso questo risultato è evidente se si ritiene che il coefficiente cF sia
approssimativamente costante nel tratto di condotto considerato.
Nell’ipotesi di condotto conico il termine dA A può essere così riscritto:
D dx tan 4 D dx dx dD 2 D dD 2 A dA θ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = = (A.3)
dove θ è l’angolo di semiapertura del condotto conico.
Per quanto riguarda la variazione di temperatura totale, nell’ipotesi che essa sia dovuta al solo scambio di calore con le pareti esterne si avrà, per il primo principio: dx D q dx cos D q dT c
m& p 0 =−&wπ θ ≅−&wπ (A.4) dove si è supposto che l’angolo θ sia sufficientemente piccolo (come d’altronde è richiesto anche dall’ipotesi di flusso unidimensionale) da poter considerare il suo coseno unitario.
Introducendo nella (A.4) il numero di Stanton
) ( aw w P w h Vc T T q C − ρ = &
e considerando che m& =ρVπD2/4, si ottiene
D dx T T T C 4 T dT 0 w aw h 0 0 =− − (A.5)
Se il fattore di recupero è supposto unitario la (A.5) può essere scritta come: D dx T T 1 C 4 T dT 0 w h 0 0 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = (A.6)
e quindi nell’ipotesi che lungo la parete del tratto di condotto considerato il rapporto Tw/T0 si mantenga all’incirca costante così come Ch, si ottiene il risultato
cercato.
Sostituendo le espressioni di dA A e dT0 T0 trovate nel sistema (A.2) si
ottiene il seguente modello ad un grado di libertà:
(
)
(
)
(
)
D dx 4 M K c 2 tan 2 K M 1 2 M 1 1 M dM 2 h F h 2 2 2 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − γ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + θ − − γ + − = (A.7.1)(
)
D dx 4 M K 2 1 c 2 tan K M 1 1 V dV 2 h F h 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ γ− − γ + θ + − − = (A.7.2)(
)
(
)
D dx 4 M K c 2 1 M K 2 1 tan 1 K M 1 1 T dT 4 h F 2 h h 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − γ γ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ γ+ + θ − γ + − − = (A.7.3) D dx 4 M tan K 2 1 c 2 K M 1 1 d 2 h F h 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛γ − γ− − θ − − = ρ ρ (A.7.4)(
)
D dx 4 M K c 2 1 M 2 c K tan M 1 1 p dp 4 h F 2 F h 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − γ γ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ θ+ − γ − = (A.7.5)dove per semplicità con Kh si è indicato ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛ − 0 w h T T 1 C .
Ricavando dx/D dalla (A.7.1) e sostituendolo nelle altre, si ottengono le derivate logaritmiche delle variabili dipendenti V, T, ρ e p in funzione della sola variabile M2 e con Kh, tanθ e cF come parametri che rappresentano rispettivamente i
contributi di scambio termico, variazione dell’area e attrito.
A.3 Soluzione delle equazioni
Sostituendo la (A.7.1) nelle (A.7.2-5) si ottengono quattro espressioni che sono tutte appartenenti alla seguente classe
(
)(
)
dZ
Z
q
p
Z
n
m
c
Z
b
Z
a
Z
1
X
dX
i i 2 i i i+
+
+
+
=
(A.8) dove si è posto Z=M2.I coefficienti m,n,p e q sono ricavabili dalla (A.7.1) e valgono
m = 2 , n = γ-1 , p =
−
−
tan
θ
2
K
h , q =(
)
h FK
c
2
−
γ
mentre i coefficienti a, b, c sono ricavabili dalle (A.7.2-5) e valgono: - per la velocità aV = 0 , bV = F Kh 2 1 c 2 − γ − γ , cV = −Kh−tanθ - per la temperatura aT =
(
cF Kh)
2 1 − − γ γ − , bT =(
)
Kh 2 1 tan 1 θ+γ+ − γ , cT = -Kh - per la densità aρ = 0 , bρ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛−γ− + γ − θ − c tan 2 K 2 1 F h , cρ = Kh - per la pressione ap =(
cF Kh)
2 1 − − γ γ − , bp = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + θ γ 2 c K tan F h , cp = 0L’integrazione della (A.8) può essere effettuata ponendola nella forma
(
) (
p qZ)
dZ C Z n m B Z A X dX i i i i i ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + + + + = (A.9) con i i mpc 1 A = i i i i np mqc n m n b mq np n a mq np m B − − − + − − = i i i i np mqc q p q b mq np q a mq np p C − + − − − = da cui si ottiene: ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 0 i 0 i 0 i 0 i i Z q p Z q p ln q 1 C Z n m Z n m ln n 1 B Z Z ln A X X ln e quindi:q C 0 n B 0 A 0 0 i i i i i Z q p Z q p Z n m Z n m Z Z X X ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = (A.10)
dove Xi0 e Z0 fanno riferimento alle condizioni all’ingresso del tratto di condotto.
A.4 Risultati
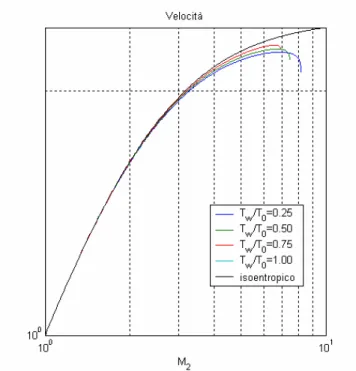
A titolo di esempio sono di seguito riportati i risultati della (A.10) applicati al caso di un flusso in un condotto divergente con angolo di semiapertura di 5°, coefficiente di attrito cF=0.003 e numero di Stanton Ch=0.0015. I grafici riportano,
al variare del numero di Mach all’uscita del condotto (in regime supersonico), i valori delle variabili del flusso adimensionalizzate con il loro valore in corrispondenza di M=1. I grafici sono stati tracciati per diversi valori del rapporto Tw/T0 compresi tra 0.25 e 1 (caso adiabatico), con tratto nero si è inoltre riportato
la curva relativa al caso isoentropico come termine di paragone.
Figura A.1 Rapporto di velocità al variare del numero di Mach (in questo caso la curva adiabatica coincide con quella isoentropica).
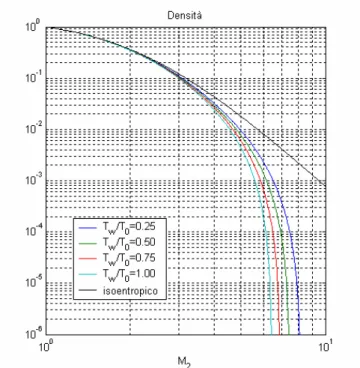
Figura A.2 Rapporto di densità al variare del numero di Mach.
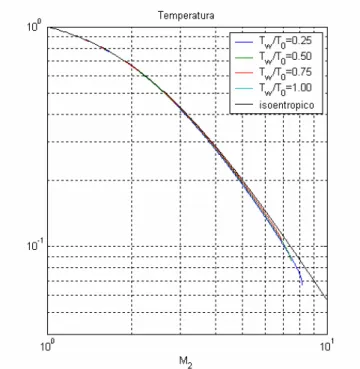
Figura A.6 Rapporto di temperatura totale al variare del numero di Mach.
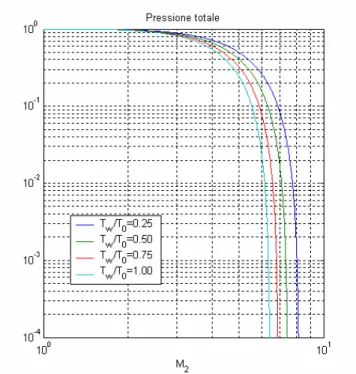
L’aspetto più interessante che emerge dai grafici precedenti è sicuramente il comportamento divergente che le curve assumono ad elevati numeri di Mach e che non ha riscontro nella teoria isentropica. Fisicamente questo fatto si traduce nell’impossibilità di espandere il flusso oltre un certo numero di Mach anche avendo a disposizione un rapporto delle aree infinito.
Il valore del Mach ‘asintotico’ MA è funzione dei parametri perturbativi Kh, tanθ
e cF, come risulta dalla (A.7.1), infatti il valore di dM2/M2 si annulla quando si
verifica la condizione
(
)
2 h F h c K M 2 tan 2 K − γ = θ + (A.11) ovvero per(
)
(
F h w 0)
h A T T 1 C c tan 2 K M − − γ θ + = (A.12)Dalla (A.12) segue che MA esiste solo se il termine razionale sotto radice
quadrata è positivo, in base all’analogia di Reynolds si può ritenere che il denominatore sia maggiore di zero, mentre per quanto riguarda il numeratore, il segno dipende prevalentemente dal termine 2tanθ che già per valori molto modesti dell’angolo del condotto assume valori molto maggiori di Kh. Se ne deduce quindi
che il valore ‘asintotico’ del numero di Mach esiste solo per condotti divergenti per i quali tanθ>0, ovvero il numero di Mach è superiormente limitato, ma non inferiormente.
Allo scopo di ottenere valori di MA più elevati è possibile aumentare l’angolo di
apertura del condotto e/o mantenere bassa la temperatura della parete. Nel caso esaminato, dalla (A.12) risulta:
49 . 9 MA= per Tw T0=0.2 36 . 8 MA= per Tw T0=0.4 55 . 7 MA= per Tw T0 =0.6 94 . 6 MA= per Tw T0 =0.8 45 . 6 MA= per Tw T0=1.0
Bibliografia dell’Appendice A
[1]. Shapiro, A.H. – “The Dynamics and Thermodynamics of Compressible Fluid Flow” – Ronald Press, New York, 1953.