Capitolo 3 METODO PER LA DETERMINAZIONE DEGLI EFFETTI TERMICI IN TRANSITORIO

Capitolo 3

METODO PER LA DETERMINAZIONE DEGLI EFFETTI

TERMICI IN TRANSITORIO

Nella progettazione di un edificio è molto importante conoscere gli effetti termici legati all’inerzia della struttura, in particolare se è destinata ad avere un impianto alimentato ad energia solare. I modelli che vengono presentati in questo Cap. 3 sono modelli previsionali a parametri concentrati, che non vogliono essere alternativi, ma preliminari ad altri più complessi, quali per esempio quelli che adottano griglie di discretizzazione del dominio come il metodo degli elementi finiti.

Quindi sono stati analizzati gli effetti termici principali sfruttando varie approssimazioni ed ipotesi a seconda del caso.

In primo luogo bisogna considerare l’inerzia termica dell’edificio,in seguito si passa alle parti della struttura, infatti sono stati fatti diversi casi cambiando la densità del materiale per poterne considerare gli effetti. In seguito partendo dall’equazione del calore di Fourier si è determinato il periodo di transitorio del muro e come varia la temperatura al suo interno, in seguito si è cercato di ricreate l’andamento giornaliero della temperatura durante le 24 ore approssimando la curva fornita dalla NORMA UNI EN ISO 13791 [7]. Una volta trovata tale funzione si è utilizzata come condizione al contorno dell’ equazione di Fourier per trovare l’attenuazione e lo sfasamento nel tempo della temperatura operato da parte del muro.

3.1 Effetti termici inerziali

Dovendo analizzare la trasmissione del calore attraverso un edificio, si deve considerare l’effetto inerziale della massa di questo e cercare un sistema per approssimare il modo e il tempo che tale costruzione impiega a disperdere il calore che ha al suo interno, tuttavia tale problema non ha facile soluzione, a causa della complessità della schematizzazione della struttura, quindi si parte da un modello più semplice e più dominabile.

Infatti in questo primo modello l’intero edificio è stato schematizzato come un guscio applicando la teoria monodimensionale, dato che il numero di Biot rientra nell’intervallo di valori che permettono di sfruttare tale teoria [11]. Comunque sia, in questo modo si

riesce ad avere una soluzione abbastanza indicativa del comportamento dell’edificio dovuto all’aspetto dell’inerzia termica. In particolare l’obiettivo di questo modello è quello di vedere approssimativamente quanto tempo impiega la struttura in questione a scambiate un T fissato a parità di spessore, ma variando la densità del muro, ovvero variando l’inerzia globale della struttura. Questo può essere utile per valutare gli effetti provocati dall’abbassamento di temperatura notturno, cioè quale temperatura aspettarsi la mattina quando si riapre l’edificio per essere di nuovo frequentato.

Ipotesi:

√ Schematizzazione: guscio

√ Comportamento: monodimensionale √ Temperatura iniziale Ti: uniforme √ Temperatura all’infinito T∞: costante

√ Coefficiente di scambio convettivo h: costante ed uniforme √ Simmetria: asse centrale

Considerando la funzione rappresentata dell’Eq. (3.1):

( )

( )

θ

valida nel corso del periodo invernale, (nel caso estivo si prende il valore assoluto di tale differenza) questa si comporta secondo l’Eq. (3.2),

( )

θ

dove rappresenta il numero di Fourier Eq. (3.3):

hS V C_p

ρ

τ

è la densità del materiale della struttura, Cp il suo calore specifico,

V il volume,

h coefficiente di scambio convettivo S la superficie di scambio per la struttura.

Nel caso specifico è stata considerata l’inerzia termica della sola struttura esterna, approssimando il fatto che le dispersioni causate dalle superfici vetrate vengano compensate dal fatto che sicuramente l’inerzia dell’edificio, completo di strutture interne, sarà maggiore e quindi maggiore la sua capacità di trattenere il calore. Lo spessore adottato per le pareti di seguito è 0,2 metri, valore intermedio che presenta buoni risultati a livello di trasmissione del calore e costi di realizzazione.

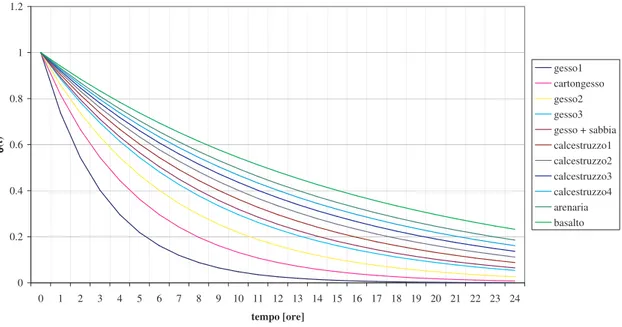
Il grafico in Fig. 3.1 mostra come, a parità della altre condizioni, andando verso materiali di maggiore densità, l’inerzia termica della struttura cresce.

Andamento della funzione θθθθ(t) al variare della densità del materiale ( Cp = 1000 J/kgK ) 0 0.2 0.4 0.6 0.8 1 1.2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 tempo [ore] θθθθ( t) gesso1 cartongesso gesso2 gesso3 gesso + sabbia calcestruzzo1 calcestruzzo2 calcestruzzo3 calcestruzzo4 arenaria basalto

Figura 3.1 Andamento della funzione (t) al variare della densità del materiale del muro

In Fig. 3.2 si vuole mettere in evidenza anche l’influenza di un altro parametro, ovvero il calore specifico del materiale. Infatti come si vede dalle curve relative al cartongesso e alle tavole a fibre orientate che hanno pari valore di densità ( = 900 kg/m3), ha maggiore inerzia termica il materiale con Cp più alto. Quindi, anche se l’effetto della densità del materiale risulta predominante, perché comunque la curva che rappresenta l’inerzia maggiore è quella relativa al vetro ( = 2500 kg/m3_{; Cp = 750 J/kgK), non è da}

sottovalutare neppure l’influenza che produce il calore specifico, che risulta legato al relativo valore di conducibilità termica.

Andamento della funzione θθθθ(t) al variare del materiale 0 0.2 0.4 0.6 0.8 1 1.2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 tempo [ore] θθθθ( t) vetro cartongesso calcestruzzo1 legno compensato pannello truciolare tavole fibre orientate

Figura 3.2 Andamento della funzione (t) al variare del materiale del muro

3.2 Analisi del transitorio termico

Nel paragrafo precedente si è visto come varia la temperatura in funzione del tempo, in base all’inerzia termica dell’edificio, invece con questo secondo modello si vuole osservare come si comporta la temperatura nel tempo lungo lo spessore di un muro preso singolarmente. L’obiettivo di tale schematizzazione è quello di capire, in base all’avanzamento della temperatura nello spessore, quale capacità può avere il muro di sfasare nel tempo i picchi della temperatura esterna, in modo da comprendere quali margini si possono avere tra le condizioni in cui sarebbe necessaria la massima potenza refrigerante (o riscaldante) e quelle in cui si hanno veramente.

Gli effetti dovuti al transitorio termico sono maggiormente comprensibili adottando un altro modello analitico. Invece dell’edificio intero, si passa a simulare un muro soltanto, considerandolo come una parete piana infinita e adottando ancora una volta la teoria monodimensionale. In questo modo si riesce ad approssimare l’andamento della temperatura nello spessore della parete durante il trascorrere del tempo, questo permette di capire come si abbia la propagazione dell’onda termica attraverso il muro e quindi anche lo sfasamento che esso provoca sulla temperatura.

Ipotesi:

√ Comportamento: monodimensionale √ Equazione: omogenea

√ Condizioni al contorno: non omogenee √ Temperatura interna Tint: uniforme e costante √ Temperatura esterna Test: uniforme e costante

√ Coefficiente di conducibilità termica: costante, uniforme ed isotropo √ Coefficiente di scambio convettivo h: costante ed uniforme

√ Simmetria: centrale

Per trovare la soluzione è stata studiata l’equazione di Fourier.

2 2 x T t T ∂ ∂ = ∂ ∂

_α

Con condizioni al contorno di scambio convettivo:

( )

(

)

( )

(

)

Il problema è schematizzabile come monodimensionale non stazionario, con condizioni al contorno non omogenee; per questo è necessario suddividere il problema in due sottoproblemi.

( )

( ) ( )

T , − _int =

η

θ

dove η

( )

( )

θ

In teoria si risolve prima il caso stazionario, in questo testo invece verrà trascurato perché comunque non influisce in alcun modo sul variare della funzione nel tempo.

Si passa subito all’altra funzione.

Si definisce

θ

( ) ( )

2 2 1 x t ∂ ∂ = ∂ ∂

θ

θ

α

con le sue condizioni al contorno di terzo genere:

0 0 = ∂ ∂ x k

θ

( )

questa condizione, Eq. (3.11), corrisponde ad una situazione abbastanza frequente, durante i mesi estivi nella città di Pisa, ovvero che la temperatura esterna sia Test = 34°C, come si può evincere dalla NORMA UNI EN ISO 13791. Inoltre in questo modo si fa un’approssimazione abbastanza importante e cioè che per tutto lo spessore del muro la funzione valga inizialmente 8 K, in realtà non è così, perchè man mano che aumenta la coordinata x e cioè si va verso l’esterno, tale valore diminuisce.

Per risolvere tale equazione in genere si usa il problema di Sturm – Liouville e si applica la tecnica della separazione delle variabili, in questo caso si è semplificato considerando il problema simmetrico e seguendo la trattazione di Eckert e Drake [12].

Per prima cosa bisogna trovare gli autovalori n della funzione, in particolare sono le soluzioni della funzione:

L h L n e n _β β = tan (3.12)

di questi n ne sono stati trovati tre, sfruttando il metodo grafico con l’ausilio del software Excel del pacchetto Microsoft Office 2003.

L

n

n β

δ = (3.13)

Quindi note le caratteristiche del materiale di cui è costituita la parete in esame si può calcolare la funzione risolvente:

( )

_{( ) ( )}

( )

δ

δ

δ

δ

δ

θ

θ

dove 0 è la funzione all’istante t = 0.

Tale funzione è mostrata nel grafico di Figura 3.3 dal quale per esempio si deduce che il valore che assume la funzione dal lato esterno del muro e dopo che è trascorsa 1 ora, ovvero circa -5 K, dal lato interno lo si trova dopo 4 ore. È importante non dimenticare che la funzione riguarda esclusivamente il muro, e non l’aria circostante, quindi va considerato che tale sfasamento termico non riguarda direttamente la temperatura dell’ambiente interno.

Per questa simulazione si è adottato un materiale da costruzione con le seguenti caratteristiche:

= 1430 kg/m3 k = 0,73 W/mK Cp = 1200 J/kgK

Andamento di θθθθ(t) nello spessore della lastra durante le prime 24 ore (intervalli di 60') -9 -8 -7 -6 -5 -4 -3 -2 -1 0 0 0.004 0 0.008 0 0.012 0 0.016 0 0.020 0 0.024 0 0.028 0 0.032 0 0.036 0 0.040 0 0.044 0 0.048 0 0.052 0 0.056 0 0.060 0 0.064 0 0.068 0 0.072 0 0.076 0 0.080 0 0.084 0 0.088 0 0.092 0 0.096 0 0.100 0 spessore [m] θθθθ( t) t = 0 t = 1h t = 2h t = 3h t = 4h t = 5h t = 6h t = 7h t = 8h t = 9h t = 10h t = 11h t = 12h t = 13h t = 14h t = 15h t = 16h t = 17h t = 18h t = 19h t = 20h t = 21h t = 22h t = 23h t = 24h Figura 3.3 Andamento della temperatura nello spessore della lastra durante le prime 24 ore

Un altro aspetto che viene messo in rilievo dal grafico di Fig. 3.3 è che durante le prime 6 – 8 ore la temperatura diminuisce molto velocemente, mentre con il passare del tempo non è più così, per approfondire questo aspetto è stato sviluppato un terzo modello. Molto simile alla seconda, questa terza schematizzazione si differenzia dalla precedente perché in questo caso si sono considerate le condizioni al contorno di scambio convettivo variabili nel tempo.

Risolvendo l’Eq. (3.14) con diversi 0 si sono ottenute alcune curve della funzione (x,t) che sono state graficate rispetto al tempo e non allo spessore, infine è stata costruita la curva risultante ottenuta considerando l’evoluzione del sistema in successivi stadi di equilibrio, variando la condizione di scambio termico.

L’obiettivo di tale modello è rappresentare come al diminuire della differenza di temperatura rispetto alla quale si ha lo scambio termico la pendenza della curva che rappresenta la funzione diminuisca a sua volta. (Fig. 3.4)

Andamento nel tempo della funzione θθθθ(x,t) al variare di θθθθi

-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [ore] θθθθ [K ]

Soluzioni per i = 8 K Soluzioni per i = 7 K Soluzioni per i = 6 K Soluzioni per i = 5 K Soluzioni per i = 4 K Soluzioni per i = 3 K teta (t) [K] Poli. (teta (t) [K]) Figura 3.4 Andamento nel tempo della funzione (x,t) al variare di i

3.3 Sfasamento dei picchi di temperatura

L’ultima fase per poter meglio approfondire l’argomento consiste nel ricreare l’andamento giornaliero della temperatura durante le 24 ore, rispettando il più possibile i picchi di massimo e di minimo, al fine di capire in che modo la parete riesce a trasmettere tali variazioni all’interno del locale.

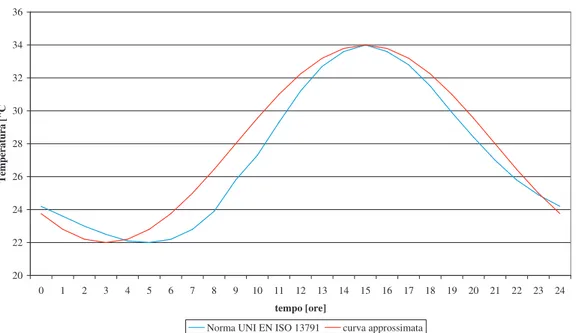
Nella norma UNI EN ISO 13791 [7] viene indicato l’andamento giornaliero della temperatura estiva di una località situata a 40° di latitudine Nord, cioè dove si trova la città di Napoli. Dato che l’edificio in questione è a Pisa località San Rossore, 43.66° latitudine Nord, si può assumere la curva indicata dalla norma valida anche per il caso suddetto. La temperatura oscilla tra un minimo di 22°C raggiunti alle ore 5 ed un massimo di 34°C raggiunti alle 15.

Per facilitare la trattazione e soprattutto rendere più maneggevole la soluzione del problema si fa un’approssimazione tramite una funzione sinusoidale.

La Fig. 3.5 mostra i due andamenti.

Tabella 3.1 Valori degli andamenti giornalieri della temperatura estiva

Andamento giornaliero della temperatura latitudine 40° Nord

20 22 24 26 28 30 32 34 36 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 tempo [ore] T em pe ra tu ra [" C

Norma UNI EN ISO 13791 curva approssimata

Figura 3.5 Andamento della temperatura giornaliera estiva

Quindi la funzione approssimante è (Eq. 3.15):

( )

( )

ω

φ

T *cos (3.15)

A questo punto per studiare come varia la temperatura all’interno del locale, grazie alla presenza della parete, è necessario risolvere l’equazione di Fourier, ma con condizioni al contorno diverse dai casi precedenti.

Ipotesi:

√ Schematizzazione: lastra piana semi – infinita √ Comportamento: monodimensionale

√ Equazione: omogenea

√ Condizioni al contorno: omogenee √ Temperatura esterna T0: periodica

√ Temperatura iniziale: valore finito pari a 0

√ Coefficiente di conducibilità termica: costante, uniforme ed isotropo Si fissano le condizioni al contorno:

0 0 = = T t ) ( 0 T0 f t x= = ∞ ≠ ∞ → T_∞ x

La funzione rappresentata nell’Eq. 3.15 si può anche scrivere come:

t t n T T _M 0 0 0 2 cos

π

ω

π

t = periodo della funzione espresso in secondi, in questo caso vale 1 giorno (86400 s) 1

= n

Nello svolgimento della soluzione si tralascia la costante

φ

( )

α

π

π

α = diffusività termica del materiale [m2/s]

Nell’Eq. (3.16) si nota che la temperatura è, sì funzione del tempo e della coordinata x, ma anche della diffusività termica α, essa influenza sia lo sfasamento che lo smorzamento che la parete provoca rispetto alla temperatura esterna.

Infatti al variare del materiale di cui è costituito l’edificio, all’interno si verificano situazioni assai differenti tra loro.

Prendendo in considerazione alcuni de materiali da costruzione frequentemente adottati se ne possono verificare gli effetti.

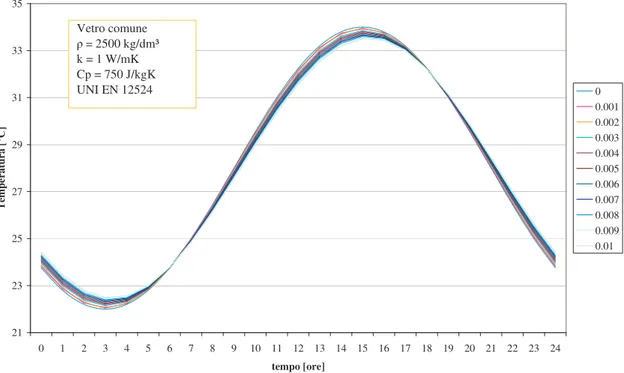
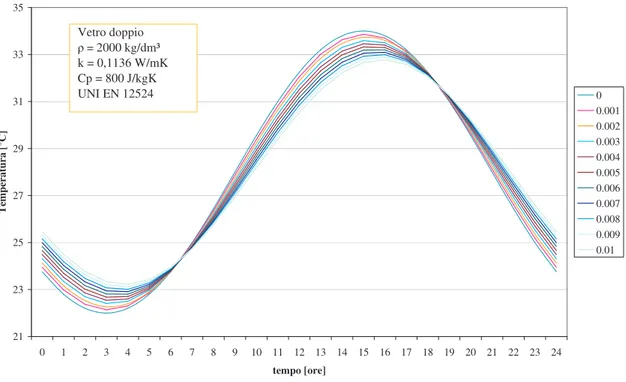
Come primo esempio si mostra il comportamento di superfici vetrate di spessore 0,01 m. Ne sono state analizzate due tipologie (Fig. 3.6 e Fig. 3.7):

• vetro comune = 2500 kg/m3 k = 1 W/mK Cp = 750 J/kgK • vetro doppio eq = 2000 kg/m3 keq = 0,1136 W/mK Cp,eq = 800 J/kgK

I valori delle caratteristiche del vetro comune sono state prese dalla NORMA UNI EN 12524 [13], mentre nell’altro caso di fa riferimento a grandezze equivalenti, non essendo il materiale omogeneo. 21 23 25 27 29 31 33 35 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 tempo [ore] T em pe ra tu ra [° C ] 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01 Vetro comune = 2500kg/dm³ k = 1 W/mK Cp = 750 J/kgK UNI EN 12524

21 23 25 27 29 31 33 35 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 tempo [ore] T em pe ra tu ra [° C ] 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01 Vetro doppio = 2000kg/dm³ k = 0,1136 W/mK Cp = 800 J/kgK UNI EN 12524

Figura 3.7 Andamento della temperatura interna dovuta alla presenza di superfici vetrate

Come evidenziato dai grafici le superfici vetrate riescono a sfasare ed attenuare i carichi esterni molto poco, per facilitare il confronto si riportano in Tab. 3.2 i valori ottenuti per ogni spessore.

Sfasamento [s] Ampiezza [°C]

x [m] Vetro comune Vetro doppio Vetro comune Vetro doppio

0 0 0 34,00 34,00 0,001 114 311 33,95 33,87 0,002 227 622 33,90 33,73 0,003 341 934 33,85 33,61 0,004 454 1245 33,81 33,48 0,005 568 1556 33,76 33,36 0,006 681 1867 33,71 33,24 0,007 795 2178 33,66 33,12 0,008 908 2490 33,62 33,01 0,009 1022 2801 33,57 32,89 0,01 1135 3121 33,52 32,78

Come si evince dalla Tab. 3.2 le superfici vetrate riescono ad attenuare ben poco la temperatura esterna e lo stesso si può affermare per quanto riguarda lo sfasamento che riescono a produrre. In ogni caso, come era intuibile il vetro doppio offre migliori prestazioni in entrambi i casi: dato uno spessore di 1 centimetro riduce la temperatura esterna di 1,64 °C e riesce a sfasare la curva della temperatura esterna di 36’40”.

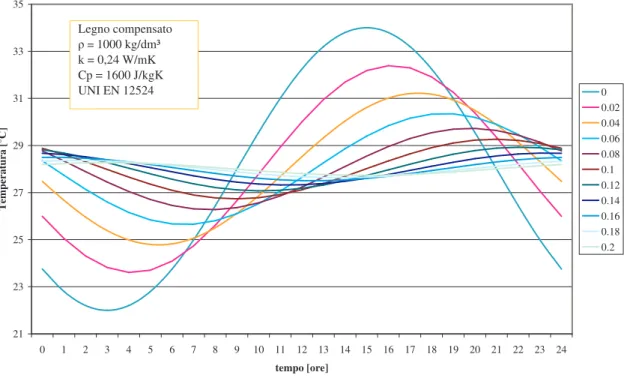
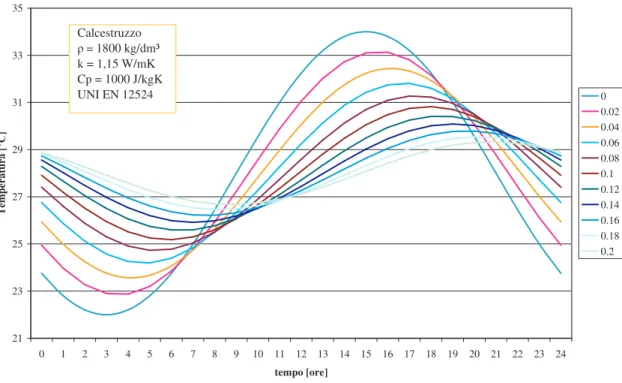
Inoltre si è analizzato il caso in cui si abbiano superfici opache, ma si è aumentato lo spessore a 0,2 m (Fig. 3.8 e Fig. 3.9):

• legno compensato = 1000 kg/m3 k = 0,24 W/mK Cp = 1600 J/kgK • calcestruzzo = 1800 kg/m3 k = 1,15 W/mK Cp = 1000 J/kgK

In entrambi i casi i valori sono tratti dalla NORMA UNI EN 12524.

21 23 25 27 29 31 33 35 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 tempo [ore] T em pe ra tu ra [° C ] 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2 Legno compensato = 1000kg/dm³ k = 0,24 W/mK Cp = 1600 J/kgK UNI EN 12524

21 23 25 27 29 31 33 35 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 tempo [ore] T em pe ra tu ra [° C ] 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2 Calcestruzzo = 1800kg/dm³ k = 1,15 W/mK Cp = 1000 J/kgK UNI EN 12524

Figura 3.9 Andamento della temperatura interna dovuta alla presenza di superfici opache

I dati specifici relativi alle Figg. 3.8 e 3.9 sono riportati in Tab. 3.3.

Sfasamento [s] Ampiezza [°C]

x [m] Legno comp. Calcestruzzo Legno comp. Calcestruzzo

0 0 0 34,00 34,00 0,01 2141 1037 33,13 33,56 0,02 4282 2075 32,39 32,16 0,03 6423 3112 31,76 32,78 0,04 8564 4150 31,22 32,44 0,05 10705 5187 30,75 32,11 0,06 12846 6224 30,36 31,82 0,07 14987 7262 30,02 31,54 0,08 17128 8299 29,73 31,28 0,09 19269 9336 29,48 31,04 0,1 21409 10374 29,26 30,82

Tabella 3.3 Confronto tra gli effetti dei due materiali da costruzione

Confrontando i valori riportati in Tab. 3.3 si può osservare che una parete di legno di 10 centimetri attenua di la temperatura esterna più di una parete di calcestruzzo dello stesso

spessore, anche se la differenza è solo 1,57°C. La vera differenza sta nella capacità di sfasamento, mentre il primo riesce a spostare il picco di temperatura di ben 6 ore circa (21409 s), il secondo soltanto di 3 ore circa (10374 s), quindi da questo punto di vista sembrerebbe preferibile il legno, ma è necessario prestare attenzione al fatto che tale materiale ha bassa densità e ciò comporterebbe una diminuzione di quei benefici che si ottengono tramite una medio – alta inerzia termica.

I materiali presi in considerazione presentano comportamenti diversi rispetto alle superfici vetrate, anche se, confrontando sia il legno compensato, sia il calcestruzzo con il vetro doppio si nota che, a parità di spessore (0,01 m), quest’ultimo offre migliori prestazioni. In base a quest’ultima considerazione si evince che ciò che permette al materiale di operare uno sfasamento temporale soddisfacente è il coefficiente di conducibilità k. Infatti al di là della altre caratteristiche fisiche, i materiali riescono meglio nel compito dell’attenuazione e dello sfasamento in funzione del fatto che hanno una bassa conducibilità termica.

Concludendo si potrebbero riassumere le caratteristiche che dovrebbe avere un ipotetico materiale ideale per la costruzione di edifici destinati all’utilizzo di sistemi elio assistiti per il loro raffrescamento:

• densità medio – alta per garantire una grande inerzia termica 1500 – 1800 kg/m3

• conducibilità termica bassa per poter contare su una attenuazione ed uno sfasamento della temperatura esterna significativi 0,2 – 0,5 W/mK

• calore specifico alto influisce positivamente sia sull’inerzia termica, che sullo sfasamento della temperatura esterna 1100 – 1300 J/kgK

Per ottenere caratteristiche del genere si potrebbero pensare di utilizzare materiali che presentano una o due delle particolarità richieste e costituire una sorta di materiale composto a strati. Per esempio si è preso una parete tipo costituita da due strati di calcestruzzo di 0,08 m ed uno di un altro materiale all’interno di 0,04 m.

Il calcestruzzo ha una alta densità (1800 kg/m3_{), ma sia la conducibilità (1,15 W/mK) che}

è troppo alta, che il calore specifico (1000 J/kgK) che è troppo basso non sono ottimali, servirebbe quindi un materiale che riuscisse a bilanciare queste caratteristiche. Dei vari materiali visti in [12], quello che si presenta come ideale è il polietilene in schiuma dato che ha conducibilità termica bassissima (0,05 W/mK) ed un Cp abbastanza alto (2300 J/kgK). Infatti considerando il materiale composto dai vari strati (calcestruzzo – PE schiuma – calcestruzzo) con gli spessori sopra indicati, si ottengono le seguenti caratteristiche:

•

ρ

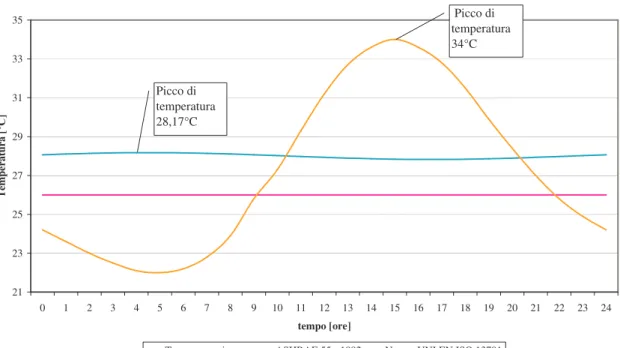
Potendo avere a disposizione tale materiale si otterrebbe un’attenuazione di quasi 6°C ed uno sfasamento di quasi 12 ore (Fig. 3.10).

Temperatura interna all'edificio

21 23 25 27 29 31 33 35 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 tempo [ore] T em pe ra tu ra [° C ]

Temperatura interna ASHRAE 55 - 1992 Norma UNI EN ISO 13791

Picco di temperatura 28,17°C Picco di temperatura 34°C

Figura 3.10 Sfasamento ottenuto con il materiale composito ideale

3.4 Conclusioni

In questo capitolo si è analizzato il comportamento del sistema edificio, partendo dalla sua inerzia termica fino ad arrivare allo sfasamento provocato sulla temperatura esterna al quale è soggetto.

Attraverso l’analisi inerziale, in base al volume del muro è possibile fare un’approssimazione di come varia la sua temperatura all’interno dello spessore. In particolare fissato lo spessore si evidenzia come al variare della densità del materiale cambi l’inerzia termica dell’edificio (Fig. 3.1), inoltre si mette in evidenza anche l’incidenza del calore specifico del materiale sugli effetti inerziali, anche se sembra avere un effetto secondario. In questo modo si ha già una misura indicativa della capacità di trattenere il calore, anche se è necessario ricordare che quando l’edificio sarà funzionante sicuramente la sua inerzia sarà maggiore.

Con l’analisi del problema transitorio la situazione viene chiarita ancora di più, la simulazione rappresenta una situazione estiva quotidiana e cioè quando a fine giornata, si spegne l’impianto di raffrescamento e l’edificio rimane vuoto. A questo punto si vuole vedere come si comporta il muro, infatti nel grafico di Fig. 3.3 le curve rappresentano la temperatura ora per ora, in funzione dell’ascissa dello spessore. Come è facile aspettarsi le maggiori variazioni si hanno durante le prime ore.

In realtà però, man mano che il tempo passa e la temperatura del muro diminuisce, si riduce anche il T al quale la struttura è sottoposta, quindi calcolando la stessa funzione ma con valori iniziali via via minori, si ottiene una curva più realistica della situazione, che approssima la variazione di temperatura per successivi stati di equilibrio. Si ha un andamento quasi lineare e pendenza poco marcata, infatti per ottenere un mezzo del valore iniziale della temperatura occorre quasi un giorno, a differenza del caso di prima in cui si impiegavano molte meno ore.

Infine è stato approssimato l’andamento della temperatura giornaliero e questa funzione è stata adottata come condizione al contorno nell’equazione di Fourier. Le soluzioni, graficate nelle Figg. 3.6, 3.7, 3.8, 3.9 mostrano come al variare del materiale si hanno comportamenti della parete diversi. In particolare si hanno diversi valori di attenuamento della temperatura all’interno e diversi valori dello sfasamento che la parete riesce ad operare. Le superfici vetrate non hanno grandi effetti, non tanto per le loro caratteristiche fisiche e termiche, quanto per il loro spessore. Al contrario i materiali da costruzione confrontati possono beneficiare di spessori più consistenti e quindi offrire migliori prestazioni sia dal punto di vista dell’attenuazione che dello sfasamento.

Infine viene indicato un materiale composto da due strati di calcestruzzo ed uno interno di polietilene in schiuma che produce le caratteristiche di inerzia, sfasamento ed attenuazione ideali ( Fig. 3.10).